Abstract
Lead-free relaxor ferroelectrics have been regarded as superior candidates for dielectric energy storage applications. Nonetheless, the degradation of energy storage performance resulted from the trade-off between high polarization and low hysteresis in RFEs under superhigh electric fields has become a bottleneck. Here, a chemical framework is established based on NaNbO3-based RFEs, bridging atomic-scale structural control to realize excellent energy storage performance. The framework design leads to unique local lattice distortion with both inhomogeneous polarization and antiferrodistortion configurations, including locally disordered polarization distribution, continuous polarization deflection and the co-existence of ordered and disordered oxygen octahedral tilts, as confirmed by phase-field simulation and scanning transmission electron microscopy. As a result, negligible polarization switching hysteresis as well as the large and delayed saturated polarization simultaneously contribute to the excellent energy storage performance. For instance, two NaNbO3-based RFEs with different compositions show ultrahigh recoverable energy densities of 16.48 and 20.08 J cm-3, respectively, as well as near-zero energy loss (η ~ 90.38% and 95.09%). This work presents new avenues toward designing high-performance lead-free RFEs.
Similar content being viewed by others
Introduction
Amidst the increasing global energy demand, it is crucial to develop efficient, eco-friendly, and cost-effective electrical energy-storage devices to advance environmental protection, ensure energy security, and drive economic sustainability. Dielectric ceramic capacitors with unique electrostatic energy storage mechanisms have the fastest charge/discharge rates (~ nanoseconds level) and the highest power density (~108 MW kg–1) among existing energy storage devices, which have been widely utilized in modern power electronic systems1,2,3. Nevertheless, compared to current mainstream storage devices, including batteries and electrochemical capacitors, the poor energy storage capability of dielectric ceramic capacitors significantly restricts their advancement in miniaturized, lightweight, and integrated device applications4,5. Large energy dissipation, i.e., low energy efficiency, makes it difficult to obtain high energy capacitance. Consequently, the combination of high energy-storage density (Wrec) and high conversion efficiency (η) is the focus of designing the next generation of high-performance dielectric ceramic capacitors6,7,8,9,10.
Generally, the energy storage capability of dielectric ceramic capacitors is mainly defined by the maximum polarization (Pmax) and breakdown strength (EB) of the dielectric material, while η is related to the energy loss calculated from the remnant polarization (Pr) and hysteresis (H) in the P-E loop11,12. Consequently, effective control of the fluctuation and saturation behavior in P-E loops at the highest possible EB is imperative to achieve high Wrec and η simultaneously. In the past decade, numerous Pb-free relaxors have been investigated to optimize the energy storage properties (ESPs) on the basis of the high chemical pliability of ABO3 type perovskites (a variety of combinations at the A/B sites)13,14,15,16,17,18,19,20,21,22,23. Examples include BiFeO3 (BF)-based19,21,24, K0.5Na0.5NbO3 (KNN)-based17,25,26, Bi0.5Na0.5TiO3 (BNT)-based27,28,29, Bi0.5K0.5TiO3 (BKT)-based16,30,31, BaTiO3 (BT)-based3,32,33, NaNbO3 (NN)-based34,35,36 and AgNbO3 (AN)-based37,38,39 relaxors, whose Wrec in the form of film have been even beyond 200 J cm−3[26], while the majority of their ESPs (Wrec < 15 J cm−3, η < 85%) in bulk ceramic is still at a level that needs to be improved8,9,12,40,41. Ultrahigh EB (MV cm−1 level) results from thinner thickness, lower defect concentration and more homogeneous structure in film than in bulk ceramics, which is the main reason for the difference in energy storage density. However, bulk ceramics exhibit structural integrity and operational stability in extreme environments that cannot be matched by thin films. Therefore, it is urgent to enhance the ESPs of bulk ceramic capacitors. It is widely believed that RFEs, possessing lower domain switching barriers, exhibit low H on account of their unique nanoscale polar structure (i.e., polar nanoregions, PNRs)2,42. Therefore, various tactics, such as “designing superparaelectric state43”, “diminishing the scale of PNRs3”, “heterogeneous structures coexisting36” and “enhancing configuration entropy6” were utilized to modulate the polar structure of RFEs to improve ESPs. Regrettably, these approaches are generally implemented through combining weakly/non-ferroelectric ions or components into the FE matrix, which would lead to a sharp decrease in Pmax under an external electric field, thus limiting the optimization of Wrec44. Very recently, numerous research works have shown that multiple polarization, and antiferrodistortion configurations resulting from oxygen octahedral tilts both contribute positively to the optimization of the ESPs45,46. The energy barrier for polarization rotation diminishes with the symmetry of the crystal structure decreases under the induction of multiple polarization configurations, thus resulting in a larger polarization difference (ΔP = Pm - Pr)47,48. Likewise, the adjustment of oxygen octahedral tilt induces a larger coercive field, which delays polarization saturation49. Coincidentally, NN with multi-phase demonstrates exceptional tunability in the ordering of both polarization and oxygen octahedral tilt, establishing it as a highly promising matrix for high-performance dielectric energy storage applications34,50,51. For example, in our previous work36, a crossover between high polarization and high efficiency was achieved through the regulation of the co-existence of the relaxor AFE/RFE polarization configurations in NN-BF-SBTT, obtaining a Wrec of 12.25 J cm−3 with η ~ 83%. Liu52 et al. have constructed a superparaelectric state NN-CZ relaxor with large antiferrodistortion ordering, which results from the ordered oxygen octahedral tilt. Wu53 et al. designed slush-like polar clusters in NN-BNT-CT, where multiple polarization configurations embedded in labyrinthine antiferrodistortion, realizing a Wrec (7.1 J cm−3) and a high η (90%) simultaneously. Considerable advancements have been made in the antiferrodistortion adjustment and polarization configuration design of NN-based energy storage ceramics. However, the lack of atomic-level rules for the collaborative tuning of oxygen octahedral tilt and polarization configuration limits the efficient engineering of NN-based RFEs with high capacitive energy storage.
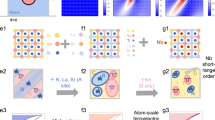
Herein, we present a rational chemical framework for the collaborative design of local polarization and antiferrodistortion configurations in NN-based RFEs after fully considering the significant differences of A/B-site ions in terms of size, polarizability and ferroelectric activity, as shown in Fig. 1. All the ions can be classified into four functional groups: framework ions, high polarizable ions, rattling ions and ferroelectrically active ions54 (Fig. 1a). Bi and La ions with high polarizability at the A-site and Ti, Ta, Fe and Nb ions with large theoretical polar displacement (D) values at the B-site are usually accompanied by large Pm55,56. Besides, the remaining ions at the A-site are framework ions with a large ionic radius (Na) and rattling ions with a small ionic radius (Li), respectively. Remarkably, the ionic radius of Na is almost twice as large as that of Li, with a difference of more than 0.6 Å, which is comparable to the D value of the Bi ion57. Based on the above chemical composition, a detailed framework for NN-based RFEs is presented in Fig. 1b: (1) The A-site comprises about 55 - 65 % framework ions, approximately 20–30% high polarizable ions and the remaining 5–15% rattling ions. (2) The B-site is occupied by ferroelectrically active ions. (3) The resulting solid solution has an ultra-small tolerance factor (t). As revealed in Fig. 1c, high polarizable ions and rattling ions induce strong fluctuations of the local polarization vectors in both magnitude and orientation, disturbing the long-range polar order, while ferroelectrically active ions in the B-site with strong covalent bonding enable continuous polarization deflection29,42,45,47,58. Furthermore, the small tolerance factor drives enhanced oxygen octahedral tilting, which nucleates localized structural disorder through dynamic octahedral rotation frustration46, leading to the co-existence of both ordered and disordered oxygen octahedral tilts. Therefore, the unique relaxor state established through the collaborative design of local polarization and antiferrodistortion configurations is mainly manifested in disordered polarization distribution, continuous polarization deflection and the co-existence of both ordered and disordered oxygen octahedral tilts (Fig. 1d). Macroscopically, these properties would provide a linear-like P-E loop with both large Pm and high EB (Fig. 1e), thus obtaining both high Wrec and η.
To verify the effectiveness of the chemical framework, we have designed two ceramics based on 0.94NaNbO3-0.06BiFeO3 (AFE P phase) and Na0.85Bi0.05NbO3 (AFE R phase) (Fig. S1), respectively: 0.7(0.94NaNbO3-0.06BiFeO3)-0.3Bi0.5Li0.5TiO3 (NN-P1) and 0.75Na0.85Bi0.05NbO3-0.25Li0.2La0.6Ti0.75Ta0.2O3 (NN-R2). Excitingly, a high Wrec ~ 16.48 J cm−3 with a η ~ 90.38 % at 75 kV mm−1 is achieved in NN-P1, as well as a Wrec ~ 20.08 J cm-3 with a η ~ 95.09 % at 90 kV mm−1 is also obtained in NN-R2, which shows a huge breakthrough in comprehensive energy storage performance over the bulk energy storage ceramics reported so far. Unique local polar structure and antiferrodistortion are identified through atomic resolution scanning transmission electron microscopy and phase-field simulation.
Results and discussion
Modulation of polarization and antiferrodistortion configurations
For the identification of the local polar structure of the designed NN-based RFEs, the detailed polar structures of both samples were carried out by transmission electron microscopy. Figure 2a–f shows the hierarchical structural features of NN-P1. Generally, structural synergy between long-range polarization ordering and coherent oxygen octahedral tilting in conventional AFE or FE systems drives the formation of macroscopic domains46. Conversely, compositional disorder-induced random fields in relaxors fragment these domains into nanodomains or PNRs2. In NN-P1, large distorted anomalous stripe domains are detected with micro-grade lengths and non-uniform widths spanning from tens to hundreds of nano-meters along the [110]c direction (Fig. 2a). Regions of non-homogeneous lattice fringes with shapes and sizes different from the PNRs in RFEs can be observed in HR-TEM images (Fig. 2b), which are the origins of bright/dark stripe domains, indicating the polarization is disordered. Another speckled domain morphology (Fig. 2d) is observed along the [100]c direction without significant ferroelectric domains, also indicating the absence of long-range ordered polarization. The HR-TEM image and corresponding Fourier inverse transform pattern (Fig. 2e) show distinct localized lattice distortions and PNRs (~1–5 nm). The complex oxygen octahedral tilt features in NN involve multiple metastable phases (P/Q/R/S/T/U), distinguished by their superlattice diffraction signatures: the P and R phases with 1/4 and 1/6 type superlattice diffraction dots, respectively, exhibit antiferroelectricity; the Q phase with 1/2 type superlattice is ferroelectricity, and the S/T/U phase is a paraelectric (PE) phase51. Only 1/2 type superlattice diffraction dots (Fig. 2c, f) can be observed in the selected area electron diffraction (SAED) pattern, suggesting that the local PNRs are ferroelectric, corresponding to the FE Q phase. Notably, the asymmetric (ooo)/2 in Fig. 2c and symmetric (eoo)/2 in Fig. 2f diffraction spots arise from competing long-range oxygen octahedral tilt ordering and local tilt disorder. Long-range ordered oxygen octahedral tilt forms micro-ferroelastic domains, leading to partial occupation of superlattice diffraction dots that cause this asymmetry34,46. Therefore, the large distorted anomalous strip domains in Fig. 2a along [110]c can be considered as micro-ferroelastic domains resulting from ordered oxygen octahedral tilt, while the oxygen octahedral tilt of the speckled domain in Fig. 2d is disordered. The NN-P1 can be defined as an RFE with disordered polarization as well as ordered and disordered oxygen octahedral tilt coexisting. Furthermore, atomic resolution scanning transmission electron microscopy (STEM) with high-angle angular dark-field (HAADF) imaging is adopted to explore the local symmetry, as shown in Fig. 2g-k and Fig. S3. The atomic displacement vectors of center B-site cations relative to the corner O anions can describe the local polarization clearly47. Arrows with various lengths and colors are adopted to denote the magnitude and direction of the polarization vectors, as presented in Fig. 2g. Randomly dispersed clusters indicate both the polarization magnitude and polarization angles are disordered, which can also be proved by the polarization magnitude mapping and the polarization angle mapping (Fig. 2j, k). About 1–3 nm island atomic-clusters are not sequestered by a nonpolar matrix but are linked by the clusters with low symmetry. The coexistence of FE Q phase clusters and various PE phases, including orthorhombic (S) and tetragonal (T) symmetric, leads to the occurrence of multiple local distortions, forming a progressive transition among different clusters. Local FE Q phases are randomly embedded in the PE (S/T) matrices, forming PNRs, indicating the reduced polarization anisotropy and the presence of random electric/stress fields, which can significantly lower the switching energy barriers, resulting in desired relaxor behavior44,45,58. The scattered statistical distribution of polarization vector magnitude and angle (Fig. 2h, i) also suggests the strong local polar fluctuation and the low polarization reorientation energy barrier between different clusters47. The above properties demonstrate that the engineered local polar structure will promote the rotation, extension and fast response of the PNRs to electric fields, leading to the ideal polarization behavior.
Bright-field TEM images, high-resolution TEM images and the corresponding SAED patterns: along the a–c [110]c, d–f [100]c directions of NN-P1; g Atomic-resolution polarization vector mapping according to the HAADF-STEM image along [100]c. The accompanied statistic distribution of h magnitude and i angle of the polarization vectors. j Polarization magnitude mapping, and k Polarization angle mapping.
Figure S4 presents the local structure of NN-R2 along the [100]c direction. A speckled domain morphology akin to NN-P1 is observed, with non-uniform lattice fringes and PNRs confirming a disordered polarization state. In addition, the (eoo)/2 superlattice diffraction dots can be detected at all equivalent positions in the SAED pattern, revealing the ferroelectricity of PNRs and the disordered oxygen octahedral tilt. To further explore local polarization and antiferrodistortion configurations of NN-R2 in more detail and accuracy, STEM with HAADF and annular bright-field (ABF) imaging is adopted, as shown in Fig. 3. The tilt angle of the oxygen octahedron can be computed through the deviation degree between the O-O bond y-axis. Obviously, two regions with different configurations of antiferrodistortion can be detected along the [100]c axis (Fig. 3a, d). In the first region, the oxygen octahedron exhibits a long-range ordering feature with alternating clockwise and anti-clockwise rotations (Fig. 3a), corresponding to the a−b+c− oxygen octahedral tilt feature in the FE Q phase46, which would lead to long-range ordered structure (similar to Fig. 2a) and ultrahigh Pmax. Inter-nested polar and weakly-polar clusters can be viewed from the STEM-HAADF images (Fig. 3c). The randomly distributed oxygen octahedral tilt angles (Fig. 3b) and weakly polar region indicate that the FE Q phase is separated by numerous PE matrices and forming PNRs, which is similar to the local polar structure of NN-P1. This phenomenon can also be proved by the strong random distributions of polarization magnitude mapping and the polarization angle mapping (Fig. S5). Interestingly, the more intensive local polarization distortions observed in Fig. 3c may be attributed to the fact that the PE matrix due to differences in component undulations and framework features is not some single PE phase but a composite of PE phases (S/T, etc.)53. The scattered polarization magnitude and isotropic orientation distribution of polarization angles (Fig. 3c1, c2) reiterate the anisotropy of the PE matrices with weak polar features, further confirming the existence of a composite PE matrix with multiple polar angles. From a thermodynamic perspective, these anisotropic polarization vectors not only severely disrupt long-range polar ordering but also reduce the domain-switching barriers, flatten the domain switching paths, and thus reduce the hysteresis loss and improve the energy storage efficiency. In another region, short-range ordered oxygen octahedral tilt regions are separated by some weak-tilt regions (Fig. 3d, e). It leads to an overall disordering in both rotation directions and tilt angles, which would consume part of the electrical energy during crystal polarization, impeding the formation of a textured domain state along the electric field direction and resulting in the delayed polarization saturation6. No near-zero polarization vectors are detected in the STEM-HAADF images (Fig. 3f) and the generally high polarization intensities in the statistical distribution of polarization vectors (Fig. 3f1), mean that the FE Q phase is separated by some domain boundaries with small oxygen-octahedral distortions rather than by PE phases. These domain boundaries effectively limit the long-range extension of the polarization so that the polarization direction shows a certain orientation on the microscopic scale without forming a macroscopic FE domain. It shows that this region is analogous to the RFE with a slush-like polar structure42. These unique properties are also evident in the polarization magnitude mapping and the polarization angle mapping (Fig. S6). Of great importance is that polarization with orientation characteristics but without long-range polarization expansion contributes to fast polarization response to an external electric field. Moreover, atomic-resolved energy dispersive X-ray spectroscopy (EDS) mapping is employed to delve into the element distribution (Fig. 3g). All cations in the lattice periodically occupy the corresponding sublattice and show slight random fluctuations (Na/La/Bi at the A-site, Nb/Ta/Ti/ at the B-site). Ordered ionic arrangements and disordered element fluctuations suggest atomic-scale chemical heterogeneity59,60. The combination of both local polar structures effectively decouples the inverse relationship between high polarization and low hysteresis under a high electric field, providing a linear-like P-E loop with both large Pmax and small H, significantly enhancing the energy storage performance.
a, d ABF-STEM image as well as the calculated oxygen octahedral tilt along y axis, blue and red indicate clockwise and anticlockwise tilt. b, e Statistic distribution of angles of oxygen octahedral tilts. c, f HAADF-STEM images and the accompanied statistic distribution of magnitude c1, f1 and angle c2, f2 of the polarization vectors. g HAADF image of atomic structure and the corresponding EDS maps for individual Na, La, Bi, Nb, Ta, Ti elements, and the A-site and B-site holistic EDS maps for NN-R2.
Phase field simulations
Figure S7 illustrates the Rietveld refinement result from high-resolution synchrotron X-ray diffraction (SXRD) of NN-R2 ceramic. It is interesting to find that the NN-R2 sample can be well identified by the orthorhombic FE Q phase with P21ma space group. This is because that the rattling ion (Li+) can stabilize the FE phase of the NN matrix at room temperature60. According to the crystal structure model from the SXRD refinement result, the specific tilt angles (ω) of the oxygen octahedron can be calculated (Fig. S8). The investigated NN-R2 ceramic has a large ω ~ 10.64°, much larger than other reported RFEs and even FEs and AFEs (Table S3). It is well known that large oxygen octahedral tilt would generally contribute to the formation of long-rang ordered textured domains (i.e., antiferrodistortion or (A)FE structure)46, which has already been observed through transmission electron microscopy in Figs. 2 and 3. However, SXRD cannot distinguish the local symmetry of PNRs due to resolution limitations. Therefore, phase field simulation was conducted to gain insight into the evolution of oxygen octahedral tilt and polarization configurations. Figure 4a, b shows the mapping of oxygen octahedral tilt and polarization configurations of NN-R2 ceramic. Obviously, the type and magnitude of oxygen octahedral tilt are consistent with the analyses in the ABF images (Fig. 3a, d), with the coexisting long-range ordered domains (alternating clockwise/anticlockwise rotations) and disordered regions with irregular tilt patterns. These ordered and disordered oxygen octahedral tilt regions would provide a large and delayed polarization. Polarization configuration also shows similar results with HAADF image analysis. The strongly polar FE Q phases are surrounded by weakly-polar PE phases (S/T phase), forming PNRs, indicating a remarkable enhancement of the local random field and an effective disruption of the long-range polar ordering of the matrix phase (Na0.85Bi0.05NbO3) by the incorporated guest phase (LLTT). Notably, the absence of the cubic-structured PE U phase in both the analytical results of the phase field simulations and the HAADF images is also an important reason for the high polarization in NN-R2 ceramic. Moreover, NN-R2 and its initial matrix Na0.85Bi0.05NbO3 were taken to deeply investigate the evolution of the polarization configurations and P-E loops with an external electric field. For the Na0.85Bi0.05NbO3, only long-range FE ordering can be established owing to the irreversible AFE-FE phase transition upon loading an electric field8,9. After unloading the electric field, the polar regions cannot be restored to the initial state and maintain a high polarization state, leading to unavoidable large hysteresis and remanent polarization (Fig. 4c). Instead, the local structure of multiphase coexistence in NN-R2 flattens the energy barrier between different phases and eradicates the loss of polarization rotation between PNRs2,3. Therefore, the polarization distribution of NN-R2 can be restored to the initial state without hysteresis after unloading the electric field (Fig. 4d). The fact indicates that the highly dynamic PNRs and the approximately hysteresis-free polarization response during the entire charging/discharging process significantly improve the η, resulting in near-zero energy loss in NN-R2 ceramic.
Dielectric and electrical properties in bulk ceramic capacitors
In accordance with the engineered route, NN-P1 and NN-R2 can be indexed as a single orthorhombic FE Q phase by Rietveld refinements (Fig. 5a). The RFE states of both samples can also be characterized by the broad dielectric peaks (Fig. 5b, c) with the diffuseness parameter γ of 1.89 and 1.8 (Fig. S9), respectively. Unipolar P-E loops at low electric fields for both samples exhibit linear polarization behavior (Fig. S10a), but exhibit higher dielectric constants compared to linear dielectrics, which can result in higher polarization capability. Therefore, the excellent low-field ESPs presented in Fig. S10b demonstrate their potential for efficient capacitive energy storage. Furthermore, on the basis of the largely delayed polarization and linear-like polarization behavior, a high EB is essential for achieving a high Wrec. Notably, the relatively small grain size (NN-P1 ~ 1.16 μm, NN-R2 ~ 1.04 μm), low tanδ and oxygen vacancy concentration, ultrahigh electrical resistivity, along with exceptional mechanical properties in both samples contribute to the high EB (Fig. 5b, c and Fig. S11–14). Finite element simulations further validate suppressed electrical breakdown pathways (Fig. S15), consistent with experimental EB. These features are all conducive to obtaining ultrahigh EB, which is also a major reason for realizing high Wrec in ceramic-based RFEs.
a Rietveld refinement results of XRD patterns based on the P21ma model. b, c Temperature and frequency dependence of the dielectric spectrum. d, g P-E loops and e, h Wrec and η. f, i Performance comparison with other lead-free energy storage ceramics. The detailed information is listed in Tables S4 and S5.
P-E loops and the corresponding energy storage performance of NN-P1 and NN-R2 ceramics were measured with thicknesses of 50 ~ 60 μm and an electrode diameter of 1.5 mm (Fig. 5d–i and Fig. S16). Benefiting from the local inhomogeneous polarization and antiferrodistortion configurations, unipolar P-E loops still exhibit near-linear polarization behavior even at EB, which demonstrates the excellent energy storage capability of both compositions. NN-P1 shows higher polarization capacity compared to NN-R2, which can be attributed to the higher dielectric constant of NN-P1. It is exciting that an encouraging Wrec ~ 16.48 J cm−3 accompanied by a high η ~ 90.38% has been realized at an EB of 75 kV mm−1. The outstanding ESPs obtained in NN-P1 are a large breakthrough in the energy storage ceramic field compared to other lead-free relaxor systems reported so far. For NN-R2, near-zero loss ESPs are obtained (Wrec ~ 20.08 J cm−3, η ~ 95.09%) under an EB of 90 kV mm−1. NN-R2 exhibits a record Wrec in the systems with η > 95%32,58,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80. The highest WF value displayed in Fig. S17 suggests that the NN-R2 has the best overall ESPs among lead-free bulk ceramic systems to date. Additionally, both NN-P1 and NN-R2 exhibit good charge/discharge performance (Fig. S18). High discharge energy densities (Wdis: NN-P1 ~ 5.64 J cm−3, NN-R2 ~ 7.81 J cm−3) are achieved in ultrafast discharge times (t0.9: NN-P1 ~ 31 ns, NN-R2 ~ 17 ns) for both components. Large power densities (PD) of ~277.8 and ~367.6 MW cm−3 are also gained in NN-P1 and NN-R2, respectively. All these values demonstrate the feasibility of the designed atomic-level chemical framework.
Reliability of the bulk ceramic capacitors
High reliability, including excellent temperature/frequency/cycling stability of the energy storage performance, would give the capacitors an enormous application range. Taking NN-P1 for example, measurement of in-situ Raman spectra to evaluate the temperature stability is presented in Fig. S19. It can be seen that the variation in temperature has no obvious impact on the Raman spectra of NN-P1. The active Raman modes show the pronounced widening and diffusion with increasing temperature, e.g., the peak position of the modes ν5 and ν1, which are associated with the vibrations of the B-O bond and the oxygen octahedra tilt, decreases from ~232 to ~219 cm−1 and ~594 to ~582 cm−1, respectively, while the full width at half maximum (FWHM) of both modes exhibits the opposite trend, indicating an enhancement of local structural disorder81,82. In especial, no variation in the deconvolution result suggests no local symmetry changes in the wide temperature range. Furthermore, in-situ XRD measurements over the same temperature range are conducted to confirm the stability (Fig. S20). No obvious splits or mergers occur on the major peaks of (100), (110), and (200). And the peak widths of all major peaks are almost constant. It is believed that dynamic nanodomains and PNRs can preserve at high temperatures (even above Tm), which ensures the stability of phase structure83. Therefore, the broader temperature range for the ER state (Fig. S21) in dielectric spectra is also an indication of no any local structural phase transition over the test temperature range. These results together demonstrate the temperature stability of NN-P1. Consequently, the high Wrec (∼8.8 ± 0.6 J cm−3) and η (88 ± 4%) under 50 kV mm−1 over the temperature range can be sustained. In addition to the excellent thermal reliability, NN-P1 also presents satisfactory energy storage behavior under other conditions. Specifically, NN-P1 exhibits outstanding frequency insensitivity (1–500 Hz: Wrec ~ 8.8 ± 0.6 J cm−3, η ~ 90 ± 2%) and fatigue resistance behavior (1–105: Wrec ~ 9 ± 0.1 J cm−3, η ~ 91 ± 1%) under the same electric field of temperature reliability measurement. Analogously, NN-R2 also shows the superior temperature/cycling/frequency reliability (Fig. S22). The remarkable temperature/frequency/cycling stability is superior compared to energy storage systems reported so far (Fig. S23).
In summary, we demonstrate a chemical design strategy for NaNbO₃-based RFEs, where tailored A/B-site ion combinations and tolerance factor engineering enable atomic-level control over polarization and antiferrodistortion configurations. Based on the intrinsic properties of selected ions, A/B site ions are classified into four functional groups: framework ions, high polarizable ions, rattling ions and ferroelectrically active ions. Combining these four types of ions at specific concentrations can achieve NN-based RFEs with linear-like polarization behavior. Two new NN-based RFEs developed show record comprehensive energy storage performance (Wrec ~ 16.48 and 20.08 J cm−3, η ~ 90.38% and 95.09%). Inhomogeneous polarization and antiferrodistortion configurations are identified by STEM atomic displacement mapping and phase field simulation. These results demonstrate the flexibility and versatility of the designed atomic-level chemical framework, providing a new idea for the development of high-performance RFEs.
Methods
Samples preparation
Dielectric ceramics of 0.7(0.94NaNbO3-0.06BiFeO3)-0.3Bi0.5Li0.5TiO3 (NN-P1) and 0.75Na0.85Bi0.05NbO3-0.25Li0.2La0.6Ti0.75Ta0.2O3 (NN-R2) were prepared by a traditional solid-state reaction. Raw materials, including Na2CO3 (99.99%), Nb2O5 (99.9%), Bi2O3 (99%), Fe2O3 (99.9%), TiO2 (99.5%), Li2O3 (99.99%), La2O3 (99.9%) and Ta2O5 (99.5%) were weighed according to the corresponding chemical formula. Subsequently, the oxides were mixed and ball milled in ethanol for 16 h. The mixtures were dried and then calcined at 850 °C for 5 h. The calcined powders were re-milled in ethanol for 24 h and then dried, ground and cold isostatically pressed into pellets with ∼ 10 mm in diameter and ∼ 1 mm in thickness under a pressure of 200 MPa. Finally, the pressed pellets were sintered at 1000–1250 °C for 2–3 h. During the sintering process, the pellets were covered with sacrificial powders of the same composition.
Structural characterization
Phase structure and purity of the prepared ceramics were monitored by X-ray diffraction (XRD; Philips X’Pert Pro MPD, Netherlands). For Rietveld refinements, the data of the ceramic powders on micron scale were collected in 2θ range of 10–110 ° with a step size of ∼0.01°. Raman spectra of the ceramics were collected by using a Raman spectrometer (Renishaw, inViaTM, UK). The microstructure of the ceramics was characterized by scanning electron microscope (SEM; FEI, Quanta FEG250, USA). Transmission electron microscopy (TEM), high-resolution transmission electron microscopy (HR-TEM), high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) and selected area electron diffraction (SAED) images were obtained by using an electron microscope equipped with energy-dispersive X-ray spectroscopy (EDS) (aberration-corrected Thermo Scientific, Themis Z (3.2), Netherlands).
Electrical performance measurement
Temperature dependence of dielectric property was measured by using a dielectric analysis instrument (Tongguo Technology, HCT1821, China) at various frequencies (1k, 10k, 100k, and 1 M Hz). P-E hysteresis loops of the samples were measured with thicknesses of ~ 50–60 μm and platinum electrodes with a diameter of 1.5 mm by using a ferroelectric analyzer (Aix ACCT TF-3000, Germany). Impedance spectra of the samples were carried out from 0.1 to 1 M Hz by using a Princeton P4000A electrochemistry system. Actual charging/discharging performance was evaluated by using a capacitor charge discharge test system (Tongguo Technology, CFD-003, China).
Simulation calculation
Details of the phase field simulation and finite element simulation are in the Supplementary information.
Data availability
All data supporting this study and its findings are available within the article and its Supplementary Information. Any data deemed relevant are available from the corresponding author upon request.
References
Li, Q. et al. Flexible high-temperature dielectric materials from polymer nanocomposites. Nature 523, 576–579 (2015).
Pan, H. et al. Ultrahigh-energy density lead-free dielectric films via polymorphic nanodomain design. Science 365, 578–582 (2019).
Zhang, M. et al. Ultrahigh energy storage in high-entropy ceramic capacitors with polymorphic relaxor phase. Science 384, 185–189 (2024).
Pan, H. et al. Ultrahigh energy storage in superparaelectric relaxor ferroelectrics. Science 374, 100–104 (2021).
Qi, H. et al. Local structure engineered lead-free ferroic dielectrics for superior energy-storage capacitors: a review. Energy Storage Mater. 45, 541–567 (2022).
Chen, L. et al. Giant energy-storage density with ultrahigh efficiency in lead-free relaxors via high-entropy design. Nat. Commun. 13, 3089 (2022).
Feng, M. et al. Recent advances in multilayer-structure dielectrics for energy storage application. Adv. Sci. 8, e2102221 (2021).
Ma, J. et al. Achieving ultrahigh energy storage density in lead-free sodium niobate-based ceramics by modulating the antiferroelectric phase. Chem. Mater. 34, 7313–7322 (2022).
Qi, H. et al. Ultrahigh energy-storage density in NaNbO3-based lead-free relaxor antiferroelectric ceramics with nanoscale domains. Adv. Funct. Mater. 29, 1903877 (2019).
Yang, B. et al. High-entropy enhanced capacitive energy storage. Nat. Mater. 21, 1074–1080 (2022).
Wang, G. et al. Electroceramics for high-energy density capacitors: current status and future perspectives. Chem. Rev. 121, 6124–6172 (2021).
Cao, W. et al. Interfacial polarization restriction for ultrahigh energy-storage density in lead-free ceramics. Adv. Funct. Mater. 33, 2301027 (2023).
Che, Z. et al. Phase structure and defect engineering in (Bi0.5Na0.5)TiO3-based relaxor antiferroelectrics toward excellent energy storage performance. Nano Energy 100, 107484 (2022).
Chao, W. et al. Enhanced energy storage density in Ca and Ta co-doped AgNbO3 antiferroelectric ceramics. J. Am. Ceram. Soc. 103, 7283–7290 (2020).
Dong, X. et al. (1-x)[0.90NN-0.10Bi(Mg2/3Nb1/3)O3]-x(Bi0.5Na0.5)0.7Sr0.3TiO3 ceramics with core–shell structures: a pathway for simultaneously achieving high polarization and breakdown strength. Nano Energy 101, 107484 (2022).
Li, F. et al. Fine-grain induced outstanding energy storage performance in novel Bi0.5K0.5TiO3–Ba(Mg1/3Nb2/3)O3 ceramics via a hot-pressing strategy. J. Mater. Chem. C. 7, 12127–12138 (2019).
Li, Z. et al. High performance lead-free Na0.5K0.5NbO3 piezoelectric ceramics obtained via oscillatory hot-pressing. Ceram. Int. 46, 11617–11621 (2020).
Liu, G. et al. Ultrahigh dielectric breakdown strength and excellent energy storage performance in lead-free barium titanate-based relaxor ferroelectric ceramics via a combined strategy of composition modification, viscous polymer processing, and liquid-phase sintering. Chem. Eng. J. 398, 125625 (2020).
Liu, L. et al. Multi-scale collaborative optimization of SrTiO3-based energy storage ceramics with high performance and excellent stability. Nano Energy 109, 108275 (2023).
Luo, B. et al. Enhanced energy-storage density and high efficiency of lead-free CaTiO(3)-BiScO(3) linear dielectric ceramics. ACS Appl. Mater. Interfaces 9, 19963–19972 (2017).
Montecillo, R. et al. Achieving superb electric energy storage in relaxor ferroelectric BiFeO3-BaTiO3-NaNbO3 ceramics via O2 atmosphere. J. Eur. Ceram. Soc. 43, 7446–7454 (2023).
Montecillo, R. et al. Tailoring energy storage in Nb2O5-added 0.7BiFeO3–0.3BaTiO3 ceramics via A-site Gd3+ substitution. J. Alloy. Compd. 963, 171144 (2023).
Wang, J. et al. Enhancing energy storage density of (Ba, Sr)TiO3 ceramic particles by coating with Al2O3 and SiO2. J. Mater. Sci.-Mater. El 24, 3309–3314 (2013).
Qi, H. et al. Superior energy-storage capacitors with simultaneously giant energy density and efficiency using nanodomain engineered BiFeO3-BaTiO3-NaNbO3 lead-Free bulk ferroelectrics. Adv. Energy Mater. 10, 1903338 (2019).
Zhang, M. et al. Giant energy storage efficiency and high recoverable energy storage density achieved in K0.5Na0.5NbO3-Bi(Zn0.5Zr0.5)O3 ceramics. J. Mater. Chem. C. 8, 8777–8785 (2020).
Li, D. et al. Improved energy storage properties achieved in (K, Na)NbO3‑based relaxor ferroelectric ceramics via a combinatorial optimization strategy. Adv. Funct. Mater. 32, 2111776 (2021).
Long, C. et al. Excellent energy storage properties with ultrahigh Wrec in lead-free relaxor ferroelectrics of ternary Bi0.5Na0.5TiO3-SrTiO3-Bi0.5Li0.5TiO3 via multiple synergistic optimization. Energy Storage Mater. 65, 103055 (2024).
Deng, T. et al. Excellent energy-storage performance in Bi0.5Na0.5TiO3-based lead-free composite ceramics via introducing pyrochlore phase Sm2Ti2O7. Chem. Eng. J. 465, 142992 (2023).
Liu, H. et al. Chemical design of Pb-free relaxors for giant capacitive energy storage. J. Am. Chem. Soc. 145, 11764–11772 (2023).
Wang, H. et al. Significantly enhanced energy storage performance in high hardness BKT-Based ceramic via defect engineering and relaxor tuning. ACS Appl. Mater. Interfaces 14, 54021–54033 (2022).
Chen, L. et al. Outstanding energy storage performance in high-hardness (Bi0.5K0.5)TiO3-based lead-free relaxors via multi-scale synergistic design. Adv. Funct. Mater. 32, 2110478 (2021).
Long, C. et al. Simultaneously realizing ultrahigh energy storage density and efficiency in BaTiO3-based dielectric ceramics by creating highly dynamic polar nanoregions and intrinsic conduction. Acta Mater. 256, 119135 (2023).
Luo, S. et al. Construction of a 3D-BaTiO3 network leading to significantly enhanced dielectric permittivity and energy storage density of polymer composites. Energy Environ. Sci. 10, 137–144 (2017).
Qi, H. et al. Tunable phase structure in NaNbO3 ceramics by grain-size effect, electric field and heat treatment. Acta Mater. 248, 118778 (2023).
Lv, Z. et al. NaNbO3-based multilayer ceramic capacitors with ultrahigh energy storage performance. Adv. Energy Mater. 14, 2304291 (2024).
Wei, K. et al. Enhancing comprehensive energy storage properties in Pb-free relaxor AFE/FE system via heterogeneous structure tuning and defect engineering. Acta Mater. 278, 120278 (2024).
Yuan, H. et al. Simultaneous enhancement of breakdown strength, recoverable energy storage density and efficiency in antiferroelectric AgNbO3 ceramics via multi-scale synergistic design. Chem. Eng. J. 456, 141023 (2023).
Lu, Z. et al. Mechanism of enhanced energy storage density in AgNbO3-based lead-free antiferroelectrics. Nano Energy 79, 105423 (2021).
Li, B. et al. Achieving ultrahigh energy storage density of La and Ta codoped AgNbO(3) ceramics by optimizing the field-induced phase transitions. ACS Appl. Mater. Interfaces 15, 4246–4256 (2023).
Jiang, J. et al. Enhanced energy storage properties of lead-free NaNbO3-based ceramics via A/B-site substitution. Chem. Eng. J. 422, 130130 (2021).
Jiang, J. et al. Ultrahigh energy storage density in lead-free relaxor antiferroelectric ceramics via domain engineering. Energy Storage Mater. 43, 383–390 (2021).
Shu, L. et al. Partitioning polar-slush strategy in relaxors leads to large energy-storage capability. Science 385, 204–209 (2024).
Duan, J. et al. High-entropy superparaelectrics with locally diverse ferroic distortion for high-capacitive energy storage. Nat. Commun. 15, 6754 (2024).
Chen, L. et al. Local diverse polarization optimized comprehensive energy-storage Performance in lead-free superparaelectrics. Adv. Mater. 34, 2205787 (2022).
Liu, H. et al. Local chemical clustering enabled ultrahigh capacitive energy storage in Pb-free relaxors. J. Am. Chem. Soc. 145, 19396–19404 (2023).
Qi, H. et al. Large (anti)ferrodistortive NaNbO3-based lead-free relaxors: Polar nanoregions embedded in ordered oxygen octahedral tilt matrix. Mater. Today 60, 91–97 (2022).
Sun, Z. et al. Superior capacitive energy-storage performance in Pb-free relaxors with a simple chemical composition. J. Am. Chem. Soc. 145, 6194–6202 (2023).
Guo, J. et al. Multi-symmetry high-entropy relaxor ferroelectric with giant capacitive energy storage. Nano Energy 112, 108458 (2023).
Zhang, Y. et al. High-performance ferroelectric based materials via high-entropy strategy: Design, properties, and mechanism. InfoMat 5, 12488 (2023).
Qi, H. et al. Emerging antiferroelectric phases with fascinating dielectric, polarization and strain response in NaNbO3-(Bi0.5Na0.5)TiO3 lead-free binary system. Acta Mater. 208, 116710 (2021).
Zhang, M.-H. et al. Electric-field-induced antiferroelectric to ferroelectric phase transition in polycrystalline NaNbO3. Acta Mater. 200, 127–135 (2020).
Liu, G. et al. Energy storage properties of NaNbO3-based lead-free superparaelectrics with large antiferrodistortion. Microstructures 3, 2023009 (2023).
Wu, S. et al. Superb energy storage capability for NaNbO(3)-based ceramics featuring labyrinthine submicro-domains with clustered lattice distortions. Small 19, e2303915 (2023).
Liu, H. et al. Chemical framework to design linear-like relaxors toward capacitive energy storage. J. Am. Chem. Soc. 146, 3498–3507 (2024).
Shannon, R. D. et al. Empirical electronic polarizabilities in oxides, hydroxides, oxyfluorides, and oxychlorides. Phys. Rev. B 73, 235111 (2006).
Balachandran, P. V. et al. Predicting displacements of octahedral cations in ferroelectric perovskites using machine learning. Acta Crystallogr. B 73, 962–967 (2017).
Grinberg, I. et al. Nonmonotonic TC trends in bi-based ferroelectric perovskite solid solutions. Phys. Rev. Lett. 98, 037603 (2007).
Li, D. et al. A high-temperature performing and near-zero energy loss lead-free ceramic capacitor. Energy Environ. Sci. 16, 4511–4521 (2023).
Fu, J. et al. A highly polarizable concentrated dipole glass for ultrahigh energy storage. Nat. Commun. 15, 7338 (2024).
Jiménez, R. et al. Stabilization of the ferroelectric phase and relaxor-like behaviour in low Li content sodium niobates. J. Phys. Condens. Matter 16, 7493–7510 (2004).
Chen, L. et al. Near-Zero energy consumption capacitors by controlling inhomogeneous polarization configuration. Adv. Mater. 36, e2313285 (2024).
Duan, J. et al. High-entropy tungsten bronze ceramics for large capacitive energy storage with near-zero losses. Adv. Funct. Mater. 34, 2409446 (2024).
Yang, L. et al. High comprehensive energy storage properties in (Sm, Ti) co-doped sodium niobate ceramics. Appl. Phys. Lett. 122, 192901 (2023).
Chen, Z. et al. Novel BCZT-based ceramics with ultrahigh energy storage efficiency and outstanding high temperature fatigue endurance and stability for practical application. Ceram. Int. 49, 34520–34528 (2023).
Nayak, R. L. et al. Enhanced dielectric, thermal stability, and energy storage properties in compositionally engineered lead-free ceramics at morphotropic phase boundary. Ceram. Int. 47, 17220–17233 (2021).
Ning, Y. et al. Achieving high energy storage performance below 200 kV/cm in BaTiO3-based medium-entropy ceramics. Ceram. Int. 49, 20326–20333 (2023).
Zhou, M. et al. Combining high energy efficiency and fast charge-discharge capability in novel BaTiO3-based relaxor ferroelectric ceramic for energy-storage. Ceram. Int. 45, 3582–3590 (2019).
Huan, Y. et al. Achieving ultrahigh energy storage efficiency in local-composition gradient-structured ferroelectric ceramics. Chem. Eng. J. 425, 129506 (2021).
Yan, F. et al. Sandwich structured lead-free ceramics based on Bi0.5Na0.5TiO3 for high energy storage. Chem. Eng. J. 425, 130669 (2021).
Ding, Y. et al. Simultaneously achieving high energy-storage efficiency and density in Bi-modified SrTiO3-based relaxor ferroelectrics by ion selective engineering. Compos. B Eng. 230, 109493 (2022).
Li, C. et al. Superior energy storage performance in (Bi0.5Na0.5)TiO3-based lead-free relaxor ferroelectrics for dielectric capacitor application via multiscale optimization design. J. Mater. Chem. A 10, 9535–9546 (2022).
Liu, J. et al. A synergistic two-step optimization design enables high capacitive energy storage in lead-free Sr0.7Bi0.2TiO3-based relaxor ferroelectric ceramics. J. Mater. Chem. A 11, 609–620 (2023).
Pu, Y. et al. Enhancing the energy storage properties of Ca0.5Sr0.5TiO3-based lead-free linear dielectric ceramics with excellent stability through regulating grain boundary defects. J. Mater. Chem. C 7, 14384–14393 (2019).
Zhang, X. et al. Ultrahigh energy storage with superfast charge-discharge capability achieved in linear dielectric ceramic. J. Mater. Sci. Technol. 177, 59–67 (2024).
Wang, T. et al. Relaxor ferroelectric BaTiO3-Bi(Mg2/3Nb1/3)O3 ceramics for energy storage application. J. Am. Ceram. Soc. 98, 559–566 (2014).
Wang, W. et al. Enhanced energy storage density and high efficiency of lead-free Ca1-xSrxTi1-yZryO3 linear dielectric ceramics. J. Eur. Ceram. Soc. 39, 5236–5242 (2019).
Zhang, L. et al. Extreme high energy storage efficiency in perovskite structured (1-x)(Ba0.8Sr0.2)TiO3-xBi(Zn2/3Nb1/3)O3 (0.04 ≤ x ≤ 0.16) ceramics. J. Eur. Ceram. Soc. 40, 3343–3347 (2020).
Zhao, W. et al. Broad-high operating temperature range and enhanced energy storage performances in lead-free ferroelectrics. Nat. Commun. 14, 5725 (2023).
Yan, F. et al. Boosting energy storage performance of lead-free ceramics via layered structure optimization strategy. Small 18, e2202575 (2022).
Yan, F. et al. Ultrahigh energy storage density and efficiency of lead-free eielectrics with sandwich structure. Small 20, e2306803 (2024).
Xie, A. et al. NaNbO3-(Bi0.5Li0.5)TiO3 lead-free relaxor ferroelectric capacitors with superior energy-storage performances via multiple synergistic design. Adv. Energy Mater. 11, 2101378 (2021).
Zhang, Y. et al. Superior energy-storage properties in Bi(0.5)Na(0.5)TiO(3)-based lead-free ceramics via simultaneously manipulating multiscale structure and field-induced structure transition. ACS Appl. Mater. Interfaces 14, 40043–40051 (2022).
Hu, Q. et al. Achieve ultrahigh energy storage performance in BaTiO3–Bi(Mg1/2Ti1/2)O3 relaxor ferroelectric ceramics via nano-scale polarization mismatch and reconstruction. Nano Energy 67, 104264 (2020).
Acknowledgements
This work was supported by the National Key R&D Program of China (No. 2023YFB3508200, H.Q.), Science and Technology Innovation Program of Hunan Province (2023RC3094, H.L.), Scientific Research Fund of Hunan Provincial Education Department (24B0047, H.L.).
Author information
Authors and Affiliations
Contributions
This work was conceived and designed by K.W., H.Q., and H.L. Sample fabrication was performed by K.W. and J.H.D., who also conducted energy storage, dielectric, and charge-discharge performance tests, as well as analyzed relevant data. Finite element simulations of breakdown characteristics were conducted by H.F.Y. Phase field simulations of BO6 tilt and polarization configurations were conducted by X.M.S. and H.Y.W. SEM and Raman spectroscopy were performed by H.L. and K.W. XPS spectroscopy were performed by Z.K.S. HAADF-STEM imaging was carried out by H.Q. and G.S.L., processed accordingly. Temperature-dependent Raman and XRD data were collected by H.Q. and analyzed by K.W. XRD testing and corresponding data analysis were carried out by K.W. The manuscript was drafted by K.W. and revised by H.L., Q.B.D., L.Z.M., G.S.L., and H.Q. All authors participated in data analysis and discussions.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Pierre-Eymeric Janolin, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wei, K., Duan, J., Qi, H. et al. Collaborative design of polarization and antiferrodistortion configurations in high energy capacitive relaxor ferroelectrics. Nat Commun 16, 7833 (2025). https://doi.org/10.1038/s41467-025-62335-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-62335-3