The oceanic physical injection pump of organic carbon

Abstract

The contribution of the ocean biological carbon pump to the export of organic carbon at depth has predominantly been assessed by considering sinking particulate matter and vertically migrating organisms. Despite growing recognition of the importance of dynamical pathways that export carbon through upper-ocean mixing and advection, observation-based estimates of their global impact are still lacking. Here, we quantify the values and uncertainties of the export driven by the physical injection pump (PIP) and its interannual variability by leveraging a 4D data-driven time series (1997-2018) of particulate organic carbon concentration (POC) and ocean circulation, as well as 3D fields of climatological dissolved organic carbon (DOC). Vertical diffusion dominates our POC export estimates, but remains the most uncertain process. Assuming maximal diffusivity estimates that are consistent with observations, POC and DOC export amount to 0.37 Pg C yr⁻¹ and 0.48 Pg C yr⁻¹, respectively. The contribution from entrainment and advection is strongly modulated by the POC annual cycle, revealing the critical coupling between biological production and upper-layer mixing in driving the net annual export. Observed interannual signals correlate with a linear combination of El Niño–Southern Oscillation and Southern Annular Mode indices, suggesting that the PIP is connected to intermediate- and mode-water formation dynamics in the Southern Ocean.

Introduction

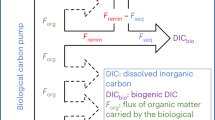
The oceanic biological carbon pump (BCP) refers to the mechanisms responsible for transferring organic carbon, mainly produced by small plant-like organisms (i.e., phytoplankton) through net primary production, from the sunlit ocean to the twilight zone (~100–1000 m). At depth, organic carbon can either be remineralized to dissolved inorganic carbon (DIC) and then re-exchanged with the atmosphere or sequestered for climate-relevant time scales. This process plays a crucial role in global climate regulation by creating a vertical gradient in DIC that enhances the ocean’s capacity to absorb atmospheric CO₂¹. Globally, the BCP exports approximately 10 Pg C yr⁻¹ from the ocean’s surface, contributing to maintaining a deep-ocean pool of around 1300 Pg C^1,2. It is thus crucial to accurately characterize and quantify all components of the BCP that are modulated by both regional and global processes^3,4,5,6.

The BCP is based on three primary pathways: gravity, migrant, and physical injection pumps of both dissolved and particulate organic carbon (DOC and POC, respectively). The gravity pump consists of organic matter sinking from the base of the euphotic zone and is the main contributor to net carbon export (e.g., 4–9 Pg C yr⁻¹ of POC) and sequestration³. The migrant pump transports organic carbon to deeper depths through the activities of vertically migrating animals, such as zooplankton or fish, from short (daily) to longer time scales (months)^3,7, (e.g., 0.9–3.9 Pg C yr⁻¹ of POC). The physical injection pump (PIP), instead, refers to the dynamical processes that transfer surface properties, including inorganic and organic carbon, to depth⁸. The PIP is associated with the transport of both DOC and POC below the euphotic zone through ocean circulation and mixing processes, and it is also referred to as the “mixing pump”^2,3 (e.g., 0.1–2.1 Pg C yr⁻¹ of POC).

The PIP encompasses all the dynamical processes exporting organic carbon across different spatial and temporal scales. Involved mechanisms include lateral and vertical transport by Ekman pumping, eddies and fronts leading to large- and small-scale subduction, as well as micro-scale turbulence events. Mixing and subduction driving water-mass formation and additional carbon export represent fundamental components of the global meridional overturning circulation^9,10. Investigating the effects of these processes on carbon export thus requires reconstructing how both dynamical variables and organic-carbon distributions evolve over large periods at relatively high temporal resolution and across different spatial scales^2,11,12. However, the PIP estimates presently available are either based entirely on numerical models or combine observation-based data and inverse modeling approaches that involve steady-state assumptions (see Supplementary Table 1 and reference therein)^11,12,13,14. As an example, the vertical component of oceanic currents, critical to estimate the exchange rate between surface and deep layers, is notoriously difficult to measure. However, significant progress has been made with the advent of in-situ autonomous robotic platforms (e.g., Biogeochemical-Argo floats; hereafter BGC-Argo) and the availability of advanced data-driven POC reconstructions and dynamical diagnostic models^15,16. Conversely, quantifying the stocks and export dynamics of DOC remains a challenge as only climatological reconstructions are currently available¹².

Here, we present a global estimate of the PIP obtained from observation-based data that refrains from any steady-state dynamical assumption. We computed it by taking advantage of state-of-the-art data-driven reconstructions of four-dimensional POC concentration and ocean circulation fields, including both horizontal and vertical current variability and temporal variations of the euphotic and mixed-layer depths. While our focus is mostly on assessing POC export and evaluating the impact of different 4D-POC reconstruction algorithms, we also provide an estimate of physically-induced DOC export based on available DOC climatology (see Methods). POC data were obtained by combining in-situ data from Argo floats and satellite observations, machine-learning techniques and advanced diagnostic tools^15,16. These weekly data cover the global ocean over the period 1997–2018 at 1/4° horizontal resolution. Quasi-geostrophic currents were available at the same resolution but only outside the equatorial band¹⁶.

We estimated the PIP at the mesoscale and large scale¹¹ and separately quantified the contributions of entrainment, horizontal and vertical advection, as well as of vertical diffusion and lateral eddy mixing. We paid specific attention to the discussion of the sources of uncertainties in POC export estimates and provided a quantification of their relevance in the “Methods” section.

Results and discussion

A consistent framework for the calculation of organic carbon export

Organic carbon (DOC and POC) export by the physical pump and water-mass formation are related to the same physical processes^17,18,19. Nevertheless, POC is an active tracer, and the availability of light is as important as upper-ocean dynamics to properly define the export depth. In specific cases (e.g., in the subtropical gyres), when the mixed layer depth (z_mld) is shallower than the euphotic depth (z_eu), and primary production can occur below z_mld, POC export should be estimated as the flux crossing z_eu. On the contrary, when z_eu < z_mld, phytoplankton can photosynthesize when mixing exposes them to light and export should be computed through z_mld. Consequently, the productive-export depth (z_p) was defined as the deepest value between the euphotic and mixed-layer depths. A similar definition was adopted to include the effect of the penetrative solar radiation in upper-ocean water-mass transformation^18,20. Our estimates of carbon export for both POC and DOC are therefore driven by temporal variations in z_p that can be due to both entrainment (i.e., variations in z_mld) and variations in z_eu. Yet, for simplicity, we have maintained the term “entrainement” in the following.

Different classifications of physical/mixing pump mechanisms have been proposed in the literature, even though consistent definitions are not always provided in terms of physical processes or separation between scales^2,8,13,21 (see Supplementary Text). To avoid confusion, we have adopted the mathematical definition of the different physical processes presented in the Methods section (Eq. (2). We then adopt the following operational definitions to separate spatial scales:

(i) The large-scale subduction pump (LSP) is defined as the export of organic carbon by large-scale processes, estimated by spatially low-pass filtering, O(500 km)¹³, all fields before computing the export (see the “Methods” section);

(ii) The eddy-subduction pump (ESP) is estimated as the residual between the export estimated from the PIP and the LSP component.

We note that all physical processes described by Eq. (2) contribute to both LSP and ESP. The mixed-layer pump (MLP) is only one of these processes (i.e., the net contribution of entrainment/detrainment^17,18,19) and occurs when the surface layer re-stratifies and the organic carbon in the waters below the export depth is no longer in contact with the atmosphere^10,20,22.

Total export values

The global spatially integrated PIP exports approximately 0.37 Pg C yr⁻¹ of POC (Table 1), and it is dominated by the vertical diffusive term (0.29 Pg C yr⁻¹). To the best of our knowledge, this dominant contribution has not been identified before explicitly^3,11. Yet, its impact is strongly dependent on the parameterization adopted for the vertical diffusivity, which remains highly uncertain due to scarce observations²³. Indeed, the contribution of vertical diffusion to POC export can vary up to a factor of 10 if the entire range of observed diffusivity values is considered. This underscores the critical role of diffusion in transporting POC from the surface to the ocean interior, and also the strong sensitivity to the way diffusion is estimated. The values discussed hereafter are based on a conservative choice of 10⁻³ m² s⁻¹, but linearly scaling this value would proportionally adjust the contribution of diffusion to the export estimates. As such, differences between our values of the net export and those found in the literature lie within the uncertainty range associated with vertical diffusion processes (see the “Methods” section). The net entrainment/detrainment contributes to a lesser extent with values (0.07 Pg C yr⁻¹; Table 1) in the range reported in the literature²² (Table S1). Globally, vertical advection exports ~0.03 Pg C yr⁻¹ of POC, and is almost completely compensated by the horizontal contribution (~−0.03 Pg C yr⁻¹). Export by lateral eddy mixing does not exceed 0.01 Pg C yr⁻¹. Notably, using a spatially constant lateral diffusivity coefficient, almost negligible variations are found (<10%, see the “Methods” section).

Table 1 Summary of net POC export (with also standard deviation of the yearly values) due to PIP, LSP, and ESP

In these estimates based on z_p, vertical diffusion and “true” entrainment (specifically, the flux associated with changes in z_mld driven by turbulence) contribute less than when considering z_mld as the export depth (see Table S2), but significantly more than when using z_eu (see Table S3). This is because whenever z_eu is sufficiently deeper than z_mld, the diffusivity reaches extremely low values. Vice versa, the vertical-diffusion component computed from z_eu is overestimated whenever z_eu lies within the mixed layer, where diffusivity is always maximal. In fact, in that case, carbon is still in the ventilated layer, so it should not be considered as exported.

Geographic variability

The PIP displays significant geographical variability in POC export, with its largest values found at high latitudes in the Labrador Sea, north-Atlantic and north-Pacific subpolar gyres, as well as in the Indo-Pacific and Atlantic sectors of the Southern Ocean, especially along the Antarctic Circumpolar Current (ACC, Fig. 1a). In these areas, the PIP is mostly linked to areas of mode- and deep-water formations²⁴.

Fig. 1: Geographical variability of POC flux by PIP.

Total POC flux by PIP (a) and by the different contributors as entrainment/detrainment (b), horizontal advection (c), vertical advection (d), vertical diffusion (e), and eddy mixing (f). Note that the vertical diffusion is strictly dependent on the parameterization. The values shown here correspond to a choice of the maximum diffusivity of O(10⁻³ m² s⁻¹). Lateral eddy mixing always attains values at least one order of magnitude lower than the other mechanisms.

The contribution of vertical diffusion and the mixed-layer pump display maxima in the most productive areas of the North Atlantic^21,22,25 and along the ACC in the Southern Ocean (Figs. 1b and S1). On the contrary, low POC export is found in correspondence with the subtropical gyres.

Vertical advection dominates POC export at mid-latitudes, particularly in the Southern Ocean (Fig. 1d). In the intertropical region and at high latitudes, instead, it drives a large negative contribution to physical export (i.e., net POC flux towards the surface, Fig. 2).

Fig. 2: Latitudinal variability of POC flux by the different components.

Latitudinal pattern of total POC flux (black line) and by entrainment/detrainment (red line), horizontal advection (green line), vertical advection (blue line), vertical diffusion (orange) and lateral eddy mixing (light blue).

Horizontal advection displays relatively strong positive and negative spatial features, especially in the Southern Ocean (Fig. 1c). When averaged, its net export is almost zero, except in the northern high latitudes (Fig. 2).

Globally, lateral eddy mixing plays a relatively minor role in exporting POC, its impact being roughly one order of magnitude smaller than that of other physical processes¹¹. Nevertheless, some notable hotspots of its activity are observed, particularly in the Gulf Stream and in the Indian sector of the Southern Ocean (Fig. 1f). A significant proportion (~80%) of the POC export attributed to lateral eddy mixing is driven by the ESP (Table 1). This emphasizes the importance of mesoscale dynamics in specific regions, despite its relatively minor role in global POC fluxes.

Considering the base of the productive layer (z_p) as the reference export depth introduces different regional impacts of mesoscale dynamics and vertical mixing with respect to considering either the mixed layer or the euphotic depth alone (Figs. S2 and S3). Specifically, when using z_p, the contribution from horizontal advection displays a slightly minor impact with respect to the estimates obtained at the base of z_mld. The same term, however, is almost zero when computed at z_eu, as z_eu is generally deeper than z_mld, and dominant mesoscale dynamics are surface intensified. Since in the tropics, z_p coincides with z_eu, the final effect is to filter out the mesoscale contribution. In the inter-tropical band, the vertical diffusive term consistently reflects the fluxes at the base of the euphotic layer, while the export estimated at the base of the shallow mixed layer would imply a negative export, due to the increasing POC concentrations down to the base of the euphotic layer, associated with marked deep chlorophyll maxima.

Spatial scales

The large-scale pump dominates the PIP, exporting around 0.31 Pg C yr⁻¹ of POC and follows the large-scale oceanic circulation and large-scale Ekman-transport patterns (Fig. S4). Globally, the LSP is mostly the result of the combined effects of vertical diffusion, entrainment/detrainment and vertical advection. The horizontal-advection component of the LSP mostly upwells POC from below z_p to the ocean surface (Fig. S4, Table 1). The ESP is concentrated along western-boundary currents (Fig. S5). At the global scale, the eddy-subduction pump exports 0.06 Pg C yr⁻¹, namely only 15% of the PIP, which is consistent with previous findings emphasizing that when the eddy pump is active, both obduction and subduction occur¹³. However, the ESP can have a substantial regional impact in the North Atlantic and in the Southern Ocean^{19,25,26,27,28,29} (Fig. S5, Table 1).

DOC physical pump

Since DOC export is driven by physical mechanisms, we applied our framework to estimate also the physical pump of DOC. This computation was based on a single 3D climatology of DOC coupled with the same weekly fields of ocean dynamics used for the POC-export estimates (see the “Methods” section). We found that 0.48 Pg C yr⁻¹ of DOC is exported yearly (Table 2, Fig. S6). Three main terms are responsible for this net flux: (i) vertical diffusion (0.39 Pg C yr⁻¹) resulting from vertical DOC gradients at the reference export depth that have similar strength to the POC gradients; (ii) vertical advection (0.36 Pg C yr⁻¹) that is driven by large-scale Ekman pumping and is the net result of large positive and negative fluxes (Fig. S6d); and (iii) horizontal advection that results in a net export of −0.29 Pg C yr⁻¹, where the negative sign suggests a net flux of DOC from subtropical regions, where DOC is maximal and z_mld is shallow, to high-latitude regions, where the mixed layer is deeper and DOC lower (mostly through the ACC, Fig. S6c)⁹.

Table 2 Summary of net DOC export (with also standard deviation of the yearly values) due to the PIP and contributions of the different physical pumps

Our DOC export is lower by a factor of about four than a model-based estimate¹⁴ computed through z_eu (1.9 Pg C yr⁻¹) and similarly lower than the values of 1.9–2.3 Pg C yr⁻¹ computed from different data-constrained models but taking a fixed depth as reference export surface^9,12. Yet, when we estimate global DOC export through z_eu we obtain higher values (0.87 Pg C yr⁻¹), but not enough to explain all the difference with pure model-based estimates. Conversely, if we take a fixed depth reference at 74 m, DOC export value reaches 1.5 Pg C yr⁻¹ (see Tables S4, S5). The residual differences with previous data-constrained assessments are reasonably explained by the differences in the dynamics and spatial domains between our method and the reported models (see the “Methods” section).

Temporal variability in organic carbon export

The time series of global POC-export displays strong interannual variability on top of a small but statistically significant (at the 95% confidence level) positive linear trend of 0.003 ± 0.002 Pg C yr⁻². Interannual fluctuations are almost completely driven by the vertical physics (i.e., entrainment, vertical advection and diffusion), with relative maxima observed in 2002–2004, 2009, 2016 (Fig. 3). These signals are primarily guided by the export occurring in the Southern Ocean¹¹ (Fig. 4), which suggests a link between the PIP and the processes that transform water masses in the Southern Ocean.

Fig. 3: Time-series of POC flux and dynamical components.

Panel a shows the time-series of total POC flux and corresponding dynamical components. Panel b is the same as above but using a single 3D POC climatology. Panel c shows the monthly SAM and ONI climate indices normalized.

Fig. 4: Time-series of POC flux on a global scale and along different latitudinal sectors.

The time-series of POC flux is on a global scale and along different latitudinal sectors (Northern Ocean (30–90°N), Southern Ocean (30–90°S) and Subtropical Ocean (30°S/30°N).

Along the ACC, circumpolar deep water (CDW) is first upwelled and then follows two principal pathways: one branch moves southward and subducts to form the Antarctic Bottom Water, while the other branch flows northward, mixing with the thermocline waters (TW) to generate mode and intermediate waters. Consequently, Subantarctic mode water (SAMW) emerges as a composite of CDW, Antarctic intermediate water (AAIW), older SAMW, and TW, formed through deep winter mixing and heat loss^18,30. Once subducted, these well-homogenized water masses penetrate the ocean interior, with SAMW predominantly forming in the Indian and Pacific sectors, where winter mixed layers reach their greatest depths.

The time series of POC export displays distinct signals in these two sectors (Fig. 5), which can be related to differences in the SAMW formation. SAMW variability is modulated by dominant Southern Hemisphere climate modes. Specifically, the southern annular mode (SAM) exerts a strong influence on wintertime mixed-layer depth anomalies, which in turn regulate the volume of subducted mode water^30,31,32. In the Pacific sector, however, SAMW formation is primarily modulated by the El Niño–Southern Oscillation (ENSO)^30,32. The interplay between ENSO and SAM phases thus governs the interannual variability in SAMW mean properties^30,32.

Fig. 5: Time-series of total POC flux in sectors of the Southern Ocean.

Time-series of total export of POC driven by ocean dynamics and by the corresponding components for the Indian (50°–168°W, 30–90°S; panel a) and Pacific (170°–290°W, 30–90°S; panel b) sectors of the Southern Ocean.

Linking organic carbon export and climate modes

To elucidate the possible relationship between the inter-annual variability of our PIP estimates and climatic modes, we regressed POC and DOC exports against the Oceanic Niño Index (ONI) and Southern Annular Mode (SAM), both separately and through multilinear computations. Separately, the ONI and SAM showed a Spearman correlation to POC export of 0.57 and 0.05, respectively. The best fit (Spearman correlation = 0.617, p-value = 0.001) was then obtained by considering a linear combination of both indexes, ONI impacting positively and SAM impacting negatively on the POC export values (but SAM weighing approximately 1/10, when considering normalized indexes, namely with coefficients 1.9 × 10⁻² and −0.4 × 10⁻², respectively). The correlation increases to 0.660 (p-value = 0.003) when diffusive terms are removed from the POC flux (see also Table S6).

Therefore, POC export appears to be modulated by the interannual variability in Subantarctic mode water (SAMW) formation and reflects the different responses of SAMW dynamics to the relative phases of SAM and El Niño–Southern Oscillation (ENSO). As reported in the literature, the thickness of the SAMW layer in the eastern (central) pool is generally positively (negatively) correlated with the SAM and ENSO, with in-phase reinforcing modes from 2005–2008 and 2012–2017 driving observed differences between the pools³². The variability of the dynamical fields, however, is not sufficient to explain the observed signals: computing the PIP using POC climatological values not only reduces the mean export to less than one third (Table S7), but also shows a substantially lower correlation with climatic indexes (Spearman correlation = 0.49, p-value = 0.025). Consistently, the interannual variations in DOC export (given only by the variability of the dynamical fields) were not significantly correlated to the climatic indices (Spearman correlation = 0.35, p-value = 0.13). This further evidences the complex interplay between the variability of physical mechanisms and that of bio-geochemical processes in determining the net flux of organic carbon to the deep ocean layers.

Perspectives

The analysis of observation-based time series of the export driven by the physical injection pump offers key insights into the dynamics of the carbon cycle. Nevertheless, large uncertainties remain that are related to the quantification of vertical diffusive processes that emerge as the dominant contribution to the export driven by the physical injection pump, a finding overlooked in prior studies. This underscores the urgent need for community efforts to better constrain mixing processes³¹, especially in observation-based studies and to evaluate the impact of the different turbulence closure models used in numerical simulations. Moreover, the large difference (~22%) between export values estimated from climatological POC data and those obtained from weekly fields points to the need to extend this 4D coupled biogeochemical and physical framework also to other components of the carbon pool. While the seasonal variability of DOC is known to be lower than that of POC³³, one critical step will thus be to develop 4D DOC reconstructions (e.g., by exploiting recent advances in techniques based on Artificial Intelligence). Furthermore, specific efforts will be needed to extend the reconstruction also to shallower regions (i.e. by including areas where the bathymetry is <1000 m, and the coastal regions) which are not covered by present POC products (e.g. the area at the South of Iceland or the Patagonian shelf) and to extend the dynamical reconstructions to the full equatorial band. Yet, our simple analysis of the link between interannual signals of POC export and selected climatic indices paves the way to deeper investigations of the impact of climate change and internal dynamical modes on global biogeochemical cycles.

Methods

3D particulate organic carbon dataset

This product consists of 3D fields of particulate organic carbon (POC), particulate backscattering coefficient (b_bp) and chlorophyll-a concentration (Chl) at depth. The reprocessed product is provided at 1/4° horizontal resolution, over 36 levels from the surface to 1000 m depth. A neural network method has been employed to estimate both the vertical distribution of Chl concentration and b_bp, a bio-optical proxy for POC, from merged surface ocean color satellite measurements with hydrological properties and additional relevant drivers¹⁵.

More details about the products can be found at: https://data.marine.copernicus.eu/product/MULTIOBS_GLO_BIO_BGC_3D_REP_015_010/description; https://catalogue.marine.copernicus.eu/documents/QUID/CMEMS-MOB-QUID-015-010.pdf.

3D Quasi-geostrophic vertical and horizontal ocean currents

We have estimated horizontal and vertical fluxes starting from a data-driven 3D reconstruction of quasi-geostrophic ocean currents provided by the Copernicus Marine Service. This product, called OMEGA3D, covers the period from January 1993 to December 2018 with a weekly sampling (representative of each Wednesday). It has been fully described and validated¹⁶. OMEGA3D data are provided over a regular grid at 1/4° horizontal resolution, with 75 non-uniformly spaced vertical levels between the surface and 1500 m depth. The velocities are obtained by solving a Q-vector formulation of the Omega equation that explicitly considers the effect of both geostrophic advection and upper layer turbulent mixing. Omega forcings are estimated from the CMEMS observation-based ARMOR3D temperature and salinity multi-year data and ERA-Interim surface fluxes. More details can be found at: https://data.marine.copernicus.eu/product/MULTIOBS_GLO_PHY_W_3D_REP_015_007/description.

Mixed layer depth dataset

Mixed layer depth (MLD) data were extracted from the CMEMS ARMOR3D dataset, which is an observation-based 4D reconstruction of the global ocean state obtained from the combination of in-situ and satellite data³⁴. ARMOR3D provides weekly fields of temperature, salinity, mixed layer depth and geostrophic currents at a nominal 1/4° horizontal resolution, over 50 vertical levels from the surface down to 5500 m depth. More information can be found at: https://data.marine.copernicus.eu/product/MULTIOBS_GLO_PHY_TSUV_3D_MYNRT_015_012/description.

Euphotic depth dataset from ocean color data

Daily euphotic depth (z_eu) was estimated starting from daily gap-free surface chlorophyll-a concentration (Chl) data (Global Ocean Colour (Copernicus-GlobColour), Bio-Geo-Chemical, L4 (monthly and interpolated) from Satellite Observations (1997-ongoing) | Copernicus Marine Service) downloaded from Copernicus portal and generated by the Copernicus Glob Color processor. z_eu was computed by applying Morel’s algorithm³⁵. The z_eu data were remapped at 1/4° horizontal resolution to be consistent with the other key datasets for the entire period of analysis (1998–2018).

Dissolved organic carbon climatology

The 3D dissolved organic carbon (DOC) climatology¹² is a global, gridded dataset with a 1° × 1° horizontal resolution that provides DOC distributions over 102 depth levels based on observational data and inverse modeling. It integrates DOC measurements from the surface to the deep ocean, offering a comprehensive representation of DOC spatial variability. Climatology is constructed using an ocean circulation inverse model that optimally combines observational constraints with modeled transport processes. DOC observations are compiled from multiple field campaigns, including historical datasets and more recent measurements from the Climate and Ocean: Variability, Predictability and Change (CLIVAR) and World Ocean Circulation Experiment (WOCE) programs. The dataset captures large-scale DOC gradients driven by ocean circulation, remineralization, and biological production. It resolves regional differences in DOC stocks, particularly across major ocean basins and water masses¹². We re-gridded the DOC climatology over the POC grid before carrying out the flux calculations.

Global ocean surface diffusivity map

The climatological surface horizontal diffusivity map used to investigate mesoscale mixing in the global ocean³⁶ (see k_mix uncorrected dataset). In their work, they employed the suppressed mixing length theory, which integrates satellite-derived surface velocities to estimate lateral eddy diffusivities. The resulting climatology offers insights into the spatial variability of unresolved (sub)mesoscale-driven mixing. Before any computation, the surface horizontal diffusivity climatological map has been regridded to the 3D POC grid. At high latitudes, the gaps are filled by the mean values of the map.

Gap-filling procedure

To fill the gaps in the 3D POC weekly fields, we have applied the multi-channel singular spectral analysis (M-SSA) technique. M-SSA is a non-parametric spectral estimation method relying on data only^{37,38,39,40,41}. The method uses temporal correlation to fill in the missing data and represents a generalization of the spatial empirical orthogonal functions (EOFs)-based reconstruction⁴². Here, the MSSA has been applied to 3D POC fields, which have been previously remapped at 1° resolution. After the application of MSSA on the remapped dataset, the filled dataset at 1° resolution has been re-gridded at 1/4°, and only original gaps are filled with corresponding new data.

Export computation

The evolution of any ocean tracer $C$ follows the general transport equation:

$${{{\partial }}}_{t}C=-w{{{\partial }}}_{x}C-u\cdot {{{\nabla }}}_{{{\rm{H}}}}C+{{{\rm{\partial }}}}_{z}({k}_{z}{{{\rm{\partial }}}}_{z}C)+{E}_{{{\rm{c}}}}+{S}_{{{\rm{c}}}}$$

(1)

where $w$, $u$, ${k}_{z}$ are the vertical velocity, horizontal velocity, and vertical diffusion coefficient of seawater, respectively. The mixing term ${E}_{{{\rm{c}}}}$ represents the dynamics at unresolved scales. The source terms do change when one is considering POC, so that ${S}_{{{\rm{c}}}}$ generically accounts for gas exchange, river discharges, flux to the sediments, gravitational sinking, and other biological and chemical/photochemical processes. Here, we are focusing on the terms that contribute to the tracer evolution that are directly linked to the transport by oceanic currents at mesoscale and larger scales. Neglecting the source terms, the vertical integration of Eq. (1) from the surface of the ocean to the export depth, h, thus leads to:

$${{{P}}{{O}}{{C}}}_{{{f}}{{l}}{{u}}{{x}}}=h\cdot {{{\partial }}}_{t}{C}_{h}=-{C}_{h}\cdot ({{{\partial }}}_{t}h+{u}_{h}\cdot {{{\nabla }}}_{{{H}}}h+{w}_{h})+({k}_{z}{{{\partial }}}_{z}C)h+{\int }_{0}^{h}{E}_{{{c}}}{{d}}z$$

(2)

where ${C}_{h}$, ${u}_{h}$, and ${w}_{h}$ are the values of POC, u, and w at the export depth, h, which is defined as the depth below the organic carbon is considered exported⁴³. Equation (2), written here as presented in Eq. (1), is obtained by considering the equivalence between the divergence of the tracer flux integrated over a volume and the integral of the flux across the volume surface (a.k.a. Gauss theorem), plus the impact of the volume change itself.

We have computed the export depth as the maximum depth between the mixed layer and the euphotic depth for each pixel, at weekly time scales^15,16. At high latitudes, during polar night conditions, h is assumed to coincide with the MLD.

As our data are available on an Arakawa A-grid, the tracer export is finally defined as the concentration at the base of the upper layer, ${C}_{h}$, multiplied by the instantaneous subduction rate⁴⁴ given by the sum of the local change in export depth (which we somehow improperly call “entrainment/detrainment”, whatever the reference surface considered), of the horizontal advection across the sloping base of the export depth, and of the vertical advection at the base of the export depth (–w_h).

We calculated the contribution of vertical diffusion to POC flux (k_z∂_zC)h by parameterizing the vertical diffusion coefficient. Data-driven reconstructions do not provide the same amount of information available within prognostic models to apply more sophisticated parameterizations. As such, we applied a simplified approach that modulates the upper-layer diffusivity based on the mixed-layer depth and imposes an analytical dumping of mixing intensity below the base of the mixed layer. Our methodology fundamentally follows the same strategy to estimate viscosity from limited in situ data⁴⁵, as follows:

$${k}_{z}=\frac{{k}_{z{{m}}{{a}}{{x}}}}{2}\left[1+\tanh \left(\frac{2\pi (h+{z}_{{{\rm{m}}}{{\rm{l}}}{{\rm{d}}}})}{\delta z}\right)\right]$$

(3)

where $\delta z$ is the thickness of the transition layer and has been set to 40 m, h is the export depth in our computation. The key parameter in our calculation is thus the maximum vertical diffusion coefficient ${k}_{z{{m}}{{a}}{{x}}}$. Resulting diffusivity is always maximal at the surface and reduces to half the surface value at the base of the mixed layer.

The last term of Eq. (2) (POC flux due to eddy mixing, unresolved scale) has been computed by using the single climatology of surface diffusivity map³⁷ and by imposing a decreasing exponential curve to obtain a vertical profile of horizontal diffusivity⁴⁶. We have also tested the impact of using a single mean value, which led to a decrease in the eddy mixing contribution to export by around <10%.

Following Eq. (2), we have computed the weekly ${{{P}}{{O}}{{C}}}_{{{f}}{{l}}{{u}}{{x}}}$ from 1998 to 2018. After that, the weekly ${{{P}}{{O}}{{C}}}_{{{f}}{{l}}{{u}}{{x}}}$ was averaged to compute monthly maps and an annual climatology. We have computed both the total export of POC and the separate contributions from entrainment/detrainment, horizontal and vertical advection.

The entire approach has been replicated to estimate DOC export, following the same computational framework described above. The only distinction lies in the use of a single 3D DOC climatology rather than the weekly 3D POC fields. This means that DOC export was computed using the DOC climatology¹² as the input dataset, while maintaining the same methodological steps applied in the POC-based estimates. This ensures consistency in the assessment of organic carbon exports while accounting for the distinct behavior of DOC in the ocean.

Sources of uncertainty in POC export estimation and sensitivity analyses

The quantification of uncertainties is a fundamental step for a robust and scientifically sound discussion on the mechanisms driving carbon export. However, a distinction needs to be made between the numerous possible sources of uncertainties, keeping in mind that the majority of them can, at best, be presented in terms of sensitivities rather than actual error budgets. In the literature, both model-based and observation-based estimates of the global net export never include true uncertainty estimates, as those would require direct observations that are not available. Whatever the model and approach followed, the sources of uncertainties in POC export estimates include:

• 1. errors in the dynamical variables (velocities and parameterization of diffusion)

• 2. errors in the estimation of POC

• 3. errors due to the sampling.

Concerning point 1.: Quantifying dynamical variables’ errors and their impact on export estimates remains a persistent challenge in the literature, with no established methods currently available. In fact, those errors are sometimes evaluated based on ensemble modeling in pure model-based approaches, which cannot be replicated with the observation-based approach followed here. As such, to assess the uncertainty due to errors in the water mass velocities, we have repeated the export computations, adding a Gaussian noise to the observation-based fields (either taken as 10% of the velocity values and as a fixed error of 10 cm/s). While we are aware that this approach is only very roughly simulating the errors in our input observation-based data (especially because true errors include spatially correlated signals), in both cases, the POC fluxes changed by <3%.

We then carried out a sensitivity analysis on the parameterization of vertical diffusion by allowing ${k}_{{{z}}{{m}}{{a}}{{x}}}$ to vary between 10⁻³ and 10⁻⁴ (m² s⁻¹). These values were chosen based on in-situ measurements collected at the global scale²⁴. The parameterization⁴⁹ was applied to each pixel on a weekly basis. The contribution of diffusion to POC export depends linearly on the value of ${k}_{z{{m}}{{a}}{{x}}}$, so that the uncertainty related to this term remains extremely high.

Concerning point 2.: To assess how the bbp-based POC algorithm affects net export estimates, we conducted a sensitivity analysis. Initially, we employed specific empirical algorithms^47,48,49 focusing only on the terms associated with advection and entrainment (i.e., neglecting the effect of parameterized diffusion) (see Main text). Using the Stramski ‘salgorithm⁴⁷, we observed a 13% increase in net POC flux (0.097 Pg C yr⁻¹) compared to the flux computed with the Copernicus product (0.086 Pg C yr⁻¹). Applying Cetinic’s and Koestner’s algorithms^47,49 resulted in a greater reduction in net POC flux (0.05 and 0.06 Pg C yr⁻¹, respectively). These algorithms utilize linear empirical relationships at the surface that are extrapolated through the depth.

It’s important to note that the relationship of Cetinic et al. ³⁵ applied to this global database shows a mean absolute percentage difference (MAPD) of 72% and root mean square deviation (RMSD) of 54 mg m⁻³ compared to Copernicus products, which provide POC estimates for the global ocean across all seasons with a MAPD of 21% and RMSD of 35 mg m⁻³ (for more details see https://catalogue.marine.copernicus.eu/documents/QUID/CMEMS-MOB-QUID-015-010.pdf).

Furthermore, those discrepancies between POC fluxes may also arise because the latter was derived from a specific cruise in a particular season in the North Atlantic Ocean⁴⁹. Finally, we also compared results using Gali’s algorithm⁵⁰, which shows a difference <20% (0.07 Pg C yr⁻¹). However, recent studies have revealed significant variability in the POC:b_bp ratio as a function of depth and region⁵⁰. As such, the 3D weekly POC fields utilized in our study have been adjusted using this algorithm⁵⁰, which accounts for variations in the POC:b_bp ratio throughout the water column. To assess the influence of the b_bp-based POC algorithm on net export estimates within our framework, we also conducted a sensitivity analysis by looking at the changes in POC flux with and without such correction⁵⁰. When the depth-dependent correction was excluded, the estimated net POC flux decreased by roughly 5%, primarily due to the vertical diffusion term (Table 3), which is consistent with the reduced vertical gradient entering the diffusive term computation.

Table 3 POC export values computed with and without the correction of Gali et al. (2022)

Concerning point 3.: We assessed the impact of making estimations based on climatological averages with respect to weekly sampled data and also working on high spatial resolution vs. low-pass filtered data. First of all, we compared the values obtained from the full high-resolution 3D dynamical and POC data with those found by taking POC climatology, only allowing physics to evolve over time. This has been thoroughly covered in the main text.

The impact of the resolution of the input data has been assessed by looking at the LSP (see main text), which was computed by applying a spatially low-pass filtering of 500 km (through a boxcar average). The procedure was applied to all the variables used (POC, horizontal and vertical velocities, mixed layer and euphotic depths, horizontal diffusion map). As discussed in the main text, we also tested various definitions of the “horizon” export depth, i.e., of the depth below which organic carbon can be considered exported⁴³. The most common choices include the mixed layer depth (z_mld), the euphotic depth (z_eu), or a fixed-depth surface of 100 m (z₁₀₀)^10,20,21,43. Table 4 resume all the analyses described above.

Table 4 % of difference between the POC export values presented in Table 1 and the results of the sensitivity tests, computed as: 100*[(export_observed-export_test)/export_observed]