Introduction

Non-Abelian physics, a field that focuses on physical systems exhibiting non-Abelian symmetry, has played a central role in various physical disciplines such as describing fundamental forces and interactions1,2. Non-Abelian systems satisfy non-Abelian statistics3,4, that is, the symmetry operations acting on the eigenfunction of the system are generally non-commutative. This is mainly since the symmetry operations are described by a non-Abelian group5 in which the group elements typically do not commute with each other. As an example of great current interest, non-Abelian braiding that exploits the non-Abelian statistics of non-Abelian anyons6,7,8, has been proposed in condensed matter systems towards the application of topological quantum computing9,10,11,12,13,14. The braiding of non-Abelian anyons follows a non-Abelian holonomy process15, giving rise to a geometric phase matrix via a global effect that is immune to local perturbations such as noise. The idea of non-Abelian braiding has been recently introduced to systems beyond fermion systems16,17,18,19,20,21. Other intriguing non-Abelian phenomena and applications associated with non-Abelian holonomy22,23,24,25,26,27,28,29, non-Abelian gauge fields30,31,32,33,34 and non-Abelian topological insulators35,36,37 have also been proposed.

Photonics is an ideal platform to study non-Abelian physics, since photons possess various degrees of freedom that can be exploited to realize non-Abelian gauge fields38,39 and associated non-Abelian phenomena. On the other hand, non-Abelian physics provides new application scenarios for photonics, especially integrated photonics, since the non-Abelian geometric phase matrix can be directly employed for on-chip applications that rely on matrix operations such as optical computing40 and quantum computing41. Current integrated photonic devices are typically designed based on dynamical phase associated linear optics principles42, which are resonant effects that lead to on-chip devices (e.g., directional couplers and microring resonators) exhibiting narrow working bandwidths and performances vulnerable to perturbations. The non-Abelian geometric phase matrix, arising from a non-resonant global effect that is protected by the topology of the system in Hilbert space15, manifests itself as an effective scheme to realize broadband and robust photonic chips20,26. Oriented on practical applications, the developed non-Abelian photonic devices must meet two key requirements: scalability and reconfigurability. The former has been recently demonstrated in various integrated platforms19,20,21,26,27,28, while the latter, that is, making non-Abelian devices reconfigurable such that one photonic circuit can be programmed to implement fruitful algorithms, remains out of reach, which hinders non-Abelian integrated photonics from further developments and practical applications.

Here, we propose a universal approach to reconfigurable non-Abelian integrated photonics and experimentally realize it in a double-layered polymer photonic chip. The proposed photonic chip performs the task of non-Abelian braiding of multiple photonic modes. It consists of multiple tunable two-mode braiding structures as building blocks, in which electrode heaters are introduced to tune the refractive index of specific waveguides and thus the holonomy-induced non-Abelian geometric phase matrix. By separately modulating each building block, reconfigurable non-Abelian braiding of multiple photonic modes can be realized in a single device. As a proof of concept, a four-mode non-Abelian braiding photonic chip was fabricated, and up to 24 unitary matrices (that form a permutation group S4) belonging to the braid group B4 have been realized in this single chip upon modulations. The proposed tuning scheme is expected to be implemented for other non-Abelian photonic devices towards abundant applications.

Results

Design of the reconfigurable non-Abelian photonic chip

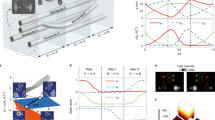
Figure 1a illustrates a schematic diagram of the proposed reconfigurable non-Abelian photonic chip, which is double-layered and mainly consists of four single-mode polymer waveguides A, B, C, and D (gray) located in layer II. The photonic chip is designed to realize the non-Abelian braiding of these four modes, i.e., the output and input of the chip are associated with a non-Abelian holonomy induced geometric phase matrix belonging to the braid group B443. To achieve this goal, some auxiliary waveguides (blue) and coupling waveguides (red) are introduced in layers I and II, respectively. At specific regions, electrode heaters (yellow) are placed on top of layer II, which can be exploited to tune the refractive index of the braiding waveguides (i.e., A, B, C, or D) and thus the braiding-induced geometric phase matrix. The chip consists of six sets of tunable two-mode braiding structure, which acts as building blocks.

Fig. 1: Schematic diagram of a reconfigurable non-Abelian photonic chip.
figure 1

a Schematic diagram of a double-layered polymer photonic chip which performs the task of non-Abelian braiding of four photonic modes located in waveguides A to D (gray), respectively, with the assistance of several auxiliary waveguides (blue) and coupling waveguides (red). The chip consists of six two-mode braiding structures as building blocks (dashed region), where electrode heaters (yellow) are introduced on top of the braiding waveguides to tune their refractive index via the thermo-optic effect. b An enlarged view of one building block, where an auxiliary waveguide (S) is placed in layer I, while braiding waveguides (A and B) and coupling waveguides (X1, X2, and X3) are located in layer II. The whole two-mode braiding process can be divided into steps I, II, and III, plus a crossing step for the repositioning of the waveguides. When electrode heaters are turned off, the braiding results in a swap of the two modes in waveguides A and B via a non-Abelian holonomy process. When electrode heaters are turned on, the refractive index of the braiding waveguides is significantly lowered down, leading to that the output and input are in the same braiding waveguide. c A braiding diagram of the photonic chip, where each green box represents a tunable two-mode braiding building block. The abbreviation “TB” is short for tunable block, which has two working conditions associated with two geometric phase matrices U2, depending on the modulation. By separately tuning the six TBs, a variety of unitary matrices associated with the braid group B4 can be achieved in this single chip.

Full size image

We study the physical mechanism of the chip by focusing on the tunable braiding building block. Figure 1b shows an enlarged view of one building block (i.e., the one enclosed by the dashed line in Fig. 1a) where two modes in waveguides A and B are braided. These two braiding waveguides, together with three coupling waveguides, namely X1, X2, and X3, are in layer II, while an auxiliary waveguide S is placed below them in layer I. The interlayer distance is 5.4 μm, and all the waveguides share the same rectangular cross section of 4.5 × 4 μm2. Apart from the input region, the process that light propagates in the building block can be mainly divided into three steps, while there is a crossing step between steps II and III for the repositioning of the waveguides. Since the refractive index contrast between the waveguide and the cladding is ~0.0144, light propagating in the paraxial waveguides can be described by a Hamiltonian

$$H\left(z\right)=\left[\begin{array}{cccc}{\beta }_{{{\rm{X}}}}(z) & {\kappa }_{{{\rm{AX}}}}(z) & {\kappa }_{{{\rm{BX}}}}(z) & {\kappa }_{{{\rm{SX}}}}(z)\\ {\kappa }_{{{\rm{AX}}}}(z) & {\beta }_{{{\rm{A}}}}(z) & 0 & 0\\ {\kappa }_{{{\rm{BX}}}}(z) & 0 & {\beta }_{{{\rm{B}}}}(z) & 0\\ {\kappa }_{{{\rm{SX}}}}(z) & 0 & 0 & {\beta }_{{{\rm{S}}}}(z)\end{array}\right],$$
(1)

where \({\kappa }_{{{\rm{AX}}}}\), \({\kappa }_{{{\rm{BX}}}}\) and \({\kappa }_{{{\rm{SX}}}}\) denote the position-dependent coupling strength between waveguides A, B, S, and Xi in the ith step (i = 1, 2, 3), respectively, and \({\beta }_{{{\rm{A}}}}\), \({\beta }_{{{\rm{B}}}}\), \({\beta }_{{{\rm{S}}}}\) and \({\beta }_{{{\rm{X}}}}\) are the propagation constant of the fundamental mode in the corresponding waveguides.

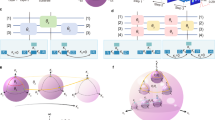
We first consider the situation that the electrode heaters are turned off. In this case, the diagonal terms of the Hamiltonian are constants, i.e., \({\beta }_{{{\rm{A}}}}\left(z\right)={\beta }_{{{\rm{B}}}}\left(z\right)={\beta }_{{{\rm{S}}}}\left(z\right)={\beta }_{{{\rm{X}}}}\left(z\right)={\beta }_{0}\), leading to a braiding result that the two modes in waveguides A and B are swapped. We focus on the wavelength of 1550 nm and show the fitted coupling coefficients in the upper panel of Fig. 2a (see Supplementary Note 1 and Supplementary Fig. 1 for fitting details). By enforcing this Hamiltonian with chiral symmetry13,19, the system supports four eigenmodes, as shown by their propagation constants in the lower panel of Fig. 2a. Among them, two photonic “zero” modes with \({\beta=\beta }_{0}\) are degenerate, forming a degenerate subspace in which the braiding takes place. The whole braiding process can be interpreted as follows. At step I, the waveguides A, X1, and S are coupled via a stimulated Raman adiabatic passage45, leading to a complete energy transfer from the waveguide A in layer II to S in layer I, in the form of a photonic “zero” mode. Meanwhile, the waveguide B is isolated so that a “zero” mode injected there remains there. Steps II and III follow the same principle. At step II, the waveguides A, X2, and B in the same layer II are so coupled to pump a “zero” mode from waveguide B to A, while the waveguide S is uncoupled. At step III, a “zero” mode is adiabatically transferred from the waveguide S to B with the help of X3, while another “zero” mode in waveguide A is isolated. The building block then accomplishes the task of two-mode braiding, i.e., the two injected modes in waveguides A and B are swapped. Figure 2b, c shows the calculated light intensity distributions in the building block when light is injected in the waveguides A and B, respectively, by employing a 3D finite-difference beam propagation method (RSoft 3DFD-BPM). The light trajectory and mode conversion behavior are in accordance with the above analysis.

Fig. 2: Physics of the tunable two-mode braiding building block.
figure 2

a The fitted coupling coefficients between adjacent waveguides (upper panel) and the calculated propagation constants \(\beta\) (lower panel) in the two-mode braiding building block when electrode heaters are turned off. The non-Abelian holonomy occurs following the flat band with \({\beta=\beta }_{0}\), resulting in a swap of the two modes supported in waveguides A and B. The simulated light intensity distributions in the two-mode braiding building block with electrodes turned off, when the input is via the waveguide A (b) and B (c). d The fitted diagonal terms of the Hamiltonian (upper panel) and the calculated propagation constants \(\beta\) (lower panel) in the two-mode braiding building block when the electrode heaters are turned on. Following the red and blue bands, a mode remains in the same waveguide where it is injected. The simulated light intensity distributions in the two-mode braiding building block with electrodes turned on, when the input is via the waveguide A (e) and B (f).

Full size image

These two processes exactly follow the double-degenerate flat band in Fig. 2a. Since the bending parts in waveguides A, B and S in the whole braiding process (including the crossing step) are judiciously designed to ensure that these three waveguides share the same total length, the two accumulated dynamical phases in the two braiding processes with “zero” modes are the same. In contrast, the non-Abelian holonomy gives rise to different geometric phases obtained in the two braiding processes. They are related to the off-diagonal terms of a 2 × 2 geometric phase matrix that can be calculated via \({U}_{2}={{\mathcal{P}}}\exp \left(i\int {A}_{{mn}}(\lambda )d\lambda \right)\{m={1,2},n={1,2}\}\), with \(\lambda\) and \({{\mathcal{P}}}\) being the evolution path and order, respectively, and \({A}_{{mn}}\left(\lambda \right)=i{{\langle }}{\psi }_{m}\left(\lambda \right)|{\partial }_{\lambda }|{\psi }_{n}\left(\lambda \right){{\rangle }}\) is the Berry connection matrix15. For this two-mode braiding, the geometric phases when injecting light in A and B are 2π and π, respectively. This leads to \({U}_{2}=\left[\begin{array}{cc}0 & -1\\ 1 & 0\end{array}\right]\) that satisfies \({U}_{2}|{\psi }_{{{\rm{A}}}}{{\rm{\angle }}}={|\psi }_{{{\rm{B}}}}{{\rm{\angle }}}\) and \({U}_{2}|{\psi }_{{{\rm{B}}}}{{\rm{\angle }}}=-|{\psi }_{{{\rm{A}}}}{{\rm{\angle }}}\) where \(|{\psi }_{{{\rm{A}}}}{{\rm{\angle }}}={[{\mathrm{1,0}}]}^{{{\rm{T}}}}\) and \({|\psi }_{{{\rm{B}}}}{{\rm{\angle }}}={[{\mathrm{0,1}}]}^{{{\rm{T}}}}\) are the eigenfunctions of the modes in waveguide A and B, respectively.

We turn to the situation that the electrode heaters are turned on. In this case, the braiding is avoided, meaning that the input and output are in the same waveguide (A or B). To realize this, four rectangular electrode heaters with a thickness of ~200 nm are used to tune the building block (see Fig. 1b). Two out of them are placed on top of the waveguide A at steps I and II, while the other two are put on top of the waveguide B at steps II and III. The refractive index of the waveguide and cladding adjacent to the electrode is significantly lowered down since the polymer material has a large thermo-optic coefficient of approximately −1 × 10−4/K (see Supplementary Fig. 2 for the induced refractive index distributions). As a result, the propagation constant of those waveguides near the electrode is no longer a constant. The upper panel in Fig. 2d shows the calculated heating-induced position-dependent diagonal terms of the Hamiltonian. We find that as expected, \({\beta }_{{{\rm{A}}}}\left(z\right)\) and \({\beta }_{{{\rm{B}}}}\left(z\right)\) at steps with electrodes are greatly changed, while \({\beta }_{{{\rm{X}}}}\left(z\right)\) is affected slightly. Since the waveguide S is sufficiently far away from the electrodes, \({\beta }_{{{\rm{S}}}}\left(z\right)={\beta }_{0}\) still holds (not represented in Fig. 2d). Although the off-diagonal terms (i.e., coupling strengths) are almost the same as those in Fig. 2a, the large detuning introduced in waveguides A and B associated with the diagonal terms can greatly change the eigenvalues of the Hamiltonian and thus the light transmission behavior, as the chiral symmetry is broken (see Supplementary Note 2 for a detailed theoretical analysis). The lower panel in Fig. 2d shows the calculated propagation constants of the two modes associated with waveguides A (red) and B (blue). We note that the original degenerate flat band is split into two nondegenerate bands with electrodes turned on, following which the light transportation remains in the same waveguide. This can be verified by Fig. 2e, f, which represents the calculated light intensity distributions with input in the waveguides A and B, respectively. We emphasize that the accumulated dynamical phases in these two processes are still the same, since the two bands are symmetric with respect to the center. Obviously, no geometric phase is obtained in this case, which leads to \({U}_{2}=\left[\begin{array}{cc}1 & 0\\ 0 & 1\end{array}\right]\). We also calculate the wave transmission by directly using the fitted Hamiltonian, and the results (see Supplementary Fig. 3) are found to match well with those in Fig. 2b, c, e, f.

After demonstrating the working mechanism of the tunable two-mode braiding building block, the reconfigurable functionality of the chip is easy to understand. Figure 1c shows a simplified schematic of the four-mode braiding chip, where each green box represents a tunable building block that has two working conditions and associated geometric phase matrices. By separately tuning these building blocks, a variety of unitary matrices associated with the braid group B4 can be realized in the same photonic chip. In what follows, we will experimentally demonstrate up to 24 unitary matrices that exactly form a permutation group S4.

Experimental demonstration of the two-mode braiding building block

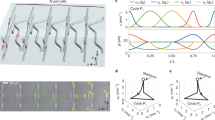
We fabricated the double-layered photonic chip using spin-coating, photolithography, and wet-etching processes in sequence (see Methods and Supplementary Fig. 4 for details). To characterize the modulation performance, we first fabricated three devices containing only steps I, II, and III of the building block, respectively (see Supplementary Fig. 5 for microscope images of the sample). The corresponding measured output light intensity images when a single waveguide was launched by a laser at 1550 nm (see the red arrows) are shown in Fig. 3a–c, respectively. We note that when the waveguide A is injected at step I (Fig. 3a), light exits mainly via the waveguide S with electrodes turned off, while it remains in the waveguide A by turning on the electrode heaters. At step II (Fig. 3b), a “zero” mode is adiabatically pumped from the waveguide B to A when the electrodes are turned off. By turning on them, in contrast, the mode remains in the injected waveguide (either A or B). At step III (Fig. 3c), the same phenomenon regarding the modulation occurs between the waveguides S and B.

Fig. 3: Experimental demonstration of the tunable two-mode braiding building block.
figure 3

a Measured output light intensity images of a structure featuring only step I with a laser of 1550 nm injected from the waveguide A, when the electrode heaters are turned off (upper panel) and on (lower panel). b Measured output light intensity images of a step II structure, where the input is from the waveguide B with electrodes turned off (upper panel), from the waveguide B (middle panel), or A (lower panel) with electrodes turned on. c Measured output images of step III, where light is injected from the waveguide S with electrodes turned off (upper panel) and from the waveguide B with electrodes turned on (lower panel). d Measured output light intensity images of the two-mode braiding structure when the electrode heaters are turned off (left column) and on (right column). In (a–d), the red arrows mark the waveguide in which light is injected. Measured transmission coefficients TA,A, TB,A, TA,B, and TB,B (see main text for definition) in the two-mode braiding building block as a function of wavelengths when the electrode heaters are turned off (e) and on (f).

Full size image

Since the three structures related respectively to the three steps work well, we combined them and fabricated a two-mode braiding building block. The experimentally measured output patterns at 1550 nm are shown in Fig. 3d. As expected, the output and the input are located in different waveguides with electrodes turned off, while they are in the same waveguide when all the electrode heaters are turned on. The applied driving power for each electrode heater is ~120 mW. The switching exhibits a response time of ~1 ms, primarily attributed to the low thermal conductivity inherent to polymer materials. The response time of the device can be further improved by employing the polymer/silica hybrid waveguide structure46.

We emphasize that since the braiding is a non-resonant effect which is protected by the system topology in Hilbert space, the geometric phase matrix and mode switching phenomenon are robust and apply to broadband wavelengths. To demonstrate this point, we measured the transmission coefficient Tj,i, defined as the light transmission from an input waveguide i to an output waveguide j {i,j = A,B}, in the wavelength range of 1500–1630 nm. The measured results by excluding the insertion loss and outcoupling effects are given in Fig. 3e, f, for the case when electrode heaters are turned off and on, respectively. We note that for the former case, the transmission coefficient TB,A (TA,B) is significantly higher than the crosstalk TA,A (TB,B) in the whole wavelength range of interest, with an average extinction ratio of ~17.2 dB (~14.4 dB). The situation is reversed when the electrode heaters are turned on, where the transmission coefficient TA,A (TB,B) is larger than the crosstalk TB,A (TA,B), with an average extinction ratio of ~17.8 dB (~14.2 dB). These experimental results clearly demonstrate the broadband feature of the proposed tunable two-mode braiding building block. As the multi-mode braiding device is consisted of multiple two-mode braiding building blocks, the proposed photonic chip can also work in broadband, as long as the waveguide fundamental mode is well supported in the wavelength of interest. A systematic study on the broadband and robust features is provided in Supplementary Note 3 and Supplementary Figs. 6−10.

Experimental demonstration of reconfigurable multi-mode non-Abelian braiding devices

The tunable building blocks can be cascaded to realize reconfigurable non-Abelian braiding of multiple photonic modes. We first take a three-mode non-Abelian braiding as example (see Supplementary Fig. 11 for the structure) and show the braiding diagram and experimentally measured output patterns of light intensity at the wavelength of 1550 nm in Fig. 4a–f. The device consists of three tunable blocks namely TB-1, TB-2 and TB-3. Figure 4a shows the case that all the electrode heaters are turned off. In this case, a mode injected from the waveguide A, B and C exits the device via the waveguides C, B and A, respectively, leading to a geometric phase matrix \({U}_{3}=\left[\begin{array}{ccc}0 & 0 & 1\\ 0 & -1 & 0\\ 1 & 0 & 0\end{array}\right]\) that connects the input and output via \(|{\psi }_{{{\rm{OUT}}}}{{\rm{\angle }}}={U}_{3}|{\psi }_{{{\rm{IN}}}}{{\rm{\angle }}}\), with the input \(|{\psi }_{{{\rm{IN}}}}{{\rm{\angle }}}\) being \(|{\psi }_{{{\rm{A}}}}{{\rm{\angle }}}={[{\mathrm{1,0,0}}]}^{{{\rm{T}}}}\), \(|{\psi }_{{{\rm{B}}}}{{\rm{\angle }}}={[{\mathrm{0,1,0}}]}^{{{\rm{T}}}}\) or \(|{\psi }_{{{\rm{C}}}}{{\rm{\angle }}}={[{\mathrm{0,0,1}}]}^{{{\rm{T}}}}\). By exerting modulations, the proposed device can be reconfigured to realize various geometric phase matrices belonging to the braid group B3. Figure 4b–d shows the cases that only the TB-1, TB-2 or TB-3 is turned on, where the geometric phase matrix is correspondingly changed to be \(\left[\begin{array}{ccc}0 & -1 & 0\\ 0 & 0 & -1\\ 1 & 0 & 0\end{array}\right]\), \(\left[\begin{array}{ccc}1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & -1\end{array}\right]\) or \(\left[\begin{array}{ccc}0 & 0 & 1\\ 1 & 0 & 0\\ 0 & 1 & 0\end{array}\right]\), respectively. When the TB-1 and TB-2 are simultaneously turned on, a geometric phase matrix \({U}_{3}=\left[\begin{array}{ccc}1 & 0 & 0\\ 0 & 0 & -1\\ 0 & 1 & 0\end{array}\right]\) is obtained (Fig. 4e). Another configuration \({U}_{3}=\left[\begin{array}{ccc}0 & -1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 1\end{array}\right]\) can be accessed by simultaneously turning on the TB-1 and TB-3 (Fig. 4f). When considering the mode switching behavior only (that is, without the phase information), the above six group elements in Fig. 4a–f form a permutation group S3. The corresponding geometric phase matrices for each case are summarized in Supplementary Table 1.

Fig. 4: Experimental demonstration of a reconfigurable three-mode non-Abelian braiding device.
figure 4

a Measured output light intensity images of a reconfigurable three-mode non-Abelian braiding device consisting of three TBs at 1550 nm, when all the TBs are turned off. b–f Experimental results of the three-mode non-Abelian braiding device when some of the TBs are turned on (see the braiding schematic for details). The red arrows mark the waveguide in which light is injected.

Full size image

The principle can be expanded to achieve the reconfigurable non-Abelian braiding of more photonic modes. We come back to the four-mode non-Abelian braiding photonic chip illustrated in Fig. 1a. The braid group B4 has three generators: \({\sigma }_{1}\), \({\sigma }_{2}\), and \({\sigma }_{3}\), which can be realized using a two-mode braiding building block with waveguides A and B (see Fig. 1b), B and C, and C and D, respectively. With these definitions, the group element representing the reconfigurable device in Fig. 1a is given by \({({\sigma }_{1})}^{{n}_{1}}{({\sigma }_{3})}^{{n}_{2}}{({\sigma }_{2})}^{{n}_{3}}{({\sigma }_{1})}^{{n}_{4}}{({\sigma }_{3})}^{{n}_{5}}{({\sigma }_{2})}^{{n}_{6}}\), where each \({n}_{i}\in \{{\mathrm{0,1}}\}\) depends on whether the corresponding electrode heater TB-i is turned on (\({n}_{i}=0\)) or off (\({n}_{i}=1\)). In this way, our device can be reconfigured to realize a total of 26 = 64 settings of braiding operations. In our experiment, we choose 24 settings out of them by turning on at most three sets of electrode heaters simultaneously. These 24 unitary transformations also form a permutation group S4. Figure 5 shows the experimentally measured light output patterns of 9 settings by exerting different modulations (see the inset for details), while the experimental results for the other 15 settings where one, two and three building blocks are turned on, are given in Supplementary Figs. 12–14, respectively. The corresponding geometric phase matrices for each case are given in Supplementary Table 2.

Fig. 5: Experimental demonstration of a reconfigurable four-mode non-Abelian braiding device.
figure 5

a–i Measured output light intensity images of a reconfigurable four-mode non-Abelian braiding device consisting of six TBs at 1550 nm, when some of the TBs are turned on (see the braiding schematic for details). The red arrows mark the waveguide in which light is injected. These results, together with the experimental results in Supplementary Figs. 12–14, demonstrate that the device can be reconfigured to achieve a fruitful set of four-mode non-Abelian braiding.

Full size image

The braid group B4 is an infinite group, and a general element can be written as \({({\sigma }_{1})}^{{n}_{1}}{({\sigma }_{2})}^{{n}_{2}}{({\sigma }_{3})}^{{n}_{3}}{({\sigma }_{1})}^{{n}_{4}}{({\sigma }_{2})}^{{n}_{5}}{({\sigma }_{3})}^{{n}_{6}}\ldots\), where \({n}_{i}{\mathbb\,{\in }}{\mathbb\,{Z}}\). A universal solution could be a reconfigurable device in which six tunable building blocks associated with the six basic braids of the group are cascaded in sequence, i.e., \({\sigma }_{1}\), \({\sigma }_{1}^{-1}\), \({\sigma }_{2}\), \({\sigma }_{2}^{-1}\), \({\sigma }_{3}\), and \({\sigma }_{3}^{-1}\), where the inverse braids (i.e., \({\sigma }_{1}^{-1}\), \({\sigma }_{2}^{-1}\), \({\sigma }_{3}^{-1}\)) can be realized by simply reversing the device structure of Fig. 1b along the x axis. By controlling the array of electrode heaters according to the values of \({n}_{i}\) and repeatedly feeding back the output of the device to the input in situ using auxiliary circuits (see Supplementary Fig. 15 for a schematic), the reconfigurable non-Abelian braiding device can in principle realize any element associated with the braid group B4. In addition, by adding or removing necessary working waveguides (i.e., gray ones in Fig. 1a), a reconfigurable braiding belonging to a general braid group Bi can also be achieved. These results and outlook demonstrate the scalability and versatility of the proposed reconfigurable approach.

At last, we discuss how to eliminate the dynamical phase effect in the reconfigurable non-Abelian braiding process. In the design in Fig. 1a, we have introduced various bending to the braiding waveguides A to D, to guarantee that they share the same total length (see Supplementary Fig. 16 for details). In this sense, the accumulated dynamical phase for each working mode is solely related to the propagation constant, which is always equal to \({\beta }_{0}\) except in the building block with electrodes turned on (see Fig. 2d). To tackle such difference, one can introduce an extra electrode heater for each braiding waveguide after each braiding step. By turning on specific electrode heaters, the difference of the dynamical phase accumulation in different braiding waveguides could be compensated (see Supplementary Fig. 17 for details).

Discussion

Beyond non-Abelian braiding associated with the braid group, our reconfigurable approach can also realize reconfigurable unitary matrices belonging to the SO(N) group, which can be employed for various matrix related applications. A scalable approach utilizing arrays of tripod-configured photonic waveguides has been experimentally demonstrated in femtosecond-laser-written photonic chips27, with subsequent implementation extended to the silicon nitride platform20. By implementing our reconfigurable approach to these devices, the geometric phase matrix associated with the SO(N) group has the potential to be tuned continuously, since the thermal effect induced refractive index change is continuous. By replacing conventional tunable Mach-Zehnder interferometers with these reconfigurable units based on continuous non-Abelian groups, the resulting broadband and robust non-Abelian device may also enable novel deep learning applications47.

To conclude, we have proposed a universal solution to reconfigurable non-Abelian integrated photonics by employing the thermo-optic effect to tune the refractive index of photonic waveguides, leading to a change in the Hamiltonian of the system and therefore the generated non-Abelian geometric phase matrix. We have demonstrated the concept in a double-layered polymer photonic chip that performs the task of non-Abelian braiding of multiple photonic modes. The multi-mode non-Abelian braiding chip consists of multiple tunable two-mode braiding structures as building blocks. Reconfigurable three-mode and four-mode non-Abelian braiding have been experimentally realized in a single device by judiciously exerting modulations on specific building blocks. The versatile and scalable platform can realize the reconfigurable non-Abelian braiding of an arbitrary number of photonic modes. Since the polymer waveguide used in our experiments exhibits a non-negligible propagation loss for light, we have only demonstrated the application of the reconfigurable photonic device for manipulating classical light in this work. By replacing our material with lower-loss polymers48, the proposed platform may be employed for quantum applications in the future. The proposed idea can also be employed for the design of other types of reconfigurable non-Abelian devices such as non-Abelian Thouless pumps24,26,28. It is also expected to expand the idea to other integrated platforms such as silicon photonics and lithium niobate photonics towards the design of robust and broadband on-chip non-Abelian photonic devices.

Methods

Sample fabrication and measurement

The proposed device was fabricated using standard ultraviolet (UV) photolithography, spin-coating and wet-etching procedures. Supplementary Fig. 4 shows the fabrication process of the device. The dimensions of the waveguides can be controlled precisely by adjusting the exposure time and spin-coating speed. First, a 5 µm-thick EpoClad polymer film was spin-coated on the Si substrate and cured at 120 °C for 5 min to remove the solvent, then the wafer was exposed by UV lithography machine (ABM Co. Inc., USA) at 15 mW/cm2 for 10 s and cured at 120 °C for 30 min to enhance the material cross-linking. A 4 µm-thick lower-core layer was formed onto the sample by spin-coating, and the pattern of the device was transferred from a properly designed chromium mask to the core layer by conventional contact photolithography and wet-etching. The sample was then covered with a 1.4 µm-thick EpoClad middle-cladding. After that, a 4 µm-thick upper-core layer was prepared by the same fabrication process as the lower-core layer. In this step, the upper-layer was carefully positioned to guarantee the precise alignment to the lower-layer. The sample was then coated with a 4.0 µm-thick EpoClad upper-cladding. Finally, a 0.2 µm-thick Al thin film was deposited onto the sample by thermal evaporation, and the electrode heaters were patterned using UV lithography and wet-etching. The propagation loss of light in the fabricated waveguide is ~1.9 dB/cm, which can be further reduced by leveraging lower-loss polymers48. The fiber-waveguide coupling loss is ∼1.4 dB in the measurement.

To characterize the performance of the fabricated device, the light from a tunable semiconductor laser (TSL-510, Santec) was launched into the input waveguide of the device through a single-mode fiber. At the output end, the output power was monitored by an optical power meter (2832-C, Newport) through a single-mode fiber, and the output near-field patterns were obtained by using an infrared charge-coupled device (CCD) camera (C2741-03, Hamamatsu). The driving voltage from a direct-current source was applied to the electrode heater via two metal probes.

Numerical simulations

Model Hamiltonian

The fitted coupling strengths (i.e., the off-diagonal terms of the Hamiltonian) in the upper panel of Fig. 2a are obtained by calculating the propagation constants of a corresponding two-waveguide system (see Supplementary Note 1 and Supplementary Fig. 1 for details). The on-site energies of the system (i.e., the diagonal terms of the Hamiltonian) with electrodes turned on, shown in the upper panel of Fig. 2d, are obtained using the following procedure. We first calculate the temperature distribution with the electrode heater by using a finite element method. A typical result is shown in Supplementary Fig. 2. The modified distribution of the refractive index in the device can then be obtained by considering the thermo-optic coefficient of the polymer material (approximately −1 × 10−4/K). Then we consider the proposed two-mode building block in which the distance between the electrode heater and the waveguide (A, B, or X) varies along the waveguiding direction. We study the three waveguides respectively. For each waveguide, we choose a variety of cross sections along the waveguiding direction and calculate the effective mode index of the fundamental mode in the corresponding waveguide (A, B, or X) by using the heating-induced refractive index distribution. In this regard, we obtain modified \({\beta }_{{{\rm{A}}}}(z)\), \({\beta }_{{{\rm{B}}}}(z)\), and \({\beta }_{{{\rm{X}}}}(z)\), as shown in the upper panel of Fig. 2d. In addition, \({\beta }_{{{\rm{S}}}}(z)\) is the same as the case without heating since the waveguide S is sufficiently far away from the electrode heater. The coupling strengths are assumed the same as the case without the electrode heater, since the heating only affects the effective mode index, while the eigenfield profile is nearly not changed. In this way, we have obtained the modified Hamiltonian with electrode heaters turned on.

Eigenvalues of the system

The lower panels of Fig. 2a, d are obtained by using the finite element method, i.e., we calculate the propagation constants in a variety of cross sections along the waveguiding direction. In fact, we can also calculate the eigenvalues by directly solving the model Hamiltonian (i.e., upper panels of Fig. 2a, d). The corresponding results are found to be almost the same as the results in the lower panels of Fig. 2a, d, indicating that the fitted Hamiltonian works well for the proposed system.

Simulation of light transmission in the device

The fitted Hamiltonian is then used to simulate the wave dynamics in the system by solving the Schrödinger-like equation \(H\left(z\right)|\phi \left(z\right){{\rm{\angle }}}=-{j\partial }_{z}|\phi \left(z\right){{\rm{\angle }}}\), where \(H(z)\) is the position-dependent Hamiltonian and \(|\phi \left(z\right){{\rm{\angle }}}\) is the state vector. The corresponding numerical results are given in Supplementary Fig. 3. For comparison, we also simulate the wave transmissions in the paraxial waveguides directly using a beam propagation software RSoft (e.g., results in Fig. 2b, c, e, f). All these numerical results match each other well, and are also consistent with experimental results.