Introduction

Manipulation of single atoms or molecules promotes a “quantum leap” in the fabrication of designer quantum materials that are otherwise challenging to achieve with conventional material growth approaches1,2,3. Compared to atoms/molecules, manipulating single charges, including both electrons and holes, opens up a platform for yet more appealing synthetic strategies4, which allows quantum simulations of prototypical theoretical models5,6, designing atomic-scale charge/spin devices7, tailoring chemical reactions at single electron level8, etc. Nevertheless, the laws of quantum mechanics dictate the motion of single charges, making their manipulation less straightforward compared to the manipulation of single atoms and molecules. Meeting that goal requires the feasibility of getting individual electrons or holes trapped at the atomic limit and ultimately assembling them one-by-one in a controlled manner.

Polaron, as a composite quasiparticle of excess electron or hole dressed with local lattice distortion, can trap the excess charge into a potential well, which is induced by anti-adiabatic displacements of adjacent ions due to strong electron–phonon coupling9,10,11. Polarons govern multiple physicochemical processes, influencing charge transport12, surface reactivity13, catalytic activity14, thermoelectric and multiferroic functionality15,16, etc. Small polarons can confine excess charges into one atomic lattice10, making them ideally suited for positioning embedded electrons or holes at atomic precision. However, due to the Coulomb repulsion between like charges, the same category of polarons repel each other, preventing the assembly of the same charges in close proximity. Only under rare circumstances of strong electron–phonon coupling and/or large dielectric screening, may two charges share the same trapping potential of lattice distortions to form a bipolaron17,18. Bipolarons have attracted extensive interest, owing to their critical roles in material dynamics and superconducting pairing19,20. Multipolaron, which contains multi-charges trapped in the same potential, has been theoretically proposed to exist21,22,23, but has never been observed in experiments to the best of our knowledge.

Previous experimental probes on bipolarons are mainly based on ensemble-averaged techniques, including optical spectroscopy24, electron spin resonance25, electrical transport26, angle-resolved photoemission spectroscopy27, and neutron scattering28, etc. Despite their important results, signals of bipolarons are frequently entangled with coexisting monopolarons, and the interpretation is not straightforward. In contrast, scanning tunneling microscopy (STM) allows atomic-resolution imaging, spectroscopic characterization, and tip manipulation of atomic species on surfaces, which is ideal to investigate individual polarons29,30, bipolarons and potential multipolarons. Recently, polarons and bipolarons have been observed on the polar surface of KTaO3(001) with STM31.

Here, using STM, we report the creation and spectroscopic characterization of the multipolaron in a monolayer insulator, CrBr3. They are crafted by assembling single monopolarons one-by-one with the STM tip, whose contained electron number reaches nine but can be larger. All multipolarons exhibit polaronic states and increased local upward band bending with increased apparent charge. Notably, the apparent charge can be noticeably smaller than the electron number. As is unveiled with first principles calculations, this discrepancy comes from the formation of a polaron–exciton droplet, wherein the multipolaron binds holes from the substrate and forms excitons, significantly releasing the inner Coulomb repulsion. Our work provides critical insights into the many-body physics of polarons at the atomic limit.

Results and discussion

The experiments were performed with a Unisoku 1300 STM system at 4.2 K32. Monolayer CrBr3 films are grown by molecular beam epitaxy on a highly oriented pyrolytic graphite (HOPG) substrate. The topography and atomic resolution STM images of the HOPG and monolayer CrBr3 indicate high sample crystalline quality (Supplementary Fig. 1a–d). The first principles calculations are carried out by VASP with the hybrid functional method.

HOPG is the substrate of choice, which is a layered semimetal with low carrier density and excellent chemical stability33. Those properties render it an ideal substrate for the growth of two-dimensional (2D) materials, such as the CrBr3 here, because (1) The interface is of weak van der Waals interactions with minute influence from the lattice mismatch and no dangling bonds; (2) The low carrier density of HOPG minimizes its screening effect on the grown 2D materials.

CrBr3 is a layered van der Waals ferromagnet, whose magnetism persists to the monolayer limit34, and exhibits a magnetic transition in its bilayer depending on the interlayer stacking configuration35. Each layer consists of one Cr layer sandwiched by two Br layers, the Br (Cr) layer forms a triangle (honeycomb) lattice (Supplementary Fig. 2a). The apparent height of monolayer CrBr3 on HOPG (7.9 ± 0.15 Å) is larger than its actual value (6.3 Å) (Supplementary Fig. 2b, c), reflecting the vdW gap at the interface36,37. Its STM image resolves a triangular lattice of characteristic trimer-shaped units, whose lattice constant (6.36 ± 0.04 Å) is consistent with the previous report35. Each trimer is composed of three top-layer Br anions centered on the hollow site of Cr cations (Supplementary Fig. 2b, insert). Conductance spectra of the monolayer CrBr3 exhibit an insulating gap that conforms to the previous report35, with spatial uniformity (Supplementary Fig. 1e).

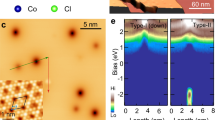
There are some dark entities randomly distributed over the CrBr3 surface (Fig. 1a, Supplementary Fig. 3 and Supplementary Note 1), whose population density increases with elevating the substrate temperature during the sample growth (Supplementary Fig. 4). Those dark entities are monopolarons, instead of crystal defects, since their surrounding lattices are intact (Supplementary Figs. 5, 6), and further evidenced below. A 2D conductance plot (Fig. 1b) acquired traversing a typical monopolaron features an upward band bending of the conduction band, implying it is negatively charged and thus is attributed as an electron polaron. While the valence band edge is invisible within the measured spectroscopic range, the in-gap state is prominently seen, which is ascribed to a polaronic state. In accordance with the induced upward local band bending and the polaronic state, STM images of the polaron appear as a bright spot at the polaronic state energy and a depression that shrinks in size with increasing bias from 0.8 to 1.4 V (Supplementary Fig. 7). At a low bias of −0.8 V, the polaron becomes a tiny dark spot without notable local lattice distortions (Supplementary Fig. 5), suggesting it is a small polaron. By superimposing the atomic lattice structure onto the STM image, the monopolaron is determined as occupying the Cr-site (Supplementary Figs. 5, 6).

Fig. 1: Spectra and manipulations of monopolarons.
figure 1

a STM image showing two naturally formed monopolarons as marked by black arrows. b Constant height 2D conductance plot taken across a monopolaron as indicated by a white arrow in (a). A white arrow indicates the polaronic state. Spectroscopic condition: Vs = 1 V, It = 50 pA, Vmod = 40 mV. c STM image showing the creation of a monopolaron as indicated by the red arrow. d STM image showing the movement of the created monopolaron, whose original location and moving trajectory are marked with a red dashed circle and an arrow, respectively. From (d) to (a), the polaron is erased, and its original location is marked with a yellow dashed circle in (a). Scanning conditions for (a, c, d): Vs = 1 V, It = 10 pA.

Full size image

The monopolarons can be more directly evidenced by their manipulation, including the creation, movement and erasure with ~96% success rate. This contrasts with the low success rate of manipulating defects38. Approaching the tip towards a polaron-free region (Fig. 1a) with a bias of 1.8 V causes the current to exponentially increase until it jumps (Supplementary Fig. 8a), signifying the polaron creation (Fig. 1c). The created monopolaron is identical to the naturally formed ones. Upon positioning the tip above a monopolaron at 1.8 V while keeping a constant current, the tip height switches between two discrete values, resulting in a telegraph-like noise. Such switching is caused by the polaron hopping between two neighboring Cr-sites (Supplementary Fig. 9a–c). By counting the number of times the polaron hops within 1 min, we can obtain its hopping frequency, which statistically gives an average value. The hopping frequency (R) and the tunneling current (I) follow the relation of \(R\propto {I}^{N}\) with the fitting parameter N ~ 1, demonstrating that the electron hopping is activated by an inelastic electron tunneling process (Supplementary Fig. 9d and Supplementary Note 2). This inelastic electron-driven hopping allows the polaron to stably follow the tip trajectory at 1.8 V/10 pA, thus controllably moving the polaron with low tip speeds (Fig. 1d). At the tip speed exceeding 4.8 nm/s, the polaron cannot follow the tip anymore (Supplementary Fig. 10 and Supplementary Note 3). Compared to creation, the polaron can also be erased by approaching the tip towards it even further at 1.8 V with disabled feedback (Fig. 1a and Supplementary Note 4), ruling out that it’s a crystal defect. We note that similar manipulations can be realized with negative bias settings, as is exemplified in Supplementary Fig. 8b for the polaron erasure under −1 V. The various manipulation conditions are summarized in Supplementary Table 1. The atomic lattice in the same field of view remains intact before and after the creation, movement and erasure of the polaron (Supplementary Fig. 11), further augmenting that it is not a crystal defect. We speculate that the electric field generated from the tip may reduce the barrier for the electron transfer into or out of the Cr-site, creating or erasing the polaron. On the other hand, the in-plane barrier involved in the polaron motion is much smaller.

Having characterized monopolarons, we study their mutual interactions. With the above manipulation protocol, we assemble monopolarons one-by-one into a multipolaron, whose electron number characterizes the number of contained monopolarons. This approach makes it feasible to craft multipolarons with any desired electron numbers without the signature of limitations. In our experiment, up to 9 electrons are assembled into a multipolaron. Figure 2a, b shows STM images before and after crafting three typical multipolarons, containing 1, 2, and 3 electrons, respectively. Superimposing the atomic structure model of CrBr3 unveils that the bipolaron occupies Cr-sites of nearest neighbors (Supplementary Fig. 12) that are 3.7 Å apart, demonstrating the multipolaron is of intersite type39. Their apparent depths deepen with the increasing electron number, suggesting their enhanced local band bending (Fig. 2b, inset and Supplementary Note 5). Indeed, the amount of upward band bending increases monotonically with the increasing electron number, and the polaronic state concomitantly shifts upward in energy (Fig. 2c, d). At the energy of the polaronic states, the multipolarons appear as bright protrusions, whose apparent heights increase with their contained electron number (Supplementary Fig. 13). Those observations conform to the enhanced Coulomb energy with the increasing electron number in the multipolaron. As such, the apparent depth of the multipolaron at a certain bias hallmarks its contained electron number. In the following, we choose a fixed bias of 1 V to characterize the apparent depth of the multipolaron.

Fig. 2: Assembly and spectra of multipolaron.
figure 2

a, b STM images (Vs = 1 V, It = 10 pA) of the same region of monolayer CrBr3 before (a) and after (b) the assembly of a monopolaron, a bipolaron and a tripolaron. The multipolarons in (b) are assembled with the monopolarons in (a) circled with corresponding colors, the inset shows the height profile of the multipolarons taken along the red line. c Constant height 2D conductance plot of the multipolarons, that is taken along the red line in (b). Two white arrows indicate the polaronic states of bipolaron and tripolaron, respectively. d Tunneling spectra taken on the centers of the monopolaron, bipolaron, tripolaron, and polaron-free area. Spectroscopic condition for (c, d): Vs = 1 V, It = 100 pA, Vmod = 40 mV. Note that the polaronic state of monopolaron in (d) is absent, due to the smaller spectroscopic range compared with that in Fig. 1b.

Full size image

Apart from the generation of multipolarons through assembling monopolarons, it can also be directly created upon a larger tip electric field applied to the surface, and the number of electrons in the created multipolarons is positively correlated with the tip electric field (Supplementary Figs. 14, 15 and Supplementary Note 6). Once the multipolaron is assembled, it can be moved with the STM tip as a whole entity. However, the multipolaron containing larger electron numbers is more difficult to move and becomes unmovable upon the contained electron number exceeding 5. Nevertheless, if the tip is moving fast, the multipolaron can be separated into individual monopolarons (Supplementary Fig. 16). This makes it possible to assemble and disassemble the multipolaron reversibly.

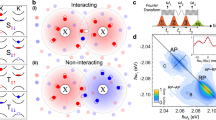
When moving the multipolaron, we found that a given multipolaron may change to several shallower apparent depths, implying its apparent charge is reducible (Fig. 3a–e). As such, apart from the electron number depicting the contained monopolarons in a given multipolaron, another characterizing parameter is its expressed apparent charge, which is determined from its induced band bending and its associated apparent depth at 1.0 V (Supplementary Note 7). Figure 3a shows three spatially separated monopolarons. Two of them are assembled into a bipolaron, which appears obviously darker than the monopolaron (Fig. 3b). However, moving the bipolaron occasionally changes its apparent depth to the same as that of the monopolaron (Fig. 3c), demonstrating that its apparent charge is reduced to one. Moreover, the polaron can be separated into two individual monopolarons again with tip manipulation (Fig. 3d). This demonstrates the polaron still contains two electrons, instead of a partial erasure of charge (Supplementary Note 8), as is also confirmed in a tetrapolaron (Supplementary Fig. 17) and a pentapolaron (Supplementary Fig. 18). Similar apparent charge reduction behaviors, as are also confirmed from tunneling spectra (Supplementary Note 9 and Supplementary Fig. 17), are observed in all the multipolarons containing up to nine electrons (Supplementary Table 2).

Fig. 3: Apparent charge reduction behavior of multipolaron.
figure 3

a–d STM images (Vs = 1 V, It = 10 pA) showing the sequence of assembling and disassembling a bipolaron. The white circles mark the bipolaron and its two monopolarons. e Height profiles were taken at the corresponding-colored arrows in (a–c), and the horizontal dashed lines indicate the depth of the monopolaron. f Statistics showing the apparent depth of a pentapolaron during many sequences of lateral manipulations. The dashed lines represent the averaged apparent depths of the multipolarons with indicated apparent charges. g Histogram of the statistics in (f).

Full size image

Notably, irrespective of the increasing electron number, the apparent charges of those multipolarons are limited to ≤ 5. Moreover, the multipolarons exhibiting reduced apparent charge are still difficult to move, implying the amount of local lattice distortions may not change and further ruling out the possibility of partial erasure of charge. To scrutinize the apparent charge reduction behavior, we performed statistics over the apparent charge distribution histogram of a given multipolaron upon tens of tip disturbances. As is exemplified in Fig. 3f, g, the apparent depth of a pentapolaron exhibits several discrete values corresponding to the apparent charges of 2–5. Statistics on the apparent charges of bipolaron, tripolaron, and tetrapolarons are shown in Supplementary Figs. 19–21.

Density functional theory40 is used to understand the formation and apparent charge reduction of a multipolaron. The electronic densities of states of the polaron-free region and multipolarons are calculated in Fig. 4a. CrBr3 monolayer is a 3 eV gap insulator (Supplementary Fig. 22), of which the conduction band minimum (CBM) and valence band maximum are dominated by Cr-d and Br-p orbitals. The polaron levels are located at −0.8, −0.6, and −0.4 eV below CBM for mono-, bi-, and tri-polaron, and all the electrons of multipolarons occupy the Cr-\({d}_{{z}^{2}}\) orbital. We tested the hybrid functional mixing factor α from 0.20 to 0.40 and consistently found a stable polaronic state (Supplementary Table 3). The stability of the multipolaron depends on the balance between the Coulomb repulsion and the coherence of the phonon field41. If the potential energy lowering due to the phonon field coherence exceeds the Coulomb repulsion increase due to the assembling of electrons, the multipolaron will be stabilized with an inner attraction. However, taking the bipolaron as an example, we find that the Coulomb repulsion is stronger than the phonon field coherence (Supplementary Fig. 23 and Supplementary Note 10). In Fig. 4b, the formation energy of a bipolaron monotonically reduces as a function of electron-electron distance, indicating a repulsive interaction. Notably, the influence of finite supercell size has already been ruled out (Supplementary Fig. 24).

Fig. 4: Electronic structure, energy, and transition barrier of multipolaron.
figure 4

a Electronic density of states of the polaron-free region and multipolarons. Conduction band minima are set as zero. The black triangles denote the highest polaron levels. Insets show the multipolaron wavefunctions. The light blue, the dark blue and the orange spheres represent the top Br atoms, the Cr atoms and the bottom Br atoms, respectively. The yellow clouds represent the negatively charged wavefunctions. b The bipolaron formation energy as a function of electron–electron distance. The energy of the nearest (first) neighbor bipolaron is set to zero. Inset defines different bipolaron configurations. c The hopping barrier of a monopolaron between two nearest-neighbor Cr sites. d The separation barrier of a bipolaron beyond which one electron can jump from the nearest neighbor to the second nearest neighbor of the other electron. The wavefunction of the initial (final) state is shown in the blue (red) inset panel. Configuration coordinate is an even interpolation of the polaron distortion from initial (0.0) to final (1.0) states, and the vertical axis shows the energy. Black circles are the calculated results, and the blue/red lines are quadratic fittings.

Full size image

In the experiments, the stability of multipolarons can be attributed to two key factors: (1) the significant energy barrier associated with polaron hopping between neighboring Cr-sites, and (2) the stabilizing effect of the graphene substrate through its screening mechanism. Regarding the energy barriers, the hopping barrier for a single polaron is 270 meV (Supplementary Fig. 25 and Supplementary Note 11), while the separation barrier for a bipolaron is 220 meV (Fig. 4c, d). Both values far exceed the thermal energy at the experimental temperature of 4.2 K, effectively preventing the multipolarons from diffusing once they are formed via STM manipulation. The screening effect of the graphene substrate also plays a crucial role in stabilizing multipolarons. This is evidenced by the experimental observation that assembling a multipolaron becomes infeasible on the second layer of CrBr3, where the influence of the substrate is much weakened (Supplementary Fig. 26). Using a model detailed in the supplementary information (Supplementary Fig. 27 and Supplementary Note 12), we incorporated the screening effect of the graphene substrate and found that the energy of a bipolaron in the CrBr3 monolayer reaches a minimum at an electron–electron distance of \(d=5.4 \,{{\text{\AA}}}\), comparable to the experimentally observed \({d}_{\exp }=3.7\,{{\text{\AA}}}\). This indicates that the substrate screening weakens the repulsive interaction between polarons, thereby enhancing the stability of the multipolaron system. While substrate screening affects the long-range Coulomb repulsion in multipolarons, it has a limited impact on individual polaron configurations due to the short-range nature of electron–phonon coupling in small polarons. Despite contributing to the stability of multipolarons, the substrate can never fully screen the multipolaron charges since graphene is a semimetal. The polaron levels will rise with the increase of electron number \(N\), so there must exist a critical electron number \({N}_{{{\rm{C}}}}\), above which the polaron level goes above the Fermi level to cause a destabilization. We infer\(\,{N}_{{{\rm{C}}}}=5\) from the experiments, as indicated in Supplementary Table 2, at which the apparent depth of multipolaron reaches saturation.

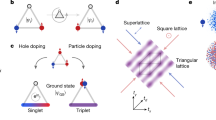
The variation in apparent depth suggests changes in the net charges within the multipolaron. A multipolaron assembled by \(N\) electrons, while exhibiting a reduced apparent charge, can always be decomposed into exactly \(N\) individual monopolarons, indicating strict conservation of electron number. The apparent charge reduction must therefore originate from the binding of holes, forming a compensated quasiparticle state. To explain this, we propose a scenario in which the polarons are coupled to local holes in the graphite substrate, which is a half-filled semimetal with the existence of free holes (Supplementary Fig. 28), offering a possible mechanism for the observed variation in apparent charge. Specifically, a positive hole at the Fermi level is captured by the negative polaron, forming an exciton-like42 pair, as illustrated in Fig. 5. This state, which contains both polarons and excitons, is referred to as a polaron–exciton droplet. It comprises self-trapped electrons (multipolarons) bound to a smaller number of holes naturally supplied by the semimetallic graphite substrate. In this configuration, no free electron-hole pair needs to be pre-excited (e.g., to overcome the band gap), thereby avoiding the associated energy cost and stabilizing the polaron-exciton droplet as a ground state (see Supplementary Note 13), or at least as a long-lived metastable state. The energetic stability of the polaron-exciton droplet can be considered from the interplay between two effects: the recombination of excitons reduces the internal Coulomb repulsion of the multipolaron, but it also eliminates the exciton binding energy associated with the recombined polaron-hole pair. Experimental observations indicate that the exciton binding energy exceeds the internal Coulomb repulsion, so that the system energetically favors the coexistence of polarons and holes. Thus, the polaron-exciton droplet stands in contrast to conventional phonon-dressed excitons, which are charge-neutral, photoinduced by external illumination, and typically exhibit short lifetimes43,44,45.

Fig. 5: Polaron–exciton droplet.
figure 5

Multipolaron changes net charges and apparent depth by capturing a hole. Band energy (vertical axis) changes as a function of position (horizontal axis) due to band bending, reaching the maximum at the multipolaron position. The Fermi level (\({E}_{{{\rm{F}}}}\)) is denoted by a black dashed line at the Dirac point. a, b Illustrate the multipolaron (polaron–exciton droplet), which is an unstable (stable) state above (below) the \({E}_{{{\rm{F}}}}\) without (with) capturing a hole through exciton binding.

Full size image

Multipolarons with larger \(N\) are easier to capture holes and even capture more than one hole in line with the observed apparent charge reduction, enabling a multipolaron with \(N\) > 5 to exist. On the other hand, too many holes give rise to hole–hole repulsion and increase the total energy. Thus, beyond the saturation limit \({N}_{{{\rm{C}}}}=5\), there should exist a lower limit on the apparent depth associated with the maximum hole number. As shown in Supplementary Table 2, the maximum hole number depends on the size of the multipolaron.

As observed experimentally, the polaron-exciton droplets exhibit limited mobility under the influence of the STM tip. This is likely because the tip-induced electric field primarily affects the upper Br atoms, which are directly involved in the manipulation of multipolarons. In contrast, the holes stay in the substrate and couple to the lattice via the lower Br atoms, which lie farther from the tip and are therefore less responsive to its electric field. This asymmetric coupling results in an additional “pinning force” from the hole side, making the entire droplet more resistant to lateral displacement and increasing the energy barrier for motion.

In summary, multipolarons with clearly defined electron numbers were crafted reversibly via a manipulation of monopolarons, exhibiting increasing local band bending and in-gap polaronic-state energy with the increasing electron number, due to increased Coulomb interaction. The multipolaron exhibits an apparent charge reduction behavior, which is ascribed to the formation of the polaron-exciton droplet, reducing its inner Coulomb repulsion. Our study unveils the intricate polaron–polaron interactions at the atomic scale and opens up a direction to engineer multipolarons for in-depth studies, such as examining multipolaron theories21,46,47, probing their internal spin coupling10, building an artificial electron lattice for designing quantum states1,2,3,4, and building miniaturized charge-storage devices.

Methods

Sample growth and STM measurements

The monolayer CrBr3 film is grown on HOPG. The HOPG substrate was cleaved ex situ and further degassed in a vacuum chamber at ~1170 K for 0.5–2 h before growth. High-purity ultra-dry CrBr3 powder (99% PrMat) is evaporated at 600 K from a home-made K-cell evaporator, and the substrate temperature is kept around 523 K during the sample growth. The base pressure is better than 5 × 10−9 torr. The STM measurement is conducted at 4.2 K. An electrochemically etched W wire was used as the STM tip, which had been cleaned on the Ag (111) surface before conducting the measurements. The STS is taken by the lock-in technique with a modulation of 21.2 mV (rms) at 983 Hz.

First-principles calculations

First principles calculations are performed with the VASP code48 and the hybrid functional HSE06 method41. Multipolarons are simulated by a \(3\,\times \,2\sqrt{3}\) orthogonal supercell with experimental in-plane lattice constant, 20 Å vacuum, and fully relaxed atomic positions (Supplementary Fig. 24). A Γ-point sampling of reciprocal space is used. The plane-wave basis cut-off is 400 eV and the threshold of residual force in atomic relaxation is 0.01 eV/Å. The position of electrons in the multipolaron is initialized by slightly enlarging the local Cr-Br bonds of the Cr atoms at the polaron centers. Marcus’s theory is used to calculate the hopping and separation barrier of multipolarons; the details of this method can be found in ref. 49.