Compromise-free scaling of qubit speed and coherence

Abstract

Across leading qubit platforms, a common trade-off persists: increasing coherence comes at the cost of operational speed, reflecting the notion that protecting a qubit from its noisy surroundings also limits control over it. This speed-coherence dilemma limits qubit performance across various technologies. Here, we demonstrate a hole spin qubit in a Ge/Si core/shell nanowire that triples its Rabi frequency while simultaneously quadrupling its Hahn-echo coherence time, boosting the Q-factor by over an order of magnitude. This is enabled by the direct Rashba spin-orbit interaction, emerging from heavy-hole-light-hole mixing through strong confinement in two dimensions. Tuning a gate voltage causes this interaction to peak, providing maximum drive speed and a point where the qubit is optimally protected from charge noise, allowing speed and coherence to scale together. Our proof-of-concept shows that careful dot design can overcome a long-standing limitation, offering a new approach towards building high-performance, fault-tolerant qubits.

Introduction

Spins in semiconductor quantum dots (QD) have emerged as one of the leading contenders for encoding and processing quantum information^1,2,3. Their success is attributed to their competitive coherence times^4,5, the demonstration of robust multi-qubit operations^6,7,8, coherent spin control above 1 K^9,10,11,12 and their compatibility with industrial fabrication techniques^13,14,15.

Among the various semiconductor systems capable of hosting spin qubits, material systems exhibiting strong, intrinsic spin-orbit interactions (SOI) have received increasing attention in recent years^16,17. Taking advantage of the SOI, all-electrical spin driving can be implemented via electric dipole spin resonance (EDSR), without the requirement for on-chip micro magnets or microwave antennas. While SOI-mediated EDSR allows for compact device architectures^18,19, it has more importantly led to ultrafast Rabi oscillations ranging from 80MHz in electrons²⁰, to several 100MHz^21,22 and even up to 1.2 GHz²³ in holes, alas, at the expense of coherence. These remarkable gate speeds have thus raised a pivotal concern for the future of spin qubits with strong SOI²⁴: Do strong couplings to the qubit driving field inevitably lead to increased decoherence due to enhanced couplings with undesired noise sources²⁵?

First steps towards reducing the coupling to charge noise have been taken via the modification of global system parameters such as the external magnetic field orientation^26,27,28, however, the fundamental trade-off between speed and coherence has so far prevailed.

Here we provide experimental evidence for compromise-free scaling, through the demonstration of a coherence sweet spot that coincides with maximal Rabi driving speeds. Our observations are in agreement with previous theoretical predictions on group IV hole spin qubits^{24,29,30,31,32}. Additionally, we achieve this Fast and Coherent Tunable Operating Regime (FACTOR) all-electrically, by controlling static gate voltages at the individual qubit level. Such local optimizations allow us to respond to the variable electrostatic environments that each qubit experiences, which can be comprised of electric stray fields from neighboring gates or non-uniform strain.

Realizing a compromise-free qubit requires navigating the intricate interplay between the tuning parameter, driving mechanism and decoherence channel. Remarkably, certain systems naturally exhibit the conditions for a FACTOR, such as hole spins in quasi 1D systems with strong SOI. In these systems, the g-tensors often display a high level of anisotropy, which can be notably influenced by electric fields. Consequently, random charge fluctuations couple to the qubit energy, resulting in reduced coherence³³. In order to mitigate this issue, configurations with vanishing derivatives of the g-factor, with respect to voltage changes, are most promising, as they indicate a reduced coupling of g to charge noise. To realize such a sweet spot, we exploit the properties of a spin qubit hosted inside a squeezed, elongated hole quantum dot, subject to strong SOI, as is naturally provided by the geometry of a Ge/Si core/shell nanowire (NW)²¹.

In such structures, the strong biaxial confinement causes heavy- and light-hole (HH-LH) states to intermix, giving rise to a strong and electrically tunable direct-Rashba spin-orbit interaction (DRSOI)^34,35. At an optimal HH-LH mixture, the spin-orbit strength is expected to reach a maximum as a function of an externally applied electric field. In the presence of strong SOI, when the spin-orbit length l_SO becomes comparable to the dot size l_dot, the g-factor is reduced^34,35,36,37. This gives rise to a minimum in g at the point where SOI reaches a maximum. This minimum in g as a function of electric field corresponds to the coherence sweet spot. By additionally employing iso-Zeeman EDSR driving of the qubit³⁸, the Rabi frequency f_Rabi can be maximized at this very same spot. This ensures an operating regime where the qubit is both fast and long-lived without compromising speed or coherence, thus defining our FACTOR.

Results

Coherent spin control at 1.5 K

We first demonstrate the operation of our Ge/Si NW hole spin qubit at 1.5 K, adding it to the list of previously demonstrated hot qubits^9,10,11,12. A scanning electron micrograph showing a representative device is presented in Fig. 1a. The device consists of a Ge/Si core/shell NW lying on top of nine bottom gates. For details on the device fabrication, we refer to the materials and methods section. By applying positive voltages to the first five bottom gates from the left, the intrinsic hole gas inside the NW is depleted to form a hole double quantum dot (DQD)³⁹ with a net-effective hole occupation (m, n) on the left and right dot. The true total hole occupation has been estimated to be in the range of several dozen^39,40, where DRSOI is still predicted to be present due to the large sub- band splittings of  ~40 meV^34,37,41.

Fig. 1: Measurement of a NW hole spin qubit at 1.5 K.

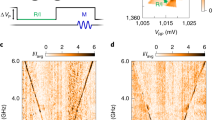
a False-color scanning electron micrograph of a representative NW-device. The Ge/Si NW is highlighted in yellow, lying on top of nine bottom gates, and is further connected to source and drain contacts from above, marked S and D. The first five bottom gates from the left were used to form a DQD, whose expected location is indicated by the yellow and pink ovals. The color code is consistently used throughout the manuscript. The scale bar corresponds to 100 nm. b Schematic of PSB. In the absence of a magnetic field and for detunings ε < ε_ST, charge transport is blocked when the system is initialized in a triplet state T(1, 1). c Measurement of bias triangles with lifted spin-blockade at B = 350 mT (x-direction) and bias of V_SD = +5 mV. The pink star marks the qubit initialization/readout spot, and the pink circle indicates the manipulation point. Inset: Same bias triangle at B = 0 mT, manifesting PSB via the suppressed current at the baseline. d Schematic of the pulse scheme applied to V_RP, consisting of the readout/initialization stage (R/I) and the manipulation stage, for which a MW burst is applied while in Coulomb blockade. e Measurement of the current as a function of f_MW and B showing characteristic EDSR at a fixed microwave burst duration. f Current as a function of microwave burst duration and magnetic field B at f_L = 2.79 GHz, showing Rabi-oscillations with a frequency f_Rabi = 130 MHz and coherence time ${T}_{2}^{{{{\rm{Rabi}}}}}=40$ ns.

The device is operated at a net-effective charge-transition from (1, 1) to (2, 0) that exhibits Pauli spin blockade (PSB). We apply a positive bias across the NW and measure the current through the DQD, which provides spin to charge conversion due to PSB. This allows to read out the state of the effective spin-1/2 system, as shown in Fig. 1b. The characteristic DC transport signature of PSB can be seen in Fig. 1c, where the baseline of the bias triangle disappears in the absence of magnetic field (inset 1c).

In our setup, the right plunger gate RP, colored in magenta in Fig. 1a, is connected to a high frequency line via a bias-tee. This allows for the application of square voltage pulses and microwave bursts to the gate, in addition to DC voltages. The measurements were performed employing a common two-stage pulsing protocol^11,21,42,43, as schematically shown in Fig. 1d.

The system is initialized in a spin-blockaded effective (1,1) triplet state by employing a specific plunger gate voltage V_RP, represented by the magenta stars in Fig. 1c, d. After a short waiting time, the system is pulsed into Coulomb blockade by applying a square voltage pulse, as indicated by the magenta circles in Fig. 1c, d. While in Coulomb blockade, a microwave (MW) burst of duration t_burst is applied. Pulsing back to the initial voltage of V_RP allows for recording a current signal I, proportional to the likelihood of a singlet configuration after coherent manipulation. Figure 1e shows typical EDSR measurements where the applied MW frequency f_MW is swept against the external magnetic field B, and from which the g-factor is extracted. On resonance, the spin is rotated, lifting the spin-blockade which leads to an increased current. By varying the burst duration as a function of magnetic field detuning at a fixed frequency of the microwave drive f_MW, coherent Rabi oscillations can be observed as shown in Fig. 1f, with a gate quality factor of ${}^{g}Q={f}_{{{{\rm{Rabi}}}}}\times {T}_{2}^{{{{\rm{Rabi}}}}}\approx 5$. These results establish coherent qubit control at 1.5 K.

To gather information about the level of control over the qubit, similar scans to those presented in Fig. 1e, f were repeated for different electrostatic environments experienced by the qubit whilst remaining within the same charge occupation of the DQD. Each electrostatic configuration of the qubit is defined by the three barrier gate voltages V_L, V_M and V_R, while the plunger gate voltages V_LP and V_RP were compensated to remain at a fixed readout point.

SOI in a squeezed quantum dot

We characterize each qubit configuration by measuring the Rabi frequency f_Rabi and Landé g-factor, g, and show their functional dependence on the three individual barrier voltages in Fig. 2a–c. In each of the three studies, the voltages on the other two barrier gates are held at a constant value, indicated by the vertical dashed lines in Fig. 2a–c. The larger responses of g and f_Rabi to the barrier voltages V_L and V_M, compared to V_R, suggest that the driven qubit is the spin located above the left plunger gate (LP). Moreover, the opposite trends of g and f_R with respect to voltage are consistent with the theoretical description of an elongated quantum dot in the presence of SOI³⁶. To understand the observations made in Fig. 2a–c, we first explain how SOI renormalises the g-factor, followed by how it can be related to f_Rabi by choosing a specific EDSR driving mechanism.

Fig. 2: SOI mediated g-factor renormalization of an elongated dot.

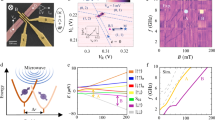
a–c Experimental data of the qubit g-factor (solid black discs), the corresponding Rabi frequency f_Rabi (empty discs) and the estimated gtm-EDSR contribution ${f}_{{{{\rm{Rabi}}}}}^{{{{\rm{gtm}}}}}$ (white bars), as a function of the barrier gate voltages V_L, V_M and V_R, respectively. For each of the datasets (a–c), the values on the other two barrier gates are fixed at the value marked by the vertical dashed line. The yellow colored regions highlight the voltage ranges for which the qubit driving mechanism is dominantly iso-EDSR, whereas the brown regions show the ranges for which the contribution to the measured f_Rabi originating from gtm-EDSR, ${f}_{{{{\rm{Rabi}}}}}^{{{{\rm{gtm}}}}}$, is ≥15% (5% above the spread of data points, see Supplementary Information). These colors are used consistently in all other panels. The estimated ${f}_{{{{\rm{Rabi}}}}}^{{{{\rm{gtm}}}}}$ is represented by the white bar charts. d Schematic visualization of how the Zeeman vector ${\hat{{{{\bf{g}}}}}}_{0}\cdot {{{\bf{B}}}}$ is affected when subject to an infinitesimal voltage change dV in the presence of SOI represented by ${\alpha }_{{{{\rm{SO}}}}}^{\perp }$ and a fixed magnetic field ∣B∣. Left shows pure iso-EDSR coming from displacements of the dot potential. Right shows the additional appearance of gtm-EDSR, when the dot is displaced and deformed. e Shows the extracted ∂g/∂V_RP, as a function of the voltage V_L in blue, and f as a function of V_M in red. These derivatives are used to calculate an upper bound of the g-modulated contribution to f_Rabi. g Values of the g-factor plotted versus their according f_Rabi from panels a (blue) and b (red). We exclusively show the data points for which iso-EDSR is the dominant driving mechanism (yellow regions), i.e., the gtm-EDSR contribution is ≤15% of the measured f_Rabi. We fit the data using Eq. (1), which assumes iso-EDSR (fit shown by black line with yellow highlight symbolizing iso-EDSR), yielding an intrinsic NW g-factor of g_NW ≈ 1.

In the case of a quasi 1D, elongated quantum dot, as it is reasonable to assume for our NW, the longitudinal axis of gate-defined confinement is well described by a harmonic potential resulting in a Gaussian envelope of the hole wave function. In the presence of SOI, the spins acquire a helical texture along the NW^34,35,36,37, provided the external magnetic field B acting on the g-tensor $\hat{{{{\bf{g}}}}}$ gives rise to a Zeeman vector $\hat{{{{\bf{g}}}}}\cdot {{{\bf{B}}}}$ with a component perpendicular to the SOI axis α_SO. As a result, the whole wave function averages over different spin orientations, leading to a renormalization of the dot g-factor (see Eq. (1) I). This effect is especially relevant when the dot extension along the NW, l_dot, and spin-orbit length l_SO, which represents the distance a hole must traverse to undergo a spin rotation due to SOI, are comparable in size. This leads to a minimum in g-factor where the SOI is strongest, i.e., l_SO shortest. Relating g to f_Rabi, however, additionally requires an assumption on the underlying qubit driving mechanism.

We assume that all effects arising from SOI, induced by a change in voltage ΔV, are captured by a modulation of the g-tensor⁴⁴ while keeping the magnetic field constant, that is ${\hat{{{{\bf{g}}}}}}_{0}\cdot {{{\bf{B}}}}{\to }^{\Delta V}{\hat{{{{\bf{g}}}}}}_{\Delta V}\cdot {{{\bf{B}}}}$. We represent this as a rotation of the Zeeman vector around the perpendicular component of the spin-orbit vector ${{{{\boldsymbol{\alpha }}}}}_{{{{\rm{SO}}}}}^{\perp }$. Periodic displacements of the wave function along the NW can result in SOI-mediated Rabi oscillations. We refer to them as iso-Zeeman EDSR (iso-EDSR), if they conserve the modulus of the Zeeman vector $| \hat{{{{\bf{g}}}}}\cdot {{{\bf{B}}}}|$, Fig. 2d left. In this case, f_Rabi ∝ 1/l_SO³⁸, and g can be directly related to f_Rabi (see Eq. (1) II),

$$g\,{=}^{{{{\rm{I}}}}}\,{g}_{{{{\rm{NW}}}}}\cdot {e}^{-{({l}_{{{{\rm{dot}}}}}/{l}_{{{{\rm{SO}}}}})}^{2}}{=}^{{{{\rm{II}}}}}{g}_{{{{\rm{NW}}}}}\cdot {e}^{-C\cdot {f}_{{{{\rm{Rabi}}}}}^{2}}.$$

(1)

Here, g denotes the measured g-factor as extracted from Fig. 1e, C is a fitting parameter, and g_NW is the confinement-dependent intrinsic NW g-factor without renormalization due to SOI, and is assumed constant to first order, thus not capturing residual g-modulations from voltage-induced changes of the confinement or other higher order contributions. The derivation is provided in the Supplementary Information. We further note that the functional form of Eq. (1) results from the harmonic confinement along the longitudinal axis of the NW and is independent of the microscopic origin of the SOI.

As seen in Eq. (1), when reducing l_SO (thereby increasing SOI), g is suppressed and f_Rabi is increased. This behavior can be observed in Fig. 2a, b. To obtain a minimum in g and a maximum in f_Rabi, as seen in Fig. 2a, the governing SOI has to plateau or show a maximum, as an implicit function of voltage. Ge/Si core-shell NWs, as the one used here²¹, like Ge-hut wires¹⁹ and Si-FinFETs¹¹, particularly benefit from DRSOI, which is expected to reach a local maximum at moderate electric fields below 10MV/m^21,30,34,35. These predicted electric field ranges are consistent with the voltage range of  ~100 mV around the extrema of g and f_Rabi shown in Fig. 2a, assuming a voltage drop over  ~ 50 nm (gate-pitch). Within the experimental error (see Supplementary Information) the maximum in f_Rabi coincides with the minimum in g. The small shift between the extrema can primarily be attributed to residual g-modulations, not captured by our model in Eq. (1).

In order to facilitate iso-EDSR, displacements of the hole wave function along the NW are desirable, while only minimally varying the dot potential. To this end the MW drive is chosen at gate RP, located as far as possible from the qubit on gate LP. To see where the driving mechanism is consistent with iso-EDSR, we measure the response of g to variations ΔV_RP, to extract ∂g/∂V_RP at a fixed magnetic field B. These responses are shown in Fig. 2e, f, as a function of V_L and V_M.

If, while driving, the voltage shifts ΔV_RP cause significant variations of the target dot potential, the induced Rabi oscillations can be significantly influenced by g-tensor modulated EDSR (gtm-EDSR). Such modulations of the g-tensor do not conserve the modulus of the Zeeman vector $\hat{{{{\bf{g}}}}}\cdot {{{\bf{B}}}}$, Fig. 2d right. Since the response ∂g/∂V_RP is computed from the difference in lengths of Zeeman vectors $| {\hat{{{{\bf{g}}}}}}_{0}\cdot {{{\bf{B}}}}| -| {\hat{{{{\bf{g}}}}}}_{\Delta {V}_{{{{\rm{RP}}}}}}\cdot {{{\bf{B}}}}|={\Delta }_{| \hat{{{{\bf{g}}}}}\cdot {{{\bf{B}}}}| }$ under ΔV_RP, we can only provide a rough upper bound to the g-tensor modulated Rabi contribution ${f}_{{{{\rm{Rabi}}}}}^{{{{\rm{gtm}}}}}$, which is proportional to a transverse modulation of the Zeeman vector ${\Delta }_{| \hat{{{{\bf{g}}}}}\cdot {{{\bf{B}}}}| }^{{{{\rm{gtm}}}}}$. These approximate upper bounds for ${f}_{{{{\rm{Rabi}}}}}^{{{{\rm{gtm}}}}}\,\propto \,| {\Delta }_{| \hat{{{{\bf{g}}}}}\cdot {{{\bf{B}}}}| }^{{{{\rm{gtm}}}}}/\Delta {V}_{{{{\rm{RP}}}}}| \,\le \,| {\Delta }_{| \hat{{{{\bf{g}}}}}\cdot {{{\bf{B}}}}| }/\Delta {V}_{{{{\rm{RP}}}}}|$ are represented by the bars in Fig. 2a, b. For the calculation of ${f}_{{{{\rm{Rabi}}}}}^{{{{\rm{gtm}}}}}$ and a qualitative description of the EDSR driving mechanisms, we refer to the Supplementary Information.

As seen in Fig. 2a, b, e, f, we qualitatively divide the measured data points into two regions, driven primarily by pure iso-EDSR (yellow) and a mix of both, iso- and gtm-EDSR (brown). If ∣∂g/∂V_RP∣ → 0, also the component attributed to gtm-EDSR, ${f}_{{{{\rm{Rabi}}}}}^{{{{\rm{gtm}}}}}\to 0$. This leaves iso-EDSR as the only available mechanism that can induce Rabi oscillations.

The pairs of f_Rabi and g at specific gate voltages V_L and V_M in Fig. 2a, b, that were classified as pure iso-EDSR (Supplementary Information), are plotted against each other in Fig. 2g, where they are fitted using Eq. (1). From the fit parameter g_NW ≈ 1 and the experimental values of g, the corresponding l_SO were calculated, yielding a range from 65 nm to 150 nm, assuming l_dot = 50 nm (gate-pitch). It is worth noting that this estimation of l_SO does not rely on knowledge of the effective mass m_eff, which can be challenging to estimate in systems with HH-LH mixing, as the one studied here. Further, the calculated values of l_SO are in agreement with those obtained via magnetic field spectroscopy³⁷ and qubit measurements in ref. ²¹ assuming HH-LH mixing.

Compromise-free operation

Given the extremal behavior of the g-factor and f_Rabi from Fig. 2a, we measured the Hahn-echo decay times ${T}_{2}^{{{{\rm{Hahn}}}}}$ as a function of V_L and compared them in Fig. 3a. We note that our estimate of ${T}_{2}^{*}\approx 5$ ns was on the order of the duration of the gate pulse duration ranging from 2 to 8 ns. These pulse durations can therefore not be assumed to be instantaneous⁴⁵, rendering ${T}_{2}^{*}$ too short to be reliably extracted. We attribute the comparably short ${T}_{2}^{*}$ to the measurement’s sensitivity to low-frequency noise, due to the long integration times required by our transport measurements. Details about the dominant noise source in our device are provided in the Supplementary Information.

Fig. 3: Compromise-free operation.

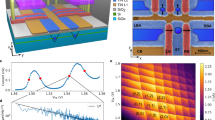
a Top: Experimental data of f_Rabi and g as a function of V_L. Bottom: Dark blue circles show coherence times ${T}_{2}^{{{{\rm{Hahn}}}}}$ obtained from fits of the time-dependent readout current measured in Hahn-echo experiments at different voltages V_L. Light blue circles show modeled coherence times taking into account ${g}_{i}^{{\prime} }({V}_{{{{\rm{L}}}}})$ from panels b–f using Eq. (2), yielding ${S}_{{{{\rm{G}}}}}\,=\,29\,{{{\rm{nV}}}}/\sqrt{{{{\rm{Hz}}}}}$. Vertical dashed line at V_L = 1330 mV shows sweet spot, where ${T}_{2}^{{{{\rm{Hahn}}}}}$ is maximal. This spot coincides with fastest f_Rabi within experimental errors. Error bars correspond to standard deviations that result from fitting. Inset: Pairs of f_Rabi and ${T}_{2}^{{{{\rm{Hahn}}}}}$ from V_L = 1330–1360 mV in 10 mV steps. b–f Show ${g}_{i}^{{\prime} }({V}_{{{{\rm{L}}}}}):=\partial g/\partial {V}_{{{{\rm{i}}}}}({V}_{{{{\rm{L}}}}})$, as a function of different static voltages on gate V_L. Dark blue data represent values of V_L for which ${g}_{i}^{{\prime} }({V}_{{{{\rm{L}}}}})$ were measured. Light blue line represents linearly interpolated data needed to match the number of measured data points between ${g}_{i}^{{\prime} }({V}_{{{{\rm{L}}}}})$ and ${T}_{2}^{{{{\rm{Hahn}}}}}$, which was fitted in (a). Vertical dashed line marks the sweet spot at V_L = 1330 mV where all five ${g}_{i}^{{\prime} }({V}_{{{{\rm{L}}}}})$ reach near zero, defining the sweet spot. Horizontal dashed line marks the zero-line of the ${g}_{i}^{{\prime} }({V}_{{{{\rm{L}}}}})$. g The FACTOR: 2D voltage space showing ${T}_{2}^{{{{\rm{Hahn}}}}}$ as function of V_M and V_L. Filled circles represent measured coherence times ${T}_{2}^{{{{\rm{Hahn}}}}}$ extracted analogously to panel a. Data trace corresponding to the dark blue trace on panel a is referenced by the blue arrow on the 2D plot. An additional trace of ${T}_{2}^{{{{\rm{Hahn}}}}}$ as a function of V_L for fixed V_M = 630 mV is indicated by the vertical dark blue dashed line to the left end of the plot, as well as a trace of ${T}_{2}^{{{{\rm{Hahn}}}}}$ as a function of V_M for fixed V_L = 1320 mV which is indicated by the horizontal red dashed. Background is obtained by a Gaussian process interpolation serving as a guide to the eye. Black contours show a Gaussian process interpolation of measured Rabi frequencies, highlighting the overlap of maxima in ${T}_{2}^{{{{\rm{Hahn}}}}}$ and f_Rabi.

The applied pulse sequence involved a π_x/2 pulse, a refocusing π pulse, and a π_φ/2 pulse with a sinusoidally varying phase as a function of the free evolution time τ, allowing for a more robust fit of the Hahn decay. Assuming 1/f^β noise, the exponent of the Hahn-echo decay α = 1 + β was defined as a global fit parameter, shared among all data sets, and converged to α ≈ 1. This value for α was extracted for the frequency range sampled by the Hahn-echo experiment from approximately $1/{\tau }_{\max }=12.5$ MHz up to f_Rabi, where ${\tau }_{\max }$ is the longest waiting time between pulses in the Hahn experiment. Given the operation temperature of 1.5 K, a white noise spectrum could be expected, as observed in other spin qubit experiments^11,12,46,47. Above 1.7 K, the qubit readout in this device significantly degrades. As seen in Fig. 3a, the coherence peaks at a gate voltage V_L where the g-factor is minimal and f_Rabi is maximal, within the experimental error margin. This observation clearly indicates a compromise-free scaling regime in which the fastest qubit operation times coincide with the coherence sweet spot. As seen in the inset of Fig. 3a the FACTOR is characterized by a simultaneous fourfold increase in coherence and threefold increase in operation speed. Defining ${Q}^{{{{\rm{Hahn}}}}}={f}_{{{{\rm{Rabi}}}}}\cdot {T}_{2}^{{{{\rm{Hahn}}}}}$ as a quantitative measure for quality, this improvement corresponds to a more than tenfold increase in performance, from  ~2 to  ~21. Further, the qualitative signature of the sweet spot remains robust regardless of the choice of noise color β, as shown in the Supplementary Information.

Next, we analyze the response of g to small voltage fluctuations of the gate voltages V_i as a function of V_L, denoted as ∂g/∂V_i(V_L). We refer to ∂g/∂V_i(V_L) as ${g}_{i}^{{\prime} }({V}_{{{{\rm{L}}}}})$ for brevity. Figure 3b–f show the ${g}_{i}^{{\prime} }({V}_{{{{\rm{L}}}}})$ of the five gates used in our experiments. One striking commonality among all five ${g}_{i}^{{\prime} }({V}_{{{{\rm{L}}}}})$ is the near-zero point crossing at the sweet spot voltage ${V}_{{{{\rm{L}}}}}^{*}=1330$ mV, indicating minimal modulations of the Zeeman vector magnitude $| \hat{{{{\bf{g}}}}}\cdot {{{\bf{B}}}}|$. Slight variations of the readout point between experimental runs and residual modulations of g_NW can lead to minor offsets in the zero-point crossing and residual decoherence^29,36.

We suspect the noise mainly originates from charge traps in the self-terminated, native SiO₂ layer, uniformly covering the NW shell, see Supplementary Information. This brings a source of noise very close to the Ge core, where the hole wave function resides. We model the noise as voltage fluctuations on all the gates with one common noise spectrum, characterized by a spectral density S_G and exponent β. Considering the appropriate noise filter function for a Hahn-echo and β = 0 (as determined before), the characteristic decay rate can be expressed as²⁷,

$$\frac{1}{{T}_{2}^{{{{\rm{Hahn}}}}}}=2{\pi }^{2}\,\left({\sum}_{i}{\left(\frac{\partial g}{\partial {V}_{i}}{S}_{{{{\rm{G}}}}}\right)}^{2}\right).$$

(2)

The best fit to the measured ${T}_{2}^{{{{\rm{Hahn}}}}}$, employing Eq. (2), is obtained with a white noise spectral density of ${S}_{{{{\rm{G}}}}}({f}_{0}/f)=29\,{{{\rm{nV}}}}/\sqrt{{{{\rm{Hz}}}}}$. In keeping with ref. ²⁷ we choose ${f}_{0}=1/{\tau }_{\max }=12.5$ MHz, corresponding to the frequency above which the noise was probed. This is an approximate value set by the duration of our shortest Hahn-experiments, and provides an estimate of the noise frequencies our Hahn-experiment is susceptible to. The modeled coherence times are shown in Fig. 3a. No additional lever arms are required in Eq. (2), as they are already captured by the ${g}_{i}^{{\prime} }({V}_{{{{\rm{L}}}}})$. Lastly, we repeat similar coherence measurements for different values of V_M and show in Fig. 3g that the FACTOR is not limited to a point in voltage space. In fact, the existence of a “sweet ridge" can be observed, which shows a weaker dependence of the coherence time ${T}_{2}^{{{{\rm{Hahn}}}}}$ on V_M as compared to V_L, over comparable voltage ranges. As shown by the black contours in Fig. 3g, the Rabi frequency f_Rabi follows the trend of ${T}_{2}^{{{{\rm{Hahn}}}}}$, reaching frequencies above 100 MHz surrounding the coherent region in green. The experimental data points for the contour plot of f_Rabi are shown in the Supplementary Information.

Discussion

We report on the existence of a FACTOR for which the coherence sweet spot coincides with the fastest qubit operation speeds. We demonstrate that our FACTOR originates from the renormalization of the g-factor, yielding a minimum in g and thus ${g}_{i}^{{\prime} }({V}_{{{{\rm{L}}}}})=0$, when the SOI is maximized for a hole quantum dot subject to strong, quasi-1D confinement. Further, maximal Rabi frequencies are achieved for iso-EDSR driving of the qubit. We favor this driving mechanism by applying the MW drive to a remote gate and we identify static gate voltage ranges for which the qubit is indeed dominantly driven by iso-EDSR. Our experimental observations thus overturn the conventional wisdom that fast qubit operations impose a toll on qubit lifetimes.

While the presented data were recorded on a single device, experiments on devices fabricated with NWs from the same growth batch^39,48 suggest broad gate tunability and low levels of disorder, reducing the likelihood that the observed behavior arises from an anomalous disorder effect. However, due to the manual NW deposition method used in the fabrication of our devices, some additional strain may be applied to the NWs. This could induce slight offsets in the position of the extremum of the SOI with respect to gate voltage. While homogenous strain would lead to offsets in the chemical potential, inhomogeneous strain could influence the direction and amplitude of the effective DC-electric field applied across the dot, which breaks the inversion symmetry to induce SOI.

Nevertheless, such static electric fields can be readily compensated for in situ, at the individual qubit level, via corresponding gate voltage adjustments, making our FACTOR independent of any global experimental parameters. We thus expect additional strain not to affect the results qualitatively. Our observed non-monotonous behavior of a Rashba-type SOI of holes confined to quasi 1D remains best explained by the electric-field tunable HH-LH mixing described within the DRSOI framework³⁴. The required electric field ranges are consistent with our experiments^24,35,36.

Furthermore, we have established coherent control of a hole spin qubit in a Ge/Si NW at 1.5 K, with qubit operation speeds and coherence times on par with previous experiments performed at mK temperatures²¹. This achievement renders our platform compatible with on-chip classical control electronics⁴⁹. While better qubit performance can be expected at lower T⁵⁰, other device aspects may also play a crucial role. In particular, the proximity of noisy interfaces such as a native SiO₂ layer⁵¹, which in our device is  ~2.5 nm away from the qubit. However, since our demonstrated mechanism changes the qubit’s susceptibility to the noise, we expect our observations to change quantitatively but not qualitatively when changing the operating temperature or the distance of noise sources relative to the qubit.

The transferability of our concept to other spin qubit platforms is described by a set of key criteria: (i) The principal mode of qubit control is intrinsic or synthetic SOI. Dephasing is dominated by electric noise fluctuations coupling to the spin through SOI. (ii) A non-monotonic SOI tuning response as a function of the noise parameter is essential. In an elongated dot, when l_SO ≈ l_dot, the effective g-factor is renormalized. When SOI is maximal (minimal l_SO) this yields a minium in g with reduced voltage sensitivity and minimal decoherence. (iii) Under iso-Zeeman driving, this same point corresponds to a maximum in f_Rabi, creating an optimal operation point where speed and coherence are simultaneously maximal. (iv) For hole systems, the non-monotonic SOI response relies on controlling the mixing of HH and LH states. This is achieved when the transversal confinement in both axes becomes comparable in strength and aspect ratio, and is significantly stronger than the longitudinal confinement.

Within this framework, the question may be raised whether the conditions leading to the observed compromise-free operation might be translated to 2D hole spin qubit platforms. Thanks to their relaxed lithographic constraints resulting from the comparatively low in-plane effective hole masses¹⁶, lateral squeezing gate electrodes could be used to induce strong, quasi 1D confinement³⁶ to planar Ge systems such as the one presented in, e.g., ref. ⁴³, where a  ~16 nm thick quantum well is buried  ~22 nm below the surface. To define the lateral squeezing axis, we suggest the fabrication of parallel finger gates (squeezing gates) separated by  ~20 nm, on the order of the thickness of the quantum well. Systems with significantly deeper wells and effective masses comparable to that of the HH (light in-plane effective mass)⁵² have achieved similar confinement lengths. These remain feasible even for in-plane effective masses approaching that of the LH^49,53,54. A second gate layer oriented perpendicular to the squeezing axis could then be used to divide the longitudinal axis into  ~50 to 100 nm segments, which should be on the order of l_SO. A driving gate that is offset along the longitudinal confinement axis would favor iso-Zeeman driving.

One may pose the question whether compromise-free operation can be transferred to electron-based systems. Conventional Rashba SOI could potentially also be tuned by electric fields to reach a maximum in SOI, but might require larger electric fields than the ones used here, as the SOI is primarily governed by the fundamental band gap of the semiconductor obtained in the third order of a multi-band perturbation theory^55,56. For electron systems using synthetic SOI, we cautiously note that nanomagnet arrays could induce g-factor renormalization if engineered to produce a spatial winding of the magnetic field on the order of the spread of the wavefunction. Motivated by recent nanomagnet structures⁵⁷, we propose designing magnetic field gradients that are maximal on the longitudinal axis of the elongated quantum dot and roll off perpendicular to the axis of elongation. Again, using lateral squeezing gates, the QD could be positioned on the extremum of the magnetic field gradient, yielding a similarly maximal artificial SOI as a function of lateral electric field, making fluctuations of the confinement voltage perpendicular to the elongated dot axis less detrimental. While the transferability of compromise-free operation may be more straightforward for holes, it is more speculative for electron-based platforms whose coherence is not dominantly limited by spin-orbit-induced dephasing. Should nanomagnet-based architectures, however, prevail, strategic positioning of the quantum dots relative to the magnetic field gradients may become an important consideration to prevent coherence from being compromised by the stronger couplings associated with synthetic SOI.

Finally, it is important for either electrons or holes that the SOI is strong enough to enter the strong SOI regime, where l_SO ≈ l_dot holds. By demonstrating the feasibility of a FACTOR in a hole spin qubit, our work offers a new angle from which to approach fault-tolerant quantum computation without sacrificing high qubit operation speeds.

Methods

Device fabrication

The QD device featured a set of nine bottom gates, each with a width of  ~20 nm and a pitch of  ~50 nm. The gates were fabricated on an intrinsic Si (100) chip with 290 nm of thermal SiO₂ using electron beam lithography (EBL). After cold development, the bottom gates were metallized with 1 nm/9 nm of Ti/Pd, respectively. To provide electrical insulation between the bottom gates and the NW, 175 cycles (~20 nm) of Al₂O₃ were grown by atomic layer deposition at approximately 225^∘C using atomic layer deposition. In an effort to improve the quality of the gate dielectric, the chip underwent annealing in a 20 mbar forming gas atmosphere (N₂92%, H₂8%) for 15 min at 300 ^∘C, prior to NW deposition. Details on the impact of the annealing process on gate hysteresis and qubit coherence are described in the Supplementary Information.

A single Ge/Si core/shell NW was deterministically placed in a perpendicular orientation to the nine bottom gates. The NW has a core radius of  ~10 nm and a shell thickness of  ~2.5 nm. The exact in-plane angle, however, remains unknown. Subsequently, ohmic contacts were patterned by EBL and metallized with Ti/Pd layers of 0.3 nm/50 nm of Ti/Pd, respectively, following a 10-s dip in buffered hydrofluoric acid to locally remove the native SiO₂ layer in the defined contact region. Figure 1a presents a scanning electron micrograph of an analogously fabricated device from the same batch, representative of the measured device.

Measurement apparatus

The experimental setup featured a variable temperature insert (VTI) in a liquid helium bath with the sample mounted below the 1 K pot (base temperature 1.5 K). The VTI was equipped with a solenoid magnet controlled by an Oxford Instruments IPS magnet power supply. DC voltages were supplied by a Basel Precision Instruments digital-to-analog converter (LNHR 927) and filtered on a dedicated filter PCB (second-order RC low-pass filter, cutoff frequency 8 kHz). Fast gate pulses and IQ control pulses were generated on a Tektronix AWG 5204. A Rohde & Schwarz SGS100A Vector Signal Generator was used to generate the qubit control pulses through IQ modulation. The gate- and control pulses were combined using a Wainwright WDKX11 diplexer and delivered to the sample PCB using attenuated coaxial lines. A bias-tee on the sample PCB was used to combine the high-frequency pulses with a DC bias. The DC current through the NW was amplified by a Basel Precision Instruments current-to-voltage converter (LSK389A) with a gain of 10⁹ and measured using a National Instruments DAQ card (USB-6363). The Vector Signal Generator output was pulse-modulated by a Zurich Instruments MFLI lock-in amplifier at 77.777 Hz to enhance the signal-to-noise ratio of the qubit measurements.

Data analysis

The g-factors were measured as described in Fig. 1e, and were extracted for each considered electrostatic configuration defined by the barrier voltages V_L, V_M and V_R. The positions of the resonance condition, with respect to f_MW at fixed B, are obtained by fitting each column to a Gaussian. The slope of a linear fit to the center positions of the Gaussians then yields the g-factor. The Rabi frequencies f_Rabi were extracted from fits to $I(t)={I}_{{{{\rm{offset}}}}}+{I}_{0}\sin (2\pi {f}_{{{{\rm{Rabi}}}}}{t}_{{{{\rm{burst}}}}}+\,{\phi }_{0})\exp (-{t}_{{{{\rm{burst}}}}}/{T}_{2}^{{{{\rm{Rabi}}}}})$. Here, I_offset is an offset, I₀ the amplitude, ϕ₀ a phase shift and ${T}_{2}^{{{{\rm{Rabi}}}}}$ the characteristic decay time. The characteristic decay times of each individual Hahn-echo experiment ${T}_{2}^{{{{\rm{Hahn}}}}}$ were obtained from a global fit of all echo-experiments using $I(t)\,=\,{I}_{{{{\rm{offset}}}}}\,+\,{I}_{0}\sin (2\pi {f}_{\varphi }{\tau }_{{{{\rm{wait}}}}}\,+\,{\phi }_{0})\exp (-{(\tau /{T}_{2}^{{{{\rm{Hahn}}}}})}^{\alpha })$, and one shared parameter α = β + 1. Furthermore, f_φ describes the frequency at which the phase of the pulse π_φ/2 was artificially varied as a function of the free evolution time τ.

Measurement details

The derivatives $\partial g/\partial {V}_{i}({V}_{j}):={g}_{i}^{{\prime} }({V}_{j})$ presented in Fig. 3b–f were extracted in three different ways at fixed f_MW: (i) ${{{{\boldsymbol{g}}}}}_{i}^{{\prime} }({{{{\boldsymbol{V}}}}}_{{{{\bf{L}}}}})$, for i ∈ {LP, M, R} : The readout point was defined by fixing all gate voltages. The derivatives were then obtained by recording the g-factors at manually varied voltages ΔV_i = 2–4 mV, without losing readout. (ii) ${{{{\boldsymbol{g}}}}}_{{{{\rm{RP}}}}}^{{\prime} }\,({{{{\boldsymbol{V}}}}}_{{{{\boldsymbol{j}}}}})$, forj ∈ {L, M}: For a fixed readout point, the depth ΔV_CP, by which the system was pulsed into Coulomb blockade, was varied by up to 10 mV while all other voltages were held constant. Only the DC voltage on V_RP was algorithmically adjusted for each ΔV_CP by a linear correction factor in order to keep the readout point fixed. As in (i), the derivatives were computed by fitting the slope of the recorded g-factor versus the variation of ΔV_CP. (iii) ${{{{\boldsymbol{g}}}}}_{{{{\rm{L}}}}}^{{\prime} }({{{{\boldsymbol{V}}}}}_{{{{\bf{L}}}}})$ : We first computed the derivative of the recorded g(V_L) presented in Fig. 2a with respect to V_L, yielding ${g}_{{{{\rm{L}}}}}^{{\prime} }({\tilde{V}}_{{{{\rm{L}}}}})$. Here, ${\tilde{V}}_{{{{\rm{L}}}}}$ is used to highlight that for each value of V_L, the voltage V_LP was compensated as otherwise the readout point would have been lost over the considered range of V_L due to the large cross-capacitance. Therefore, in order to obtain the true derivative ${g}_{{{{\rm{L}}}}}^{{\prime} }({V}_{{{{\rm{L}}}}})$, the influence of V_LP was subtracted to first order via ${g}_{{{{\rm{L}}}}}^{{\prime} }({V}_{{{{\rm{L}}}}})={g}_{{{{\rm{L}}}}}^{{\prime} }({\tilde{V}}_{{{{\rm{L}}}}})-{g}_{{{{\rm{LP}}}}}^{{\prime} }({V}_{{{{\rm{L}}}}})\cdot \Delta {V}_{{{{\rm{LP}}}}}/\Delta {V}_{{{{\rm{L}}}}}$. Here, ${g}_{{{{\rm{LP}}}}}^{{\prime} }({V}_{{{{\rm{L}}}}})$ is taken from (i) and the compensation ΔV_LP/ΔV_L ≈ −0.49.

All qubit measurements were performed at a microwave frequency of 2.79 GHz, to accommodate the specifications of the diplexer and to avoid resonances of the RF-wiring, requiring the qubit to be operated at fields between  ~100 and 400 mT, given range of g-factors. The power of the microwave frequency was fixed at P_MW = −13.4 dBm power and V_IQ = 300 mV IQ voltage amplitude, corresponding to an AC excitation of V_ac = 7.8 mV at the driving gate RP. The Rabi chevron shown in Fig. 1f was taken near the optimal operating regime at V = 1320 mV, V_M = 660 mV, V_R = 1020 mV. The EDSR resonance shown in Fig. 1e was recorded at a fixed t_burst = 4 ns.

The Hahn-echo experiments were taken at 2 s integration time, and depending on the amplitude of the transport current, up to 50 averages were taken of each trace to improve the signal-to-noise ratio.