Introduction

An isolated quantum system undergoes unitary dynamics, generated by a Hermitian Hamiltonian. Since no system can be perfectly isolated from its surrounding environment, however, non-Hermiticity appears naturally in describing the non-unitary, irreversible evolutions that real-world open systems undergo1. Non-Hermitian effective Hamiltonians have long been used to model a variety of open-system behavior phenomenologically, from the decay of unstable states to anomalous wave propagation and localization2,3, to gain-and-loss phenomena4,5,6 and parity-time (\({{{\mathcal{PT}}}}\)) symmetry-breaking transitions7,8,9,10,11,12. Within a more rigorous treatment in the framework of open quantum systems13, a broad class of systems undergoing Markovian dissipation may be accurately described by a Lindblad master equation14. A probability-non-conserving evolution described by a non-Hermitian effective Hamiltonian then arises in a semiclassical or a measurement-post-selected regime, where quantum fluctuations and quantum jumps can be neglected. Remarkably, as a sole consequence of quantum statistics, effectively non-Hermitian dynamics may also arise for closed systems of non-interacting bosons, despite their Hamiltonian remaining Hermitian at the many-body level15,16,17,18.

Systems evolving under explicitly or even effectively non-Hermitian dynamics can exhibit a wealth of distinctive features, which are both of fundamental interest and can be harnessed for practical applications. Notably, non-Hermiticity makes it possible for a system to sustain non-reciprocal couplings, which offers new opportunities for realizing unidirectional, phase-dependent transport and amplification16,19,20, and may be ultimately traced back to the non-trivial topology of the underlying dynamical generator21,22. Likewise, enhanced sensing modalities are being predicted to stem from both non-reciprocity23 and uniquely non-Hermitian spectral singularities associated with loss of diagonalizability and the emergence of exceptional points24. Renewed interest in non-Hermitian dynamics is driven by the realization that, in connection with ideas from many-body and topological physics, non-reciprocal interactions may underpin a range of emergent phenomena of broad relevance to photonics, optics, acoustics, and condensed-matter physics1,25,26. Representative examples include novel time-dependent27 or transient metastable phases28,29, as well as exotic strongly-correlated phases of matter with non-Hermitian topology30 or broken time-translation symmetry31,32.

By now, numerous experimental platforms have successfully demonstrated non-Hermitian dynamics and the resulting non-reciprocal transmission in the classical regime. In particular, optomechanical oscillators coupled in a non-reciprocal, nonlinear regime have revealed \({{{\mathcal{PT}}}}\)-symmetry-breaking phase transitions and limit-cycle oscillations33,34,35, and the use of a parametrically driven nano-optomechanical network has led to initial implementations of a paradigmatic (effectively) non-Hermitian model described by a bosonic Kitaev chain Hamiltonian36. Meanwhile, real-world acoustic experiments have demonstrated loss-compensated, non-reciprocal scattering and self-oscillations as well37. Within circuit quantum electrodynamics (QED) setups, existing approaches for breaking reciprocity often rely on active cavities38 or complex schemes that require magnetic-field-tunable components like Yttrium-Iron-Garnet (YIG) spheres39,40. Circuit QED platforms have proven instrumental for realizing exotic topological lattices with complex connectivities and non-Euclidean geometries41,42,43,44. While they are thus ideally positioned for studies of strongly correlated photonic materials and synthetic gauge fields, the above-mentioned schemes lack the degree of flexibility and tunability that would be desirable for explicitly engineering non-Hermiticity and non-reciprocal hopping dynamics in these systems.

With the above challenge in mind, in this work we demonstrate a highly tunable non-Hermitian device as a fundamental building block toward realizing scalable synthetic photonic lattices. We construct this building block using two coupled three-dimensional (3D) aluminum cavities acting as classical harmonic oscillators at room temperature, and forming a dimer system. Our key idea for engineering non-reciprocal interactions in a way that can be precisely calibrated and controlled is to combine a novel realization of non-Hermitian hopping dynamics, obtained via the insertion of a digital phase shifter, with the intrinsic nonlinearities stemming from amplifier saturation. This effectively results in a closed-feedback network of active and passive elements, which permits access to a regime where gain surpasses inherent loss, forcing the onset of dynamical instability at the linear level. Under these conditions, the system undergoes a supercritical Hopf bifurcation45, and the nonlinear dynamics eventually result in a self-sustained, stable limit cycle (LC).

Besides characterizing the stability phase diagram in the undriven case, we explore the effects of frequency entrainment46 (a form of synchronization) that the LC undergoes in the presence of an external microwave tone. Phase-locking47 and synchronization phenomena have long been recognized as hallmark features in understanding the classical-to-quantum transition of various nonlinear oscillators48,49,50,51,52, and they show significant promise for device applications, particularly in injection-locking techniques53. Here, we systematically investigate the interplay of gain, loss, non-reciprocity, and nonlinear saturation through experiments, and quantitatively account for all the observed effects using numerical simulations and analytical calculations based on a proposed phenomenological model.

Results

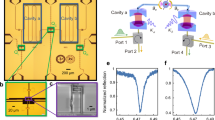
Figure 1 a illustrates the 3D microwave cavities used in our system, each with four ports featuring adjustable coupling rates, tunable (identical) resonance frequency, ωc, and fixed internal loss rates, κint. Figure 1b presents an exploded view of the cavities, showing the length-adjustable couplers, each formed by the center conductor of a coaxial connector that controls the input, output, and coupling rates, labeled as κin, κout, and κc, respectively. The resonance frequency is tuned by adjusting a post at the base of the device, with locking pins ensuring the stability of all mechanically-tunable parameters after calibration.

Fig. 1: Tunable, non-Hermitian, nonlinear microwave dimer.
figure 1

a Depiction of individual cavities with a mechanically-adjustable resonance frequency and coupling rates. b An exploded view of the cavity, showing how cavities are assembled with locking pins to set experimental parameters after calibration. c Schematic of the dimer system formed from two tunable microwave harmonic oscillators with frequencies ωc/2π = 6.027(5) GHz and internal quality factors of Qint = ωc/κint ≈ 1488. The oscillators are connected with a characteristic coupling strength of κc/2π = 8.7(1) MHz. When the amplifier is in its normal operating regime, this coupling is determined by a characteristic gain, G0 = 20.3(2) dB, and subsequently adjusted through digital attenuation, Γ. On the return path (cavity 2 → cavity 1), a phase shifter introduces a relative phase, ϕ, between the two coupling paths. We couple photons into and out of the cavity at an average rate κin,out/2π = 4.0(2) MHz.

Full size image

As shown in Fig. 1c, cavity 1 is driven by a coherent signal with strength ϵ and frequency ωd at an input rate κin. Hence, we define \(\epsilon \equiv \sqrt{{\kappa }_{{{{\rm{in}}}}}{P}_{{{{\rm{in}}}}}/\hslash {\omega }_{d}}\), where Pin is the input drive power (in watts), converted from the corresponding value Pd (in dBm) using \({P}_{{{{\rm{in}}}}}=1{0}^{({P}_{d}-30)/10}\).

Both cavities are coupled to unidirectional amplifiers with a characteristic gain G0, followed by a digital attenuator with a dynamic range of Γ ∈ [0, 50] dB, adding to the intrinsic insertion loss of the passive components. A digital phase shifter is inserted to make the relative phase, ϕ, of the reverse propagating path (cavity 2  → cavity 1) tunable over [0, 2π), and the output is collected from cavity 2 at a rate κout. In what follows, we characterize our system using the quantity ΔG ≡ G0 − Γ, representing the net hopping gain. By utilizing a conversion factor of 10ΔG/20, we adjust the intrinsic κc of each oscillator to produce an effective, tunable hopping coefficient at low power given by J0(ΔG) = 10ΔG/20κc.

Before describing the full nonlinear model of our system, we present a linear model that accurately describes the essential features of the dynamics in the low-power regime. This is achieved by considering the following semiclassical equations of motion (EOMs):

$$\dot{{{\alpha }}}={A}_{0}{{\alpha }}+\epsilon {{{\rm{B}}}},$$
(1)

where the state variables \({{\alpha }}\equiv {\left[\begin{array}{c}{\alpha }_{1}{\alpha }_{2}\end{array}\right]}^{T}\) represent complex amplitudes of the cavity field, \({{{\rm{B}}}}\equiv {\left[\begin{array}{c}10\end{array}\right]}^{T}\) accounts for the external drive on cavity 1, and the dynamical matrix A0 takes the form

$${A}_{0}=\left[\begin{array}{cc}-i({\omega }_{c}-{\omega }_{d})-{\kappa }_{0}&-i{J}_{0}(\Delta G){e}^{-i\phi }\hfill \\ -i{J}_{0}(\Delta G)\hfill &-i({\omega }_{c}-{\omega }_{d})-{\kappa }_{0}\end{array}\right].$$
(2)

In this way, tuning the phase ϕ takes the system from a regime where the hopping dynamics is perfectly reciprocal (ϕ = 0), to one where the couplings are skew-Hermitian (ϕ = π). Thus, phase non-reciprocity occurs in our system when the relative phase of the hopping terms differ, despite the hopping rates remaining equal. As a key difference from existing non-reciprocal devices, our dynamical matrix A0 is non-Hermitian but nonetheless normal (hence diagonalizable) throughout the undriven parameter regime.

In Eq. (2), we have introduced the parameter κ0 to describe the total intra-cavity dissipation rate. Experimental observations suggest that κ0 is also influenced by J0(ΔG). This influence can be explained by the increase in state amplitudes within the cavities, αi, which leads to the amplifiers introducing and amplifying existing incoherent noise over a finite bandwidth determined by the inherent linewidth of the cavities. Since this amplified noise competes directly with the intrinsic dissipation of each cavity, the overall effective dissipation rate is reduced. We model this process phenomenologically as:

$${\kappa }_{0}\equiv {\kappa }_{0}(\Delta G)=2\,({\kappa }_{{{{\rm{int}}}}}+{\kappa }_{{{{\rm{in}}}}/{{{\rm{out}}}}}+{\kappa }_{c})-{J}_{0}(\Delta G).$$
(3)

Generally, Eq. (1) admits a unique stable equilibrium point when \(\max {{\rm{Re}}}\,[\sigma ({A}_{0})] < 0\), where σ(A0) ≡ σ(A0(ΔG, ϕ)) denotes the eigenvalue spectrum of A0 as a function of the tunable parameters. Thus, a necessary and sufficient condition for dynamical stability is that

$$\frac{{J}_{0}(\Delta G)}{{\kappa }_{0}(\Delta G)}\sin (\phi /2) < 1.$$
(4)

The associated stability phase boundary as a function of ϕ and ΔG is illustrated in Fig. 2a. From Eq. (4), we can immediately see that for ϕ ≠ 0 and sufficiently high ΔG, it is possible that J0(ΔG) can balance and exceed κ0(ΔG), resulting in the onset of instability. This condition selects two relevant regions, namely,

$$\,{{\rm{Region I:}}}\,0\le {J}_{0}(\Delta G)\le {\kappa }_{0}(\Delta G),$$
(5)
$$\,{{\rm{Region II:}}}\,{\kappa }_{0}(\Delta G) < {J}_{0}(\Delta G).$$
(6)

Region I is always stable, while Region II is only stable for those ϕ satisfying Eq. (4). Physically, in the gain-dominated (Region II) unstable regime, the field amplitudes ∣αi∣2 diverge, pushing the amplifiers into saturation and reducing the gain in a power-dependent fashion.

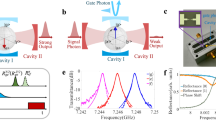
Fig. 2: Stability phase diagram and transmission spectra (S21) for our tunable non-Hermitian nonlinear microwave dimer.
figure 2

a Stability phase diagram depicting the vacuum-stable and unstable regimes determined by the dynamical matrix in Eq. (2) or Eq. (9). b(d), Experimental, and c(e) numerical simulations for S21 as a function of net gain, ΔG, for ϕ = 0(π). In both cases, data are plotted with the same colorbar for direct comparison. Numerical simulations (squares) and experimental measurements (circles) of maximum transmission, \({S}_{21}^{\max }\), are shown in (f) and (g). A comparison of the experimental full width at half maximum (FWHM) with corresponding numerical results for ϕ = π is included in (g), showing a dramatic reduction in linewidth as ΔG increases. \({S}_{21}^{\max }\) and FWHM are extracted from single- or double-Lorentzian fits to the spectra in b-c and d-e, with error bars indicating one standard deviation from the fit covariance matrix. FWHM is shown on a logarithmic scale to highlight the sharp transition to sub-MHz linewidths above threshold. Experimental and numerical results in (b)–(g) consider an input drive power of Pd = − 30 dBm. The dashed line at ΔG = 4.78 in a-g denotes the onset of instability at ϕ = π.

Full size image

While the linear model captures the correct asymptotic behavior in the stable, loss-dominated (Region I) regime, to obtain a description of the dynamical behavior valid in both the above regions, we must allow the hopping function to depend nonlinearly upon ∣αi∣2. We account for such a dependence through the following continuous piecewise function:

$$\frac{J(\Delta G;| {\alpha }_{i}{| }^{2})}{{\kappa }_{c}1{0}^{\Delta G/20}}=\left\{\begin{array}{ll}1\hfill \quad &\,{{\rm{if}}}\,\,| {\alpha }_{i}{| }^{2}\le | {\alpha }_{{{{\rm{sat}}}}}{| }^{2},\\ \frac{{b}_{G}+\hslash {\omega }_{c}| {\alpha }_{{{{\rm{sat}}}}}{| }^{2}{\kappa }_{c}}{{b}_{G}+\hslash {\omega }_{c}| {\alpha }_{i}{| }^{2}{\kappa }_{c}}\quad &\,{{\rm{if}}}\,\,| {\alpha }_{i}{| }^{2} > | {\alpha }_{{{{\rm{sat}}}}}{| }^{2},\end{array}\right.$$
(7)

where bG = 8.6 mW and ∣αsat∣2 is the saturation threshold of the amplifier, which is determined by ∣αsat∣2 = Psat/ℏωcκc, with Psat = 0.9981 mW derived from experimental characterization (see Supplementary Information Sec. VI). Note that for sufficiently low ∣αi∣2, Eq. (7) consistently recovers the hopping coefficient for the linear model, namely J0(ΔG). However, as ∣αi∣2 exceeds ∣αsat∣2, J(ΔG, ∣αi∣2) becomes monotonically reduced, illustrating the saturation effect that drives the nonlinear behavior of the system.

As we will further discuss in the next section, transmission experiments (Fig. 2b,d) show that peak-splitting at ϕ = 0 is first resolved at a significantly lowerΔG than the one at which instability sets in for ϕ = π. However, Eq. (2) indicates that the two normal modes become spectrally resolvable, namely when their splitting equals the peak linewidth, only at ΔG ≃ 4.78 dB, so it predicts that the resolvable splitting and the instability threshold should coincide. This suggests an additional coherent hopping effect that is stronger at ϕ = 0, allowing for earlier mode splitting (see also Supplementary Information, Sec. IB). We make this intuition precise by directly modifying the off-diagonal hopping coefficients via a phase-dependent function, \(f(\phi )=i{J}_{c}\cos \left(\frac{\phi }{2}\right){e}^{i\phi /2},\) where Jc/2π = 11.5 MHz represents the strength of this additional coherent hopping. While a complete explanation of the origin of f(ϕ) is lacking, and its proposed ϕ-dependence is phenomenological, we believe it stems from constructive interference between the two modes. The incorporation of f(ϕ) accurately captures the frequency splitting observed in Fig. 2b–e without altering the stability characteristics of the system in Fig. 2a.

At this point, we have already introduced all of the terms required to define the final form of our EOMs:

$$\dot{{{\alpha }}}=A(| {\alpha }_{1}{| }^{2},| {\alpha }_{2}{| }^{2}){{\alpha }}+\epsilon {{{\rm{B}}}},$$
(8)

with the full dynamical matrix being given by

$$ A(| {\alpha }_{1}{| }^{2},| {\alpha }_{2}{| }^{2})\\ =\left[\begin{array}{cc}-i({\omega }_{c}-{\omega }_{d})-{\kappa }_{1}(\Delta G;| {\alpha }_{1}{| }^{2})&[-iJ(\Delta G;| {\alpha }_{2}{| }^{2})-f(\phi )]{e}^{-i\phi }\\ -iJ(\Delta G;| \alpha {| }_{1}^{2})-f(\phi )\hfill &-i({\omega }_{c}-{\omega }_{d})-{\kappa }_{2}(\Delta G;| {\alpha }_{2}{| }^{2})\end{array}\right],$$
(9)

where κ1(2) = 2(κint,1(2) + κin(out) + κc) − J(ΔG, ∣α1(2)∣2), and J(ΔG, ∣α1(2)∣2) is defined in Eq.(7). In the linear limit of small ∣αi∣2, A(∣α1∣2, ∣α2∣2) reduces to A0 as described in Eq.(2), up to the phase-dependent correction introduced via f(ϕ). By explicitly solving the dynamics defined by Eqs. (8) and (9), we can directly reproduce and capture the main features observed in our experiments, such as weak-drive transmission (Fig. 2b–g), undriven LC solutions (Figs. 2a and 3), as well as the phase locking synchronization phenomena (Fig. 4). We provide an in-depth discussion in the sections that follow.

Fig. 3: Phase diagram of the amplitude and frequency of the LC solutions without external driving.
figure 3

a–c Power emitted from the LC extracted experimentally (a), numerically (b), and analytically (c). d–f Frequency detuning of the LC relative to ωc, δωLC, extracted experimentally (d), numerically (e), and analytically (f). The contour in each plot represents the stability phase boundary from the dynamical matrix in Eq. (9), also corresponding to ∣α2∣2 = ∣αsat∣2 for the analytical solution in Eq. (10), which is depicted in (c) and (f). Numerical and analytical amplitudes in the vacuum-stable phase in (b)–(c) are set at -44 dBm, corresponding to the baseline amplitude observed experimentally in a, and this same threshold is used to white out the corresponding region in (d). The vertical dashed line in all plots marks the value of net gain ΔG = 4.78 dB at which the phase ϕ = π becomes unstable. In the experimental data, we removed an outlier near ϕ = 5.287 rads., corresponding to the set value on the digital phase shifter moving from 2π → 0.

Full size image
Fig. 4: Synchronization of the LC mode and an external drive.
figure 4

Experimental (a) and numerical (b) contours representing regions containing a distinct LC away from ωc/2π as a function of drive power. For the experimental and numerical data presented in (a) and (b), we applied an external drive at ωd/2π = ωc/2π = 6.027 GHz. Note that in the LC region of a and b, if ϕ = π, then ωc = ωd = ωLC, whereas for ϕ ≠ π, we have ωc = ωd ≠ ωLC. Experimental (c) and numerical (f) power of the drive peak as a function of the drive frequency for the panels presented in (d)–(e) and (g)–(h) depicted as blue and red dashed lines for Pd = 0 and 4 dBm, respectively. Experimental (d–e) and numerical (g–h) emission from the dimer at ϕ = π and ΔG = 8.4 dB as an external drive is swept from low to high frequency around ωc/2π for Pd = 0 dBm (d, g), and for Pd = 4 dBm (e, h) drive strengths, showing mixing and phase locking synchronization with the external drive. In both experimental and numerical simulations, the LC synchronizes in a larger range in frequency as Pd increases, consistent with the expansion of synchronized regions shown in c and f, which explains the trend observed in the vicinity of ϕ = π for the contours depicted in (a)–(b), respectively.

Full size image

Weak-drive transmission spectra

To probe the steady-state S21, we drive the system at an input power of Pd = − 30 dBm and sweep the drive frequency ωd/2π over the range 5.98 to 6.09 GHz using a scalar network analyzer. Numerically, we compute S21 as the ratio of the steady-state output power from cavity 2 and the input drive power in cavity 1. Hence,

$${S}_{21}({\omega }_{d},\Delta G,\phi )=\frac{{P}_{{{{\rm{out}}}}}}{{P}_{{{{\rm{in}}}}}}=\frac{\hslash {\omega }_{d}{\left\vert {\alpha }_{2}^{{{{\rm{eq}}}}}\right\vert }^{2}{\kappa }_{{{{\rm{out}}}}}}{\hslash {\omega }_{d}{\epsilon }^{2}/{\kappa }_{{{{\rm{in}}}}}}={\kappa }_{{{{\rm{in}}}}}{\kappa }_{{{{\rm{out}}}}}\frac{{\left\vert {\alpha }_{2}^{{{{\rm{eq}}}}}\right\vert }^{2}}{{\epsilon }^{2}},$$

where \({\alpha }_{2}^{{{{\rm{eq}}}}}\) is the DC-component of the unique asymptotic solution α2(t). Note that the dependence on ΔG and ϕ is implicitly contained in the solutions for \({\alpha }_{2}^{{{{\rm{eq}}}}}\). Moreover, to directly compare numerical solutions to experimental results, the conversion to dB is accomplished via S21 [dB] \(=10{\log }_{{{{\rm{10}}}}}({S}_{21})\).

Figure 2b–g present the experimental and numerical S21 data for the two special phases, ϕ = 0 and ϕ = π, for which, as noted, the hopping amplitudes are Hermitian and skew-Hermitian, respectively. Specifically, Fig. 2b–c depict the experimental and numerical S21 spectra for ϕ = 0 across various ΔG values. At low ΔG, the S21 spectra show a single, very broad peak, indicating that the two modes are decoupled due to the high effective loss in the hopping path. As ΔG increases, two distinct peaks emerge and move further apart, demonstrating enhanced coupling and symmetric energy distribution between the two modes. The increasing separation of the peaks and higher S21 magnitudes (indicated by brighter colors at higher ΔG in Fig. 2b–c) confirm the successful experimental implementation of reciprocal hopping with tunable rates, as predicted by the dynamical matrix in Eq. (9) at ϕ = 0. Additionally, the excellent agreement between experimental results and numerical simulations presented in Fig. 2b–c validates the accuracy of our model by capturing the S21 characteristics when the coupling coefficients in both paths are engineered to be nominally equal.

Figure 2d–e show the experimental and numerical S21 spectra at ϕ = π. At low ΔG values, we observe a minimal S21 signal, again indicating that the two modes are essentially decoupled. As ΔG increases to intermediate levels, the signal response increases, but the transmission spectra differ significantly from the typical frequency splitting seen in symmetrically coupled modes. Instead of two peaks in frequency, we observe a single peak centered at ωc/2π. When ΔG ≃ 4.78 dB and beyond, the amplitude of the peak at ωd ≃ ωc suddenly and dramatically increases, followed by asymptotic saturation, while its linewidth sharply narrows (Fig. 2g), consistent with the onset of a stable LC.

Since the scalar network analyzer performs homodyne detection at the drive frequency, the experimental S21 measurements effectively collect the steady-state transmission amplitude at ωd/2π. We account for this effect into our numerical framework to generate the data presented in Fig. 2 by breaking down the time-domain signal into its frequency components and extracting the DC component, as described in the Methods section. Overall, the tunable S21 behavior highlights a fundamental difference in the system dynamics when the hopping coefficients have equal magnitude but opposite signs, yielding a skew-Hermitian dynamical matrix in Eq. (9), which is realized when ϕ = π.

Furthermore, Fig. 2f shows \({S}_{21}^{\max }\) at ϕ = 0, where both experimental (solid circles) and numerical (open squares) data display a monotonic increase with ΔG. This trend demonstrates the reduction of intra-cavity dissipation rates in the system as ΔG increases, which is captured by Eq. (3). Similarly, Fig. 2g presents \({S}_{21}^{\max }\) and FWHM at ϕ = π. Here, near ΔG ≈ 4.78 dB, \({S}_{21}^{\max }\) suddenly increases and saturates, while the FWHM sharply decreases due to amplifier saturation. This behavior indicates that the system has transitioned into a dynamically unstable regime, which we analyze in detail next.

Undriven, self-sustained, limit cycles

So far, we have explored the dynamics of our system under the influence of a (weak) coherent external drive applied to cavity 1, specifically at two phases, ϕ = 0 and ϕ = π. However, the system hosts a self-sustained LC in the unstable regime. The stability condition in Eq. (4), which is depicted in Fig. 2a, determines the existence of this LC, in the absence of external driving. Figure 3 presents the experimental, numerical, and analytical results for the amplitude (a-c) and frequency (d-f) of these LC solutions. Each subplot includes the onset of instability for comparison, with the red dashed line indicating the lowest ΔG value where instability occurs at ϕ = π.

Figure 3a presents the experimentally measured amplitude of the LC, obtained from the emission spectra for multiple values of ϕ and ΔG (see Supplementary Information Sec. IIE). In regions where the system is dynamically stable, Fig. 3a shows a nominally constant baseline, indicating the absence of a self-sustained emission signal. However, as the system enters the unstable regime, a distinct peak emerges, seeded by thermal noise at room temperature. The limit cycle arises from a dynamical instability of the zero-amplitude state and does not require external driving. Once the linear stability condition is violated, small fluctuations are amplified by the system’s effective net gain, resulting in a self-sustained steady-state oscillation that is accurately captured without the need to explicitly model noise. This manifests as a sharp increase in amplitude and an ultra-narrow linewidth, on the order of kHz. Notably, the transition into the unstable regime is marked by a sudden increase in the intensity of the emitted light (or LC amplitude), indicating that the system has undergone a supercritical Hopf bifurcation45.

We perform numerical simulations to determine the amplitude of the LC solutions, as shown in Fig. 3b. In our numerical simulations, we time-evolve the EOMs with ϵ = 0 in Eq. (8) and ωd = ωc in Eq. (9). This allows us to calculate the steady-state intensity of the emitted light from cavity 2 (\(\propto | {\alpha }_{2}^{{{{\rm{eq}}}}}{| }^{2}\)). Additionally, we derive an analytical expression for the LC-amplitude. We do this by transforming the EOMs into the normal mode basis, excluding the eigenvalue corresponding to the stable normal mode and solving for the amplitude ∣αi∣2 that yields non-trivial solutions. We obtain the following expression for the amplitude of the LC, nLC, (see the Methods section for a summary, and the Supplementary Information, Sec. II for a full derivation):

$$ {n}_{{{{\rm{LC}}}}}\equiv | {\alpha }_{1}(t){| }^{2}\equiv | {\alpha }_{2}(t){| }^{2}\\ =\frac{1{0}^{\Delta G/20}\left(1+\sin \left(\frac{\phi }{2}\right)\right)\left({\kappa }_{{{{\rm{c}}}}}^{2}\hslash {\omega }_{{{{\rm{c}}}}}{| {\alpha }_{{{{\rm{sat}}}}}| }^{2}+{\kappa }_{{{{\rm{c}}}}}{b}_{{{{\rm{G}}}}}\right)-2{b}_{{{{\rm{G}}}}}\left({\kappa }_{{{{\rm{c}}}}}+{\kappa }_{{{{\rm{in/out}}}}}+{\kappa }_{{{{\rm{int}}}}}\right)}{2{\kappa }_{{{{\rm{c}}}}}{\omega }_{{{{\rm{c}}}}}\hslash \left({\kappa }_{{{{\rm{c}}}}}+{\kappa }_{{{{\rm{in/out}}}}}+{\kappa }_{{{{\rm{int}}}}}\right)},\quad \forall t.$$
(10)

In addition to characterizing the amplitude of the self-sustained mode, we also investigate the tunable frequency response. Figure 3d–f displays experimental, numerical, and analytical data that describe the frequency of the LC solutions for a range of ΔG and ϕ values. Specifically, Fig. 3d presents the experimentally measured frequency of the LC, identified as the frequency at which the emission spectra exhibit its highest amplitude (see Supplementary Information Sec. IIE). We calculate the difference δωLC ≡ ωc − ωLC. We see that δωLC shifts monotonically with changes in ϕ, and it is anti-symmetric around ϕ = π. Specifically, δωLC/2π is positive for ϕ < π and negative for ϕ > π, thus demonstrating remarkable tunability over a  ~60 MHz frequency range. Importantly, δωLC shows negligible dependence on ΔG, which aligns with our numerical and analytic solutions, as discussed next.

To numerically determine δωLC/2π, we perform a Fourier analysis of the time-domain solutions to Eq. (8), and extract the dominant frequency from the spectra, as discussed in the Methods section. Analytically, we derive an expression for δωLC, revealing that this quantity is independent of ΔG, and entirely determined by ϕ:

$$\delta {\omega }_{{{{\rm{LC}}}}}\equiv {J}_{c}\cos \left(\frac{\phi }{2}\right)+\frac{2\left({\kappa }_{{{{\rm{in/out}}}}}+{\kappa }_{{{{\rm{int}}}}}+{\kappa }_{c}\right)\cos \left(\frac{\phi }{2}\right)}{1+\sin \left(\frac{\phi }{2}\right)}.$$
(11)

Figure 3e–f present numerical and theoretical calculations of δωLC for various ϕ and ΔG values. These results accurately reproduce the key experimental observations, including the monotonic tuning of δωLC with ϕ over a wide frequency range and a 4π-periodicity. This mechanism enables precise control over the frequency of the self-sustained mode by tuning the relative phase between the hopping paths. Overall, the remarkable agreement between our experimental, numerical, and analytical results demonstrates the effectiveness of our model in explaining the key characteristics of the self-sustained emission process observed in the unstable, gain-dominated regime.

Synchronization dynamics

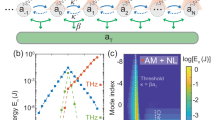
To further probe the nonlinear dynamics of our device, we now examine a particular synchronization effect, namely, the frequency entrainment phenomenon or phase locking between the LC and an external microwave tone46,47. In our experiments and simulations, shown in Fig. 4a–b, we employ a fixed microwave tone set at ωd = ωc, and vary the drive power, Pd, from 0 to 16 dBm. We then analyze the spectra to identify regions of the phase diagram with at least two distinct peaks, indicating the coexistence of self-oscillation and external drive. These regions define the contours in Fig. 4a–b. From here, we observe that increasing the drive power progressively reduces the area where LC solutions exist. This is more pronounced when the LC frequency is close to the drive frequency, which occurs when ϕ = π. Everywhere else, the dynamics converge to a unique stable equilibrium point, where no self-sustained oscillatory behavior occurs. Moreover, we observe a slight asymmetry in the experimental contours of Fig. 4a, which we attribute to minor experimental imperfections not captured by the model, as discussed further in the Methods section.

To better understand the interaction between the LC mode and the external drive, we perform experiments and numerical simulations sweeping an external tone around ωc/2π at fixed drive powers (0 and 4 dBm), keeping the dimer set at ϕ = π and ΔG = 8.4 dB, as shown in Fig. 4c–h. As shown in d-e and g-h, when ωd/2π is below ωc/2π, the measured spectra show three distinct peaks: the drive-response peak at ωd/2π (left), a central peak at ωc/2π from the LC, and a higher harmonic at higher frequencies created by nonlinear wave mixing. As the drive frequency approaches the LC frequency, a pronounced line-pulling effect causes all peaks to coalesce into a single resonance. Moreover, we can see from Fig. 4c, f that in this synchronization window, the power of the drive peak increases and then saturates, further confirming the onset of synchronization. This convergence and line-pulling is a clear signature of a frequency entrainment effect46, and phase locking47, where the LC, with its time-dependence composed of generated higher-order harmonics, coalesces into a single frequency corresponding to that of the external drive. In our setup, phase locking is evidenced by the progressive shift of the dominant spectral peak toward the drive frequency and the merging of harmonics into a single tone, distinct from suppression of natural dynamics, which would result in a stationary peak fading with increasing drive power (see Supplementary Information Sec. III). Furthermore, the synchronization window around ωc/2π expands with increased drive power, as evident from Fig. 4c, f, hence explaining the observed widening of the gap around ϕ = π in Fig. 4a–b. At higher drive frequencies, the self-oscillation reappears as a distinct resonance, accompanied by asymmetric higher harmonics, mirroring the behavior observed for drive frequencies below ωc/2π.

Discussion

We have presented a tunable platform for investigating phase-non-reciprocal hopping dynamics between two spatially separated microwave oscillators. We explored uncharted parameter regimes where coupling significantly exceeds inherent losses at room temperature, by utilizing low-loss passive components and high-gain unidirectional amplifiers. We investigate the transmission behavior, LC, and synchronization phenomena that emerge when non-reciprocal amplifiers provide enough gain to compensate for loss in the hopping paths and to exceed the total loss in the system. The remarkable quantitative agreement between numerical, analytical, and experimental results demonstrates the effectiveness of our model in adequately describing the dynamics of the system.

Our platform holds significant potential across various fields in science and engineering, by facilitating tunable non-Hermitian and nonlinear dynamics. The ability to finely control the self-sustained LC frequency with phase opens new possibilities for cavity-magnonic and optomechanical systems38,54,55,56, as well as low-cost signal generators. Future characterization of the phase noise, output power, and linewidth, alongside comparisons with established microwave sources, could clarify whether the intrinsic phase-locking dynamics in the unstable regime contribute to phase noise suppression, enabling compact, frequency-tunable emitters with potentially enhanced spectral stability. Additionally, the observed frequency entrainment offers valuable insights for sensing applications57, since the LC frequency shows enhanced sensitivity to the drive frequency at the onset of synchronization. Also promising for sensing is the non-Hermitian nature of our dimer: while, as noted, the undriven dynamics is normal, the combination of external drive and nonlinearity renders the linearized dynamics around the displaced steady state non-normal, enabling the exploration of exceptional points – including in a nonlinear regime, where the sensitivity may potentially be enhanced without sacrificing the signal-to-noise ratio as is typical of linear exceptional-point-based sensors58,59,60,61. In turn, the sigmoid-like transmission profile we observe (Fig. 2g) offers opportunities for generating nonlinearities in analog neural networks across radio-to-optical frequencies62,63,64.

Furthermore, as mentioned, the dimer building block presented here can serve as a tunable edge in synthetic photonic materials, which can be extended to higher degrees of connectivity and enable non-planar geometries39,43,65. Although the current system operates in a classical regime, its components can be adapted to cryogenic environments using parametric amplifiers66,67,68,69 and YIG-based phase shifters, with promising implications for quantum information processing70,71,72. For example, one may envision that the coupling method introduced here may be useful in the context of novel implementations of driven-dissipative cat qubits73,74.

Although the coupling that we introduced here is realized through a network of passive and active circuit elements, the dynamics are well captured by a two-mode coupled-mode model with phase-tunable non-reciprocal coupling. This phenomenological approach avoids unnecessary complexity while preserving generality and predictive power, and it reproduces the experimental behavior with excellent accuracy. Further characterization of cross-correlations between scattering elements across multiple phases and drive configurations, including simultaneous cavity driving, also represents a promising direction to deepen our understanding of the phase-nonreciprocal interaction between the coupled oscillators. Theoretically, we expect that a Lindblad master equation encompassing a novel combination of phase-dependent correlated loss and gain mechanisms will be needed to microscopically describe the system in a fully quantum Markovian regime. We leave this promising step to future investigation.

Methods

Full device description

Our setup includes a tracking generator (SignalHound TG124A), synchronized with a spectrum analyzer (SignalHound SA124B), which serves as a scalar network analyzer and is utilized for collecting the data displayed in Fig. 2. Our dimer comprises two microwave cavities with mechanically tunable frequency and coupling rates. Each cavity is directly connected to an amplifier (Minicircuits CMA-83LN+), followed by a digital attenuator (Vaunix LDA-5018V) for tunable gain control. A phase shifter (Vaunix LPS-802) modifies the phase for the hopping path from cavity 2 to cavity 1. SMA coaxial pins (Minicircuits SM-SM50+) bridge connections between components where necessary. A 50 Ω terminator is connected to the driving port for LC experiments without an external drive. When a drive of precise strength and frequency is required, as shown in Fig. 4, an external signal generator (SignalCore SC5511A) is utilized.

Calibration of ΔG and ϕ

The tunable parameters, namely, symmetric net gain in hopping, ΔG, and relative phase, ϕ, we use in the theoretical model are not quantities directly adjustable experimentally. Instead, they are inferred from actual experimental parameters, namely, the settings of the two digital attenuators Γ1→2 and Γ2→1 expressed in dB and the setting of the phase shifter \({\phi }_{\exp }\) expressed in degrees. The calibration, or mapping, from \(({\Gamma }_{1\to 2},{\Gamma }_{2\to 1},{\phi }_{\exp })\mapsto (\Delta G,\phi )\) is achieved using a lookup table, referred to as the hash map, which was constructed from a series of calibrations. This hash map establishes the relationship between the experimental and model parameters, ensuring consistent ΔG for arbitrary ϕ (see Supplementary Information, Sec. VII).

Weak-drive transmission experiments

The experimental results shown in Fig. 2b–g were obtained using the following procedure. First, we calibrate our operational ϕ = 0 by identifying the actual phase set on the device, \({\phi }_{\exp }\), that makes the two peaks in Fig. 2b symmetric at the largest ΔG = 8.4 dB value. Because the attenuator introduces phase shifts at different values of attenuation, Γ, we then iteratively adjust \({\phi }_{\exp }\) to preserve this symmetry for all ΔG values displayed in Fig. 2b,f. At ϕ = π, the primary goal was to update \({\phi }_{\exp }\) to align the frequency of \({S}_{21}^{\max }\) at ωc/2π for different Γ. We then iteratively adjusted the digital attenuators to ensure a consistent ΔG value for all the data displayed in Fig. 2d,g. These additional phase offsets are mainly influenced by the inherent phase shift from increasing attenuation in the digital devices and by phase shifts due to amplifier saturation. These effects are challenging to characterize and control, thus requiring additional manual calibration. The spurious feature near ωd/2π ≃ 6.01 GHz in Fig. 2d arises from limit-cycle emission leaking into the scalar network analyzer during homodyne detection, not from a separate cavity mode, as confirmed by simulations in Fig. 2e. To extract the peak transmission (\({S}_{21}^{\max }\)) and linewidth (FWHM) in Fig. 2f–g, we fit each spectrum using double Lorentzians for ϕ = 0 and a single Lorentzian for ϕ = π. Above threshold, increased uncertainties in \({S}_{21}^{\max }\) and FWHM arise due to spectral narrowing and the development of Fano-like asymmetries at ϕ = π. The log-scale plot in Fig. 2g highlights these effects more clearly. Minor deviations in \({S}_{21}^{\max }\) at low ΔG are also visible, possibly due to slightly lower attenuation than expected.

Experimental characterization of the limit cycle

We used our hash-map for the LC characterization to ensure accurate ΔG across all ϕ values (Supplementary Information). The output port of cavity 2 is connected to a spectrum analyzer, and the emission spectrum is recorded for ΔG values ranging from 4.0 to 8.4 dB and ϕ from 0 to 2π, with the previously determined \(({\phi }_{\exp }\to \phi=0)\) as the reference phase. A 50 Ω terminator is connected to the input port of cavity 1 to maintain the loading of the cavity during data collection. For each recorded emission spectrum, we extracted the highest amplitude and its corresponding frequency, identifying the LC amplitude and frequency for each ΔG and ϕ, as shown in Fig. 3a and d, respectively (for more details see Supplementary Information Sec. IIE).

Sketch of the analytical analysis for the undriven limit cycle

When the system is not driven, ϵ = 0, the relevant asymptotic behavior of the system can be solved for exactly. In Sec. II of the Supplementary Information, we achieve this by introducing the normal modes amplitudes \({\beta }_{\pm }\equiv \left(\pm {e}^{i\phi /2}{\alpha }_{1}-{\alpha }_{2}\right)/\sqrt{2}\), and working towards a suitable normal form for the EOMs of β+, in polar coordinates \({\beta }_{+}=i{R}_{+}{e}^{i{\theta }_{+}}\), while assuming β− ≡ 0, ∀t.

The radial EOM for \({\dot{R}}_{+}\), which is decoupled from that of \({\dot{\theta }}_{+}\), allows for a unique stable equilibrium point R+ = RLC, when R+ = 0 becomes unstable. We describe this supercritical Hopf bifurcation explicitly, and obtain the exact expression for \({n}_{{{{\rm{LC}}}}}={R}_{{{{\rm{LC}}}}}^{2}\) in Eq. (10). The uniqueness of RLC is a straightforward consequence of the monotonicity of \({R}_{+}\mapsto J({R}_{+}^{2}/2;\Delta G)\), with J as defined in Eq. (7), allowing applying its inverse on \(({| {\alpha }_{{{{\rm{sat}}}}}| }^{2},\infty )\ni {R}_{{{{\rm{LC}}}}}\). Since \({| {\alpha }_{{{{\rm{sat}}}}}| }^{2} > 0\), and \(J({R}_{+}^{2}/2;\Delta G)\) is perfectly constant for \({R}_{+}^{2} < {| {\alpha }_{{{{\rm{sat}}}}}| }^{2}\), the bifurcation described is technically no longer local, since for the LC amplitude RLC, we have that \({R}_{{{{\rm{LC}}}}} > {| {\alpha }_{{{{\rm{sat}}}}}| }^{2}\), immediately after R+ = 0 becomes unstable.

Next, we additionally derive an explicit expression for the LC linewidth by linearizing the radial EOM around R+ = RLC. Lastly, the expression for the LC frequency in Eq. (11) is obtained by substituting R+ = RLC in the angular EOM for \({\dot{\theta }}_{+}\). This yields insight into the physical reason for δωLC not depending on ΔG.

Synchronization experiments

To investigate the synchronization dynamics between a self-sustained mode and an external drive, we connect the input port of the dimer to an external local oscillator (SignalCore SC5511A), which allows us to generate signals of precise frequency and power. Initially, we set the external drive to ωd = ωc and record the emission spectra for different ΔG and ϕ, adjusting the drive power, Pd, from 0 to 16 dBm. In each case, we identify regions where the spectrum displays two or more distinct peaks, indicating the coexistence of the drive and LC tones. These regions define the contours in Fig. 4a. We acknowledge the asymmetry observed in the contours of Fig. 4a and attribute it to minor experimental imperfections, such as slight mismatches in resonance conditions, parasitic phase shifts under amplifier saturation, or minor hysteresis in the phase tuning, which may cause the limit cycle to latch earlier on one side of ϕ = π (Supplementary Information Sec. III).

Next, we focus on characterizing the gap widening around ϕ = π. We set the dimer parameters to ΔG = 8.4 dB and ϕ = π, which effectively fixes the LC frequency to ωc/2π. We then sweep ωd/2π over an 8 MHz span around ωc/2π at constant drive strengths of 0 and 4 dBm. The resulting spectra are displayed in Fig. 4c–d, respectively.

Time-domain numerical analysis

All simulated data in Figs. 2-4 are obtained using the Dormand-Prince method75 to solve Eq. (8). To systematically analyze the time-domain traces, we applied the fast Fourier transform expressed as \(y[k]\equiv {\sum }_{n=0}^{N-1}x[n]{e}^{-2\pi ikn/N}\), where N = 1 × 105 is the total number of time samples. This transformation allows us to break down our time-domain signal into its frequency components. Hence, to numerically calculate S21, we focus specifically on the DC component of the resulting spectra when the system is driven at ωd/2π. This DC component represents the average signal value over a given time interval and accurately represents the experimental homodyne detection, which measures the output signal at the drive frequency ωd/2π.

Extending this analysis, we can also determine the frequency of the LC, \(\delta {\omega }_{{{{\rm{LC}}}}}^{{{{\rm{num}}}}}/2\pi\), by extracting the dominant frequency in the computed spectra, \(f({k}_{\max })\), namely, \(\delta {\omega }_{{{{\rm{LC}}}}}/2\pi=2\pi f({k}_{\max })\), where \({k}_{\max }=\arg \mathop{\max }_{k}| y[k]|\), and \(f({k}_{\max })=\frac{{k}_{\max }}{N\Delta t}\). Here, \(f({k}_{\max })\) defines the dominant frequency in the transformed spectra corresponding to the index \({k}_{\max }\), and Δt denotes the sampling interval. Numerical results in Figs. 2-4 were achieved by time-evolving the system in the range 0 ≤ t ≤ 10000/κc, under initial conditions set as α(0) = [107, 0, 107, 0]. We excluded the initial 20% of the data to ignore transient effects, and whenever ∣α2∣2 < 0.001%∣αsat∣2, to avoid spurious sampling effects from numerical traces corresponding to the vacuum solution. We convert the photon numbers to absolute power using P[W] = ℏωc∣α2∣2κout, and then calculate the amplitude in dBm using the conversion \(10{\log }_{10}\left(P/1\,\,{{\rm{mW}}}\,\right)\). We also refer to the Supplementary Information Sec. ID for more details regarding the numerical parameters used in simulations.