Introduction

Felsic calderas often exhibit cryptic unrest behavior, occasionally leading to monogenetic eruptions1. Among the most challenging problems of modern volcanology is to provide constraints on magma recharge and eruption triggering processes at restless caldera systems. The presence of deep-rooted caldera structures and, more broadly, volcano-tectonic structures significantly influences the location of eruptions2. The most relevant task for monitoring centers and decision-makers is to anticipate the precursory signals indicating the formation and propagation of magmatic dykes toward the surface. An improved understanding of these processes may offer crucial and timely aid for volcano monitoring and eruption forecasting. Seismology and geodesy are among the most powerful tools for identifying critical phases prior to/during magma injection3.

For the initiation of a dyke, the magmatic excess pressure (exceeding the lithostatic pressure) roughly equals the rock tensile strength4. The escalation towards this point by intermediate steps of magma recharge can be identified by geodetic signals, such as source pressurization linked to volume change5. Once initiated, the propagation of the dyke is driven by the magmatic overpressure6. In this regard, Geshi et al.7 demonstrated that the dyke aspect ratio is positively correlated to the overpressure, in turn related to the discharge rate of magma containing pressurized vesicles through the conduit. Hence, the explosivity of an eruption is mutually linked to the magmatic overpressure for a given volcano, which produces deformation in the surrounding host rock during its movement. Since the dyke aspect ratio can be inferred from geodetic data inversion, it follows that it can be evaluated based on real-time monitoring of ground deformation and seismic activity7. All of the above is extremely relevant to highly urbanized volcanic regions, such as the Campi Flegrei caldera in southern Italy (Fig. 1a). This volcanic field has produced eruptions for at least 200 kyr8. It has experienced multiple large-magnitude eruptions throughout its history, including the caldera-forming eruptions of Campanian Ignimbrite (CI) at ~39 ka9 and the Neapolitan Yellow Tuff (NYT) at ~15 ka10, as well as the Maddaloni/X-6, the oldest known large-magnitude eruption at ~109 ka emerging as a further caldera-forming eruption11 (Fig. 1a). The activity of the last 15 kyr has been characterized by over 70 eruptions in three volcanic epochs12,13 (Fig. 1b), where low and moderate-sized activity has been punctuated by larger Plinian eruptions, e.g., Pomici Principali (PP) and Agnano-Monte Spina (AMS) (Fig. 1b). Specifically, the third epoch of activity13, is further divided into two sub-Epochs (3a and 3b; 5.5–4.5 and 4.4–3.8 ka, respectively), due to a rapid subsidence-uplift sequence following the AMS eruption and preceding the last 4.4 kyr of activity14,15,16. The last eruption, which offers a prime example of a low-magnitude monogenetic eruption, occurred in 1538 CE and was preceded by a century of precursory signals, including ground deformation and seismicity17,18,19. Numerous petrological and geophysical studies helped define the depth and extent of the plumbing system feeding the eruptions of the last 4.4 kyr20 (Fig. 1c). Most of the eruptions have been fed by a magma reservoir located at a depth of 5–7 km, hosting latite to trachytic/phonolitic magmas, which in turn are recharged by a mafic reservoir from a depth of 8–10 km20,21,22,23. During magma uprise towards the surface, the magma often gets stalled at shallower depth (2–4 km), where the presence of evolved magma batches20,24, and/or a fluid-trapping weak mechanical layer25 may halt the ascent of magma towards the surface. However, despite the extensive knowledge about the plumbing system, no reference threshold value for magma chamber rupture is known. At present, the need is particularly urgent, as the volcano has been experiencing a series of short-lived uplift episodes in the caldera center since the 1950s, and escalating seismicity in the last few years26. The surface deformation pattern27, including localized anomalies28 and seismic activity29,30, is similar and qualitatively resembles that of the ramp-up to the 1538 CE eruption17,18,19 (Fig. 1c). For this reason, the study of recent (<4.4 kyr) eruptions is crucial for gathering information about the potential processes that may lead to the next eruption. We focus our attention on the Nisida eruption (~3.9 ka), which occurred in the south-eastern caldera ring fault zone and was recently reappraised in terms of structure and erupted volume31, being the result of a fissure phreatomagmatic eruption yielding a volume of at least 0.15 ± 0.01 km3 DRE31. This is a moderate-sized eruption for the Campi Flegrei, similar in magnitude to the single events of the Astroni cluster13 (~4.2 ka). The Nisida fissure eruption was fed by a latite-trachyte magma reservoir32, without interaction with shallower bodies and thus representing an ideal case study to retrieve information on the rupture conditions of the main magma reservoir. Moreover, this eruption has the same isotopically distinct mafic magma component as the other Epoch 3b and Monte Nuovo (1538 CE) eruptions21,24, indicating that it tapped a shared magma reservoir. In this work, relying on the diagnostic dyke-related features identified on the southern part of the Nisida island31, and together with the length of the feeding fissure, we reconstruct the crucial geometric elements needed for dyke overpressure estimations. By combining and expanding the approaches of Geshi et al.8 and Browning et al.6, we adopted crustal and magma properties specific to the Campi Flegrei caldera to estimate the magmatic overpressure and failure threshold of the main magma chamber before dyke formation. In addition, we simulated the geodetic signature of the calculated excess pressure values, providing a benchmark to catch the transition from unrest to eruption at the world’s most urbanized volcanic area, currently experiencing escalating magma-driven unrest33,34.

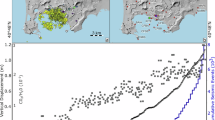
Fig. 1: Outline of the main features of the Campi Flegrei caldera.
figure 1

a Simplified geological map of the Campi Flegrei caldera indicating caldera rims, volcano-tectonic faults, and lineaments58,95, and post-NYT vent location subdivided by Epochs. The top right inset shows a simplified chronostratigraphic scheme from Fernandez et al.11. b Plot showing the erupted volume of post-NYT eruptions (in log scale), yellow boxes indicate volcanic epochs13. Error bars indicate uncertainties on the erupted volume. c Schematic diagram summarizing the Campi Flegrei sub-volcanic plumbing system storage depth based on petrologic constraints20 and independent constraints such as geodetic inversion and seismic tomography. G: Geothermal system101; U: current volcanic unrest28; T: seismic tomography35,36; Petrologic constraints (Stock et al.20 and references therein), including P: Phase equilibria; MIs: Melt inclusions 1-2: Fondo Riccio; Minopoli 2; 3: Agnano-Monte Spina; 4: Averno 283; 5: Astroni 684; 6: Nisida32; M: Melts modeling on post-NYT eruptions92. E: Cooling and decompression experiments: Monte Nuovo24. Pressure estimates were converted to depths using a crustal density of 2600 kg m−3 (see “Methods” and Supplementary Fig. S1).

Full size image

Results

Upper-crust mechanical properties

Here, we present the evaluation of crucial crustal parameters necessary to appropriately characterize the host rock. The host-rock compressibility βr is obtained as in Eqs. (17 and 20 in “Methods” section) and is equal to ~6.5 × 10−11 ± 2.4 × 10−11 Pa−1. The Poisson’s ratio v using Eq. (18)33 is 0.24 ± 0.08, based on the average Vp/Vs ratio of 1.72 ± 0.17 for the upper 6 km of crust35,36. With a shear modulus G (or modulus of rigidity)5,7, equal to 9.4 ± 2.1 GPa, Vs = 1900 ± 190 m s−1 and a representative crustal density of 2600 ± 100 kg m−3, in agreement with the value proposed by tomographic studies35, and reassessment of depth/density profiles from up to 3 km-deep geothermal boreholes25,37,38 (Supplementary Fig. S1). We calculated the dynamic Young’s modulus Ed by Eq. (19), yielding a value of 23.4 ± 5.0 GPa.

Magma properties

Physical properties of the erupted magma during the Nisida eruption have been gathered from the detailed work of Arienzo et al.32. Among the available analyses, we retrieved MI (melt inclusion) compositions and entrapment pressures hosted within clinopyroxene phenocrysts. Four available pressure determinations (ranging between 145 and 229 MPa) have been used to assess the minimum dip-dimension of the feeder dyke, and consequently, the minimum depth of the magma reservoir feeding the eruption (Fig. 1c)21,32. The pressure has been converted to depth using the reassessed average density of the Campi Flegrei crust in the first 6 km (see previous paragraph). The resulting average magma density (see “Methods”) is 2400 kg−1 m−3, to which we added a conservative uncertainty of ±50 kg−1 m−3. As a reference temperature to calculate the density of molten magma, we used the value of 1218 K (944 °C) provided by Arienzo et al.32 (see “Methods” section). The bulk modulus of melt and crystal is ∼3 × 1010 Pa39,40,41. The bulk modulus of the vapor phase ranges between 1 × 108 and 2 × 108 Pa at 4–8 km depth, assuming an ideal gas behavior42,43,44. We considered a value of 1.5 × 108 Pa at 6 km depth. It must be noted that the gas phase compressibility, which affects the magma chamber bulk compressibility depending on the amount of exsolved volatile fraction, may be up to 103 times higher than that of non-vesicular magmas43,44,45,46. The bubble fraction x is controlled by the initial magma water content, which is still in solution at the investigated depths, and by the amount of decompression. The abundance of H2O measured in Nisida melt inclusions ranges from ~1 to ~4.5 wt.%, with a mode at around 2 wt.%, which is a recurrent value in the majority of Campi Flegrei products, regardless of their age and compositions32. The compressibility of magma βm is thus equal to ~1.66 × 10−10 Pa−1 at 6 km depth, overlapping with available compressibility values47,48. We consider all these magma parameters to be constant and involved in isothermal conditions. The crystallinity of the juvenile, which is a proxy of the melt fraction, is in the range of 15–25%49, within the values of crystal content found in the post-NYT products13,49.

Feeder dyke of Nisida eruption

The feeder dyke of the Nisida eruption is a circumferential/oblique dyke, with respect to the caldera center, which fed the fissure phreatomagmatic eruption, building up a tuff cone complex along a ~1400 ± 50 m long fissure31. The length approximates the centroids of the aligned craters31 (Fig. 2a). The estimated width of the dyke (see “Methods”) gives a value of 4 ± 1 m (Fig. 2b, c). The dyke width-to-length w/L ratio is ~0.0030 ± 0.0007. The graben width Wg is ~220 ± 30 m, inferred roughly constant along its length, and an average dip angle α is 75 ± 10°, indicating a dyke upper tip depth at 410 ± 290 m below the free surface at the time of the intrusion (see “Methods”). Phreatomagmatic explosions during the Nisida eruption produced thick sequences of massive to stratified lapilli tuff, with very frequent juvenile ballistic ejecta31,32. Due to the lack of direct observations of the feeder dyke, the minimum conduit vesicularity has been inferred from the quenched erupted juvenile materials found in the eruption deposit7,32, estimated as much as 20% vol. in glassy latite ballistics in Arienzo et al.32.

Fig. 2: UAV photograph of the Nisida tuff cone (Photo courtesy of Dr. Enrico Cascella) and simplified illustration of the feeder dyke.
figure 2

a Simplified sketch describing the main geometrical features of the Nisida feeder dyke, where Ed and v are the dynamic Young’s Modulus and the Poisson ratio, respectively. L and h are respectively the strike and dip dimensions of the dyke, while w and P0 are the dyke width and overpressure. The bottom left pop-up shows the length of the dyke and its relationships with the caldera ring fault zone. b Interpreted field photographs showing the dyke-induced faults; only the cut-offs of the main fault have been considered. White and blue dots represent fault tips and branch points, respectively. The bottom right plot shows equiareal lower-hemisphere plane projections of the faults. c Simplified sketch showing the relationships between dyke-induced graben features and dyke syn-emplacement depth and width.

Full size image

Magmatic overpressure

In general terms, the failure of a magma chamber roof occurs following the relation5,6,48,50:

$${P}_{l\,}{P}_{e}={\sigma }_{3}{\,T}_{0}$$
(1)

where Pl is the lithostatic or overburden pressure, Pe is the magmatic excess pressure within the chamber \(({P}_{e}={P}_{t}-{P}_{l})\), σ3 is the local minimum compressive principal stress, and T0 is the local tensile strength of the host rock. Since σ3 is the local stress at the margin of the chamber, stress-concentration effects due to magma-chamber shape and loading are automatically considered, since any irregularity in its shape would promote instability5,50. The host-rock tensile strengths typically range from 0.5 to 9 MPa, with the most common values being 1–6 MPa4,5,6. It follows from Eq. (1) that, unless Pe reaches the local value of T0, the chamber is in lithostatic equilibrium with the surrounding host rock. In the absence of an external source of σ3 stress acts (e.g., regional tectonic stress), then a magma chamber can be assumed in lithostatic equilibrium (non-deviatoric state) where all the principal stresses at the chamber boundary are mutually equal (σ1 = σ2 = σ3) and equal to the lithostatic stress (Pl). Hence, from Eq. (1), the assumed equivalence \({P}_{e}\approx {T}_{0}\) can be envisaged and used to derive Eq. (2). When \({P}_{e}\ge {T}_{0}\), the magma chamber fails and injects the magma in a tensile (mode I) fracture, following the linear elasticity theory6; its driving pressure, or overpressure P0, can be described in the general form4,6,50:

$${P}_{0}={P}_{e}+\left({\rho }_{r}-{\rho }_{m}\right){gh}+{\sigma }_{d}$$
(2)

where \({\rho }_{r}-{\rho }_{m}\), namely, the difference between the average host rock density and the average dyke-magma density, respectively, represents the buoyancy term. The other terms are the gravitational acceleration g (9.81 m s−2), the height of the dyke between the chamber and the observation point h (i.e., the dip dimension of the dyke), and the differential stress σd (σd = σ1 − σ3), i.e., the difference between vertical stress and the minimum principal horizontal stress in the rock layer, where the dyke overpressure is calculated. On the other hand, the overpressure P0 of a magma-filled fracture in an elastic medium can be related to the dyke aspect ratio w/L of a two-dimensional elliptical crack as follows7:

$${P}_{0}=\frac{w\,{E}_{d}}{2\,L\,(1-{v}^{2})}$$
(3)

where the dyke width is 4 m, L is 1400 ± 50 m, the dynamic Young’s modulus Ed, calculated using Eq. (19), is equal to 23.4 ± 5.0 GPa, in line with that calculated in Vanorio and Kanitpanyacharoen51, who already noted the remarkable difference with values obtained in laboratory experiments on tuff samples from Campi Flegrei52,53. The Poisson’s ratio v, following Eq. (18)33, is equal to 0.24 ± 0.08, although its deviation from the standard value of 0.25 is not critical for the sake of our results, as depicted in Di Traglia et al.54. Thus, using the abovementioned values, the calculated dyke overpressure P0 is equal to 35.5 ± 11.0 MPa (Fig. 3a).

Fig. 3: Physical parameters of the Nisida feeder dyke.
figure 3

a Relationship between dyke aspect ratio (w/L) and overpressure (P0) of the magma in the dyke based on Eq. (18). Density of host rock (ρr) is fixed as 2600 kg m−3. Variations of the dynamic Young’s modulus of the host rock from 1 MPa to 50 MPa are shown. The solid line represents the relationship between w/L and P0 at Ed = 23.4 GPa, as suggested by the velocity of the S-wave (VS) at 1900 m s−1 in the host rock. Error bars denote the error on the w/L ratio and dyke overpressure. b Relationship between dyke aspect ratio (w/L) and vesicularity of magma (p) based on Eq. (5). The calculations are based on two different magma chamber depths (h = 6 km (solid red lines) and 9 km (solid blue lines). The cases of Pe = 0, 2, 4, 6, 8, and 10 MPa are shown for each case. For a depth of 5.7 km, a 9.3 MPa curve is indicated with a dashed black line. The filled triangle indicates the calculated vesicularity of the least-vesiculated bombs of the Nisida eruption, which agrees with the qualitative estimation provided by Arienzo et al.32. The scale at the top of the figure indicates the overpressure corresponding to the dyke aspect ratio (w/L) shown in the horizontal axis of the figure based on Eq. (5) at Ed = 23.4 GPa. Error bars denote the error on the dyke vesicularity and dyke overpressure.

Full size image

Magma vesicularity and excess pressure

As seen in Eq. (2), the magmatic overpressure Po in a conduit is the sum of several terms, including the buoyancy force. As magma decompresses during ascent, the exsolution of volatiles and consequent vesiculation decrease its overall density. Following Geshi et al.7, we assume that the density of the water vapor in bubbles is negligible. Therefore, the bulk density ρvm of a vesicular magma is given as follows:

$${\rho }_{m}=(1-p){\rho }_{0}$$
(4)

where p is the vesicularity of magma, and ρm is the density of liquid magma. The bulk density of the magma ρ in a magma chamber close to the equilibrium is at least similar to that of non-vesiculated magma ρ0. However, potential instabilities due to small amounts of exsolved volatiles could promote unrest8. Yet if this amount cannot reach the rock’s tensile strength, it would contribute to maintaining equilibrium in the chamber. The density of non-vesiculated magma ρ0 is 2400 ± 50 kg m−3 (see “Methods”). Therefore, the vesicularity (p) of magma in a dyke can be estimated using Eq. (5):

$$p=\frac{{P}_{0}-({P}_{e}+{\sigma }_{d})}{{\rho }_{0}{gh}}$$
(5)

where depth to the magma chamber (h) was estimated from the clinopyroxene-hosted Melt Inclusions32, which indicate the shallowest entrapment depth at 5.7 km (in a range of 5.7–7.8 km depth, see “Methods”). In agreement with the existing literature20,32, although the similar isotopic compositions do not necessarily place constraint on depth21, it is consistent with the extraction of magma from a similar reservoir as the other Epoch 3b (<4.4 kyr) eruptions. As for Eq. (2), the differential stress is considered negligible, as no direct influence of regional tectonics on vent distribution has been documented for the recent volcanism2,55. When the volatile content (mainly H2O)20 exceeds solubility, they begin to exsolve from the magma. Rewriting Eq. (2) and using the magma density as in Eq. (4), the buoyancy is the primary driver of magma propagation within the shallow crust at Campi Flegrei. Since CO2 exsolves from magma at greater depths, we imply that Eq. (4) only reproduces the effect of exsolving H2O at investigated depths20,22. With Eq. (3) we have estimated the overpressure of the Nisida feeder dyke at 35 ± 11 MPa. The magma reservoir will fail when Pe reaches the tensile strength of T05. Experimental analyses of Campi Flegrei rock samples23,56 indicated that the upper limit of representative tensile strengths of these rocks can be as high as 10 MPa. However, wall rock rupture may occur at lower excess pressures than the laboratory-measured tensile strengths, owing to stress concentrations at the edge of the wall rock and/or local failures within the wall rock5,6,50. In our specific case, we have estimated the value of Pe adopting the assumption that the volume added to a sill-like chamber before rupture ΔVm is roughly equal to the magma volume leaving the chamber with the dyke intrusion. This is, the sum of the erupted volume at the surface, plus the volume quenched within the feeder dyke, assumed of homogeneous strike dimension and width from the surface down to the magma chamber (i.e., planar dyke57) which is, a simplification, yet provides a crude estimate of 0.03 ± 0.01 km3, for a total considered volume Ve of 0.18 ± 0.01 km3. We can estimate the value of Pe for a sill-like reservoir, using6:

$${P}_{e}=\frac{3{E}_{d}\Delta V}{16(1-{v}^{2}){R}^{3}}$$
(6)

where Ed is equal to 23.4 ± 5.0 GPa, and R is the inferred radius of a sill-like magma chamber encompassing the inner caldera rim58, fixed at 4.5 ± 0.5 km, which gives a value of 9.3 ± 3.8 MPa, higher than the other value estimated with Eq. (S1). The vesicularity of the quenched juvenile material is estimated at around 20%32. We now estimate the vesicularity of the magma using Eq. (5), which gives a value of 0.20 ± 0.09 when the excess pressure Pe is considered. Its relationship with dyke aspect ratio and overpressure is shown in Fig. 3b. On the other hand, neglecting the excess pressure, necessary to initiate a dyke intrusion and assuming that the buoyancy force solely supports the magma overpressure, then the vesicularity of the magma in the feeder dyke is estimated with Eq. (5) to be 0.26 ± 0.08. Both modeled values are consistent with the observed vesicularity of the least vesicled quenched material32. Rearranging Eq. (5) for Pe, it becomes:

$${P}_{e}={P}_{0}-p\,{\rho }_{0}{gh}$$
(7)

and yield a value of ~8.6 ± 1.6 MPa, which is similar to that calculated with Eq. (6), within the range of realistic values of rock tensile strength5,6,23,50 allowing us to consider the value of 9 MPa as an appropriate upper limit of tensile strength T0 for the shallow crust hosting the Campi Flegrei plumbing system.

Depth of dyke nucleation

The buoyancy term is the leading factor to dyke overpressure, thus neglecting the magma excess pressure upon propagation within the crust, overpressure P0, derived from Eq. (2) can be rewritten as follows59,60:

$${P}_{0}=|(\,{\rho }_{r}-{\rho }_{m}){|gz}$$
(8)

which in terms of the depth of dyke formation z, becomes:

$$z=\frac{{P}_{0}}{g|\left({\rho }_{r}-{\rho }_{m}\right)|}$$
(9)

where ρm is the density of vesicular magma. The estimated depth of dyke formation is 5.3 ± 1.8 km.

Constraining the magma chamber volume during the last 4.4 kyr

Small-to-moderate-sized volcanic eruptions are fed by magma chambers that only drain a limited proportion of the hosted magma in eruptible conditions61. Other external factors may force the expulsion of higher proportions of magma, for instance, the onset of caldera collapse, graben subsidence, or involvement of interconnected reservoirs39,40,62,63. The erupted volume of “ordinary” eruptions relates to that of a molten magma chamber (Vm) according to the relation6:

$${V}_{e}={P}_{e}\left({\beta }_{r}+{\beta }_{m}\right){V}_{m}$$
(10)

where host rock βr and magma βm compressibility are calculated as described in the “Methods” section. To estimate the ratio of erupted material to the volume of the shallow magma chamber, we assumed the chamber to be fully molten. This is the usual assumption implied in the inversion of geodetic data to infer the depths and volume of magma chambers associated with inflation and deflation (unrest) periods5,64.

If the erupted volume is known, Eq. (10) can be rearranged as follows5:

$${V}_{m}=\frac{{V}_{e}}{{P}_{e}({\beta }_{r}+{\beta }_{m})}$$
(11)

Remembering that the rock tensile strength T0 is roughly equal to the magmatic excess pressure Pe6, we see that an upper bound value for the Nisida eruption is ~9 MPa. Using Eq. (11), the volume of the molten magma chamber is 84 ± 35 km3 (Fig. 4a). Consequently, the ratio between extrusive Ve (erupted + intruded) and magma chamber volume Vm, Ve/Vm ratio, is ~2.1 × 10−4 (for Pe = 9 MPa) or rewritten in terms of Vm, \({V}_{m}=464\,\pm 193\,{V}_{e}\).

Fig. 4: Magma domain of the Campi Flegrei.
figure 4

a Sketched cartoon of the magmatic plumbing system of the Campi Flegrei illustrating the volume of the active sill-like magma chamber, the volume variation ΔVm, and the erupted volume Ve. b Binary diagram showing the relationship between the recharge volume and the magmatic excess pressure necessary to bring the main chamber to rupture. The yellow dashed line indicates the median value of juvenile crystallinity (reciprocal of melt fraction) in Epoch 3b erupted rocks49. SMG Santa Maria delle Grazie, OL Olibano, AC Accademia, PA Paleoastroni, SO Solfatara, A1-7 Astroni, FL Fossa Lupara, AV Averno-2, CM Capo Miseno, MN Monte Nuovo, subscripts s source, e erupted. Triangles indicate erupted magma DRE of post 4.4 kyr eruptions; Inverted triangle indicates the shallow source of Monte Nuovo.

Full size image

However, extensive petrologic evidence13,20,49 indicates that magma reservoirs are pictured as poroelastic mush in transcrustal systems65,66. Therefore, this implies that only a fraction, not less than 50% to ensure eruptible conditions67, of the bulk magma chamber is molten, and reciprocally proportionate, is made up of compressible pores of the crystal mush68,69, so that Eq. (10) is rewritten as:

$${V}_{e}=f{P}_{e}\left({\beta }_{r}+{\beta }_{m}+{\beta }_{p}\right){V}_{{mp}}$$
(12)

Where f is the multiplier factor accounting for the magma crystal mush molten fraction, βp is the undrained mush compressibility65,68 equal to ~2.67 × 10−11 Pa−1 specifically modulated for the molten fraction f (0.5)69, and Vmp is the bulk volume of the poroelastic mush reservoir. Thus, introducing the melt fraction f and adding βp in Eq. (12) becomes:

$${V}_{{mp}}=\frac{{V}_{e}}{f\,{P}_{e}({\beta }_{r}+{\beta }_{m}+{\beta }_{p})}$$
(13)

On that basis, we estimate a bulk volume of the poroelastic magma reservoir at 151 ± 62 km3, which would be equal to a 2.4 ± 1.1 km thick sill-like magma domain encompassing the shallow crust between 5.7 and 8.1 km depth. Using these values, the ratio between extrusive (erupted + intruded) and magma chamber volume rewritten for Vmp becomes: \({V}_{{mp}}=\,833\,\pm 346\,{V}_{e}\).

Magma chamber failure upon recharge

When the magmatic excess pressure Pe equals the rock tensile strength T0, the pressure promotes dyke initiation, and assuming that the erupted volume is approximately equal to the volume ΔVm added to the reservoir before the chamber rupture, we can rewrite Eq. (11) for Pe5:

$${P}_{e}=\frac{{\Delta V}_{m}}{{V}_{m}\left({\beta }_{r}+{\beta }_{m}\right)}$$
(14)

The addition of new magma to the fully molten chamber may disrupt the lithostatic equilibrium, producing a deviation from background seismic, geochemical and geodetic observables related to the increase in excess magmatic pressure and degassing. Therefore, using the total volume Ve of the Nisida eruption as input (0.18 ± 0.01 km3 of magma), the magma recharge produces an upper-bound value of excess pressure Pe equals to 9 MPa for a fully molten magma chamber (Fig. 4b). Hence, in the case of a partially molten magma chamber, to which βp must be added, Eq. (14) becomes:

$${P}_{e}=\frac{{\Delta V}_{m}}{{V}_{{mp}}\left({\beta }_{r}+{\beta }_{m}+{\beta }_{p}\right)}$$
(15)

Considering the bulk volume of a poroelastic magma chamber Vmp for a lower-bound value for eruptible conditions of 50% molten fraction during a volcanic epoch49,67,68,69, the addition of ~0.2 km3 of magma may reach lower values of Pe (~5 MPa), yet sufficient to reach critical rock tensile strength values proposed in literature (Fig. 4), while larger ΔVm volumes would be required to reach the upper bound threshold of ~9 MPa. A summary of the complete set of physical parameters used above is provided in Table 1.

Table 1 List of physical parameters and variables used in this work
Full size table

Geodetic signature of magma chamber recharge

As described above, the top of the magma reservoir feeding the <4.4 kyr eruptions is averagely located at 5–6 km depth (Fig. 1c). Since we have estimated the volume change required to bring the magma chamber into critical condition, we have explored different combinations of source depth and magmatic excess pressure for a sill-like reservoir, and how this affects the maximum displacement value at the deformation center and the spatial pattern of deformation if this would occur at present time, centered in Pozzuoli (UTM coordinates 425794, 4518206). In Fig. 5a, we show that for a fully molten chamber, the addition of 0.075 km3 can produce a maximum uplift of ~1 m at the deformation center for a 6 km deep, 4.5 km radius magma chamber. Higher volume variations, up to 0.15 km3, would produce up to ~1.8 m of uplift. On the other hand, this value is lower than 0.5 m for an 8 km deep sill-like reservoir70. In Fig. 5b, we show the comparison between normalized curves of the deformation of the 1980–198371 levelling and the GNSS (Global Navigation Satellite Systems) data from the INGV (Istituto Nazionale di Geofisica e Vulcanologia) network72 (both vertical and horizontal displacement), for which we obtained a best fit with an idealized a Mogi point source73 between 3 and 4 km depth, in agreement with Giudicepietro et al.30. On the other hand, the vertical displacement reconstructed for the 1251–1538 CE period during the unrest predating the 1538 Monte Nuovo eruption18 is best fit with a sill-like, 4.5 km radius, reservoir at ~6 km depth19. This deformation pattern is significantly broader than the one observed today. The best fit at ~6 km depth gives RMSE (Root Mean Square Error) of 0.03. These curves are superimposed based on the assumption that the deformation shares the same axis of symmetry as the shallow deformation and that the source is confined by an elastic half-space (Fig. 5b).

Fig. 5: Geodetic modeling of Campi Flegrei magmatic source.
figure 5

a 3D plot showing the tradeoff between the source depth and magmatic excess pressure of a sill-like source in producing a spectrum of uplift values at the deformation center. The source radius is fixed at 4.5 km. b Plot showing the comparison between normalized vertical displacement of a Mogi point source and a Fialko sill-like source displaying a bell-shaped pattern as computed for different source depths with a fixed radius of 4.5 km. Blue circles are 1980–1983 vertical levelling data71; Green and cyan circles are the vertical and horizontal components of the 2010–2021 GNSS data72; Red circles are geoarchaeological data of ground deformation preceding the Monte Nuovo eruption in 1538 CE18. Dashed and dotted colored lines show the vertical and horizontal components modeled with a Mogi source fitting the current deformation. Dashed shaded-red lines show the vertical component modeled with the Fialko model of a sill-like source fitting the geoarchaeological data18,19.

Full size image

Discussion

The 1400 ± 50 m long feeder dyke of the Nisida eruption is rather similar to the eruptive fissures of Baia-Fondi di Baia, Averno 2, and Monte Nuovo, characterized by a length of ~1900, 1300, and 1700 m, respectively18,74,75. Some non-feeder dykes have also been recognized along the southern caldera rim76, having a length between up to 750 ± 150 m, closer to the average crater width of single vent Campi Flegrei eruptions77, suggesting that laterally propagating fissure eruptions are rather uncommon. The combination of the inferred dyke width and length leads to a w/L aspect ratio of 0.003 ± 0.001 like those obtained in the literature. The spectrum of such values spans from 0.0001 and 0.001 for the fissure swarms in east Iceland59 and Santorini dykes exposed on the caldera walls5, to 0.001 to 0.01 at Miyakejima volcano7,78, tectonic-controlled carbonate-seated dykes79, and mafic dykes emplaced within granites of the Western Dharwar Craton (India)80. Thus, our estimation of w/L appear to be reasonable for the Nisida feeder dyke. The calculated magmatic overpressure using Eq. (3) gives a value of 35 ± 11 MPa, which is significantly higher, by a factor of 3, than those calculated for the Miyakejima historical fissure eruptions. Still, this is well justified by the higher H2O content and explosivity of the Nisida phreatomagmatic eruption when compared to the lava effusion to fire fountaining activity (P0 between 3 and 13 MPa) at Miyakejima, yet in line with larger dykes59. Moreover, the maximum inferred dyke upper tip depth of 410 ± 290 m is, within uncertainties, consistent with the valid depth range expected for phreatomagmatic explosions81, this value decreases down to ∼250 m, accounting for overstimation implicit in the applied method82. Our predicted vesicularity values are remarkably similar to those qualitatively assessed on quenched juvenile material32 and are compatible with the computed dyke overpressure and aspect ratio for a 5–6 km depth magma chamber (Fig. 3b), supporting the findings of Geshi et al.7. The value of ~9 MPa of excess pressure, which is roughly equal to the upper limit of the host rock tensile strength, has been calculated using a sill-like geometry, and the vesicularity value, as well as for a sphere geometry (see Supplementary Results), the latter yielding lower Pe values due to its dependence with higher magma chambers volumes for a spherical reservoir (Supplementary Fig. S2). It should be noted that most of the post-NYT eruptions are fed by magma reservoirs between 5 and 7 km, with magma interacting and eventually stalling at shallower depth (2–4 km) only briefly before eruptions83,84. Therefore, in agreement with the entrapment depth of melt inclusions, our estimation of ~5.3 km, based on the depth of origin of a buoyancy-driven dyke, is consistent with independent petrologic data.

All of the above furnish the backdrop for further evaluation of the magma chamber volume and the threshold for its failure due to incremental or short-lived recharge. The volume of the molten magma chamber active during the Nisida eruption, and representative of the Epoch 3b volcanism, is 84 ± 35 km3 (Fig. 4a), meaning that around 0.1–0.2% of the volume of a molten magma chamber would be transported out of the chamber, feeding a moderate-sized volcanic eruption. It is worth noting that, considering a realistically sill-like shaped reservoir of radius 4.5 km, accounting for the surface of the inner caldera enclosing eruptive sites and deformation pattern27,55,85, the inferred thickness of the magma chamber region would be ~1.3 km, ranging from 5 to 6 km depth, consistent with the estimation provided by melt inclusions and phase equilibria in the vast petrological literature of Campi Flegrei (Stock et al.20 and references therein). It should also be stressed that such a molten magma reservoir volume should produce significant positive Vp/Vs anomalies86 detectable by seismic tomography.

On the other hand, although the complete characterization of the magma chamber geometry is beyond the scope of this work, the surface projection of the recently active magma chamber could be smaller than the existing caldera structure, implying that the thickness of the active magma chamber would encompass a wider depth range. The availability of such a large volume of magma, concurrently with a deep-rooted network of volcano-tectonic faults, could also represent the predisposing conditions viable for the occurrence of large (M ≥ 5–6) eruptions8, in which the gravitational collapse of overburden blocks would allow a larger volume of magma to be erupted39,40.

In contrast, during the post-NYT eruptive activity, uprising magma has often interacted with shallow, smaller, more evolved magma pockets located in the upper 3–4 km20,83,84, possibly favored by the presence of a weak layer25, including the process implicated in the last eruption in historical times (Monte Nuovo18,24). We acknowledge that the architecture of the plumbing system may be more complex, inhomogeneous and compartmentalized50, with regions of crystal-rich mush testified from antecrysts and microlites frequently found in the erupted juvenile material13,49. In general, melt fraction values may vary dramatically, ranging from 5–10% in long (>100 kyr) dormant volcanoes (e.g., Datong volcanoes87) to approximately 30% in quiescent caldera systems (e.g., Yellowstone Caldera88). At Campi Flegrei, melt fraction values have been proposed based on magnetotelluric data66 (10–30%) and seismic reflection studies35 (65–90%) at around 8 km depth. On the other hand, the melt fraction of the shallow plumbing system during a volcanic epoch can range from a minimum of value of 50% to 85–90% based on the crystallinity of erupted material13,49, also agreeing with the input parameters used in Mullet and Segall69 and Weber et al.89, and considering that eruptible magma usually contains less than 50% volume of crystals67. The effect of considering down to 50% of melt fraction entails that the magma intrudes in a medium with a bulk compressibility higher than the host rock, but still much lower than the molten magma. It implies that the undrained mush bulk compressibility can be up to 20% higher for a 50% mush melt fraction69, partially damping the overpressure generated by a magma injection into the magma reservoir (Fig. 4b). Given the implied simplifications which represent an end member for our calculations, the results indicate an increase in the modeled bulk magma chamber volume, up to 151 ± 62 km³, considering a sill-like reservoir of radius 4.5 km, encompassing depths from 6 to 8 km, which it still be a reasonable value. The uncertainty decreases to ±16 km³, neglecting the error propagation related to Pe when fixed at 9 MPa. Generally, the values of melt fraction may vary significantly along the vertical axis of a sill system90, with higher degrees of melt fraction up to a totally molten magma reservoir being inferred below a depth of 7.5 km35. It must also be considered that as a volcanic epoch progresses, the melt fraction gradually increases, implying that less magma needs to be added to a molten reservoir before initiating rupture. On the other hand, although the thermal fingerprint91 of past recharges vanishes at greater time scales than the current interval since the last eruption, low melt fractions (10–30%) might be expected at the onset of unrest at a dormant volcano. This may provide a possible explanation for the failure to image in seismic tomography, to date, the main Campi Flegrei magma chamber at 5–7 km depth92, also accounting for the resolution limits of these techniques, as, due to its current state, predominantly made of crystal mush. This could be remobilized by hot gases93, or remelted by the recharge of more mafic magma20,21.

We have obtained an upper bound value of magmatic excess pressure Pe for a fully molten reservoir, hence of rock-tensile strength T0, close to 9 MPa, which is consistent with realistic values of tensile strengths4,5,6,25,53,56. It is worth noting that such high tensile strength is not unexpected due to the positive correlation with low rock porosity56, which can be envisaged at magmatic depths and in the presence of thermo-metamorphic and geothermal supercritical fluids, able to mineralize the rock fractures and primary (likely compacted) pores25,38. The applied model predicts the required volume variation needed for a magma chamber of known volume to reach the critical excess pressure and cause dyke initiation5 (Fig. 4b). A lower bound of ~4 MPa can be considered a critical threshold5 (Fig. 4b). Our reconstructed curve yields a ratio of ΔVm/Pe, i.e., the slopes of the correlation lines, of 0.02 and 0.04 km³/MPa, for a fully molten and a poroelastic reservoir, respectively. This means that, for the latter, the system can store more magma before reaching critical values for ordinary eruptions. This may also explain why moderate-sized eruptions are the most frequent at Campi Flegrei in the post-NYT activity, having a recurrent magma chamber rupture threshold and tapping a similar reservoir. Possibly also explaining the observed temporal clustering of the volcanic eruptions into epochs at Campi Flegrei94. Therefore, we suggest that in the condition of a molten chamber and a poroelastic magma chamber, 0.075 and 0.175 km3 of magma, respectively, would be enough to promote chamber failure (Fig. 4b). Moreover, the values of crystallinity of erupted magma (15–25 vol. %13,49) is within the considered spectrum of melt fraction (50–100 vol. %), for which we have calculated the magmatic excess pressures. We underscore that this model only applies to ordinary eruptions that do not involve volcano-tectonic collapses or interaction between different magma batches, which can cause more magma to reach the surface40. This observation has implications for the growth of magma chambers over time, as magma accumulation preceding an eruption, which most likely occurs through incremental steps of recharge, must arise on shorter timescales than those leading to solidification65,69. As a volcanic epoch progresses, lower and lower volume variation would be required as the melt fraction eventually increases (Supplementary Fig. S2). Overall, this represents the first attempt to estimate a threshold for magma chamber failure potentially associated with geodetically detectable signals despite the presence of a poroelastic mush system, which is able to affect the accurate determination of volume variations at the surface69. Critically, the compression of poroelastic media may lead to a significant underestimation of intruded volumes, and this most likely explains the misfit between erupted volumes and geodetic-derived volume estimates47,69.

The magma reservoir feeding the Nisida eruption can be reasonably assumed to be representative of those feeding the Campi Flegrei eruptions of Epoch 3b (4.4-3.8 kyr). Given this, it is striking to note from Fig. 4 that while most of the eruptions are within the 4–9 MPa range, some of these eruptions fall below the critical values of 4 MPa, required to bring a chamber to rupture5. Here, we provide some possible explanations considering their age and location with respect to the caldera structure (Fig. 6). The large volume eruption of Agnano-Monte Spina, closing the Epoch 3a, triggered the volcano-tectonic collapse of the Agnano Plain14,95 and the apical region of the uplifted dome76,96. The subsequent activity occurs within a frame of intense volcano-tectonic activity associated with rapid ground uplift14,15, which followed a short-lived subsidence phase. The first post-AMS activity occurred in the central sector (VT zone 1, Fig. 6), where small-volume lava domes, phreatic explosions, and small Vulcanian eruptions have taken place along volcano-tectonic faults dissecting the shallow geothermal system97. This activity involved the simultaneous eruptions of Solfatara and Averno 298 (Fig. 6), the former anticipated by phreatic eruptions. The Astroni cluster13 erupted ~0.7 km3 of magma through 7 distinct explosive episodes (~0.1 km3 DRE on average) and further minor intra-crater activity, vented in correspondence with the previously formed AMS caldera (VT zone 2, Fig. 6). Epoch 3b then concluded with the three peripheral eruptions of Nisida, Capo Miseno, and Fossa Lupara, distantly vented across the ring fault zone (VT zone 3, Fig. 6). Some alternative explanations can be given about the eruption in zone 1, either being erupted at the culmination of caldera unrest, with the erupted volume representing the deviation from the minimum threshold for chamber rupture of ~0.075 km3 DRE of magma (4 MPa). Alternatively, since these small-scale eruptions occur along volcano-tectonic faults, it is likely that they represent the eruptive material of more evolved shallow magma pockets squeezed out through the faults dissecting the geothermal system, as suggested by the phreatic activity (e.g., Olibano and Solfatara eruptions)14. If this were the case, then the threshold for the 5–6 km depth magma chamber provided here would not be applicable for this shallower system, which needs further characterization. On the other hand, it becomes evident that deep-rooted caldera structures, i.e., both the broad caldera ring fault zone and the AMS caldera, can facilitate larger magma volumes towards the surface. Isotopic studies21 suggest that most of the Epoch 3b eruptions are fed by a common mafic “Astroni-like” component recharging a 5–7 km depth reservoir, allowing us to consider these eruptions as related to the main magma storage region constrained by petrologic evidence (Figs. 1c, 4a), regardless of the incidental interaction with shallower magma pockets intercepted during the ascent21,84. The eruption of Monte Nuovo in 1538 CE erupted only 0.03 km3 of magma DRE13, but, in agreement with geodetic inversion of geoarchaeological data18, and petrologic constraints24, up to 0.16 km3 left the main reservoir region before briefly stalling at ~2 km depth, and remaining mostly trapped. Thus, this suggests that our model provides a reasonable approximation to forecast the initiation of a magmatic dyke from the main magma reservoir. We note that this model is not necessarily capable of predicting the match of the excess pressure threshold due to crystallization-induced second boiling and late-stage volatile saturation99 of shallower magma pockets, but rather is only related to first boiling of the main reservoir61. In fact, volatile saturation may occur due to first boiling, resulting from the injection of volatiles-rich mafic magma into a more evolved magma body49,61, or to late-stage differentiation and segregation of mineral phases20,92,99, as occurred for the Monte Nuovo eruption49.

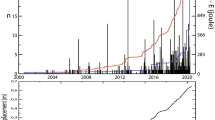
Fig. 6: Volcano-tectonic zones of Epoch 3b eruptions.
figure 6

Plot showing the temporal distribution of volcanic vents for the three volcano-tectonic zones (VT1, VT2, VT3) of the Epoch 3b. Map insets show the location of the caldera ring fault zone (shaded red58) and the collapsed area associated with the AMS eruption (shaded blue76,95,96); and the surface hydrothermalized area (shaded yellow37,97).

Full size image

Our results are consistent with petrology work20,92, indicating that most volcanic eruptions are fed by a magma reservoir located below 5 km depth49,100. This also agrees with geodetic inversion of geoarcheological data related to the Monte Nuovo eruption18,19, that suggests a 6 km source depth (Fig. 5b). This depth is significantly different from that estimated for the current deformation (Fig. 5b), which coincides with the pressurization of the geothermal system101 and/or smaller magma intrusions at shallow levels36 recharged by the main reservoir. Eruptions fed from shallow levels occur following late-stage differentiation99, or by passive extraction of degassed magma14 due to volcano-tectonic control (Fig. 6). Overall, this implies that a significantly different, likely wider (Fig. 5), deformation pattern would be superimposed on the one characterizing the current unrest. In the simplest approximation, assuming that the two superimposed sources share the same axis of symmetry, the pressurization of a sill-like reservoir70, with a radius of 4.5 km and a depth between 5–7 km, in relation to a volume change around 0.075 km3, would, in theory, produce a readily detectable change in the deformation pattern, as evident from the normalized curves (Fig. 5b). The greatest sensitivity to this change in patter would be in the widening of the deformation field, beyond the 8 km radial distance from the center, as well as an outward shift of the steeper portion of the curve between 3 and 4 km of radial distance (Fig. 5b). The change in pattern would be even more evident in the case of non-correspondence of symmetry axis. It is also important to bear in mind that a pressurization linked to a magma recharge of the order of that feeding the last 4.4 kyr eruptions, would produce some meters of ground deformation anticipating the dyke enucleation (Fig. 5a). Therefore, we contend that, under the assumption of an elastic half-space, it should be possible to catch the precursory phase leading to an impending eruption at Campi Flegrei. On the other hand, if the actual rheological structure of the Campi Flegrei crust is not represented by an elastic half-space at the investigated depths, detection of such deformation could be more difficult, but the ascent of mafic magma can still be detected, and its volume estimated, from geochemical data34. In this regard, we underline that starting from 2018, the anomalous H2S content found in the monitored fumaroles34, is consistent with the ascent of mafic, volatile-rich (2 wt. % CO2, 4 wt. % H2O) magma degassing at 150 MPa, which point to ascent depths of 6 km, strikingly similar to our calculations for the recharge of the main magma chamber34. As of today, such magma recharge seems to be escaping geodetic/seismological detection, suggesting it is below a minimum detection threshold of the network. Yet, this should stimulate actions towards improved preparedness of the population living inside the caldera and further development of the volcano multiparametric monitoring network in constraining deeper sources, testing its sensitivity to such signals, and enhancing effective management of volcanic crises in one of the world’s most hazardous volcanic areas. Hence, our results can be valuable to the scientific community in informing forward models of ground deformation, testing geodetic network sensitivity in the presence of superimposed deformation sources. Our model provides a threshold for a timely detection of the precursory phases before dyke formation, attempting to catch the critical state of the magma reservoir before magma movements. This is crucial in a condition of escalating unrest, like the one experienced in the last decade at Campi Flegrei, characterized by extensive evidence of magma-related observables. Moreover, we have provided realistic values of dyke aspect-ratio and reference for magmatic overpressure, which are critical values for testing dyke intrusion scenarios. Finally, long-lasting, low-volume injections, instead of discrete, recharge episodes102, might be more efficient to represent incremental steps in magma recharge growing magma chambers103. The effect of long-lasting magma injection would promote magma preservation in eruptible conditions49.

Methods

This section describes the technical approach we have pursued to estimate reliable geometric and mechanical properties suitable to be representative for the Nisida feeder dyke, Campi Flegrei magma and hosting shallow crust.

Estimation of feeder dyke geometry

At Campi Flegrei no direct information about dyke dimensions are available but based on recent results31 we have assessed the one feeding the eruption of Nisida tuff cone complex. We estimated the dyke width (w) considering the geometry of the dyke-induced deformation at the surface, which commonly produces a set of opposite-dipping conjugate faults of a partially preserved fissure-related graben104. The heave, i.e., the horizontal component of the displacement (Fig. 2), is considered a proxy for dyke thickness w employing the extension at surface across dyke-induced fault pairs (i.e., their cumulative heave)105,106. We estimate the cumulative heave using the relationship: \(w\approx 2\,\times {heave}\) of a single observed dyke-induced fault105. Although there are no direct measurements of the dyke in the field and available seismic datasets, its presence is suggested by a localized seismic reflection blanking disturbance31. Moreover, graben width (wg) and the dip of bounding faults measured at the surface are commonly used to estimate the dyke upper-tip depth (Htip) as follows: \({H}_{{tip}}=\frac{{{{{\boldsymbol{w}}}}}_{{{{\boldsymbol{g}}}}}}{2}\,\times \tan \alpha\). Where α is the average fault dip, assumed constant with depth104,107. We are also aware that this method may have some limitations, as it can overestimate the dyke upper tip depth by up to 40%82, therefore we consider this potential bias accordingly.

Magma properties

To seek an accurate calculation of the magma buoyancy term, the chemical composition of melt inclusions has been used to estimate the density of the magma, adopting the Python script of Iacovino and Till108.

The magma bulk Modulus km (modulus of incompressibility) is obtained using equation39,40:

$$k=\Delta P\frac{V}{\Delta V}=\Delta P\frac{V}{(\Delta {V}_{g}+{\Delta V}_{m})}=\frac{{k}_{g}{k}_{m}}{{k}_{m}x+{k}_{g}(1-x)}$$
(16)

where k is the Bulk Modulus of the multi-phase magma, x is the bubble fraction (i.e., the H2O content of the magma), kg is the bulk modulus of the gas component, km is that of the melt component, ΔP is the pressure change, ΔVg is the volume change of bubbles, and ΔVm is the volume change of melt and crystals.

The compressibility of magma βm is then obtained as the reciprocal of the bulk modulus:

$${\beta }_{m}=\frac{1}{k}$$
(17)

Host-rock properties

We estimated the elastic properties of the host rock from the seismic velocities of P-waves and S-waves (VP, VS, respectively) retrieved using travel-time tomography of natural earthquakes that occurred during the ongoing unrest by Giacomuzzi et al.36. We used the seismic velocity values of the upper 6 km of the crust at Campi Flegrei, representative of the host rock crossed by feeder dykes and of the upper plumbing system20, and assuming a conservative uncertainty of 10%. We have calculated the Poisson ratio v, based on the VP/VS ratio33 given by:

$$v=\frac{{\left(\frac{{V}_{P}}{{V}_{S}}\right)}^{2}-2\,}{2\,\left({\left(\frac{{V}_{P}}{{V}_{S}}\right)}^{2}\right.-\,\left.2\right)}$$
(18)

Where VP and VS are in m s−1.

The dynamic Young’s modulus Ed (modulus of elasticity, in Pa) has been calculated using:

$${E}_{d}=2G\left(1+v\right)=2\left(1+v\right){\rho }_{r}{V}_{S}^{2}$$
(19)

where G is the shear modulus.

To estimate the host-rock bulk modulus Kr (or modulus of incompressibility, in Pa), we considered that the infill of the caldera of Campi Flegrei is mainly composed of tuffs, loose pyroclastic deposits, hydrothermally altered rocks, and subordinately by thermometamorphic rocks having a similar average density25,37,38,51,52,109 (Supplementary Material). Hence, we used its mutual relationship with the dynamic Young’s Modulus Ed as:

$${K}_{r}=\frac{{E}_{d}}{3(1-2v)}$$
(20)

The compressibility of host-rock βr is then obtained as the reciprocal of the bulk modulus.

Ground deformation associated with a magma chamber inflation

To estimate the ground deformation due to volume variation in the magma chamber, we used the sill model of Fialko et al.70. The current deformation, instead, is best fitted using the point-source Mogi model, in agreement with Giudicepietro et al.28, assuming an elastic half-space above the source. We used a Matlab script provided by Battaglia et al.110, and employing the crustal characteristics of Campi Flegrei calculated in this work (see “Results”).