Introduction

Thermoelectric materials, capable of directly converting heat into electricity and vice versa, have attracted increasing attention for their potential in waste heat recovery, power generation, and solid-state refrigeration. The efficiency of thermoelectric materials is governed by the dimensionless figure of merit, zT, which is maximized by achieving high electrical conductivity (σ), a large Seebeck coefficient (S), and low thermal conductivity (κ). Over the past decades, considerable progress has been made in reducing thermal conductivity through strategies such as enhanced phonon scattering, lattice anharmonicity, and nanostructuring1,2. However, many thermoelectric materials with intrinsically low thermal conductivity suffer from poor mechanical integrity — particularly brittle fracture — which impedes their processability and scalability in device integration3,4,5.

Layered thermoelectric materials, such as bismuth telluride (Bi2Te3) and tin selenide (SnSe), exemplify this trade-off. Bi2Te3 achieves a benchmark zT above 1.0 at room temperature due to its anisotropic lattice bonding that effectively suppresses phonon transport. However, its weak interlayer bonding leads to mechanical fragility and susceptibility to cleavage under mechanical stress6,7. Similarly, SnSe exhibits an impressive zT of ~3.0 owing to its ultralow thermal conductivity and favorable electronic properties, yet its orthorhombic crystal structure features low-energy cleavage planes that result in poor mechanical robustness1,2. Efforts to improve their structural integrity—such as incorporating secondary phases, engineering grain boundaries, and introducing nanocomposites—often come at the expense of thermoelectric performance or introduce processing complexity, posing challenges to industrial scalability6,8,9.

P-type Zintl-based thermoelectric compounds, including YbZn2Sb2 and YbCd2Sb2, face similar limitations, despite their n-type counterparts having demonstrated promising potential in both thermoelectric and mechanical properties. These materials exhibit excellent thermoelectric properties due to their complex atomic bonding networks, which combine covalent and ionic interactions that reduce lattice thermal conductivity and enhance the Seebeck coefficient10,11. However, their layered crystal structure also makes them prone to brittle failure, complicating processing and device assembly. For instance, p-type YbZn2Sb2 prepared via conventional one-step ball milling often develops cracks after sintering, and the resulting samples fragment easily during handling or machining—hindering their practical implementation3,4.

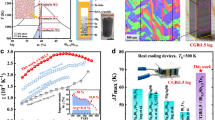
To address these limitations, we propose a fresh graded ball milling strategy that fundamentally restructures the microstructure to improve mechanical durability while preserving thermoelectric functionality. This two-stage process generates finer, more rounded grains, increased dislocation density, and promotes the formation of intermediate-angle grain boundaries (Fig. 1a). These microstructural modifications enhance Griffith’s fracture energy (Gc) and fracture toughness, shifting the mechanical failure mode from rapid, catastrophic transgranular fracture to a more ductile-like and controlled intergranular tearing12,13,14. This enables the fabrication of crack-free, large-size p-type YbZn2Sb2 disks (20 mm in diameter) via spark plasma sintering that can be precision-cut into uniform microscale dices (500 μm × 500 μm), addressing a long-standing barrier to device-level integration (Fig. 1b). Importantly, this approach demonstrates strong versatility across a broad family of brittle Zintl compounds, including AZn2Sb2, AMg2Sb2, and ACd2Sb2 (A = Yb, Mg, Ca, Sr, Ba). By compositional optimization, we further develop p-type Yb0.5Mg1.3Zn1.2Sb2, which exhibits a pre-formation cohesive energy of 9.1 eV atom-1 and maintains a relatively low lattice thermal conductivity of 0.5 W m−1 K−1 (Fig. 1c) at room temperature15,16,17,18,19,20,21,22. Carrier concentration is further enhanced through Yb deficiency at the grain boundaries, resulting in high thermoelectric performance without compromising processability. Building on this, we construct a fully integrated thermoelectric module by pairing p-type Yb0.5Mg1.3Zn1.2Sb2 with n-type Mg3.1Nb0.1Sb1.5Bi0.49Te0.01, achieving a conversion efficiency of exceeding 10% under a temperature difference of 458 K (Fig. 1d)23,24,25,26. Together, these results establish a robust, scalable strategy for designing mechanically durable and high-performance thermoelectric materials, offering a promising route toward practical energy conversion technologies.

Fig. 1: Visualizing cohesive fracture energy for mechanical integrity, processability, and thermoelectric performance.
figure 1

a Schematic illustrating how cohesive fracture energy correlates with key microstructural parameters —including grain roundness, size, dislocation density, and fracture surface characteristics— driving a transition from transgranular to intergranular fracture. b Images of low fracture energy (L-FE) and high fracture energy (H-FE) YbZn2Sb2 samples after spark plasma sintering (left) and subsequent precision machining (right), highlighting improved processability in H-FE samples. c Correlation between lattice thermal conductivity (κl) and pre-formation cohesive energy15,16,17,18,19,20,21,22. Here, the pre-formation cohesive energy (Epre) represents the total cohesive energy of the constituent pure elements (A/B) before the formation of compound AxBy, serving as a baseline for calculating the cohesive energy of AxBy compounds. d Maximum energy conversion efficiency (ηmax) of thermoelectric modules based on Zintl, CoSb3, PbTe, and half-Heusler (HH) systems23,24,25,26. The cold-side temperature for all modules is near room temperature. The Zintl-based modules demonstrate strong potential for energy harvesting in low- to medium-grade waste heat regimes.

Full size image

Results

Enhanced mechanical properties and broader applicability

To address the inherent brittleness and limited processability of p-type Zintl-phase thermoelectric materials, we employed a graded ball milling (G-BM) approach (Methods and Supplementary Fig. 1). This method involves a two-stage milling process with varying rotational speeds, distinguishing it from conventional ball milling (C-BM). Unlike conventional methods that rely primarily on centrifugal force, the graded ball milling incorporates gravitational effects at lower speeds, resulting in optimized milling dynamics and controlled microstructure evolution. In this study, samples of YbZn2Sb2 prepared via graded ball milling are referred to as H-FE (high fracture energy), while those synthesized by conventional ball milling are designated as L-FE (low fracture energy) for comparison. Comprehensive structural and chemical analyses, including X-ray diffraction (XRD), scanning electron microscopy (SEM), and energy dispersive spectroscopy (EDS), confirm the high phase purity and uniform elemental distribution in both sets of samples (Supplementary Figs. 2 and 3). However, fractured surfaces of L-FE sample exhibit pronounced porosity and tear-like features (Supplementary Fig. 4), indicative of brittle behavior that complicates thermoelectric optimization and limits processability (Fig. 1b)27. In contrast, the G-BM method yields H-FE samples with substantial improvements in moldability and processability, enabling precise shaping and integration (Fig. 1b). These advances offer a reliable platform for investigating the mechanical origins of fracture resistance in brittle thermoelectrics.

To evaluate mechanical performance, we employed modified small punch (MSP) testing, which requires flat disks 10 mm in diameter and less than 1 mm thick28,29. Due to their low structural integrity, L-FE samples could not be processed to meet this specification. H-FE samples, however, exhibit a mean MSP strength of ~38.2 MPa and a fracture energy of 2.9\(\times\)10-5 J, with fracture path similar with the commercial p-type Bi2Te3 ingots after MSP testing30 (Fig. 2a and Supplementary Fig. 5a). The strength distribution shows positive skewness, suggesting a greater prevalence of samples with above-average strength. Post-MSP fractured surfaces reveal a higher density of tear-like microstructures in H-FE samples compared to L-FE (Supplementary Figs. 4 and 5b). These structures are likely instrumental in impeding crack propagation and dissipating stress27, which likely contribute to stress dissipation and crack deflection27,31. Compressive strength is also markedly improved in H-FE samples, rising by more than 40% from 391.8 MPa to 556.5 MPa, along with reduced variability across measurements (Fig. 2b and Supplementary Fig. 6). True stress-strain profiles further reveal that H-FE samples could sustain strains up to ~9% before failure, with compressive fracture energy reaching ~3.7 \(\times\) 10-4 J (nearly double that of L-FE samples), highlighting enhanced resistance to cracking (Fig. 2c)32.

Fig. 2: Robust mechanical properties and broad applicability of the graded ball milling strategy.
figure 2

Comparison of mechanical properties between L-FE and H-FE samples: a modified small punch (MSP) strength, b compressive strength, c true stress and corresponding fracture energy, d Vickers hardness, and e residual stress profiles. f The graded ball milling strategy is successfully extended to a wide range of AB2Sb2-based Zintl compounds (A = Yb, Mg, Ca, Sr, Ba; B = Mg, Zn, Cd). Insets show optical images of the synthesized samples (the diameters of all samples are 10 mm), highlighting their superior moldability and machinability compared to those produced by conventional methods. Here, we use Origin 2021 Software to calculate the box plots. Every point contains at least 5-time measurements. Error bars denote mean ± standard deviation.

Full size image

Hardness measurements reveal substantial heterogeneity in L-FE samples (ranging from 2.75 to 4.25 GPa), reflective of microstructural disorder. In contrast, H-FE samples exhibit a consistent hardness of ~4.24 GPa, corresponding to an ~20% enhancement and improved homogeneity (Fig. 2d and Supplementary Fig. 7). This uniformity is critical for applications requiring mechanical reliability under thermal or vibrational stress. The fracture toughness of H-FE samples is also improved, as indicated by reduced crack propagation lengths and narrower data dispersion. To further assess mechanical stability, residual stress was measured according to the GB/T 7704 standard. L-FE samples display a heterogeneous stress profile with steep gradients ranging from -16 MPa to 48 MPa (Fig. 2e), leading to localized strain accumulation and increased risk of failure33. In contrast, H-FE samples exhibit a uniform residual stress distribution (12 ± 2 MPa), minimizing internal stress concentrations and enhancing long-term reliability.

Beyond YbZn2Sb2, the graded ball milling strategy was successfully extended to a broad family of brittle Zintl compounds, including AZn2Sb2, AMg2Sb2, and ACd2Sb2 (A = Yb, Mg, Ca, Sr, Ba). XRD patterns confirm consistently high phase purity and improved crystallinity in these samples compared to those produced via C-BM (Supplementary Fig. 8). This enhancement stems from the controlled energy input during graded ball milling, which stabilizes the phase and mitigates premature fracture during synthesis. It can be clearly observed that the G-BM samples generally exhibit higher densities than the C-BM samples, closer to the theoretical values, which is likely due to the smaller grain size and increased surface energy in the G-BM samples (Supplementary Table 1). Despite natural variability in mechanical response, all compounds prepared by graded ball milling achieve mean MSP strengths above 30 MPa (much higher than the raw commercial p-type Bi2Te3 ingots, ~16.97 MPa)30, demonstrating the broad applicability of this strategy across multiple compositions (Fig. 3f).

Fig. 3: Microstructure characterization and fracture response.
figure 3

a, b Distributions of the shortest distance from grain interiors to the grain boundaries. c1, c2 Grain size statistics based on circle-equivalent diameter. d, e Maps of geometrically necessary dislocations (GND). f, g Crack propagation responses under uniaxial tensile loading, where the grey lines delineate individual grains. h Cohesive fracture energy extracted from the fracture zones shown in (f, g), comparing L-FE and H-FE samples.

Full size image

By addressing key limitations, such as poor mechanical resilience and low synthetic yield, the graded ball milling approach offers a practical and effective pathway for the scalable fabrication of brittle thermoelectric materials, bridging the gap between mechanical integrity and functional performance.

Microstructural optimization and enhanced fracture resistance

For brittle materials with limited plastic deformation under stress, fracture resistance is often governed by Griffith’s fracture energy \({W}_{{frac}}\), which can be expressed as \({W}_{{frac}}={G}_{c}{\varGamma }_{l}\), where \({G}_{c}\) is the critical energy release rate and \({\varGamma }_{l}\) denotes a phase-field regularized crack surface, approximated by a volume integration towards the crack density function34,35,36. Gc is strongly influenced by microstructural factors such as grain roundness (R), grain size (D), and dislocation density (ρd). Grain roundness could impact the stress concentration near grain boundaries. Angular grains with sharp edges and corners lead to higher local stress concentrations, promoting crack initiation and propagation, tending to lower Gc. In contrast, rounded grains distribute stress more uniformly, potentially enhancing fracture energy. Grain size influences the crack path and the energy required for crack propagation. Smaller grains, particularly when uniformly distributed, introduce more grain boundaries, which serve as obstacles to crack propagation. In brittle materials, dislocations can influence crack propagation by modifying the local stress field. While their mobility is limited, localized dislocation activity may contribute to crack tip shielding, leading to an increase in Gc. Additionally, fracture behavior is sensitive to crystallographic anisotropy, with grain orientation and slip angles (θ) further modulating the fracture response13,36,37,38,39. Therefore, materials with smaller rounded grains, high dislocation densities, and intermediate-angle grain boundaries tend to exhibit higher Wfrac.

To evaluate these relationships, we analyzed the microstructural attributes of L-FE and H-FE YbZn2Sb2 samples. The shortest distance to grain boundaries was analyzed to evaluate grain roundness. Over 65% of grains in H-FE samples exhibit a shortest distance of approximately 0.1 μm to the grain boundaries, compared to only ~35% in L-FE samples, where the maximum distance extends to 0.6 μm (Fig. 3a, 3b, and Supplementary Fig. 9). This substantial difference underscores the improvement in grain morphology for the H-FE samples, with a more cohesive and homogeneous microstructure. Grain size analysis shows a dramatic refinement in H-FE samples, with average diameters reduced from ~0.79 μm to ~0.26 μm and a near elimination of grains larger than 0.4 μm (Fig. 3c1 and Supplementary Fig. 10a). This size reduction aligns with the Hall-Petch relationship, which predicts increased yield strength with finer grains, due to impeded dislocation motion.

Geometrically necessary dislocation (GND) mapping further highlights differences between the two sample types (Fig. 3d and 3e). In H-FE samples, the probability of the Nye tensor equaling 1 × 1015 m−2 surpasses 20%, which is approximately 9.3% higher than that in L-FE samples (Supplementary Fig. 11). This elevated dislocation density suggests a more complex internal stress state of H-FE samples, enabling the material to accommodate deformation more effectively and resist fracture40. Additionally, in L-FE samples, a distinct orientation is observed, particularly along [0001], with dislocation densities concentrated within specific grains. In contrast, H-FE samples exhibit a more homogeneous grain inclination angles (Supplementary Fig. 12), which reduces stress localization and improves resistance to deformation and fracture41. This microstructural homogeneity optimizes the balance between strength, modulus, and toughness, contributing to improved mechanical stability42,43,44.

To further understand these improvements, we applied a phase-field regularized cohesive fracture model to analyze the relationship between the reaction force and loading displacement36,45 (Methods). Simulation results indicate that L-FE samples fracture under a maximum tensile strength of 367 MPa, with crack propagation occurring primarily via a transgranular model along a linear trajectory with minimal fracture path deflection (Fig. 3f, Supplementary Fig. 13a and b). This behavior stems from the alignment of microstructures, which generate localized stress concentrations, facilitating crack penetration through large grains. In contrast, H-FE samples exhibit a nearly twofold increase in effective tensile displacement and a significantly higher tensile strength of 542 MPa. Influenced by intricate microstructural transformation (grain structure, dislocation density, and cohesive interactions), the fracture pattern shifts towards an intergranular pattern with greater path deflection, resulting in a more stable fracture process and reduced crack propagation velocity (Fig. 3g, Supplementary Fig. 13c and d).

Between the parameters governing fracture behaviors, the critical energy release rate (Gc) emerges as the dominant factor. As demonstrated in the model with modifications exclusively to the critical energy release rate (from 1.05 × 10−4 J mm−2 to 1.85 × 10−4 J mm−2), the fracture pattern transitions from abrupt, catastrophic failure to a more gradual and stable process, accompanied by a significant increase in tensile strength to 548 MPa, comparable to the H-FE samples (Supplementary Fig. 14a)36. In contrast, the model incorporating variations in grain orientations retained pronounced fracture exhibiting localized stress intensification and ultimate tensile strengths confined to ~380 MPa (Supplementary Fig. 14b). Moreover, among the grain structure, dislocation density, and cohesive interactions, the ~67% reduction in grain size, as observed experimentally, is expected to play a pivotal role in Gc to enhance mechanical properties.

Finally, standard notched specimen tests reveal that H-FE samples demonstrate not only higher strain energy but also nearly double the cohesive fracture energy compared to L-FE samples (Fig. 3h, Supplementary Figs. 15 and 16)46,47. This elevated fracture energy threshold indicates an enhanced resistance to crack propagation, reinforcing the superior toughness and durability of H-FE samples under tensile loading conditions. These findings accentuate the direct correlation between microstructural optimization and fracture resistance, highlighting the effectiveness of the graded ball milling strategy in enhancing mechanical durability while preserving thermoelectric functionality—an essential advance for scalable device fabrication.

Optimized thermoelectric performance and module integration

Among the various Zintl-phase materials enhanced through the graded ball milling approach, Yb0.5Mg1.3Zn1.2Sb2 emerging as a particularly promising candidate following targeted compositional tuning (Supplementary Fig. 17). This compound exhibits a remarkable zT exceeding 1.0 at 773 K, attributed to its favorable combination of enhanced electrical transport and suppressed thermal conductivity. Specifically, its electrical conductivity increases with temperature, consistent with semiconducting behavior, while the Seebeck coefficient reaches a peak of approximately 230 μV K-1 supported by a carrier concentration of ~2 × 1019 cm-3 (Fig. 4a–c). Hall measurements and first-principles calculations indicate that the relatively weak Yb-Sb bond plays a vital role on the lifted carrier concentration (Supplementary Fig. 18). Elemental mapping and integrated EDS intensity profile (Fig. 4d) show that Yb is deficient at the grain boundaries, which is due to its non-stoichiometric behavior and the relatively weak atomic bonding48,49,50. In the 122-type Zintl structure, Yb atoms occupy the Mg1 site, contributing to the electron-crystal characteristic of the compound, and simultaneously reinforcing the role of vacancies in promoting p-type conduction and thermoelectric performance (Fig. 4e, f). Compared with other synthetic routes, our samples show reduced carrier mobilities, ~28 cm2 V-1 s−1 (Supplementary Fig. 19), caused by abundant grain boundaries, ensuring a favorable balance between thermoelectric and mechanical properties.

Fig. 4: Exceptional thermoelectric performance for low-to-medium grade waste heat harvesting.
figure 4

Temperature-dependent a electrical conductivity (σ), b Seebeck coefficient (S), and c Hall carrier concentration (nH), and mobility (μH) of Yb0.5Mg1.3Zn1.2Sb2 compounds. d HAADF-STEM images showing a grain boundary in Yb0.5Mg1.3Zn1.2Sb2 with corresponding EDS mapping showing Yb deficiency. e Atomic resolution HAADF-STEM image of Yb0.5Mg1.3Zn1.2Sb2 along the [11\(\bar{2}\)0] orientation and the corresponding fast Fourier transform pattern. f Integrated EDS intensity profile along the y-axis with quantification after multi-variate analysis48. g Temperature-dependent thermal conductivity (κ)17,18,19. h1 Temperature-dependent zT and h2 average zT (zTave) in comparion with literature17,18,19. i Simulated maximum conversion efficiency (ηmax) of a Zintl-based unicouple depending on the geometrical configuration, where the y-axis shows the ratio between height of Zintls and Bi2Te3-based (BT) compounds and the x-axis shows the ratio of cross section between p- and n-type legs. j Measured and predicted inner resistance (Rin) and open-circuit voltage (Voc) as a function of temperature difference. k Conversion efficiency (ηout) of the Zintl-based module under different temperature differences.

Full size image

Contrary to typical trends where improved mechanical stability leads to increased thermal conductivity due to enhanced phonon transport, the H-FE Yb0.5Mg1.3Zn1.2Sb2 samples exhibit relatively low thermal conductivity across the entire temperature range. This suppression arises from multiple microstructural factors: the fine grain size reduces phonon mean free paths, while elevated dislocation density at grain boundaries increases phonon scattering and boundary resistance51 (Fig. 4g). Moreover, the graded ball milling strategy introduces engineered grain roundness and disorientation, further intensifying grain boundary scattering and reducing lattice thermal conductivity toward its theoretical minimum (Supplementary Fig. 20)18,52,53. These combined effects decouple phonon and electron transport, allowing simultaneous optimization of mechanical and thermoelectric properties—firmly positioning Yb0.5Mg1.3Zn1.2Sb2 as a leading p-type Zintl material for energy conversion17,18,19 (Fig. 4h and Supplementary Fig. 21). In contrast, while several previously reported materials offer high zT, their scalability, mechanical reliability, and integration feasibility remain uncertain. Furthermore, the thermal stability evaluation of the material is conducted. The mass variation of Yb0.5Mg1.3Zn1.2Sb2 sample remains below 0.5% throughout a 10-cycle thermogravimetric analysis (Supplementary Fig. 22), indicating negligible thermal decomposition or structural degradation. Thermoelectrical performance of Yb0.5Mg1.3Zn1.2Sb2 sample exhibits a variation consistently below 5% over three thermal cycles from 300 K to 773 K (Supplementary Fig. 23). Moreover, the sample retains stable thermal conductivity after being exposed to air for over one year (Supplementary Fig. 24), indicating excellent oxidation resistance.

To validate the practical potential of this material, we constructed a Zintl-based thermoelectric module, pairing p-type segmented Yb0.5Mg1.3Zn1.2Sb2/bismuth telluride with n-type Mg3.1Nb0.1Sb1.5Bi0.49Te0.01. Prior to fabrication, finite element simulations were conducted to determine the optimal geometrical configuration for maximizing conversion efficiency (ηmax) (Fig. 4i). Each interfacial contact resistivity for both n-type and p-type junctions is ensured below 15 μΩ cm2, fulfilling practical operational requirements (Supplementary Fig. 25). The resulting module exhibits an internal resistance of ~91 mΩ and an open-circuit voltage of ~0.41 V under a 458 K temperature gradient—values that align closely with theoretical predictions, indicating excellent electrical connectivity and minimal parasitic losses (Fig. 4j). A conversion efficiency of 10% is achieved at a temperature difference of 458 K (Fig. 4k and Supplementary Fig. 26) and keeps stable over more than 25 thermal cycles (~40 h) (Supplementary Fig. 27), underscoring the viability of graded-ball-milling-engineered Zintl materials for waste heat recovery and low-to-medium temperature power generation.

Discussion

This work establishes graded ball milling as an effective strategy to simultaneously enhance the mechanical robustness and thermoelectric performance of brittle Zintl-phase materials. Through grain refinement, elevated dislocation density, and promotion of intermediate-angle grain boundaries, this approach substantially improves mechanical stability and processability while preserving ultralow thermal conductivity and optimized electronic transport. The enhanced workability enables precise sample shaping and reliable module assembly, leading to a robust Yb0.5Mg1.3Zn1.2Sb2-based thermoelectric module that achieves 10% conversion efficiency under a 458 K temperature gradient, operating for more than 40 hours steadily. More broadly, this fracture-energy-guided strategy offers a general framework for improving the manufacturability of brittle thermoelectric materials without compromising functional properties. By bridging the long-standing gap between mechanical reliability and high zT, it provides a scalable path toward the integration of robust, high-performance thermoelectric modules for practical energy harvesting applications.

Methods

Material synthesis and module fabrication

High-purity elements were used for synthesis: magnesium (pieces, 99.9%, Sinopharm Chemical Reagent Co., Ltd), zinc (powder, 99.999%, Sinopharm Chemical Reagent Co., Ltd), ytterbium (junks, 99.9%, ThermoFisher Scientific (China) Co., Ltd.), calcium (granules, 99.5%, Aladdin Reagent Co., Ltd.), strontium (particles, 99%, Shanghai Macklin Biochemical Technology Co., Ltd.), barium (particles, 99%, Aladdin Reagent Co., Ltd.), cadmium (powder, 99.999%, Shanghai Titan Technology Co., Ltd.), antimony (powder, 99.999%, Sinopharm Chemical Reagent Co., Ltd), bismuth (powder, 99.999%, Sinopharm Chemical Reagent Co., Ltd), niobium (powder, 99.99%, Shanghai Titan Technology Co., Ltd.), and tellurium (powder, 99%, Sinopharm Chemical Reagent Co., Ltd). These elements were weighed according to stoichiometric ratios for the following p-type Zintl compounds: (Yb, Mg, Ca, Sr, Ba)A(Zn, Mg, Cd)B2Sb2, (YbZn2Sb2)0.6(YbMg2Sb2)0.4, (MgZn2Sb2)0.6(MgMg2Sb2)0.4, (CaZn2Sb2)0.2(CaMg2Sb2)0.8, (MgZn2Sb2)0.2(CaZn2Sb2)0.4(CaMg2Sb2)0.4, (YbZn2Sb2)0.1(MgZn2Sb2)0.5(YbMg2Sb2)0.4. The n-type compound is Mg3.1Nb0.1Sb1.5Bi0.49Te0.01. All mixtures were sealed in stainless-steel ball-milling jars inside an argon-filled glovebox. The conventional ball milling (C-BM) process was conducted using an oscillating ball mill (MSK-SFM-3-II, Hefei Kejing Material Technology Co., Ltd., China) with the first-stage ball-milling process. For the graded ball milling (G-BM) process, it included the two stages shown in the Supplementary Table 2. For the n-type material, a high-energy ball milling process at 875 rpm for 20 hours was applied. The resulting powders were loaded into cylindrical graphite dies (10 mm diameter) and consolidated by spark plasma sintering (SPS) (Dr. Sinter 725, Sumitomo Coal Mining Co., Ltd., Japan). The p-type Zintl samples were sintered at 823 K for 5 minutes under a uniaxial pressure of 70 MPa, while the n-type materials were sintered at 1023 K for 3 minutes under 50 MPa. Bulk n- and p-type joints were fabricated with Fe/Fe-Sb diffusion barrier layers. The sintered pellets were cut into dices of 3.0 mm × 3.0 mm × 6.0 mm, with 0.1 mm-thick barrier layers applied to the top and bottom surfaces. These were assembled into thermoelectric modules using nano-silver paste and Al2O3 ceramic plates as substrates24.

Characterization

Phase composition and crystal structure were examined using X-ray diffraction (XRD, Rigaku D/Max-2550 PC, Japan) with Cu Kα radiation (λ = 1.5406 Å) operated at 40 kV and 100 mA. Sample densities were measured using the Archimedes method with alcohol as the immersion medium. Micro-pellets were sectioned using a precision slicer (DS623, Shenyang Hoyan Technology Co., Ltd., China). Mechanical properties were evaluated as follows: modified small punch (MSP) strength and compressive strength were tested using a universal testing machine (AGS-X-10kN, Shimadzu Co., Ltd., Japan) equipped with appropriate fixtures. Hardness and fracture toughness were determined using a microhardness tester (HV-1000, Shenzhen Lunjie Technology Co., Ltd., China). Residual stress was measured with a SmartLab residual stress system (Hangzhou Research Interest Information Technology Co., Ltd., China). Microstructural analysis, elemental distribution, and crystallographic orientation mapping (EBSD) were conducted using a thermal field emission scanning electron microscope (FE-SEM: MAIA3, TESCAN, Czech Republic) equipped with an EBSD detector (Bruker QUANTAX CrystAlign 400i). EBSD data were analyzed using the ATEX software package54. High-resolution structural and compositional characterization at the atomic scale was performed using a spherical aberration-corrected transmission electron microscope (Fischione Model M3000, USA).

The temperature-dependent relative length change (ΔL/L0) was measured by a thermal dilatometer (DIL 402C, Netzsch, Germany). Electrical resistivity and Seebeck coefficient were simultaneously measured under a helium atmosphere using a commercial system (ZEM-3, ULVAC-RIKO, Japan), with a combined measurement uncertainty of ~7%. Thermal conductivity (κ) was calculated using the relation \(\kappa=D{C}_{p}\rho\), where D is the thermal diffusivity measured by a laser flash apparatus (LFA 457, Netzsch, Germany), \({C}_{p}\) is the specific heat capacity estimated from the Dulong–Petit law, and ρ is the sample density. The overall uncertainty in κ is estimated to be within 5%, resulting in a total uncertainty in zT of less than 12%. Hall carrier concentration and mobility were measured using the van der Pauw method on a Hall measurement system (Lakeshore 8400 Series HMS, USA). Contact resistivity was determined using a linear resistance scanning technique with a custom-built four-probe setup. The conversion efficiency of thermoelectric modules was measured using a commercial performance evaluation system (Shanghai Fuyue Vacuum Technology Co., Ltd., China)24.

Damage mechanics modeling

To evaluate fracture behavior, we employed a phase-field regularized cohesive fracture model designed for brittle materials. This framework is rooted in Griffith’s fracture theory and captures crack initiation and propagation through a smeared damage formulation. As for the material model, an anisotropic cohesive fracture model35,36,55,56 and its post-processing are implemented using the finite element programming packages AceGen and AceFEM45,57, respectively. The detailed material model is based on the phase-field regularized cohesive model, which is rooted in Griffth’s fracture theory. The total energy density \({\psi }_{{total}}\) is calculated as:

$${\psi }_{{total}}\left({{\boldsymbol{\varepsilon }}},d,\nabla d,\phi \right)={\psi }_{{bulk}}\left({{\boldsymbol{\varepsilon }}},d\right)+{\psi }_{{frac}}\left(d,\nabla d,\phi,{G}_{c}\left(R,p,{GBs}\right)\right)+{\psi }_{{ext}}\left({{\boldsymbol{u}}}\right)$$
(1)

\({\psi }_{{total}}\) is decomposed into bulk energy density \({\psi }_{{bulk}}\), fracture energy density \({\psi }_{{frac}}\), and external energy density \({\psi }_{{ext}}\). \({{\boldsymbol{u}}}\), \({{\boldsymbol{\varepsilon }}}\), and \(d\) denote the displacement vector, strain tensor, and phase-field variable, respectively. Therefore, the fracture energy \({W}_{{frac}}\) is calculated based on Griffith’s fracture theory.

$${W}_{{frac}}= {\int }_{V}{G}_{c}\left(R,p,{\rho }_{d}\right)\gamma \left(\phi,d \right){dV},{\Gamma }_{l}={\int }_{V}\gamma \left(\phi,d \right){dV} \\= {\int }_{V}\frac{1}{{c}_{0}}\left(\frac{\omega \left(d\right)}{{l}_{f}}+{l}_{f}\nabla d\,\bullet \,{{\boldsymbol{A}}}\,\bullet \,\nabla d\right){dV}$$
(2)

\(\omega \left(d\right)=2d-{d}^{2}\) denotes a crack geometric function. The coefficient \({c}_{0}\) is defined as \({c}_{0}=\pi\). The fracture energy \({W}_{{frac}}\) is expressed as: \({W}_{{frac}}={G}_{c}{\varGamma }_{l}\), which formulates the fracture energy using a volume integral form. Here, the critical energy release rate possesses a positive dependence on some quantities of grains \({G}_{c}\left(R,p,\,{\rho }_{d}\right)\propto \left\{R,{\left(\frac{1}{p}\right)}^{2},\,{\rho }_{d}\right\}\). R, p, ρd, and ϕ denote the grain roundness, grain size, dislocations, and misorientations of the targeted compounds. A second-order anisotropic structure tensor A is employed to formulate the grain’s fracture performance.

$${{\boldsymbol{A}}}=\left[\begin{array}{cc}{\cos }^{2}\left(\phi \right) & \cos \left(\phi \right)\sin \left(\phi \right)\\ \cos \left(\phi \right)\sin \left(\phi \right) & {\sin }^{2}\left(\phi \right)\end{array}\right]$$
(3)

As for the bulk energy density function, it is expressed with a quadratic function based on cohesive degradation function \(g\left(d\right)\) as:

$${\psi }_{{bulk}}\left({{\boldsymbol{\varepsilon }}},d\right)=g\left(d\right){\psi }_{e}^{+}\left({{\boldsymbol{\varepsilon }}}\right)+{\psi }_{e}^{-}\left({{\boldsymbol{\varepsilon }}}\right)$$
(4)

where \({\psi }_{e}^{+}\) and \({\psi }_{e}^{-}\) denote the tensile and compressive strain energy densities, respectively. The degradation is expressed with linear cohesive softening parameters \({a}_{1}\), \({a}_{2}\) and \({a}_{3}\).

$$g\left(d\right)=\frac{{\left(1-d\right)}^{2}}{{\left(1-d\right)}^{2}+{a}_{1}\left(1+{a}_{2}d+{a}_{3}{d}^{2}\right)}$$
(5)