Introduction

Heat transfer in nanometre-sized gaps is of great importance for various technologies such as thermophotovoltaics1, thermal imaging2, or thermal management3,4,5. From a fundamental point of view, heat transfer between bodies separated by a distance of the order of 1 nm or smaller is extremely interesting because in this crossover regime between heat conduction and radiative heat transfer, up to three different heat carriers can give a significant contribution, namely electrons, phonons, and photons. Focusing on metallic systems, two limiting cases of nanoscale thermal transport are relatively well-understood by now. On the one hand, when two metallic surfaces are separated by gaps larger than a few nanometres, the heat transfer is dominated by thermal radiation in the so-called near-field regime3,4,5. In this case, the thermal radiation exchange is dominated by evanescent waves that lead to overcoming Planck’s blackbody limit by several orders of magnitude6. This radiative heat transfer between metallic materials has been experimentally investigated in the extreme near-field regime using cantilevers with embedded thermocouples down to gap sizes ~3 nm7, and the results were found in excellent agreement with the predictions of the theory of fluctuational electrodynamics, which is considered as the standard model for near-field radiative heat transfer (NFHRT)8,9. For larger gaps, this physical picture has been verified using a variety of techniques, see ref. 10 and references therein.

On the other hand, in the contact regime, i.e., when metallic surfaces are in direct contact, it has been shown that the heat conductance is dominated by electron conduction, with phonons marginally contributing 5–10% of the total signal. This fact has been established with the help of picowatt-resolution calorimetric scanning probes11,12 and detailed simulations of both electron and phonon conduction in metallic atomic-sized contacts11,13,14. Overall, these studies have confirmed that the Wiedemann–Franz law is approximately fulfilled all the way down to single-atom contacts. This law relates the electronic contribution of the thermal conductance, \(K\), to the electrical conductance, \(G\), by \(K={L}_{0}{TG}\), where \(T\) is the absolute temperature and \({L}_{0}=\left(\frac{{\pi }^{2}}{3}\right){\left(\frac{{k}_{{{{\rm{B}}}}}}{e}\right)}^{2}\) is the Lorentz number15, \({k}_{{{{\rm{B}}}}}\) being the Boltzmann constant and \(e\) the electron charge. In the case of an Au single-atom contact, where \(G\) is typically equal to the electrical conductance quantum \({G}_{0}=\frac{2{e}^{2}}{h}\approx 12.9\) kΩ, this law predicts a thermal conductance approximately equal to \(2{K}_{0}\), where \({K}_{0}={\pi }^{2}{k}_{{{{\rm{B}}}}}^{2}T/3h\) is the thermal conductance quantum. Thus, an Au single-atom contact exhibits a room temperature (300 K) thermal conductance of ~0.57 nW/K, as it was experimentally reported11.

However, in the crossover between these two limiting cases, the situation is much less satisfactory, and the two main experiments realised in this regime have reported largely contradictory results. Kloppstech et al.15 carried out heat transfer measurements between an Au-coated near-field scanning thermal microscope tip and a planar Au surface for distances ranging from 7 nm down to 2 Å. They found heat fluxes four orders of magnitude larger than the values predicted by fluctuational electrodynamics, i.e., these results are largely incompatible with conventional NFRHT. Moreover, they reported a linear decay of the thermal conductance with the gap size, which is very difficult to reconcile with electron or phonon tunnelling across a vacuum gap. In fact, all theory attempts to elucidate these results, irrespective of the invoked heat carriers, have failed to reproduce both the order of magnitude and the gap-size dependence of the measured heat transfer16,17,18,19,20,21,22,23,24,25. On the other hand, Cui et al.26 reported heat transfer measurements in a few Å to 5 nm gap sizes between an Au-coated probe featuring embedded nanoscale thermocouples and a heated planar Au substrate. It was found that the thermal conductance of these metallic gaps depended drastically on the cleaning conditions, and upon aggressive cleaning signals could be decreased below the detection limit (~900 pW/K in that setup). Based on these observations, it was suggested that the large heat transfer reported by Kloppstech et al.15 could be to the presence of surface contaminants bridging the gap between the tip and the surface26.

Part of the problem to elucidate the origin of these contradictory results is the lack, thus far, of an experimental technique able to investigate the crossover between nanometre-sized gaps and the contact regime. To solve this controversy, here we present a systematic study of the heat conductance of Au atomic-sized contacts ranging from gap sizes of the order of 10 nm to deep into the contact regime (for electrical conductance values up to 100 \({G}_{0}\)). Our measurements are based on a scanning tunnelling microscope (STM) incorporating novel, custom-designed thermoelectric-resistive probes. Upon approaching the Au STM tip (at ~400 K) to an Au surface (at ~300 K), we typically find the onset of thermal signals at gap sizes of a few nm, much before there is any measurable electrical signal. These thermal signals grow approximately in a linear fashion up to the contact regime with thermal conductance values of a few nW/K, and they are reversible upon retracting the tip. These observations are in qualitative agreement with those by Kloppstech et al.15 and Cui et al.26, and, as we show here using state-of-the-art simulations, they are not compatible with electron tunnelling, phonon transfer across the gap, or NFRHT. In the contact regime, we typically observe a change in slope in the thermal conductance versus elongation curves. The slope in this regime is compatible with the Wiedemann–Franz law, while we observe background signals, reminiscence of the tunnel regime, that persist and decrease slowly up to very large contacts. Overall, our experimental results strongly suggest that the unusual heat transfer in our nanoscale metallic gaps is due to the presence of water menisci that bridge the gap between tip and sample and that are very difficult to avoid in standard high-vacuum conditions (\(2\times {10}^{-6}\) mbar in our case). We back up this hypothesis by providing molecular dynamics simulations of the heat conduction through gold-water meniscus-gold contacts that reproduce both the order of magnitude of the experimental thermal conductance as well as its unconventional gap-size dependence.

Results

Experimental setup

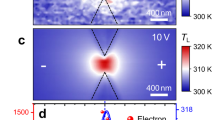
We use a custom-built STM incorporating a thermoelectric-resistive probe that also acts as a STM tip to experimentally study the thermal conductance between a tip and a substrate in the transition from the tunnelling to the contact regime. The probe (see Fig. 1a, b) consists of two welded Wollaston wires of approximately \(5\) µm in diameter and \(500\) μm in length, where the apex of one of the wires serves as STM tip (see Supplementary Notes 1 and 2 for details on the probe fabrication and modelling). Similar probes have been used before as thermal probes in SThM27. In the conventional approach, these probes are used as thermocouples, in contrast, we follow a novel approach using the welded Wollaston wires as both thermoelectric and resistive probes by utilising a multifrequency sensing technique (Fig. 1c). This approach has the important advantage of enabling in situ calibration of the probe (see “Methods” section). These Wollaston wire probes are far simpler to build than those previously used11,12,15,26.

Fig. 1: Experimental setup and measurement technique.
figure 1

a SEM picture of the STM thermoelectric-resistive sensor consisting of two welded Wollaston wires of Pt (right-hand-side wire) and PtRh10 (left-hand-side wire), of approximately 5 µm in diameter and 500 µm in length. b Zoom of the welded junction, which acts as an STM tip. The orientation of the substrate with respect to the sensor in working conditions is indicated by the golden horizontal line, and the effective apex of the tip is indicated by the red ellipse. c Schematics of the multifrequency measuring system. The ac voltages applied to the probe are \({V}_{1}=\left[{V}_{{{{\rm{heat}}}}}\left({f}_{{{{\rm{heat}}}}}\right)+{V}_{{{{\rm{bias}}}}}\left({f}_{{{{\rm{bias}}}}}\right)\right]/2\) and \({V}_{2}=Z\left[{-V}_{{{{\rm{heat}}}}}\left({f}_{{{{\rm{heat}}}}}\right)+{V}_{{{{\rm{bias}}}}}\left({f}_{{{{\rm{bias}}}}}\right)\right]/2\), where \({f}_{{{{\rm{heat}}}}}=31.123\) kHz and \({f}_{{{{\rm{bias}}}}}=51.987\) kHz. Differential amplifier #1 measures the voltage drop at the calibrated resistor \({R}_{{{{\rm{b}}}}}\) to extract the heating current; differential amplifier #3 measures the voltage drop at the sensor; and resistor \({R}_{{{{\rm{v}}}}}\) is used via differential amplifier #2 to set a variable offset for the voltage drop at the sensor. Resistors \({R}_{{{{\rm{b}}}}}^{{\prime} }\) and \({R}_{{{{\rm{v}}}}}^{{\prime} }\) are used to balance the circuit, and \({V}_{{{{\rm{A}}}}}\) measures the tip-substrate current.

Full size image

To measure the thermal conductance, the probe is heated above ambient temperature by applying an antisymmetric ac voltage to the probe to maintain the tip at zero volts. This ac voltage is applied at a frequency higher than the inverse of its thermal relaxation time (\(50\) ms, see Supplementary Note 3), \({f}_{{{{\rm{heat}}}}} \sim 31\) kHz, resulting in a constant temperature profile for the probe. Heat currents flowing between the tip and the sample alter the probe temperature and reflect in changes in its resistance, which are monitored by measuring the voltage drop \(\Delta V\) in the probe at the heating frequency. The tip temperature is obtained from the thermoelectric DC voltage drop of the probe, which reflects the temperature of the welded junction and consequently of the tip, which is in its proximity. In addition to the heating current, an ac bias voltage with 100 mV amplitude at a different frequency, \({f}_{{{{\rm{bias}}}}} \sim 51\) kHz, is applied symmetrically to the probe, keeping the substrate grounded, enabling the measurement of the tip-substrate current \(I\), both in the tunnelling regime and in contact via an IV amplifier connected to the sample. This tip-substrate electrical current contributes to the heat current at the tip and must be considered to obtain the thermal conductance of the contact. Indeed, the heat current at the tip is given by

$${Q}_{{{{\rm{t}}}}}=-K\left({T}_{{{{\rm{t}}}}}-{T}_{{{{\rm{s}}}}}\right)+\frac{{I}^{2}}{2G}$$
(1)

where \(K\) is the thermal conductance of the contact, \({T}_{{{{\rm{t}}}}}\) and \({T}_{{{{\rm{s}}}}}\) are the temperatures of the tip and substrate, respectively, and \(G\) is the electrical conductance of the contact. The second term is the Joule dissipation at the tip, assuming that the contact is symmetric.

The experiments are conducted in high-vacuum conditions (\(2\times {10}^{-6}\) mbar), avoiding convection effects and providing a relatively clean environment. The experimental procedure consists in approaching the apex of the probe to a gold substrate to form an atomic contact while both the thermal conductance and electrical conductance are simultaneously monitored. This is a variation of the widely used STM break-junction technique used to study electrical transport in atomic contacts28 and single-molecule junctions29. In this case, we use our thermoelectric-resistive probe as a STM tip, where the tip is the apex of the probe. The tip is further prepared in situ by indenting the gold surface repeatedly, which results in the coverage of the apex of the probe with gold. This procedure leads to an effective clean gold tip (see Supplementary Note 4 for further details). This in situ cleaning by repeated indentation is a standard procedure in experiments on atomic contacts28,30,31. After preparation, the tip is moved to a different region of the substrate.

The gold substrate is cleaned and flattened by flame annealing (see “Methods” section and Supplementary Note 5 for more details). After the flame annealing, the substrate is rapidly (within 5 min) introduced into the vacuum chamber and pumped down to minimise contamination by airborne contaminant species (the so-called adventitious carbon contamination32) (see Supplementary Note 6 for more details).

Experimental thermal conductance in the transition from tunnelling to contact

The substrate is scanned at constant current to find clean atomically flat terraces where no adsorbates are observed. In these clean regions, the apparent tunnelling barrier observed as the tip approaches the surface are of the order of 1 eV33,34, and no molecular signatures are detected in the approach conductance traces35 (see Supplementary Note 6). These values for the apparent tunnelling barrier, which are much lower than the work function, are typically observed in experiments on Au surfaces in ambient conditions (see Supplementary Note 6), and they are probably due to the presence of adsorbed water on the surface. Indeed, the gold surface is hydrophilic after the annealing, and some of the water condensed on the surface before entering the vacuum chamber will stay on the surface36. X-ray photoelectron spectroscopy (XPS) analysis of substrates prepared following the same protocol as those used in the experiment shows evidence of the presence of adsorbed water in addition to carbon species (see Supplementary Note 7). These XPS measurements were performed in another setup in UHV conditions at ambient temperature.

In these clean regions we find that at large tip-substrate distances (>20 nm) the thermal and electrical conductances are below the detection limits of our probe (\(K < 0.1\) nW/K, \(G < {10}^{-4.6}{G}_{0}\)), while the electrical conductance increases exponentially for decreasing tip-sample separations reaching a value \(G\approx {G}_{0}\) when a one-atom contact is established, this is the point of metallic contact (PMC). The tip is pushed further into the sample until the contact reaches a conductance of several \({G}_{0}\).

Figure 2a, b respectively show the electrical and thermal conductance of four different contacts in a clean region. For better visibility, the traces are shifted along the \(z\)-axis in increments of 6 nm, ensuring the PMC aligns with these \(z\)-offset multiples. The onset of thermal conductance in all traces occurs at about 3 nm from the PMC, and the thermal conductance at the PMC, which is highly variable from contact to contact and reaches a minimal value of 1.5 nW/K for traces #1 and #2. These results are consistent with those reported in previous works15,26 that investigated the thermal conductance for nanometre and subnanometre gaps just before metallic contact is established. In Fig. 2b, we also show the thermal conductance of refs. 15,26, as magenta and green shadowed areas, respectively. The large variability in the thermal conductance at the PMC will be discussed below.

Fig. 2: Thermal conductance in the crossover between tunnelling and contact regime.
figure 2

a, b show the tip-substrate electrical and thermal conductance vs tip displacement traces, \(G\)-\(z\) and \(K\)-\(z\), respectively, both for approach and retraction to the sample after a clean region of the contact area. The shadowed areas in (b) represent the results reported in ref. 15. (green) and ref. 26 (magenta). For representation purposes, traces are displaced in \(z\) by multiples of 6 nm.

Full size image

Thermal conductance in the contact regime

Let us now consider the relation between thermal conductance and electrical conductance after metallic contact is established. After several indentations on a pre-annealed Au surface (at ~300 K) the apex of the type-S Wollaston wire thermoelectric-resistive probe is covered with a thin gold layer, so the atomic junction can therefore be assumed to consist only of gold atoms (see Supplementary Note 4). Figure 3a shows that \(K\) vs \(G/{G}_{0}\) for contacts 1 and 4 in Fig. 2a, b are linear with slopes of 0.66 and 0.71 \(G/{G}_{0}\) nW/K and offsets of 2.1 and 4.4 nW/K, respectively. Subtracting the offset from the thermal conductance and dividing by the slope (see Fig. 3b) shows that thermal conductance closely follows the electrical conductance, showing the features related to the atomic rearrangements in the contact11,12. This behaviour suggests that the thermal conductance observed in contact consists of a thermal conductance characteristic of a metallic contact, which is proportional to the electrical conductance of the contact, and an additional component, which is rather constant and different for different contacts due to adsorbates on the substrate and tip. The thermal conductance of a metallic contact is expected to have contributions from electrons and from phonons. The contribution from electrons, \({K}_{{{{\rm{WF}}}}}\), is given by the Wiedemann–Franz law \({K}_{{{{\rm{WF}}}}}={L}_{0}G{T}_{{{{\rm{av}}}}}\) where \({L}_{0}\) is Lorentz number and \({T}_{{{{\rm{av}}}}}\) is the average temperature of the electrodes26. In our experiment, we have \({T}_{{{{\rm{t}}}}}={126}^{\,\circ}{{\rm{C}}}\) and \({T}_{{{{\rm{s}}}}}={24}^{\,\circ}{{\rm{C}}}\), then \({K}_{{{{\rm{WF}}}}}=0.658G/{G}_{0}\) nW/K. The contribution from phonons is expected to be much smaller (5–10% for Au)11,13,14. In addition to these two contributions the contact shows another contribution that appears to be constant (for relatively small contacts \(G < {20G}_{0}\)) but different for different contacts.

Fig. 3: Thermal conductance in the contact regime.
figure 3

a shows \(K\) vs \(G\) for the traces #1 and #4 in Fig. 2a, b. b shows the normalised thermal conductance \(\widehat{K}\) superimposed to the electrical conductance. \(\widehat{K}=\left[K-K\left(G=0\right)\right]/{s}_{{{{\rm{K}}}}}\), where \({s}_{{{{\rm{K}}}}}\) is the slope of \(K\) vs \(G\). c shows \(K\) vs \(G\) for large contacts, while the black dashed line represents the theoretical WF values.

Full size image

To investigate the evolution of this additional contribution to the thermal conductance, we make larger contacts. In Fig. 3c it is shown that for large contacts the thermal conductance tends to the WF value denoted by the dashed black line, indicating that the additional contribution to the conductance decreases slowly with the size of the contact.

Thermal conductance tunnelling regime

As we mentioned above, in clean regions, we detect heat transfer between the tip and the substrate at distances of a few nm, with the thermal conductance increasing linearly up to the PMC as shown in Fig. 2a, b. In contrast, other regions (unclean regions) of the sample show much larger thermal conductances before the PMC (see Supplementary Note 8), demonstrating the role of adsorbates between the tip and sample play an important role in heat transfer26. In the clean regions, the thermal conductance is largely variable from contact to contact as illustrated in Fig. 4. In Fig. 4a, several traces are shown with values of thermal conductance at the PMC \(\left({K}_{{{{\rm{contact}}}}}\right)\) ranging from 1.2 to 11 nW/K and values of the onset of the thermal conductance \(\left({z}_{{{{\rm{K}}}}}\right)\) from 2 to 6 nm. In Fig. 4b, this information is condensed for 200 different contacts in a 2D histogram.

Fig. 4: Thermal conductance in the tunnelling regime.
figure 4

a Portion of the \(K\)-\(z\) traces before the PMC for several different clean contacts, showing approach in brown and retract in red. All traces have been cut when the electrical conductance jumps to \({G}_{0}\). b 2D histogram of the conductance at the PMC \(\left({K}_{{{{\rm{contact}}}}}\right)\) vs the onset of the thermal conductance \(\left({z}_{{{{\rm{K}}}}}\right)\) for 200 clean contacts.

Full size image

Simulations of heat conductance of clean gold contacts

To elucidate the origin of the anomalous conductance values observed in the tunnelling regime, now we analyse the contribution of the different potential carriers in clean Au contacts. To estimate the contribution of electrons, we make use of the fact that, as shown in Fig. 3 and previous work11,13,14, the electronic thermal conductance in Au atomic-sized contacts satisfies Wiedemann–Franz law very precisely. Thus, through the measured electrical conductance we estimate the electronic contribution to the total thermal conductance. Figure 5a shows two characteristic thermal traces constructed from electrical conductance data, for both tip-retract and approach. Notice that beyond the PMC, the electronic thermal conductance decays exponentially with the gap size and drops well below 1 pW/K in 2–3 Å, which is clearly at variance with our experimental observations.

Fig. 5: Simulations of the heat conductance of clean contacts in the tunnelling regime.
figure 5

a Computed electronic thermal conductance as a function of the tip-sample distance for two characteristic traces (approach and retract). The inset shows the same, but in a logarithmic scale. The thermal conductance was computed using the experimental results for the electrical conductance and the Wiedemann–Franz law with the average temperature of the electrodes (363 K). b Thermal conductance due to phonons computed with NEMD simulations. The two traces correspond to the approach and retract of the tip, and the insets show the contact geometries at different states. The scale bar is 3 nm long. c Radiative thermal conductance as a function of the gap size for the geometry shown in the inset with corresponding dimensions. The conductance was calculated within the framework of fluctuational electrodynamics. The temperatures used in all panels are Tt = 428 K and Ts = 298 K, for the tip and the sample, respectively.

Full size image

To evaluate the contribution of phonons, we carried out non-equilibrium molecular dynamic (NEMD) simulations using the LAMMPS37 (see Supplementary Notes 9 and 10 for details). These allow describing the formation and rupture of the Au contacts, whilst evaluating the phononic thermal conductance arising from the tip-surface temperature difference. To reproduce experimental geometries, we start from a parallel tip-surface conformation, and then we indent/retract the tip from the surface as shown in Supplementary Movie 1. During the retraction, a plastic deformation gives rise to atomically sharp gold contacts, which are experimentally confirmed through the observation of the electrical quantum of conductance. From such geometries, we then compute heat conductance at different tip-surface distances during both the approach and the retract, see Fig. 5b. For single-atom contacts (d = 0.5 nm), we obtain a phononic thermal conductance of ~40 pW/K in accordance with previous results11,13,14, which is less than 10% of the typical electronic contribution11. More importantly, the phononic thermal conductance beyond PMC (d = 0 nm) decays very rapidly (in a few Å) to values clearly below our experimental sensitivity. These results rule out phonons as a candidate for the observed thermal signals in the tunnelling regime.

Finally, we also considered the photon contribution towards heat transfer through NFRHT. For this purpose, we performed state-of-the-art simulations within the theory of fluctuational electrodynamics8,9 using the SCUFF-EM code38 (see Supplementary Note 11 for details). To accurately represent the contact region as in experiments, we modelled a tip-substrate geometry with dimensions extracted from the SEM images of our thermal probes (see Fig. 5c inset). Note the difference between the tip-surface contacts considered in Fig. 5b, c insets. This is motivated by the different nature of both heat carriers. Electromagnetic modes, responsible for the photonic contribution, slowly decay across distances on the order of microns7. Consequently, a larger contact region must be simulated. On the other hand, phonon transport experiences a much faster decay (d < 1 nm), and thus it suffices to model the few last nanometres of the tip. Apart from the contact geometry and the experimental temperatures, the only input information in our simulations is the frequency-dependent Au dielectric function, which we took from tabulated data39. The results for the radiative thermal conductance between the gold tip and the gold substrate are shown in Fig. 5c for gap sizes from 2 to 10 nm. Notice that the thermal conductance for the smallest gap is of the order of 90 pW/K, which is below the noise floor in our experiments. The weak decay of the photonic thermal conductance with gap size is due to the fact that the NFRHT in these gold nanogaps is dominated by evanescent transverse electric modes resulting from total internal reflection. The contribution of these electromagnetic modes saturates at single-nanometre gaps, as predicted by Chapuis et al.6 and experimentally confirmed7,10. These results indicate that the large signals observed in our experiments in the tunnelling regime cannot be attributed to near-field thermal radiation.

Simulations of the heat conductance in the presence of a water meniscus

As evident from the previous discussion, the abnormal heat conductance measured across nanometre-sized gaps, although in line with previous reports15,26, cannot be reconciled with conventional heat transfer mechanisms. Both the unusual gap-size dependence and the large variability of the thermal signals in the tunnelling regime (Fig. 4) strongly suggest that residual adsorbates are responsible for these observations, and water is the most obvious candidate in view of the hydrophilicity of gold after annealing, as mentioned above. Water is one of the most pervasive surface contaminants40,41,42,43, both for its atmospheric abundance and its high surface-adhesion energy44,45. Although one could argue that such conductance measurements15,26 are performed in high-vacuum conditions (\(2 \times {10}^{-6}\) mbar), recent experiments have conclusively demonstrated the presence of a 1.4 nm-thick water layer adsorbed over gold in high vacuum46. More importantly, and as mentioned above, we have carried out an XPS analysis of our gold substrates and found evidence of the presence of adsorbed water even in UHV conditions (see Supplementary Note 7).

For these reasons, we explored the role of water in the heat transport across nanometre-sized gaps. To this end, we performed NEMD simulations in which we considered a gold tip (with a contact area of 29.4 nm) at a fixed distance from an Au(111) surface, as shown in Fig. 6a snapshots and in Supplementary Movie 2. Also, we included sufficient water molecules for both surface and tip to be fully covered with a 1.5 nm-thick hydration layer46 (see Supplementary Notes 12–14). Then, by maintaining a temperature difference of 130 K between the tip and the surface (see Supplementary Note 9), we computed the heat flux as a function of the tip-surface distance. The results, shown in Fig. 6a, agree with the thermal conductance measured experimentally (see Fig. 2). Specifically, not only we obtain a conductance of similar magnitude (few nW/K), but more reassuringly, we recover its hallmark linear dependence with the distance between the gold contacts. These results, both for bulk and water menisci, are robust against changes in the tip geometry as shown in Supplementary Note 15 associated with a representative trajectory shown in Supplementary Movie 3.

Fig. 6: Heat conductance simulations in the presence of a water meniscus.
figure 6

a Thermal conductance as a function of the tip-sample distance for a water meniscus as computed from NEMD simulations. The upper panels show different snapshots of the evolution of the water meniscus. The gold tip has an area of 29.4 nm2, while temperatures used in the simulations are \({T}_{{{{\rm{t}}}}}=428\) K and \({T}_{{{{\rm{s}}}}}=298\) K, for the tip and the sample, respectively. b Computed thermal conductance per unit of area of extended gold-water-gold contacts as a function of the distance between the Au reservoirs. The symbols are the results of the NEMD simulations, and the dotted line to the fit with Eq. (2). The temperatures of the thermal baths were fixed to \({T}_{{{{\rm{t}}}}}=42\) K and \(\mp{{T}_{{{{\rm{s}}}}}=298}\) K. c Representative examples of the fits of the experimental traces for the conductance as a function of the tip-sample distance using Eq. (2) and the Ansatz for the meniscus’ cross section as a function of the tip-sample distance (see text). The colour lines are the experimental results and the black lines the fits. d 2D histogram of the conductance at PMC versus the breaking distance as obtained from the fit of 200 traces using the model described in the text.

Full size image

In what follows, we shall show that these results for the gap-size dependence of the thermal conductance of a water meniscus can be understood as an interplay between the diffusive thermal conduction through water and the evolution of the meniscus’ geometry with the tip-sample distance. Concerning the first aspect, we performed NEMD simulations of the thermal conduction through extended water layers of varying thickness sandwiched between Au electrodes (see Supplementary Note 12). The dependence of the thermal conductance per unit of area with the water layer thickness is displayed in Fig. 6b. The decay with the distance between the Au reservoirs can be understood with a simple three-resistor model in which two resistances are associated with the gold-water interfaces and the third one is related to the diffusive thermal conduction inside the water layer of thickness \(d\). In this model, the total thermal conductance (\(K\)) is given by

$$K\left(d\right)=\frac{A}{\left(\frac{2}{{\kappa }_{{{{\rm{Au}}}}-{{{\rm{w}}}}}}+\frac{d}{{\kappa }_{{{{\rm{w}}}}}}\right)}$$
(2)

where \(A\) is the area of the contacts, \({\kappa }_{{{{\rm{Au}}}}-{{{\rm{w}}}}}\) is the gold-water interfacial thermal conductance, and \({\kappa }_{{{{\rm{w}}}}}\) is the water thermal conductivity. Fitting the results of Fig. 6b with Eq. (2), we obtained \({\kappa }_{{{{\rm{w}}}}}=0.78\) W/Km and \({\kappa }_{{{{\rm{Au}}}}-{{{\rm{w}}}}}=120\) MW/Km2, both in agreement with previous literature47,48. The slow decay shown in Fig. 6b, where the conductance is only reduced by ~30% from 2 to 6 nm, is because the thermal resistance of contacts with water layers of a few nanometres is dominated by the Au-water interfacial resistance. This slow decay is not compatible with the gap-size dependence obtained experimentally (Fig. 2) or in our NEMD simulations (Fig. 6a). This brings us to the second key ingredient, namely, the evolution of the meniscus’ geometry with the gap size.

The shape and size of water menisci formed between a tip and a surface have been extensively studied in the context of atomic force microscopy (AFM)49,50,51,52,53,54,55. In particular, the measurement of the capillary force between a tip and a sample (mediated by a water meniscus) has enabled to establish the relation between the geometry of a meniscus and physical properties like the pressure difference between the liquid and the vapour and the liquid vapour pressure. This has been achieved with the help of Laplace–Young’s equation55 and Kelvin’s equation51,53, respectively. To account for the fact that a water meniscus shrinks as the tip-sample distance increases, we assumed that the meniscus’ cross section changes with the interelectrode distance \(d\) as \(A\left(d\right)=C\left({d}_{{{{\rm{c}}}}}-d\right)\), where \({d}_{{{{\rm{c}}}}}\) is the distance at which the meniscus breaks and \(C\) is related to the meniscus area when the tip and the substrate are in contact. This relation reproduces well the evolution of the cross section in our simulations (see Supplementary Notes 13 and 14) and remains valid independently of the tip shape (see Supplementary Note 15). More importantly, it can be justified with the help of Kelvin’s equation, assuming that the vapour pressure remains constant during the elongation process54. Using this Ansatz in Eq. (2) with \({d}_{{{{\rm{c}}}}}\) and \(C\) as fit parameters and the values of \({\kappa }_{{{{\rm{w}}}}}\) and \({\kappa }_{{{{\rm{Au}}}}-{{{\rm{w}}}}}\) obtained in our simulations (see above), we were able to reproduce very accurately our experimental results (Fig. 6c), as well as the results of our NEMD simulations (see Supplementary Note 14). Using this simple model, we fitted the 200 experimental conductance traces of Fig. 4b. The results for the thermal conductance at the PMC \(\left({K}_{{{{\rm{contact}}}}}\right)\) as a function of the breaking distance are summarised in Fig. 6d. The excellent agreement with the experimental results of Fig. 4b further supports our conclusions on the origin of these anomalous thermal signals.

Discussion

In summary, our results show that in the contact regime, the thermal conductance down to a single-atom gold contact follows closely the electrical conductance showing the features related to the atomic rearrangements in the contact, in agreement with the results from Cui et al.11 and Mosso et al.12. The slope of the thermal conductance versus the electrical conductance in this regime is compatible with the Wiedemann–Franz law, while background signals, reminiscence of the tunnelling regime that persist and decrease slowly up to very large contacts are observed. When the contacts are broken, we observe anomalously large thermal conductance values compatible with previous reports15,26. The ensemble of our results strongly suggests that these signals are due to the formation of water menisci that are very difficult to avoid in the standard conditions under which these experiments are conducted.

Our work also explains the origin of the background signals reported to date in the measurements of the thermal conductance of single-molecule junctions56,57,58. In all those cases, the analysis of the thermal conduction through molecular contacts was largely hindered by the presence of extraneous background signals, which we now understand that are due to the presence of water menisci. This presence has impeded thus far the proper investigation of many fundamental questions in the context of phonon transport and heat conduction in single-molecule junctions. The challenge now is to come out with strategies to avoid the presence of water in this kind of experiments, such as working under ultra-high-vacuum conditions, which is not an easy task.

On the flip side, the unavoidable presence of water in our experiments has allowed us to investigate a different aspect of water menisci in nanoscale gaps, namely their thermal conduction properties. These liquid nanostructures are very important for many engineering and science disciplines, and thus far, their properties have been mainly studied in the context of capillary forces measured with AFM49,50,51,52,53,54,55. Our work provides an alternative way to investigate the properties of these liquid nanostructures.

On the technical front, the thermal probes developed in this work are much easier to fabricate than those currently employed for probing the thermal conduction of atomic-scale junctions11,12,15,26,56,57,58. So, in this regard, our work might encourage other experimental groups to join the endeavour of investigating thermal transport at the nanoscale, which continues to be one of the most fascinating open problems in all of nanoscience.

Methods

Substrate preparation

The substrate is a 200 nm-thick gold layer grown over a borosilicate glass base of 0.7 mm thickness (Arrandee). It is cleaned and flattened by flame annealing with a butane torch using the standard procedure, melting superficially the evaporated gold, allowing it to reorganise in a polycrystalline (111) surface (see Supplementary Note 5 for more details).

Calibration of the probe

The calibration of the response of the probe’s voltage drop, \(\Delta V\), caused by a local heating at the tip due to a heat current, is conveniently performed using the Peltier effect as a local source of heat at the welded junction. To achieve this, a DC current is added to the main AC heating current \({f}_{{{{\rm{heat}}}}} \sim 31\) kHz. For small DC currents, the Peltier effect dominates Joule heating and heats or cools the welded junction depending on the sign of the current. By measuring the \(\Delta V\) at the ends of the thermoelectric-resistive probe simultaneously with the injected DC current, an offset parabola is obtained whose linear term can be related to the resolution of the thermoelectric-resistive probe. Following this procedure, the \(\Delta V\) measured at the ends of the probe can be transformed directly into the heat changes experienced by the probe’s apex. When the tip is heated at 127 °C with an ac current \({I}_{{{{\rm{heat}}}}}=8.9\) mA at a frequency of \({f}_{{{{\rm{heat}}}}} \sim 31\) kHz, a resolution of 26.80 V/W is obtained (see Supplementary Note 16 for more details).

Multifrequency demodulation

Using the thermoelectric-resistive sensors as a STM probe requires a multifrequency approach (Fig. 1c). Two distinct frequencies are employed to generate two currents simultaneously: the tip-substrate current and the thermoelectric-resistive probe heating current. To establish the tip-substrate current \(I\), a symmetric bias voltage is applied to the probe (voltages \({V}_{1}\) and \({V}_{2}\) in Fig. 1c) at a frequency \({f}_{{{{\rm{bias}}}}} \sim 51\) kHz, whereas for the heating current (\({I}_{{{{\rm{heat}}}}}\)), voltages are applied antisymmetrically at a frequency \({f}_{{{{\rm{heat}}}}} \sim 31\) kHz. The selection of frequencies was based on the choice of prime numbers, which serves to circumvent the generation of artefacts resulting from the subharmonics of the main frequency. A HF2LI Zurich Instruments Lock-in amplifier is used to separate the components of the measured signals at these frequencies.

Following the schematic in Fig. 1c, differential amplifier #1 measures the voltage drop at the calibrated resistor \({R}_{{{{\rm{b}}}}}\) to extract the heating current; differential amplifier #3 measures the voltage drop at the sensor; and differential amplifier #2 is used to set a variable offset for the voltage drop at the sensor. These two signals, which are differentially demodulated by the Lock-in amplifier, reflect the changes in the probe resistance and are directly related to the heat current. The base noise of this resulting signal is approximately 250 nV with a 200 Hz bandwidth with a 4th order filter. In addition to the AC current at \({f}_{{{{\rm{heat}}}}}\), a DC thermovoltage is generated in the probe’s welded junction, producing a thermocurrent in the thermal circuit which can be extracted demodulating at zero frequency. Having previously calibrated the sensor’s Seebeck coefficient (see Supplementary Note 17) and knowing the ambient temperature, placing a thermocouple on the tip holder, the measured DC voltages can be directly translated into the probe’s apex temperature.

The current passing through the junction is limited by a series resistor RS = 104 Ω before reaching the IV amplifier, which gain is set at RG = 104 Ω. This current has two components at \({f}_{{{{\rm{bias}}}}}\) and \({f}_{{{{\rm{heat}}}}}\), which will be separated using the Lock-in amplifier. The former is related to the electrical conductance of the junction and the latter to the heat losses due to the heating current leakage from the probe to the sample. To cancel this heat leakage, it is necessary to shift \({V}_{1}\) and \({V}_{2}\) accordingly. For more details, see Supplementary Note 18.