Introduction

Antiferromagnetic (AFM) materials have alternating magnetic moments on individual atomic sites1. This unique property leads to zero stray fields, immunity to external perturbations, and ultrafast spin dynamics1,2,3. Despite its significant potential for ultrafast and ultrahigh-density storage, the outstanding problem is efficiently detecting and manipulating the AFM state2. For colinear antiferromagnets (AFMs), they are usually read by imprinting the state on a ferromagnetic tunnel junction (MTJ). The detected electrical signal for collinear AFMs due to transverse Hall response or anisotropic magnetic resistance (AMR) is very small4,5,6,7,8,9,10. Therefore, it is very important to develop a new method to detect collinear antiferromagnetic Néel vectors. Recently, the magnetic tunneling effect suitable for detecting the AFM order11, in which electrical readout is enhanced between two magnetic electrodes, has been utilized in magnetic random-access memory (MRAM) and in-memory computing chips12,13,14. Especially the potential control of the tunneling anisotropic magnetoresistance (TAMR) through a two-step magnetization offers a rich phenomenology that opens new directions in spintronics research. The TAMR is distinguished from the tunneling magnetoresistance (TMR), which is the influence of the detailed electronic structure of the MTJ on the bias voltage dependence of the spin-polarized tunneling15. An effective way to explore TAMR is to consider the angular dependence of tunneling resistance when the electron spins are rotated under a large magnetic field.

Recent first-principles theory has predicted a promising route toward spintronics based on spin-neutral currents phenomena, in particular on the AFM tunneling magnetoresistance (ATMR)16,17. The ATMR has hitherto been experimentally demonstrated only in non-collinear AFMs15,18. However, collinear AFMs have unique advantages: they exhibit greater magnetic stability compared to noncolinear AFMs19,20. The parallel or antiparallel alignment of magnetic moments leads to more regular and stable magnetic structures which have more immunity to external magnetic perturbations. Secondly, the collinear AFMs have stronger exchange interaction between neighboring magnetic moments.

In this article, we report large TAMR in RuO2 (100) /MgO (110) / RuO2 (100) tunnel junctions. The efficient rotation of the RuO2 moments in the bottom RuO2 will cause a large TAMR response. It is shown that due to the spin-flop effect, the TAMR exceeds 60% at room temperature by measuring all-epitaxial RuO2 AFM-TJ with different magnetic field orientations using the magneto-transport method. Our findings demonstrate the prevailing influence of spin-flop TAMR over alternative magnetic resistance factors, aligning with atomic simulations and first-principles calculations. This holds significant promise for advancing spintronics applications.

Results

While altermagnetism or spin-neutral currents could potentially induce TMR16,17, the existence of altermagnetism in RuO₂ has recently become a topic of debate21,22, leaving the presence of an altermagnetism-induced TMR effect in this system uncertain. Regarding the antiferromagnetic nature of RuO₂, angle-resolved photoemission spectroscopy (ARPES) alone may not provide conclusive evidence, as similar spectral features can be interpreted within both magnetic and non-magnetic theoretical frameworks23. Importantly, we observe a clear X-ray Magnetic Linear Dichroism (XMLD) signal originating from antiferromagnetic ordering in the films (Supplementary Fig. 1), which closely matches the features reported by other research groups24. Furthermore, in our ferromagnetic/antiferromagnetic heterojunction, a pronounced exchange bias (EB) effect is observed (Supplementary Figs. 2–3). Owing to the high-quality epitaxial growth of the film, the EB field at low temperatures reaches up to 700 Oe, exceeding previously reported values4. These results collectively provide strong evidence for the robust antiferromagnetic nature of RuO₂. Ruthenium dioxide (RuO2) is a typical rutile antiferromagnet with a tetragonal crystal structure4,25. The RuO2 has two sublattices RuA and RuB (Fig. 1a, b). Each magnetic atom (Ru) is surrounded by six nonmagnetic oxygen atoms (O). The arrangement of atoms forms a lattice structure with alternating layers of ruthenium and oxygen (Fig. 1a, b). RuO2 has been reported to host high-temperature antiferromagnetism with a Néel temperature TN > 300 K26,27. RuO2 also shows efficient and broadband terahertz radiation at room temperature due to electrical anisotropy28. In recent studies, RuO2 has exhibited intriguing phenomena such as the anomalous Hall effect, spin splitting, and tilted spin current in epitaxial single crystal films4,25,29. Despite these advancements, electrically detecting the AFM order of RuO2 remains a significant challenge with the associated readout electrical signal proving very faint. The spin-flop effect combined with TAMR could bypass those obstacles. The initial state of collinear anti-ferromagnetism is that neighboring magnetic moments align in opposite directions, canceling each other and resulting in a zero magnetic moment. After increasing the external magnetic field, the alignment of the moments slightly tilted toward a perpendicular direction because of the competition between the Zeeman energy gained from the external magnetic field and the exchange energy associated with the AFM exchange interaction between neighboring moments.

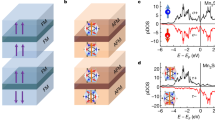
Fig. 1: Spin structure and device geometry.
figure 1

a Atomic structure of RuO2 where the red (blue) spheres denote O (Ru) atoms. b Front view along the [010] axis of the 2D atomic spin structure. c Schematic of the AFM-TJ. The bottom RuO2 and top Au/Ti serve as the writing and detecting channel in the perpendicular direction. d Magnetization data measured at 300 K with the magnetic field parallel to the [100] axis after deducting the paramagnetic background.

Full size image

To observe the spin-flop tunneling magnetoresistance in collinear AFM materials, it is necessary to fabricate collinear AFM-TJ (Fig. 1c). The all-epitaxial collinear AFM-TJ stacks composed of RuO2 (10 nm)/MgO (2 nm) /RuO2 (20 nm) sandwich structure were grown atop the SrTiO3 (STO) substrate. The RuO2 (100) grown on the STO (001) was used in the recent study due to the high-temperature collinear Néel order, zero magnetic moment (Fig. 1d) and abundant electronic-magneto transport phenomena of RuO230. We chose the MgO as the tunneling layer because the MgO-based MTJ, currently used in MRAM12,31,32, exhibits the largest TMR33,34. In addition, the lattice constant of RuO2 can match that of MgO very well as shown (Supplementary Fig. 10). Transmission electron microscopy (TEM) imaging was employed to identify the presence of stacked films distinguished by a seamless interface between RuO2 and MgO, with a measured lattice constant of a = 4.5 Å (Fig. 2a). Furthermore, the thickness and the surface roughness were fitted from XRR spectra and atomic force microscopy (AFM) [Supplementary Fig. 9, 10] to be close to the measured value of TEM. Furthermore, the Néel vector of RuO2 was found to be in-plane, allowing us to characterize the films and measure tunneling conduction in the RuO2/MgO/ RuO2 trilayer film, as discussed below. The selected area electron diffraction (SAED) investigations corresponding to this observation unveiled that both the top and bottom collinear antiferromagnetic (AFM) RuO2 exhibit predominantly single crystal characteristics oriented along the (100) direction. In the crystal configuration, the out-plane anomalous Hall effect is almost zero when the Néel vector is in-plane direction [Supplementary Fig. 8]. The tunneling MgO film similarly displays a single crystal structure oriented along the (110) direction, exhibiting excellent lattice matching (Fig. 2b–d). This facilitated the preparation of an all-epitaxial AFM-TJ in our experiments.

Fig. 2: Crystal structure and spin flop tunneling effect.
figure 2

a Transmission electron microscopy (TEM) image of the RuO2/MgO/RuO2 MTJ. b–d Selected-area electron diffraction (SAED) patterns of MTJ obtained by TEM. e, f Schematic of the two states of the bottom RuO2 layer, that is, perpendicular and parallel states of MTJ, respectively. g MTJ resistance RA and X-ray Absorption Spectroscopy (XAS) signal, as a function of external magnetic field.

Full size image

The stacks were then patterned into circular nanopillars with diameters (D) of 3–15 μm on the STO substrate, The Au/Ti top electrode was used for the MTJ readout. The resistance of the tunnel junction depends on the thickness of the MgO layer. Previously, we observed a resistance of 2.6 kΩ for a 1.7 nm MgO barrier, corresponding to an RA value of 1.84 × 104Ω·μm², which is slightly lower than our experimental value of 2.3 ×  104 Ω·μm² (2 nm MgO)35. The top and bottom RuO2 are required to have two distinctive spin-flop magnetic fields (SP-MF) so that the parallel and perpendicular configurations of the Néel vector arise as a function of the magnetic field (Fig. 2e–g). The applied 1μA d.c. current along the [001]-axis flowing through the junction, yields a perpendicular measured voltage. Under sweeping magnetic fields along the x direction ([001]- axis) of a device with D  =  15 μm, the magnetoresistance loop can be observed at room temperature (Fig. 2g). Because the spin flop (SP) field Hsp is larger than 5 T, the Néel vectors of the RuO2 top and bottom layers fully stay in the in-plane direction at zero fields, corresponding to an initial parallel state of the MTJ with small tunneling resistance. After increasing the magnetic field to 6 T, the spin-flop behavior occurs, causing a final perpendicular state of the MTJ with huge tunneling resistance. This behavior is also observed in other devices, (Supplementary Information Note 6 and Note 15), with similar Hsp. In addition, the X-ray absorption spectroscopy (XAS) was performed on the 20 nm RuO2 (100) at 300 K. We measured the XAS spectra under different magnetic fields and analyzed the peak characteristics (Supplementary Fig. 4). The peak of Ru L2, 3 edge exhibits significant signal changes under the application of large magnetic fields.

To further confirm the spin-flop tunneling effect of the all-epitaxial pure AFM-TJ, we conducted TAMR examinations in the configuration illustrated in Fig. 3a. The Néel vector is aligned along the [001]-axis at zero magnetic field, the current is along the out-of-plane direction, and θ refers to the angle between the in-plane magnetic field and the [001]-axis. Subsequent to the spin flop event, the Néel vectors of bottom RuO2 align along the out-plane direction (Fig. 3b). However, the spin of Ru atom in the top RuO2 maintains the original in-plane spin structure due to larger SP-field. We observed magnetic field-dependent magnetoresistance at various angles θ (Fig. 3c). For each angle θ, we measured the magnetoresistance by sweeping the in-plane magnetic field up to 8 T during which only the bottom RuO2 spin moments were switched (explained later). We observed 60% magnetoresistance only when the magnetic field and Néel vector were parallel and zero magnetoresistance when the magnetic field and Néel vectors were perpendicular, validating the in-plane AFM magneto-crystalline anisotropy. The angular dependence of the magnetoresistance is proportional to \(\sin 2\theta\) function (Fig. 3d). Based on macrospin approximation, the total AFM magnetic energy density \({{{{\rm{E}}}}}_{{{{\rm{m}}}}}\) of AFM is1:

$${{{{\rm{E}}}}}_{{{{\rm{m}}}}}={J}_{{AF}}{M}_{s}^{2}\cos 2\theta+{{{{\rm{E}}}}}_{{{{\rm{K}}}}}-{E}_{D}-{\mu }_{0}H{M}_{s}\cos \theta$$
(1)
Fig. 3: TAMR effect at RuO2 (10 nm)/MgO (2 nm) /RuO2 (20 nm).
figure 3

a Schematic of the tunnel junction device, where the current is along the perpendicular direction. b Crystal and spin structure of RuO2 TJ at saturated magnetic field. Blue arrows and red spheres represent Ru and O atoms, respectively. c MTJ resistance, RA, as a function of the external magnetic field applied at different angles between the in-plane magnetic field and [001] axis. d TAMR ratio, TAMR = (R⊥-RII)/ RII, as a function of angle at room temperature. e Sheet resistance of 20 nm RuO2, Rxx, as a function of temperature at zero magnetic field. f TAMR ratio, TAMR = (R⊥-RII)/ RII, as a function of temperature at θ =0 deg.

Full size image

Here, \({J}_{{AF}}{M}_{s}^{2}\cos 2\theta\) is the exchange interaction term, \({E}_{D}={{D}_{{ij}}S}_{i}\times {S}_{j}\) is the Dzyaloshinskii-Morriya interaction term, \(-{\mu }_{0}H{M}_{s}\cos \theta\) is the Zeeman energy under a uniform magnetic field. The magnetic anisotropy \({{{{\rm{E}}}}}_{{{{\rm{K}}}}}=K{\sum}_{i}{S}_{i}\cdot {S}_{i}\) can be explained as: \({{{{\rm{E}}}}}_{{{{\rm{K}}}}}={K}_{u}{\sin }^{2}\theta+{K}_{c}{\sin }^{2}2\theta\), where \({K}_{u}\) is the uniaxial anisotropy and Kc is the cubic anisotropy. The exchange interaction and magnetic Zeeman energy term have very weak contribution due to the vanishing Ms. Our observation of a twofold symmetric TAMR in conjunction with the uniaxial in-plane anisotropy, where the TAMR maximum aligns with the in-plane easy axis, suggests a common underlying origin (Fig. 3d). The sheet resistance Rxx of 20 nm RuO2 gradually increases at the higher temperature, indicating the metallic behavior, and there is no phase transition during our measurement (Fig. 3e). Temperature (T) dependent TAMR values of RuO2/MgO/RuO2 AFM tunnel junctions are then presented (Fig. 3f). Interestingly, the in-plane TAMR values slightly increase, from 60 to 73% as T decreases from 300 to 3 K. It is worth noting that the different devices exhibit significant variation, which impacts our analysis of the trends associated with varying thickness (Supplementary Information Note 6).

To better understand the TAMR mechanism, we have carried out first-principles electronic transport calculations of the transmission properties for the RuO2[100]/MgO[110]/RuO2[100] tunnel junction versus the Néel orientations of one of the RuO2 leads. To the lowest order in the Néel orientations of the two RuO2 leads, \({\vec{n}}_{1,2}\), the transmission is in general expected to follow,

$$T\left({\vec{n}}_{1},{\vec{n}}_{2}\right)={T}_{0}+{T}_{{TMR}}{\vec{n}}_{1}\cdot {\vec{n}}_{2}+{\sum}_{\alpha }{T}_{{TAMR}}^{\alpha }\left({\left({\vec{n}}_{1}\cdot {\vec{e}}_{\alpha }\right)}^{2}+{\left({\vec{n}}_{2}\cdot {\vec{e}}_{\alpha }\right)}^{2}\right),$$
(2)

where, \({\vec{e}}_{\alpha }\,\), with \(\alpha=y,z\), is the unit vector, \({\vec{e}}_{z}\) is a unit vector normal to the interface, \({\vec{e}}_{x}\) is along the c-axis of RuO2 and the TAMR transmission is assumed to be the same for both interfaces. While the TMR transmission is obtained by considering parallel and anti-parallel configurations, \({T}_{{TMR}}=\left(T\left(\vec{n},\vec{n}\right)-T\left(\vec{n},-\vec{n}\right)\right)/2\), in the case of TAMR, one needs to consider an additional noncollinear configuration, e.g. orthogonal configuration, whereby, the TAMR transmission along the αth direction can be calculated from \({T}_{{TAMR}}^{\alpha }=T\left({\vec{e}}_{x},{\vec{e}}_{\alpha }\right)-{T}_{0}\), where \({T}_{0}=\left(T\left({\vec{e}}_{x},{\vec{e}}_{x}\right)+T\left({\vec{e}}_{x},-{\vec{e}}_{x}\right)\right)/2\). Since, in the case of transport along the [100] direction in RuO2, the k-resolved spin polarization does not flip under reversal of the Néel orientation, assuming that the interface is compensated, we do not expect a finite TMR effect. Therefore, only TAMR is expected to be present in this system, where the relative in-plane and out-of-plane TAMR strength are given by, \({{TAMR}}^{\parallel }={T}_{{TAMR}}^{y}/{T}_{0}\) and \({{TAMR}}^{\perp }={T}_{{TAMR}}^{z}/{T}_{0}\), respectively.

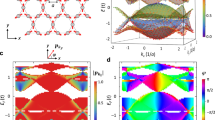
We present in Fig. 4a the ab-initio results for the in- (y) and out-of-plane (z) TAMR in RuO2[100]/MgO [110]/RuO2[100] tunnel junction with 2.1 nm thick MgO versus the shift of the chemical potential. For the chemical potential around the Fermi energy, E = EF, which corresponds to an undoped structure, we find TAMR values around −5% and −10% for the in-plane and out-of-plane cases, respectively. We observe a significant enhancement of TAMR when doped 0.2 eV below the Fermi level that reaches about −50% which agrees with the experimental measurement both in amplitude and sign. The negative shift of the chemical potential can be justified by the diffusion of O dopants around the interface region which is not explicitly considered in the ab initio calculations. In the top left inset of Fig. 4a, we present the calculated transmission for bulk RuO2 along [100] (a-axis) versus the chemical potential for different orientations of the Néel vector. We find a very small modulation of bulk transmission under reorientation of the Néel vector, thus ruling out the bulk origin of the observed large TAMR. Additionally, we confirmed that the TAMR value remains unchanged when the fixed RuO2 lead is made nonmagnetic.

Fig. 4: Calculated TAMR and transmission.
figure 4

a Calculated of the in- (y) and out-of-plane (z) TAMRy(z) for the RuO2[100]/MgO[110]/RuO2[100] tunnel junction versus rigid shift of the chemical potential. The top left inset shows the calculated transmission in bulk RuO2 along [100] versus the chemical potential for various Neel orientations; the bottom right inset shows the transmission of the tunnel junction for various configurations of the two RuO2 Néel orientations versus chemical potential. In the parallel (antiparallel) configurations, \({\vec{n}}_{1}\) and \({\vec{n}}_{2}\) are along [010], in the orthogonal in-plane \({\vec{n}}_{1}\) and \({\vec{n}}_{2}\) are along [010] and [001] respectively, and in the orthogonal out-of-plane \({\vec{n}}_{1}\) and \({\vec{n}}_{2}\) are along [010] and [100,] respectively. b Layer resolved change in DoS, \({\delta ({LDoS})}_{i}^{{{{\rm{in}}}}-{{{\rm{plane}}}}}={{LDoS}}_{i}^{[001]}-\,{{LDoS}}_{i}^{\left[010\right]}\) of the ith layer of the top RuO2 for two in-plane orthogonal spin configurations. At \({{{{\rm{E}}}}}_{{{{\rm{F}}}}}=-0.2\,{{{\rm{eV}}}}\) we observe a significant change of interfacial DoS which is a signature of interfacial resonant states. c Interfacial change of \({\delta {DoS}}_{{inplane}}\) of top RuO2 versus chemical potential demonstrating a strong correlation with the calculated in-plane TAMR in (a).

Full size image

In order to investigate the microscopic origin of the large TAMR, we calculated the layer-resolved local density of states (LDoS) of the top RuO2 for two orthogonal in-plane orientations of the top RuO2, one along the y-axis ([010]) and the other along the x-axis ([001]). In Fig. 4b we present the results for the change in LDoS \({\delta ({LDoS})}_{i}^{{{{\rm{in}}}}-{{{\rm{plane}}}}}={{LDoS}}_{i}^{[001]}-\,{{LDoS}}_{i}^{[010]}\) of the ith layer for three values of the chemical potential (−0.2, 0 and 0.2 eV). The calculations reveal a large modulation of the LDoS at the interface for EF = −0.2 eV, suggesting the emergence of the interfacial resonant states36. The significant role of the interfacial resonant states on TAMR is further corroborated in Fig. 4c, which depicts the interfacial LDoS versus the shift of the chemical potential, demonstrating a strong correlation with the in-plane TAMR shown in Fig. 4a. This suggests that the observed giant TAMR, consistent with both experimental and theoretical findings, originates from the emergence of the resonant interfacial states that together with the the tunneling transmission across the MgO barrier and the relatively large spin-orbit coupling (SOC) strength of Ru coupled with the oxygen doping effect result in the giant value of the observed TAMR. The bottom right inset in Fig. 4a shows the calculated transmission of the tunnel junction versus the chemical potential for various configurations of the two Néel orientations of the RuO2 leads. The presence of a finite TMR is an artifact of the non-compensated interfaces. For a 2.1 nm MgO barrier, the calculated transmission coefficient at the Fermi level (≈5 × 10⁻⁹; see Fig. 4a, inset) translates to a RA product of about 3 × 10⁵ Ω µm². This value closely matches our experimental result and falls within the typical range reported for conventional ferromagnetic MgO tunnel junctions37.

The AFM spin-flop dynamic can also be understood by the following mechanism. We have investigated the magnetic field-induced behavior of RuO2 multilayer membranes. In our simulations, we set the atomic magnetic moment to be 0.1 \({\mu }_{B}\), the lattice structure to be a tetragonal lattice. Specifically, our model features a trilayer film system, incorporating a central MgO layer sandwiched between two RuO2 layers. For each RuO2 layer, the slender RuO2 layer is denoted as the “A-layer”, and its counterpart as the “B-layer”. Initialized with Néel vectors and net magnetic moments of both A and B layers parallel to the x-axis, we subjected the system to an in-plane magnetic field along the negative x-axis during the simulations. In our model, we have considered the exchange interactions between the ruthenium (Ru) atoms, as well as the magnetic anisotropy in the RuO2 crystal. Concurrently, in agreement with the experimental observations, we have considered the impact of magnetic anisotropy at the RuO2 interface. Specifically, the magnetic anisotropy at the interface could prompting the inclusion of a non-uniform distribution of magnetic moments in our model. Subsequently, an external magnetic field was applied to the system to facilitate the simulation-based investigation of spin dynamics within the system (see Fig. 5). The simulation results reveal that the magnetic field can induce the flipping of Ru spins, consistent with our initial hypothesis. Under the influence of the magnetic field, the spins undergo nearly 90-degree switching. Remarkably, this behavior mirrors the experimentally observed switching.

Fig. 5: Atomistic simulation of spin-flop dynamics.
figure 5

a Schematic of RuO2/MgO/RuO2 MTJ in the atomistic simulations. The red balls denote Ru atoms, the white balls denote O atoms in RuO2, and the black balls denote MgO atoms. b The switching curve of the top layer (A-layer) of RuO₂ under the influence of an external magnetic field. The inset illustrates the final state of the switching process, where the red and blue vectors represent the spin directions of Ru atoms. The inset shows that the Ru atoms in the top layer do not undergo switching under the external magnetic field. c The switching curve of the bottom layer (B-layer) of RuO₂ under the influence of an external magnetic field. The inset illustrates the final state of the switching process, where the inset shows that the Ru atoms in the bottom layer do undergo switching under the external magnetic field.

Full size image

The AFM spin-flop dynamics can also be understood through the following mechanism. We employed atomic-level simulations to investigate the magnetic field-induced behavior of RuO₂ multilayer membranes. In our simulation, we constructed a RuO₂/MgO/RuO₂ multilayer membrane model with dimensions of 10 nm × 10 nm × 50 nm, where one RuO₂ layer, designated as the A-layer, was set to a thickness of 10 nm, and another RuO₂ layer, designated as the B-layer, was set to a thickness of 20 nm. The lattice structure was modeled as a tetragonal lattice, with the MgO layer having a thickness of 2 nm. In the simulations, we accounted for various physical effects, including magnetic anisotropy, exchange interactions, and Dzyaloshinskii–Moriya interaction (DMI). The system’s Hamiltonian can be expressed as:

$$H=-{\sum}_{{ij}}\,\,{J}_{{ij}}\left({{{{\bf{s}}}}}_{i}\cdot {{{{\bf{s}}}}}_{j}\right)-\frac{{k}_{u}}{2}\sum {\left({{{{\bf{S}}}}}_{i}\cdot {{{{\bf{e}}}}}_{i}\right)}^{2}-{{{{\boldsymbol{D}}}}}_{{ij}}\cdot ({{{{\bf{s}}}}}_{i}\times {{{{\bf{s}}}}}_{i})$$

Concurrently, we considered the influence of magnetic anisotropy on the RuO₂ interface. Specifically, we observed that magnetic anisotropy at the interface necessitated the incorporation of a non-uniform distribution of magnetic moments into our model. To illustrate the spin-flop process, we initialized the Neel vectors and net magnetic moments of both the A and B layers to be parallel to the x-axis, then applied an in-plane magnetic field along the negative x-axis during the simulations. The simulation parameters are listed in our Supplementary Material. The schematic of model is illustrated in Fig. 5a.

In Fig. 5b, c, we present the dynamic process in the two RuO₂ layers under the influence of an 9 T external magnetic field. As shown in Fig. 5b, the Néel vector of the A-layer exhibits minimal deflection under the applied magnetic field. Under the influence of the magnetic field, the Néel vector in the B-layer undergoes a flip, as depicted in Fig. 5 c, where the snapshots of the magnetic moment states reveal that the spins undergo a nearly 90-degree switching—a behavior that closely resembles the experimentally observed switching. The simulation results demonstrate that the magnetic field can induce the switching of Néel vector in bottom RuO2 layer, consistent with our initial hypothesis.

Discussion

The giant TAMR in all epitaxially-grown AFM-TJ is mainly based on the spin-flop tunneling resistance. The large magnetic field can effectively flip the spin of the Ru atom in the bottom RuO2 layer. However, the spin of Ru atom in the top RuO2 maintains the original in-plane spin structure due to larger SP-MF. By sweeping the magnetic field from +8 T to −8T, we found two evident transitions SP-MF at BSP (about 5 T and −5 T) which is close to the SP-MF estimated by the atomic simulation above. When the absolute value of the magnetic field is less than 3 T, both the top and bottom RuO2 layers maintain the in-plane spin configuration. When the magnetic field is slightly greater than 3 T (less than 5 T), the RuO2 at the bottom evolves into a multi-magnetic domain state. When the magnetic field is greater than 5 T, the RuO2 spin structures at the bottom and top are perpendicular to each other.

We simultaneously discover giant TAMR exceeding 60% at room temperature and the evident in-plane anisotropy in all antiferromagnetic tunneling junction (RuO2/MgO/RuO2). Additionally, we elucidated the spin flop dynamic by atomic simulation, revealing magnetic field induced two distinct AFM configurations. The ab-initio calculations are consistent with our experiment and provide insights into the TAMR in AFM-TJ. This work demonstrates the origin of the TAMR on the interfacial resonance states, the strong SOC of Ru and establishes the existence of giant TAMR in a pure collinear AFM system, enhancing our comprehension of tunneling effects in collinear antiferromagnetic materials, thus advancing the development of AFM based spintronic devices.

Our experiments provide fresh outlook on tunnel magnetoresistance in structures with two collinear AFM contacts. As demonstrated, the presence of a spin-flop effect necessitates a significant magnetic field. Furthermore, the change of AFM configurations in the bottom RuO2 layer contribute to the observed TAMR. Previous studies have demonstrated that IrMn-based tunnel junctions exhibit a significant tunneling anisotropic magnetoresistance (TAMR) effect; however, traditional TAMR devices typically necessitate a ferromagnetic layer. In this work, we observed a substantial TAMR effect at room temperature using a pure antiferromagnetic device. This approach effectively mitigates the interference of stray fields on the antiferromagnetic device. Additionally, we employed pure epitaxial growth techniques to achieve a high-quality single-crystal antiferromagnetic tunnel junction, which likely contributes to the relatively large TAMR value observed. We have also investigated how the dependence of TAMR on the Néel vector direction is determined by the specific form of the Zeeman field resulting from time-reversal symmetry breaking. We which will lead to anisotropies in the tunneling resistance. We find that the in-plane Néel vector magnetic configuration results in a small tunnel magnetoresistance, whereas the out-of-plane Néel vector configuration leads to a large magnetoresistance state. This behavior may be attributed to the time-reversal symmetry breaking and the subsequent changes in the electronic band structure with the Néel vector direction. However, our measurements are inseparable from giant auxiliary magnetic fields. It’s worth noting that achieving field free electrical-current-induced writing in AFM-TJ remains an exciting challenge for the spintronics device.

Methods

Material growth

RuO2 thin films were sputtered from a RuO2 target onto (001)-oriented STO single-crystal substrates (10 × 10 × 0.5 mm3) with a base pressure of 5 × 10–7 Pa. The deposition was performed at 600 °C. After deposition, RuO2 MTJ films were kept at 600 °C in a vacuum for annealing for 1 h.

XRD

XRD measurements were performed by a Bruker D8 diffractometer with a five-axis configuration and Cu Kα (λ = 0.15419 nm).

STEM

Cross-sectional wedged samples were prepared by mechanical thinning, precision polishing and ion milling. An electron-beam probe was utilized to scan thin films to achieve high resolution of local regions.

Electrical measurements

Electrical measurements were performed in a Quantum Design physical property measurement system. The electrical current used for resistance measurements was 5 µA.

Magnetic measurements

Magnetic measurements were performed in a Quantum Design superconducting quantum interference device magnetometer with 10–11 A.m–2 sensitivity.

Density functional theory simulations

Structural relaxations are carried out using the Vienna ab-initio Simulation Package (VASP) code38 on a RuO2[100] layer, 3.5 nm in thickness, interfaced with a 1.8 nm thick MgO layer. The system was treated with periodic boundary conditions, namely no vacuum was included. The two in-plane lattice constants were fixed at 4.53 Å and 3.12 Å, corresponding to the bulk RuO2 lattice constant b and c, respectively. Additionally, the interlayer distances of RuO2 away from the interface were kept fixed as a/2 = 2.265 Å. We minimized the total energy with respect to the ionic positions and layer spacings of three monolayers of the RuO2 near the interface and the entire MgO film. The relaxation was performed using the PBE+U39exchange correlation functional and a Monkhorst-Pack40 6 × 8 × 1 k-points mesh with plane-wave cut-off energy of 450 eV. Hubbard correction, U − J = 2 eV, is applied to Ru-d orbital. Using the relaxed coordinates of RuO2/MgO, we employed the OpenMX DFT package41,42,43 to obtain the Hamiltonian in the atomic orbital basis sets. A 14 × 14 × 1 k-points mesh was used for the self-consistent field (SCF) calculation. The unit cells in the middle of the RuO2 film were utilized to calculate the self-energies of the left and right leads. The self-energies were calculated using Sancho-Rubio’s fast recursive method44. The RuO2 film was divided in half by removing the hopping elements between the top and bottom halves. The lead self-energies were added to the corresponding surface layers to extend them into the semi-infinite limit. In the case of the anti-parallel tunnel junction, we multiplied the exchange splitting of one side of the junction by a negative sign. Subsequently, we employed Landauer-Buttiker’s formula45 to calculate the transmission across the tunnel junction for various magnetic configurations. A broadening value of, \(\eta=25{meV}\) was introduced to account for the decoherence effect due to the finite temperature and structural disorder.