Introduction

Ferroelectric materials, known for their capacity to interconvert electrical and mechanical energy, have found widespread applications in sensors, actuators, and ultrasound transducers. Over the past 70 years, various perovskite-type ferroelectric systems with remarkable electromechanical properties have been developed1,2,3,4,5. These systems include commercially available Pb-based materials, such as Pb(ZrxTi1-x)O3 (PZT)- and Pb(Mg1/3Nb2/3)O3-PbTiO3 (PMN-PT)-derived systems6, as well as Pb-free materials, such as (KxNa1-x)NbO3 (KNN)7,8 - and BaTiO3 (BT)- based systems9,10. Understanding the mechanisms underlying high piezoelectricity in these diverse materials has long been a focal point of research, as it holds the potential to shape and enhance strategies for developing new high-performance piezoelectric systems.

Over time, several theories have been proposed from different perspectives to account for the observed rise in piezoelectricity within chemically complex perovskite oxide solid solutions10,11,12,13. One prevailing idea is the coexistence of long-range rhombohedral (R), tetragonal (T), and/or orthorhombic (O) phases at the morphotropic phase boundary (MPB) or polymorphic phase boundary (PPB). The multi-phase coexistence can accommodate a variety of polarization variants and thereby facilitates field-induced phase transitions or domain reorientation processes10,14,15. The existence of a low-symmetry monoclinic (M) phase, where spontaneous polarization lies within a crystallographic plane, enables easy and continuous polarization rotation under external stimulus11,12,16,17,18,19. Coupled with strong polarization-strain interactions, this enhances the piezoelectric response through intrinsic lattice contributions11,12. However, beyond these well-established intrinsic factors, other physical phenomena, such as nanodomains with a reduced coherent length of unit-cell polarizations, and the mobility of the high-density domain walls, could further enhance the piezoelectricity as extrinsic factors20,21. Additionally, local structural heterogeneity, represented by the polar nanoregions in relaxor ferroelectric crystals, contributes to a large shear piezoelectric response associated with the softening of the transverse acoustic mode22,23.

While existing theories or phenomena can explain high piezoelectricity in specific systems, there is still a lack of consensus that potentially applied across Pb-based and Pb-free perovskite piezoelectric systems, such as PZT-, PMN-PT-, BT-, and KNN-based. For instance, the development of a low-symmetry phase and the corresponding argument on the enhanced piezoelectricity maybe valid for several Pb-based high-performance systems, but it cannot be applied straightaway in the cases of many Pb-free alternatives. Despite decades of research, an atomic-level understanding for high piezoelectricity that is applicable to both Pb-based and Pb-free perovskite oxide ferroelectrics is yet to be established. Moreover, the piezoelectric response of ferroelectric materials depends on the polarization variation under external stimulus13. Recent studies indicate that modifications of local cation environments can heavily impact the piezoelectricity even without altering the long-range average symmetry6,23,24,25. This highlights the importance of local polarization characteristics in identifying a generic phenomenon that explains elevated piezoelectricity across different perovskite oxide systems.

Herein, we elaborate a generic fingerprint of the fluctuating local polarization (PFL), a quantitative descriptor of local polarization characteristics that directly correlates with the enhanced piezoelectric performance in perovskite ferroelectrics. This is achieved by capturing the characteristics of local polar displacement vectors (D) in 16 compositions, covering both Pb-based and Pb-free piezoelectric systems. The PFL-driven piezoelectricity can further explain the performance gap between Pb-based and Pb-free systems, stemming from the larger polar displacement of A-site cations in Pb-based materials compared to those in Pb-free systems.

Results and discussion

Quantitative description of local polarization state

High-performance piezoelectric materials are typically chemically complex solid solutions, where multiple cations occupy equivalent crystallographic sites. Differences in the ionic polarizability, atomic radius, or valence states of these cations cause them to deviate away from their crystallographic positions, manifesting as disorder that disrupts the average polarization that is constrained by the long-range structural symmetry. Considering the weak polarization anisotropy typically associated with the diverse local polarization variants in a system, the disorder of local polar displacements induced by the chemical complexity would impact the piezoelectricity. The study of atomic pair-distribution function (PDF), calculated from the total scattering function, incorporates both the Bragg diffraction and diffuse scattering26,27,28, therefore allows for study of local and nanoscale structures that go beyond the long-range symmetry of crystalline materials29,30.

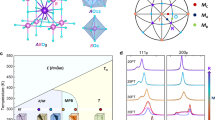
To characterize the features of the local polarization disorder, we employed advanced neutron total scattering experiment combined with RMC modelling31,32,33. The steps are illustrated in Fig. 1, taking the relatively high-performance Pb-free piezoelectric K0.48Na0.52Nb0.955Sb0.045O3 (KNNS) as an example. The starting supercells were constructed based on the average crystal structure derived from the Rietveld refinements of the neutron powder diffraction data. During the RMC modelling process, the atoms undergo random iterative movements and position-swaps to fit multiple experimental datasets, including the neutron Bragg data, the real-space data G(r), and the reciprocal-space data S(Q) (Fig. 1a–d). From the refined atomic configurations, the local polarization states, represented by the local polar displacement vectors (D), can be directly calculated as the off-centering displacement vector in the AO12 and BO6 cages (Fig. 1e). Unlike the single specific D obtained from the average structure refinement, this method provides a more comprehensive description of D by providing a distribution. Additionally, we focus on the orientation and magnitude of D to explore the characteristics of local spontaneous polarization across different piezoelectric systems.

Fig. 1: The workflow schematic of extracting local polarization characteristics based on the neutron total scattering and RMC modelling.
figure 1

a–d Bragg, reciprocal-space S(Q), and real-space G(r) data simultaneously fitted by RMC algorithm to get the refined 3D atomic configurations for KNNS. The black dots, red lines, and blue lines represent the observed data, the fitted calculated data, and the difference curve, respectively. e The local oxygen environment of A-site and B-site cations in a perovskite-type structure. f Stereographic projection along the [001]c direction and (g), the orientation disorder parameter of local polar displacement vectors (D). The <D> indicates the average vector, while the θ represents the deviation of Di from the direction of <D>.

Full size image

We have extracted the degree of orientation disorder and the mean magnitude of D (<D>) to quantify the characteristics of the local polarization state. The orientation order parameter S, often used to describe nematic ordering in liquid crystals34, is calculated as 1.5 < cos2θ > −0.533,35, where θ represents the angle of each displacement vector away from the direction of average polar displacement vector (<D>), the notation < > indicates averaging (Fig. 1g). A detailed definition of S is provided in the supplementary information. However, according to the definition of S, it should be noted that this order parameter is suitable for ferroelectric-based systems but may not be applicable to paraelectric, antiferroelectric, or fully disordered relaxor systems. The disorder parameter ξ is defined as 1 – S to quantify the degree of disorder in the orientation of the D33. ξ = 0 signifies perfect ordering, indicating that all polar displacement vectors are along the same direction in the ferroelectric-based systems, while ξ ~ 1 represents high directional disorder of these vectors. To validate the accuracy of our modelling, the polarization feature of PbTiO3 (PT) were calculated. The obtained mean magnitude polarization value is 55 μC/cm2 with a disorder parameter ξ of 0.03 (Supplementary Fig. 1), which are in good agreement with previously reported results35,36. Therefore, a combined evaluation of the magnitudes as well the orientation disorder of D can be provided to describe deeply the local polarization state in a ferroelectric system.

Configuration of local polar displacement vectors

Two chemically modified Pb-free KNN-based materials, namely (K0.5Na0.5)NbO3 (KNN50) and its modified variant KNNS, as well as the classical PZT-based composition of PbZr0.53Ti0.47O3 (PZT53) and its chemical modified counterpart 0.135PbZrO3-0.315PbTiO3-0.55Pb(Ni1/3Nb2/3)O3 (PZT-PNN), were investigated first to explore the relationship between the piezoelectric performance and the local polar displacement vectors. Specifically, KNN50 exhibits inferior piezoelectricity (d33 = 120 pC/N), while KNNS displays relatively high piezoelectricity (d33 = 400 pC/N). In a similar way, the PZT53 demonstrates inferior piezoelectricity (d33 = 220 pC/N), whereas PZT-PNN exhibits ultrahigh piezoelectricity (d33 = 1050 pC/N).

The configurations of A-site polar displacement vector (DA) and B-site polar displacement vector (DB) were extracted from the refined atomic configurations (Fig. 2), following the procedure outlined in Fig. 1. The left panel displays stereographs depicting the directional disorder, while the right panel presents histograms of the displacement magnitudes and their angular deviations relative to the average vector. Evidently, for the KNN-based system, the DB-distribution of KNN50 demonstrates a statistical preference along [011]c with a moderate level of angular deviations (Fig. 2a), while the DB-directions in KNNS exhibit a much broader range of deviations covering a larger area of the stereograph (Fig. 2b). On the other hand, the distributions of DA remain notably similar in both compositions. These observed direction-distributions of DB are consistent with the reported long-range orthorhombic phase in KNN5037 and align with the concept of multi-phase coexistence in KNNS24,38. Statistical analysis of the polar displacement vectors indicates a minor difference of DA, not only from the magnitude, but also from the angular distribution. Interestingly, there is a significant diffusion of θ for the DB in KNNS compared to KNN50 (Fig. 2d). This suggests an increased disorder of DB may lead to enhanced piezoelectricity in Pb-free systems.

Fig. 2: Characteristics of A/B-site polar displacement vectors in two KNN-based and two PZT-based systems.
figure 2

a, b, e, f The stereographic projection of local polar displacement vector with respect to [001]c. The right color bars represent the density of polar displacement vectors. c, g the magnitude and d, h the angle histograms of local polar displacement vectors. θ indicates the angle of each displacement vector away from the direction of average polar displacement vector <D>.

Full size image

For PZT-based system, the directions of both DA and DB display a much more dispersed distribution in the high-performance PZT-PNN compared to inferior performance PZT53, while the magnitude changes mildly (Fig. 2e–h). This suggests that a broader direction distribution of D generally leads to elevated piezoelectricity in both Pb-free and Pb-based systems. Interestingly, these two PZT-based compositions possess a large mean magnitude of DA (0.35 Å in PZT-PNN, 0.44 Å in PZT53) compared to the two KNN-based compositions (both about 0.2 Å), while there is not much difference in the mean magnitude of DB (about 0.21 Å). As the magnitudes of DB remain comparable among those systems, it is highly indicative that the performance gap between the Pb-free and Pb-based materials may exclusively originate from the distinct behaviour of the A-site cations.

The atomic resolution scanning transmission electron microscopy (STEM) technique was further employed to complement the observations from RMC method, with KNN50 and KNNS serving as examples (Fig. 3). KNNS, with its relatively high piezoelectricity, exhibits a wider variation of local distortions compared to KNN50, as revealed by the inverse Fast Fourier Transform (IFFT) of HRTEM (Fig. 3a, b and Supplementary Fig. 2a, b). The 2D atomic displacement mapping is extracted from the high-angle annual dark field (HAADF)-STEM, based on the position of A/B-site atomic columns (Fig. 3c–h and Supplementary Fig. 2c, d). In KNN50, predominant displacement occurs along the [011]c, with small fluctuations, resulting in a consistent color distribution within a 5-10 nm range. In contrast, KNNS displays smaller clusters of displacement vectors. Statistically, over 8000 displacement vectors were analyzed to confirm the distribution of displacement vector angles. The results clearly illustrate a broader angle distribution in KNNS compared with KNN50, confirming the observation in Fig. 2a–d. Such a continuous and broad distribution of polar displacement vectors, observed in other ferroelectric materials with high piezoelectricity, can therefore be considered to facilitate polarization rotation and thus enhancing piezoelectricity39,40. This observation again suggests that higher disorder in local polar displacement vectors favors higher piezoelectricity.

Fig. 3: Distributions of local polarization states revealed by the high-resolution STEM of KNN-based piezoelectric system.
figure 3

a, b The IFFT images obtained by masking the (110) spots in HRTEM images. c, d the STEM-HADDF images recorded along the [001]c zone axis along with the A-site displacement vectors mapping. e, f representative enlarged images from (c and d), respectively. g, h the schematic of displacement vector calculation. i angle histograms of the A-site and B-site displacement vectors. The angle of 0° indicates the [110]c direction.

Full size image

Fluctuating local polarization and piezoelectricity

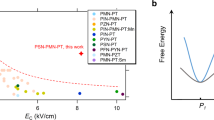
The above results suggest clearly that the macroscopic piezoelectric response is highly correlated with the local polarization configuration, and a ferroelectric system with higher piezoelectricity possesses a more disordered local polarization state. To gain a deeper understanding of how local polarization configuration influence piezoelectricity, we studied several prominent perovskite-type Pb-based and Pb-free piezoelectrics with varying piezoelectric coefficient d33. The detailed compositions are listed in Supplementary Table 1, with Pb-based systems exhibiting piezoelectric coefficients ranging from 80 to 1050 pC/N, and Pb-free systems showing values between 120 and 600 pC/N. The respective RMC fitting results for each composition are provided in Supplementary Fig. 3. The Rwp values of the RMC fitting results (Supplementary Table 2) for all systems indicate that the data were well-fitted simultaneously. Note that the extracted stereographic projections of local polar displacement vectors of PZT45, PZT53, PT, BT, and BCZT (Supplementary Fig. 4) agree well with previous studies29,31,35,41.

The critical parameters, including the disorder parameter ξ and the mean magnitude of D (<D>), both for A-site and B-site polar displacements in various piezoelectric systems, were extracted and presented in Fig. 4a, b. Two distinct subgroups are observed for Pb-based and Pb-free systems in the plot of ξ vs. <D> of the A-site, while no significant difference exists in the case of B-site cations. A common characteristic of a high ξA value close to 1 occurs in the Pb-free systems, which is notably higher than that in Pb-based systems. While the mean magnitude <DA> in the Pb-free systems is considerably lower than Pb-based systems. For example, both the Ba2+ and Ca2+ have a large ξ value of near 1 in the relatively high-performance BCZT (d33 = 600 pC/N), which is higher than the ξA value of 0.77 in the ultrahigh-performance PZT-PNN (d33 = 1050 pC/N). Despite this, PZT-PNN has a larger <DA> of Pb2+ of 0.35 Å compared to 0.22 Å for Ca2+, and 0.13 Å for Ba2+ in BCZT. Note that these compositions with high piezoelectricity, whether Pb-based or Pb-free, typically have a relatively high ξ value. For example, La-PZT65 and PZT-PNN have ξ values above 0.7, while KNNS and BCZT have ξ values above 0.8 for both the A-site and B-site. This scenario is also observed in individual solid solutions, such as the PZT and PMN-PT systems with varying Ti content, where MPB compositions exhibit higher ξ values as compared to the non-MPB compositions. Interestingly, although the Pb-free systems present high ξA, and similar values of ξB and <DB>, their piezoelectric d33 is still lower than that of the Pb-based systems. This indicates that piezoelectricity is governed not only by the orientational disorder of local polarization vectors but also by their magnitude.

Fig. 4: Strong correlation between fluctuating local polarization and piezoelectricity in various piezoelectric systems.
figure 4

a, b the plots of disorder parameter ξ and the mean magnitude <D> of A-site and B-site local polar displacement vectors, respectively. Different colors correspond to different atoms, while different shapes represent various systems. c the piezoelectric coefficient d33 as a function of fluctuating local polarization PFL, defined as ZA·<DA>·ξA + ZB·<DB>·ξB. The red bars represent Pb-based systems, and the blue bars represent Pb-free systems.

Full size image

To integrate these two critical parameters, disorder parameter and the magnitude of D, we introduced a new parameter called fluctuating local polarization (PFL), which is defined as PFL = ΣiZi·<Di>·ξi, where Zi represents the charge of the different cations, and the nominal charge was utilized to simplify the calculation. The PFL reflects the accumulated states of electric dipole moments (Z·<D>) from both A-site and B-site. In other words, PFL effectively captures the directional distribution and the magnitude of A/B-site electric dipole moments. A larger value of PFL requires not only a large magnitude but also high disorder characteristics of A/B-site electric dipole moments. Interestingly, the plot of d33 as a function of PFL reveals a compelling correlation in both Pb-based and Pb-free systems (Fig. 4c). The piezoelectric d33 demonstrates a strong positive correlation with the PFL value, where a larger PFL value corresponds to a higher d33. For example, the considerable enhancement in disorder of both DA and DB from PZT65 to La-PZT65, leads to a PFL value increases from 0.85 to 1.31, and corresponding to a d33 enhancement from 100 to 850 pC/N. Similarly, the rise in ξB from KNN50 to KNNS, results in a PFL value increase from 0.8 to 1.07, leading to a d33 increase from 120 to 400 pC/N.

Notably, despite BCZT exhibits very high ξ ~ 1 values for both A-site and B-site, its relatively low <DA> value results in a moderate PFL value of 1.1, yielding a relatively high d33 of 600 pC/N. This highlights that enhancing piezoelectricity requires not just the orientation disorder of local polar displacement vectors, but also maintaining a significant magnitude. From thermodynamic theory, the critical role of high PFL stems from the interplay between significant orientational disorder—reducing polarization anisotropy—and large local polarization magnitudes, which collectively contribute to a flattened free-energy landscape across a broad polarization range. These features enable larger polarization variations under small external fields, enhance polarization-lattice coupling, and ultimately lead to a heightened piezoelectric response.

Piezoelectric performance gap between Pb-based and Pb-free materials

Based on the quantifiable relationship between PFL and d33, the individual piezoelectric contributions from the A-site and B-site can be evaluated. The piezoelectric contribution from A-site in the Pb-free systems (dark blue shaded columns, typically below 30%) is much smaller than that in Pb-based systems (dark red shaded column, typically 45%), owing to the lower values of <DA> (Fig. 4c and Supplementary Fig. 5). The observed piezoelectricity gap in Pb-based and Pb-free systems can be attributed to the distinct behaviour of A-site polar displacement, wherein Pb-free systems exhibit smaller magnitude of A-site local polar displacement compared to Pb-based systems. For example, the piezoelectric contribution from B-site (ZB·<DB>·ξB) is similar for BCZT (d33 = 600 pC/N) and La-PZT65 (d33 = 850 pC/N). However, BCZT has a lower value of ZA·<DA>·ξA compared to La-PZT65 despite having a higher value of ξA (Supplementary Fig. 5). Importantly, in Pb-free systems, it appears challenging to largely increase the PFL from the A-site by enhancing the disorder (Fig. 4a), due to the inherently high disordering. In these systems, the piezoelectric enhancement through chemical modifications mainly arising from B-site disordering (Supplementary Fig. 6). In contrast, Pb-based systems still have considerable potential to improve disorder, as both the A-site and B-site can accommodate large polar displacement. This atomic-level observation aligns with the greater ease of achieving a d33 value of 1000 pC/N in Pb-based ceramics3, while Pb-free KNN-based and BT-based ceramics are typically limited to below 700 pC/N8. The different behaviour of A-site atoms in Pb-based and Pb-free systems thus provides a key insight into why Pb-free piezoelectric systems generally exhibit inferior performance compared to Pb-based systems.

DFT calculations and A-site susceptibility

To further explore the atomic-level mechanisms underlying the relationship between PFL and piezoelectricity, density functional theory (DFT) calculations were employed. DFT calculations were performed on relatively simple systems with representative compositions, including Pb-based PZT65 and La-PZT65, as well as Pb-free KNN50 and KNNS. A broadened DB distribution from DFT calculations is observed in high piezoelectric performance compositions such as La-PZT65 (d33 = 850 pC/N) and KNNS (d33 = 400 pC/N), compared with their lower-performing counterparts, PZT65 (d33 = 120 pC/N) and KNN50 (d33 = 120 pC/N) (Supplementary Fig. 7c). This observation is consistent with the results obtained from RMC fitting and STEM analysis.

To understand the role of local polarization in piezoelectricity, we examined the sensitivity of local potential energy (<k>) of each A-site ions, which measures the position shift from small perturbation40. A smaller value of <k> corresponds to the larger ions shift under a small external field, thus reflecting a higher piezoelectric response. Significantly, the higher value of PFL also suggests easier ions shifting, analogous to the smaller <k>. As depicted in Fig. 5, an increase in the PFL from PZT65 to La-PZT65, as well as from KNN50 to KNNS, corresponds to a decrease in the <k> value, consequently resulting in a significant enhancement in the piezoelectric response.

Fig. 5
figure 5

Correlation between d33 and the susceptibility (<k>) from DFT calculation.

Full size image

Interestingly, a pronounced difference in the <k> values between Pb-based and Pb-free systems is observed, with the <k> values of the PZT65-based compositions being considerably lower than those of the KNN-based compositions. This coincides with the performance gap elucidated in Pb-based and Pb-free system. Notably, the <k> value of La-PZT65 is smaller than that of KNNS, corresponding to its higher piezoelectric performance. The different <k> values for A-site atoms in Pb-based and Pb-free systems contribute to the understanding of the piezoelectricity gap. The weak coupling between A-site atoms and oxygen in Pb-free systems (Supplementary Fig. 7b) contrasts with the strong A-O hybridization in Pb-based systems42 (Supplementary Fig. 7a) due to the lone pair of Pb2+, accounting for a smaller value of <k> observed in Pb-based systems. These features suggest lower local potential energy stiffness and stronger polarization-lattice coupling in Pb-based systems, which contribute to their superior piezoelectric performance.

The high value of PFL indicates a larger variety of polarization states, signifying a broader spatial configuration of polar displacement available for polarization variation. The orientation disorder in polar displacements corresponds to the reduced polarization anisotropy, accompanied with large magnitude of polar displacements, corresponds to a flattened energy landscape over wide polarization length range. This feature leads to a large effective polarization variation and enhances polarization-lattice coupling with external stimulus, and resulting heightened piezoelectricity. Notably, this diversity in polar displacement is reflected in the polarization within the unit cell, leading to the presence of multiple polarization orientations in perovskite ferroelectric materials. Established piezoelectric mechanisms, such as multi-phase coexistence, local heterogeneity, and low-symmetry phase, also emphasize the role of increased polarization orientation diversity. For example, the phase coexistence at MPBs or PPBs correlates with diverse polarization variants from different phases. These phenomena are linked to the reduction of polarization anisotropy, correspond to a low energy barrier for polarization reorientation under external fields, and ultimately leading to enhanced piezoelectric performance1,4,8,43.

From a materials design perspective, achieving a high value of PFL is crucial for attaining high piezoelectricity. This study suggests chemical composition design principles for both high-performance Pb-based and Pb-free systems. It is important to maintain a large <D> when introducing high disorder ξ. The prime examples include our recently reported high piezoelectricity in high-entropy compositions, such as PNN-PIN-PT (d33 = 920 pC/N), PNN-PSN-PT (d33 = 804 pC/N)40, and the designed PNN-PIN-PZT (d33 = 1010 pC/N) (Supplementary Fig. 8). In these examples, since the Pb atoms effectively maintain large A-site polar displacement, the improvement in piezoelectric performance is primarily achieved by introducing disorder through chemical substitution. Conversely, in Pb-free systems, the low <DA> (such as Ba2+, Ca2+, Sr2+, K+, Na+) limits the performance enhancement, even though a high degree of disorder can be achieved. The 6s2 lone pair electron is crucial for the high <DA> in Pb-based systems. Looking at the periodic table, the Bi3+ and Tl+ possess a similar lone pair configuration to Pb2+. However, the small ionic radius of Bi3+ results in long-range oxygen octahedron tilting44, typically leading to a high local polar displacement ordering that hinders the piezoelectric performance enhancement. Additionally, Tl+ is a highly toxic element. Therefore, Pb-free materials are unlikely to achieve the same high level of d33 as Pb-based materials solely through chemical compositional design. Overall, the concept of PFL can provide a theoretical framework for designing high-performance Pb-based piezoelectric materials, and offers insight into the difficulties in developing high-performance Pb-free materials.

In summary, we have introduced a phenomenological model—called fluctuating local polarization—as a quantitative measure to describe the atomic-level polar displacement characteristics, demonstrating a strong correlation with the observed piezoelectricity in both Pb-based and Pb-free systems. The model considers both the magnitudes and disorder of local polarization vectors, which ultimately influence the local potential energy surfaces and determine the adaptability of inherent polarizations under external stimuli. This quantitative measure, derived from nanoscale structural information, not only explains the development of piezoelectric activity within specific systems and the distinct macroscopic properties of Pb-based and Pb-free materials, but also complements existing theories, such as the role of low-symmetry monoclinic phases in Pb-based materials, in describing enhanced piezoelectric activity as a function of composition. As such, the proposed concept offers a potential fingerprint for understanding the evolving local structural correlations that drive extraordinary piezoelectricity in both Pb-based and Pb-free systems. It provides a theoretical foundation for designing high-performance perovskite piezoelectric materials. Furthermore, this simple concept could be extended beyond ferroelectric systems, making it applicable to other ordered/disordered functional materials, including those exhibiting magnetic and/or charge-ordering phenomena.

Methods

The detailed sample preparation and structural characterization methods are provided in the Supplementary Information file.