Introduction

Electrons confined to two spatial dimensions and subjected to a strong perpendicular magnetic field exhibit quantum Hall effects1,2. Charge transport is governed by one-dimensional chiral edge modes3,4,5,6,7, enabling coherent transport and interferometry. Fabry-Pérot interferometers serve as powerful probes for studying quasiparticle charge, anyonic braiding statistics, and Coulomb interactions between localized charged excitations and gapless edge modes. Fabry-Pérot interferometers have been extensively explored in both theoretical8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29 and experimental works30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46. While much recent effort has focused on interrogation of braiding statistics in the fractional quantum Hall regime, Fabry-Pérot interferometers also expose interesting phenomena in the integer quantum Hall regime. Unexpectedly, experiments47,48,49 have revealed a halved magnetic flux period of ϕ0/2 and a halved voltage period while interfering with the outermost edge mode for filling factors 2.5 < ν < 5. Here \({\phi }_{0}\equiv \frac{h}{e}\) is the quantum of magnetic flux. The authors of refs. 47,48,49 proposed that the periodicity of ϕ0/2 was due to the pairing of electrons, resulting in an interference charge of e*  =  2, where e* is normalized to the magnitude of the charge of a single electron ∣e∣. However, the mechanism that generates the putative pairing was not established. Subsequent theoretical work50 argued that the period halving may be understood as an effect not of electron pairing but of electrostatic interaction between multiple independent edge channels. A recent experiment in a graphene-based Fabry-Pérot interferometer concluded that edge–edge coupling and charge quantization were enough to generate the observed period halving without invoking electron pairing51.

In a quantum Hall Fabry-Pérot interferometer, two quantum point contacts are used to partially reflect incident edge modes. Interference is generated by coherent transport within the interferometer chamber. In the limit of weak backscattering and negligible Coulomb coupling, the interference phase evolves as11,19,28,29,

$$\frac{\theta }{2\pi }={e}^{*}\frac{AB}{{\phi }_{0}}+{N}_{L}\frac{{\theta }_{a}}{2\pi }$$
(1)

Here, B is the magnetic field, A is the area enclosed by the interference path, e* denotes the quasiparticle charge normalized to the elementary electron charge ∣e∣, NL is the number of quasiparticles localized within the device, and θa is the statistical phase of the quasiparticles. Eq. (1) incorporates both the Aharonov–Bohm phase and the statistical (anyonic) phase contributions to the interference phase. For integer quantum Hall states, the discrete change in phase associated with the addition or subtraction of a localized electron is an unobservable factor of 2π. Hence, the variation of the interference phase in integer states in the absence of Coulombic couplings can be expressed as δθ/2π = (AδB + BδA)/ϕ0, where δA = αδVPG is the variation in area due to the modulation of the plunger gate and α is the constant of proportionality relating the change in the interferometer area to the variation of the plunger gate voltage. The expected magnetic field and plunger gate voltage periods are:

$$\Delta B=\frac{{\phi }_{0}}{A}$$
(2)
$$\Delta {V}_{PG}=\frac{{\phi }_{0}}{\alpha B}$$
(3)

Equation (1) neglects two important couplings active in real interferometers: bulk-edge coupling, which may alter the area of the interference path when the charge configuration in the interior of the interferometer changes, and capacitive edge–edge coupling that may contribute when isolated edge modes are present at the boundary of the quantum Hall liquid. At integer filling factors greater than ν = 1 and in certain fractional states, multiple edge modes are typically present. In these cases, we must consider the capacitive interaction between multiple edge modes.

Theoretical work has extensively examined a minimal capacitive model to describe the energetics of a Fabry-Pérot interferometer15,19,23,28,29,50. As a specific example, we consider an interferometer in which the bulk filling factor is ν = 2 bounded by two circulating edge modes. For small variations in the charge in the interior of the interferometer and the interferometer area, the total electrostatic energy of the system may be expressed to quadratic order as:

$${E}_{tot}= \frac{{K}_{1}}{2}\delta {q}_{1}^{2}+\frac{{K}_{2}}{2}\delta {q}_{2}^{2}+\frac{{K}_{L}}{2}\delta {q}_{b}^{2}+{K}_{1L}\delta {q}_{b}\delta {q}_{1}\\ +{K}_{2L}\delta {q}_{b}\delta {q}_{2}+{K}_{12}\delta {q}_{1}\delta {q}_{2}$$
(4)

The variation in charge in the interior of the interferometer is represented by δqb, the variation of charge on the outer edge is δq1, and the variation of charge on the inner edge mode is δq2. A set of effective interactions parameterizes the total electrostatic energy. The stiffness of the edge modes, K1 and K2, represents the energy cost associated with the variation of the area of the edge channels for the outer edge and the inner edge, respectively; bulk-edge couplings, K1L and K2L, quantify the electrostatic coupling between charge in the interior of the interferometer and each of the two edge modes, and the edge–edge coupling, K12, captures the electrostatic (capacitive) interaction between the two edge modes.

The variations of charge in Eq. (4) may be further specified as:

$$\delta {q}_{b}={e}^{*}{N}_{L}+2\frac{\bar{A}B}{{\phi }_{0}}-\gamma \Delta {V}_{PG}$$
(5)
$$\delta {q}_{1}=\left({N}_{1}-\frac{\bar{A}B}{{\phi }_{0}}\right)$$
(6)
$$\delta {q}_{2}=\left({N}_{2}-\frac{\bar{A}B}{{\phi }_{0}}\right)$$
(7)

Here \(\bar{A}\) is the average area of the interferometer that does not include variations δA due to bulk-edge and/or edge–edge coupling. N1 is the charge in N = 0 spin-down Landau level, and N2 is the charge in the N = 0 spin-up Landau level that forms the quantum Hall condensate in the interior of the interferometer, not including localized excitations. γ is the proportionality constant that relates the change in the voltage of the plunger, ΔVPG, needed to induce the charge ∣e∣ on the interferometer. In a configuration where the QPCs are set to partially transmit the outer mode while fully reflecting the inner mode, the charge dynamics are constrained. Charge variations in the interior of the interferometer and on the inner isolated edge are quantized to integer values because the inner edge is effectively disconnected from the reservoir of charge in the ohmic leads.

Minimization of the total energy with respect to the variations of the charge on the interfering outer edge is achieved by setting \(\frac{\partial {E}_{tot}}{\partial (\delta {q}_{1})}=0\). This condition leads to the following relation for modifications of charge in the interior of the interferometer (bulk and isolated inner edge mode) and on the outer interfering edge mode:

$$\delta {q}_{1}=-({K}_{1L}/{K}_{1})\delta {q}_{b}-({K}_{12}/{K}_{1})\delta {q}_{2}.$$
(8)

Using the established relationships between δqi’s, the expression for the total interference phase (Eq. (1)) may be rewritten as:

$$\frac{\theta }{2\pi }= {e}^{*}\frac{\bar{A}B}{{\phi }_{0}}-{e}^{*}\frac{{K}_{1L}}{{K}_{1}}\left({e}^{*}{N}_{L}+2\frac{\bar{A}B}{{\phi }_{0}}-\gamma \Delta {V}_{PG}\right)\\ -{e}^{*}\frac{{K}_{12}}{{K}_{1}}\left({N}_{2}-\frac{\bar{A}B}{{\phi }_{0}}\right)$$
(9)

The normalized charge of the interfering particles is retained as e* to maintain generality, even though we may expect e*  =  1 for the integer states. For simplicity, we neglect the anyonic phase term \({N}_{L}\frac{{\theta }_{a}}{2\pi }\) in Eq. (1) as we do not expect anyonic statistics at the integer states ν  =  2 and ν  =  3. In Eq. (9), the second term on the right-hand side reflects the contribution from the bulk-edge coupling, while the third term is the phase variation attributable to edge–edge coupling.

The interplay between bulk-edge and edge–edge couplings significantly modifies the interference. Eq. (9) is generally applicable and does not rely on a particular regime of interferometer operation. For interferometer operation in incompressible regimes, where the number of localized quasiparticles is fixed such that δNL = 0, modifications to the interference periods induced by these couplings can be expressed in a simple form. For an incompressible regime at ν = 2, Eq. (9) implies magnetic field and gate voltage periods given by the following expressions:

$$\Delta B=\frac{{\phi }_{0}}{{e}^{*}(1-2\frac{{K}_{1L}}{{K}_{1}}+\frac{{K}_{12}}{{K}_{1}})\bar{A}}$$
(10)
$$\Delta {V}_{PG}=\frac{1}{{e}^{*}}{\left(\left(1-2\frac{{K}_{1L}}{{K}_{1}}+\frac{{K}_{12}}{{K}_{1}}\right)\frac{\alpha B}{{\phi }_{0}}+\gamma \frac{{K}_{1L}}{{K}_{1}}\right)}^{-1}$$
(11)

These particular expressions for the magnetic field and plunger gate voltage periods are valid when N2 is constant and δNL = 0, such that the interference phase evolves continuously. Even within an incompressible region, if the number of localized quasiparticles varies, discrete phase slips can also be observed, as predicted in theoretical studies19,23,28,50. Between these discrete phase slips, NL remains fixed, and the interference phase evolves continuously. The periodicity of phase evolution between phase slips is described by Eq. (10) and Eq. (11) and may be determined experimentally through Fourier decomposition of the interference data. The interference charge in the integer quantum Hall regime can be determined by analysis of the discrete phase slips, while the ratios K1L/K1 and K12/K1 can be accurately determined by analyzing the interference periods in compressible and incompressible operating regimes, and through analysis of differential conductance measurements42,43. The effective area of the interferometer and the proportionality constants can be extracted by measuring the differential conductance in the tunneling regime at B  = 0 T and the interference at ν = 140,41,42,43.

If interference occurs in the compressible regime, the analysis of the expected magnetic field period, which we used to evaluate K12/K1, is modified slightly. In the compressible regime, the total charge density in the interior of the interferometer remains fixed (∂(δqb)/∂B  = 0) when the magnetic field is varied so that the flux changes by ϕ0. Examination of Eq. (9) indicates that the magnetic field period is modified in the compressible regime to be the following:

$$\Delta B=\frac{{\phi }_{0}}{\bar{A}(1+\frac{{K}_{12}}{{K}_{1}})}$$
(12)

Here we report on an experiment designed to determine the magnitude of the interfering charge and understand the origin of the unusual ϕ0/2 periodicity for the interference of the outermost edge mode at ν = 2 and ν = 3 in an AlGaAs/GaAs Fabry-Pérot interferometer. Toward this end, we designed and examined an interferometer that expresses measurable bulk-edge coupling and edge–edge coupling to highlight the important role played by these Coulomb coupling mechanisms in determining interferometer periodicity and phase evolution in the integer quantum Hall regime. We describe and apply a method to extract in operando the effective interference charge, the edge–edge coupling constant, and the bulk-edge coupling constant42,43. The magnitude of the couplings extracted by this analysis quantitatively explains the observed ϕ0/2 periodicity and constrains the possible magnitude of the interfering charge. The central findings of our study can be summarized as: (1) the observed periodicity ϕ0/2 is quantitatively explained by capacitive coupling to isolated inner edge modes, and (2) the magnitude of discrete phase slips at ν = 2 and ν = 3 for interference of the outer edge mode indicate that the interfering charges are single electrons, ruling out for our experiments an effective charge e* = 2 postulated previous experimental works47,48,49.

Results

Device design

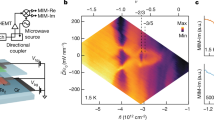
Our device was fabricated on the AlGaAs/GaAs heterostructure40,52,53 shown in Fig. 1a. Our heterostructure design incorporates three GaAs wells populated with electrons: a 30 nm wide primary quantum well flanked by two additional 12.5 nm wells situated on either side of the primary well separated by 25 nm AlGaAs spacer layers. The 2DEG located in the primary GaAs quantum well has an electron density ns = 0.65 × 1011 cm−2. The additional populated quantum wells serve to partially screen long–range Coulomb interactions, allowing the interferometer to operate in an intermediate regime that exhibits features associated with both Aharonov–Bohm interference and Coulomb-dominated interference. Electron beam and optical lithography techniques were employed in the fabrication process. In Fig. 1b, an atomic force microscopy image of the interferometer is presented. QPCs form narrow constrictions, and a pair of plunger gates defines the interference path. The QPCs are negatively biased to adjust the transmission of the individual edge modes, while the plunger gates are biased just past the depletion point to delineate the interference path. The central top gate was grounded during the course of this experiment. In Fig. 1c, the Hall resistance, Rxy, and the diagonal resistance across the interferometer, RD, as a function of magnetic field are plotted with the QPCs and plunger gates biased just past depletion. Parallel conduction through the ancillary wells is suppressed by negatively biasing gates near the ohmic contacts40,41,42,43.

Fig. 1: Device design.
figure 1

a Schematic of our GaAs/AlGaAs heterostructure consisting of a primary GaAs quantum well flanked by ancillary GaAs screening wells. b False color atomic force microscopy image of the interferometer studied in this work. Yellow regions are the metallic gates that define the interference path with a lithographic area 0.58 μm2. c Bulk Rxy and diagonal resistance RD across the interferometer, demonstrating overlapping plateaux at integer quantum Hall states. The QPCs are biased at VQPC = −0.9 V, and the plunger gate is biased at VPG = −0.7 V, just past depletion. The top gate in the center of the interferometer is grounded during all measurements.

Full size image

Measurements at B = 0 and ν = 1

Figure 2a illustrates the variation in conductance, δG, as a function of the voltage variation of the plunger gate, δVPG, and the variation of the DC source-drain bias, δVSD, in the tunneling regime at B = 0 T. The height of the Coulomb diamonds indicates that the charging energy is EC ≈ 95 μeV. The spacing between crossings at zero DC bias yields 1/γ ≈ 5.1 mV. In Fig. 2b, the conductance variation, δG, (with a smooth background subtracted) is plotted against magnetic field B and plunger gate voltage variation, δVPG, at the integer quantum Hall state ν = 1. The QPCs have been set to ~90% transmission. Note that δVPG is relative to −0.7 V in all measurements. At the center of the ν = 1 plateau (B ≈ 2.6 T), the magnetic field period is ΔB ≈ 19 mT. The period in the center of the plateau is longer than that observed in the low and high field flanks, indicating that the chemical potential lies in the bulk gap and the state is incompressible19,26,28. At higher and lower fields, the magnetic field period is shorter, indicating that the localized electron number varies by 1 when the flux changes by ϕ0, returning the magnetic field period to the base value of ϕ0/A. The change in periodicity in the higher and lower fields is consistent with a transition from an incompressible regime in the center of the plateau to compressible regimes on the flanks19,26,28,41,42. The average magnetic field period at the higher and lower fields, ΔB = 16.2 mT, yields an effective area of the interferometer A = ϕ0/ΔB ≈ 0.26 μm2. The gate voltage oscillation period at B = 2.3 T is ΔVPG = 9.07 mV, which yields ∂A/∂VPG = ϕ0/(BΔVPG) ≈ 0.198 μm2 V−1. The ratio of periods in the incompressible regime and in the compressible regime can be used to estimate KIL/KI  ≈ 0.16, indicating a relatively weak bulk-edge coupling at ν = 1 for this device, consistent with the observed Aharonov–Bohm interference pattern19,23,26,28,42,43,50.

Fig. 2: Measurements at B = 0 and ν = 1.
figure 2

a Differential conductance measurements at zero magnetic field in the Coulomb blockade regime. The height of the diamonds gives the charging energy of \(\frac{{e}^{2}}{C}\approx 95\) μeV. Additionally, the spacing between crossings at zero bias yields \(\frac{1}{\gamma }\approx 5.1\) mV. b Interferometer conductance oscillations versus magnetic field and gate voltage at ν = 1. The magnetic field oscillation period is larger near the plateau center, indicating an incompressible bulk and moderate bulk-edge coupling. In the compressible regions at high and low fields, the interference oscillation period yields an effective area of A  ≈  0.26 μm2 and \(\alpha=\frac{\partial A}{\partial {V}_{PG}}\approx 0.198\) μm2 V −1.

Full size image

Interference at ν = 2

Our primary objective is to determine the interfering charge and to understand the origin of the unusual flux periodicity ϕ0/2 for the interference of the outermost edge mode at ν = 2 and ν = 3 that has been attributed to electron pairing in previous experiments. Setting the magnetic field to B = 1.25 T places the interferometer at ν = 2. The conductance of an individual QPC at ν = 2 is shown in Fig. 3a. The complete transmission of two edge modes is revealed by the quantized plateau at G = 2e2/h. The absence of a clear plateau G = e2/h suggests coupling between the inner and outer edges, likely associated with a small spin gap at B = 1.25 T. We first set the QPCs to partially reflect the inner edge mode. We eventually interfere with the outer edge mode by applying more negative bias. The operating points are indicated by red circles in Fig. 3a.

Fig. 3: Interference at ν = 2.
figure 3

a QPC conductance versus gate voltage at ν = 2. A robust conductance plateau at \(G=2\frac{{e}^{2}}{h}\) is observed, indicating full transmission of two edge modes of the N = 0 Landau level. However, a sharp plateau at \(G=\frac{{e}^{2}}{h}\) is not evident, likely due to the smallness of the spin gap at B = 1.25 T. Red circles indicate the QPC settings for partial transmission of the inner mode and outer mode of the N = 0 Landau level. b Interference while partially transmitting the inner edge mode (spin-up N = 0 Landau level). c 2D FFTs of interference for the inner mode and the outer mode in the compressible and incompressible regimes at ν = 2. d Interference while partially transmitting the outer edge (spin-down N = 0 Landau level). For interference of both the inner and outer modes, the data display a larger magnetic field period near the plateau center, indicating an incompressible bulk. At lower fields, a smaller period accompanied by numerous phase modulations is observed, suggesting a compressible bulk. Black dashed lines in panel d highlight the discrete phase slips within the incompressible region when interfering the outer edge mode at ν = 2. e Plot of the magnitude of discontinuous phase slips observed in Fig. 3d with \(\overline{\Delta \theta }/2\pi \approx 0.38\). f Differential conductance versus DC source-drain bias and plunger gate voltage. g FFT amplitude of the differential conductance vs. DC source-drain bias. The FFT amplitude minimum corresponds to the nodes in the interference, allowing extraction of ΔVSD1 ≈ 132 μV.

Full size image

Figure 3b displays interference when weakly backscattering the inner mode and fully transmitting the outer mode. On the low-field flank of ν = 2 (B < 1.18 T), the magnetic field and the plunger gate periods are, respectively, ΔB ≈ 17.0 mT and ΔVPG ≈ 18.0 mV. The magnetic field period is close to that extracted at ν = 1 in the compressible regime, as expected for Aharonov–Bohm interference. The plunger gate period for the inner mode is ΔVPG = 18.0  mV, approximately twice the period observed at ν = 1, consistent with the reduction in magnetic field needed to reach ν = 240. Using ∂A/∂VPG = 0.198 μm2 V−1 and the effective area A = 0.26 μm2 extracted at ν = 1, the expected period for pure Aharonov–Bohm interference at ν = 2 is calculated as ΔB = ϕ0/A = 15.9 mT and ΔVPG = ϕ0/(B∂A/∂VPG) = 18.1 mV, which align well with our experimentally observed periods. The observation of phase modulations in the low-field data suggests a compressible regime where the number of localized electrons in the interferometer varies with magnetic field and gate voltage.

Near the center of the ν = 2 plateau (1.18 T < B < 1.28 T), the periods change and a small number of discrete phase slips are observed, indicative of an incompressible regime in which disorder lowers the energy of a few discrete localized electronic states. The magnetic field period is larger in this regime, revealing the influence of bulk-edge coupling. In the incompressible regime the magnetic field period is measured to be ΔB ≈ 32.9 mT and the plunger gate period is ΔVg ≈ 15.0 mV. Predominantly Aharonov–Bohm interference is maintained as the system transitions to the incompressible regime. At fields above B = 1.30 T, the interference changes dramatically, suggesting a transition to a highly compressible regime and increased decoherence for the inner edge mode. This regime is not explored further in this study.

Setting the QPCs to achieve total conductance G = 0.8 e2/h induces total reflection of the inner edge mode and partial transmission of the outer mode. As seen in Fig. 3d, at magnetic fields below B = 1.21 T, the interference pattern exhibits lines of constant phase with negative slope with prominent modulations, reminiscent of the observations on the high magnetic field side of ν = 1. These additional modulations observed along lines of otherwise constant phase are consistent with periodic changes in the localized electron number in the interior of the interferometer. These phase modulations are only visible in the integer quantum Hall regime due to finite bulk-edge coupling; otherwise, the phase change associated with the addition or removal of an electron is an unobservable factor of 2π.

For B ≤ 1.21 T, the interference periods are determined using a 2D fast Fourier transform (FFT) that yields ΔB ≈ 8.45 mT and ΔVPG ≈ 8.32 mV as shown in Fig. 3c. Intriguingly, this magnetic field period is approximately half of the magnetic field period observed at ν = 1 in the compressible regime. This observation of ϕ0/2 periodicity is noteworthy as it is in conflict with naive expectations for interferometers in the Aharonov–Bohm limit15,19,23,26,28,50. The observation of ϕ0/2 periodicity when partially backscattering the outermost edge mode has previously been attributed to interference of charge e* = 2 quasiparticles in the integer quantum Hall regime in experiments using AlGaAs/GaAs interferometers47,48,49. Although the ϕ0/2 period observed in our device is consistent with observations in previous experimental works47,48,49,51,54, it does not provide evidence for charge e* = 2 excitations. As we will demonstrate, our data are consistent with the interference of charge e* = 1 electrons in the integer quantum Hall regime.

The transition to an incompressible region near the center of the plateau at B = 1.25 T is seen in the data of Fig. 3d. In this incompressible regime, ΔB ≈  12.5 mT and ΔVPG ≈ 6.50 mV. Interestingly, the magnetic field period is smaller than that observed at ν = 1 in the incompressible regime. In the interferometer studied here, the combined effects of bulk-edge coupling and edge–edge coupling associated with the fully reflected inner mode modify the periodicity in the incompressible regime at ν = 2. These coupling parameters can be determined in operando and constrain the possible value of the interfering charge. As seen in Fig. 3d, a few discrete phase slips are evident in the incompressible regime at ν = 2 for interference of the outer edge mode. The average magnitude of these phase slips is measured to be \(\frac{\overline{\Delta \theta }}{2\pi }\approx 0.38\), as shown in Fig. 3e, and is described in greater detail in  Supplementary Information. Referring to Eq. (9), we may now consider the discontinuous change in interference phase associated with the removal or addition of a localized charged excitation while keeping all other parameters fixed such that \(\delta (\bar{A}B)/{\phi }_{0}=0\), δVPG = 0, and δN2 = 0. Under these circumstances, the expression for the change in phase Δθ associated with the removal of a localized excitation in the interior of the interferometer reduces to:

$$\frac{\Delta \theta }{2\pi }=\frac{{{e}^{*}}^{2}{K}_{1L}}{{K}_{1}}$$
(13)

The magnitude of the observed phase slips is determined by the effective charge and the coupling parameters K1L and K1. To determine the effective interference charge experimentally, we must determine K1L and K1. We utilize the model detailed in refs. 42,43 to determine K1L, and K1 from the measurements. It should be noted that the sign of the phase slips observed in our experiment is opposite to those observed in ref. 51. The positive phase slips observed here suggest that the phenomenon is attributable to a change in the occupation of localized excitations in the interior of the interferometer.

In order to relate K1 and K1L to experimentally measurable quantities, we note that the total energy of the interferometer, Etot, may be written as a combination of electron–electron interaction energy, Eint, and the single-particle energy, Esp, due to electrostatic confinement in the interferometer: Etot = Eint + Esp. To determine Eint, we model the interferometer as a quantum dot. The energy of the electron–electron interaction is then given by \({E}_{int}={(e\delta {q}_{tot})}^{2}/2{C}_{0}\), where eδqtot = e(δq1 + δq2 + δqb) is the total charge within the interferometer, and C0 is the self-capacitance of the interferometer. The interaction energy can be written as:

$${E}_{int}= ({e}^{2}/{C}_{0})\left(\delta {q}_{1}^{2}/2+\delta {q}_{2}^{2}/2+\delta {q}_{b}^{2}/2+\right.\\ \left.\delta {q}_{1}\delta {q}_{2}+\delta {q}_{1}\delta {q}_{b}+\delta {q}_{2}\delta {q}_{b}\right)$$
(14)

As illustrated in Fig. 2a, the measurement of the differential conductance in the Coulomb blockade regime at B = 0 T produces a charging energy of e2/C ≈ 95 μeV. We can refine our determination of C0 by subtracting the contribution from the single particle level spacing at B = 0 T determined by the finite density of states in a 2D system42. For a device with an area A ≈ 0.26 μm2, the contribution of the quantum capacitance is e2/Cquantum = πℏ2/(m*A) ≈ 11 μeV. This yields e2/C0 = e2/C − e2/Cquantum = 95 μeV–11 μeV = 84 μeV.

The single-particle energy, Esp, is the energy cost to add charge to each edge mode in the presence of the external electrostatic confining potential when the area of the interferometer changes. This energy is given by \({E}_{sp}=e\delta {q}_{i}^{2}{\phi }_{0}{v}_{i}/2L\), where L is the perimeter of the interference path calculated from the effective area A as \(L\approx 4\sqrt{A}\approx 2.04\)μm, and vi is the velocity of the ith edge state42. The edge velocity is experimentally determined by the node spacing, ΔVSD, observed in finite DC source-drain bias measurements of the interference signal, expressed as ΔVSD = hvi/(ee*L)11,24,42,43,55. At ν = 2, two edge modes contribute to the single-particle energy such that \({E}_{sp}=\frac{{e}^{*}\delta {q}_{1}^{2}}{2}e\Delta {V}_{SD1}+\frac{{e}^{*}\delta {q}_{2}^{2}}{2}e\Delta {V}_{SD2}\). ΔVSD1 and ΔVSD2 are the node spacings determined by finite bias measurements for the outer mode and inner mode, respectively.

Combining Eq. (4) with the expressions for the electron–electron interaction energy and the single particle energy allows us to write expressions for the bulk-edge coupling, K1L, and the stiffness of the edge mode, K1, in terms of experimentally measurable quantities42,43:

$${K}_{1L}=\frac{{e}^{2}}{{C}_{0}}$$
(15)
$${K}_{1}=\frac{{e}^{2}}{{C}_{0}}+{e}^{*}e\Delta {V}_{SD1}$$
(16)

Eq. (15) yields K1L = e2/C0 = 84 μeV. In the integer quantum Hall regime, the edge stiffness K1 can be determined from the measurement of the charging energy at B = 0 T and the measurement of the spacing of the nodes with finite source-drain bias as shown in Fig. 3f for the outer mode at ν = 2. The FFT amplitude versus VSD is shown in Fig. 3g which yields ΔVSD1 = 132 μV. For our analysis of ϕ0/2-periodic interference for the outer mode at ν = 2, we have retained the magnitude of interfering charge as a variable to be determined in experiment. In this case, the identification of an incompressible regime punctuated by few discrete phase slips for interference of the outer mode at ν = 2 provides crucial information. We may combine Eq. (13) with our expressions for K1L and K1 (Eqs. (15) and (16)) into a simple quadratic equation for the interfering charge in terms of the measured average phase slip \(\overline{\Delta \theta }\) and the experimentally determined values for K1 and K1L:

$$\frac{\overline{\Delta \theta }}{2\pi }=\frac{{{e}^{*}}^{2}{K}_{1L}}{{K}_{1}}=\frac{{{e}^{*}}^{2}\frac{{e}^{2}}{{C}_{0}}}{{e}^{2}/{C}_{0}+e{e}^{*}\Delta {V}_{SD1}}$$
(17)

which may be combined with the measured values eΔVSD1 = 132 μeV and e2/C0  = 84 μeV to yield,

$$\frac{\overline{\Delta \theta }}{2\pi }=0.38=\frac{{{e}^{*}}^{2}84\mu eV}{84\mu eV+{e}^{*}132\mu eV}$$
(18)

Solving Eq. (18) yields an interfering charge e* = 0.98 and therefore we conclude e* = 1 for the outer edge mode at ν = 2. Hence, our in operando determination of all relevant coupling parameters directly indicates that the interfering charge is e* = 1 for the outer mode at ν  = 2.

To complete our characterization of all coupling constants, we need to determine K12, the edge–edge coupling strength at ν = 2. This may be achieved through examination of Eq. (10) and measurement of the magnetic field period ΔB ≈ 12.5 mT in the incompressible regime. The interferometer area A =  0.26 μm2 and the interference charge e* = 1. The edge stiffness is K1 = 216 μeV, while K1L was determined to be 84 μeV. Therefore, K1L/K1 ≈ 0.39. These measured parameters may be used with Eq. (10) to calculate K12/K1.

$$\frac{{K}_{12}}{{K}_{1}}=\frac{{\phi }_{0}}{{e}^{*}A\Delta B}+2\frac{{K}_{1L}}{{K}_{1}}-1$$
(19)

Equation 18 yields K12/K1 ≈ 1. The strong edge–edge coupling derived here is consistent with the observation of periodicity ϕ0/2 in the compressible regime at ν = 2. Examination of Eq. (12) indicates that the magnetic field period becomes \(\Delta B=\frac{{\phi }_{0}}{2\bar{A}}\) when K12/K1 = 1. Our analysis at ν = 2 demonstrates that the interfering charge is e* = 1 and strong capacitive edge–edge coupling generates periodicity ϕ0/2 in the absence of an exotic electron pairing mechanism. The tunable bulk-edge and edge–edge coupling strengths afforded by the screening well heterostructure design facilitate quantitative analysis.

Interference at ν = 3

At ν = 3, we sequentially set the transmission of the QPCs to G = 2.8 e2/h, 1.8 e2/h, and 0.6 e2/h to selectively interfere the innermost, the middle, and the outermost edge modes as illustrated in Fig. 4a. As shown in Fig. 4b, for the innermost edge mode, constant phase lines within the B − δVPG plane exhibit a positive slope, a characteristic of interference in the Coulomb-dominated regime15,19,23,28,50. For the innermost mode, the magnetic field period is 6.68 mT and the plunger gate voltage period is 37.5 mV. The strength of the bulk-edge coupling K3L and the edge stiffness K3 are estimated from the B = 0 T Coulomb blockade data and finite DC source-drain bias measurements at ν = 3 using the model developed in refs. 42,43. We extract the ratio K3L/K3 ≈ 0.58 for this edge mode. Given that K3L/K3 > 0.5, the interference for the innermost mode occurs in the Coulomb-dominated regime as theoretically described in refs. 19,23,28,50. This data provides an example of how an interferometer can switch from the Aharonov–Bohm regime to the Coulomb-dominated regime depending on device tuning.

Fig. 4: Interference at ν = 3.
figure 4

a QPC conductance versus gate voltage at ν  = 3. \(G=3\frac{{e}^{2}}{h}\) and \(G=2\frac{{e}^{2}}{h}\) plateaus are observed. The \(G=\frac{{e}^{2}}{h}\) plateau is not well-formed, likely due to the small N = 0 Landau level spin gap at B = 0.9 T, which prevents formation of a wide incompressible region between the spin-down and spin-up N = 0 Landau level edge modes. However, an inflection near \(G=\frac{{e}^{2}}{h}\) is observed, indicating a transition from backscattering the spin-down N = 0 edge mode to backscattering the spin-up N = 0 edge mode. Red circles indicate the transmission used to interfere each mode at ν = 3. b Interference generated by partially backscattering the innermost edge mode (spin-down N = 1 Landau level). (c) Interference produced when backscattering the middle edge mode (spin-up N = 0 Landau level). Black solid lines are drawn along lines of nearly constant phase in (b) and (c). d Interference when partially backscattering the outermost edge mode (spin-down N = 0 Landau level). e 2D FFT for interference of the outermost edge mode at ν = 3 identifying the most significant frequencies in the interference. f Plot of the magnitude of discontinuous phase slips observed in Fig. 4d with \(\overline{\Delta \theta }/2\pi \approx 0.44\). g Differential conductance measurement for the outermost mode at ν = 3. h Plot of FFT amplitude vs. δVSD1 used to determine the node spacing for the outermost mode.

Full size image

When the innermost edge is fully reflected and the middle edge mode is weakly backscattered, Aharonov–Bohm-like interference with lines of nearly constant phase displaying negative slope is observed, as shown in Fig. 4c. The periods of this interference are extracted using a 2D FFT. The measured magnetic field period is ΔB ≈ 12.6 mT, and the plunger gate voltage period is ΔVPG ≈ 21.5 mV. Note that the magnetic field period is approximately twice that measured for the innermost mode, consistent with theoretical expectations as the number of fully transmitted modes has now decreased to one19,23,28,50 while maintaining fixed filling factor in the interior of the interferometer. For the middle mode, K2L/K2 ≈ 0.37 is determined by analyzing finite DC bias interference and Coulomb blockade spectroscopy at B = 0 T, indicating a reduction in the ratio of bulk-edge coupling to edge stiffness compared to the innermost mode. This reduction is consistent with the transition from Coulomb-dominated interference for the innermost edge mode to a predominantly Aharonov–Bohm-like pattern for the middle edge mode. Additional amplitude modulations along the negatively sloped lines of constant phase are also clearly observed. The occurrence of these modulations for Aharonov–Bohm-like interference is associated with moderate bulk-edge coupling in a compressible regime in an integer quantum Hall state19,23,28,50.

It is interesting to note that, unlike ν = 1 and ν = 2, the interference pattern throughout the ν = 3 plateau appears to reflect only a compressible regime of operation. There are no visible changes in periodicity that are normally associated with the transition from a compressible state on the flanks of the quantum Hall plateau to an incompressible state near the center of the quantum Hall plateau. The moderately strong Coulomb coupling and the smaller bulk excitation gap at ν = 3 at B = 0.9 T in this instance make it energetically favorable to keep the total charge in the interior of the interferometer fixed rather than to keep the filling factor fixed26. The magnetic field range of an incompressible region is expected to be proportional to the ratio of the quantum Hall state energy gap to the charging energy required to add one electron to the interferometer, as described in ref. 26 and confirmed by previous experimental observations41,42,43. One of our previous experiments reported an incompressible regime when partially backscattering the outermost edge mode at ν = 340. In that interferometer, the charging energy was measured to be e2/C ≈ 17 μeV40. In our current experiment, the interferometer has a significantly higher charging energy of e2/C ≈ 95 μeV. Furthermore, the effective energy gap at ν = 3 is reduced because of the significantly lower electron density used here compared to the value used in ref. 40. The reduced excitation gap-to-charging-energy ratio likely results in the absence of a detectable incompressible region at ν = 3 in the current experiment.

When interfering the outermost edge mode and isolating the two inner modes from the ohmic leads, a complex lattice-like pattern of interference develops, as seen in Fig. 4d. Dramatic phase slips, interspersed within short stretches of continuous phase evolution, are evident. The periodicities for this configuration are determined via 2D FFT, as shown in Fig. 4e. The strongest component in the 2D FFT decomposition corresponds to a magnetic field period of ΔB ≈ 7.05 mT and a gate voltage period of ΔVPG ≈ 10.0 mV. Similar to the outer mode at ν = 2 in the compressible regime, this magnetic field period is consistent with an approximate flux periodicity ϕ0/2 for the outermost edge mode at ν = 3. The lattice-like interference pattern represents an admixture of Aharonov–Bohm and Coulomb-dominated oscillations, consistent with the theoretical predictions for moderate bulk-edge coupling and strong edge–edge coupling19,23,28,50. The observation of short stretches of constant phase evolution interrupted by periodic phase slips indicates that the interference occurs in a compressible regime. As was done at ν = 2, we can quantify the magnitude of the discrete phase slips as shown in Fig. 4f with \(\overline{\Delta \theta }/2\pi=0.44\).

As was done at ν = 2, we must determine the interfering charge for the outermost edge at ν = 3 that gives rise to the approximate periodicity ϕ0/2. K1L = 84 μeV has already been determined. The differential conductance measurements of interference for the outermost mode at ν = 3 are shown in Fig. 4g, resulting in the node spacing ΔVSD1 = 93 μeV shown in Fig. 4h. The quadratic equation relating the average value of the measured phase slips with the effective charge now reads:

$$\overline{\Delta \theta }/2\pi=0.44=\frac{{{e}^{*}}^{2}84\mu eV}{84\mu eV+{e}^{*}93\mu eV}$$
(20)

The interfering charge for the outermost mode at ν = 3 is also e* = 1. Once the effective charge is specified, the ratio K1L/K1 ≈ 0.47 is determined.

Unlike ν = 2, where we observed interference in both the incompressible and compressible regimes, interference occurs only in the compressible regime at ν = 3. As discussed in the Introduction, we can evaluate K21/K1 using Eq. (12). Using \(\bar{A}=0.26\,\mu\)m2 and the magnetic field period extracted from the FFT of the data in Fig. 4d, ΔB = 7.05 mT, yields K12/K1 ≈ 1. The extracted edge–edge coupling ratio of K12/K1 ≈ 1 indicates a strong interaction between the outermost interfering edge and the isolated inner edges. This strong capacitive edge–edge coupling is consistent with the observed approximately ϕ0/2 flux periodicity. The specification of the coupling parameters for interference at ν = 3 is complete. Again, the analysis indicates that an interference charge of e* = 1 and strong edge–edge coupling are sufficient to generate periodicity ϕ0/2.

Discussion

Recent developments in Fabry-Pérot interferometry experiments47,48,49,51,54 and theory25,50 have drawn attention to the origin of the flux period ϕ0/2 in the integer quantum Hall regime when interfering the outermost edge mode. In previous experiments using GaAs/AlGaAs 2DEGs, the observed ϕ0/2 flux period in the integer quantum Hall regime was attributed to electron pairing47,48,49. A recent experiment in a graphene interferometer51 explains the transition in periodicity from ϕ0 to ϕ0/2 in the integer quantum Hall regime as a result of edge–edge coupling and single-electron interference without invoking an electron pairing mechanism. In this graphene experiment, the importance of edge–edge capacitive coupling is highlighted; our results in an AlGaAs/GaAs interferometer substantiate the conclusions of ref. 51 with the quantification of the edge–edge coupling parameter in the regime in which ϕ0/2 periodicity is observed. In this regard, our data and analysis support the conclusions of ref. 51. However, in the graphene interferometer, the magnitude of the interfering charge could not be specified in the strong edge–edge coupling limit because discrete phase slips were not observed. The ability to determine the interfering charge through in operando extraction of all the necessary coupling parameters in our experiment removes ambiguity. To amplify this point, another recent experiment in graphene by a different group has claimed evidence for even more exotic pairing behavior involving electronic triplets54 in the integer quantum Hall regime, adding a new and confounding twist to this evolving story of electron correlations in interferometers operated in the integer quantum Hall regime. In a device with minimal bulk-edge coupling and strong edge–edge coupling, it is challenging to discriminate between the effects of electron pairing, however improbable, and edge–edge capacitive coupling. The introduction of moderate bulk-edge coupling in our AlGaAs/GaAs interferometer allows the disambiguation of these two phenomena by examining the magnitude of phase slips at ν = 2 and ν = 3 in the strong edge–edge coupling limit.

It is important to note that an assumption of an interfering charge e* = 2 on the outer edge at ν = 2 and ν = 3 is not consistent with our experimental results. We have intentionally studied a structure that simultaneously possesses finite bulk-edge coupling and edge–edge coupling to explore the impact of each mechanism and explore how control of these couplings may be used to determine the charge of the interfering particles. The observation of phase slips with magnitude that is a precise, but non-integer, multiple of 2π, at ν = 2 and ν = 3 is a key feature of our experiments that allows us to determine the charge of the interfering particles in the integer quantum Hall states. Our observations are clearly in variance with a model of interference with the charge e* = 2, and strongly indicate that the interfering particles carry the charge of a single electron. The internal consistency of multiple independent measurements and the minimal capacitive model of interferometer energetics that can explain multiple experiments conducted with several interferometers40,41,42 support a picture in which ϕ0/2 flux periodicity in the integer quantum Hall regime is generated by edge–edge coupling and the interfering charge is a singly charged electron.

To conclude, we studied a device characterized by moderate bulk-edge coupling and strong edge–edge coupling, enabling a quantitative assessment of the impact of these coupling mechanisms on the flux periodicity of interference. We determine the charge of interfering particles in the integer quantum Hall regime using the magnitude of discrete phase slips associated with the introduction of localized charged excitations in the interior of the interferometer. Using a simple capacitive model, we analyze the interference phenomena for 1 ≤ ν ≤ 3, providing information on the underlying source of the different frequencies observed in Fabry-Pérot interferometers with multiple edge modes. The interfering charge is determined to be e* = 1.

Methods

Mesas were defined by optical lithography and 50:5:1 H2O:H3PO4:H2O2 wet etching. 8 nm Ni/80 nm Ge/160 nm Au/36 nm Ni ohmic contacts were deposited and annealed to make electrical contact with the 2DEG. Electron beam lithography and electron beam evaporation of 5 nm Ti/10 nm Au were used to define the interferometer gates. Optical lithography and electron beam evaporation of 20 nm Ti/150 nm Au were used to define bond pads and surface gates in the vicinity of ohmic contacts. The substrate was thinned to ~70 μm, and metallic back gates were defined to deplete the 2DEG in the bottom screening well in the vicinity of the ohmic contacts. The back gates were patterned by optical lithography and 100 nm Ti/150 nm Au was deposited by electron beam evaporation.

Conductance measurements were made using standard lock-in amplifier techniques, employing an excitation voltage Vex ≤ 20 μV at a frequency of 43 Hz. These measurements were carried out in a dilution refrigerator at a mixing chamber temperature of T = 10 mK, unless otherwise specified. All data were obtained with the plunger gate biased at −0.7 V. For finite DC bias measurements, a 5 μV AC voltage was typically used, and the DC source-drain voltage was swept using a programmable digital-to-analog converter.