Introduction

Flatbands are dispersionless energy levels that extend over a wide region in momentum space. In crystalline materials, they are widely recognized as a versatile playground for novel material properties with profound implications for quantum information sciences (QIS) and microelectronics1,2,3,4,5,6,7,8. Notable material platforms for electron and magnon flatbands include twisted-angle van der Waals materials with unconventional superconductivity4,5,6,7,8, as well as spin ice and Kagome lattices hosting topological magnons9,10,11,12,13,14,15,16,17. While less explored, phonon flatbands have been shown to induce or stabilize ferroelectricity18, frustrated magnetism19, and superconductivity20. In all these cases, the material properties of interest arise fundamentally from the dramatic increase in the density of states at the eigenenergy of the flatband, which leads to strong coupling between the associated quasiparticles and other degrees of freedom.

Utilizing flatbands for QIS and other applications requires precise manipulation using external stimuli and, most preferably, the ability to turn flatbands on and off. However, most flatbands are protected by the configurations and symmetries of the lattices and electrons at thermal equilibrium, preventing them from being created or eliminated at will. There is a lack of understanding as to how to achieve switchable flatbands in appropriate material systems that can be excited by external means. One possible approach involves the use of coherent phonons – collective lattice vibrations with a well-defined phase of atomic motions21. These coherent phonon modes may modulate the lattice configurations in the time domain, allowing the creation of flatbands. Coherent phonons can be generated with femtosecond laser pulses through impulsive Raman scattering or displacive excitation processes22,23,24,25,26,27. They have been observed in many crystalline materials and proven effective in manipulating electronic and magnetic properties at ultrafast time scales28,29,30,31,32. However, coherent phonon flatbands (CPFB) have neither been theoretically predicted nor experimentally observed.

In this study, using time-resolved X-ray diffraction (tr-XRD), we demonstrate the generation of CPFB in a GaAs/AlAs superlattice (SL) with ultrafast double pump excitation at 800 nm. The CPFB has an eigenfrequency of 0.31 THz, extending across at least 60% of the folded Brillouin zone (FBZ). As a non-equilibrium excitation, the CPFB exhibits a half lifetime of approximately 75 ps and couples coherently to the low-energy acoustic phonon branches. Molecular dynamics (MD) simulations reveal a generalized pathway for obtaining CPFBs via coherently and spatially modulated excitation of SL structures. Our results provide a versatile approach whereby transient flatbands are generated via an external stimulus in a wide range of SL systems. Compared to single-mode coherent phonons, the high density of states and wide-range momentum of CPFB offer a highly efficient method for manipulating other energy carriers, with promising applications in future QIS and microelectronics.

Results

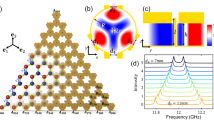
We performed tr-XRD (Fig. 1a) of an 8 nm/8 nm GaAs/AlAs SL with 30 periods and a total thickness of 480 nm, epitaxially grown on a GaAs (001) substrate (Fig. 1b). For the optical excitation and manipulation of the coherent phonons, we employed two nearly identical optical pump pulses, both with 800 nm wavelength and 35 fs full width at half maximum (FWHM). The pump photon energy (1.55 eV) lies between the optical bandgaps of GaAs (1.49 eV) and AlAs (3.03 eV). Hence, only the GaAs layers absorb the pump energy and are excited. The first pump pulse launches initial lattice vibrations in the GaAs layers that propagate into the AlAs layers. The second pump pulse then manipulates the vibrations generated by the first one, where the relative arrival time between two pumps (\(\Delta \tau\)) is controlled with a motorized delay stage. The two optical pumps spatially overlap on a steering mirror before arriving on the sample surface at an incident angle of \({11}^{\circ }\), with a penetration depth of 743.2 nm, sufficiently long to excite all the GaAs layers in the SL (Figs. 1a, b). A 50 fs (FWHM) X-ray pulse with a photon energy of 10 keV was used at the Bernina instrument of the SwissFEL free electron laser source to measure the diffracted X-ray intensity from the SL in the vicinity of the (1 1 3) Bragg peak of the GaAs substrate as a function of time relative to the two optical pumps. The sample was oriented such that the X-ray beam was incident at an angle of \({1}^{\circ }\) to match the optical excitation depth and the SL thickness.

Fig. 1: Layer-selective, double-pump excitation of coherent phonons in a GaAs/AlAs SL detected using ultrafast X-rays.
figure 1

a Schematic of the experimental setup. A pair of ultrafast 800 nm optical pulses with variable relative delays excite the coherent phonons in GaAs/AlAs SL, while a 10 keV X-ray pulse at glancing incidence resolves the temporal evolution of the SL lattice response via stroboscopic X-ray diffraction. b Structure of GaAs/AlAs SL. With an 800 nm pump, only the GaAs layers are excited since the AlAs layers are optically transparent. The optical penetration depth exceeds the total SL thickness. c The reciprocal space map (RSM) of the static (unpumped) GaAs/AlAs SL near the (1 1 3) Bragg peak of the GaAs substrate. The white arrow marks the GaAs (1 1 3) substrate peak, while the orange arrows point to the Bragg peaks of the GaAs/AlAs SL. The H and L are in the relative lattice unit (r.l.u.) of the folded Brillouin zone (FBZ) of the SL. The even orders of the SL Bragg peaks are structurally allowed but substantially weaker than the odd orders. The color of the L = +/− 1 SL Bragg peaks is saturated in panel (c) to highlight the higher-order SL peaks.

Full size image

Figure 1c shows the reciprocal space map (RSM) of the SL at thermal equilibrium (no excitation). Pronounced intensity modulations along the film’s surface normal confirm the high quality of the GaAs/AlAs interfaces. The equally spaced local maxima of the diffraction intensity around the substrate Bragg peak correspond to the SL Bragg peaks. The separation between nearest-neighbor SL peaks is determined by the FBZ of the 16 nm GaAs/AlAs supercell. To obtain the SL phonon dispersion, we chose five momentum transfer (Q) points along L within the FBZ between the -1 and -2 order SL peaks to minimize the X-ray scattering intensity contributions from the GaAs substrate (Fig. 1c). Throughout this paper, we define the L components of these points and represent them as out-of-plane Q (in reciprocal lattice units, r. l. u.) with the SL -1 Bragg peak as the reference. This highlights the FBZ boundary and periodicity of the phonon dispersions in the reciprocal space.

We first demonstrate that the optical pump pulses excite multiple coherent phonon branches by monitoring their dispersions across the FBZ. The existence of coherent phonons can be seen from periodic XRD intensity oscillations at frequencies corresponding to the phonon mode energy27,31. Figure 2a, b show the temporal evolutions of the XRD intensities at all five Q points under coincidental optical excitations, i.e., when the two pump pulses excite the SL simultaneously (\(\Delta \tau=0\)). At all Q points, strong oscillations are observed, featuring beating-like patterns that indicate the presence of multiple phonon frequencies. These include fast oscillations on the order of a few picoseconds (Fig. 2a) and slower ones extending up to at least 200 picoseconds (Fig. 2b). The periods of the slower oscillations are highly Q-dependent, suggesting the presence of highly dispersive phonon modes.

Fig. 2: Coherent phonon oscillations and dispersions of the 8 nm/8 nm GaAs/AlAs SL excited with coincidental double pump.
figure 2

a, b X-ray diffraction intensity oscillations at different Q points throughout the FBZ. XRD intensities are normalized to the respective average intensity before time zero. c, d Characteristic oscillation frequencies at each Q point, obtained from the Fourier Transform of the signals in a, b. Three distinct branches of coherent phonons can be identified: the CPFB, the FLA and FLA2. For comparison, red open circles in (d) show the phonon dispersions of the 8 nm/8 nm GaAs/AlAs SL at thermal equilibrium from the lattice dynamics calculations, including FLA1 and all the transverse phonon eigenmodes, which were not detected in the experimental data.

Full size image

We apply the Fourier Transform to the time traces in Fig. 2a, b to convert them to the frequency domain (Fig. 2(c, d)), allowing us to identify the coherent phonons. Three branches can be clearly resolved, with one flat branch independent of Q at 0.31 THz, which we name as coherent phonon flatband (CPFB), and two dispersive branches. We compare the dispersive branches with the theoretical phonon dispersions of an 8 nm/8 nm GaAs/AlAs SL obtained from the equilibrium-state lattice dynamics calculation33 (red open circles in Fig. 2d). Direct agreement is obtained between the experiment and the calculation without scaling factors, confirming that the optically-induced XRD oscillations do come from coherent phonons, rather than squeezed phonons, which would have resulted in oscillation frequencies twice that of the phonon frequency27,34. (See SI for details) We assign the two dispersive branches as the fundamental and second-order folded longitudinal acoustic branches (FLA and FLA2, respectively). These two branches are eigenmodes of the SL vibrations at thermal equilibrium that can be coherently excited. FLA and FLA2 have positive group velocities with similar values, 4671 m/s for FLA and 4550 m/s FLA2. Interestingly, our experimental data do not show the first-order folded longitudinal acoustic phonon (FLA1, with a negative group velocity), nor any transverse phonon branches. This absence can be attributed to the small dynamic structure factor of the FLA1 branch35,36 or the inability of FLA1 to be coherently excited27,34,37.

The most striking observation in our experiment is that the CPFB extends over a wide Q-range in the FBZ. Indeed, there is no resolvable change in the energy of the CPFB over more than 60% of the FBZ within the energy resolution of our measurement (0.005 THz, or 0.0207 meV corresponding to the 200 ps time window used for the Fourier transformation). This number is at least ten times smaller than previously reported phonon flat band in other solid-state materials under thermal equilibrium35. This flatband cannot be generated in the equilibrium-state lattice dynamics simulation and cannot be explained as from phonon band folding due to the SL. The flatband appears only under femtosecond laser excitation far from equilibrium, in contrast to the FLA and FLA2 branches. Consequently, our results provide direct confirmation that the CPFB is not a phonon eigenmode of the SL but rather a state that only exists at nonequilibrium.

To explore the tunability of the CPFB, we varied the delay times between two pumps, Δτ*, and tracked the evolution of the XRD intensity at Q = 0.02 (Fig. 3a). Here, Δτ* is labeled in units of the CPFB oscillation period. Coherent oscillations were observed for all delay times, with a suppression of the amplitude at Δτ* = 0.5 (half period of the CPFB) and a slight enhancement at Δτ* = 1.0 (one complete cycle). Like for the coincidental pump configuration, Fig. 3b, c show the coherent phonon dispersions for the anti- (Δτ* = 0.5) and in-phase (Δτ* = 1.0) cases. Notably, the CPFB was observed in both cases.

Fig. 3: CPFB at selected delays between the two pump pulses.
figure 3

a The temporal evolution of the XRD intensity at Q = 0.02 for various pump delay times, Δτ*, indicated in the units of the CPFB oscillation periods. Time zero (t = 0 ps) on the horizontal axis marks the arrival of the second optical pump pulse. b, c Coherent phonon dispersions for two cases of pump delay time: (b) Anti-phase (Δτ* = 0.5 is half the oscillation period of the CPFB) and c in-phase (Δτ* = 1.0 is one oscillation period of the CPFB). For comparison, the red open circles represent the phonon dispersions of an 8 nm/8 nm GaAs/AlAs SL obtained from equilibrium-state lattice dynamics calculation.

Full size image

The persistence of the CPFB is unexpected compared with double-pump measurements in other materials, e.g., bismuth or chromium thin films38,39, where the amplitude of the coherent oscillations excited by the first optical pump can be effectively manipulated by the relative delay of the second pump. For bismuth or chromium, in the case of in-phase excitation, significant amplitude enhancement can be achieved, while for the anti-phase case, the oscillations are almost completely suppressed. The key differences between previous studies and this work lie in the use of the SL structure and the layer-selective optical pumping. Specifically, when the first pump arrives, only the GaAs layer in the SL absorbs the photons and can be excited. The oscillations of the GaAs layers then immediately extend to the AlAs layers and form CPFB in the entire SL. When the second pump arrives, it can only manipulate the oscillations in the GaAs layers, limiting the effect on the CPFB, which involves the entire SL.

We further quantified the lifetime of the CPFB by applying a short-window Fourier transform (SWFT) to the tr-XRD datasets over the full 200 ps time range for all three double-pump configurations. In Fig. 4, we show the time-dependent SWFT amplitudes of the FLA, CPFB, and FLA2 branches at Q = 0.12 r.l.u, for all three configurations. Compared to the coincidental case, the initial amplitudes of CPFB for the anti-phase case are somewhat lower, while those for the in-phase case are slightly higher, which is consistent with Fig. 3a. The amplitudes of FLA1 and the CPFB decrease with time, while that of the FLA increases, indicating a transfer of energy from FLA2 and CPFB to FLA. The oscillation amplitudes of both the CPFB and FLA2 branches reduce to 50% of their initial values by approximately 75 ps, which we assign as the half lifetime of the two modes. By ~150 ps, the XRD intensity oscillations are dominated by the FLA branch.

Fig. 4: Lifetimes of the coherent phonon branches.
figure 4

Time-dependent amplitudes of the coherent phonon branches obtained with SWFT for a coincidental, b anti-phase and c in-phase double-pump measurements at Q = 0.12 r.l.u. The time step was chosen as 25 ps with a window duration of 87.5 ps to maintain an adequate signal-to-noise ratio for the oscillation amplitudes. The time step is smaller than the window size to differentiate the amplitude evolutions of the three coherent phonon branches.

Full size image

The energy dissipation from FLA2 and CPFB into FLA is significant and reveals a strong coupling between the three coherent branches. In previous studies, excited coherent phonons in the higher energy branches usually dephase and dissipate the energy into the incoherent phonon bath at lower energies27. However, when the interactions between coherent phonon modes are much higher than the coherent-incoherent phonon coupling, the material can enter a regime of quantum coherent coupling (QCP), which features the superposition of a set of coherent phonon states with simultaneous momentum and energy conservation. First proposed by Orbach in 1966, QCP is feasible only when the population of the excited phonon (referred to as the driving mode) reaches a threshold40. Phonon QCP usually only occurs among three discrete phonon modes, each with a distinct momentum and energy41. In our case, however, QCP occurs among three coherent branches, which is highly unusual. This occurs because the CPFB offers an exceptionally large number of coupling channels that comply with momentum conservation. Therefore, it can effectively enhance coherent coupling among phonons. Thus, understanding the conditions under which the CPFB forms is critical.

Based on the experimental results, we argue that the CPFB in GaAs/AlAs emerges due to the ultrafast coherent excitations of the GaAs layers within the SL. Specifically, at time zero, the 800 nm optical laser induces displacements that are in phase across all GaAs layers since they are excited by the same pump laser pulse at the same time. The pump laser travels at the speed of light (~2.0 \(\times\) 108 m/s in GaAs) and it takes 2.5 fs to go through the 0.5 µm-thick SL. In comparison, the AlAs layers are transparent to the laser and remain un-excited. As a result, the entire SL hosts periodically modulated displacements with the coherent vibrations spatially localized within the discrete GaAs layers. After time zero, all the AlAs layers also vibrate synchronously with each other but not with GaAs, due to the difference in force constants between the GaAs and AlAs. This corresponds to a spatially localized and periodically modulated energy distribution in real space. In the reciprocal space, such modulations lead to a delocalized mode that is Q-independent, which is commonly referred to as a flatband in the transient phonon spectrum. Therefore, the coherent motion from the selective optical pumping of the GaAs layer is crucial to the CPFB.

From the discussion above, a more general approach towards CPFB is possible where ultrafast laser pulses induce coherent and spatially modulated excitations within the SL. Such an approach can extend CPFB to various SL systems beyond GaAs/AlAs.

To illustrate the general applicability of our approach, we performed non-equilibrium MD simulations on Lennard-Jones (LJ) SLs equipped with the LAMMPS package42. Specifically, the conceptual SLs were constructed by alternately stacking thin films of the two conceptual materials: m90 (atomic mass: 90 g/mol, artificially assigned) and m40 (atomic mass: 40 g/mol, equivalent to that of real Argon). Each SL possesses a cross-sectional area of 4 unit cells by 4 unit cells in the x and y directions, respectively, and 20 periods in the z direction, as illustrated in Fig. 5a. Interatomic interactions were modeled by the Lennard-Jones potential. Both m40 and m90 atoms are modeled as solid Argon, which crystallizes in a face-centered cubic (FCC) structure with a conventional unit cell of approximately 0.53 nm in each dimension. Each layer is 1.05 nm thick, corresponding to two unit cells, resulting in a SL period thickness of 2.12 nm. To stimulate the selective optical excitation, coherent and spatially modulated excitations were implemented in the MD simulations by introducing an initial atomic displacement profile in alternating layers, consistent with the zone center phonon mode. The relative lengths and directions of the initial displacement are illustrated by the yellow arrows in Fig. 5a.

Fig. 5: Simulated CPFB generation via MD simulations.
figure 5

a A schematic drawing of the m40/m90 Argon SL employed in MD simulations, with the layer-selective coherent displacement at time zero marked using yellow arrows in the m90 layer. Logarithmic SED maps of an m40/m90 SL under different excitation conditions: b No excitation, (c) Coherent displacive excitation by dT/T = 0.1 across all m90 layers. d Uniform temperature increases of dT/T = 0.1 across all m90 layers. e Coherent excitation in pure m90. The red circle marks the phonon mode coherently excited at time zero in (b). Red dashed lines depict the phonon dispersions of corresponding m40/m90 SL obtained from the lattice dynamics calculation.

Full size image

As a reference, we first calculated the phonon dispersion of the m40/m90 SL model in its unexcited equilibrium state at a temperature of T = 2 K, as shown in Fig. 5b. The temperature is chosen to be below the onset of anharmonic lattice effects around 9 K. This choice is consistent with our experiment at 300 K, where the GaAs lattice is widely considered as harmonic. The phonon dispersion was obtained by tracking peaks in the calculated spectral energy density (SED) at various Q points and then projecting components of atomic positions from the MD model onto the normal modes of vibrations39,40,43. At thermal equilibrium, the phonon dispersion displays the characteristic backfolding typical of SL systems, resembling those observed in GaAs/AlAs SLs.

Secondly, we extract the nonequilibrium phonon dispersions resulting from selective excitation of the SL through coherent atomic displacements. At time zero, the zone center FLA1 phonon mode is excited within all m90 layers by displacing the atoms to introduce a standing wave, as depicted in Fig. 5a. The maximum displacement amplitude was converted to a temperature rise proportional to the square of the amplitude. We choose a temperature increase dT/T~0.1, consistent with the increase in the effective lattice temperature of GaAs in our experiment. With coherent atomic displacements, the SED simulations generated a CPFB resembling our experimental observations (Fig. 5c). The mode energy of the CPFB is equal to the zone center intercept of the phonon backfolded from the FLA1 and, therefore, consistent with the experiments. The CPFB becomes more prominent with increasing amplitude of the initial coherent atomic displacements (Fig. S3a). All other phonon branches remained nearly identical to those of the equilibrium case.

To illustrate the critical role of the coherent excitation, we conducted simulations of selective excitation in the SL via incoherent (random) atomic displacement. At time zero, the temperature of Argon atoms within each m90 layer was raised by adding kinetic energy (heat) in the form of random atomic displacement, and in subsequent time steps, this energy diffuses to the adjacent m40 layers. This leads to a temperature increase in the entire SL identical to that in Fig. 5c. As shown in Fig. 5d, no CPFB was observed in this case, indicating that coherent displacement is indeed necessary for CPFB generation.

Finally, to verify the need for an SL structure, we also performed an MD simulation using only heavy Argon (m90), still under coherent excitation. One specific phonon mode was selected for excitation, and coherent long-range atomic displacements were introduced to the m90 atoms commensurate with the LA phonon mode at time zero to simulate a coherent excitation. Figure 5e does not show the existence of the CPFB, indicating the necessity of the SL structure.

The simulations featured in Fig. 5c–e demonstrate that the CPFB can be generated by coherent and spatially modulated excitations of the SL structures. It is noteworthy that this prediction emerged from a seemingly simple MD model of Argon atoms employing a Lennard-Jones interatomic potential. The ability of this simple model to replicate key aspects of our experimental results indicates that generating CPFB could be feasible in a variety of SL systems under excitation conditions, regardless of the specific materials used.

Discussions

Previous time-resolved optical reflectivity measurements have revealed a coherent phonon mode between 0.305 and 0.310 THz at the center of the FBZ of GaAs/AlAs SL41. However, this mode was not identified as a CPFB because only two Q points were probed. Hints of CPFBs were also observed by varying the optical probe wavelength in the vicinity of the BZ center in systems such as YBa2Cu3O7/La1/3Ca2/3MnO3 SLs44. However, this was interpreted as an “artificial” effect based on the assumption that only the phonon mode at the zone center was excited45,46,47,48,49. The lack of direct evidence for the CPFB in previous experiments is mainly due to technical limitations in probing phonon modes across the momentum space during optical-pump optical-probe studies. In our experiment, we leverage the capability of tr-XRD to achieve momentum transfer covering over two-thirds of the BZ to unveil the nature of the atomic oscillations. Furthermore, it is important to distinguish the CPFB from intrinsic localized modes, which also appear as phonon flatbands over a broad range of reciprocal space, and are associated with lattice instabilities and anharmonicities50,51. Such modes do not require an SL structure or coherent pumping.

In summary, we successfully generated a CPFB in a GaAs/AlAs SL through selective coherent excitations. A CPFB that is non-Eigen and exists only under nonequilibrium conditions was identified in this system. Simulations reveal the pathway for creating such a CPFB in a wide range of SLs. Recently, phononic qubits have been realized using GHz-frequency acoustic wave resonators52,53. The CPFB observed in this work has an energy of several hundred GHz and, in principle, can be above THz with a thinner SL, which will extend mechanical qubits to higher frequencies and more diverse material platforms. Furthermore, due to the increased phonon-phonon scattering channels, the CPFB has significant potential for dynamically controlling phonon-phonon, phonon-electron, and phonon-magnon interactions54,55,56,57. This could enable new functionalities for electronic and magnetic devices and beyond.

Methods

Synthesis and X-ray characterization of the GaAs/AlAs SL: GaAs/AlAs SLs are synthesized via molecular beam epitaxy, on a GaAs (0 0 1) substrate coated with a 150 nm GaAs buffer layer. A 500 nm AlAs etching layer was added between the GaAs buffer layer and the SL film. The reciprocal space map of the GaAs/AlAs SLs was measured at beamline 33-ID-D of the Advanced Photon Source. The pronounced intensity oscillations along the [0 0 1] direction in Fig. 1c illustrate the high quality of the SL.

Time-resolved X-ray diffraction (tr-XRD) with double-pulse optical excitations

We utilized the SwissFEL Aramis hard X-ray free-electron laser (XFEL) operating in self-amplified spontaneous emission (SASE) mode at the Bernina endstation58. The XFEL delivered pulses with a photon energy of 10 keV, a pulse duration of 50 fs, and a repetition rate of 100 Hz, achieving a monochromatic beam with 0.1% bandwidth using a Silicon (111) double-crystal monochromator. Experiments were conducted with the sample mounted on a six-circle surface diffractometer in a horizontal scattering geometry, and measurements were taken at ambient conditions. The X-ray beam was focused to a spot size of 5 (H) × 75 (V) µm² on the sample, with an incident angle of 1° relative to the sample surface.

Simultaneously, the optical pump, a commercial 100 Hz Ti:sapphire amplifier system emitting at 800 nm with a 30 fs pulse duration and p-polarized, was synchronized with the XFEL pulses using the Bunch Arrival-time Monitor (BAM) and Laser Arrival Monitor (LAM). These monitors provided real-time, shot-to-shot data on the arrival times of electron and laser pulses, allowing for adjustments in pulse timings and corrections for temporal jitter (~140 fs) to ensure precise alignment for accurate time-resolved measurements. The optical pump laser was split into two beams with equal energy, with a mechanical stage placed in the path of one of the beams to control the relative arrival time. The two beams were then combined through a second beam splitter and came out at a 10° incident angle relative to the XFEL. Considering the projection of the optical laser footprint, the pump fluence on the sample surface was estimated to be 2.5 mJ/cm2 from each of the split beams for the majority of this work.

The absorption depth for GaAs at 800 nm is 743.2 nm, significantly exceeding the thickness of the SL film, ensuring uniform excitation of all GaAs layers. The effective lattice temperature of the GaAs was raised by 32.63 K above room temperature, calculated based on optical absorption and specific heat of the material. The scattered XFEL radiation was captured by a Jungfrau 1.5 M detector with 75 µm pixel size positioned at 400 mm from the sample, which provided detailed shot-to-shot readouts of the scattered intensity.

The tr-XRD experiments focused on the SL FBZ. By first aligning the sample to access the Bragg peaks of the GaAs substrate, we were able to find a series of satellite peaks next to the substrate Bragg peaks. We used a sample ϕ scan to access the (1 1 3) Bragg peak of the GaAs substrate along with +2, +1, −1, −2 SL peaks. For each tr-XRD measurement, the azimuth angle (ϕ) was rotated to access the Q points between -1 and -2 order SL peaks. Each tr-XRD measurement was conducted twice, once with the pump laser on and once off. The tr-XRD intensity, referring to the integrated intensity in the region of interest, which includes the diffuse scattering next to the Bragg peak, was used to calculate the intensity ratio between the measurements with the pump on and off, providing the final dataset for future Fourier Transform processes.

In the FBZ we examined, the X-ray diffraction intensities are dominated by the longitudinal acoustic phonon modes, which capture the atomic motions normal to the layering of the SL. We rotated the azimuth angle of the sample to access the different Q points while keeping the X-ray and laser incidence angles identical, thereby ensuring the spatiotemporal overlap between the pump laser and the probe XFEL pulses.

Lattice dynamics calculations

Lattice dynamics simulations were performed using the ALAMODE package33 to acquire the phonon dispersion relations for both GaAs/AlAs and m40/m90 SLs under the harmonic approximation, corresponding to a background temperature of 0 K. Furthermore, the polarization of each phonon mode was also determined through this process, which was then utilized to set up the subsequent transient SED simulations.

Molecular dynamics (MD) simulations

MD simulations were conducted to perform transient SED calculations and to evaluate the degree of lattice anharmonicity using the LAMMPS package42. Specifically, for the transient SED calculation of the m40/m90 SL, the zone center phonon mode, with a wavevector of zero and a frequency of approximately 0.54 THz, was selectively excited to mimic the coherent selective pumping with femtosecond laser pulses as achieved in our experiments. This excitation was confined exclusively to the m90 layers, achieved by displacing atoms according to the polarization information obtained from lattice dynamics, while the m40 layers remained undisturbed initially. The simulation setup theoretically generates a standing wave with a specific wavevector Q and polarization υ centered at position \({{{\bf{x}}}}_{{{\bf{0}}}}\). The atomic displacement, \({u}_{l,b}\), of the bth atom in the lth unit cell of such a standing wave can be described based on the equation59:

$${u}_{l,b}=\frac{A}{\sqrt{{m}_{b}}}{{{\bf{e}}}}_{\upsilon,{{\bf{Q}}},b}\exp \left\{i\left[{{\bf{Q}}}\cdot \left({{{\bf{x}}}}_{{{\bf{l}}}}-{{{\bf{x}}}}_{{{\bf{0}}}}\right)-\omega t\right]\right\}$$
(1)

where A is the amplitude of the standing wave,\(\,{m}_{b}\) is the mass of the bth atom, \({{{\bf{e}}}}_{\upsilon,{{\bf{Q}}},b}\) is the eigenvector for the bth atom for the phonon mode of wavevector Q and polarization \(\upsilon\). \({{{\bf{x}}}}_{{{\bf{l}}}}\) is the position of the lth unit cell, \({{{\bf{x}}}}_{{{\bf{0}}}}\) is the center position of the standing wave, and ω is the angular frequency.

The displacement amplitude A can be converted into an increase in temperature denoted as dT, which is proportional to the square of the amplitude60, as

$${dT}\propto {A}^{2}$$
(2)

The average SED was obtained over a period of 50 ps within the microcanonical ensemble (NVE), immediately following the excitation of zone center mode. Additionally, the degree of lattice anharmonicity at a specific temperature was evaluated with the harmonically-mapped averaging (HMA)61,62 method.