Abstract
Inorganic solid electrolytes have emerged as promising candidates for realizing all-solid-state batteries because they eliminate flammable, low boiling-point liquids in lithium-ion battery cells, improving safety and cycle life. In this study, we present a highly lattice-matched composite solid electrolyte consisting of an antiperovskite-perovskite system, offering the benefits of both antiperovskites as melt-infiltratable solid electrolytes and perovskites as fast-ion conductors. Atomistic simulations predict significant lithium-ion diffusion at the interface between cubic Li2OHCl and Li0.31La0.56TiO3. The incorporation of fluorine enables room-temperature operation by stabilizing the high-temperature cubic phase of Li2OHCl1-xFx and reduces the lattice mismatch ratio to 0.8% at the interface through lattice contractions. The composite solid electrolyte was synthesized via pressure-assisted melt infiltration. The solid electrolyte effectively infiltrates conventional lithium-ion battery electrodes while maintaining a stable interface structure. Electrochemical testing demonstrates promising charge-discharge characteristics, including long cycle life and rate performance. Intricate infiltration of the solid electrolyte into an electrode structure composed of active materials with microcracks and high surface area enables stable operation by mitigating degradation phenomena typically observed in liquid electrolyte-based lithium-ion batteries.
Similar content being viewed by others
Introduction
High-performance energy storage demand has risen owing to the widespread use of portable devices, electric vehicles, and renewable energy technologies1,2,3. Lithium-ion batteries (LIBs) are favored for their energy density and long cycle life4,5. However, their safety issues, capacity limitations, and environmental impact have prompted the exploration of alternative technologies1,6. All-solid-state batteries (ASSBs) are a potential next-generation solution to these concerns7,8, but technical challenges hinder their commercialization. They require low-temperature processing, especially when utilizing oxide solid electrolytes8,9. Conventional manufacturing involves high-temperature sintering, which hampers scalability and is incompatible with temperature-sensitive components. Using low-temperature, formable, sulfide-based solid electrolytes carries safety risks, as they react quickly with moisture8, generating toxic hydrogen sulfide and compromising battery reliability. Additionally, introducing solid electrolytes into the interior of cost-effective, environmentally friendly conventional LIB electrodes in ASSBs remains challenging. Therefore, the search for solid electrolytes that can be incorporated into conventional LIB electrodes while being less toxic and not reliant on rare elements is crucial for ASSB development.
Molten-salt solid electrolytes with a melt infiltration process using Li2OHCl antiperovskite10 materials, composed of rare-element-free and environmentally friendly raw materials, have been proposed by Xiao et al.11. These antiperovskite materials exhibit low melting points (523–573 K) and high wettabilities toward oxides and metals, facilitating penetration into electrode voids. However, Li2OHCl undergoes a structural phase transition from a low-temperature orthorhombic phase (o-Li2OHCl) to a high-temperature cubic phase (c-Li2OHCl) at approximately 345 K. The o-Li2OHCl has low ionic conductivity (approximately 1 × 10-7 S cm-1)12,13, rendering room-temperature ASSB operation problematic.
Here, we propose a composite solid electrolyte utilizing an antiperovskite-type fluorine-doped c-Li2OHCl1-xFx combined with a perovskite-type Li0.31La0.56TiO3 (LLTO) with a high lattice-matched system. Fluorine-doped Li2OHCl1-xFx maintains its high-temperature phase and exhibits high ionic conductivity even at room temperature14,15. LLTO is a perovskite-type oxide solid electrolyte composed of two perovskite units stacked together in a unit cell8,16. Its bulk ionic conductivity exceeds 1.0 × 10-3 S cm-1 at room temperature16,17, but it requires sintering above 1400 K and is therefore unsuitable as a standalone ASSB solid electrolyte17,18. A lattice-matched composite solid electrolyte system can effectively utilize both Li2OHCl and LLTO as solid electrolytes.
In this paper, we discuss the possibility of composite solid electrolytes based on the lattice-matched system of Li2OHCl1-xFx/LLTO interface and demonstrate ASSB using the composite solid electrolytes with melt infiltration processes.
Results
Modeling of lattice-matched composite solid electrolytes
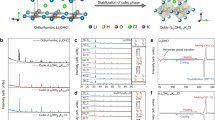
Figure 1a shows structure models of antiperovskite c-Li2OHCl, perovskite LLTO, garnet Li7La3Zr2O12(LLZO)8, and NASICON Li1.3Al0.3Ti1.7(PO4)3 (LATP)8. The corresponding structures are available in Supplementary Data 1. The antiperovskite structure of c-Li2OHCl exhibits similarities to the LLTO perovskite structure, which is characterized by a reversed arrangement of cations and anions. However, LLZO and LATP have different atomic arrangements compared to the c-Li2OHCl, implying more complex interface states with c-Li2OHCl. Reciprocal lattice projections for each crystal structure are shown in Fig. 1b. Antiperovskite c-Li2OHCl (a = b = c = 3.911 Å) exhibits remarkably high lattice matching with perovskite LLTO (a = b = 3.869 Å and c = 7.742 Å (3.871 Å in the cubic unit)), achieving a mismatch ratio of only 1.1% for energetically favorable surfaces, indicating suitable epitaxial relationships as a composite solid electrolyte. The detailed mismatch ratios based on energetically favorable surfaces and lattice parameters are shown in Supplementary Fig. 1.
a Crystal structure models of antiperovskite c-Li2OHCl, perovskite LLTO, garnet LLZO, and NASICON LATP. Two-color spheres indicate mixed occupancy at the same crystallographic site. The size of each color segment corresponds to the occupancy ratio. b Calculated two-dimensional reciprocal lattice projections for c-Li2OHCl, Li2OHCl/LLTO, Li2OHCl/LLZO, and Li2OHCl/LATP. White patterned dots and numerical indices in each reciprocal lattice projection represent their Miller indices relative to the energetically favorable (100) surface of Li2OHCl. Red, light green, and light blue dots represent projection patterns against the LLTO(001), LLZO(100), and LATP(012) surfaces, respectively. Each projection pattern is overlaid on the white pattern of c-Li2OHCl(100). c Calculated interfacial energies between LLTO(100), LLZO(100), and LATP(012) against c-Li2OHCl(100). d Schematic illustration of the energetically favorable interface between c-Li2OHCl(100) and LLTO(100), showing the effects of fluorine substitution to enhance the lattice matching and coherence of atomic arrangement. e Dependence of halogen substitution on cell volume and formation energy of c-Li2OHCl0.875X0.125 (X: F, Cl, Br, and I). f Dependence of halogen substitution on the interfacial energy between c-Li2OHCl(100) and LLTO(100). Source data are provided as a Source Data file.
Next, we discuss the interface stability of composite solid electrolytes based on atomistic simulations. The detailed structural modeling procedure is described in the Methods section. Briefly, for modeling composite solid electrolytes, each material was optimized using the replica exchange Monte Carlo (REMC) method19 with the Preferred Potential (PFP)20, a machine learning potential provided by Matlantis20,21,22. The REMC method and subsequent structural relaxation for interface modeling, along with energy evaluation during MD simulations, were comprehensively verified by DFT calculations (Supplementary Fig. 2c, d, and e). The simulation results obtained in this study, based on PFP, enabled a quantitative evaluation of interface stability and the effects of Li-ion diffusion.
Figure 1c shows interfacial energies between LLTO(100), LLZO(100), and LATP(012) against c-Li2OHCl(100), using energetically favorable surfaces. The corresponding structures are available in Supplementary Data 2. Among these combinations, Li2OHCl(100)/LLTO(100) has the lowest interfacial energy, suggesting a thermodynamically stable interface. In contrast, LATP exhibits much higher interfacial energy compared to LLTO, which is likely attributed to its polyanionic framework containing PO4 groups that differ from the atomic arrangement of c-Li2OHCl. Figure 1d shows a schematic representation of the energetically favorable interface between c-Li2OHCl(100) and LLTO(100). The coherence between the lattice matching and atomic arrangements of these two materials minimizes atomic disorder at the interface, emphasizing their critical role in forming stable interfaces for composite solid electrolytes.
To further enhance lattice matching between these materials, we propose a strategy involving halogen substitution of c-Li2OHCl with fluorine. Figure 1e shows the elemental dependence of halogen substitution on the cell volume and the formation energy for c-Li2OHCl0.875X0.125 (X: F, Cl, Br, I). Substituting chlorine (ionic radius: 1.81 Å) with fluorine (ionic radius: 1.33 Å) induces lattice contraction in c-Li2OHCl. The lattice parameter decreases to a = b = c = 3.87 Å for F substitution, reducing mismatch with LLTO to 0.1%. Additionally, the formation energies imply that substitution of Cl with F enhances chemical stability due to high electronegativity of fluorine. Figure 1f illustrates the elemental dependence of halogen substitution on the interfacial energy between c-Li2OHCl0.875X0.125(100) and LLTO(100). As expected, F-substituted c-Li2OHCl exhibits lower interfacial energy compared to other halogen substitutions. These results indicate that F substitution is an effective strategy for achieving both chemical stabilization of c-Li2OHCl and optimal interfacial properties in composite solid electrolytes with LLTO.To address the limitations of pure Li2OHCl, particularly its low ionic conductivity at room temperature and the cubic-to-orthorhombic phase transition around 345 K, we investigated the effects of halogen substitution on the structure and ionic transport properties of Li2OHCl. MD simulations were conducted in an NVT ensemble with a Nosé-Hoover thermostat. Before conducting the large-scale MD simulations involving over 400 atoms with durations of 2 ns, both PFP-MD and AIMD (ab initio MD) simulations were performed to validate their reliability in the Li2OHCl and Li2OHCl0.875F0.125 systems, each consisting of 40 atoms. The corresponding initial and final configurations are available in Supplementary Data 3. As shown in Supplementary Fig. 2, the mean-squared displacement (MSD) of Li and H during these MD simulations exhibits results consistent with those previously reported by Wang, F. et al.23 and Howard, J. et al.24. No evidence of free diffusion of H⁺ was observed in this study, confirming that ionic conductivity is solely derived from Li ions. For this study, PFP-MD was employed for the quantitative evaluation of interface stability and Li-ion diffusion effects, with its reliability verified through comparisons with corresponding total energies obtained via DFT.
Figure 2a shows the dependence of halogen substitution on the Li-ion diffusivity of c-Li2OHCl0.875X0.125 based on MD simulations, as well as the volume fraction of available Li⁺ sites determined using the bond valence sum (BVS) method25,26. The corresponding halogen-substituted structures are available in Supplementary Data 4. The ionic conductivity of c-Li2OHCl0.875F0.125 was calculated to be higher than that of other halogen substitutions, even though the lattice parameter of c-Li2OHCl0.875F0.125 is smaller compared to those of other halogen substitutions (Fig. 1e). Generally, a decrease in lattice parameter reduces the available volume for ion passage, which typically leads to increased activation energy and decreased ion diffusivity27. However, despite a reduced cell volume following F substitution, an increased volume fraction of available Li⁺ sites was observed (Fig. 1e). Figure 2b illustrates three distributions related to Li-ion movement: volumetric distribution for available Li+ sites from the BVS analysis, energy isosurfaces from the Bond Valence Energy Landscape (BVEL)24, and probability density distributions derived from MD simulations. Geometrical rearrangements around F sites with smaller ionic radius create additional space in the Cl-based framework; conversely, Br or I substitutions with larger ionic radii reduce this effect by decreasing available volumes for Li+. The distribution of available volumes closely matches migration pathways identified in both BVEL isosurfaces and MD simulations (Fig. 2b). Detailed results of MD simulations regarding F substitution are provided in Supplementary Fig. 3, and the corresponding initial and final configurations are provided in Supplementary Data 5. An increase in F dopant concentration leads to a reduction of the activation energy for Li transport, accompanied by a decrease in the lattice parameter (Supplementary Fig. 3j). Therefore, F-doped c-Li2OHCl emerges as a promising candidate for an effective lattice-matched system in conjunction with LLTO as a composite solid electrolyte.
a Dependence of halogen substitution on the Li-ion diffusivity of c-Li2OHCl0.875X0.125 (X = F, Cl, Br, and I) calculated from Li-MSD, as well as the volume fraction of available Li+ sites determined using the BVS method. b Visualized distributions related to Li-ion movement: volumetric distribution of available Li+ sites derived from BVS shown in blue; energy isosurface for Li+ obtained from the BVEL shown in purple; and probability density distribution of Li+ obtained from MD simulations shown in yellow. Isosurfaces from MD simulations are plotted at an isovalue of 0.005 au. c Temperature dependence of Li-MSD with and without F substitution. d Reconstructed isosurface illustrating the probability density distribution of Li ions during MD simulations. Isosurfaces are plotted at an isovalue of 0.0001 au. The isosurfaces representing Li ions are shown in yellow. e Temperature dependence of Li-ion diffusivities in LLTO, c-Li2OHCl, and Li2OHCl(100)/LLTO(100), as well as along the z-direction in c-Li2OHCl, and c-Li2OHCl(100)/LLTO(100). f F concentration dependence of interfacial ionic conductivity in the z-direction for the c-Li2OHCl1-xFx/LLTO interface. Source data are provided as a Source Data file.
We then confirmed the phenomenon of the cubic-to-orthorhombic phase transition in F-substituted Li2OHCl for the room temperature operation of ASSBs. The phase transition of Li2OHCl is driven by changes in OH- orientation26,27,28. At low temperatures, o-Li2OHCl adopts an ordered structure where Li ions occupy specific Wyckoff sites (2a and 2b) within the Pmc21 space group, with local charge compensation achieved through OH- alignment toward vacancies (Supplementary Fig. 4). In contrast, at higher temperatures, increased thermal vibrations promote site hopping and rotational motion of OH- ions26,27,28. This results in a disordered c-Li2OHCl structure where approximately 66.6% of 3c Wyckoff sites (Pm-3m) are occupied by Li ions while others remain vacant. This transition involves pendulum-like rotational motion of OH- ions coupled with enhanced Li migration. Figure 2c shows the temperature dependence of MSD of Li ions (Li-MSD) calculated from MD simulations with and without F substitution. In pure Li2OHCl, Li is localized at the 2a and 2b sites, with no hopping observed to 3c sites; consequently, Li-MSD remains unchanged up to approximately 325 K. A discontinuity in Li-MSD is observed between 325 K and 350 K as Li begins occupying the 3c sites. Our simulation results (Supplementary Fig. 3, 4 and Supplementary Data 6) confirm random angular variations in OH- orientations above the phase transition temperature, consistent with previous studies26,27,28. In the case of F substitution, continuous changes in Li-MSD are observed even at temperatures as low as 275 K (Fig. 2c). Li occupies all three sites, 2a, 2b, and 3c, in the cubic arrangement. As shown in Supplementary Fig. 4, the bond length of Li-F is shorter than that of Li-Cl, resulting in the displacement of Li+ from their original ordered positions in o-Li2OHCl to disordered positions associated with disturbances in OH- orientation. Radial distribution function (RDF) of the optimized Li2OHCl0.875F0.125 structure closely resembles that of the c-Li2OHCl (Supplementary Fig. 4c), indicating that F substitution modifies the atomic arrangement toward the disordered cubic structure.
Li-ion transport within a Li2OHCl/LLTO interface model was investigated using MD simulations. The corresponding initial and final configurations are provided in Supplementary Data 7. The LLTO model generated using REMC exhibits a two-dimensional structure with alternating La-rich and La-poor layers, where the La-rich layers tend to hinder Li-ion conduction16,17. In this model, the La layers are aligned along the x-z plane, restricting Li+ transport to two dimensions within the x-z plane and effectively prohibiting conduction in the y-direction (Fig. 2d). MD simulations were performed at temperatures below 800 K to prevent an unsuitable rare event of O-H bond breakage at the Li2OHCl(100)/LLTO(100) interface. Figure 2d shows a reconstructed isosurface of the Li-ion probability density distribution observed during MD simulations of the Li2OHCl(100)/LLTO(100) interface model, visually illustrating the diffusion trajectory of Li ions. Li-ion transport occurs actively within both the bulk regions of Li2OHCl and LLTO, as well as across their interface, as illustrated by the BVEL isosurface in Supplementary Fig. 5. Figure 2e compares the temperature dependence of Li-ion diffusivity for the Li2OHCl(100)/LLTO(100) interface model with those observed in c-Li2OHCl and LLTO bulk crystals. Li-ion diffusivity for the interface model lies between those of each bulk material. The ionic conductivity contribution of bulk LLTO is prominent in the x-direction where LLTO forms a continuous pathway, whereas its contribution is negligible in the y-direction due to low Li-ion conductivity along this axis. In contrast, in the z-direction, where Li2OHCl and LLTO are arranged with equal thickness under periodic boundary conditions, the bulk ionic conductivity (σ) contributions can be expressed as 1/σtotal = 1/2σLi2OHCl + 1/2σLLTO. Consequently, Li2OHCl, which exhibits lower ionic conductivity, plays a significant role in determining overall ionic transport properties along the z-direction. To validate this observation, z-directional diffusivity was analyzed and found to be nearly identical to that in bulk-phase c-Li2OHCl crystals (Fig. 2e), suggesting that ion diffusion in bulk-phase c-Li2OHCl is likely the rate-limiting step for total conductivity in the z-direction. Figure 2f shows the F concentration dependence of interfacial ionic conductivity in the z-direction, determined by MD simulations for the c-Li2OHCl1-xFx/LLTO interfaces. The ionic conductivity across the interface increases with increasing F content, while F substitution also reduces the activation energy (Supplementary Fig. 5d). The enhancement of ionic conductivity across the interface by F substitution can be attributed to two factors: (1) the intrinsic improvement in the conductivity of bulk c-Li2OHCl1-xFx due to extended migration pathways, and (2) improved interfacial lattice matching with LLTO achieved through tuned lattice parameters. These findings demonstrate that halogen substitution, particularly fluorination, effectively addresses key challenges associated with Li2OHCl and enables its seamless integration into high-performance composite solid electrolytes suitable for ASSBs.
Synthesis and analysis of Li2OHCl1-xFx-LLTO composite solid electrolytes
Composite solid electrolytes of Li2OHCl1-xFx-LLTO were synthesized. The detailed synthesis procedures are described in the Method section. Briefly, the composite solid electrolytes were prepared by hot pressing Li2OHCl1-xFx with LLTO powders. Infiltration of LLTO with molten Li2OHCl1-xFx achieved a pellet density of 99%. Adding LLTO as a filler29 reduces the fluidity of the molten Li2OHCl0.9F0.1, minimizing leakage and facilitating pellet formation through hot pressing. The photographs of Li2OHCl0.9F0.1 and Li2OHCl0.9F0.1-LLTO pellets kept at different temperatures are shown in Fig. 3a. In the case of the LLTO composite, although Li2OHCl0.9F0.1 melts, the pellet structure remains intact. The experimental results demonstrate that Li2OHCl1-xFx exhibits high wettability with LLTO, as shown in Fig. 1c, f, and indicate that Li2OHCl1-xFx/LLTO has low interfacial energy. However, because this process utilizes the Li2OHCl1-xFx melt, even slight temperature changes significantly impact the internal structure of the composite pellet (Fig. 3b). By processing at 548 K (corresponding to the melting onset temperature), a dense and well-infiltrated composite with no distinct grain boundaries in the Li2OHCl0.9F0.1 region was obtained. At 543 K (below its melting onset temperature), both Li2OHCl0.9F0.1 and LLTO particles were observed. At 553 K (above the melting point), excessive melt was generated, leading to leakage caused by a decrease in viscosity, which resulted in the formation of cavities within the composite material.
a, Photographs of Li2OHCl0.9F0.1 and Li2OHCl0.9F0.1-LLTO pellets stored at different temperatures. b Cross-sectional SEM images of Li2OHCl0.9F0.1-LLTO pellets synthesized at 543, 548, and 553 K. The scale bars in b are 10 μm. c XRD patterns at room temperature for the synthesized Li2OHCl, Li2OHCl-LLTO, Li2OHCl0.98F0.02-LLTO, and Li2OHCl0.9F0.1-LLTO composite solid electrolytes. d Enlarged view of c with Rietveld analyses included for detailed structural assignments. e Relationship between changes in lattice parameters due to F doping in Li2OHCl1-xF and the measured Li ionic conductivity of Li2OHCl1-xFx at 298 K. f Nyquist plots of impedance at 298 K for Li2OHCl0.9F0.1, Li2OHCl0.9F0.1-LLTO, Li2OHCl0.9F0.1-LLZO, and Li2OHCl0.9F0.1-LATP composite solid electrolyte pellets. g Nyquist plot, fitted curve, and the corresponding equivalent circuit of Li2OHCl0.9F0.1-LLTO composite solid electrolyte pellets. Source data are provided as a Source Data file.
Figures 3c, d show the XRD results and enlarged patterns for Li2OHCl, Li2OHCl-LLTO, Li2OHCl0.98F0.02-LLTO, and Li2OHCl0.9F0.1-LLTO composite solid electrolyte pellets. Li2OHCl exhibits an orthorhombic phase at room temperature as expected. In the Li2OHCl-LLTO composite solid electrolyte, both orthorhombic and cubic phases coexist, unlike standalone Li2OHCl. With increasing F dopant concentration, the orthorhombic phase decreases while the cubic phase increases in Li2OHCl1-xFx. The cubic/orthorhombic ratios for x = 0, 0.02, 0.05, and 0.1 were calculated to be 59, 91, 95, and 100%, respectively, using Rietveld analysis (Supplementary Fig. 6). The c-Li2OHCl1-xFx peak position, referenced to the LLTO(110) peak at 32.8°, shifts toward higher angles for x = 0.1 compared to x = 0.02, indicating contraction of the crystal lattice. As shown in Fig. 3e and Supplementary Fig. 6c, the lattice parameter decreases with increasing x, particularly at x = 0.1, where it contracts to 3.9025 Å, approximately 0.2% smaller than that of typical c-Li2OHCl (3.911 Å). This lattice contraction reduces the lattice mismatch with LLTO to approximately 0.8%. The ionic conductivity of the synthesized Li2OHCl0.9F0.1 at 298 K also improves to 3.3 × 10-6 S cm-1 from 1.1 × 10-7 S cm-1 in Li2OHCl, demonstrating an inverse correlation with lattice parameters (Fig. 3e). These results align with theoretical calculations in Figs. 1e and 2a, supporting the validity of F substitution effects. It is worth noting that an increasing trend of small LiF precipitates is observed at higher F dopant concentrations, as shown in Supplementary Fig. 7. These observations suggest that a composition around x = 0.1 likely represents a practical solubility limit.
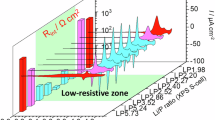
Figure 3f shows Nyquist plots of impedance at room temperature for c-Li2OHCl0.9F0.1, Li2OHCl0.9F0.1-LLTO, Li2OHCl0.9F0.1-LLZO, and Li2OHCl0.9F0.1-LATP composite solid electrolyte pellets. The Li2OHCl0.9F0.1-LATP composite solid electrolyte exhibited higher resistance than c-Li2OHCl0.9F0.1, indicating that the high ionic conductivity of LATP was not effectively realized. This may be attributed to the evidently high interfacial energy, as shown in Fig. 1c, which suggests that an appropriate interface for Li-ion transport could not be formed. In contrast, it was found that composites with LLTO or LLZO resulted in lower resistance compared to c-Li2OHCl0.9F0.1, with a significant reduction in resistivity observed for the c-Li2OHCl0.9F0.1-LLTO composite solid electrolyte. Notably, two distinct semicircles were clearly observed for both composites with LLTO and LLZO in Fig. 3f. As shown in Fig. 3g and Supplementary Fig. 8, equivalent circuit model analysis suggests that the first and second semicircles represent the ionic conductivity at the Li2OHCl0.9F0.1-LLTO interface (1.7 × 10-4 S cm-1) and the bulk ionic conductivity of Li2OHCl0.9F0.1 (9.7 × 10-6 S cm-1), respectively. The low resistance of the Li2OHCl0.9F0.1/LLTO interface, attributed to its energetically stable lattice-matched structure, was comparable to the resistance observed at sintered LLTO grain boundaries27. The total ionic conductivity of the c-Li2OHCl0.9F0.1-LLTO composite solid electrolyte was calculated to be 5.0 × 10-5 S cm-1 (Supplementary Fig. 8). This value is approximately one order of magnitude higher than that of c-Li2OHCl0.9F0.1, facilitating ASSB operation at room temperature.
Pressure-assisted melt-infiltrated ASSBs with conventional LIB electrodes
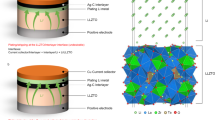
ASSBs were fabricated using the Li2OHCl0.9F0.1-LLTO composite solid electrolyte via melt infiltration into conventional LIB electrodes. A tape-cast NCA (LiNi0.8Co0.15Al0.05O2) secondary particle positive electrode and a tape-cast Li4Ti5O12 (LTO) secondary particle negative electrode were utilized, with relatively higher calendar pressing applied to induce significant microcracks in the active materials, thereby accelerating melt infiltration. A compacted Li2OHCl0.9F0.1-LLTO composite solid electrolyte sheet was sandwiched between the positive and negative electrodes, and ASSBs were fabricated by heating and melt-infiltrating the solid electrolytes. Xiao et al. previously reported a thermal melt infiltration method11. As discussed above, handling Li2OHCl melt poses significant challenges due to leakage during processing. In the fabrication of ASSBs, issues arise from incomplete infiltration into fine voids within the electrode, as well as the potential for short circuits between the positive and negative electrodes. In contrast, with Li2OHCl0.9F0.1-LLTO composite solid electrolytes, stable pressure-assisted melt infiltration30 by hot pressing is feasible. As shown in Fig. 4a, LLTO functions as a separator filler to prevent short circuits when pressurization. Figure 4b shows SEM images of the cross-section of the negative electrode after thermal and pressure-assisted melt infiltrations. In thermal melt infiltration, Li2OHCl0.9F0.1 infiltrates into the negative electrode; however, many cavities smaller than 200 nm are observed. In contrast, pressure-assisted melt infiltration achieves higher penetration, effectively filling both the interior of the electrode and the secondary particles of negative electrode active materials. External pressure allows molten solid electrolytes to penetrate delicate and complex pathways. The packing density of the entire ASSB after pressure-assisted melt infiltration reached approximately 96%, compared to 91% for thermal melt infiltration. Our investigation revealed that pressure-assisted melt infiltration provides improved penetration compared to conventional thermal methods and allows for effective infiltration into complex electrode geometries. This increased packing density is crucial for maximizing ionic conductivity throughout the composite electrode system. However, as shown in Fig. 3b, this process has a very narrow temperature range: above 548 K, Li2OHCl0.9F0.1 begins to melt, and under pressure, molten salt may flow outward from the electrode. Accurate temperature control is essential for stable penetration into the electrode. At an optimized temperature for pressure-assisted melt infiltration (548 K) and pressing pressure (5 MPa), controlled melting occurs on the Li2OHCl0.9F0.1 surface while minimizing external leakage of molten salt and promoting efficient penetration into electrode voids. Notably, these optimal values may vary depending on equipment or material compositions.
a Schematic illustration of the cross-sectional structure of ASSB with Li2OHCl0.9F0.1-LLTO and conventional tape-cast LIB electrodes. b Cross-sectional SEM images of LTO negative electrodes with Li2OHCl0.9F0.1-LLTO composite solid electrolyte prepared by thermal and pressure-assisted melt infiltrations. c SEM and ToF-SIMS mapping images of the NCA positive electrode cross-section after pressure-assisted melt infiltration. d STEM and STEM-EDX mapping image of an NCA positive electrode after pressure-assisted melt infiltration; Green, blue, and red represent Ni, Cl, and C, respectively. e Three-dimensional SEM cross-sectional image and the EDX mappings of Li2OHCl0.9F0.1-LLTO composite solid electrolyte prepared by pressure-assisted melt infiltration. The scale bars in b, c, d, and e are 2, 10, 2, and 10 μm, respectively.
Figure 4c shows an SEM image and time-of-flight secondary ion mass spectrometry (ToF-SIMS) mapping images of the positive electrode cross-section after pressure-assisted melt infiltration. It was confirmed that Li2OHCl0.9F0.1, serving as the ionic pathway, penetrated deeply into the densely compacted electrode. Figure 4d shows scanning transmission electron microscopy (STEM) and energy-dispersive X-ray spectroscopy (STEM-EDX) images of the positive electrode active material region, where Li2OHCl0.9F0.1 effectively filled microcracks in the active material, providing a path for Li-ion conduction. This infiltration structure was found to replicate the behavior of liquid electrolytes by creating efficient pathways for Li ions. Three-dimensional (3D) reconstruction images (Fig. 4e), generated from SEM cross-sectional and SEM-EDX mapping obtained through continuous focused ion beam (FIB) processing, suggest that the interior of the tape-cast negative electrode is densely filled with solid electrolyte, exhibiting an electrode porosity of less than 1%. This low porosity helps maintain the mechanical integrity of the electrode while also enhancing ionic conductivity within the electrode. The curvature of the Li2OHCl0.9F0.1 ion pathway, calculated from these 3D images, is 2.29, comparable to an equivalent value of 2.11 for ionic pathways in liquid LIB electrodes as evaluated by ionic conductivity. Additionally, smaller LLTO particles were observed to be dispersed throughout the electrode interior alongside infiltrated Li2OHCl0.9F0.1 (as shown in the La mapping in Fig. 4e). This phenomenon is likely attributed to capillary effects, indicating transport of small LLTO particles during the infiltration of Li2OHCl0.9F0.1 into complex pathways. Such dispersion of LLTO is presumed to enhance ionic conductivity within the electrode interior.
The electrochemical properties of the pressure-assisted melt-infiltrated ASSB coin cells were evaluated. Figure 5a, b, and c show a photograph of the ASSB coin cell, a detailed schematic of its internal structure, and a processed image of the ASSB junction obtained through SEM-EDX imaging, respectively. The highly infiltrated solid electrolyte in the electrode enables the ASSB junction to be tightly solidified, eliminating the need for excessive cell pressure. For instance, the ASSB junction can operate by simply embedding it in an external casing (Fig. 5a, b) and has been verified to retain functionality even when cut into smaller pieces. As shown in Fig. 5c, the infiltrated solid electrolyte allows for the use of tape-cast electrodes designed for conventional LIBs, significantly reducing electrode costs. This design is straightforward and accommodates various cell configurations. Common winding or stacking structures used in liquid LIBs can also be implemented.
a Photograph of an ASSB coin cell. b Detailed schematic of the internal structure of the ASSB coin cell. c Processed image of the ASSB junction obtained through SEM-EDX imaging. d, e Nyquist plots of impedance and initial charge-discharge characteristics at 298 K for ASSBs with different oxide solid electrolyte fillers. f Cycle performance of the ASSB using Li2OHCl0.9F0.1-LLTO composite solid electrolyte at 333 K under a charging/discharging current of 50 mA g-1 (corresponding to 0.3 C). The last data point after 100 cycles was obtained using a charging/discharging current of 10 mA g-1 (corresponding to 0.1 C) to minimize the effect of cell resistance. g, h Rate performance at 298 K for ASSBs utilizing small NCA particles (D50: 5 µm) and a thin solid electrolyte layer (thickness: 50 µm), selected to reduce ionic resistance and enhance rate performance. Source data are provided as a Source Data file.
Figure 5d shows the Nyquist plots of the ASSBs before charging at 298 K utilizing composite solid electrolytes containing LLTO, LLZO, and LATP. In the ASSB configuration, tape-cast LIB electrodes were combined with relatively higher calendar pressing to induce microcracks and enhance specific surface area. Consequently, the cell resistance was reduced to approximately one-tenth that of the composite solid electrolyte with Pt-sputtered electrodes shown in Fig. 3f. Among these composites, LLTO demonstrated a relative low cell resistance, while LATP exhibited a relatively high cell resistance, consistent with the trends observed in Fig. 3f.
Figure 5e shows the initial charge-discharge characteristics of the ASSBs at 298 K using composite solid electrolytes containing LLTO, LLZO, and LATP. The low resistivity of the Li2OHCl0.9F0.1-LLTO composite solid electrolyte significantly enabled the room-temperature operation of this ASSB. In comparison to LLTO, incorporating other oxide solid electrolytes as filler materials increased cell resistivity (Fig. 5d), leading to higher overpotentials in the ASSBs and a reduction in achievable charge-discharge capacity (Fig. 5e).
Figure 5f shows the cycle performance of the ASSB using Li2OHCl0.9F0.1-LLTO composite solid electrolyte at 333 K. The capacity retention of 92% was maintained after 100 cycles. A slight increase in overpotential (0.1 V for both charge and discharge) was observed in the charge-discharge curves after 100 cycles (Supplementary Fig. 9a). The capacity retention was recovered to 99.4% through low-rate operation (0.067 C), indicating limited degradation of the active materials during the cycling test. The Nyquist plots before and after cycling are shown in Supplementary Fig. 9c. Based on the equivalent circuit model analysis of the impedance components (Supplementary Fig. 9d and 9e), the ohmic resistance component, which is attributed to electronic conduction within the electrode and at the electrode interface, remains stable. However, both the high-frequency and low-frequency components, which are likely associated with charge transfer resistance at the negative electrode and positive electrode interfaces, are observed to increase. Notably, the second semicircle exhibits a significant increase. The impedance value corresponding to the peak of this second semicircle at 1 kHz demonstrates a slight linear upward trend with repeated charge-discharge cycles (Supplementary Fig. 10b). Supplementary Fig. 10 shows the dependence of the capacity retention and interface resistivity (impedance value at 1 kHz) of the ASSB cell on calendar pressing of the positive and negative electrodes. The effect of calendar pressing on the porous negative electrode was negligible, whereas its impact on the interface resistivity at the positive electrode was significant for both capacity retention and interface resistivity. Supplementary Fig. 10c shows the Nyquist plots of the ASSB at the 100th cycle with and without calendar pressing of the positive electrode. An increase in the ohmic resistance component was observed, suggesting delamination at the positive electrode interface. Furthermore, an increase in the second semicircle was confirmed, indicating an increase in charge transfer resistance at the positive electrode interface. The high-pressure pressing induces cracks in dense NCA secondary particles, promoting solid electrolyte infiltration into these cracks (Fig. 4d). For liquid electrolytes, increased reaction surface area due to cracks within active material can cause surface degradation, leading to reduced cycle life and safety performance31. However, for the infiltrated solid electrolyte, it is speculated that cracks within NCA secondary particles contribute to the formation of a robust self-binding electrode via an anchoring effect while also reducing resistance through enhanced solid electrolyte penetration. This phenomenon likely stabilizes interface resistance and improves cycle performance.
To reduce resistivity and enhance the adaptability of ASSBs, the use of smaller NCA positive electrode particles with a higher surface area was demonstrated. The rate performance at 298 K for an ASSB employing smaller NCA particles (D50: 5 µm) and a thinner solid electrolyte layer (thickness: 50 µm) is shown in Figs. 5g and 5h. Stable operation was achieved at rates up to 0.5 C, whereas ASSBs with larger NCA particles (D50: 15 µm) exhibited a maximum rate of 0.2 C (Supplementary Fig. 11). These results suggest potential for further improving electrochemical performance by optimizing electrode configurations, as well as enhancing the ionic conductivity of Li2OHCl and reducing the interfacial resistivity at the Li2OHCl/LLTO interface through increased fluorine doping.
In summary, while composite solid electrolytes aim to effectively leverage the advantages of their constituent materials, our study demonstrates that lattice matching and interfacial stability at their interfaces have a profound impact on ionic conductivity and electrochemical performance. Moreover, well-designed interface modeling based on structurally compatible materials can enhance lattice matching and interfacial stability, thereby enabling more stable operation of ASSBs. Additionally, we have demonstrated that pressure-assisted melt infiltration using molten salts plays a pivotal role in achieving such optimized interfacial structures. This underscores the importance of exploring molten salt-based solid electrolytes as a key strategy for realizing all-solid-state batteries that outperform conventional liquid LIBs.
Building upon these findings, the combination of lattice-matched composite solid electrolytes and pressure-assisted melt infiltration in ASSBs demonstrates several attributes and performance enhancements, including stable structural integrity, improved cycling stability, flexible design options, and room-temperature operation. These advancements represent a contribution to progress in the development of advanced energy storage systems, providing useful insights for future research while supporting further work in high-performance all-solid-state batteries.
Methods
Calculation of reciprocal lattice projections
Recipro32, a crystallographic software specialized in simulating diffraction patterns and reciprocal lattice projections, was used to calculate reciprocal lattice projections for several solid electrolyte crystals. The structures considered were Pm-3m for Li2OHCl26, P4mmm for Li0.31La0.56TiO333, Ia-3d for Li7La3Zr2O1234, and R-3c for Li1.3Al0.3Ti1.7(PO4)335. The reciprocal lattice projections were generated using the Recipro diffraction simulator by overlaying individual reciprocal lattice patterns of Li2OHCl and the other solid electrolytes. The lattice plane indices of each structure were identified based on energetically favorable surfaces calculated via DFT, as referenced in studies36,37,38.
Preparation of Li2OHCl1-xFx, LLTO, LLZO, LATP, and those interface models with Li2OHCl1-xFx
The stable configurations of randomly structured crystals of Li2OHCl1-xFx (240 atoms), LLTO (234 atoms), LLZO (372 atoms), and LATP (440 atoms) (shown in Supplementary Fig. 2a and Supplementary Data 1) were obtained through replica exchange Monte Carlo (REMC)19 calculations using the PFP universal neural-network potential (version 5.0.0) provided by Matlantis20, which was integrated into the Atomic Simulation Environment (ASE)39. This machine learning surrogate model for ab initio calculations supports the elements utilized in this study, which include H, Li, O, F, Cl, Ti, and La. The reliability of the PFP during these simulations was verified by comparing the corresponding energy calculations and RDFs obtained via DFT, with a Mean Absolute Error (MAE) of less than 10-3 eV/atom, as shown in Supplementary Fig. 2. The Metropolis sampling was performed on system replicas at different temperatures in parallel. The selected temperatures ranged from 300 to 2100 K to enable enhanced sampling and exploration of diverse energy landscapes.
The interface models were prepared by combining each structure and enlarging the supercell size to ensure compatibility. Li2OHCl1-xFx/LLTO (474 atoms), Li2OHCl1-xFx/LLZO (5348 atoms), and Li2OHCl1-xFx/LATP (5732 atoms) were successfully constructed (Supplementary Data 2).
DFT calculations were performed using the Vienna ab initio Simulation Package (VASP)40,41. The Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional42 was combined with the projector augmented wave (PAW) method43,44, a plane-wave basis set with an energy cutoff to 520 eV. Long-range dispersion forces were accounted for using the Grimme DFT-D3 method45. Due to the large supercell employed in these simulations, only Γ-point sampling was performed. The following valence electron configurations were adopted: 1s1 for H; 1s22s1 for Li, 2s22p4 for O; 3s23p5 for Cl; 3d34s1 for Ti; and 5s25p65d16s2 for La.
The VESTA software package46 was used to visualize crystal structures and isosurfaces.
MD calculations for Li2OHCl1-xFx, LLTO and Li2OHCl1-xFx-LLTO interface models
MD simulations were performed using the PFP provided by Matlantis. The reliability of the PFP during these simulations was verified by comparing the corresponding energies, forces, RDFs, and MSDs with those obtained via DFT, as shown in Supplementary Fig. 2. To further ensure the reliability of PFP-MD, AIMD simulations were performed on Li2OHCl and Li2OHCl0.875F0.125 systems, each consisting of 40 atoms over a duration of 20 ps (40,000 steps). All simulations were conducted with a timestep of 0.5 fs to account for the movement of hydrogen atoms in the simulation. The temperature was controlled using the Nosè-Hoover thermostat for maintaining equilibrium at constant temperature and Parrinello-Rahman barostat for enabling isotropic pressure control in phase transition analysis. To analyze the phase transition behavior of Li2OHCl1-xFx, MD simulations were performed using both the NVT and the NPT ensembles. Analyses of Li and OH ion dynamics were conducted in the NVT ensemble for 2 ns across a temperature range of 250–400 K, with increments of 25 K, to capture detailed dynamic behavior near and beyond the phase transition temperature (345 K). Lattice parameter analyses during the phase transition were conducted in the NPT ensemble, with the temperature incrementally increased by 5 K at each step over a duration of 20 ps. The calculated lattice parameters at each step were obtained by averaging measurements taken after excluding the initial 10 ps of each step. The simulation temperature was determined from the time-averaged kinetic energy. Additionally, a combination of the Berendsen thermostat and Berendsen barostat was also employed to verify reproducibility of phase transition behavior under a temperature gradient.
MD simulations to study Li-ion diffusion were performed using the NVT ensemble with varying temperatures controlled by the Nosé-Hoover thermostat using the PFP. O-H bond breakage was observed in the Li2OHCl/LLTO interface at temperatures above 825 K; this phenomenon could affect structural stability and ionic conductivity predictions under such high temperature conditions; therefore, temperatures of 650, 675, 700, 725, 750, and 775 K were selected to evaluate ion dynamics while maintaining the structural integrity of the simulated systems. The simulations were run for 2 ns. The isosurface of Li-ion probability density distribution was visualized using atomic trajectories generated from the MD simulations. The self-diffusion coefficients of Li ions were calculated from the MSD using the Einstein relation. The activation energies for Li-ion diffusion were calculated using Arrhenius plots of the self-diffusion coefficients. The corresponding initial and final snapshots of MD trajectories, saved as CIF files, are provided in the Supplementary Data.
BVEL calculations for Li ion migration pathway
Bond Valence Energy Landscape (BVEL) calculations were performed using the BondStr24 program with the softBV23 model, which provides an enhanced description of ionic interactions compared to traditional BVS models, to simulate Li ion migration pathways and evaluate migration barrier heights. Structural models optimized via PFP and DFT were used as input structures. BVELs of Li ions were calculated on a 3D point grid with a resolution of 0.1 Å. The ion migration pathway was determined by calculating an isosurface using graph theory and the marching cubes algorithm24, which constructs the isosurface as a triangular mesh in the program.
Synthesis of composited solid-state electrolytes
All materials used in this study were handled in a dry-room environment with a dew point below 223 K. The synthetic precursors of Li2OHCl1-xFx were LiOH (anhydrous, 99.9%, Sigma-Aldrich), LiCl (anhydrous, 99.95%, Sigma-Aldrich), and LiF (≥99.99%, Sigma-Aldrich). All precursors were dried at 373 K under vacuum for 24 h prior to the experiments.
LiOH, LiCl, and LiF were mixed at an appropriate molar ratio and ground using a ball mill (P-7, Fritsch) at room temperature for 10 h at 300 rpm without intermittent rest periods. Throughout the entire ball milling process, a 45 mL zirconia jar and 50 g of zirconia balls (3 mm diameter) were used, with approximately 20 mL of total powder volume, corresponding to a ball-to-powder weight ratio of 2:1. The mixture was then heated to 603 K for 30 min at a ramping rate of 10 K/min in a box furnace until it melted into a transparent molten state, ensuring homogeneity of the solid electrolyte composition upon cooling. The molten samples were subsequently cooled to room temperature. The resulting white brittle salts were ground into fine powders using a mortar and ball milling for 30 min at 300 rpm without intermittent rest periods. These steps were repeated three times to obtain Li2OHCl1-xFx solid electrolyte powders.
Perovskite Li0.29La0.57TiO316,17 powder (TP-02F, Toho Titanium) and Li0.33La0.55TiO3 powder (Li0.33La0.55TiO3, Toshima Manufacturing) were used as the LLTO materials. The obtained solid electrolyte powders of Li2OHCl1-xFx were mixed with LLTO powder by using ball milling for 30 min at 100 rpm without intermittent rest periods. Weight ratios of 3:1 (Li2OHCl1-xFx: LLTO) were used for ASSB configurations, and 1:1 for analyses of the composite solid electrolyte itself. These ratios were optimized to achieve consistent ionic conductivity while maintaining structural stability in the composite electrolytes. Additionally, they ensured compatibility and reliable performance in melt-infiltrated electrolytes within electrodes for ASSBs. The mixture of solid electrolyte powders was heated to 558 K for 10 min in a preheated box furnace until it melted into a whitish molten state. The molten samples were cooled to room temperature, and the resulting white brittle salts were ground into fine powders using a mortar and ball milling for 10 min at 200 rpm without intermittent rest periods. These processes were repeated three times to obtain Li2OHCl1-xFx-LLTO composite solid electrolyte powders.
Preparation of active materials and electrodes
Positive electrode active materials: The precursors for synthesizing NCA (LiNi0.8Co0.15Al0.05O2) secondary particles were Li2CO3 (99.99%, Kojundo Chemical), NiSO4·6H2O (99.9%, Kojundo Chemical), NaOH (99%, Kojundo Chemical), NH4OH (28.0–30.0%, Sigma-Aldrich) and Al2(SO4)3·18H2O (Sigma-Aldrich). The Ni0.8Co0.15Al0.05(OH)2 precursor was prepared in a continuously stirred tank reactor via the hydroxide co-precipitation method47. NaOH(aq) solution was used as the base source for the reaction, while NH3(aq) solution facilitated spherical and dense particle growth. The reactor temperature was maintained at 323 K, and the contents were stirred at 1200 rpm. A pH controller automatically regulated NaOH injection using a peristaltic pump connected to the reactor. After 20 h, the hydroxide precursor was rinsed several times with water and dried at 393 K for 10 h. The Ni0.8Co0.15Al0.05(OH)2 precursor was then mixed with Li2CO3 by ball milling, with a Li-to-transition metal molar ratio of 1.02 maintained during preparation. The mixed powder was heated in a box furnace under an oxygen flow at 993 K for 20 h at a ramping rate of 10 K/min to synthesize NCA powders. The final NCA powders were mechanically ground and passed through a 53 μm sieve prior to electrode fabrication.
Negative electrode active materials: The materials used for synthesizing Li4Ti5O12 (LTO) secondary particles were Li4Ti5O12 (<200 nm, Sigma-Aldrich) and sucrose (C12H22O11, Kanto Chemical). Sucrose was dissolved in deionized water to achieve a 0.2 wt% solution. LTO powder was then suspended in the solution, and the suspension was ultrasonicated for 15 min to form a homogeneous dispersion. This suspension was processed in a spray dryer to obtain spherical secondary particles48. Sucrose served as both a binder and a carbon source for the LTO secondary particles. To obtain carbon-coated LTO secondary particles, calcination under argon flow was performed at 973 K for 5 h at a ramping rate of 10 K/min. The resulting LTO powders were mechanically ground and passed through a 53 μm sieve before electrode fabrication. Electrode fabrication: NCA powders, LTO powders, vapor-grown carbon nanofibers (VGCF, Showa Denko), and polyvinylidene fluoride (PVDF; Kureha, molecular weight: >1,000,000) were used to prepare electrodes. The weight ratio of active materials, VGCF and PVDF, was set at 92:5:3 in N-methyl-2-pyrrolidone (NMP) to form a slurry. Single-side-coated positive and negative electrodes were prepared by casting the slurry onto aluminum foils (thickness: 12 μm, purity: >99.5%), followed by drying in an oven at 363 K for 30 min. The casting was performed using the doctor blade method. Both the positive and negative electrodes were punched out to a 16 mm diameter. The electrodes were then calendared under a pressure of 20 MPa and dried further in a vacuum oven at 393 K for 12 h before cell assembly.
Pressure-assisted melt infiltration process
All procedures were conducted in a dry-room environment with a dew point below 223 K. Positive and negative electrode discs with a diameter of 15 mm were prepared. Li2OHCl1-xFx-LLTO composite solid electrolyte powders were calendared under a pressure of 20 MPa to form pellets with a thickness of 120 μm. The composite solid electrolyte pellet was placed between the positive and negative electrodes and heated to 533–553 K for 20 min while applying hot pressing with a pressure of 0-10 MPa (P5058, NPa SYSTEM). Careful control of temperature and pressure was crucial to prevent melting and leakage of the molten solid electrolyte, thereby ensuring cell quality.
Fabrication of ASSB coin cells
The fabricated LTO | Li2OHCl0.9F0.1-LLTO | NCA assembled samples were sealed in CR2016 coin cells for electrochemical measurements. The thickness of the composite electrolyte was 100 μm, with mass loadings of the NCA (D50: 15 µm) positive electrode and LTO negative electrode at 10 mg cm-2 and 8 mg cm-2, respectively. For the rate capability tests, the composite electrolyte thickness was reduced to 50 µm, and the mass loadings for the NCA (D50: 5 µm) positive electrode and LTO negative electrode were adjusted to 10 mg cm-2 and 8 mg cm-2, respectively.
Characterizations
FE-SEM (S-4800, Hitachi) and FIB-SEM (SMF2000, Hitachi) were used to examine the cross-sectional and three-dimensional images of the electrodes after melt infiltration. Elemental distribution was analyzed by EDS mapping at identical positions. TEM (JEM-ARM200F, JEOL) and ToF-SIMS (TOF.SIMS5-AD-GCIB, ION-TOF) were employed to characterize the electrode interface before and after electrochemical measurements. ImageJ49 and Avizo (Thermo-Fisher Scientific) were used to prepare two-dimensional and three-dimensional images, respectively.
An X-ray diffractometer (D8 ADVANCE, Bruker) was used to characterize phases and lattice parameters in the solid electrolytes. Rietveld diffraction pattern analysis was performed using the crystallographic analysis software GSAS-II50.
Electrochemical measurements
Electrochemical impedance spectroscopy (Solartron 1470E, Solartron Analytical; E4990A, Keysight) was employed to measure Nyquist and Bode plots, evaluating both the ionic conductivity of the solid electrolyte in symmetric cells and interfacial resistivity in CR2016 coin cells (full cells). The impedance spectra were measured using an AC voltage amplitude of 10 mV under potentiostatic control, superimposed on the open-circuit voltage, over a frequency range of 7 MHz to 0.1 Hz at various temperatures (298–333 K (±1 K)). DC magnetron sputtering was employed to deposit 40 nm Pt films on both sides of the composite solid electrolyte pellet for fabricating symmetric cells.
A TOSCAT-3100 (Toyo system) connected to climate chamber was used to perform charge–discharge tests on the ASSB coin cells. The initial charge–discharge tests were conducted at 298 K ± 1 K with a rate of 0.05 C in the voltage ranges of 0.5–2.5 V. Cycle performance tests were carried out at 333 K ± 1 K with a rate of 0.3 C. Rate performance tests were conducted at 298 K with varying discharge rates from 0.1 C to 1 C.
Data availability
The data that support the findings of this study are included within the article, its Supplementary Information, Source Data, and Supplementary Data files.The key calculation data generated in this study are provided in the Supplementary Data as CIF files. Due to company policy, data deposition in public repositories is not possible. Additional data supporting the findings of this study are available from the corresponding author upon request. Source data are provided with this paper.
References
Lu, J., Wu, T. & Amine, K. State-of-the-art characterization techniques for advanced lithium-ion batteries. Nat. Energy 2, 17011 (2017).
Schmuch, R. et al. Performance and cost of materials for lithium-based rechargeable automotive batteries. Nat. Energy 3, 267 (2018).
Manthiram, A. An outlook on lithium ion battery technology. ACS Cent. Sci. 3, 1063 (2017).
Lu, Y. & Chen, J. Prospects of organic electrode materials for practical lithium batteries. Nat. Rev. Mater. 2, 17011 (2017).
Liu, J. et al. Pathways for practical high-energy long-cycling lithium metal batteries. Nat. Energy 4, 180 (2019).
Cao, Y. et al. Bridging the academic and industrial metrics for next-generation practical batteries. Nat. Nanotech. 14, 200 (2019).
Manthiram, A., Yu, X. & Wang, S. Lithium battery chemistries enabled by solid-state electrolytes. Nat. Rev. Mater. 2, 16103 (2017).
Chen, R. et al. Approaching practically accessible solid-state batteries: stability issues related to solid electrolytes and interfaces. Chem. Rev. 120, 6820 (2020).
Schnell, J. et al. Prospects on production technologies and manufacturing cost of oxide-based all-solid-state lithium batteries. Energy Environ. Sci. 12, 1818 (2019).
Xia, W. et al. Antiperovskite electrolytes for solid-state batteries. Chem. Rev. 122, 3763 (2022).
Xiao, Y. et al. Electrolyte melt infiltration for scalable manufacturing of inorganic all-solid-state lithium-ion batteries. Nat. Mater. 20, 984 (2021).
Yamamoto, T. et al. Synthesis of the metastable cubic phase of Li2OHCl by a mechanochemical method. Inorg. Chem. 59, 11901 (2020).
Gao, L. et al. Boosting lithium ion conductivity of antiperovskite solid electrolyte by potassium ions substitution for cation clusters. Nat. Comm. 14, 6807 (2023).
Effat, M. B. et al. Stability, elastic properties, and the Li transport mechanism of the protonated and fluorinated antiperovskite lithium conductors. ACS Appl. Mater. Interfaces 12, 55011 (2020).
Gao, L. et al. Effects of fluorination on crystal structure and electrochemical performance of antiperovskite solid electrolytes. J. Energy Chem. 77, 521 (2023).
Hasegawa, G. et al. Lithium-ion diffusion in perovskite-type solid electrolyte lithium lanthanum titanate revealed by pulsed-field gradient nuclear magnetic resonance. Chem. Mater. 35, 3815 (2023).
Hasegawa, G. et al. Visualization and evaluation of lithium diffusion at grain boundaries in Li0.29La0.57TiO3 solid electrolytes using secondary ion mass spectrometry. J. Mater. Chem. A 12, 731 (2024).
Ping, W. et al. Printable, high-performance solid-state electrolyte films. Sci. Adv. 6, eabc8641 (2020).
Hukushima, K. & Nemoto, K. Exchange Monte Carlo method and application to spin glass simulations. J. Phys. Soc. Jpn. 65, 1604 (1996).
Takamoto, S. et al. Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements. Nat. Commun. 13, 2991 (2022).
Bekaert, L. et al. Assessing the reactivity of the Na3PS4 solid-state electrolyte with the sodium metal negative electrode using total trajectory analysis with neural-network potential molecular dynamics. J. Phys. Chem. C. 127, 8503 (2023).
Iwasaki, R. et al. Universal-neural-network-potential molecular dynamics for lithium metal and garnet-type solid electrolyte interface. Commun. Mater. 5, 148 (2024).
Wang, F. et al. Dynamics of hydroxyl anions promotes lithium ion conduction in antiperovskite Li2OHCl. Chem. Mater. 32, 8481 (2020).
Howard, J., Hood, Z. D. & Holzwarth, N. A. W. Fundamental aspects of the structural and electrolyte properties of Li2OHCl from simulations and experiment. Phys. Rev. Mater. 1, 075406 (2017).
Adams, S. Energy landscapes for mobile ions in ion conducting solids. Bull. Mater. Sci. 29, 587 (2006).
Katcho, N. A. et al. An investigation of the structural properties of Li and Na fast ion conductors using high-throughput bond-valence calculations and machine learning. J. Appl. Cryst. 52, 148 (2019).
Bachman, J. C. et al. Inorganic solid-state electrolytes for lithium batteries: mechanisms and properties governing ion conduction. Chem. Rev. 116, 140 (2016).
Spychala, J., Wilkening, A. & Wilkening, H. R. M. The batteries’ new clothes: Li and H dynamics in poorly conducting Li2OHCl directly probed by nuclear spin relaxation. J. Phys. Chem. C. 127, 7433 (2023).
Koca, H. D. et al. Effect of particle size on the viscosity of nanofluids: a review. Renew. Sustain. Energy Rev. 82, 1664 (2018).
de Jongh, P. E. & Eggenhuisen, T. M. Melt infiltration: an emerging technique for the preparation of novel functional nanostructured materials. Adv. Mater. 25, 6672 (2010).
Myung, S.-T. et al. Nickel-rich layered cathode materials for automotive lithium-ion batteries: achievements and perspectives. ACS Energy Lett. 2, 196 (2017).
Seto, Y. & Otsuka, M. ReciPro: free and open-source multipurpose crystallographic software integrating a crystal model database and viewer, diffraction and microscopy simulators, and diffraction data analysis tools. J. Appl. Cryst. 55, 397 (2022).
Zinkevich, T. et al. Effect of sintering temperature on Li diffusivity in Li0.29La0.57TiO3: Local hopping and long-range transport. Solid State Ion. 357, 115486 (2020).
Buschmann, H. et al. Structure and dynamics of the fast lithium ion conductor “Li7La3Zr2O12”. Phys. Chem. Chem. Phys. 13, 19378 (2011).
Case, D. et al. Structure and ion transport of lithium-rich Li1+xAlxTi2−x(PO4)3 with 0.3<x<0.5: A combined computational and experimental study. Solid State Ion. 346, 115192 (2020).
Wang, T. et al. Oriented crystal growth of La0.557Li0.330TiO3 in bulk ceramics induced by LaAlO3 single-crystal fibers. ACS Appl. Mater. Interfaces 13, 33102 (2021).
Gao, B. et al. Surface-dependent stability of the interface between garnet Li7La3Zr2O12 and the Li metal in the all-solid-state battery from first-principles calculations. ACS Appl. Mater. Interfaces 12, 16350 (2020).
Tian, H.-K. et al. Electron and ion transfer across interfaces of the NASICON-type LATP solid electrolyte with electrodes in all-solid-state batteries: a density functional theory study via an explicit interface model. ACS Appl. Mater. Interfaces 12, 54752 (2020).
Larsen, A. H. et al. The atomic simulation environment—a Python library for working with atoms. J. Phys. Condens. Matter 29, 273002 (2017).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15 (1996).
Perdew, J. P. et al. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Grimme, S. et al. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 7, 1456 (2011).
Momma, K. & Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Cryst. 44, 1272 (2011).
Li, J. et al. Structural and electrochemical study of the Li−Mn−Ni oxide system within the layered single phase region. Chem. Mater. 26, 7059 (2014).
Wagner, A. C. et al. Hierarchical structuring of NMC111-cathode materials in lithium-ion batteries: an in-depth study on the influence of primary and secondary particle sizes on electrochemical performance. ACS Appl. Energy Mater. 3, 12565 (2020).
Schindelin, J. et al. Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676 (2012).
Toby, B. H. & von Dreele, R. B. GSAS II: the genesis of a modern open-source all purpose crystallography. Softw. Package J. Appl. Cryst. 46, 544 (2013).
Acknowledgements
This work was supported by the NIMS Materials Open Platform (MOP) for All Solid-State Battery. We thank the NIMS Battery Research Platform for its support. A part of this work was supported by JST Grant Number JPMJPF2016 (all authors). This work used computational resources of the supercomputer Fugaku provided by the RIKEN Center for Computational Science through the HPCI System Research Project (Project ID: hp220404), utilized by S.T. and D.I.
Author information
Authors and Affiliations
Contributions
D.I. conceived the idea and conducted the proof-of-concept experiments. N.K., K.K., and G.H. performed microscopic analyses (TEM, SEM, ToF-SIMS). S.T. and D.I. performed the theoretical calculations. K.T. provided suggestions on the work. All authors participated in the data analysis and reviewed and approved this paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Wei Xia and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Ito, D., Kuwata, N., Takemoto, S. et al. Lattice-matched antiperovskite-perovskite system toward all-solid-state batteries. Nat Commun 16, 7372 (2025). https://doi.org/10.1038/s41467-025-62860-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-62860-1