Supramolecular chirality largely modulates chemical doping of conjugated polymers

Xu, Zhuang; Saiev, Shamil; Qian, Peisen; Nabei, Yoji; Wang, Ziming; Rinehart, Joshua M.; Österholm, Anna M.; Jones, Austin L.; Lee, Jong-Hoon; Hwang, Changhyun; Wang, Siqing; Sun, Rui; Shin, Dongguen; Jeon, Sanghyun; Elangovan, Kavinraaj Ella; Vura-Weis, Josh; Coropceanu, Veaceslav; Rodríguez-López, Joaquín; Reynolds, John R.; Sun, Dali; Brédas, Jean-Luc; Diao, Ying

doi:10.1038/s41467-025-62915-3

Download PDF

Article
Open access
Published: 25 September 2025

Supramolecular chirality largely modulates chemical doping of conjugated polymers

Nature Communications volume 16, Article number: 8381 (2025) Cite this article

1713 Accesses
1 Altmetric
Metrics details

Subjects

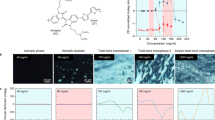
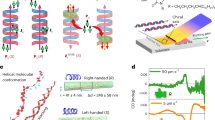
Abstract

Chemical doping has unlocked the touted potential of conjugated polymers by significantly boosting their conductivity and device performance. Yet, the relationship between doping and the polymers’ complex, multiscale morphology remains elusive. Herein, we report a surprising find that supramolecular chirality, which up to now had not been considered a parameter relevant to doping, significantly boosts the underpinning redox reaction in conjugated polymer thin films. The chiral helical structures arise during an evaporative assembly process upon meniscus-guided coating, when the originally racemic conjugated polymer chains aggregate first and assemble into chiral twist-bent nematic mesophases which “imprint” their solution-state structure into solid thin films. By manipulating the solution aggregate structures through only subtle variations in the solvent nature, we modulate the structures of the liquid crystal phases to access a broad spectrum of supramolecular chirality, from achiral, to weakly chiral, and to strongly chiral. The differential solubilities of the side-chains and backbones in various solvent environments—elucidated by molecular dynamics simulations—underpin transitions in solution assembly behaviors. Upon sequential doping, the strongly chiral film exhibits a markedly higher charge carrier concentration leading to the highest doping efficiency and electrical conductivity, followed by the weakly chiral and the achiral films. Such increased conductivity in chiral structures is observed across three sets of polymer systems. We further suggest that enhanced crystallinity from chiral assembly facilitates the doping process, while chirality-induced spin selectivity may accelerate oxidation over reduction, together resulting in increased doping efficiency in chiral structures.

Chiral emergence in multistep hierarchical assembly of achiral conjugated polymers

Article Open access 18 May 2022

Unravelling emergence of chirality in click-chemistry polymers down to the single-chain level

Article Open access 22 July 2025

Inverse chirality-induced spin selectivity effect in chiral assemblies of π-conjugated polymers

Article 15 March 2024

Introduction

Doping is a ubiquitous technique for enhancing the electrical properties of traditional semiconductor materials^1,2. Since the pioneering reports from decades ago^{3,4,5,6,7,8,9}, its extension to organic semiconductors has significantly boosted their conductivity by several orders of magnitude reaching as high as thousands of S/cm upon doping^10,11,12. This adaptation has been critical in improving the device performance of organic light-emitting diodes, transparent conductors, electrochromic devices, bioelectronics and beyond^{13,14,15,16,17,18}. Meanwhile, there has been tremendous progress in understanding the fundamental mechanisms of chemical doping in organic semiconductors^19,20,21,22. Nevertheless, knowledge of doping in organic systems still lags that of their inorganic counterparts with fundamental mechanisms still being unraveled²³.

For organic polymeric semiconductors, one of the critical challenges is to understand the complex interactions between chemical doping and morphologies such as polymer conformation, packing, and crystallinity²⁴. For instance, the presence of significant morphological disorder is usually responsible for charge trapping and low doping efficiency²⁴. Consider the extensively studied case of 2,3,5,6-tetra-fluoro-7,7,8,8-tetracyanoquinodimethane (F4TCNQ) doped poly(3-hexylthiophene) (P3HT), where only about 5% of the generated charge carrier pairs are found to dissociate and contribute to a free hole for electrical conduction²⁵. Therefore, it has been proposed that films with higher crystallinity yield significantly higher doping efficiency compared to those with amorphous ones, attributed to the better delocalization of charge carriers within crystallites and the suppression of trapped charges^26,27,28. On the other hand, there are proposals that low-crystallinity films can be doped more efficiently than their high-crystallinity counterparts as they can tolerate more dopants in loosely packed structures^29,30. Furthermore, the microstructures can be significantly modified by introducing dopants, and both beneficial and detrimental effects on morphological ordering and charge transport have been reported^22,31. We believe the key to resolving these conflicting results lies in unraveling the little known assembly pathways from solution to solid states and the resultant microstructures³², which have been rarely investigated in the context of chemical doping of conjugated polymers. Recently, some of us have discovered chiral assembly pathways of several achiral/racemic conjugated polymers^33,34,35, which provides the opportunity to explore how chirality influences chemical doping. Notably, chirality has been shown to play a crucial role in various chemical reactions, including the oxygen evolution reaction and organic electrosynthesis^36,37, by means of the chiral-induced spin selectivity (CISS) effect³⁸. It remains an open question how chirality re-writes rules for redox reactions that underpin chemical doping of electronic materials – a topic not explored thus far.

In this study, we significantly modulated the chiral liquid crystal (LC) mediated assembly pathways of a racemic conjugated polymer and identified the crucial role of chiral helical assemblies in dictating the extent of redox reactions during doping. By manipulating the solution aggregate structures into networks, rigid fibers, and semiflexible fibers, we obtained three distinct assembly pathways, mediated by an isotropic phase, a continuous twist-bend nematic (N_tb) mesophase, and a striped N_tb mesophase, respectively. These pathways further resulted in the formation of three types of films with distinct multiscale morphologies: amorphous films with randomly oriented polymer chains, semicrystalline films with uniaxially-oriented helical fibers characterized by a large pitch length, and semicrystalline films with zigzag-oriented helical fibers with a small helical pitch. Also, the films exhibited varying degrees of supramolecular chirality—from achiral to weakly chiral, and to strongly chiral—corresponding to the presence or absence of N_tb mesophases. Following sequential doping, the strongly chiral film demonstrated the highest doping level, with a charge carrier concentration more than two-fold higher than that of the other two films. We discuss potential mechanisms underpinning this observation based on morphological distinctions and the chirality-induced spin selectivity (CISS) effect: The highest crystallinity and closest packing in the strongly chiral film may facilitate doping by promoting charge delocalization and reducing charge trapping; in addition, the doping process may also be facilitated by supramolecular chirality through the CISS effect by enhancing the redox reaction asymmetry. Notably, across three sets of polymer systems—a dioxythiophene copolymer (PE₂-biOE2OE3), a diketopyrrolopyrrole-based polymer (DPP2T-TT), and two 1,4-(2-thienyl)−2,5-dialkoxyphenylene-based polymers (TPT-2T and TPT-T)—we observed increased conductivity in chiral structures. We present an in-depth analysis of the PE₂-biOE2OE3 results and provide a summary of the findings for DPP2T-TT and TPT polymers in the final section of this manuscript.

Results

Solution-state structure and assembly pathway

A model polymer, PE₂-biOE2OE3, a dioxythiophene copolymer comprised of 2, 2’-bis-(3,4-ethylenedioxy)thiophene (biEDOT) and 3,4-propylenedioxythiophene (ProDOT) substituted with branched oligo(ether) side chains³⁹, displays distinct assembly pathways from solution to solid state in three ether solvents: 1,4-dioxane, diglyme, and 1,3-dioxane, despite the solvents being close structural analogs (Fig. 1). This is evidenced by the emergence or absence of LC mesophases beyond a critical concentration, observed both under nonequilibrium droplet-drying processes and in equilibrium solution states with progressively increased concentrations^34,35,40. As shown in Fig. 2A and Movie S1, while observing a drying droplet of a 5 mg/mL 1,4-dioxane solution under a cross-polarized optical microscope (CPOM), we found the concentrated edge exhibits no birefringence, indicative of an isotropic phase-mediated polymer assembly. This is consistent with the equilibrium phases at high concentration (up to ~150 mg/mL) where the solution displays no birefringence under CPOM (Fig. 2B and S2). Furthermore, circular dichroism (CD) spectra confirm the achiral nature of the solution (Figure S2). To accurately capture the true CD signal, we used a four-scan method to eliminate linear anisotropic contributions, as previously reported⁴¹. We note that the sp³ carbon chiral centers on the side chains likely existing in a racemic form, not contributing to molecular chirality in isotropic solutions. In contrast, the droplet edge of a diglyme solution displays a continuous birefringence with a uniform texture (Fig. 2A and Movie S2). In the equilibrium solution state, we reproduced this uniform texture along with a singularity characterized by four surrounding schlieren brushes⁴², which resembles the texture of a nematic phase (Fig. 2B and S2)⁴². Additionally, CD spectra reveal the emergence of chirality in the mesophase, characterized by an anisotropic dissymmetry factor (g-factor) of 10^-3 in magnitude (Fig. 2C and S2; see definition of g-factor in “Methods section”). We define the mesophase as a continuous N_tb phase. In the case of the 1,3-dioxane solution, the drying meniscus exhibits stripe-like textures (Fig. 2A and Movie S3). This resembles the morphology of a striped N_tb phase that we previously identified in the solution of several conjugated polymers adopting helical chain conformation^33,35. The morphology is reproducible at solution concentrations of 90–150 mg/mL (Fig. 2B and S2), featuring twin domains that extinguish cross-polarized light at mirroring angles (Figure S3). Additionally, CD spectra uncovered the emergence of strong chirality in the mesophase, characterized by a g-factor ranging from 10^-2 to 10^-1 in magnitude reaching values as high as 0.141 (Fig. 2C and S2). These findings indicate that the assembly pathways of PE₂-biOE2OE3 are mediated by an isotropic phase in 1,4-dioxane, a continuous N_tb phase in diglyme, and a striped N_tb phase in 1,3-dioxane, respectively. These phase assignments are supported by in-depth structural characterizations combining molecular scale X-ray diffraction, meso-scale imaging and micron-scale microscopy (shown later).

**Fig. 1: Distinct solution-state assembly pathways of PE₂-biOE2OE3 and their impact on film chirality and conductivity.**

**Fig. 2: Solution-state assembly pathways of PE₂-biOE2OE3 in 1,4-dioxane, diglyme, and 1,3-dioxane.**

We next uncover that the three distinct assembly pathways arise from distinct solution-state aggregate structures. We first characterized these aggregate structures using both real-space imaging and reciprocal-space scattering techniques. As shown in Fig. 2D and S4, scanning electron microscopy (SEM) reveals three-dimensional network-like aggregates with a diameter of 251 ± 87 nm in 1,4-dioxane. In contrast, polymers in diglyme aggregate into rigid fibers with an average diameter of 133 ± 31 nm, while in 1,3-dioxane, we observe flexible fiber aggregates with an average diameter of 22 ± 15 nm. These findings suggest a trend in polymer backbone rigidity and degree of aggregation in the order of 1,4-dioxane <1,3-dioxane <diglyme. Support for this inference comes from small-angle X-ray scattering (Figure S5, Table S1), which informs an increasing polymer persistence length (l_p,p) from 4.4 ± 0.2 nm in 1,4-dioxane, to 7.0 ± 0.5 nm in 1,3-dioxane, and to 9.5 ± 0.4 nm in diglyme. Further evidence is provided by UV-vis absorption spectra, which show that the absorption coefficient, the degree of red-shift in absorption peaks, and the resilience to disaggregation by heating are highest in diglyme, followed by 1,3-dioxane, and lowest in 1,4-dioxane (Figures S6 and S7). Fluorescence spectra indicate that these distinct aggregate structures are possibly different polymorphs, as detailed in the supplementary information (SI section II). Overall, these results show that formation of semiflexible fibril aggregates in solution are conducive to chiral LCs during evaporative assembly. We have found that the emergence of chirality in the lyotropic mesophases of achiral or racemic polymers is a widespread phenomenon, observed in over twenty such systems, including several previously reported examples^33,34,35,43. This chiral emergence, occurring without the addition of chiral bias (such as chiral small molecules), suggests a mechanism distinct from the classic “sergeants-and-soldiers” effect^44,45,46. We hypothesize that the formation of helical structures is entropy-driven, where polymers adopt a helical conformation to reduce excluded volume and maximize solution entropy. This proposed mechanism aligns with the theoretical model by Kamien et al.⁴⁷, based on classic depletion interaction theory. We have also substantiated generality of chiral emergence across 20 polymer systems in a subsequent manuscript⁴⁸. In this work we choose to focus on the role of chirality in chemical doping specifically.

We further explored the molecular underpinnings behind the distinct helical assemblies, identifying side-chain aggregation as a key factor through molecular dynamics (MD) simulations. To investigate this, we used MD simulations to highlight specific trends of polymer behavior in different solvents. We first calculated the cumulative angle (∆θ_tot) between conjugated rings along the polymer backbone to evaluate helical propensities (Figs. 2E and 2F). Ideally, in the absence of helical preference, ∆θ_tot should be ~0°. Our simulations indicate that isolated chains (consisting of 12-mers) maintain a ∆θ_tot near 0° across all solvents, showing no inherent helicity. However, upon aggregation, ∆θ_tot significantly diverges, reaching 132.1–142.8° in 1,3-dioxane and 89.2-91.9° in diglyme, while remaining unchanged in 1,4-dioxane. These results align with the experimental observations of g-factors (Fig. 2C), confirming that PE₂-biOE2OE3 exhibits the highest extent of helicity in 1,3-dioxane, lower in diglyme, and negligible in 1,4-dioxane. It’s important to note that Δθ_tot is not indicative of rigidity or persistence length—e.g., both flexible coils and rigid rods can show Δθ_tot = 0. Instead, Δθ_tot reflects the consistency of helical twist along the polymer contour, correlating with helicity rather than with rigidity or aggregate size.

We then assessed the Flory–Huggins interaction parameter (χ) for the backbone, side chains, and the entire polymer in three solvents: 1,4-dioxane, diglyme, and 1,3-dioxane, which provides an established metric for evaluating solubility and aggregation tendencies (Fig. 2G). The calculated χ values for the polymer backbone in all three solvents remain below the critical χ threshold for phase separation, indicating good solubility. Among them, 1,4-dioxane displayed the lowest χ value, followed by diglyme, and the highest χ was found in 1,3-dioxane, though still within the miscible regime. A similar solvent dependence was observed for the side chains; however, in 1,3-dioxane, the χ value sharply increased to 2.2 well above the critical point, revealing a strong thermodynamic driving force for side-chain aggregation. This trend is also reflected in the χ values for the entire polymer, which follow the same order: 1,4-dioxane <diglyme <1,3-dioxane, with the polymer in 1,3-dioxane crossing the miscibility limit.

These results suggest that the enhanced helicity observed in 1,3-dioxane is primarily driven by side-chain aggregation, which overrides backbone planarity and induces a packing motif favoring side-chain interactions. Such a competition between side-chain ordering and backbone planarity in conjugated polymers has been previously reported, albeit not in the context of helical assemblies⁴⁹. In contrast, diglyme promotes more balanced interactions: the χ values for side chains and backbone are comparable, reducing competition and allowing backbone-driven packing into planar conformations. In 1,4-dioxane, the polymer is the most soluble across all solvents resulting in weak driving force for either side-chain aggregation or backbone stacking, which in turn contributes to disordered chain conformation and network structures. While these results do not explicitly validate the proposed model, they offer valuable molecular-level insights that align with experimental observations, reinforcing the model’s relevance in elucidating the mechanisms driving the observed chiral assembly.

Solid-state morphology and electrical conductivity

The solution-state structures and assembly pathways directly determine the morphology of thin films prepared by meniscus-guided coating from three solvents (Figs. 3 and 4). These films, coated in the evaporation regime⁵⁰, maintain a thickness of ~400 nm (Figure S10). This thickness approaches the optimal level previously identified for enhancing this polymer’s electrical conductivity³⁹. We first examined the micron- and meso-scale morphology using CPOM, SEM and atomic force microscopy (AFM) (Fig. 3). The film coated from 1,4-dioxane solution displays no birefringence under CPOM, and its AFM phase image shows an isotropic structure, indicating the preservation of the polymer’s disordered state from the isotropic solution into the film. CD spectra further confirm the film’s achiral nature (Fig. 3D and S11). The film from diglyme exhibits an aligned, birefringent morphology under CPOM, resembling the texture of the continuous N_tb phase in solution. SEM images show the film is comprised of twisted fibers with a diameter D_{fiber, WC} of 171 ± 28 nm and a large helical pitch l_{1/2p, WC} of 617 ± 117 nm, giving rise to g-factors ranging from 0 to 10^-4 (Fig. 3D and S11). The film from 1,3-dioxane solution displays a twinned morphology with an 8.9 ± 2.4 µm periodicity, which resembles the texture of the striped N_tb mesophase observed in solution. AFM phase image reveals the mesoscale helically twisted fibers with an average diameter D_{fiber, WC} of 47 ± 13 nm and a helical pitch l_{1/2p, WC} of 83 ± 14 nm, much smaller than in the diglyme case. Such highly twisted fibers give rise to high g-factors ranging from 10^-3 to 10^-2 (Figure S11). Henceforth, we have designated the films from 1,4-dioxane, diglyme, and 1,3-dioxane as achiral, weakly chiral, and strongly chiral, respectively, based on their g-factor and helical pitch across scales. It should be borne in mind that ‘achiral’ here refers to structural rather than chemical achirality in the film coated from 1,4-dioxane, as racemic side chains are attached to the polymers.

**Fig. 3: Multiscale characterization of film morphology.**

**Fig. 4: Schematic illustration of multiscale morphology of three printed films, with white arrows indicating film printing directions.**

We further analyzed the polymer packing at molecular scale using grazing-incidence X-ray diffraction (GIXD) (Fig. 3C and S12–S17)⁵¹. The chiral emergence correlates with a 45° tilted peak at q_r = 1.35 Å⁻¹ attributed to the helical backbone stacking (Figs. 3C and 4). This feature is the most pronounced in strongly chiral films, less so in weakly chiral films, and absent in achiral films (Fig. 3E). Such tilted peaks are also noted in other chiral material systems^52,53, and it has been suggested that the 45° tilt indicates a tightly packed helical structure^54,55. We indeed observed a decrease in backbone π-π packing distances (d_π-π) from 3.80 Å in achiral films to 3.75 Å in weakly chiral films, and further to 3.68 Å in strongly chiral films, implying a tighter backbone packing in helical structures (Fig. 3G and Table S3). Conversely, the lamellar stacking distance (d_lamellar) follows an opposite trend, increasing from 24.26 Å to 25.96 Å and then to 26.97 Å. This may result from the difference in side chain solubilities as suggested by χ interaction parameter shown in Fig. 2G. Poor side chain solubility in 1,3-dioxane promotes side chain aggregation and extended conformations, increasing lamellar spacing. In contrast, good solvents like 1,4-dioxane keep side chains solvated, enabling reorganization and tighter packing during film formation, resulting in smaller lamellar distances. Additionally, we observed an in-plane alkyl stacking peak at q_xy = 1.417 Å⁻¹ in the strongly chiral film, corresponding to adjacent side chain stacking distances of 4.43 Å. We attribute this to a pronounced side-chain aggregation tendency in 1,3-dioxane, which is corroborated by the solvation energy calculations shown in Fig. 2G. Furthermore, the strongly chiral film demonstrates the highest relative degree of crystallinity (rDoC) for both lamellar and (helical) π-π stacking, exceeding that of the weakly chiral film, while the achiral film displays the lowest rDoC values due to its amorphous structure, as shown in Fig. 3F. This suggests that chiral helical structures are thermodynamically favorable, driven by denser packing. MD simulations and X-ray reflectivity (XRR) experiments confirm this trend, where MD shows a decreasing free volume trend—37.1% in achiral, 36.1% in weakly chiral, and 35.4% in strongly chiral films—and XRR shows an increasing density trend—1.18 g/cm³ in achiral, 1.20 g/cm³ in weakly chiral, and 1.24 g/cm³ in strongly chiral films (Fig. 3H and S18, detailed in SI section IV).

To evaluate the effect of PE₂-biOE2OE3’s solution-state assembly pathway and solid-state morphology on its electronic properties, we measured the films’ electrical conductivity upon doping. After solution coating, PE₂-biOE2OE3 thin films were sequentially doped with an isopropyl alcohol solution of iron (III) tosylate (Fe(Tos)₃) or nitrosonium tetrafluoroborate (NOBF₄) placed on top of the films, allowing the dopant molecules to penetrate the film (Fig. 5A). We then obtained the electrical conductivity values using van der Pauw method (Fig. 5B). Upon doping with Fe(Tos)₃, the achiral film exhibits a conductivity of 41 ± 24 S/cm. In comparison, the weakly chiral film shows a 3.3 times higher conductivity at 136 ± 26 S/cm, while the strongly chiral film’s conductivity is 7.4 times greater than the achiral case, reaching 305 ± 42 S/cm. Films doped with NOBF₄ also exhibit a similar trend as shown in Figure S19. To explain the differences in the electrical conductivity across the three films, we quantified the extent of doping and charge carrier density using a combination of X-ray photoelectron spectroscopy (XPS) and optical absorption spectroscopy. As shown in Figure S20, the XPS S2p features from doped films were deconvoluted into two contributions: polymer sulfur peaks occur between ca.163.5 and 166.0 eV, and tosylate S = O peaks occur between 167.0 to 170.0 eV (Table S6)⁵⁶. The polymer sulfur peaks were further deconvoluted into neutral sulfur (S) and charged sulfur (S*) following previously reported procedures (detailed in SI section IV)⁵⁶. We then calculated the carrier ratio (c) of the S* peak area to the total S* + S peak area, which is assumed to be equal to the number of holes per thiophene unit⁵⁶. The carrier ratios are comparable in achiral and weakly chiral films, reaching 0.14 ± 0.02 and 0.12 ± 0.03, respectively. In contrast, the strongly chiral film demonstrates a roughly two-fold increase, achieving a ratio of 0.26 ± 0.03. The carrier concentration can be estimated from the carrier ratio, using a previously reported method described in SI Section IV. The drift mobility is then calculated by dividing the measured electrical conductivity by the estimated carrier concentration⁵⁶. As shown in Fig. 5C, the strongly chiral film shows the highest level of doping with the highest carrier concentration of (4.9 ± 0.6) × 10²⁰cm^-3. In contrast, the weakly chiral and achiral films show relatively lower carrier concentrations of (2.2 ± 0.6) × 10²⁰ and (2.5 ± 0.4) × 10²⁰cm^-3, respectively. In addition, compared to the polymer sulfur peaks before doping, the S2p peak shifts to lower binding energy with increased doping density (Figure S20)⁵⁷. The strongly chiral film shows the largest extent of shift, 0.41 eV compared to 0.26 eV in the other two films, further confirming its highest level of doping. Furthermore, the degree of oxidation can also be quantified by determining the abundance ratio of tosylate counterions (using the sulfoxide doublet between 167.0 to 170. eV) with respect to thiophene⁵⁸. As shown in Fig. 5E, this trend also aligns closely with the calculated carrier concentration and the shifts in the S2p peaks. Due to the surface-sensitive nature of XPS, which exclusively probes a limited volume close to the surface, we employ the optical absorbance of the charge carriers (i.e., polaron and bipolarons) to assess the representativeness of the results for the bulk material. As illustrated in Fig. 5D, the chiral film exhibits notably higher charge carrier absorbance; quantitative comparisons were performed by integrating the area under the curve. As shown in Fig. 5E, the relative carrier ratios obtained from S*/(S + S*) in XPS align well with those from charge carrier absorbance. In sum, all these four pieces of evidence support that the strongly chiral films exhibit the highest doping level. As for the nature of the charge carriers after doping, we believe that in all three cases, the charge carriers are predominantly di-cation fragments based on the absence of the characteristic PE₂ polaron absorption peak near 1000 nm and the presence of a broad absorbance extending deep into the near-infrared (NIR) region^39,59.

**Fig. 5: Characterization of doped films.**

We further analyzed the films’ morphological changes upon doping. As shown in Figure S21, AFM images suggest that the mesoscale morphologies closely resemble those before doping. The molecular scale packing, however, is significantly modified as revealed by GIXD and CD. First, the d_π-π reduces and the d_lamellar expands in all three films (Figure S22 and Table S4), which is commonly observed and suggests that the dopants are mostly located between the side chains²². Second, the variation in rDoC values across the three films is significantly distinct (Fig. 5F). In the strongly chiral film, the lamellar stacking rDoC increases significantly from 5.84 to 10.32, indicating a dopant-induced enhancement in lamellar order, aligning with earlier findings⁵⁶. In contrast, the change in the weakly chiral film is minor, moving from 4.20 to 5.52. The achiral film shows minimal change, with rDoC values shifting only slightly from 1.43 to 1.61, implying that the dopant preferentially resides in the amorphous regions of this low-crystallinity film²². The π-π stacking rDoC drops in both chiral films, indicating a disruption of ordering in the backbone stacking region due to enhanced side-chain ordering⁴⁹. Moreover, the characteristic 45° tilted peak in the amorphous ring region at q_r = 1.35 Å⁻¹ is significantly reduced in the strongly chiral film (Figure S23), leading to a substantial decrease in the rDoC of helical backbone stacking. In contrast, the helical backbone stacking rDoC in the weakly chiral film shows only a slight alteration, consistent with the largely unchanged tilted peak signature. This observation further aligns with the CD spectra after doping (Figure S23). The g-factors for weakly chiral films remain within the range of 0 to 10^-4, while for strongly chiral films, they decrease from 10⁻³-10⁻² before doping to predominantly 10^-4 after doping (Figure S23). Moreover, the in-plane alkyl stacking peak diminishes upon doping (Figure S22), implying dopants enter the lamellar region and disrupt the lateral packing between side chains. These inferred morphological changes upon doping are summarized in Fig. 5G. All these analyses indicate that a higher quantity of dopants has entered the strongly chiral film, resulting in more pronounced changes in the crystalline region of the films compared to the other two cases, which is consistent with the XPS elemental analysis shown in Fig. 5E.

Proposed mechanisms for enhanced doping by supramolecular chirality

What enables the strongly chiral film to incorporate substantially more dopants at the expense of pronounced structural changes? We first note that all three films exhibit similar ionization energies despite their structural differences: 4.64 eV in both the achiral and weakly chiral films, and 4.67 eV in the strongly chiral film (Figure S24). We now turn to possible morphological impact on doping efficiency. The strongly chiral film demonstrates the highest crystallinity in both backbone and side-chain stacking regions and has the highest density, factors that could typically hinder dopant penetration due to reduced ease of swelling^29,30. While it possesses slightly larger lamella spacing (by < 1 Å) and slightly larger volume of the side chain region where the dopants reside (Figures S25-S27), such small differences can hardly account for a nearly doubled doping level in this film compared to the achiral and weakly chiral cases. However, despite the potential for impeded dopant diffusion, previous works have shown or implied in a number of instances, that high crystallinity can facilitate chemical doping. For example, this phenomenon has been observed in chemical doping of graphite, polyacetylene, poly(phenylene sulfide), or poly(3-hexylthiophene)^{26,27,28,60,61}. It was proposed that the ordered structure of polymer chains in backbone crystalline domains can serve as an effective precursor for doped species^26,27. The high planarity of these chains also facilitates the delocalization of hole carriers, thereby improving doping efficiency. In this work, the close-packing nature and high crystallinity of the strongly chiral films may impose molecular-level constraints and reduce dihedral angle distribution. This could lead to fewer charge traps and lower activation energy⁶², enhancing charge delocalization and further improving doping efficiency. This suggests that the superior doping levels observed in strongly chiral films can in part be attributed to their higher degree of crystallinity and reduced structural disorder, alongside the reduced π-π stacking distance d_π-π, allowing for improved interchain charge delocalization (Fig. 6A). Nonetheless, the trend in doping levels also reflects other important factors beyond differences in crystallinity. This is evidenced by the achiral and weakly chiral films, which, despite having significant differences in their degree of crystallinity, show similar charge carrier concentrations. Further, while there is only moderate gain in crystallinity from weakly to strongly chiral films, the conductivity gain is substantial.

**Fig. 6: Hypothesis on the mechanism underpinning chirality-modulated chemical doping.**

Intriguingly, another potential contributing factor could be the impact of chirality on the redox reaction during doping. Indeed, recent studies have highlighted the presence of an unconventional spin-orbit coupling (SOC) in helical structures of chiral conjugated polymers^63,64, which underpins the spin-selective electron transport known as the CISS effect³⁸. CISS has proven effective in manipulating the electron spin, which is crucial in chemical bonding and reactive processes. For example, CISS has been shown to enhance the efficiency of oxygen evolution and reduction reactions^65,66,67, facilitate organic electrosynthesis and polymerization^37,68, and influence electron transfer kinetics in biological redox processes⁶⁹. An earlier study has indicated that the CISS effect causes an asymmetry in the oxidation and reduction rate constants during electron transfer processes through oligopeptides. This asymmetry, observed in both forward and backward electron transfers, is attributed to spin-selective electron transfer mechanisms within these chiral molecules⁷⁰. Thus, the supramolecular chirality in the strongly chiral PE₂-biOE2OE3 film along with the higher crystallinity could enhance the polymer oxidation rate relative to the reduction rate by enhancing redox reaction asymmetry during doping (Fig. 6A). To probe this hypothesis, we performed kinetic measurements of the Fe³⁺/Fe²⁺ redox couple via scanning electrochemical microscopy (SECM) on PE₂-biOE2OE3 films (Figures S30 and S31). The results reveal that the forward (oxidation) reaction is enhanced, while the reverse (reduction) reaction is reduced in the strongly chiral films (Figure S6B and Table S8). The findings reveal a significant enhancement in the oxidation reaction rates in strongly chiral films, where ${k}_{{ox}}^{\circ }$ = (9.49 ± 2.09) × 10^-6 m/s, which is more than twice the rates observed in weakly chiral films (${k}_{{ox}}^{\circ }$ = (4.36 ± 0.72) × 10^-6m/s) and achiral films (${k}_{{ox}}^{\circ }$ = (4.57 ± 1.11) × 10^-6m/s). Additionally, the reduction reaction rates increase by a factor of 33% when transitioning from ${k}_{{red}}^{\circ }\,$= (6.39 ± 0.48) × 10^-6 m/s in strongly chiral films to ${k}_{{red}}^{\circ }\,$= (8.48 ± 0.71) × 10^-6 m/s in achiral films. In comparison, only a 6% increase is observed when moving from ${k}_{{red}}^{\circ }\,$= (7.97 ± 0.27) × 10^-6 m/s in weakly chiral films to achiral films, as shown in Fig. 6B and Table S8. The extent of redox asymmetry measured by SECM is highly correlated with the extent of oxidation across the three films measured by XPS (Fig. 6C). It must be noted that, as the oxidation and reduction reactions were carried out in distinct reaction media (iron (II) and iron (III) tosylate solutions, respectively) (Figures S30 and S31), the absolute values of ${k}_{{ox}}^{\circ }$ and ${k}_{{red}}^{\circ }$ cannot be directly compared; only the oxidation-to-reduction rate comparisons are meaningful.

The possible manifestation of the CISS effect on the observed reaction asymmetry is supported by the exceptionally high SOC in the strongly chiral films inferred from the damping factors $\alpha$ measured by the ferromagnetic resonance (FMR) technique⁶³. As shown in Fig. 7, the strongly chiral film showed a larger damping factor $\alpha$ = 0.033 compared to that of weakly chiral ($\alpha$ = 0.010) and achiral ($\alpha$ = 0.022) films, reaching a value on par with that of a heavy metal such as platinum⁷¹. We further validated that the damping factor is measured in the saturation regime and thus intrinsic to the polymer material (Figure S32). This large damping factor suggests that the strongly chiral film possesses a surprisingly large chirality-induced SOC⁴² underpinning a possible CISS effect, corroborating the observed redox reaction asymmetry. The fact that the achiral film exhibits a moderately high $\alpha$ value of 0.022 can be attributed to the highly torsional chain conformation rather than chirality (Figure S28)⁶³. This trend in the magnitude of the damping factor $\alpha$ aligns with the oxidation trend, where weakly chiral films exhibit the lowest degree of oxidation, followed by an increase in achiral films, and a significant increase in strongly chiral films (Fig. 7E).

**Fig. 7: Mechanism of chirality-induced chemical doping and characterization of damping factors.**

To summarize the doping mechanism discussion above, we propose that the chiral structure increases doping efficiency through inherently higher crystallinity with a possible contribution from the CISS effect, which increases the apparent oxidation rate of the chiral film. An enhanced oxidation rate builds up a steeper dopant concentration gradient in the film, thereby driving faster dopant diffusion into the strongly chiral film to boost charge carrier concentration and doping efficiency, resulting in improved conductivity upon doping. We rule out the possibility that faster dopant diffusion may instead arise from a higher diffusion coefficient, as the relative degrees of crystallinity of both the side chain and backbone regions are the highest in the strongly chiral film, leading to the densest packing in the strongly chiral film (Figs. 3F and 3H). Such morphology characteristics can only reduce the dopant diffusion coefficient in the chiral film. Despite a lower diffusion coefficient, the more than two-fold higher oxidation rate “forces” the dopant into the strongly chiral film as to cause the most substantial morphological changes upon doping, evidenced by diminished in-plane alkyl stacking and marked changes in rDoC values after doping (Figs. 5F and 5G). Besides CISS and the crystallinity effect, variations in dopant distribution near the polymer backbone may contribute to the differences in apparent oxidation rates; however, the similar extent of changes observed in the stacking distances of both backbone and side chains upon doping across the three films suggest similar dopant distributions within the crystalline regions (Tables S3 and S4). It must be stressed that definitively proving the CISS effect requires studying the magnetic field dependence of the reaction rate asymmetries. Unfortunately, bulk doping is not compatible with such measurements given the non-directional character of the electron transfer processes. Indeed, the CISS effect is usually studied in model systems involving an oriented monolayer of chiral molecules with directional electron transfer, distinct from a practical chemical doping process shown in this work.

Generality of the role of chirality in chemical doping

To assess whether supramolecular chirality influences chemical doping in other polymer systems, we tested two additional sets of systems: DPP2T-TT and TPT-2T/TPT-T (Fig. 8). As shown in Fig. 8A-D, using chlorobenzene (CB) or anisole as solvents allowed control over supramolecular chirality in blade coated DPP2T-TT films, yielding chiral films from CB and achiral films from anisole. Films were subsequently doped with a 5:1 molar ratio of F₄TCNQ (2, 3, 5, 6-tetrafluoro-7, 7, 8, 8-tetracyanoquinodimethane) to BCF (tris(pentafluorophenyl)borane) mixture which forms Lewis-paired dopant complexes⁷². Doped chiral films showed a much higher conductivity (0.55 ± 0.05 S/cm) than achiral films (0.02 ± 0.01 S/cm). In the second system (Fig. 8E-H), TPT-2T exhibited chiral structure upon annealing due to its thermotropic liquid crystalline phases, whereas TPT-T is absent from chiral assembly upon annealing⁷³. After doped with iron (III) tosylate, chiral TPT-2T films reached a conductivity of 24.7 ± 4.0 S/cm, outperforming the achiral TPT-T films (3.3 ± 1.8 S/cm).

**Fig. 8: Supramolecular chirality enhances chemical doping in two additional sets of polymer systems (DPP2T-TT and TPT Derivatives).**

Further analysis of the TPT-2T/TPT-T system suggests that chirality, rather than high crystallinity, is the key factor enhancing doping efficiency. As shown in Figure S33, TPT-T achiral films exhibit higher crystallinity, evidenced by sharper GIXD peaks and lower paracrystalline disorder parameters (g), with values of 12.27% and 7.00% for lamellar and π-π stacking peaks, respectively, compared to the higher disorder in TPT-2T chiral films (24.46% and 17.65%, respectively). This higher crystallinity in TPT-T contradicts the expected trend if crystallinity were the dominant factor, as it would predict higher conductivity for TPT-T rather than TPT-2T. Furthermore, we found TPT-T exhibited a higher mobility than TPT-2T, which further reinforce this discrepancy. Despite its lower mobility and crystallinity, TPT-2T exhibits significantly higher conductivity, which can be attributed to the role of supramolecular chirality in enhancing doping efficiency. These findings highlight the potential of chirality in overcoming low charge-carrier mobility by facilitating effective oxidation and boosting conductivity.

Discussion

To conclude, independent of the actual extent of contribution of the CISS effect, our study points to the unprecedented observation that introducing supramolecular chirality via helical assemblies can serve as a surprisingly effective approach to significantly enhance doping efficiency and conductivity. This discovery points to previously unrecognized principles governing redox reactions. Given the pivotal role of chemical doping in a broad range of polymer materials, we anticipate that our finding will have broad impact across many technological areas spanning renewable energy and bioelectronics.

Methods

Materials

The dioxythiophene copolymer, comprised of 2, 2’-bis-(3,4-ethylenedioxy)thiophene (biEDOT) and 3,4-propylenedioxythiophene (ProDOT) substituted with branched oligo(ether) side chains (PE₂-biOE2OE3, Mn = 20.0 kg/mol, PDI = 1.7), was synthesized using direct hereto(arylation) polymerization (DHAP) as previously described (the synthetic protocol is given in the SI)³⁹. All starting materials used for DHAP were purchased from a commercial supplier and were used without further purification. The number average molecular weight was determined by gel permeation chromatography with a Tosoh EcoSEC (calibrated versus polystyrene) equipped and a refractive index detector and using stabilized chloroform at 40 °C as the eluent. The polymer solutions were prepared by dissolving the polymer (5 mg mL⁻¹) in 1,4-dioxane (anhydrous, 99.8%, Sigma-Aldrich), diglyme (anhydrous, 99.5%, Sigma-Aldrich), and 1,3-dioxane (97.0%, Sigma-Aldrich). Corning glass was used as substrates. The substrates were cleaned with toluene, acetone and isopropyl alcohol, and then dried under a stream of nitrogen to remove contaminants. The substrates were then plasma treated for 20 minutes before printing to improve the wetting of the solution. For SECM and differential pulse voltammetry measurements the substrates were ITO-coated glass substrates. Dopant iron(III) p-toluenesulfonate hexahydrate (technical grade, Sigma-Aldrich) was dissolved in isopropyl alcohol (IPA) (40 mM). The diketopyrrolopyrrole-based polymer DPP2T-TT (Mn = 60.7 kg/mol, PDI = 3.2) was synthesized following a previously published method⁷⁴. The polymer was dissolved in anhydrous chlorobenzene (99.8%, Sigma-Aldrich) and anisole (99.7%, Sigma-Aldrich) at a concentration of 5 mg/mL, and films were prepared using a meniscus-guided coating technique in the evaporation regime on glass substrates. The coating was performed at room temperature with a blade angle of 7° relative to the substrate, using coating speeds of 0.002 mm/s and 0.004 mm/s for CB and anisole solutions, yielding film thicknesses of 648 ± 42 nm and 705 ± 73 nm, respectively. The dopant, consisting of a 5:1 molar ratio of F₄TCNQ (2, 3, 5, 6-tetrafluoro-7, 7, 8, 8-tetracyanoquinodimethane) (97%, Sigma-Aldrich) to BCF (tris(pentafluorophenyl)borane) (95%, Sigma-Aldrich) mixture, was dissolved in acetonitrile ( > 99.9%, Sigma-Aldrich) at a concentration of 10 wt%⁷². Two additional polymers, TPT-2T (Mn = 15.7 kg/mol, PDI = 1.6) and TPT-T (Mn = 17.2 kg/mol, PDI = 1.6), were synthesized as previously reported⁷⁵ and dissolved in anhydrous chlorobenzene at 5 mg/mL. Films of these polymers were spin-coated at 500 rpm onto glass substrates, heated to 180 °C (above the melting temperature), and cooled to room temperature at a rate of 10 °C/min. The film thicknesses were 103 ± 8 and 110 ± 13 nm for TPT-2T and TPT-T before annealing, respectively. This annealing process induces the thermotropic liquid crystal phase of TPT-2T and promotes chiral emergence. The dopant solution was prepared with iron(III) p-toluenesulfonate hexahydrate (technical grade, Sigma-Aldrich) in isopropyl alcohol at a concentration of 40 mM.

Solution-state structures characterization

UV–visible (Agilent Cary 60 UV-Vis) and fluorescence (SLM-ISS fluorescence Spectrometer) spectroscopy was used to measure the absorption and emission of PE₂-biOE2OE3 solutions. The solution SAXS measurement was performed at beamline 12ID-E within the Advanced Photon Source at Argonne National Laboratory. Scattering profiles were acquired using an incident X-ray beam with an energy of 13.3 keV and a sample-to-detector distance of 3622.78 mm. The polymer scattering data were correction for background scattering, which was determined using solvent-only measurements. Subsequent data analysis was carried out using SAXSLee, a tool developed for MATLAB, and fitting was conducted employing models developed in our previous work⁷⁶ (Supplementary Information section II).

Freeze-drying experiments were conducted to image the structure of aggregates in solution using SEM (JEOL 7000 F). This process began with the rapid freezing of polymer solutions in a liquid ethane and propane mixture (63% propane and 37% ethane), immediately followed by storage in liquid nitrogen. The chosen mixture facilitated swift freezing owing to its high heat capacity, effectively minimizing polymer aggregation during the cooling phase. Subsequently, the frozen polymer solution was swiftly moved to a Linkam stage set at −100 °C under vacuum. There, the temperature was incrementally raised at a rate of 0.5 °C/min up to -80 °C, remaining decidedly below the solvents’ melting points (with melting points at 11.8 °C for 1,4-dioxane, -64 °C for diglyme, and -42 °C for 1,3-dioxane). The process concluded with 8–10 h of continuous observation using cross-polarized microscopy, ensuring complete solvent sublimation.

Solution characterization under CPOM (Nikon Eclipse Ci-POL) was conducted by encapsulating the polymer solutions between two microscope glass coverslips, which were then placed on a Si wafer for the CPOM measurements in reflection mode. High-concentration solutions were prepared using the drop and dry method, a process in which the concentration of the pristine solution was enhanced by evaporating a specified volume and subsequently redissolving the residue with 2 μL of the solution. This concentrated solution was then homogenized by shearing with the microscope cover glasses to further increase its concentration. The solution samples then underwent thermal annealing cycles to remove the shearing history and reach an equilibrium state before imaging under CPOM.

Film printing and doping

The PE₂-biOE2OE3 thin films were deposited onto substrates using a meniscus-guided blade coating technique, as detailed in our earlier work⁵³ In brief, an OTS-treated Si blade set at a 7° printing angle and a 100 µm gap was set from the blade to the substrate. The blade moved linearly across the stationary substrate, maintaining the ink solution within the specified gap. The PE₂-biOE2OE3 films were coated at a speed of 5.0 µm s⁻¹ at 25 °C for 1,4-dioxane and 1,3-dioxane solutions, and at 1.0 µm s⁻¹ at 55 °C for diglyme solutions. The elevated temperature for diglyme aimed to align its vapor pressure with that of the other solvents, while the reduced speed ensured a consistent film thickness of 400 nm across different solvent conditions. Printing began with a low solution concentration (5 mg/mL); as the solvent evaporated during coating, the local concentration increased, promoting the in-situ formation of chiral mesophases typically observed at higher equilibrium concentrations. To preserve these structures in the final film, coating was performed at low speeds (1–5 µm/s) within the evaporation regime, allowing near-equilibrium formation of chiral liquid crystalline phases.

When doping the film using Fe(Tos)₃, 40 μL of Fe(Tos)₃ solution was distributed across the film using a pipette. The film was then shielded with a petri dish for 2 minutes. Then around 100 μL of clean IPA was applied over the film to rinse away residual dopant solution, which was then carefully pipetted off. This washing step was repeated 5 times and the whole doping process was repeated 3 times for one film. Subsequently, the films are placed in a vacuum oven, set at room temperature under vacuum, for a duration of 10 minutes before conductivity measurement. The doping procedure is the same when using NOBF₄/IPA solution. TPT-T and TPT-2T were doped using same dopant solutions and procedures. DPP2T-TT was doped using the same procedure but with F₄TCNQ/BCF dopant solutions in acetonitrile. The dopant solution is composed of a 5:1 molar ratio of F₄TCNQ to BCF, dissolved in acetonitrile at a concentration of 10 wt%. This solution forms Lewis-paired dopant complexes that effectively dope the polymers, as previously reported⁷².

Printed film morphology and electrical property characterization

The birefringence of the PE₂-biOE2OE3 thin films was characterized using cross-polarized optical microscopy (Nikon Eclipse Ci-POL). The mesoscale morphology was characterized using tapping-mode atomic force microscopy (Asylum Research Cypher). UV–visible (Cary 60 UV-Vis and Varian Carry 5 G, Agilent) spectroscopy was used to measure the absorption of films before and after doping. GIWAXS measurements were performed at the 7.3.3 beamline of the Advanced Light Source at Lawrence Berkeley National Laboratory, using incident angles of 0.14° with an X-ray energy of 10 keV and a beam size of 30 μm × 50 μm. All samples were scanned 10 s in a helium chamber for measurement. XRR measurement was done using Bruker D8 Advance XRR system with an X-ray energy of 8.04 keV.

CD spectra were recorded using a JASCO 1500 spectrophotometer. To accurately capture the true CD signal, we used a four-scan method, as previously reported⁴¹, to eliminate artificial CD contributions from linear dichroism and linear birefringence (CD_LDLB), as well as residual static birefringence from the photoelastic modulator (PEM) (CD_α). Further details are provided in the Supplementary Information and Figure S28.

The CD g-factor quantifies the differential absorption of left- and right-circularly polarized light relative to the total absorption of unpolarized light⁷⁷. It normalizes circular dichroism (ellipticity) to eliminate dependencies on sample concentration, path length, or film thickness. Mathematically, it is given by:

$${g-{factor}}_{{abs}}=\frac{\triangle A}{A}=\frac{\theta }{32,980\,\times \,A}=\frac{2\left({A}_{L}\,-{A}_{R}\right)}{{A}_{L}\,+{A}_{R}}$$

(1)

where $\triangle A={A}_{L}-{A}_{R}$ is the difference in absorption between left- and right-circularly polarized light, $A=\frac{{A}_{L}\,+{{A}}_{R}}{2}$ is the absorption of unpolarized light, $\theta$ is the ellipticity in millidegrees,

and the constant 32,980 is used to convert ellipticity to absorbance units.

To quantify crystallinity, we extracted the relative degree of crystallinity (rDoC) from GIXD patterns. The angle χ is defined such that χ = 0° corresponds to a “face-on” π–π orientation and χ = 90° to an “edge-on” π–π orientation, as illustrated in Fig. 3C. The rDoC values for the lamellar, π–π, and helical π–π stacking peaks were calculated by integrating the corresponding peak intensities over χ according to the expression⁷⁸:

$${{rDoC}}\propto {\int }_{0}^{\frac{\pi }{2}}sin (\chi ){{{\rm{I}}}}({{{\rm{\chi }}}}){{{\rm{d}}}}\chi$$

(2)

The film sheet resistivity (${R}_{s}$) was measured using van der Pauw method in Accent HL5500PC Measurement system. The ${R}_{s}$ was then converted to conductivity $\sigma$ using equation:

$$\sigma=\frac{1}{{R}_{s}\times t}$$

(3)

where $t$ is the film thickness. To estimate the charge carrier concentration, XPS spectra were measured using a Kratos Axis Supra photoelectron spectrometer and a phi-Versa probe hemispherical analyzer system. For photoelectron excitation, a monochromatized X-ray source (Al Kα, 1486.6 eV) was used. The base pressure of the analysis chamber was maintained below 10^–8 Torr) The energy reference was calibrated using clean Au (111).

Ionization energies and charge density were determined under argon atmosphere by differential pulse voltammetry and chronocoulometry in degassed 0.5 M tetraethylammonium tosylate (TEAtos) in propylene carbonate. The potential was controlled with an EG&G PAR 273 A potentiostat/galvanostat under CorrWare control. The three-electrode measurements incorporated a Ag/Ag⁺ pseudoreference electrode (calibrated vs ferrocene/ferrocenium, E_1/2 = 90 mV) and a platinum flag counter electrode.

FMR and SECM measurements

For ferromagnetic resonance (FMR) measurement, the NiFe (6 nm) thin films were deposited on three assembled polymers by e-beam evaporation. The sample was attached to the coplanar wave guide with the Kapton tape. The FMR spectra were obtained using a commercial NanOsc Phase FMR spectrometer connected with the wave guide in the Physical Property Measurement System (PPMS, Quantum Design). The FMR spectra were fitted with the derivative of the asymmetric Lorentzian equation¹⁹,

$$S= {K}_{1}\cdot \frac{\left(\frac{\triangle H}{2}\right)\left(H-{H}_{{res}}\right)}{{\left({\left(H-{H}_{{res}}\right)}^{2}+{\left(\frac{\triangle H}{2}\right)}^{2}\right)}^{2}}+{K}_{2}\cdot \frac{{\left(\frac{\triangle H}{2}\right)}^{2}-{\left(H-{H}_{{res}}\right)}^{2}}{{\left({\left(H-{H}_{{res}}\right)}^{2}+{\left(\frac{\triangle H}{2}\right)}^{2}\right)}^{2}} \\ +{Offset}+H\cdot {Slope}$$

(4)

where $S,\,{K}_{1},\,{K}_{2},{H},\,{H}_{{res}},$ and $\triangle H$ are absorption derivative, fitting constant for the first term, constant for the second term, applied magnetic field, resonant field, and FMR linewidth (FWHM).

In SECM, an ultramicroelectrode is positioned over a substrate, and the current response at the tip and substrate depends on the potential applied to the tip and substrate. Following Tafel fitting gives the standard rate constant (k^o) and charge transfer coefficient (${\alpha }_{{SECM}}$) of the redox reaction. A similar work can be found elsewhere⁷⁹.

MD simulations

All-atom (AA) molecular dynamics (MD) simulations were performed using the LAMMPS package⁸⁰, and the Optimized Potentials for Liquid Simulations−All Atom (OPLS-AA) force field⁸¹. Atom types and parameters were defined using the LigParGen web server⁸². Long-range electrostatic interactions of charged particles were computed using the particle-particle-particle-mesh (PPPM) algorithm with a root-mean-accuracy of 10^-5⁸³. The Verlet integrator with a time step of 1 fs was used, and the Nose−Hoover thermostat/barostat was employed for temperature/pressure control. All related simulations were performed using NPT (constant number of molecules, pressure, and temperature) at pressure of 1 atm. A cutoff of 12 Å was applied for the summation of van der Waals interactions.

MD simulations were used to investigate the conformational dynamics of PE₂-biOE2OE3 chains, with an emphasis on the behavior of single chains and their collective organization in various solvents. These simulations were conducted at 300 K within the NPT ensemble, featuring 12-mer polymer chains within a solvent-filled simulation box measuring 18.0 × 10.5 × 10.5 nm³. Each system underwent an equilibration phase of 20 ns, succeeded by a production phase lasting 30 ns for the purposes of data collection and averaging. For structures involving multiple chains, an additional metadynamics simulation was implemented to expedite the packing process through the application of a biased potential.

Data availability

The authors declare that all data supporting the findings of this study are available within the Article and Supplementary Information files. All data are available from the corresponding author upon request.

References

Sze, S. M. et al. Semiconductor Devices, Physics And Technology. 2nd ed. (Wiley, 2002).
Sze, S. M. & Ng, K. K. Physics of Semiconductor Devices. 3rd ed. Wiley-Interscience: Hoboken, NJ, (2007).
Shirakawa, H., Louis, E. J., MacDiarmid, A. G., Chiang, C. K. & Heeger, A. J. Synthesis of electrically conducting organic polymers: halogen derivatives of polyacetylene, (CH) x. J. Chem. Soc. Chem. Commun. 578–580 (1977).
Chiang, C. K. et al. Electrical conductivity in doped polyacetylene. Phys. Rev. Lett. 39, 1098 (1977).
Article ADS CAS Google Scholar
Chiang, C. et al. Synthesis of highly conducting films of derivatives of polyacetylene,(CH) x. J. Am. Chem. Soc. 100, 1013–1015 (1978).
Article ADS CAS Google Scholar
Yamamoto, Y. et al. Electrical properties of phthalocyanine-halogen complexes. J. Phys. Soc. Jpn. 12, 47 (1979).
Google Scholar
Reynolds, J. R., Chien, J. C., Karasz, F. E., Lillya, C. P. & Curran, D. Iron (III) perchlorate doping of polyacetylene. J. Chem. Soc. Chem. Commun. 1358–1359 (1982).
Bredas, J. L. & Street, G. B. Polarons, bipolarons, and solitons in conducting polymers. Acc. Chem. Res. 18, 309–315 (1985).
Article CAS Google Scholar
Skotheim, T. A. Handbook of Conducting Polymers. (CRC Press,1997).
Kim, N. et al. Highly conductive PEDOT: PSS nanofibrils induced by solution‐processed crystallization. Adv. Mater. 26, 2268–2272 (2014).
Article CAS PubMed Google Scholar
Dash, A. et al. Spontaneous modulation doping in semi‐crystalline conjugated polymers leads to high conductivity at low doping concentration. Adv. Mater. 36, 2311303 (2023).
Basescu, N. et al. High electrical conductivity in doped polyacetylene. Nature 327, 403–405 (1987).
Article ADS CAS Google Scholar
Yamamori, A., Adachi, C., Koyama, T. & Taniguchi, Y. Doped organic light emitting diodes having a 650-nm-thick hole transport layer. Appl.Phys. Lett.72, 2147–2149 (1998).
Blochwitz, J., Pfeiffer, M., Fritz, T. & Leo, K. Low voltage organic light emitting diodes featuring doped phthalocyanine as hole transport material. Appl. Phys. Lett. 73, 729–731 (1998).
Lüssem, B. et al. Doped organic transistors. Chem. Rev. 22, 13714–13751 (1998).
Walzer, K., Maennig, B., Pfeiffer, M. & Leo, K. Highly efficient organic devices based on electrically doped transport layers. Chem. Rev. 107, 1233-71 (2007).
Ponder, J. F. Jr, Osterholm, A. M. & Reynolds, J. R. Conjugated polyelectrolytes as water processable precursors to aqueous compatible redox active polymers for diverse applications: electrochromism, charge storage, and biocompatible organic electronics. Chem. Mater. 29, 4385–4392 (2017).
Article CAS Google Scholar
Pittelli, S. L., Shen, D. E., österholm, A. M. & Reynolds, J. R. Chemical oxidation of polymer electrodes for redox active devices: stabilization through interfacial interactions. ACS Appl. Mater. Interfaces 10, 970–978 (2018).
Article CAS PubMed Google Scholar
Tietze, M. L. et al. Elementary steps in electrical doping of organic semiconductors. Nat. Commun. 9, 1182 (2018).
Salzmann, I., Heimel, G., Oehzelt, M., Winkler, S. & Koch, N. Molecular electrical doping of organic semiconductors: fundamental mechanisms and emerging dopant design rules. Acc. Chem. Res. 49, 370-8 (2016).
Mityashin, A. et al. Unraveling the mechanism of molecular doping in organic semiconductors. Adv. Mater. 03, 24 (2012).
Google Scholar
Scaccabarozzi, A. D. et al. Doping approaches for organic semiconductors. Chem. Rev. 122, 4420-4492 (2021).
Xu, Y. et al. Doping: a key enabler for organic transistors. Adv. Mater. 46, e1801830 (2018).
Jacobs, I. E. & Moule, A. J. Controlling molecular doping in organic semiconductors. Adv. Mater. (2017).
Pingel, P. & Neher, D. Comprehensive picture of p-type doping of P3HT with the molecular acceptor F${}_{4}$TCNQ. Phys. Rev. B. 87, 115209 (2013).
Gao, J., Niles, E. T. & Grey, J. K. Aggregates promote efficient charge transfer doping of poly(3-hexylthiophene). J. Phys. Chem. Lett. 4, 2953–2957 (2013).
Scholes, D. T. et al. Designing conjugated polymers for molecular doping: the roles of crystallinity, swelling, and conductivity in sequentially-doped selenophene-based copolymers. Chem. Mater. 31, 73–82 (2019).
Clarke, T. C. et al. Poly(P‐phenylene sulfide) hexafluoroarsenate: a novel conducting polymer. J. Polym. Sci. Polym. Physics 20, 117–130 (1982).
Wang, S. et al. Effect of backbone regiochemistry on conductivity, charge density, and polaron structure of n-doped donor–acceptor polymers. Chem. Mater. 31, 3395–3406 (2019).
Duan, J. et al. Enhancing the performance of N‐Type thermoelectric devices via tuning the crystallinity of small molecule semiconductors. Adv. Sci. 10, 2204872 (2023).
Lu, Y., Wang, J.-Y. & Pei, J. Achieving efficient n-doping of conjugated polymers by molecular dopants. Acc. Chem. Res. 54, 2871–2883 (2021).
Khasbaatar, A. et al. From solution to thin film: molecular assembly of π-conjugated systems and impact on (opto)electronic properties. Che.Rev. 123, 8395-8487 (2023).
Park, K. S. et al. Subtle molecular changes largely modulate chiral helical assemblies of achiral conjugated polymers by tuning solution-state aggregation. ACS Cent. Sci. 9, 2096–2107 (2023).
Article CAS PubMed PubMed Central Google Scholar
Xu, Z. et al. Not all aggregates are made the same: distinct structures of solution aggregates drastically modulate assembly pathways, morphology, and electronic properties of conjugated polymers. Adv. Mater. 34, e2203055 (2022).
Article PubMed Google Scholar
Park, K. S. et al. Chiral emergence in multistep hierarchical assembly of achiral conjugated polymers. Nat. Commun. 13, 2738 (2022).
Article ADS CAS PubMed PubMed Central Google Scholar
Vadakkayil, A. et al. Chiral electrocatalysts eclipse water splitting metrics through spin control. Nat. Commun. 14, 1067 (2023).
Article ADS CAS PubMed PubMed Central Google Scholar
Tassinari, F. et al. Spin-dependent enantioselective electropolymerization. J. Phys. Chem. C. 124, 20974–20980 (2020).
Article CAS Google Scholar
Bloom, B. P., Paltiel, Y., Naaman, R. & Waldeck, D. H. Chiral induced spin selectivity. Chem. Rev. 124,1950–1991 (2024).
Jones, A. L. et al. Branched oligo(ether) side chains: a path to enhanced processability and elevated conductivity for polymeric semiconductors. Adv. Funct. Mater. 31, 2102688 (2021).
Article CAS Google Scholar
Davidson, Z. S. et al. Deposition and drying dynamics of liquid crystal droplets. Nat. Commun. 8, 15642 (2017).
Article ADS CAS PubMed PubMed Central Google Scholar
Yao, Y. et al. Extracting pure circular dichroism from hierarchically structured CdS magic cluster films. ACS Nano 16, 20457–20469 (2022).
Article CAS PubMed Google Scholar
Goodby, J. W. et al. Introduction to Defect Textures in Liquid Crystals. In Handbook of Visual Display Technology, Springer, (2012).
Qu, G. et al. Lyotropic liquid crystalline mesophase governs interfacial molecular orientation of conjugated polymer thin films. Chem. Mater. 32, 6043–6054 (2020).
Article CAS Google Scholar
Green, M. M. et al. Macromolecular stereochemistry: the out-of-proportion influence of optically active comonomers on the conformational characteristics of polyisocyanates. The sergeants and soldiers experiment. J. Am. Chem. Soc. 111, 6452–6454 (1989).
Article ADS Google Scholar
Langeveld-Voss, B., Waterval, R., Janssen, R. & Meijer, E. Principles of“majority rules“and“sergeants and soldiers“applied to the aggregation of optically active polythiophenes: evidence for a multichain phenomenon. Macromolecules 32, 227–230 (1999).
Article ADS CAS Google Scholar
Smulders, M. M., Schenning, A. P. & Meijer, E. Insight into the mechanisms of cooperative self-assembly: The “sergeants-and-soldiers” principle of chiral and achiral C3-symmetrical discotic triamides. J. Am. Chem. Soc. 130, 606–611 (2008).
Article ADS CAS PubMed Google Scholar
Snir, Y. & Kamien, R. D. Entropically driven helix formation. Science 307, 1067 (2005).
Article CAS PubMed Google Scholar
Xu, Z. et al. Ubiquitous chiral symmetry breaking of conjugated polymers via liquid-liquid phase separation. ChemRxiv. https://doi.org/10.26434/chemrxiv-2025-l8kj7 (2025).
Carpenter, J. H. et al. Competition between exceptionally long‐range alkyl sidechain ordering and backbone ordering in semiconducting polymers and its impact on electronic and optoelectronic properties. Adv. Funct. Mater. 29, 1806977 (2019).
Article Google Scholar
Le Berre, M., Chen, Y. & Baigl, D. From convective assembly to Landau− Levich deposition of multilayered phospholipid films of controlled thickness. Langmuir 25, 2554–2557 (2009).
Article PubMed Google Scholar
Hexemer, A. et al. In A SAXS/WAXS/GISAXS beamline with multilayer monochromator, J. Phys: Conf. Ser. 247, 012007(2007).
Kim, H. et al. Multistep hierarchical self-assembly of chiral nanopore arrays. Proc. Natl Acad. Sci. USA 111, 14342–14347 (2014).
Article ADS CAS PubMed PubMed Central Google Scholar
Park, K. S. et al. Tuning conformation, assembly, and charge transport properties of conjugated polymers by printing flow. Sci. Adv. 5, eaaw7757 (2019).
Olsen, K. & Bohr, J. The generic geometry of helices and their close-packed structures. Theor. Chem. Acc. 125, 207–215 (2010).
Article CAS Google Scholar
Pierański, P. In search of ideal knots. Comput.Methods Sci. Technol. 4, 9–23 (1998).
Article MathSciNet Google Scholar
Kurdi, A. L. et al. Iron(III) dopant counterions affect the charge-transport properties of poly(thiophene) and poly(dialkoxythiophene) derivatives. ACS Appl Mater. Interfaces 14, 29039–29051 (2022).
Article PubMed Google Scholar
Shallcross, R. C. et al. Quantifying the extent of contact doping at the interface between high work function electrical contacts and poly (3-hexylthiophene)(P3HT). J. Phys. Chem. Lett. 6, 1303–1309 (2015).
Article CAS PubMed Google Scholar
Bubnova, O. et al. Optimization of the thermoelectric figure of merit in the conducting polymer poly (3, 4-ethylenedioxythiophene). Nat. Mater. 10, 429–433 (2011).
Article ADS CAS PubMed Google Scholar
Ponder, J. F. Jr, österholm, A. M. & Reynolds, J. R. Designing a soluble PEDOT analogue without surfactants or dispersants. Macromolecules 49, 2106–2111 (2016).
Article ADS CAS Google Scholar
Thomas, E. M. et al. X‐ray scattering reveals ion‐induced microstructural changes during electrochemical gating of poly(3‐Hexylthiophene). Adv. Funct. Mater. 28, 1803687 (2018).
McFarland, M. et al. The impact of aggregation on the p-doping kinetics of poly(3-hexylthiophene). J. Mater. Chem. C 5, 5764–5771 (2017).
Noriega, R. et al. A general relationship between disorder, aggregation and charge transport in conjugated polymers. Nat. Mater. 12, 1038–1044 (2013).
Article ADS CAS PubMed Google Scholar
Vetter, E. et al. Tuning of spin-orbit coupling in metal-free conjugated polymers by structural conformation. Phys. Rev. Mater. 4, 085603 (2020).
Article CAS Google Scholar
Sun, R. et al. Inverse chirality-induced spin selectivity effect in chiral assemblies of π-conjugated polymers. Nat.Mater. 23, 782–789 (2024).
Mtangi, W., Kiran, V., Fontanesi, C. & Naaman, R. Role of the electron spin polarization in water splitting. J. Phys. Chem. Lett. 6, 4916–4922 (2015).
Article CAS PubMed PubMed Central Google Scholar
Tassinari, F. et al. Enhanced hydrogen production with chiral conductive polymer-based electrodes. J. Phys. Chem. C. 121, 15777–15783 (2017).
Article CAS Google Scholar
Sang, Y. et al. Chirality enhances oxygen reduction. Proc. Natl Acad. Sci. 119, e2202650119 (2022).
Article CAS PubMed PubMed Central Google Scholar
Naaman, R. et al. The Electron Spin As A Chiral Reagent. Angewandte Chemie. International Edition (2020).
Wei, J. et al. Examining the effects of homochirality for electron transfer in protein assemblies. J. Phys. Chem. B 127, 6462–6469 (2023).
Article CAS PubMed PubMed Central Google Scholar
Tassinari, F. et al. Chirality dependent charge transfer rate in oligopeptides. Adv. Mater. 30, 1706423 (2018).
Article Google Scholar
Ramaswamy, R. et al. Extrinsic spin Hall effect in Cu 1− x Pt x. Phys. Rev. Appl. 8, 024034 (2017).
Article ADS Google Scholar
Zapata-Arteaga, O. et al. A universal, highly stable dopant system for organic semiconductors based on lewis-paired dopant complexes. ACS Energy Lett. 9, 3567–3577 (2024).
Article CAS PubMed PubMed Central Google Scholar
Makala, M. et al. Non-Covalent Interactions and Helical Packing in Thiophene-Phenylene Copolymers: Tuning Solid-State Ordering and Charge Transport for Organic Field-Effect Transistors. Chem. Mater. 37, 4145–4157 (2025).
Qu, G. et al. Understanding interfacial alignment in solution coated conjugated polymer thin films. ACS Appl. Mater. interfaces 9, 27863–27874 (2017).
Article CAS PubMed Google Scholar
Makala, M. et al. Non-covalent interactions and helical packing in thiophene-phenylene copolymers: tuning solid-state ordering and charge transport for organic field-effect transistors. Chem. Mater. 37, 4145–4157 (2025).
Article CAS PubMed PubMed Central Google Scholar
Kwok, J. J. et al. Understanding solution state conformation and aggregate structure of conjugated polymers via small angle x-ray scattering. Macromolecules 55, 4353–4366 (2022).
Article ADS CAS Google Scholar
Fernando, P. S., Chen, Y. C., Baek, J. M. & Diao, Y. Chiral Assemblies of pi-conjugated molecules: fundamentals, processing strategies, and applications in (opto)electronics. Annu. Rev. Chem. Biomol. Eng. 16, 59–91(2025).
Zhang, F. et al. Critical role of surface energy in guiding crystallization of solution-coated conjugated polymer thin films. Langmuir 34, 1109–1122 (2018).
Article CAS PubMed Google Scholar
Gaddam, R. et al. An SECM‐based spot analysis for redoxmer‐electrode kinetics: identifying redox asymmetries on model graphitic carbon interfaces. Chem.– Asian J. 18, e202201120 (2023).
Article CAS PubMed Google Scholar
Thompson, A. P. et al. LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Computer Phys. Commun. 271, 108171 (2022).
Article CAS Google Scholar
Jorgensen, W. L., Maxwell, D. S. & Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 118, 11225–11236 (1996).
Article ADS CAS Google Scholar
Dodda, L. S., Cabeza de Vaca, I., Tirado-Rives, J. & Jorgensen, W. L. LigParGen web server: an automatic OPLS-AA parameter generator for organic ligands. Nucleic acids Res. 45, W331–W336 (2017).
Article CAS PubMed PubMed Central Google Scholar
Hockney, R. W., Eastwood, J. W., Computer Simulation Using Particles. (CRC Press, 2021).

Download references

Acknowledgements

Z.X. and Y.D. acknowledge primary ONR support under Grant No. N00014-22-1-2202. S.S., V.C. and J.-L.B. acknowledge funding from ONR under award number N00014-22-1-2178. Y.N., R.S., D.S., S.J. and Y.D. acknowledge financial support from the Air Force Office of Scientific Research, Multidisciplinary University Research Initiatives (MURI) program under award number FA9550-23-1-0311. J.M.R., A.M.Ö., A.L.J. and J.R.R. acknowledge ONR support under grant number N00014-22-1-2185 and N00014-20-1-2129. J.V.W. acknowledge supported by the Air Force Office of Scientific Research under AFOSR Award No. FA9550-23-1-0368. This research used resources of Beamline 7.3.3 of the Advanced Light Source supported by the Director of the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. This research used resources of the Beamline 12-ID-B of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility, operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. This research also used facilities of the Materials Research Laboratory Central Research Facilities, University of Illinois.

Author information

These authors contributed equally: Zhuang Xu, Shamil Saiev, Peisen Qian, Yoji Nabei.

Authors and Affiliations

Department of Chemical and Biomolecular Engineering, Department of Chemistry, Beckman Institute for Advanced Science and Technology, University of Illinois Urbana−Champaign, 600 S. Mathews Avenue, Urbana, IL, USA
Zhuang Xu, Peisen Qian, Ziming Wang, Changhyun Hwang, Siqing Wang, Sanghyun Jeon, Kavinraaj Ella Elangovan, Josh Vura-Weis, Joaquín Rodríguez-López & Ying Diao
Department of Chemistry and Biochemistry, The University of Arizona, Tucson, AZ, USA
Shamil Saiev, Veaceslav Coropceanu & Jean-Luc Brédas
Department of Physics, North Carolina State University, Raleigh, NC, USA
Yoji Nabei, Rui Sun & Dali Sun
School of Chemistry and Biochemistry, School of Materials Science and Engineering, Center for Organic Photonics and Electronics, Georgia Tech Polymer Network, Georgia Institute of Technology, Atlanta, GA, USA
Joshua M. Rinehart, Anna M. Österholm, Austin L. Jones & John R. Reynolds
Department of Advanced Materials Engineering, Kyonggi University, Suwon, Republic of Korea
Jong-Hoon Lee
Department of Physics, Chonnam National University, Buk-gu, Gwangju, Republic of Korea
Dongguen Shin

Authors

Zhuang Xu
View author publications
Search author on:PubMed Google Scholar
Shamil Saiev
View author publications
Search author on:PubMed Google Scholar
Peisen Qian
View author publications
Search author on:PubMed Google Scholar
Yoji Nabei
View author publications
Search author on:PubMed Google Scholar
Ziming Wang
View author publications
Search author on:PubMed Google Scholar
Joshua M. Rinehart
View author publications
Search author on:PubMed Google Scholar
Anna M. Österholm
View author publications
Search author on:PubMed Google Scholar
Austin L. Jones
View author publications
Search author on:PubMed Google Scholar
Jong-Hoon Lee
View author publications
Search author on:PubMed Google Scholar
Changhyun Hwang
View author publications
Search author on:PubMed Google Scholar
Siqing Wang
View author publications
Search author on:PubMed Google Scholar
Rui Sun
View author publications
Search author on:PubMed Google Scholar
Dongguen Shin
View author publications
Search author on:PubMed Google Scholar
Sanghyun Jeon
View author publications
Search author on:PubMed Google Scholar
Kavinraaj Ella Elangovan
View author publications
Search author on:PubMed Google Scholar
Josh Vura-Weis
View author publications
Search author on:PubMed Google Scholar
Veaceslav Coropceanu
View author publications
Search author on:PubMed Google Scholar
Joaquín Rodríguez-López
View author publications
Search author on:PubMed Google Scholar
John R. Reynolds
View author publications
Search author on:PubMed Google Scholar
Dali Sun
View author publications
Search author on:PubMed Google Scholar
Jean-Luc Brédas
View author publications
Search author on:PubMed Google Scholar
Ying Diao
View author publications
Search author on:PubMed Google Scholar

Contributions

Y.D. conceived the experiments and supervised this research. Z.X. and Z.W. were responsible for the solution-state structures, film morphology characterizations and chemical doping studies under the guidance of Y.D.. S.S. and V.C. were responsible for the molecular dynamics simulations and their interpretation under the guidance of J.-L.B.. Y.N. and R.S. conducted the ferromagnetic resonance measurements under the guidance of D.Su.. P.Q. was responsible for the scanning electrochemical microscopy measurements under the guidance of J.R.-L. and J. V.-W.. A.M.Ö. conducted differential pulse voltammetry measurements and A.L.J. synthesized the polymer under the guidance of J.R.R.. J.M.R., J.-H.L., C.H., S.W., K.E.E. assisted with the electrical conductivity measurement under the guidance of Y.D. and J.R.R.. J.-H.L., D.Sh. and S.J. contributed to the X-ray photoelectron spectroscopy measurement and spectra fitting. Z.X. S.S. Y.N. and Y.D. wrote the first draft of paper. All authors contributed to editing the paper.

Corresponding authors

Correspondence to Joaquín Rodríguez-López, John R. Reynolds, Dali Sun, Jean-Luc Brédas or Ying Diao.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Description of Additional Supplementary Files

Supplementary Movie 1

Supplementary Movie 2

Supplementary Movie 3

Transparent Peer Review file

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Xu, Z., Saiev, S., Qian, P. et al. Supramolecular chirality largely modulates chemical doping of conjugated polymers. Nat Commun 16, 8381 (2025). https://doi.org/10.1038/s41467-025-62915-3

Download citation

Received: 06 November 2024
Accepted: 04 August 2025
Published: 25 September 2025
DOI: https://doi.org/10.1038/s41467-025-62915-3