Introduction

Deep neural networks (DNNs) have driven remarkable advances in various artificial intelligence (AI) applications1, yet their ever-growing computational demands strain conventional electronic hardware2,3. To sustain performance scaling, new hardware paradigms are needed to overcome interconnect, power, and parallelism bottlenecks. Optics offers a promising route to overcome these constraints by leveraging its intrinsic parallelism for signal processing4,5,6,7,8.

Specifically, summing outputs from multiple parallel-processing units (fan-in) is a core operation in computing architectures9, traditionally requiring multiple buffering stages in electronics to address Resistor-Capacitor (RC) and Inductor-Capacitor (LC) delays10,11. By contrast, optical systems can merge multiple beams in free space (using lenses12, holographic elements13, or intensifiers14) or on chip (using multimode interferometers15 or directional couplers16) without incurring the same interconnect overheads. However, for single-mode photonic integrated circuits, reciprocity imposes fundamental insertion losses during beam combining: merging multiple inputs into one single-mode waveguide typically causes partial back-reflection or scattering17, limiting the scalability of photonic computing systems. In particular, convolution operations in DNNs place a heavy load on such fan-in processes18,19,20,21,22,23,24, as they involve repeated additions of partial products. This makes convolution especially reliant on efficient fan-in, underscoring the importance of a low-loss photonic approach.

Here, we propose a photonic convolution accelerator featuring a lossless mode-division fan-in architecture that addresses the fundamental limitations of single-mode photonic computing. By exploiting the orthogonality of distinct waveguide modes, multiple signals are merged without incurring the insertion losses characteristic of conventional single-mode fan-in (SFI). Through inverse design, we have developed a high-tolerance (±15 nm) multimode 3-dB coupler and a low-power (23.6 mW) multimode kernel modulator (MKM) with a 12 dB extinction ratio in the C-band, both supporting three modes and readily scalable to higher mode counts. To validate our approach, we focus on the convolution operation as a demonstration of our design. Leveraging parallel computation across both mode and wavelength dimensions, our system achieves 6-7 bits of computational accuracy in the C-band, yielding classification accuracies of 95.2% on MNIST and 87.9% on Fashion MNIST. Moreover, we attain a theoretical arithmetic density of 125.14 TOPS/mm2, underscoring the potential of this solution to pave the way for scalable, energyefficient photonic computing.

Results

Principle

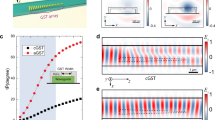
Figure 1a illustrates the conceptual difference between traditional SFI and our multimode fan-in (MFI), showing their respective scattering matrices for a 3-port device with two inputs and one output. In single-mode photonic integrated circuits, signals from multiple waveguides converge into a single waveguide mode. Due to the reciprocity of passive photonic devices, the scattering matrix S remains symmetric, i.e., Sμν = Sνμ. Consequently, merging multiple inputs into a single output inevitably induces partial back-reflections or out-of-phase interference, causing intrinsic insertion losses. In practice, this diminishes the signal-to-noise ratio and restricts the scalability of on-chip fan-in. As an illustrative example, Fig. 1a (left) shows two separate inputs (a1, a2) combining into a single output port (b3). The scattering matrix is given by:

$$\left(\begin{array}{c}{b}_{1}\\ {b}_{2}\\ {b}_{3}\end{array}\right)=\left(\begin{array}{ccc}{S}_{11} & {S}_{12} & {S}_{13}\\ {S}_{21} & {S}_{22} & {S}_{23}\\ {S}_{31} & {S}_{32} & {S}_{33}\end{array}\right)\left(\begin{array}{c}{a}_{1}\\ {a}_{2}\\ {a}_{3}\end{array}\right){{{\rm{wit}}}}{{{\rm{h}}}}\,{S}_{\mu \nu }={S}_{\nu \mu }$$
(1)
Fig. 1: Principle of a photonic multimode convolution accelerator enabled by lossless mode-division fan-in.
figure 1

a The illustration of single-mode fan-in (SFI) and multimode fan-in (MFI) and their corresponding scattering matrix. b Design of the photonic multimode convolution accelerator. MKM, multimode kernel modulator; MWR, multimode waveguide routing.

Full size image

Under the reciprocity constraints and ∣S13∣2 + ∣S23∣2 ≤ 1 (energy conservation), the output follows:

$$\frac{{\left|{S}_{31}\right|}^{2}+{\left|{S}_{32}\right|}^{2}}{{1}^{2}+{1}^{2}}\le \frac{1}{2}$$
(2)

indicating a minimum 50% fan-in loss for two input ports. As the number of inputs grows, these losses compound, ultimately constraining the scalability of on-chip fan-in. For N inputs, the output can contain at most 1/N of the total input power. This limitation is fundamental to the incoherent fan-in of optical power, a scenario highly relevant to on-chip convolution accelerators. In such systems, achieving the convolution often involves parallel multiplications and routing signals through varied optical paths, whitch makes coherent phase synchronization impractical, necessitating a direct power-summation approach.

By contrast, MFI makes use of multiple orthogonal waveguide modes to combine signals without forcing them to share the same mode profile. As shown in Fig. 1a, each input beam is mapped to a distinct spatial mode in the output waveguide, thus reducing interference and reflection between channels. The scattering matrix in the multimode design is still subject to reciprocity; however, distributing signals across orthogonal modes alleviates the inherent single-mode bottleneck. When carefully engineered, mode overlap can be minimized, allowing each mode to act as an independent channel for fan-in with negligible loss. This principle underpins our lossless mode-division fan-in architecture, where signals are effectively combined in a way that conserves total optical power and maximizes device utilization. Figure 1b illustrates our design of a multimode convolution accelerator enabled by lossless mode-division fan-in. The accelerator comprises multimode 3-dB couplers, MKMs, and multimode waveguide routing (MWR). The multimode waveguide is widened for clarity in the figure, and the structures of the multimode 3-dB couplers and MKMs are simplified for clear understanding (detailed structures are provided in Supplementary Notes 1 and 4). To process a single image, the image is first flattened into a one‑dimensional vector of length P. The accelerator then receives M = 3 vectors corresponding to M mode intensities, which propagate through cascaded multimode 3-dB couplers that split the energy into N = 4 equal parts. Subsequently, the energy from each port propagates through N MKMs, which are modulated in intensity to function as a convolutional kernel H. The kernel remains fixed during each inference, rarely requiring rapid updates, so its response time does not impact the overall inference speed. The sliding output of the convolutional kernel window is then generated by MWR (the sliding path is represented by different colors), which comprises a mode demultiplexer and an MFI, with M + N – 1 output ports. The convolution sliding process is entirely passive, with power consumption arising solely from input and kernel modulation. Additionally, each mode can transmit information across multiple wavelengths simultaneously, with the number of wavelengths (K) corresponding to the number of images that can be input at once. Only M modulators are required to encode input vectors of size M and N MKMs to encode convolution kernels of size N, completing the computation in one clock cycle. The total number of multiply-accumulate (MAC) operations is K × M × N, which corresponds to 2 × K × M × N arithmetic operations.

Multimode fan-in

MFI maps each input onto a distinct orthogonal waveguide mode, ensuring that signals do not interfere with one another. For the MFI to support multiple wavelengths simultaneously, it must exhibit broadband characteristics and high fabrication tolerance25,26,27. Inverse design28,29,30, which ensures both compactness and optimal performance, has emerged as a powerful tool in the development of various photonic components31,32,33,34,35. Figure 2 presents experimental results for high‑performance SFI and MFI realized through inverse design. Figure 2a, b show scanning electron microscope (SEM) images of the SFI, with a length of 14.1 μm, and the MFI for the TE2 and TE1 modes, with lengths of 21 and 20 μm, respectively. Detailed parameters and design processes are provided in Supplementary Notes 1 and 2. Figure 2c shows the measured insertion losses over a broadband wavelength range. In the C-band, the SFI incurs an average loss of around 3.53 dB (dashed line), while the MFI exhibits average losses of only 0.32, 0.2, and 0.21 dB for TE2-TE0 modes (solid lines). To further verify the MFI results, we fabricated a Negative-Intrinsic-Positive (NIP) germanium-on-silicon vertical multimode photodetector (MPD) for three-mode detection. The MPD enables simultaneous reception and summation of multiple modes, whereas single-mode photodetectors require separate detection and summation. As shown in Fig. 2d, we integrated the MFI with the MPD, where the multimode waveguide is widened to 2 µm, the covering Ge is widened to 4 µm, and its length is set to 20 µm to improve detector responsivity for all modes. The NIP-MPD has two metal contacts connected to the P-doped section to reduce attenuation near the peak of the modal power profiles. Figure 2e demonstrates the responsivities for the SFI and MFI. At 1.55 µm, the measured responsivity is 0.413 A/W for the SFI and 0.847, 0.84, and 0.864 A/W for the TE2-TE0 modes of the MFI, respectively. In conclusion, the loss of the designed MFI is negligible compared to that of the SFI, demonstrating that distributing signals across orthogonal modes avoids the aggregation losses inherent to the SFI.

Fig. 2: Comparison of the SFI versus the MFI.
figure 2

a, b Scanning electron microscope (SEM) images of the SFI and the MFI structures. c Measured insertion losses of SFI and MFI. d Optical microscope image of MFI cascaded with a multimode photodetector. e Responsivities for the SFI and MFI.

Full size image

Multimode kernel modulator

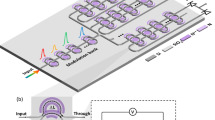
The input of the multimode convolution accelerator is split by a cascaded multimode 3‑dB coupler, but conventional designs suffer from large footprints, limited mode scalability, and fabrication challenges36,37,38,39. To address these issues, we employed inverse design—specifically the Particle Swarm Optimization combined with Direct Range Search (PSO‑DRS) optimization algorithm40—to develop a compact multimode 3‑dB coupler composed of a multimode power splitter and the MFI (Supplementary Notes 1 and 2). Simulation results of the multimode power splitter indicate that with a ± 15 nm waveguide width variation, the insertion losses remain below 0.3 dB and the crosstalk stays below –20 dB. All devices, including subsequent components, were fabricated on a commercial 220 nm silicon‑on‑insulator (SOI) platform. Figure 3a shows an SEM image of the cascaded power splitter, with TE2-TE0 mode splitter lengths of 18.5 µm, 20 µm, and 14.1 µm, respectively. Three modes input from the left port, with higher-order modes decoupled in turn and divided equally between the upper and lower ports. Figure 3b presents an optical microscope image of the complete multimode 3‑dB coupler, which is 127 µm long with an adjustable width. Three modes enter Port I1, propagate through the splitter, divide equally, and recombine via the MFI to form 3‑dB couplers at Ports O1 and O2. To evaluate insertion loss, straight waveguides with grating couplers were fabricated on the same chip (see “Methods”). Figure 3c–e display the normalized transmission spectra: at 1.55 µm, the insertion losses for the TE2-TE0 mode splitters are 0.2, 0.45, and 0.42 dB, respectively, with crosstalk below –20 dB. Across the C‑band, maximum insertion losses reach 0.4, 0.67, and 0.76 dB, with all crosstalk values remaining below—17.3 dB. Experimental results align well with the simulated data provided in Supplementary Note 1. Slight output variations between Ports O1 and O2, attributed to unavoidable sidewall etching roughness and linewidth variations during fabrication, remain within acceptable limits. The MKM40,41,42,43 is the core structure of the multimode convolution accelerator. Although cascading two multimode 3‑dB couplers with a phase shifter can achieve this function, that approach requires widening the phase‑shifter’s bus waveguide—necessitating long tapers and increasing device size. To overcome this, we designed a compact MKM (Supplementary Note 3). Figure 3f shows an optical microscope image of the centrosymmetric device (325 × 80 μm2) with a central thermal insulation slot to prevent crosstalk. Three modes enter the left port, are split by cascaded mode splitters into three single‑mode waveguides within the phase shifter, pass through another set of three cascaded splitters, and exit via the right port. The phase shifter uses three parallel waveguides (0.5 μm spacing, 2 μm width each) to avoid (de)multiplexing and long tapers and to reduce phase errors44,45. To ensure uniform temperature rise across all waveguides—avoiding excessive heating of the central waveguide—we use two parallel TiN microelectrodes (2 μm wide, 140 μm long, 0.1 μm thick) with a spacing of GW = 1.92 μm. Figure 3g plots the transmission spectra of the three modes at 1.55 μm versus voltage. At the driving voltage of 3.6 V, all modes switch simultaneously, consuming 23.6 mW for a π‑phase shift. Compared to the conventional approach using three separate microelectrodes that requires about 60 mW, our design reduces power consumption by approximately 60%46. Figure 3h–j show the normalized “on/off” spectra, with dashed lines marking the extinction ratios and solid lines indicating the inter‑mode crosstalk (values below –30 dB omitted). Over the C‑band, the insertion losses for TE2-TE0 are 2.1, 1.3, and 1.5 dB, respectively. Maximum crosstalk is –13.2, –14.3, and –17.1 dB, and extinction ratios exceed 12 dB. The designed multimode 3‑dB coupler and kernel modulator can be easily scaled to higher-order modes by cascading an additional higher-order mode splitter.

Fig. 3: Design and experimental results of the multimode 3‑dB coupler and the kernel modulator.
figure 3

a SEM image of the cascaded mode splitter. b Optical microscope image of the multimode 3‑dB coupler. c-e Measured transmission spectra in the C‑band. Dashed lines indicate the mode corresponding to the mode splitter. f Optical microscope image of the MKM. g Transmission spectra of three modes at 1550 nm under varying voltage. h–j Normalized transmission spectra in the “on” and “off” states. Dashed lines indicate variations in the same mode, whereas solid lines denote inter‑mode crosstalk (values below −30 dB are omitted).

Full size image

Multimode convolution accelerator

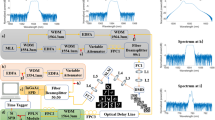
Figure 4a displays the optical and electrical packaging of the chip, with vertical grating coupling and wire bonding completed. The chip, used as a proof of concept, measures 0.6 × 0.7 mm2, and at 1.55 µm, the total insertion losses of the photonic convolution accelerator are below 2.73 dB. The chip integrates three‑mode 3‑dB couplers, three‑mode kernel modulators, and three‑mode routing. A single-wavelength input generates three vectors, while four MKMs implement the loading of a 1 × 4 convolution kernel. A microscope image of the fabricated photonic convolution accelerator chip, along with a schematic of the experimental apparatus, is provided in Supplementary Note 4. We tested 1000 sets of random input vectors and convolution kernels. Each convolution produced an output vector of length 6, yielding a total of 6000 data points. The input vector elements were random numbers between 0 and 1, and the convolution kernel elements ranged from 0 to 1/3, ensuring that the output values remained within 0 to 1. As shown in Fig. 4b, the experimentally obtained values align tightly along the diagonal, demonstrating precise computations with a high degree of reliability. The bit precision Nb is defined as:

$${N}_{b}={\log }_{2}\left(\frac{{\mu }_{max }-{\mu }_{min }}{{{{\rm{\sigma }}}}}\right)$$
(3)

where μmax and μmin are the maximum and minimum output values, respectively, and σ is the standard deviation of the error between the experimental and expected outputs. Gaussian fitting yields a normalized standard deviation of 0.0072, confirming a system computational precision of 7 bits. In Fig. 4c, we employ a CNN to perform ten‑class classification of handwritten digits (0-9), with the convolution layer implemented via optical convolution (highlighted in orange). Images are first resized to 12 × 12 pixels and flattened into a 144 × 1 vector. The photonic convolution layer then uses four 4 × 1 convolution kernels to generate four 146 × 1 feature maps. To perform convolution on long vectors, the original operation is decomposed into multiple short‑vector convolutions with subsequent encoding. We adopt the overlap–add method to compute the convolution; see Supplementary Note 5 for details. After applying the ReLU nonlinearity, the four 146 × 1 feature maps are reshaped into a 584 × 1 vector, which is then fed into a fully connected layer with 10 neurons using SoftMax activation. Although our architecture and experimental demonstrations are based on one‑dimensional (1D) convolution, two-dimensional (2D) convolution can be equivalently portrayed as a 1D convolution by applying zero-padding to the kernel19. While the architecture does not inherently support convolution kernels with negative values, the kernel can be decomposed into two positive components and subtracted at the output to accommodate real‑valued kernels. Offline training is carried out via stochastic gradient descent with backpropagation to minimize the cross‑entropy loss (see Supplementary Note 6 for details). We performed 20 iterations of training on the MNIST dataset (70,000 images total; 60,000 for training, which was split with a training‑to‑validation ratio of 5:1). In the optical‑domain test, 1000 images were loaded, yielding a classification accuracy of 95.2%, very close to the theoretical electrical‑domain accuracy of 95.8%. The corresponding confusion matrices in Fig. 4d, e indicate that the effects of optical noise or distortion (due to higher‑order dispersion) on network performance and effective precision are minimal.

Fig. 4: Experimental results of the multimode convolution accelerator.
figure 4

a Optical and electrical packaging of the chip. b Scatter plot of measured convolution accuracy. Inset: Histogram of compute errors (differences between measured and computed values). c Schematic of the CNN architecture: orange regions denote optically implemented convolutional layers. d, e Confusion matrices for recognition of 1000 MNIST test digits, comparing experimental results with computerized calculations.

Full size image

To further demonstrate the capability of wavelength‑parallel input, we utilized two different wavelengths to achieve recognition on the Fashion-MNIST dataset. As shown in Fig. 5a, b, using the same precision verification method at wavelengths of 1530 nm and 1565 nm, the normalized standard deviations are 0.0094 and 0.0075, corresponding to computational precisions of 6 bits and 7 bits, respectively. After retraining the CNN with the same architecture as in Fig. 4c and loading the training parameters onto the chip, 500 Fashion-MNIST images were processed at each of the two wavelengths, achieving an accuracy of 87.9% (the confusion matrix is shown in Fig. 5c). In the electrical domain, the recognition accuracy was 89.2% (see Fig. 5d). The slightly larger difference of 1.3% (compared to the previous 0.6% for MNIST) may be attributed to variations in precision at the different wavelengths.

Fig. 5: Experimental results of multi-wavelength parallel recognition on the Fashion-MNIST dataset.
figure 5

a, b Scatter plots of convolution accuracy at 1530 nm and 1565 nm. Insets: Histograms of compute errors. c, d Confusion matrices comparing experimental and computerized classification results for 1000 Fashion-MNIST test images.

Full size image

Discussion

The proposed multimode optical convolution accelerator, which integrates multimode 3‑dB couplers, kernel modulators, and routing, has a compact footprint of 0.6 × 0.7 mm2 and is compatible with 130–nm commercial standard manufacturing processes. At 1.55 µm, the total insertion losses of the photonic convolution accelerator are below 2.73 dB. Both the multimode 3‑dB coupler and the kernel modulator were designed using inverse design, yielding high performance and a fabrication tolerance of ±15 nm. Within the C‑band, experimental results show that the multimode 3‑dB coupler attains an extinction ratio exceeding 16 dB, while the MKM delivers an extinction ratio greater than 12 dB and requires only 23.6 mW for a π‑phase shift. The convolution window’s sliding and encoding rely entirely on passive optical components, minimizing power consumption. At 1.55 µm, the accelerator provides a computational precision of 7 bits. In MNIST handwritten digit classification, optical-domain inference achieved an accuracy of 95.2%, closely matching the theoretical electrical-domain accuracy and validating the design’s practical reliability. Additionally, wavelength‑division multiplexing (WDM) enables parallel loading of multiple wavelengths, while mode-division multiplexing (MDM) provides distinct spatial modes in a single waveguide for efficient fan-in, both significantly boosting computational throughput. To verify the performance of WDM, tests at 1530 nm and 1565 nm yielded computational precisions of 6 bits and 7 bits, respectively, while recognition experiments on the Fashion-MNIST dataset recorded an optical-domain accuracy of 87.9%, showcasing the capability for complex tasks. Finally, the device provides a 4.38 THz available bandwidth (corresponding to the C‑band) and achieves a compute density of up to 125.14 TOPS/mm2, calculated as follows:

$$\frac{2\times 3\times 4\times K\times \frac{4.38}{2K}{{{\rm{THz}}}}}{0.6\times 0.7{{{{\rm{mm}}}}}^{2}}\approx 125.14\,{{{{\rm{TOPS}}}}/{{{\rm{mm}}}}}^{2}$$
(4)

Here, 2 × 3 × 4 × K denotes the total MAC count per clock cycle across three modes, four kernels, and K wavelengths; 4.38/K THz is the bandwidth of each wavelength channel, with modulation bandwidth halved to prevent crosstalk (i.e., 4.38/(2K) THz); and 0.6 × 0.7 mm2 is the chip footprint.

Our approach complements other innovative strategies recently demonstrated for photonic convolution accelerators. For instance, high-throughput convolvers have been realized using time-domain delay-and-interleave schemes22,23,24. Other works have ingeniously exploited synthetic dimensions19,20, demonstrating convolution in the frequency domain to unlock massive computational parallelism within a single modulated ring. Furthermore, redundancy-free architectures based on arrayed waveguide gratings (AWGs) have been developed to enhance computational efficiency47. For further comparisons of photonic convolution methods, see Supplementary Note 7. While these methods significantly advance the field, our work focuses specifically on overcoming the fan-in loss bottleneck through lossless mode-division multiplexing, offering a new pathway toward scalability in large-scale linear operations. While this work concentrates on the linear convolution step, integrating efficient on-chip nonlinear activation functions remains a critical next step for creating fully integrated photonic neural networks. Neurons based on nonlinear optical materials48 and photodetector-driven modulators49,50,51,52 are both highly promising solutions to this challenge.

In summary, our lossless mode-division fan-in strategy introduces a fundamentally new approach for large-scale on-chip optical summation by circumventing the insertion-loss bottleneck in single-mode systems. Through inverse-designed multimode components, we have demonstrated the viability of leveraging multiple orthogonal modes to achieve near-ideal fan-in efficiencies. Such architectures hold promising implications for photonic accelerators, where efficient fan-in plays a critical role in convolution and other linear operations. Moving forward, further optimization of device footprint, fabrication tolerance, and broad optical bandwidth will be key to integrating more modes and wavelengths for supporting energy-efficient, high-throughput photonic computing platforms.

Methods

Chip fabrication

The device was fabricated on a commercial 220 nm SOI wafer with a 2 µm buried oxide. First, waveguide patterns were defined by deep ultraviolet (DUV) lithography and transferred into the silicon layer via dry etching. Next, for the Ge photodetectors, a localized ion implantation formed the bottom contact in the silicon waveguide, followed by heteroepitaxial growth of Ge and top‑side doping. Afterward, an interlayer dielectric (ILD) was deposited and planarized via chemical mechanical polishing (CMP). Then, in the back‑end‑of‑line (BEOL), contact vias were etched and filled with tungsten (W), and a TiN layer was subsequently deposited and patterned to form the on‑chip microheaters for the thermo‑optic phase shifters. Finally, multi‑layer metal traces and vias were fabricated using a Cu single‑Damascene process to interconnect the devices and route signals to the Al bond pads. The entire chip was then protected by a passivation layer, with windows opened over the bond pads for packaging and testing.

Measurement methods

To facilitate the measurement of the normalized losses and crosstalk of the multimode 3‑dB coupler and kernel modulator, mode (de)multiplexer connecting straight waveguides were fabricated on the same chip. The experimental setup included a broadband light source, a vertical fiber‑chip coupling stage, a spectrum analyzer, and a power meter. Prior to vertical coupling, a polarization controller was used to select the TE polarization state. Grating couplers connected single‑mode fibers to the silicon waveguides, each incurring a measured loss of approximately 4 dB. The output light was divided in a 1:9 ratio—10 % was sent to a high‑sensitivity power meter for continuous, real‑time monitoring of the coupling efficiency, and 90 % to the spectrum analyzer to ensure sufficient optical power for an adequate signal‑to‑noise ratio. All measurements were conducted at room temperature.