Introduction

Solid-state refrigeration technology based on caloric effects has emerged as a promising solution to address the environmental concerns associated with vapor compression refrigeration technology. The caloric effect refers to the phenomenon where certain materials experience a temperature change when subjected to an external field. Several types of caloric effects exist and each is named after the applied external field, including magnetocaloric, electrocaloric, elastocaloric, and barocaloric effects (BCE)1,2,3,4. Such effects can be observed as a generic thermal response to external fields regardless of whether there is a phase transition. However, they are typically more pronounced near phase transitions, where external fields can more effectively shape the energy landscape profiles. Consequently, prominent caloric effects are usually limited to a relatively narrow temperature span. For instance, Gd5Si2Ge2, the prototype room-temperature giant magnetocaloric material, exhibits a temperature range of approximately 10 K under a 2 T magnetic field5,6, and the refrigeration span might be extended through an active magnetic regenerating refrigerant cycle1. This universal characteristic has led to a long-standing limitation: a caloric material is only active within a specific temperature region, necessitating a multi-stage configuration to reach lower temperatures. As a result, caloric refrigerators become more complicated and cost-inefficient.

In conventional barocaloric materials, the pressure-temperature phase diagram typically exhibits a monotonic phase boundary, often linear at the lower pressure region7,8, but a deviation at higher pressures9. This means that the phase transition temperature shifts straightforwardly with smaller applied pressure. As illustrated in Fig. 1a for the prototype material neopentylglycol (NPG), the phase transition temperature of the pressure-induced cubic to monoclinic transition increases at a rate of about 0.103 K MPa−1 (Fig. 1b). Currently, the highest rate is achieved in NH4I, which is approximately 0.8 K MPa−110. This shift indeed determines the refrigeration temperature span under a given pressure, which is usually about 20 K or less under a reasonably high pressure, such as 100 MPa10, which is easily accessed in current commercial calorimetry.

Fig. 1: Comparison of the all-temperature BCE material and regular BCE materials.
figure 1

a, c Schematic entropy versus temperature curve of NPG as well as KPF6 in the absence of pressure and under applied pressure. The arrows depict pressurization. b, d Temperature-pressure phase diagrams of NPG8 as well as KPF6. For the latter, each symbol represents an experiment. Except for neutron diffraction data labeled with ND, other all are from Raman scattering. “C”, “M-I”, “M-II”, and “R” are abbreviated for cubic, monoclinic I, monoclinic II, and rhombohedral phase. The meaning of the legends are specified in the text. e Comparison of the operating temperature range of the regular BCE materials with that of KPF67,10,13,14,20,21,22,23,24,25,26,27,28 .

Full size image

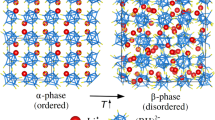
In this study, we address this limited temperature span issue by demonstrating a novel all-temperature BCE in KPF6. This compound has previously been reported as an intriguing barocaloric material11. What sets this material apart is the presence of a high-pressure phase. The pressure-induced phase transition from the disordered cubic phase to the fully ordered rhombohedral phase results in a colossal BCE around room temperature, characteristic of an entropy change of 144 J kg−1 K−1 and a large temperature span up to 50 K11. This cubic phase crystallizing in the space group of \({Fm}\bar{3}m\) exhibits extensive orientational disorder of PF6 octahedra11 and thus it can be regarded as an inorganic plastic crystal phase. The existence of this high-pressure phase inspires us to investigate the BCE at lower temperatures. We directly observed an adiabatic temperature change of 2.5 K at 77.5 K, potentially extended to even lower temperatures. As illustrated in Fig. 1c, this phenomenon is attributed to the unique entropy-temperature curve, where pressure can induce a phase transition from the low-temperature monoclinic phase to the rhombohedral phase in the wide temperature region below 219 K. Pressure-dependent experimental characterizations and first-principles calculations support this groundbreaking finding. This discovery overcomes the temperature range limitations of conventional materials and provides a novel approach for the future development of solid-state phase transition refrigeration technology.

Results and discussion

All-temperature BCE of KPF6

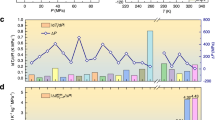
In our previous work, we investigated the BCEs associated with the cubic and intermediate-temperature monoclinic phases (here, labeled as monoclinic II phase), focusing on entropy changes under various applied pressures11. In this study, we directly measure the adiabatic temperature change (ΔTad) of the compound during pressurization-depressurization cycles at different environmental temperatures, particularly regarding the pressure-induced phase transition from the low-temperature monoclinic phase (here, labeled as monoclinic I phase) to the high-pressure rhombohedral phase. Figure 2a shows the ΔTad profiles at 300, 255, and 77.5 K, corresponding to the cubic, monoclinic II, and monoclinic I phases, respectively. These phases were identified based on previous studies11,12 and the present heat flow and dielectric data shown in Supplementary Fig. 1, where two phase transitions occur at 252 and 259 K during heating, and at 219 and 257 K during cooling, respectively, with thermal hysteresis of 33 and 2 K. In a pressure cycle of 250 MPa, ΔTad reaches approximately 9.6 K for pressurization and 9.1 K for depressurization at 300 K. This behavior is attributed to the exothermic effect of the pressure-induced cubic to rhombohedral phase transitions as well as the endothermic effect of the reverse transition, which directly characterized the refrigeration performance of a barocaloric material. This value is smaller to leading barocaloric materials like two-dimensional vdW alkylammonium halides, which achieve a ΔTad of approximately 22 K under 200 MPa at 330 K13. For the pressure-induced phase transition between the monoclinic II and rhombohedral phases, ΔTad decreases to about 5.7 K, similar to the reduction of entropy changes previously reported11. In the monoclinic I phase at 77.5 K, ΔTad further decreases to 1.65 K. The detailed pressure dependence of the monoclinic I phase is considered at 77.5 K, as shown in Fig. 2b, where ΔTad increases from 0.56 K to 1.65 K as the applied pressure increases from 100 to 250 MPa. Figure 2c illustrates the detailed temperature dependence of ΔTad. Below 200 K, for the monoclinic I to rhombohedral phase transition, ΔTad steadily decreases as temperature drops. The temperature dependence obviously differs from the trivial single-peak profile of other barocaloric materials9,13,14 due to the special high-pressure phase transitions.

Fig. 2: Adiabatic temperature change, ΔTad.
figure 2

a ΔTad profile in pressurization-depressurization cycles under 250 MPa at different base temperatures (77.5, 255, and 300 K). b ΔTad profile in pressurization-depressurization cycles at the base temperature of 77.5 K under different pressures (100, 150, 200 and 250 MPa). c Experimental and calculated ΔTad as a function of temperature. Here, several samples are surveyed.

Full size image

To ensure the accuracy of our experiments, we conducted measurements on several different batches of samples. In addition, we measured NaCl in the same temperature range as a reference, as illustrated in Supplementary Fig. 2. The adiabatic temperature changes for NaCl at 250 MPa were determined to be 0.8 K at 77.5 K and 5.04 K at 300 K. Notably, the value at 298 K is nearly identical to the prediction of 4.64 K derived from the fitting curve proposed by Boehler15.

Crystal structures and phase transitions

As previously mentioned, KPF6 undergoes two successive phase transitions at approximately 257 and 219 K under ambient pressure. Figure 3a presents a contour plot of neutron powder diffraction patterns in the temperature-sweeping mode during cooling to about 5 K. As the temperature decreases, the diffraction peaks shift and split at the two black dashed lines, indicating the occurrence of two phase transitions. These transitions are clearly identified and consistent with the heat flow data (Supplementary Fig. 1). We determined the crystal structures of the low-temperature monoclinic I phase and intermediate-temperature monoclinic II phase using neutron powder diffraction combined with first-principles calculations. Supplementary Fig. 3 displays the Rietveld refinements of their patterns based on the C2/c model. The refined parameters are summarized in Supplementary Table 1 and 2.

Fig. 3: Phase transitions of KPF6 as a function of temperature.
figure 3

a, b correspond to contour plots of the neutron diffraction patterns measured during cooling at 0.1 and 400 MPa at PLANET, respectively, where the individual phases are labeled.

Full size image

Then, we move the response to applied pressure. Under 400 MPa, the crystal structure is monitored in a similar way (Fig. 3b). The two phase transitions are suppressed, and there is a unique phase throughout all the temperature regions from room temperature to 5 K, which has been identified as the high-pressure rhombohedral phase in the previous work at room temperature11. This result points out a single high-pressure phase during a pressure-cooling process. Differing from the temperature scan under constant pressure, several pressure scans were also performed at constant temperatures. At constant temperatures of 10, 100, and 200 K, neutron powder diffraction patterns were collected under ambient pressure, 100, 400, and 700 MPa, respectively. In Fig. 4a–f, we show the patterns of 100 and 400 MPa, while the rest are given in Supplementary Fig. 4. The Rietveld refinements of the patterns at 10 and 100 K under 100 MPa indicate a single phase of the rhombohedral structure, implying a critical pressure smaller than 100 MPa. The crystallographic information of this rhombohedral phase is listed in Supplementary Table 3. Note that Bragg peaks of lead are present since it is used for calibrating the actual pressure of samples. In contrast, there is phase coexistence with a residual monoclinic phase at 200 K, suggesting that 100 MPa is insufficient for a complete transition to the rhombohedral phase. Upon applying pressure up to 400 MPa, the phase transition is completed. This difference in critical pressures reflects a positive slope of the phase boundary in the temperature-pressure phase diagram. The determined lattice dimensions are shown in Supplementary Fig. 5a. Increasing pressure from the ambient pressure to 100, 400, and 700 MPa, the unit cell volume undergoes an abrupt decrease at ~ 100 MPa, reflecting the transition from the low-pressure monoclinic I to the high-pressure rhombohedral phase.

Fig. 4: Pressure-induced phase transition at selected temperatures.
figure 4

Neutron diffraction patterns at 10 K (a, d), 100 K (b, e), and 200 K (c, f) under 100 and 400 MPa, respectively. g, h, and i Raman spectra at 4, 100, and 200 K, respectively.

Full size image

To depict phase transitions in a wide pressure and temperature space, we have collected about 100 data points of Raman scattering in the temperature region between 4 and 350 K, as well as pressures up to 1 GPa, which ensures the complete phase transition. Complete datasets are summarized in Supplementary Fig. 6. In Fig. 4g–i, we show the selected spectra at 4, 100, and 200 K, corresponding to the neutron diffraction patterns. The Raman spectra are characteristic of three bands located at about 470, 570, and 750 cm−1, respectively. The octahedral symmetry of PF6- can be described by the Oh point group, which essentially determines the lattice vibrations16. The strongest peak at 749 cm−1 is associated with the A1g mode reflecting symmetric stretching vibration. The Eg mode, which is related to asymmetric stretching, appears weaker with four peaks at 576, 581, 582, and 586 cm−1. The F2g mode, describing the bending motions, is found at 482, 476, and 472 cm−1. Under applied pressure, multiple peaks associated with Eg and F2g modes are merged to be single peaks located at 476 and 572 cm−1, respectively, while the A1g mode exhibits significant hardening.

The aforementioned pressure-dependent Raman spectra and neutron diffraction measurements allow us to establish the temperature-pressure phase diagram. All the data points are drawn in the diagram. The filled square, circle, and triangle represent the cubic, monoclinic II and monoclinic I phases, while the open diamond means the rhombohedral phase at the given temperature and pressure conditions, respectively. The half-filled square, circle, and triangle represent the phase-coexisting zone of rhombohedral cubic with monoclinic II and monoclinic I phase, respectively. As shown in Fig. 1d, the high-temperature cubic phase, intermediate-temperature monoclinic II phase, and the low-temperature monoclinic I phase are separated from the high-pressure rhombohedral phase. The phase boundaries are schematically drawn using the dash lines. In particular, given that the monoclinic I/ rhombohedral phase boundary is used to estimate the barocaloric entropy change, the slope is quantitatively determined by fitting the nearby data points to a linear function. The fitting gives rise to dT/dP ~ 2.03 K MPa−1, indicating a normal BCE.

The complete datasets of the slope of the phase boundary, dT/dP (Fig. 1d), and the unit cell volume changes (Supplementary Fig. 5a) at the pressure-induced phase transition allow us to estimate the barocaloric entropy changes in terms of the Clausius-Clapeyron relation. The determined barocaloric entropy changes are plotted as a function of temperature under different pressures in Supplementary Fig. 5b. The barocaloric ΔTad can be further calculated using specific heat (Supplementary Fig. 7), which are included in Fig. 2c. It can be seen that there are some discrepancies between the experimental and estimated values, which might be ascribed to the inaccuracy of the dT/dP due to the diamond anvil cells high-pressure technology. The estimated values are meaningful considering they provide a reference below 77.5 K, where the direct measurement is still not available at this stage.

First-principles calculations

First-principles calculations were conducted to further understand the physical properties of the low-temperature monoclinic I and high-pressure rhombohedral phases. The phonon dispersions of both phases of KPF6 are shown in Fig. 5a and b. No imaginary phonon bands are observed, indicating their dynamical stability and aligning with our experiments. Moreover, the two phases share a common feature of separate and flat phonon bands. This is due to the dominant contributions of F atoms spanning a large region of frequencies, as indicated in the atom-resolved phonon density of states (Fig. 5c). The calculated energy-volume curves in Fig. 5d showcase that the monoclinic I phase is the ground state under ambient pressure and would undergo a phase transition to the rhombohedral phase via pressure. The derived enthalpy-pressure curves in Fig. 5e show that the transition pressure at 0 K is 0.71 GPa. Furthermore, we computed the energy barrier for the phase transition from the monoclinic I phase to the rhombohedral phase at 0 K and 1 GPa using the variable cell nudged elastic band method17. The results displayed in Fig. 5f demonstrate that the phase transition from the monoclinic I phase to the rhombohedral phase needs to overcome an energy barrier of 0.27 eV/f.u. By examining the transformation trajectory, we interestingly find that the phase transition does not need to break the chemical bonds but proceeds through the concerted rotation of the PF6 octahedra accompanied by the lattice modulations. This, therefore, results in a small kinetic energy barrier and facilitates the transformation.

Fig. 5: Energy landscapes by first-principles calculations.
figure 5

a, b Phonon dispersion of the monoclinic I (at 0 GPa) and rhombohedral (at 1 GPa) phases, respectively. c Total and atom-resolved phonon density of states of the two KPF6 phases. d Energy-volume curves. e Enthalpy-pressure curves at 0 K. f Computed enthalpy at 0 K and 1 GPa as a function of the normalized transformation coordinate for the phase transitions from the monoclinic I phase to the rhombohedral phase.

Full size image

Implication to caloric refrigeration

Typically, the refrigeration span of caloric materials is relatively narrow under a reasonably large external field. For well-studied magnetocaloric materials, the refrigeration span of materials themselves — often defined as the full width at half maximum of the entropy change curves — is limited to a few kelvins. To achieve meaningful magnetic refrigeration, a series of materials with different Curie temperatures must be used in conjunction with active magnetic regenerative technology18,19. Barocaloric materials generally exhibit broader refrigeration spans. Notably, a span of 80 K can be obtained in NH4I under 100 MPa10. However, the lowest theoretically accessible temperature is typically limited to their phase transition temperature in the absence of applied pressure. In fact, in a single-stage barocaloric refrigerator, the largest refrigeration span is only the adiabatic temperature change of the material. In contrast, the present all-temperature BCE in KPF6 is unprecedented and fundamentally different, as illustrated in Fig. 1e7,10,13,14,20,21,22,23,24,25,26,27,28. Both our neutron diffraction and Raman scattering studies demonstrate that pressure can induce phase transitions at 4 K with even smaller driving pressures. In addition, the pressure-dependent Raman scattering above room temperature indicates the BCE is also potentially active up to 350 K. In principle, such a wide refrigeration span can be accessed using this single material by designing an adaptive thermodynamic cycle across the typical room temperature, liquid nitrogen, liquid hydrogen, and liquid helium refrigeration regions. Regarding the ultralow temperature region, further research is necessary to fully characterize its structural and barocaloric properties.

Summary

In summary, structural phase transitions in KPF6 have been studied down to 4 K through a combination of neutron diffraction, Raman scattering, and first-principles calculations. With cooling down from room temperature, this compound undergoes successive phase transitions from cubic to monoclinic II at 257 K, and then to monoclinic I at 219 K. Applying pressure can induce a phase transition to the rhombohedral phase, regardless of the initial phase at ambient pressure. This pressure-induced phase transition leads to the all-temperature BCE spanning a wide temperature region from room temperature to 77.5 K and potentially expanded down to 4 K, whose adiabatic temperature change is directly measured to be 2.5 K under 250 MPa at 77.5 K. The finding of the all-temperature BCE significantly extends the limited refrigeration span of caloric materials and provides a solid foundation for exploiting the continuous single-stage caloric refrigeration technology.

Methods

Sample preparation and characterization

Polycrystalline KPF6 (purity 99.98%) was purchased from Aladdin. Heat flow data of the samples were obtained using differential scanning calorimetry (TA, Q1000) at a rate of 20 K min−1 in the temperature range from 173 to 313 K. Specific heat capacity measurements were performed on a sample weighted 2.5 mg using a Physical Property Measurement System (PPMS-14 T, Quantum Design). For the dielectric measurements, a plate-like sample with a thickness of ~ 0.9 mm was prepared, and silver conductive paste deposited on the plate surfaces were used as top and bottom electrodes. The dielectric constants (εʹ) was measured using a two-probe AC impedance method with an impedance analyzer (Tonghui, TH2838)29,30. The thermal conductivity at room temperature was measured using the laser flash method (NETZSCH LFA 467HT). Similar to other plastic crystals, the thermal conductivity of KPF6 is very low, about 0.368 W m−1 K−1, but it can be significantly improved by compositing with highly-conductive materials like graphene25.

Adiabatic temperature change measurements

We utilized a homemade instrument to measure the temperature of samples pressurized in a piston-cylinder unit, which is powered by an oil pump. Powder samples of approximately 1 gram were pelletized and inserted into a Teflon cell. A Teflon cap embedded with a type-E thermocouple was mounted onto the pellet in the cell. Subsequently, the cell containing the sample was fixed in a beryllium copper pressurized mold, placed in a stainless steel container, and put on a hydraulic press for the experiment. The low-temperature environment was realized in a liquid nitrogen flow. The temperature of the samples was recorded using a high-precision cryogenic temperature controller (Lakeshore 336). This system was well-calibrated using NaCl. The applied pressures were determined by converting the pressure of the oil pump, whose error bars were estimated to be smaller than 10 MPa. Pressure ramping up time was as short as 7 s from 0 to 100 MPa and 9 s from 0 to 250 MPa, while the pressure ramping down time was set to 1 s. The response time of the thermocouple is about 0.5 s. Such time structures guarantee the adiabatic conditions. Another measurement using a PE cell is also given in Supplementary Fig. 8. Note that the profile of adiabatic temperature change is sensitive to the microstructures of the samples, and sometimes a peak appears with a shoulder.

Raman spectroscopy

Temperature- and pressure-dependent Raman spectra were obtained using an in-situ Raman spectrometer (LabRAM HR Evolution, Horiba) equipped with a 4He cryostat (S-300, Physike) and a diamond anvil cell (CryoDAC Tesla, ALmax easylab). The wavelength of the laser was 532 nm. At a constant temperature of 4, 30, 50, 70, 100, 130, 150, 180, 200, 220, 240, 250, 260, 280, 300, 310, 330, and 350 K, the diamond anvil cell was used to apply pressure to the sample. The pressure applied to the sample was determined using the ruby fluorescence method, whose error bars were usually regarded to be about 50 MPa at the current pressure region31. To access a stable temperature, we waited for a least 20 min before measurements. The Raman data were processed using LabSpec6 software.

Neutron powder diffraction

Temperature- and pressure-dependent neutron diffraction experiments were carried out using a high-pressure neutron diffraction spectrometer, PLANET32, J-PARC, at selected temperatures of 10, 50, 100, 150, 200, and 300 K and pressures of about 0.1, 100, 400, and 700 MPa. The pelletized samples, about 5 grams, were inserted into a piston-cylinder sample cell. The applied pressures were determined using the Pb reference, which gives rise to an error bar of about 50 MPa. The neutron diffraction data obtained were refined using the GSAS I software33. At a lower temperature of 3.5 K, the crystal structure was checked using the ECHIDNA34 at ACNS of ANSTO. The neutron wavelength was 2.4395 Å. The Rietveld refinements were used to analyze crystal structures by the Fullprof Suite program35.

Computational details

The first-principles density functional theory (DFT) calculations were performed using the Vienna ab initio simulation package (VASP)36,37. The interactions between nuclei and valence electrons were described by the VASP-recommended PAW pseudopotentials38,39. The PBEsol40 exchange-correlation functional was used, which yields a better description of the equilibrium properties of solids40. The plane wave energy cutoff was set to 700 eV, and a Γ-centered k-point grid with a reciprocal-space resolution of 0.21 Å−1 was used for sampling the Brillouin zone. The convergence criteria for the total energy and ionic forces were set to 10−6 eV and 5 meV Å-1, respectively. The phonon dispersions and density of states were calculated by finite displacements using the Phonopy code41. The variable cell nudged elastic band method17 was employed to obtain the energy barrier of the phase transition. The structure search for the low-temperature phase was conducted using the generic evolutionary algorithm implemented in the USPEX code42,43,44. The structures of the first generation were created based on the information available from experiments, including the space groups, lattice parameters, and the number of formula units in the unit cell. The structures of the following generations were produced by using heredity (45%), a random symmetric structure generator (15%), soft mutation (15%), transmutation (15%), and lattice mutations (15%). Five-step DFT calculations with increasing precision were used for each structure to compromise the search speed and accuracy. The structure search was terminated until the structures with a simulated X-ray diffraction pattern matching the experimental one were obtained. The electronic band structures of the monoclinic I and rhombohedral phases of KPF6 were computed and displayed in Supplementary Fig. 9, showing the insulating states for both phases.