Soft porous metamaterials using inflation-induced buckling for smart actuation

Abstract

Cellular metamaterials represent unique platforms to manipulate structure–property relationships and enhance mechanical responses. While their unconventional behaviors have traditionally been obtained via pattern-transformations under compressive loading or deflation, we theoretically investigate and experimentally realize a new class of soft, porous metamaterials that undergo buckling instability upon inflation, unlocking superior programming and sequencing capabilities for soft intelligent machines. Our inflatable metamaterial reimagines the traditional rubber slab with periodic holes by incorporating a single internal pressure cavity. Upon inflation, the structure can be engineered to exhibit global short-wavelength buckling modes with a controllable circumferential lobe count of the cylindrical pores. First, we experimentally demonstrate the programmable post-buckling behavior by tuning the geometric parameters. Then, with a combination of analytical and numerical methods, we accurately predict the critical buckling pressure and pattern reconfiguration of the cellular metamaterial. By enabling different pattern rearrangements of the collapsing pores, we achieve a new actuation mechanism to suddenly reconfigure the global structure, selectively grasp slender objects, and operate multiple fluid channels with a single input.

Introduction

Biological matter has long organized itself in cellular periodic structures such as the repeated cells of cork tree bark^1,2, the hexagonal honeycomb of beehives³, or the brilliant blue color of butterfly wings^4,5. Structural advantages, like augmented energy-absorbing capacity^6,7,8,9 and high performance index for bending strength^10,11, emerge from the internal structures of cellular solids^12,13,14. Inspired by such natural cellular materials, porous metamaterials, which are comprised of unit cells repeated in various patterns, have arisen as artificial structures able to unlock desirable properties ranging from tunable negative Poisson’s ratio^15,16,17,18, high strength-to-weight ratios^19,20,21, acoustic^22,23,24, and thermal²⁵ tunability, phononic switches^26,27 to topologically protected mechanical memories²⁸. Behind these exotic and tunable behaviors, interconnected networks of pores experience reversible morphological changes induced by the buckling instability of a network of beams²⁹. When uniaxially compressed, a simple square lattice of circular holes pierced in an elastomeric sheet undergoes a buckling-based pattern transformation into alternating, mutually orthogonal ellipses^{30,31,32,33,34,35,36}.

In 2D porous metamaterials, porosity, pore shape, and lattice type uniquely identify the reconfiguration mode obtained upon buckling. Indeed, under plane strains, the collective buckling of the ligaments connecting the pores dictates the shape transformation throughout the entire lattice. Here, we propose a shift from porous metamaterials based on beam networks to a new class of buckling-based metamaterials made of networks of cylindrical shells. This soft porous nonlinear geometric (SPoNGe) metamaterial is made of repeated unit cells of cylindrical shells surrounded by a single pressure cavity and bounded by square plates at either end (Fig. 1a). A single pneumatic inlet controls the pressure of the interior cavity, which simultaneously applies positive pressure to the entire structure and, upon reaching a programmable critical buckling pressure, activates a global structural reconfiguration. For this geometry, we demonstrate how the buckling instability and the corresponding mode shape are governed by the interplay between the cylindrical shells and the top and bottom plates. Although the buckling of cylindrical shells has been widely studied in the literature³⁷, the use of cylindrical shells as unit cells in metamaterials remains unexplored. This key transition at the building block level enables a design landscape wherein different buckling-induced reconfigurations can be obtained by varying the depth of the metamaterial, even though the shape, size, and arrangement of the pores are kept constant. Moreover, while classical metamaterials with arrays of pores are known to experience buckling under compressive forces or vacuum loading^38,39,40, the SPoNGe metamaterial platform manifests the instability upon inflation. Thanks to this family of hollow cellular metamaterial, we can unlock the potential of preprogrammable deformations with tunable circumferential waveforms (i.e., diamond mode, alternating ellipses mode, three-lobe mode, etc.) and out-of-plane 3D pattern transformations. These repeatable, large, and fast reconfigurations are attractive for multifunctional robotic applications, enabling superior programming and sequencing capabilities with a single pressure input. In previous studies, metamaterial-based soft grippers have been introduced to achieve either tunable bending in the robotic skins of bending actuators⁴¹ or to obtain grasping due to rotation of rigid appendices attached at the intersection of the metamaterials’ ligaments^42,43. However, the SPoNGe metamaterial introduces a grasping mechanism that leverages the deformation of the cylindrical soft walls of the unit cells of the porous metamaterial itself to achieve sequential and distributed forces to fragile objects and control fluidic channels.

Fig. 1: The SPoNGe metamaterial.

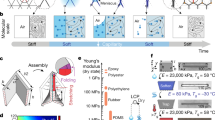
a 3D schematic of the metamaterial with its hollow interior and single pneumatic input, b 2 × 2 supercell, c Single unit cell with geometric properties, d Pressure loading acting on the unit cell for positive internal pressure, e Experimental deformed two-lobe diamond mode shape, f Experimental deformed two-lobe alternating ellipse mode shape, g Experimental deformed three-lobe mode shape. The arrows at the bottom indicate that as the height of the sample decreases, the lobe count of the deformed structure increases.

With a combination of theory, numerical simulations, and experiments, we investigate how the deformation of the cylindrical shells determines the number of lobes of the deformed cellular metamaterial, while the alignment of the lobes is governed by the deformation of the top and bottom plates. Together, the plates and the cylindrical shells define the buckled mode shapes and the critical buckling pressures of the SPoNGe metamaterial, which is preprogrammed through the selection of geometric parameters. In soft robotic applications, the number of lobes of the deformed cylindrical shells allows for control over the number of touch-points used to engage with objects to be grasped. To elicit desired functionalities, we illustrate the new features of the SPoNGe metamaterial as a soft gripper to selectively and sequentially grasp slender objects and as a fluidic controller to dispense two fluids at targeted fluidic ratios.

Results

Design and experiments of inflatable cellular metamaterials

We introduce the SPoNGe metamaterial, an inflatable cellular metamaterial made of two porous elastomeric sheets connected by a MxN square array of deformable thin cylindrical shells surrounded by a single cavity and enclosed by four side walls (Fig. 1a–d). To create the internal cavity, the elastomeric (Zhermack Elite Double 8) porous metamaterial is manufactured with a two-step mold and cast process (see Supplementary Information “Manufacturing Additional Details” section for more details). The cavity is actuated by a single pressure input p, which controls the inflation of the whole cellular metamaterial. In terms of geometrical parameters, the cylindrical shells have neutral axis radius R, length L, and thickness h while the top/bottom plates and the side walls have thickness t and a, respectively (Fig. 1c). Assuming the center-to-center distance d between aligned neighboring cylindrical shells, we introduce the porosity Φ of the cellular metamaterial as Φ = πR²/d². Considering h = 1.5 mm, t = 3 mm, a = 3 mm, Φ = π/9, R = 10 mm, we manufacture three 4 × 4 elastomeric samples with three different heights L₁ = 46 mm, L₂ = 36 mm, and L₃ = 25 mm, with M = N = 4 being chosen as the minimum size unaffected by significant boundary effects (see Supplementary Information “Finite Element Models” section for more details). Each sample is actuated by increasing the internal volume using air as working fluid until a sudden and reversible morphological change is observed at a critical buckling pressure p_cr (see Supplementary Information “PV Curves Experimental Set Up” section for more details) and see Supplementary Information “Compressibility Effects” section for more details. We notice that the three samples exhibit three distinct global buckling modes triggered at different p_cr values. The tallest sample (L₁ = 46 mm) deforms at a critical buckling pressure p_cr1 = 0.58 kPa in a two-lobe “diamond” pattern (Fig. 1e) with an alternating orientation of the deformed cylindrical shells along the diagonals of the square lattice. The sample with height L₂ = 36 mm buckles at a critical buckling pressure ${p}_{c{r}_{2}}=0.79$ kPa with a pattern of alternating, mutually orthogonal ellipses (Fig. 1f) reminiscent of the buckling mode observed in a square array of circular holes in an elastomeric matrix³¹. The shortest sample (L₃ = 25 mm) experience buckling at a critical pressure ${p}_{c{r}_{3}}=1.13$ kPa with a three-lobe pattern with 120° symmetry (Fig. 1g).

Buckling upon inflation: numerical validation of the experimental findings

To validate the experimentally observed pattern transformations, we simulate the nonlinear response upon inflation of the three samples using Finite Element (FE) simulations within ABAQUS 2020/Standard. We model the SPoNGe metamaterial using triangular shell elements (S3), and we assume a Neo-Hookean material model with the mechanical properties of the elastomer Zhermack Elite Double 8. To mimic the volume-controlled inflation experiments, we perform dynamic, implicit FE analyses of each sample by fixing the side walls and increasing the internal cavity volume filled with an incompressible fluid (see Supplementary Information “Finite Element Models” section for more details. In Fig. 2, we observe a very good agreement between the numerical and experimental results both in terms of reconfiguration patterns and pressure-volume (PV) curves for all the three samples—two-lobe diamond (Fig. 2a), two-lobe alternating ellipses (Fig. 2b), and three-lobe mode (Fig. 2c). In all the three cases, the critical buckling pressure can be observed as a sudden change in slope in the PV curves corresponding to ${p}_{c{r}_{1}}^{exp}\simeq 0.58$ kPa, ${p}_{c{r}_{2}}^{exp}\simeq 0.79$ kPa, and ${p}_{c{r}_{3}}^{exp}\simeq 1.13$ kPa for first, second, and third sample, respectively (Movie S1). These experimental findings are correctly predicted by the numerical values ${p}_{c{r}_{1}}^{num}\simeq 0.57$ kPa, ${p}_{c{r}_{2}}^{num}\simeq 0.79$ kPa, and ${p}_{c{r}_{3}}^{num}\simeq 1.16$ kPa.

Fig. 2: Buckling upon inflation in the SPoNGe metamaterial.

Experimental (solid line) and numerical (solid line with markers) pressure-volume curves together with the analytical buckling pressure prediction (dashed line) for three samples: a two-lobe diamond deformed shape, b two-lobe alternating ellipse deformed shape, and c three-lobe mode shape. In each subplot, the top left image represents the deformed physical sample and the top right image the corresponding finite element simulation, for a ΔV/V₀ = 0.36, b ΔV/V₀ = 0.44, c ΔV/V₀ = 0.43, respectively. Where ∣u∣ is the magnitude of the displacement within each element and V represents the volume of air within the SPoNGe sample. Here, the nondimensional form ΔV/V₀ is presented to represent the change in volume relative to the sample’s initial volume.

Analytical model

To investigate the role of geometry in determining the critical buckling pressure of the SPoNGe metamaterial, we develop an analytical model capturing the effect of positive pressure on a single unit cell of the metamaterial. The unit cell is composed of a cylindrical shell with square plates of side length d attached to the top and bottom of the cylinder (Fig. 1c). We decompose the effects of positive pressure, p, in the internal cavity into two components (i) normal forces acting on the top and bottom plates which tend to stretch the cylinder and (ii) radial compressive forces (Fig. 1d). The compressive radial pressure tend to buckle the cylindrical shell while the axial tension tends to delay the instability. The critical buckling pressure can be solved by considering the combined effect of each of these loads.

We introduce the following nondimensional parameters to describe the unit cell: cylindrical shell radius $\overline{R}=R/L$, thickness $\overline{h}=h/R$, center-to-center distance $\overline{d}=d/R$, and pressure $\overline{p}=p/E$, where E is the material Young’s modulus. Using the geometry of the unit cell, the nondimensional radial pressure, Q₁, and nondimensional axial pressure, Q₂, can be written in nondimensional form as a function of the internal positive pressure

$${Q}_{1}=\frac{\overline{p}}{\overline{h}}(1-{\nu }^{2})$$

(1a)

$${Q}_{2}=-\frac{\overline{p}}{\overline{h}}\left(\frac{{\overline{d}}^{2}}{2\pi }-\frac{1}{2}\right)(1-{\nu }^{2})$$

(1b)

where ν is the material Poisson’s ratio. Following the approach described in ref. ³⁷, the critical buckling pressure of the structure can be derived and written as

$${p}_{cr}=\frac{{\bar{h}}^{3}}{6({\nu }^{2}-1)}\frac{{a}_{1}{\overline{R}}^{8}+{a}_{2}{\overline{R}}^{6}+\left({a}_{3}+{a}_{4}{\overline{h}}^{-2}\right){\overline{R}}^{4}+{a}_{5}{\overline{R}}^{2}+{a}_{6}}{\left({c}_{1}+{c}_{2}{\overline{d}}^{2}\right){\overline{R}}^{6}+\left({c}_{3}+{c}_{4}{\overline{d}}^{2}\right){\overline{R}}^{4}+\left({c}_{5}+{c}_{6}{\overline{d}}^{2}\right){\overline{R}}^{2}+{c}_{7}}$$

(2)

where the coefficients a₁, . . , a₆ and c₁, . . ,  c₇ are functions of the material Poisson’s ratio ν, the m number of longitudinal half-waves, and n number of circumferential waves of the buckled mode, i.e., the number of lobes observed in the post buckled configuration (see Supplementary Information “Analytical Model” section for more details). In Fig. 2, we compare the analytically predicted critical buckling pressure to the buckling pressure found experimentally and find excellent agreement between all three experimental samples and the predicted values, with the analytical model predicting ${p}_{c{r}_{1}}=0.59$ kPa, ${p}_{c{r}_{2}}=0.96$ kPa, and ${p}_{c{r}_{3}}=1.39$ kPa for the first, second, and third samples, respectively.

The analytical model predicts not only the critical buckling pressure, but also the (m, n) buckling mode shape of the cylindrical shell. The buckling pressure and mode shape correspond to the pair of values of (m, n) which minimize non-negative values of p_cr. In our system only one longitudinal half wave (m = 1) is observed, and thus the expression for critical buckling pressure as a function of n is written as Eq. S19 (see Supplementary Information “Analytical Model” section for more details). The analytical model predicted n = 2, n = 2, and n = 3 for the first, second, and third sample, respectively.

By varying the non-dimensional radius $\overline{R}$ of the cylindrical shell in the unit cell, we predict both the critical buckling pressure and number of circumferential waves n (Fig. 3). It is seen that for tall cylindrical shells ($\overline{R} < < 1$), the structure deformed into a two-lobe mode shape, defined by two circumferential lobes (n = 2, m = 1). As the height of the cylindrical shell decreases, and thus $\overline{R}$ increases, the number of circumferential lobes increases (n = 3, 4, . . . , m = 1) as indicated by the changes in background color in Fig. 3 as well as the critical pressure required for the structure to buckle (Fig. 3). We note that although the analytical model can successfully predict the buckling mode of the cylindrical shells, the approach is unable to predict how the cylindrical shells will align in the pattern reconfiguration of the overall cellular metamaterial.

Fig. 3: Design space of SPoNGe buckling behavior.

Analytical (solid line) and numerical (markers) nondimensional critical buckling pressure ${\overline{p}}_{cr}$ as a function of the nondimensional shell radius $\overline{R}$. Three different cylindrical shell thicknesses $\bar{h}$ are considered. The shaded areas represent the analytically predicted boundaries of the two, three, and four lobe buckling mode shape. The markers indicate the critical buckling pressures found from the FE analyses with periodic boundary conditions. The markers correspond to the diamond mode shape (cross), the alternating ellipse mode shape (plus), three lobe mode shape (triangle), and four lobe mode shape (diamond), respectively. Additionally, white markers with black outlines represent experimentally collected critical pressure values. Here, ∣u∣ is the magnitude of the displacement within each element.

FE design space

To gain a more comprehensive understanding of the global buckling reconfiguration of the SPoNGe metamaterial, we create a FE model assuming periodic boundary conditions of the 2 × 2 supercell (Fig. 3) using a pressure-controlled loading (see Supplementary Information “Finite Element Models” section for more details). We perform a parametric study by varying $\overline{R}$ to evaluate and tabulate the mode shapes and buckling pressures of cellular metamaterials with parameters using linear buckling analyses (Fig. 3). In the design space, good agreement is found between the numerical and analytical predictions of the buckling pressure as well as the lobe count (n = 2, 3, 4, . . , m = 1) of the buckling mode shapes of the cylindrical shell indicated by changes in marker type in Fig. 3. Additionally, the FE model successfully predicts the pattern reconfiguration of the SPoNGe metamaterial (i.e., the mode shape of the metastructure as either two-lobe diamond, two-lobe alternating ellipses or, three-lobe) because it also incorporates the deformation of the top/bottom plates responsible for the interconnection between the cylindrical shells. Interestingly, the two-lobe alternating ellipse region arises in the design space between the two-lobe diamond and the three-lobe mode shapes (Fig. 3).

To further understand the transition between the two-lobe diamond and alternating ellipse regions, we perform a sequence of nonlinear static steps (see Supplementary Information “Finite Element Models” section for more details). By varying $\overline{R}$ across the boundary of the modes, we separately compute the bending U^b and stretching U^s energies of the top/bottom plates (${U}_{plate}^{b}$, ${U}_{plate}^{s}$) and the cylindrical shells (${U}_{shell}^{b}$, ${U}_{shell}^{s}$) to compare the contribution of each structural element to the overall deformation response.

Figure 4a, b report the ratios between bending energy U^b to total elastic strain energy U^t = U^b + U^s for the cylindrical shells ${U}_{shell}^{b}/{U}_{shell}^{t}$ and for the plates ${U}_{plate}^{b}/{U}_{plate}^{t}$, respectively, as a function of $\overline{R}$ and the nondimensional pressure p/p_cr. In Fig. 4a, the ratio ${U}_{shell}^{b}/{U}_{shell}^{t}\simeq 0.1$ for p/p_cr < 1, indicating that the majority of the elastic energy stored in the cylindrical shells arises due to stretching. At the buckling onset (p/p_cr = 1) for all $\overline{R}$, the relative contribution of bending energy ${U}_{shell}^{b}$ rises dramatically, which corresponds to the appearance and propagation of the n-lobe mode shape within the cylindrical shells. In the plate response (Fig. 4b) before the buckling point (p/p_cr < 1), the bending energy ${U}_{plate}^{b}$ contributes more to the total energy ${U}_{plate}^{t}$ than the stretching energy (${U}_{plate}^{b}/{U}_{plate}^{t}\simeq 0.8$), as the applied pressure acts transversely to the plate’s surface. At the onset of buckling, three possible scenarios can emerge depending on the nondimensional radius of the cylindrical shell $\overline{R}$. For $\overline{R}\le 0.185$, the bending energy of the plate ${U}_{plate}^{b}$ increases such that ${U}_{plate}^{b}/{U}_{plate}^{t} > {U}_{shell}^{b}/{U}_{shell}^{t}$ and the diamond mode shape arises (Fig. 4c). For $0.185 < \overline{R}\le 0.25$, after an initial rise, ${U}_{plate}^{b}$ decreases as the pressure increases and the stretching energy eventually contributes more (${U}_{plate}^{b}/{U}_{plate}^{t}\simeq 0.25$) to the response of the system (Fig. 4d). The initial appearance of the diamond mode for p = p_cr corresponds to ${U}_{plate}^{b}/{U}_{plate}^{t} > {U}_{shell}^{b}/{U}_{shell}^{t}$ as in the previous case. However, as the pressure increases, ${U}_{plate}^{b}/{U}_{plate}^{t}$ approaches and eventually becomes smaller than ${U}_{shell}^{b}/{U}_{shell}^{t}$, and consequently, the diamond mode shape transitions into the alternating ellipses configuration (Fig. 4d). For $\overline{R} > 0.25$, the buckling onset (p = p_cr) corresponds to the crossing between ${U}_{plate}^{b}/{U}_{plate}^{t}$ and ${U}_{shell}^{b}/{U}_{shell}^{t}$. Thus, for p > p_cr, ${U}_{plate}^{b}/{U}_{plate}^{t} < {U}_{shell}^{b}/{U}_{shell}^{t}$ and, in turn, the structure buckles directly into the mutually orthogonal alternating ellipses mode shape (Fig. 4e). This mode is dominated by the plate’s in-plane buckling deformation as demonstrated by the dramatic drop of the plate bending energy ${U}_{plate}^{b}$ at the occurrence of the instability (Fig. 4e).

Fig. 4: FE results of the SPoNGe elastic strain energy.

a, b Bending to total energy ratio of the cylindrical shell and the plate, respectively, as the pressure increases for varying values of $\overline{R}$ and $\overline{h}=0.15$. Slice of bending to total energy ratio for both the cylindrical shell and the plate with corresponding FE deformed mode shape for c $\overline{R}=0.18$ with the diamond mode shape (cross), d $\overline{R}=0.22$ with the deformation transitioning from the diamond and alternating ellipse mode shape (asterisk), and e $\overline{R}=0.26$ with the alternating ellipses mode shape (plus).

Exploring modal alignment

To further understand the mechanism resulting in alignment between neighboring cylinders, we developed an empirical model that relates the deflection of the plates to the deflection of the cylinders. Using results from the numerical exploration from the Section “FE Design Space”, we fit a simplified sine series function to the buckling displacements of the plates for one alternating ellipse sample (L = 37 mm) and one diamond sample (L = 57 mm) from a time step wherein the ratio of strain energy to buckling pressure is equal to U_total/p_cr = 0.0125 mm³ (see Supplementary Information “Modal Alignment Modeling Methodology” section for more details). Using the analytical mode shape for the cylindrical shell, we define an error function that depends on the rotation of the cylinder relative to the plate. Namely, we write

$${{\Xi }}(\zeta,\phi,\delta )= \!\! \int_{0}^{2\pi }\left[{({u}_{c}(\theta,x,\zeta,\phi,\delta )-{u}_{p}(\theta,x))}^{2}+{({v}_{c}(\theta,x,\zeta,\phi,\delta )-{v}_{p}(\theta,x))}^{2}\right.\\ +{\left.{({w}_{c}(\theta,x,\zeta,\phi,\delta )-{w}_{p}(\theta,x))}^{2}\right]}_{x=0}d\theta$$

(3)

wherein u, v, and w represent displacements in the three cartesian coordinate directions, ζ represents the unknown amplitude of the buckling deflection, δ represents the unknown amplitude of the cylinders’ elliptical deformation, ϕ represents the unknown rotation of the lobe relative to the plate deformation, and subscripts c and p delineate the cylinder or plate, respectively. By minimizing this penalty function, subject to the constraint that the analytical strain energy is equal to the energy of the FE model, we explore the interaction between the plate and the cylinder (Fig. 5). Figure 5a highlights the penalty function variation as the cylinder’s mode shape rotates for the diamond mode shape. The minimum of the penalty function can be found at ϕ = π/4, corresponding to the diagonal alignment highlighted in the diamond mode shape; the resulting appearance of the structure is shown as well. In contrast, for the alternating ellipse sample shown in Fig. 5b, the penalty minimum can be found at ϕ = π/2, corresponding to a direction aligned with the deflection of the plate. Using this approach wherein the plate and cylinder are modeled separately and coupled through the penalty function, we further refine our understanding that the plate deformation shape directly controls the orientation of the cylinders (see Supplementary Information “Modal Alignment Modeling Methodology” section for more details).

Fig. 5: Plate and cylinder interaction model.

a Exploration of alignment for the diamond mode shape. A minimum for the penalty function can be found when the rotation of the cylindrical shell is equal to π/4, which corresponds to the “diagonal" alignment seen for the diamond samples. b Alignment for the alternating ellipse mode shape. The penalty minimum can be found at rotation π/2, which, for a single cell, represents alignment with the in-plane deflection shape of the plates. Here, L represents the maximum depth of the sample, and d represents the side width (d = 30 mm for each sample).

Enabling selective actuation in soft machines

The programmable buckling response upon inflation of the SPoNGe metamaterial enables a complete novel strategy for grasping delicate and slender objects with tunable forces thanks to distributed touch points. This novel and gentle grasping strategy is reminiscent of the human hand posture for cylindrical grip (Fig. S16). Thanks to several touch points, the SPoNGe metamaterial enables to safely handle delicate plants made of thin and slender filament leaves, such as sprouts or grass as showcased in Fig. S17 and Movie S2 with the grasp of the flowering plant Dactylis glomerata. With a single pressure input, sequencing and selective actuation capabilities can be introduced in soft robots. We design a gripper capable of selectively grasping rows of test tubes using a single pressure input (Fig. 6). The touch points of the gripper are controlled by the buckling of the cylindrical shells that can be tuned by varying their geometrical properties, such as their thickness h, which also produces variations in grasping force (see Supplementary Information “Pressure-Force Relationship” section for more details). To grasp either only one row of test tubes or both rows of test tubes in an array, we leverage the periodic structure of a 4 × 2 cellular metamaterial (see Supplementary Information “Test Tube Gripper Experimental Set Up” section for more details) with the right and left row with cylindrical wall thickness of h₁ = 1.5 mm and h₂ = 2.5 mm, respectively (Fig. 6). Our analytical model predicts the critical buckling pressure of the right row p_1,cr = 0.94 kPa, while the left row will buckle at a pressure, p_2,cr = 3.71 kPa.

Fig. 6: SPoNGe metamaterial as a selective gripper.

By actuating the SPoNGe metamaterial to different pressures either one row (trial 1, p_1,g < p < p_2,g) or both rows (trial 2, p > p_1,g, p_2,g) of test tubes could be grasped and moved. The pressure-volume curves demonstrate that each trial consists of (i) centering material above the rows of test tubes, (ii) lowering the material onto the array of test tubes (iii) pressurizing to the corresponding pressure and selectively raising the desired rows of tests tubes (iv) moving the grasped rows of test tubes to the opposite side of the holder (v) aligning the metamaterial above the holes of the test tube rack (vi) releasing the pressure dropping the test tubes into their new location.

As the pressure continues to increase beyond p_1,cr, but below p_2,cr, the cylinders continue to deform until only the row of buckled cylinders will contact the test tubes. The pressure which makes contact with the test tubes with sufficient normal force to grasp the test tube is denoted p_1,g = 1.69 kPa. Similarly, beyond p_2,cr there will be a higher pressure which buckles and deforms the second row enough to grasp the second row of test tubes, p_2,g = 4.05 kPa. Raising the pressure beyond the first grasping pressure, but below the second p_1,g < p < p_2,g, results in grasping and moving only one row of the test tube (Fig. 6 Trial 1). However, if the applied pressure exceeds both row’s grasping pressure p > p_2,g, then all the cylindrical shells in the metamaterial will collapse to grasp and move all the test tubes (Fig. 6 Trial 2). For additional reference, see movie S3.

As a second demonstration of the multifunctional capabilities of the SPoNGe metamaterial, we harness selective buckling instabilities to control and dispense two fluids in specified ratios using only a single pressure inlet (Fig. 7). A 2 × 1 sample of the metamaterial was manufactured (see Supplementary Information “Fluidic Control Experimental Set Up” section for more details) with one cylindrical shell of thickness h₁ = 2.5 mm and buckling pressure p_1,cr = 3.17 kPa and the other cylindrical shell with wall thickness of h₂ = 1.5 mm with buckling pressure of p_2,cr = 0.63 kPa. Reservoirs were placed overhead the cellular metamaterial with plastic tubing running from the reservoir through the metamaterial’s pores (Fig. 7a). One reservoir was filled with a fluid f₁ (i.e., coffee) and ran through the cylindrical shell with the higher buckling pressure while the other reservoir was filled with another fluid f₂ (i.e., cream) and ran through the cylindrical shell with the lower pressure.

Fig. 7: SPoNGe metamaterial as a fluidic controller.

a Experimental set up consisting of coffee (fluid f₁), and cream (fluid f₂) in fluid reservoirs above the SPoNGe metamaterial with thin tubing through the sponge. b The analytical predicted concentration of f₂, η (dashed line), compared with the experimental values (points). c The time vs. pressure response for each trial indicating the amount of time spent in the critical pressure regions p_{2, g} < p < p_{1, g} and p < p_{2, g}. d Physical values of η visualized as the percentage of cream added to the coffee.

Similar to the grasping pressure of the gripper, beyond the buckling pressure of the metamaterial there are pressures where the SPoNGe metamaterial contacts and squeezes the tubes, stopping the flow of the fluid. At these pressures the pore grasps and pinches the plastic tubing, preventing flow through the tube. The fluid flow in the first tube and second tubes are stopped at p_1,g = 3.30 kPa and p_2,g = 0.92 kPa, respectively. The difference in critical grasping pressures between the two shells allows to obtain one of three states with a single pressure inlet (i) both tubes closed p>p_1,g, (ii) tube 1 open and tube 2 closed p_1,g > p > p_2,g, or (iii) both tubes open p < p_2,g. By controlling the time spent in each of these states, the ratio of the two fluids is controlled and the desired ratio of coffee to cream can be obtained.

To determine analytically the time needed at each pressure to achieve a desired ratio between the two fluids, we consider the time t₁ when only f₁ is flowing, and t₂ the time when both fluids are flowing. The f₂ tube was designed with a higher flow rate (q_f2 = 4 mL/s) than the f₁ tube (q_f1 = 2.5 mL/s) such that a larger range of f₂ concentrations can be obtained (see Supplementary Information “Fluidic Control Experimental Set Up” section for more details). The concentration η of the fluid f₂ in the mixture can then be expressed as

$$\eta=\frac{{q}_{f2}{t}_{2}}{{q}_{f1}({t}_{1}+{t}_{2})+{q}_{f2}{t}_{2}}$$

(4)

and the time ratio T between the flowing of fluid 2 and the total time (t₁ + t₂) can be expressed as

$$T=\frac{{t}_{2}}{{t}_{1}+{t}_{2}}=\frac{\eta \,{q}_{f1}}{{q}_{f2}-\eta \,{q}_{f2}}$$

(5)

Figure 7b–dreport five mixtures of f₁ and f₂ with varying concentration η = 0, 5, 20, 40, 50% from darkest coffee to lightest by controlling the time spent in each pressure range. Using a single pressure inlet and controlling the time spent in each pressure range, a personalized cup of coffee can be created with a desired percentage of cream to coffee (Movie S4). The experimental percentage of cream (η) was calculated from the recorded amount of each fluid added to the cup. To determine experimental values for T, we extract the duration of time the SPoNGe spends at steady state in state (ii) (t₁) and at steady state in state (iii) (t₂) from the gathered pressure-time response curves. Then, we manually compute the time ratio T using the resulting values in Eq. (5). Plotting the realized value of η against the predicted value shows excellent agreement between the analytically predicted values (Fig. 7b).

Discussion

We have presented a new cellular metamaterial with an internal pressure cavity acting on a network of cylindrical shells interconnected by top and bottom plates. When actuated with positive pressure, the porous metamaterial demonstrates a global reconfiguration based on the buckling instability controlled by the interplay between the response of the cylindrical shells and the top/bottom plates. By accurately tuning the geometrical properties, a variety of buckling-based pattern reconfigurations emerge spanning from two-lobe diamond, two-lobe alternating ellipses, and three-lobe. We demonstrated that the critical buckling pressure can be successfully predicted with an analytical model of a cylindrical shell subjected to a combination of radial compression and axial tension. While the analytical approach can determine the number of lobes n of the cylindrical shells’ buckling modes, the global alignment and synchronization of the mode shape is controlled by the interplay between the plates and the cylindrical shells deformations that can be successfully predicted by the FE model. Experiments were used to validate the numerical and analytical findings and novel functionalities have been explored in the field of soft robotics with a single pressure input. A selective gripper with sequencing capabilities and distributed touch points has been introduced. Finally, a soft device able to operate multiple fluidic channels to obtain a target fluidic mixture has been discussed. Future studies could explore the buckling behavior upon inflation of different lattices, such as triangular, hexagonal, and rhombi-trihexagonal lattices to further expand the design space of the SPoNGe metamaterial platform. Specifically, in triangular lattices, the role geometric frustration could be investigated to further enhance 3D buckling-based deformations upon inflation. The SPoNGe metamaterial uncovers new properties of buckling-based metamaterials upon inflation with unique applications in preprogrammable and multifunctional soft intelligent materials.

Methods

The manufacturing details and the fabrication process are reported in (Supplementary Information S1). The experimental set-up for determining the pressure-volume curves is described in (Supplementary Information S2) and (Supplementary Information S3). The FE model is described in (Supplementary Information S4) and the analytical approach in (Supplementary Information S5). The analytical method used to predict the alignment of neighboring cylinders is discussed in (Supplementary Information S6). The gripping force pressure relationship is described in (Supplementary Information S7). The test tube gripper experimental set up and the fluidic control experimental set up are reported in (Supplementary Information S8) and (Supplementary Information S9), respectively.