Solving the many-electron Schrödinger equation with a transformer-based framework

Abstract

Accurately solving the Schrödinger equation for intricate systems remains a prominent challenge in physical sciences. Here we present QiankunNet, a neural network quantum state (NNQS) framework that combines Transformer architectures with efficient autoregressive sampling to solve the many-electron Schrödinger equation. At its core is a Transformer-based wave function ansatz that captures complex quantum correlations through attention mechanisms, effectively learning the structure of many-body states. The quantum state sampling employs layer-wise Monte Carlo tree search (MCTS) that naturally enforces electron number conservation while exploring orbital configurations. The framework incorporates physics-informed initialization using truncated configuration interaction solutions, providing principled starting points for variational optimization. Our systematic benchmarks demonstrate QiankunNet’s versatility across different chemical systems. For molecular systems up to 30 spin orbitals, we achieved correlation energies reaching 99.9% of the full configuration interaction (FCI) benchmark, setting a new standard for neural network quantum states. Most notably, in treating the Fenton reaction mechanism, a fundamental process in biological oxidative stress, QiankunNet successfully handled a large CAS(46e,26o) active space, enabling accurate description of the complex electronic structure evolution during Fe(II) to Fe(III) oxidation.

Introduction

Recently, the Transformer architecture has revolutionized the field of natural language processing (NLP), giving rise to large language models (LLMs) with unprecedented capabilities^1,2,3,4,5. Intrinsic versatility and adaptability of the Transformer architecture serve as the backbone of these LLMs, making it a powerful tool for addressing complex challenges, and its applications are extending far beyond language processing, permeating various domains and revolutionizing numerous fields. Particularly, deploying this architecture within the scientific field harbors the potential to propel us towards untapped frontiers of innovation and discovery. While the Transformer has demonstrated exceptional performance in tasks like image recognition^6,7, protein representation and protein design^8,9,10, and global weather forecasting¹¹, and has shown promise in various quantum physics applications^12,13,14, its potential for solving molecular Schrödinger equations through efficient autoregressive sampling and systematic application to complex chemical systems remains underexplored. Therefore, it is both fundamentally intriguing and practically important to explore the design of efficient Transformer-based architectures specifically tailored for solving the Schrödinger equation. Such architectures are expected to unlock new levels of understanding and advancements in quantum chemistry.

In principle, the electronic structure and properties of all materials can be determined by solving the Schrödinger equation to obtain the wave function. However, in practice, it is a significant challenge to find a general approach to reduce the exponential complexity of the many-body wave function and extract its essential features. Various methods have been developed to solve the Schrödinger equation for realistic systems. Considering the fermionic nature of electrons, Slater determinants are used to represent the electron systems, ensuring that the wave function obeys exchange antisymmetric symmetries. While the full configuration interaction (FCI) method provides a comprehensive approach to obtain the exact wavefunction, the exponential growth of the Hilbert space limits the size of feasible FCI simulations. To approximate the exact energy, several strategies have been devised, including perturbation theories^15,16, the truncated configuration interaction which takes into account arbitrary linear combinations of excitations up to a certain order¹⁷, the coupled-cluster (CC) method which takes into account certain nonlinear combinations of excitations up to a certain order (e.g., CCSD, CCSD(T))¹⁸, the density matrix renormalization group (DMRG) algorithm^19,20 which uses the one-dimensional matrix product state wave function ansatz, or the variational Monte Carlo (VMC) method^21,22,23 which works for any wave function ansatz. However, these methods can fail in numerous cases, mostly due to the limited expressive power of the wave function ansatz.

In 2017, Carleo and Troyer proposed their seminal work on the neural network quantum state (NNQS) algorithm, which introduced a groundbreaking approach for tackling many-spin systems within the exponentially large Hilbert space²⁴. The main idea behind NNQS is to parameterize the quantum wave function with a neural network and optimize its parameters stochastically using the VMC algorithm. They also demonstrated that the neural network ansatz, when dealing with many-body quantum states, is more expressive than the tensor network states^{25,26,27,28,29}, and its computational cost typically scales polynomially³⁰. Moreover, as a general feature of Monte Carlo methods, large-scale parallelization can provide notable performance advantages. The NNQS framework has evolved along two distinct paths: first quantization^14,30,31, which works directly in continuous space, and second quantization^{12,13,32,33,34,35,36,37,38,39,40,41,42}, which operates in a discrete basis. While first quantization methods naturally incorporate the complete basis set limit, they face challenges in sampling efficiency, particularly for larger systems where Markov chain sampling can become ineffective. Second quantization methods, though better at enforcing symmetries and boundary conditions, encounter scalability limitations due to the rapid growth of computational costs with system size. Current implementations face two major challenges: the computational burden of energy evaluation, which scales as the fourth power of the number of spin orbitals, and the increasing complexity of neural network architectures required for larger systems^32,33. Molecular systems present additional challenges due to their complex electronic correlation patterns. This complexity demands highly expressive models that can be efficiently scaled to capture intricate quantum effects while remaining computationally tractable. The development of such models, capable of balancing expressiveness with computational efficiency, remains a central challenge in the field.

In this work, we present QiankunNet (Qiankun meaning “heaven and earth” in Chinese), a NNQS framework that combines the expressivity of Transformer architectures with efficient autoregressive sampling. At the heart of our approach lies a Transformer-based wave function ansatz that captures complex quantum correlations through its attention mechanism, effectively learning the structure of many-body states while maintaining parameter efficiency independent of system size, as illustrated in Fig. 1. Building upon the autoregressive sampling approach introduced in the Neural Autoregressive Quantum States (NAQS) method by Barrett et al.³³, we develop an efficient batched implementation that reformulates quantum state sampling as a tree-structured generation process. While NAQS demonstrated autoregressive sampling for quantum states, our implementation specifically leverages the Transformer architecture’s parallel processing capabilities and introduces several key innovations: we adopt a Monte Carlo Tree Search (MCTS)-based autoregressive sampling approach that introduces a hybrid breadth-first/depth-first search (BFS/DFS) strategy. This provides more sophisticated control over the sampling process through a tunable parameter that allows adjustment of the balance between exploration breadth and depth. Specifically, our approach first uses BFS to accumulate a certain number of samples, then performs batch-wise DFS sampling. This strategy significantly reduces memory usage while enabling computation of larger and deeper quantum systems by managing the exponential growth of the sampling tree more efficiently. We also implement explicit multi-process parallelization for distributed sampling, going beyond the single-process GPU parallelization used in NAQS. This enables our method to partition unique sample generation across multiple processes, significantly improving scalability for large quantum systems. Moreover, our implementation incorporates key-value (KV) caching specifically designed for Transformer-based architectures. While NAQS uses MLP-based models that don’t benefit from such caching, our Transformer-based approach achieves substantial speedups by avoiding redundant computations of attention keys and values during the autoregressive generation process. This approach eliminates the need for Markov Chain Monte Carlo methods, allowing direct generation of uncorrelated electron configurations. The framework is further enhanced by our physics-informed initialization scheme that incorporates truncated configuration interaction solutions, providing a principled starting point for variational optimization and significantly accelerates convergence. The framework’s efficiency stems from our parallel implementation of local energy evaluation, utilizing a compressed Hamiltonian representation that significantly reduces memory requirements and computational cost. The sampling implementation employs an efficient pruning mechanism based on electron number conservation, substantially reducing the sampling space while maintaining physical validity. This combination of architectural innovations and computational optimizations enables QiankunNet to achieve both high accuracy and robust convergence. Our systematic benchmarks demonstrate unprecedented accuracy across diverse chemical systems: for molecular systems up to 30 spin orbitals, we achieve correlation energies reaching 99.9% of the FCI benchmark; most notably, in treating the Fenton reaction mechanism, QiankunNet successfully handles a large CAS(46e,26o) active space, enabling accurate description of complex transition metal electronic structure. These advances, from weak intermolecular forces to strongly correlated transition metal systems, demonstrate QiankunNet’s broad applicability and pave the way for accurate quantum chemical calculations of previously intractable large-scale molecular systems. The remainder of this paper is organized as follows: we first present the theoretical framework of QiankunNet, followed by detailed benchmarks on various molecular systems, and conclude with discussions on future applications and potential improvements.

Fig. 1: QiankunNet: Neural Network Quantum State (NNQS) Transformer pipeline.

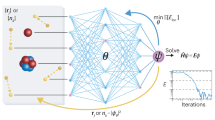
a The decoder-only Transformer architecture for the electron wave function ansatz, where the Transformer generates the amplitude ∣ψ(x)∣ and a multi-layer perceptron (MLP) generates the phase ϕ(x). The wave function is expressed as ψ(x) = ∣ψ(x)∣e^iϕ(x). b Training workflow of the variational Monte Carlo (VMC) optimization. Starting from physics-informed initialization, the model parameters are updated through gradient descent to minimize the energy expectation value. The process involves autoregressive sampling of electron configurations, local energy calculation, and parameter updates via backpropagation.

Results

To validate the effectiveness of QiankunNet, we compute the ground state energies of several molecules with an atomic basis set and compare them to results of other methods, such as Hartree-Fock (HF) and coupled cluster with up to double excitations (CCSD). Using a finite basis set, we can express the molecular Hamiltonian in the second quantized form:

$${\hat{H}}^{e}=\sum\limits_{p,q}{h}_{q}^{p}{\hat{a}}_{p}^{{{\dagger}} }{\hat{a}}_{q}+\frac{1}{2}\sum\limits_{p,q,r,s}{g}_{r,s}^{p,q}{\hat{a}}_{p}^{{{\dagger}} }{\hat{a}}_{q}^{{{\dagger}} }{\hat{a}}_{r}{\hat{a}}_{s}$$

(1)

Through the Jordan-Wigner transformation, this electronic Hamiltonian can be mapped to a spin Hamiltonian:

$$\hat{H}=\sum\limits_{i=1}^{{N}_{h}}{w}_{i}{\sigma }_{i}$$

(2)

where σ_i are Pauli string operators and w_i are real coefficients.

We also report results from NNQS methods using other neural-network ansatz (NAQS and MADE). As demonstrated in Table 1, QiankunNet achieves chemical accuracy in correlation energies, recovering 99.9% of the FCI ground-truth values across a benchmark set of 16 molecules. The method demonstrates encouraging performance when computing full potential energy surfaces, as evidenced by the C₂ and N₂ calculations with STO-3G basis set (Fig. 2). Notably, QiankunNet captures the correct qualitative behavior in regions where standard CCSD and CCSD(T) methods show limitations, particularly at dissociation distances where multi-reference character becomes significant. While more advanced methods like DMRG would provide more rigorous benchmarks for strongly correlated systems, our comparison with CCSD and CCSD(T) illustrates QiankunNet’s potential for handling challenging electronic structures. A comprehensive analysis of the model’s performance with respect to its hyperparameters and pre-training strategies is provided in the Supplementary Information (Fig. S2).

Table 1 Ground state energies (in Hartree) calculated using QiankunNet with the STO-3G basis set

Fig. 2: Potential energy curves for C₂ and N₂.

Comparison of the energies obtained using QiankunNet and other traditional quantum chemistry approaches for a C₂ and b N₂, as a function of the nuclear separation with STO-3G basis set. QiankunNet outperforms all other approximation techniques. It agrees with full configuration interaction (FCI) results well even at structures where both coupled-cluster approaches (CCSD,CCSD(T)) failed due to the presence of strong correlations. FCI represents the exact solution within a given basis set. Source data for the results are provided as a Source Data file.

When comparing with other second-quantized NNQS approaches, the Transformer-based neural network adopted in QiankunNet can exhibit heightened accuracy. For example, the second quantized approaches, such as MADE method, cannot achieve the chemical accuracy for N₂ system, while QiankunNet can achieve an accuracy two orders of magnitude higher. Another advanced second quantized method, NAQS, employs a multilayer perceptron (MLP) augmented with hard-coded pre- and post-processing steps to maintain the autoregressive property. However, the complexity of NAQS’s neural network scales with the number of spin orbitals, leading to a dramatic increase in computational demands and memory usage as the system size grows. For instance, for a C₂H₄O molecule with 38 spin orbitals, the GPU VRAM requirement soars to an unsustainable 454 GB, far surpassing the 80GB memory capacity of an A100 GPU. Conversely, QiankunNet incorporates a decoder-only Transformer, making the number of network parameters independent of the number of spin orbitals (our model can potentially be simultaneously used for systems with different numbers of spin orbitals), as a result, QiankunNet demonstrates a more favorable time scaling compared to NAQS, for systems with fewer than 24 spin orbitals, NAQS calculation is faster. However, when assessing a system with 30 spin orbitals, like Li₂O, QiankunNet boasts a computational speed 10 times faster than NAQS, and the calculations with QiankunNet can be extended to chemical systems up to 92 spin-orbitals, as illustrated in Fig. 3. Beyond speed, our QiankunNet also exhibits higher accuracy. For instance, in the Li₂O case, while NAQS captures 98.1% of the electron correlation energy, QiankunNet recovers an impressive 99.9% of the electron correlation energy. We also perform the calculation for the C₂H₄O molecule comprising 38 spin orbitals, and our method yields an energy of −151.1228 Ha, which is 2.32 mHa lower than the MADE approach (−151.12048 Ha)³⁴. A detailed analysis of QiankunNet against other state-of-the-art Neural NNQS methods is presented in the Supplementary Information (Sec. S5, Tab. S2 and Fig. S1). We have also included results for the N₂ molecule with bond length 2.118 Bohr in the cc-pVDZ basis set, which represents a significant computational challenge beyond the reach of conventional FCI methods. The N₂/cc-pVDZ system (56 qubits, 14 electrons) contains 1.402 × 10¹² configurations, making it intractable for FCI calculations. To our knowledge, no existing NNQS approaches have successfully tackled molecular systems of this scale in the full cc-pVDZ basis without approximations. Our method achieves a ground-state energy of −109.2788 Ha, which differs from the best DMRG result (−109.2821 Ha)⁴³ by only 3.3 mHa. This represents the first demonstration of an NNQS method successfully handling a molecular system with over 10¹² configurations, showcasing the method’s capability beyond small, trivially-solvable systems. It is worth noting that our current calculation employs RHF orbitals as the single-particle basis. As demonstrated in quantum Monte Carlo studies⁴⁴, using UHF orbitals typically leads to lower variational energies than using RHF orbitals. We expect that adopting UHF orbitals would further improve our energy and bring it even closer to the DMRG benchmark. However, even with RHF orbitals, our method achieves an accuracy within chemical precision (3.3 mHa), demonstrating the robustness of our approach across different orbital choices.

Fig. 3: The performance comparison between Neural Autoregressive Quantum States (NAQS)³³ and QiankunNet in simulating real chemical systems.

The measurements here refer to the wall-clock time during which these two methods perform calculations until convergence is achieved. All runtime measurements were obtained with exclusive access to computational resources to ensure accurate benchmarking. Experiments were conducted on one NVIDIA A100 GPU. Source data for the results are provided as a Source Data file.

Building upon these promising results, we now turn our attention to more complex reactions. The Fenton reaction, a fundamental process involving Fe(II) oxidation by hydrogen peroxide, plays a crucial role in biological oxidative stress and has significant implications in cellular damage mechanisms. Since its discovery in 1894⁴⁵, this reaction has been the subject of intense mechanistic debate^46,47,48. While the mechanistic details remain controversial, here we focus on examining the electronic structure of its key step using our NNQS approach. Specifically, we study the homolytic dissociation of H₂O₂ catalyzed by aqueous Fe(II) at low pH, which generates OH• radicals and Fe(III) species:

$${{{{\rm{Fe}}}}}^{2+}+{{{{\rm{H}}}}}_{2}{{{{\rm{O}}}}}_{2}\to [{{{{\rm{Fe}}}}}^{2+}({{{\rm{HOOH}}}})]\to [{{{{\rm{Fe}}}}}^{3+}({{{{\rm{OH}}}}}^{-})]+{{{{\rm{OH}}}}}^{\bullet }$$

(3)

We focus on the electronic structure of the reaction’s key step: the homolytic bond dissociation in [Fe(H₂O)₅H₂O₂]²⁺. This octahedral complex, formed by substituting one water molecule in [Fe(H₂O)₆]²⁺ with hydrogen peroxide, serves as a model system for studying the aqueous ferrous ion’s reactivity. The transition state geometry was optimized at the UB3LYP/def2-TZVP level of theory⁴⁹. Our quantum simulation employs a CAS(46e,26o) active space with cc-pVTZ basis sets, where the active orbitals are selected using the automated AVAS (Automated Virtual Active Space) method⁴⁹ (computational details are provided in Supplementary Information, Sec. S6, Tab. S3). This represents a significant expansion compared to previous studies ⁴⁹ that employed a CAS(20e,13o) active space targeting only O2s+2p and Fe 3d electron shells. As shown in Fig. 4, our calculations reveal a higher transition state barrier (83 kcal/mol compared with 65 kcal/mol in previous work). The combination of a large basis set (cc-pVTZ) and extensive active space (46e,26o) enables us to accurately capture the electronic structure evolution during Fe-O bond cleavage. This success is particularly significant for transition metal chemistry, where the multi-reference character of electronic structures often challenges traditional methods. However, for a more complete description of this system, several additional factors need to be considered. While we use the relatively large cc-pVTZ basis set, even larger basis sets might be necessary for achieving higher accuracy in transition metal systems. Additionally, relativistic effects can significantly influence the electronic structure of transition metal complexes. Furthermore, given that this reaction occurs in solution, the inclusion of solvation effects is particularly important for obtaining quantitatively accurate energetics. These factors, while beyond the scope of our current study focusing on the electronic structure of the gas phase reaction, are crucial considerations for future investigations aiming at a comprehensive understanding of the Fenton reaction mechanism.

Fig. 4: Simulation of the Fenton reaction mechanism along the intrinsic reaction coordinate (IRC).

The blue curve represents our work using an expanded (46e,26o) active space, while the green dashed curve shows previous results from ref. ⁴⁹ using a (20e, 13o) active space. The reaction pathway exhibits three distinct stages: initial formation of [Fe(H₂O)₅(H₂O₂)]²⁺ through H₂O₂ coordination to the octahedral [Fe(H₂O)₆]²⁺ complex (left molecular structure); transition state featuring O-O bond elongation (middle); and product state comprising an OH• radical and [Fe(OH)(H₂O)₅]²⁺ complex (right). Our larger active space calculations reveal a higher energy barrier (83 kcal/mol, compared with 65 kcal/mol) and more pronounced energy differences along the reaction pathway, particularly in the transition and product regions. Electronic structure calculations were performed incorporating Fe 3d and O 2s+2p shells with cc-pVTZ basis sets. Source data for the results are provided as a Source Data file.

Discussion

In this study, we introduce QiankunNet, which adapts the Transformer architecture to solve the many-electron Schrödinger equation. This marks a significant advancement in applying language model architectures to understand quantum electronic structures—the fundamental language of microscopic nature. Just as Transformer models have revolutionized NLP and protein structure prediction, we demonstrate their potential in capturing the intricate patterns of electron wave functions.

We acknowledge the pioneering work of Psiformer¹⁴ in applying attention mechanisms to electron–electron interactions. Through first-quantization approaches and complete variational treatment of basis sets, Psiformer achieved impressive absolute energies. Our approach complements this development by incorporating active space methods, allowing us to focus on chemically relevant orbitals and directly apply physical and chemical insights. This proves particularly advantageous when dealing with complex electronic structures and weak interactions. QiankunNet’s distinctive feature lies in its decoder-only Transformer architecture combined with MCTS autoregressive sampling. Unlike traditional Markov Chain Monte Carlo methods that require sample rejection and suffer from correlation issues, our autoregressive approach generates independent samples directly. The network learns during both sampling and inference phases, enhancing efficiency through parallel batch processing. This design makes QiankunNet particularly well-suited for GPU acceleration and large-scale applications.

This study establishes a fundamental connection between language modeling architectures and quantum electronic structure calculations. By adapting Transformer models to solve the many-electron Schrödinger equation, we demonstrate their capability in capturing complex quantum mechanical phenomena. The success of neural network wavefunctions in ab initio calculations, exemplified by approaches like Psiformer and QiankunNet, suggests a promising direction for quantum chemistry. These methods combine high accuracy, scalability, and computational efficiency, offering new possibilities for electronic structure calculations of complex molecular systems. The integration of physical insights through active space methods and direct sampling techniques further enhances their practical utility. We anticipate that such neural network-based approaches will become increasingly important tools in quantum chemistry, complementing existing methods in tackling challenging molecular systems.

Methods

QiankunNet with transformer architecture

In the study of quantum systems, we encounter complex structures characterized by N interacting components, each represented by discrete quantum variables $\left\vert {{{\bf{x}}}}\right\rangle=\{{x}_{1},{x}_{2},...{x}_{N}\}$. These variables might represent various physical quantities such as spin state or particle occupation numbers. The challenge lies in describing the many-body wave function, which establishes a sophisticated mapping between the configuration space and a vast landscape of complex numbers.

$$\left\vert \Psi \right\rangle=\sum\limits_{{{{\bf{x}}}}}\left\langle \right.{{{\bf{x}}}}\left\vert \Psi \right\rangle \left\vert {{{\bf{x}}}}\right\rangle=\sum\limits_{{{{\bf{x}}}}}\Psi ({{{\bf{x}}}})\left\vert {{{\bf{x}}}}\right\rangle$$

(4)

where each configuration is represented by an occupation number vector $\left\vert {{{\bf{x}}}}\right\rangle=\{{x}_{1},{x}_{2},...,{x}_{N}\}$, with x_i ∈ {0, 1} indicating whether the i-th spin orbital is occupied or not. This mapping encodes both magnitude and phase information of the quantum state, essentially serving as a transformation engine that converts a given many-body configuration x into its corresponding quantum mechanical description Ψ(x). By leveraging artificial neural networks, we aim to construct an efficient approximation of the wave function’s behavior. This neural network approach effectively creates a trainable computational framework that learns to replicate the wave function’s response to different input configurations. Among the various neural architectures available in modern machine learning, we focus our investigation on the Transformer framework, particularly in its application to quantum many-body systems. The Transformer architecture implements a sophisticated attention-based structure: an embedding layer that maps the physical configurations into a high-dimensional representation space, followed by multiple self-attention layers that capture the intricate correlations between quantum variables. The architecture is particularly well-suited for quantum systems due to its ability to model long-range interactions and complex quantum correlations through its multi-head attention mechanism. The connection between NLP and quantum chemistry represents a substantive interdisciplinary bridge rather than a superficial analogy. By establishing a formal mathematical isomorphism between configuration strings in quantum systems and sentences in language models, we address the shared challenge of exponential complexity that has long hindered progress in both fields. Specifically, the Hilbert space dimension of 2^N for N spin orbitals parallels the exponential growth of possible sentences in natural language, creating a compelling theoretical foundation for methodological transfer. In our implementation, Transformer architectures represent quantum wave functions with quantum bitstrings serving as inputs to predict the wave function. Particularly noteworthy is how the autoregressive property of Transformers enables efficient modeling of conditional probabilities in quantum states, mirroring their function in language prediction.

Our QiankunNet consists of two complementary sub-networks: the amplitude sub-network and the phase sub-network. This dual-network architecture effectively captures both the magnitude and phase information necessary to fully describe a quantum state:

$$\Psi ({{{\bf{x}}}})=| \Psi ({{{\bf{x}}}})| {e}^{i\phi ({{{\bf{x}}}})},$$

(5)

where the amplitude sub-network is constructed using a Transformer decoder to represent the probability ∣Ψ(x)∣², while the phase sub-network ϕ(x) employs a multi-layer perceptron (MLP) as shown in Fig. 1a. The Transformer architecture^1,5 is built from layers, each containing a self-attention component composed of multiple independent attention heads. These heads operate in parallel, each with its own set of parameters, allowing the network to simultaneously learn different types of correlations. Within each head, the attention mechanism works by computing how relevant each input position is to every other position, creating a rich network of relationships within the quantum state configuration. The processing of quantum states through our Transformer network follows a carefully designed sequence of steps. The initial state of the decoder is calculated using the input token vector and the position embedding matrix. We prepare the input by adding a special marker (a zero bit) at the beginning of the binary configuration. This augmented input then undergoes an embedding process, where each binary value is transformed into a rich, high-dimensional representation that captures the quantum mechanical properties of the system. The network takes as input a token/qubit vector x = {x₁, x₂, . . . , x_n} of length n, which is transformed into embeddings:

$$P{E}^{(0)}=[e({x}_{1}),e({x}_{2}),\ldots,e({x}_{n})]+P\in {{\mathbb{R}}}^{n\times {d}_{{{{\rm{model}}}}}}$$

(6)

where e(x_i) represents the d_model-dimensional learnable embedding of token x_i, P is the matrix of learnable position embeddings, and PE⁽⁰⁾ contains the combined embeddings for the input sequence at the initial layer. Position information plays a crucial role in quantum states, so we incorporate learned positional encodings for each site in the configuration. These encodings help the network understand the spatial relationships between different components of the quantum system. The embedded and position-encoded information then flows through multiple identical Transformer layers. Each layer in our architecture processes the quantum state information through several stages. The masked multi-head attention mechanism allows the network to learn complex correlations while maintaining the autoregressive property—ensuring that each position only influences those that come after it. For each decoder layer l = 1, 2, …, L, the following operations are performed: The masked multi-head self-attention mechanism computes:

$${{{{\rm{Attention}}}}}^{(l)}(Q,K,V)={{{\rm{softmax}}}}\left(\frac{Q{K}^{T}}{\sqrt{{d}_{k}}}+M\right)V$$

(7)

where $Q=P{E}^{(l-1)}{W}_{Q}^{(l)}$, $K=P{E}^{(l-1)}{W}_{K}^{(l)}$, and $V=P{E}^{(l-1)}{W}_{V}^{(l)}$ are the queries, keys, and values linearly transformed from the positionally encoded embeddings PE^(l−1), M is the mask ensuring autoregressive property, and d_k is the dimension of the keys. Residual connections and layer normalization are applied:

$${H}^{(l)}=P{E}^{(l-1)}+{{{{\rm{Sublayer}}}}}^{(l)}\left({{{\rm{LayerNorm}}}}(P{E}^{(l-1)})\right)\in {{\mathbb{R}}}^{n\times {d}_{{{{\rm{model}}}}}}$$

(8)

where Sublayer^(l)(PE^(l−1)) represents the output of the masked multi-head self-attention sublayer for layer l. Position-wise feed-forward networks with GeLU activation function process the information:

$${{{{\rm{FFN}}}}}^{(l)}(H)={{{\rm{GeLU}}}}({H}^{(l)}{W}_{1}^{(l)}+{b}_{1}^{(l)}){W}_{2}^{(l)}+{b}_{2}^{(l)}\in {{\mathbb{R}}}^{n\times {d}_{{{{\rm{model}}}}}}$$

(9)

where ${W}_{1}^{(l)}\in {{\mathbb{R}}}^{{d}_{{{{\rm{model}}}}}\times {d}_{{{{\rm{ff}}}}}}$ and ${W}_{2}^{(l)}\in {{\mathbb{R}}}^{{d}_{{{{\rm{ff}}}}}\times {d}_{{{{\rm{model}}}}}}$ are weight matrices, ${b}_{1}^{(l)}\in {{\mathbb{R}}}^{{d}_{{{{\rm{ff}}}}}}$ and ${b}_{2}^{(l)}\in {{\mathbb{R}}}^{{d}_{{{{\rm{model}}}}}}$ are bias vectors, and GeLU is the Gaussian Error Linear Unit activation function. The output for the next layer is set as:

$$P{E}^{(l)}=\left({H}^{(l)}+{{{{\rm{FFN}}}}}^{(l)}({{{\rm{LayerNorm}}}}({H}^{(l)}))\right)\in {{\mathbb{R}}}^{n\times {d}_{{{{\rm{model}}}}}}$$

(10)

which serves as input to the next layer or as the final output if l = L. After processing through L layers, the Transformer decoder’s final output undergoes linear transformation and softmax activation to produce the conditional probability distribution:

$$P({x}_{n}| {x}_{1},{x}_{2},\ldots,{x}_{n-1})={{{\rm{softmax}}}}(P{E}^{(L)}{W}_{{{{\rm{out}}}}})\in {{\mathbb{R}}}^{n\times {d}_{{{{\rm{out}}}}}}$$

(11)

where ${W}_{{{{\rm{out}}}}}\in {{\mathbb{R}}}^{{d}_{{{{\rm{model}}}}}\times {d}_{{{{\rm{out}}}}}}$ is the projection weight matrix for the output layer, and d_out is the dimension of the output space. The probability of a sequence x = (x₁, x₂, …, x_n) can be factorized as a product of conditional probabilities:

$$P(x)=P({x}_{1},{x}_{2},\ldots,{x}_{n})={\prod }_{i=1}^{n}P({x}_{i}| {x}_{1},{x}_{2},\ldots,{x}_{i-1})$$

(12)

expressing the joint probability P(x) of the sequence as the product of conditional probabilities of each element x_i given its preceding elements. The complex probability amplitude Ψ(x) for sequence x is defined as:

$$\Psi (x)=\sqrt{P(x)}{e}^{i\phi (x)}=| \Psi ({{{\bf{x}}}})| {e}^{i\phi ({{{\bf{x}}}})}$$

(13)

Here, Ψ(x) combines the square root of probability P(x) with a complex phase factor e^iϕ(x). The phase ϕ(x) is represented by a Multi-Layer Perceptron network that processes the input sequence x and outputs a real-valued phase, effectively encoding the complex quantum correlations present in the electronic wavefunction.

Efficient sampling strategy

Monte Carlo sampling is used to generate samples {x₁, x₂, …, x_N} for quantum states. A common choice is a Markov-chain Monte Carlo (MCMC) black-box sampler. MCMC is a class of algorithms based on Markov chains for random sample generation, where the production of each state depends only on the previous state. A classic example of MCMC is the Metropolis-Hastings algorithm, which uses an acceptance-rejection mechanism to decide whether to move to a new state.

$${p}_{{{{\rm{accept}}}}}=\min (1,p({{{{\bf{x}}}}}^{{\prime} })/p({{{\bf{x}}}})).$$

(14)

It can be seen that a Markov chain that gradually approximates the target distribution ${p}_{\overrightarrow{\theta }}({{{\bf{x}}}})$ is constructed, so that the distribution of states on the chain eventually matches the target distribution. However, MCMC involves the sequential assessment of proposed configurations, while the computational cost increases in relation to both the desired quality of the sample collection and the overall quantity of samples. With a Metropolis sampling scheme, Choo et al.³² observed that the performance was highly dependent on the number of samples used, but this was constrained to a maximum batch size of N_s = 10⁶. For VMC-based quantum chemistry, a more efficient scheme called autoregressive sampling can be introduced, which generates independent, uncorrelated samples directly from the target distribution. Rather than trying to model the distribution over every possible configuration of these discrete variables simultaneously, autoregressive sampling builds the distribution sequentially. It takes advantage of the fact that the probability of a specific configuration can be decomposed into the product of conditional probabilities. This approach allows for sampling one variable at a time, given the values of the previously sampled variables, thus reducing the complexity and computational burden significantly. Autoregressive sampling algorithm generates probability distributions p(x) of the special form

$$p({{{\bf{x}}}})=p({{{{\bf{x}}}}}_{1},{{{{\bf{x}}}}}_{2},\ldots,{{{{\bf{x}}}}}_{N})={\prod }_{i}^{N}p({{{{\bf{x}}}}}_{i}| {{{{\bf{x}}}}}_{ < i})$$

(15)

The autoregressive sampling scheme allows for the generation of exact samples without the need for a pre-thermalization step or the discarding of intermediate samples (which is necessary in Monte Carlo (MC) sampling to avoid autocorrelations). This makes autoregressive neural networks generally more efficient than MC sampling. As illustrated in Fig. 5, the generation of a single quantum state configuration uses QiankunNet’s sequential autoregressive sampling scheme. The architecture shows how each orbital’s occupation probability is computed conditionally based on previously sampled orbitals through the Transformer decoder layers. The probability distribution of the quantum states can be efficiently sampled by leveraging the factorization property ∣Ψ(x)∣² = ∣Ψ(x₁)∣²∣Ψ(x₂∣x₁)∣²∣Ψ(x₃∣x₁, x₂)∣² ⋯ ∣Ψ(x_N∣x₁, …, x_N−1)∣² and the masked attention mechanism that ensures the network output at position n only depends on positions m<n. We implement the sampling procedure by generating one bit at a time: we first compute ∣Ψ(x₁)∣² and sample the first bit x₁, then using the sampled x₁, we compute ∣Ψ(x₂∣x₁)∣² and sample x₂, followed by computing ∣Ψ(x₃∣x₁, x₂)∣² and sampling x₃ using all previous bits, and so on until all N bits have been sampled. This sequential sampling strategy is essential for the VMC optimization of our neural quantum states, as it enables simultaneous sampling and network training: while generating configurations for energy estimation, the network parameters can be updated through gradient computation, effectively integrating the sampling and optimization processes into a unified workflow.

Fig. 5: Generation of a single quantum state configuration using QiankunNet’s sequential autoregressive sampling scheme.

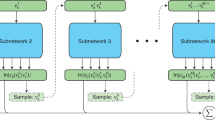
This approach consists of decoder layers that process sequential conditional probabilities, where each step computes the conditional probability of a quantum variable v_k given its previous variables. The network includes a phase subnetwork that computes the phase ϕ_k, and all components contribute to the final wave function ∣ψ_k∣. The dashed arrows indicate the autoregressive sampling process, where each variable is sampled conditionally on previously generated variables. Green boxes represent input tokens ${v}_{k}^{i}$ at different positions in the sequence. Blue boxes denote the Transformer decoder layers and phase subnetwork components. Orange boxes show the sampling operations at each step. Red dashed boxes highlight the newly sampled variables at each step, while green solid boxes indicate previously sampled variables that serve as context for subsequent sampling. The summation symbol (∑) represents the aggregation of all contributions to compute the final wave function amplitude.

Moreover, our training employs a dynamic sample adjustment mechanism that monitors the number of unique quantum states generated during sampling and automatically adjusts the total sample size accordingly. Through this adaptive approach, the sampling process naturally adjusts to the complexity of different molecular systems and the convergence state of the model, ensuring efficient training without manual tuning of sampling parameters for each specific case. The sampling process naturally forms a Monte Carlo quaternary tree structure, where each layer corresponds to a spatial orbital. While our model represents each spin–orbital as a binary token (0 or 1), the MCTS algorithm groups spin-orbitals by spatial orbital for efficiency. Since each spatial orbital contains two spin-orbitals (spin-up and spin-down), this yields four possible combined states at each tree node: “00”, “01”, “10”, or “11”. This grouping reduces the tree depth from 2N to N levels for a system with N spatial orbitals, effectively building up the complete electronic configuration through a hierarchical sampling process. Figure 6 illustrates our batched autoregressive sampling implementation. Fig. 6a presents the algorithm for generating a single configuration, showing how orbital occupations are sampled sequentially with electron number constraints. Fig. 6b depicts the tree structure used for batch generation, where multiple samples are generated simultaneously using a combination of breadth-first search (BFS) for the first few orbitals followed by depth-first search (DFS) for the remaining orbitals. This hybrid approach balances exploration diversity with memory efficiency. In the initial phase, the system explores the first few orbital positions using BFS, assigning probability weights to possible orbital configurations. This ensures reasonable coverage of the sampling space, avoiding premature convergence to local optima. Subsequently, the system shifts to a DFS strategy for processing the remaining orbital positions, a key design primarily aimed at optimizing computational resources, especially memory usage. Through this depth-first approach, the system only needs to retain state information of the current sampling path in memory, rather than simultaneously storing complete states of all possible paths, significantly reducing memory requirements, as shown in Algorithm 2 within Supplementary Information. This memory-efficient design enables the model to handle larger-scale quantum systems without being strictly limited by hardware resources. This hybrid sampling strategy is not only more efficient in computational resource utilization but also maintains sampling diversity while guiding the sample distribution to converge to the minimum energy quantum state configuration, accurately characterizing the ground state properties of quantum many-body systems. A key feature of our MCTS sampling implementation is the incorporation of physical constraints through efficient pruning strategies. Since the total number of electrons N_e is conserved in quantum chemical systems, we can significantly reduce the sampling space by eliminating invalid branches of the sampling tree. This pruning mechanism ensures that we only sample physically meaningful configurations while significantly reducing the computational cost. This tree-like structure of our sampling procedure bears resemblance to the MCTS used in AlphaGo⁵⁰, but with a crucial distinction: while AlphaGo’s MCTS relies on extensive backtracking to explore the game tree and evaluate different strategies, our method employs pure forward autoregressive sampling without any backtracking. This fundamental difference arises from the distinct nature of quantum state sampling, where our goal is to efficiently generate physically valid electronic configurations that follow the wave function probability distribution, rather than exploring multiple strategic paths as in game-playing scenarios. The absence of backtracking in our approach not only simplifies the sampling process but also significantly enhances its computational efficiency while maintaining the ability to capture the quantum state’s probability distribution accurately. This sampling strategy enables the simultaneous generation of multiple configuration samples, dramatically improving the efficiency of quantum Monte Carlo calculations. By generating independent samples directly, we eliminate both the correlation issues inherent in MCMC methods and the computational overhead of backtracking processes, while also enabling more accurate estimation of physical observables through larger sample batches. In Fig. 7, we showcase a comparison between the performance of MCMC sampling and the MCTS method for H₂O system. From this comparison, it becomes evident that the computational time of the MCMC method increases as the number of samples grows, and the low acceptance probability associated with the Metropolis-Hastings algorithm renders it inefficient for larger sample sizes. In contrast, the computational time of the MCTS method exhibits a nearly constant behavior, since it is primarily dependent on the number of unique samples. A computational efficiency improvement of several orders of magnitude is achieved compared to the MCMC method. Figure 7b illustrates that, with the same number of samples (e.g., 10⁵), the MCTS method achieves chemical accuracy within 1500 steps, whereas the MCMC method fails to attain chemical accuracy even after an extensive number of steps.

Fig. 6: Illustration of the Monte-Carlo tree search (MCTS) autoregressive sampling process which represented as a Monte-Carlo quaternary tree structure.

a The autoregressive sampling (AS) algorithm generates one sample per run. Each node in (b) corresponds to a particular local sampling outcome, and the number on the edge pointing to each circle indicates the weight. N_s can be chosen to be any number (N_s = 1000 is used as an example). Each node has four possible states (unoccupied, spin-up, spin-down, or doubly occupied). The sampling proceeds layer by layer, with each layer corresponding to one orbital’s occupation state. This sampling strategy combines Breadth-First Search (BFS) and Depth-First Search (DFS) approaches. The tree is naturally pruned based on electron number conservation: branches that would lead to configurations with incorrect total electron numbers are eliminated (shown in gray dashed lines). This pruning significantly reduces the sampling space and ensures that only physically valid configurations are generated.

Fig. 7: Comparison between different sampling algorithms.

a The time comparison of H₂O system for Markov Chain Monte Carlo (MCMC) and Monte-Carlo tree search (MCTS) autoregressive sampling methods. In both cases, the QiankunNet is used for the wave function ansatz. b The convergence comparison of H₂O between MCMC and MCTS sampling methods. N_s  = 10⁵ is used as an example, where N_s denotes the number of samples used in the variational Monte Carlo calculation for estimating the energy expectation value.

Variational Monte Carlo optimization

The VMC algorithm then proceeds iteratively to optimize QiankunNet using energy as the loss function, as illustrated in Fig. 1b: at each step, we sample configurations from the current wave function ∣Ψ(x)∣², compute the energy gradient using these samples, and update the network parameters using the AdamW optimizer, for more details, see Supplementary Information, Sec. S3 (Tab. S1). This process continues until we reach convergence, yielding a neural network representation of the ground state that minimizes the energy expectation value. To further facilitate reproducibility, a minimal working example of the code, demonstrating its core functionality, is provided in Supplementary Data 1.