Target-aware 3D molecular generation based on guided equivariant diffusion

Abstract

Recent molecular generation models for structure-based drug design (SBDD) often produce unrealistic 3D molecules due to the neglect of structural feasibility and drug-like properties. In this paper, we introduce DiffGui, a target-conditioned E(3)-equivariant diffusion model that integrates bond diffusion and property guidance, to address the above challenges. The combination of atom diffusion and bond diffusion guarantees the concurrent generation of both atoms and bonds by explicitly modeling their interdependencies. Property guidance incorporates the binding affinity and drug-like properties of molecules into the training and sampling processes. Extensive experiments prove that DiffGui outperforms existing methods in generating molecules with high binding affinity, rational chemical structure, and desirable properties. Ablation studies confirm the importance of bond diffusion and property guidance modules. DiffGui demonstrates effectiveness in both de novo drug design and lead optimization, with validation through wet-lab experiments.

Introduction

Drug discovery not only greatly impacts individuals’ physical health and the quality of their lives, but also serves as a vital catalyst for social progress and national economic prosperity. However, the development of innovative drugs is fraught with challenges and uncertainties. This process, involving retrieval of lead compound, lead optimization, preclinical evaluations, and clinical trials, typically spans 10 years and costs billions of dollars on average^1,2,3. The discovery of lead compounds is the most important stage in the entire process because it exerts huge influences on subsequent development steps and determines the fate of the project to a large extent^4,5. Traditionally, the identification of potential drug candidates mainly relied on incidental occurrences^6,7 that are inherently difficult to replicate with consistency. However, with the advancements of techniques in molecular biology, structural biology, combinatorial chemistry, and artificial intelligence (AI), the paradigm of drug discovery has been transferred from random methods to rational drug design, which can significantly increase the success rate and efficiency of drug development.

Rational drug design is composed of two approaches: ligand-based drug design (LBDD) and structure-based drug design (SBDD). LBDD designs new molecules by modifying the existing active ligands to enhance their binding affinity, selectivity, and pharmacokinetic/pharmacodynamic properties⁸. It is particularly valuable when the three-dimensional (3D) structure of the biological target is unknown. However, with the accurate prediction of biomolecular structures now widely available through AI-based methods such as AlphaFold^9,10,11, LBDD faces limitations for not incorporating the structural information of target proteins. In addition, it is also unsuitable for proteins with few or no known ligands, which is a common situation when developing drugs for novel targets. By contrast, SBDD is believed to be more effective to deliver the ligand molecules inside the binding pockets by considering the drug-target interactions at the molecular level^12,13,14. It includes two main protocols: virtual screening and molecular generation. Virtual screening employs physics-based or data-based scoring functions to estimate the binding affinities between targets and ligands, thereby selecting top-ranked molecules from chemical compound libraries for subsequent wet-lab validation and further optimization^15,16. Yet, it is computationally expensive to search the physical libraries that involve 10⁶ ~ 10⁷ molecules or the virtual on-demand libraries that contain 10¹⁰ ~ 10¹⁵ molecules, let alone the massive chemical space (10⁶⁰ ~ 10¹⁰⁰) of potential pharmacologically active molecules^17,18. Besides, the gigascale screening must be extremely accurate to guard against the false-positive hits that can cheat the scoring function by exploiting its imperfections and approximations¹⁹. Even a minimal false-positive rate of one in a million in a 10¹⁰ library would result in 10,000 false hits, which may flood out valid hit candidate selection²⁰.

Recent breakthroughs in geometric deep learning techniques^21,22,23 have facilitated the emergence of deep generative models^{24,25,26,27,28}, which are capable of directly producing pocket-aware ligands with appropriate 3D conformations. Early pioneers have attempted to represent the molecules as atomic density maps and the 3D space as voxelized grids^27,29. They harness 3D convolutional neural networks (3D CNNs) to model the protein-ligand complex and utilize conditional variational autoencoders (VAEs) to generate new molecules. Nonetheless, these models are not equivariant on molecular geometry and suffer from serious scalability problems owing to the exponential growth of the voxels’ number as the pocket size increases. To address these issues, the following approaches^{24,25,26,30,31} represent the molecules as 3D graphs and achieve SE(3)-equivariance through various techniques. For instance, GraphBP²⁶ incorporates the embeddings of atomic distance and bond angle into the training and sampling processes. Pocket2Mol²⁴ employs an E(3)-equivariant graph neural network (GNN) to ensure the rotational and translational equivariance of the system. Despite their improved performance, these models adopt an autoregressive strategy to generate the ligand atoms sequentially, which may suffer from several inherent shortcomings. Firstly, the sequential sampling models impose an unnatural generation order of atoms, thereby neglecting the global context information of the ligand. Secondly, errors introduced during the initial stages of the sampling process may gradually accumulate to promote the formation of invalid structures. Lastly, the autoregressive models frequently encounter the problem of premature termination, thus resulting in the generation of small fragments instead of complete ligands.

Diffusion-based methods^32,33,34,35 alleviate the aforementioned problems via the implementation of non-autoregressive generation scheme. By integrating diffusion probabilistic models³⁶ and equivariant neural networks^37,38,39, these methods can accomplish the task of pocket-conditioned molecular generation within continuous 3D space. Generally, each atom in the protein-ligand complex is characterized by continuous atom coordinates and discrete atom types, with noise being incrementally introduced during the forward diffusion process. The equivariant GNN is utilized to not only update the atom embeddings by message passing mechanisms, but also preserve the rotation, translation, and permutation symmetries. In reverse diffusion, atom types and positions are predicted by denoising from categorical and Gaussian distributions, respectively. However, the diffusion-based models are often inclined to produce unrealistic molecules with distorted structures, such as three- or four-membered rings, extra-large rings, and fused rings, which are energetically unstable and synthetically difficult. This may stem from the manner that the complete molecules are constructed. After acquiring the atom positions, current models typically predict the bond types based on canonical bond lengths and assemble them into intact molecules using the OpenBabel toolkit⁴⁰. As a consequence, minor deviations in atom coordinates can give rise to incorrect identification of bond types, subsequently affecting the overall structure of the generated ligand. Although DecompDiff⁴¹ incorporates molecular inductive bias into the training process by pre-decomposing ligands into arms and scaffolds, and leverages the validity guidance to instruct the sampling procedure, it cannot fully resolve the issue of ill-conformations because of the complexity and overwhelming diversity of inductive biases. On the other hand, most diffusion models aim to yield high-affinity binders without explicitly considering the essential drug-like properties such as drug-likeness^42,43, synthetic accessibility⁴⁴, and the octanol-water partition coefficient⁴⁵, which serve as crucial criteria for choosing favorable compounds. They aspire to implicitly extract the relevant information from existing protein-ligand datasets, albeit acknowledging that the molecules contained in these datasets may not uniformly exhibit optimal or satisfactory properties.

In this work, inspired by the work that solves the atom-bond inconsistency problem⁴⁶ and classifier-free diffusion guidance⁴⁷, we propose DiffGui, a novel guided diffusion model to tackle the above issues. It can not only mitigate the ill-conformational problem by introducing bond diffusion as a guidance to generate atom coordinates, but also address the attribute issue by employing property guidance during training and sampling processes. Extensive experiments presented in this study have demonstrated that DiffGui can effectively generate novel 3D molecules with high estimated binding affinities, plausible chemical structures and desired molecular properties inside the given protein pockets. It achieves the state-of-the-art (SOTA) performance on various evaluation metrics for the PDBbind dataset and exhibits competitive outcomes for the CrossDocked dataset. Case studies further confirm the superiority of DiffGui in the realms of de novo drug design and lead optimization. The generation experiments for mutated targets suggest that DiffGui is sensitive to minor changes within the protein pocket environment, underscoring its capacity to capture the complicated topological and geometrical information.

Results

This section is organized as follows: First, we describe the overall framework of the DiffGui model. Second, we compared the quality, molecular metrics and properties of the ligands generated by our method with those produced by other existing SOTA methods. Subsequently, we conducted ablation studies to determine the respective roles of bond diffusion and property guidance modules. Finally, we demonstrated the practical value of DiffGui by applying it to structure-based drug design for protein targets, lead optimization based on fragments, and molecule generation for mutated targets. Specifically, the quality of generated molecules is primarily evaluated by the Jensen-Shannon (JS) divergence between the distributions of bonds, angles, and dihedrals for the reference and generated ligands. The RMSD (root mean square deviation) values between the generated geometries and optimized/predicted conformations are also utilized as an evaluation metric for quality. The basic molecular metrics include atom stability, molecular stability, PoseBusters validity (PB-validity), RDKit validity, novelty, uniqueness, similarity with reference ligands, and similarity of protein-ligand interaction fingerprints. The molecular properties encompass estimated binding affinity (Vina Score), quantitative estimate of drug-likeness (QED), synthetic accessibility (SA), octanol-water partition coefficient (LogP), and topological polar surface area (TPSA).

Overview of DiffGui framework

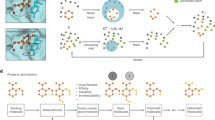
DiffGui is a bond- and property-guided, non-autoregressive generative model for target-aware molecule generation based on the equivariant diffusion framework³⁶. It integrates the mechanism of atom diffusion and bond diffusion into the forward process, while leveraging an array of molecular properties such as affinity, QED, SA, LogP, and TPSA to guide the reverse generative process (Fig. 1a). Essentially, during the forward process $q\left({{{\boldsymbol{x}}}}^{t}| {{{\boldsymbol{x}}}}^{t-1},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$ (${{\boldsymbol{p}}}$ and ${{\boldsymbol{c}}}$ represent the protein pocket and the condition of molecular properties, respectively), noise is gradually injected into the atoms and bonds of the ligand based on different noise schedules (Fig. 1b). This divides the forward process into two distinct phases. In the first phase, the bond types are gradually diffused towards the prior distribution (none-bond type), while the atom types and their positions undergo marginal disruption. Injecting a small amount of noise into the atoms, rather than rigidly fixing their states in this phase, is important for enhancing the model’s robustness. This approach provides more flexibility in predicting the bond types, as they can now be inferred from the dynamic atom distances within a specified range, rather than relying solely on the static values. In the second phase, the atom types and positions are both perturbed to their prior distributions. By this means, the model circumvents learning bond types with bond lengths that significantly deviate from the ground truth during the diffusion process. The E(3)-equivariant GNN is also modified to update the representations of both atom and bond within the message passing framework. Since atom coordinates are continuous while atom/bond types are discrete, we utilize a Gaussian distribution to model the former and categorical distributions to represent the latter. Thus, the joint molecular distribution can be formulated as a product of atom coordinate distribution and atom/bond type distributions.

Fig. 1: Overview of DiffGui framework.

a The diagram of diffusion and generative processes in DiffGui. b The details of the DiffGui structure.

In addition to the protein pocket, molecular properties are also considered as a distinct condition that is incorporated into the atomic features. Instead of sampling along the gradient direction of a label-specific classifier⁴⁸, we embrace classifier-free guidance⁴⁷ that jointly trains the unconditional and conditional models by randomly setting the property label to a null taken ø with a probability. This simplifies the training pipeline, as it eliminates the need for training an additional label classifier. During the reverse process ${p}_{\theta }\left({{{\boldsymbol{x}}}}^{t-1}| {{{\boldsymbol{x}}}}^{t},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$, the sampling can be performed using a linear combination of the conditional and unconditional score estimates, where $\gamma$ is a parameter that controls the strength of property guidance (Fig. 1b). Besides, due to the strong relationship between the bond type and bond length, the generation of atom positions is further guided by the confidence of a bond predictor, which takes the atom types and coordinates as input to predict the bond types. In this manner, the atoms can be placed in the correct positions, thus facilitating the generation of accurate 3D conformations of molecules. For an in-depth exploration of DiffGui and its underlying methodologies, please refer to the Methods section for more details.

Quality of generated molecules

As previously stated, we mainly rely on two key metrics, JS divergence and RMSD values, to compare the sub-structural and global geometry of molecules generated by diverse methods. The JS divergence⁴⁹ is a method of measuring the similarity between two probability distributions. It is a symmetrized and smoothed version of the Kullback-Leibler (KL) divergence⁵⁰, and lower JS values indicate greater similarity. Hence, JS divergence is employed here to assess the extent to which the sub-structures of generated molecules can effectively capture the true geometric distributions presented within the reference ligands. As displayed in Figs. 2 and 3, comparing with other generative models (ResGen³⁰, PocketFlow³¹, GCDM³², TargetDiff³³, DiffSBDD³⁴, and PMDM³⁵, briefly explained in the Methods section), DiffGui achieves the lowest JS divergences of 0.1815 and 0.0486 in the distributions of C-C bond distance and all-atom pairs distance, respectively, when evaluated on the PDBbind dataset. The true C-C bond distance (Fig. 2) predominantly spans the range of 1.3 to 1.6 Å, featuring two distinct peaks located approximately at 1.4 and 1.5 Å. Despite presenting two peaks, DiffSBDD and PMDM have peak densities that do not closely align with the ground truth, whereas ResGen, PocketFlow, and TargetDiff exhibit a single peak at around 1.4 Å. The JS divergence of GCDM approaches that of DiffGui, yet remains slightly higher. Regarding the distance between all-atom pairs (Fig. 3), three prominent peaks emerge approximately at 1.5, 2.5, and 3.5 Å in true distribution, accompanied by shoulders extending between 4 and 6.5 Å. In matching the true distribution, ResGen, GCDM, and PMDM perform poorly, while PocketFlow, TargetDiff, and DiffSBDD demonstrate suboptimal performance. This signifies their inability to adequately model both the short- and long-range molecular interactions. On the CrossDocked dataset, DiffGui attains the second-lowest JS divergences of 0.1923 and 0.0704 in the distributions of C-C bond distance and all-atom pairs distance, respectively, as depicted in Supplementary Figs. 1 and 2.

Fig. 2: Comparison of the distributions of C-C bond distance for the PDBbind dataset.

a ResGen, (b) PocketFlow, (c) GCDM, (d) TargetDiff, (e) DiffSBDD, (f) PMDM, (g) DiffGui. The reference molecules and generated molecules are depicted by gray and colored lines, respectively. Jensen-Shannon divergence of C-C bond distance within 2.0 Å (JS. CC_2A) is listed on the top of each sub-figure. Source data are provided as a Source Data file.

Fig. 3: Comparison of the distributions of all-atom pairs distance for the PDBbind dataset.

a ResGen, (b) PocketFlow, (c) GCDM, (d) TargetDiff, (e) DiffSBDD, (f) PMDM, (g) DiffGui. The reference molecules and generated molecules are depicted by gray and colored lines, respectively. Jensen-Shannon divergence of all-atom pairs distance within 12.0 Å (JS. All_12A) is listed at the top of each sub-figure. Source data are provided as a Source Data file.

Furthermore, to facilitate a more comprehensive evaluation, we have calculated the average JS divergences of bonds, angles, and dihedrals in generated molecules across different methods. The values are listed in Table 1. In comparison to other baselines, DiffGui exhibits the lowest JS divergence among all metrics on the PDBbind dataset, while achieving either the lowest or highly comparable values on the CrossDocked dataset. The better performance of DiffGui on PDBbind over CrossDocked is primarily because our model was trained specifically on PDBbind, which allows it to capture the underlying patterns and features within this dataset more effectively. As a result, the model is able to leverage the knowledge it has acquired to make more accurate predictions when evaluated on PDBbind. The CrossDocked dataset differs from PDBbind in various aspects, such as data distribution, complex structure, and binding affinity range. Due to the absence of a true affinity label, we cannot train DiffGui on this dataset. However, the fact that our model is able to perform reasonably well on this different dataset indicates that it has good generalization capabilities and it learns the generalizable features that are not limited to the PDBbind dataset. Overall, the results underscore the ability of our method to more accurately capture the entanglement of 3D molecular information conditioned on the protein pockets, thereby generating molecules that exhibit a higher degree of rationality on chemical structures. The detailed JS information on 20 covalent bond types, 13 bond angle types, and 15 dihedral angle types is presented in Supplementary Tables 1–6. Although DiffGui does not obtain minimum JS scores on certain individual items, it is superior to other methods in light of its lowest mean values and overall performance.

Table 1 Average JS divergences between reference ligands and generated molecules

The global geometry of the generated 3D conformation is assessed by computing the RMSD values between the original conformations extracted from the generative models and the optimized/predicted conformations produced by the RDKit software (https://www.rdkit.org/). The generated conformation is optimized by the Merck Molecular Force Field (MMFF)⁵¹, while 20 conformations are predicted for each molecule using the ETKDG conformation generation algorithm⁵², followed by relaxation using the UFF force field⁵³. In Fig. 4 and Supplementary Fig. 3, we visually depicted the RMSD distributions by violin plots, with the median RMSD values displayed at the top of each sub-figure. Among the entire spectrum of models, ResGen and GCDM stand out as they reveal the two lowest median RMSD values on both PDBbind and CrossDocked datasets. Meanwhile, the remaining models showcase comparable levels of RMSD, with the highest median value being below 1.6 Å. The lower RMSD values of ResGen and GCDM can be attributed to distinct reasons. ResGen, as an autoregressive model, is prone to premature termination during generation, often producing small molecular fragments instead of complete molecules. GCDM adopts a fully-connected 3D graph that imposes significant computational costs for large molecules. This forces the model to simplify the generation process and prioritize the fragmentary outputs. In short, DiffGui consistently achieves ~ 1 Å RMSD for all scenarios, indicating its efficacy to generate molecules with appropriate sizes and plausible 3D conformations that optimally fit protein binding pockets.

Fig. 4: Comparison of conformational similarity between generated and optimized/predicted structures for the PDBbind dataset.

a RMSD distributions between generated and optimized conformations, (b) RMSD distributions between generated and predicted conformations. Median RMSD value is listed on the top of each sub-figure. Each method samples 10,000 molecules, collecting one optimized conformation and twenty predicted conformations per molecule. The statistical descriptors for each box plot (minimum, maximum, median, and 25th/75th percentiles) are provided in Supplementary Table  17. Source data are provided as a Source Data file.

For the percentage of ring sizes (Supplementary Tables 7 and 8), five- and six-membered rings constitute the majority (exceeding 95%) of rings in the reference molecules. Conversely, rings composed of three, four, seven, eight, and nine atoms are scarce due to their low chemical stability, limited synthetic accessibility, and notably high toxicity. Among all the methods evaluated, DiffGui emerges as the one that most closely replicates the percentages of five- and six-membered rings found in the reference molecules. ResGen and PocketFlow exhibit a tendency to generate a higher proportion of six-membered rings and a corresponding decrease in five-membered rings. GCDM, TargetDiff, DiffSBDD, and PMDM, on the contrary, yield fewer six-membered rings. It is also worth noting that our method displays an elevated proportion of seven-membered rings, which account for around 10% of all rings. This feature is commonly observed in methods using diffusion models, such as GCDM, TargetDiff, DiffSBDD, and PMDM. It represents a limitation of current diffusion-based approaches and raises an intriguing direction for future improvements. Diffusion models typically treat atoms as nodes and, during the inference stage, the initialization of ligand atom’s number is primarily determined by the number of atoms within the protein pocket. Occasionally, this initialization might result in a slight excess of one or two atoms. This slight imbalance may favor the formation of seven-membered rings, which serve as a way to accommodate the extra atoms while maintaining the structural stability and connectivity within the generated molecules. Constructing diffusion models at the scale of a molecular fragment could address this issue. By focusing on pre-defined fragments rather than individual atoms, the model might be more adept at managing variations in atom number and mitigating the propensity to form seven-membered rings. This fragment-based approach could also utilize the statistical patterns and chemical properties of known fragments, guiding the generation process towards more pharmacological relevant and synthetically accessible molecules.

Molecular metrics and properties of generated molecules

We have calculated the basic molecular metrics of generated molecules to assess the generative abilities of various methods. As shown in Table 2 and Supplementary Table 9, our method, DiffGui, demonstrates superior performance over other methods in terms of atom stability, molecular stability, PB-validity, and RDKit-validity. Regarding novelty and uniqueness, except for PocketFlow, the variations among different methods are relatively minor, with their respective values all approaching 1.0. Besides, DiffGui exhibits the lowest 2D similarity and the highest protein-ligand interaction similarity when compared to other approaches. This indicates that DiffGui is capable of generating more novel molecular scaffolds while maintaining interactions with key binding site residues. In addition, the generated molecules serve as the basis for computing an array of crucial molecular properties, including Vina Score, QED, SA, LogP, and TPSA. The mean values of these properties are summarized in Table 3 and Supplementary Table 10. In terms of performance on the PDBbind dataset (Table 3), DiffGui outperforms other models on nearly all metrics except for SA, suggesting that it is capable of generating more tightly binding drug-like molecules. The AutoDock Vina program⁵⁴ is utilized to estimate the binding affinity, and three types of scores (Vina Score, Vina Min, and Vina Dock) are reported. The Vina Score is computed directly on the generated 3D conformations, while the Vina Min and Vina Dock are calculated after local minimization and redocking of the generated molecules, respectively. DiffGui reveals the lowest values (− 6.700, − 7.655, and − 8.448) in these three Vina scores, demonstrating its superiority to create potential binders with higher affinity for given pockets. Moreover, DiffGui surpasses other methods on the QED metric, which is indicative of its capability to generate more drug-like molecules. The LogP values of all methods range from 1.384 to 2.855, fitting within the universally recognized LogP range (1 ~ 3) of drug-like molecules. Although ResGen and PocketFlow show the highest SA scores of 0.784, they possess low TPSA values of 60.11 and 38.46, respectively. This validates the trend of autoregressive models to generate small fragments that may not fully occupy the entire pocket and thus compromise their specificity towards protein targets. Among the diffusion models that tend to generate complete molecules, DiffGui distinguishes itself with the highest SA score of 0.678. In brief, DiffGui excels over other baselines when assessed through the aforementioned molecular properties. This superior performance can be ascribed to the guidance of chemical bonds and property labels in our approach, which directs the reverse diffusion process toward the generation of molecules with desired characteristics.

Table 2 Basic molecular metrics of generated molecules for the PDBbind dataset

Table 3 Average molecular properties of reference ligands and generated molecules for the PDBbind dataset

In the evaluation of the CrossDocked dataset (Supplementary Table 10), even though the molecules generated by DiffGui do not attain the highest level of docking score, they showcase competitive results (highlighted in gray) against the best method. Besides, it is noteworthy that the Vina scores achieved by DiffGui are lower than those of the reference ligands for this dataset (especially after minimization and redocking), a phenomenon that is not observed in the PDBbind case. The reason could be that the PDBbind dataset, derived from experimentally determined protein-ligand complex data, involves more challenging ligands. In contrast, the ligands in the CrossDocked dataset are not native binders and may form unrealistic interactions within the binding sites. This hypothesis is further confirmed by the lower Vina scores of reference molecules in the PDBbind dataset. The SA and TPSA scores continue to expose the inherent drawback of autoregressive models (ResGen and PocketFlow), which tend to produce small fragments by sampling the local optimum atom instead of considering the global information of the ligand.

Ablation analyses

To investigate the impact of individual components on model performance, we conducted ablation experiments on the PDBbind dataset and obtained three variants of the full DiffGui model: (1) DiffGui-nobond, a model trained without the bond diffusion process; (2) DiffGui-nolab, a model trained without property label guidance; (3) DiffGui-noboth, a model trained without both above modules. The generation ability of different models and the quality of generated molecules are displayed in Supplementary Tables 11 and 12, respectively. It appears that the two techniques are devoid of any significant detrimental effect on the basic metrics, including validity, connectivity, novelty, uniqueness, and diversity (Supplementary Table 11). Notably, the validity (0.9427) of DiffGui-nolab is higher than those of other models, which is reasonable because apart from the benefits of property guidance, it also inferences with the normal generation process to a certain extent. As shown in Supplementary Table 12, the removal of bond diffusion or property guidance leads to a deterioration in model performance across the JS divergences (detailed information in Supplementary Tables 13–15), Vina scores, and QED metric. Furthermore, the simultaneous exclusion of both modules results in an even more pronounced decline in performance, thus validating their synergistic effects. The values of SA, LogP, and TPSA are all situated within reasonable ranges. Overall, the ablation study demonstrates that the components of bond diffusion and property guidance can contribute to the generation of more realistic molecules with enhanced 3D structural rationality and desired molecular attributes.

De novo drug design on protein targets

Given that GCDM underperformed all comparable methods on three Vina Scores (Table 3 and Supplementary Table 10), we excluded it from the following de novo drug design experiments. We selected 1w51, 3ctj (PDBid) from the PDBbind test set and 7ew4, 8ju6 (PDBid) outside the PDBbind dataset as protein targets. The binding sites of experimentally active compounds are utilized as pockets to enable protein-conditioned molecule generation by various methods. The protein targets of 1w51, 3ctj, 7ew4, and 8ju6 correspond to beta-secretase 1, tyrosine kinase, G protein-coupled receptor, and ion channel, respectively, covering diverse types of proteins. We generated a set of 100 molecules for each target/model and visualized the ligands with the best docking scores among those PB-valid in Figs. 5 and 6. Essentially, the molecules produced by DiffGui possess better-defined chemical structures, higher docking scores and more favorable molecular properties when benchmarked against active molecules and those produced by alternative methods. They closely resemble the binding poses of positive ligands and fully occupy the designated binding pockets. Furthermore, the binding free energies (ΔG) of these molecules are calculated by the MMGBSA method⁵⁵. As shown in Supplementary Table 16, while the binding free energy does not perfectly correlate with the docking score, the overall trend persists, and the ligands generated by DiffGui exhibit the lowest ΔG values among all produced ligands. Remarkably, with the exception of 3ctj, our model generates molecules with lower ΔG values than the reference ligands, further substantiating its capability to identify high-affinity ligands for a variety of protein targets. The 3D pharmacophore overlap between the generated molecules and reference ligands is computed by Schrödinger’s Maestro program. As displayed in Supplementary Fig. 4, the molecules generated by DiffGui possess the highest number of 3D pharmacophore overlaps for 1w51 and 3ctj. However, for transmembrane proteins (7ew4 and 8ju6) in Supplementary Fig. 5, DiffGui does not demonstrate a notable advantage over other methods. This discrepancy arises because, unlike 1w51 and 3ctj, the reference ligands in 7ew4 and 8ju6 disclose limited interactions with the binding pocket residues. Consequently, our method prioritizes the creation of novel pharmacophores to establish new interactions with crucial residues, rather than replicating the sparse binding patterns of the reference ligands.

Fig. 5: Molecules generated for targets from the PDBbind test set.

The protein targets of 1w51 (a) and 3ctj (b) are beta-secretase 1 and tyrosine kinase, respectively. The visualized molecules have the best docking scores among those PB-valid.

Fig. 6: Molecules generated for targets outside the PDBbind dataset.

The protein targets of 7ew4 (a) and 8ju6 (b) are G protein-coupled receptor and ion channel, respectively. The visualized molecules have the best docking scores among those PB-valid.

In contrast, ResGen prefers to create small molecular building blocks that are confined in sub-pockets and may cause off-target effects. Despite displaying high SA scores, their Vina scores are relatively poor, with even a positive value (2.003) in the case of 1w51 (beta-secretase 1, Fig. 5a). PocketFlow favors the generation of linear molecules with alternating single and double bonds. These molecules are fairly flexible and may possess low drug-likeness. In 3ctj (tyrosine kinase, Fig. 5b), the alkene group even protrudes outside the pocket, hindering the protein-ligand interactions and ultimately leading to the reduced docking score. Molecules generated by TargetDiff typically have superior docking scores in comparison to the molecules produced by other methods. However, there exist several limitations in their chemical structures that impair the structural rationality and synthetic accessibility. First, seven-membered rings or even larger ones, that are uncommon in drug-like molecules, frequently occur in the generated structures. Second, the fused rings are not aromatic, and these non-aromatic structures have low chemical stability and high synthesis difficulty. Last but not the least, the molecules in 7ew4 (GPCR, Fig. 6a) and 8ju6 (ion channel, Fig. 6b) incorporate six-membered rings accompanied with only two double bonds. Nonetheless, these rings are expected to be aromatic when judging from their planar conformations and overall molecular structures. Hence, we conclude that the post-operation of adding chemical bonds via the OpenBabel toolkit⁴⁰ cannot guarantee the accuracy of bond types. Moreover, the 3D conformation of the molecule in 1w51 undergoes distortion to accommodate the pocket shape, probably giving rise to its high strain energy. The other two diffusion-based methods, DiffSBDD and PMDM, generate molecules that bind more loosely than our method. Their chemical structures are also unreasonable. For instance, in the 1w51 case, the molecule of DiffSBDD has three-membered and seven-membered rings, while the molecule of PMDM forms a macrocyclic ring with two consecutive peptide bonds. In the cases of 7ew4 and 8ju6, DiffSBDD yields macrocyclic compounds with multiple hydroxy groups, which contribute to their low LogP values and reflect their high hydrophilicity. The molecules of PMDM in the pockets of 3ctj and 7ew4 both feature three seven-membered rings, whereas the ligands entirely lack aromatic groups. This structural characteristic is consistent with the high proportion of seven-membered rings (21.2% in Supplementary Table 7 and 17.6% in Supplementary Table 8) observed in PMDM-generated molecules.

In addition, to examine the diversity of molecules generated by DiffGui, we visualized the top-ranked ligands for protein targets of 4b5d, 5ni7, and 5ywy (PDBid) in Supplementary Fig. 6. These targets are Capitella teleta AChBP, nuclear receptor ROR-gamma, and prostaglandin E2 receptor, respectively. All generated molecules fit perfectly with the 3D geometry of the pockets, whether they are shallow or deep. The generated molecules are diverse and exhibit better docking scores and properties than the reference ligands. Besides, the diversity of molecules produced for the PDBbind test set is computed to be 0.7256 (Supplementary Table 11), thus proving that our method can provide various promising candidates that can be employed for further drug development. Moreover, we conducted wet-lab experimental validation on molecules generated for RSK4 (ribosomal S6 kinase 4, PDBid 6g77), a protein structure not included in the PDBbind dataset. Only two simple molecules are selected because of their rapid and straightforward synthesis. As illustrated in Supplementary Fig. 7a, b, despite their structural differences, both Compound 1 and Compound 2 demonstrate potent inhibitory activity in the HTRF assay, with IC₅₀ values of approximately 215.0 nM and 111.1 nM, respectively, highlighting their potential as lead compounds for further development. The binding modes reveal that both compounds interact with key residues (K105, D153, L155, and K221) in the binding pocket of RSK4.

Lead optimization based on fragments

In drug discovery, lead optimization is a critical task to refine the existing lead compounds for improved affinities and drug-like properties. Based on the sub-structures or fragments of known drug candidates, fragment growing and scaffold hopping are two effective strategies to perform lead optimization. Fragment growing expands the small fragments into the complete molecules by adding functional groups or larger sub-structures. Scaffold hopping replaces the core structure of the lead compound by an alternative core with the purpose of enhancing its biological activity and potency. We enable our model to implement the above task by adopting two sampling methodologies - fragment denoising and fragment conditioning. Fragment denoising manually diffuses the fixed fragment at every step, subsequently denoising it along with the remaining part from the previous step. For the next iteration, the denoised fixed fragment is discarded, while the other part is retained. Fragment conditioning inputs the fixed fragment at every step as an additional condition, and the complete molecule is obtained by denoising the fixed fragment and the denoised remaining part at the last step. For more details of these two sampling techniques, please refer to the Methods section.

As illustrated in Fig. 7, we applied the fragment denoising method on PDBid 3l13 to develop potential inhibitors based upon the structure of the active ligand. The protein target of 3l13 is phosphoinositide-3-kinase (PI3K), an enzyme involved in numerous cellular functions, such as cell growth, proliferation, differentiation, motility, survival, and intracellular trafficking⁵⁶. It plays a crucial role in the PI3K/AKT/mTOR signaling pathway, and dysregulation of PI3K signaling is often associated with various diseases, including cancer, diabetes, and autoimmune disorders. Thus, the inhibitors of PI3K can be used to treat certain cancers and inflammatory conditions. In Fig. 7a, thienopyrimidine (highlighted in orange) is fixed as a seed fragment to generate molecules via fragment growing. The generated ligands successfully replicate most of the interactions found in the native protein-ligand complex, specifically with Lys802, Ala805, Asp841, Tyr867, Val882, and Asp964. However, the interacting functional groups in these ligands are distinct from the original ones. For instance, the morpholine group is substituted by furan and pyrazole. The piperazine sulfonyl group is replaced by pyrrolidine sulfonyl, cyclized piperazine sulfonyl, and piperazine carbonyl groups. This illustrates that DiffGui can not only learn the interaction patterns in protein-ligand complexes, but also assimilate the structural information of numerous chemical groups. In Fig. 7b, c, two and three fragments are provided, respectively, to conduct scaffold hopping (fragment linking or merging), where the core scaffold of the active ligand is transformed into alternative scaffolds. The Vina, QED, and SA scores of the generated molecules are either better than or at least competitive with those of the reference compound. Therefore, taking into account the overall performance, our method effectively achieves the goal of lead optimization, whether through fragment growing or scaffold hopping strategies.

Fig. 7: Lead optimization by fragment denoising method on PDBid 3l13.

a Fragment growing, (b) Fragment linking - two fragments, (c) Fragment merging - three fragments. The seed fragments are highlighted in orange.

The fragment conditioning method is applied to PDBid 6e23, with the results visualized in Supplementary Fig. 8. The protein target of 6e23 is WD repeat-containing protein 5 (WDR5), a crucial protein involved in chromatin remodeling and gene expression regulation. It belongs to the WD-repeat protein family and plays essential roles in various cellular processes, including embryonic development, stem cell pluripotency, and cancer progression. Its dysregulation is associated with several diseases, making WDR5 an important target for therapeutic interventions and research in epigenetics and cancer biology⁵⁷. As depicted in Supplementary Fig. 8, the molecules generated by DiffGui through fragment growing, linking, and merging exhibit either superior or comparable QED and SA scores compared to those of the reference ligand. However, the estimated binding affinities of these molecules are not higher than the reference, thereby elucidating that the fragment conditioning method may not be suitable for direct use without retraining on the specialized dataset. It forcibly injects the condition of a fixed fragment at every denoising step, whereas the DiffGui model is not trained on the combined data of the fixed fragment and the denoised remaining part. This would lead to an inconsistency problem between the training and the sampling processes.

We further verified the effectiveness of lead optimization of DiffGui through wet-lab experiments on a non-kinase target, dihydroorotate dehydrogenase (DHODH). From the structures of 4zmg and 4ls1 (PDBid), the lead optimization is conducted on the basis of the fixed fragments (highlighted in orange in Supplementary Fig. 7c, d). As a result, the optimized molecules (Compounds 3 and 4) exhibit enhanced potency against DHODH, with IC₅₀ values decreasing from 8.02 μM to 4.27 μM and from 32.20 nM to 10.45 nM, respectively. Compound 3 features a thiazole ring modified with both carboxylic acid and methyl substituents. The carboxylic acid moiety engages in a salt bridge interaction with R136, while the methyl group inserts into a hydrophobic sub-pocket formed by residues V134, V143, and Y356. Compared to the original ligand, Compound 4 involves the conversion of a carboxylic acid to a hydroxamic acid, which extends the hydrogen-bonding network to incorporate additional interactions with Q47 and T360. A fluorine atom is evolved on the benzene ring to occupy the hydrophobic sub-pocket identified previously. And, a methyl group is introduced on the linker moiety to fill a distinct hydrophobic cavity surrounded by L46, A55, and L58.

Molecular generation for mutated targets

As DiffGui is a pocket-aware molecule generation model, we conducted experiments on wild-type and mutated targets to investigate its sensitivity to subtle variations within the pocket structure. We chose KRAS^G12D (PDBid 7rpz) as an example. KRAS^G12D is a specific mutation of the KRAS gene, where the glycine (G) at position 12 is replaced by aspartic acid (D). The G12D mutation leads to the constitutive activation of the KRAS protein, which drives the uncontrolled cell growth and division, contributing to cancer development and progression. Due to its significant role in oncogenesis, KRAS^G12D is a critical target for cancer research and therapeutic development⁵⁸. The distinct binding patterns of the native ligand (MRTX1133) and the generated molecules for KRAS^G12D and its mutants are shown in Supplementary Fig. 9. MRTX1133 optimally fills the switch II pocket and extends three substituents to form noncovalent interactions with seven key residues Asp12, Glu62, Tyr64, Arg68, As69, His95, and Tyr96, resulting in a K_D of 0.2 pM⁵⁸. This exceptionally high binding affinity is also evidenced by its remarkably low Vina score (− 12.877). The protein mutants include both single-point and multi-point mutations. The single-point mutations transfer each of the key residues to alanine. In multi-point mutations, Asp12Glu62Ala converts both Asp12 and Glu62 to alanine. ‘Interact’ refers to the protein in which all interacting residues are mutated to alanine, while ‘Pocket-mu’ denotes the protein where all pocket residues (residues within 10 Å of the reference ligand) are mutated to alanine.

For the wild-type protein, the generated molecule maintains the hydrogen bond with Arg68 and the salt bridges with Asp12/Glu62. As a comparison, in the Asp12Ala and Glu62Ala mutants, the relevant salt bridge disappears, and the electronegative groups, such as carboxylic acid or methyl phenyl ether, replace the positive amine groups at the corresponding positions. Since Tyr64Ala mutates Tyr64 to alanine, the π-π interaction between the resulting molecule and the residue at position 64 is absent. A phenyl group is developed to occupy the space of Arg68 in Arg68Ala, while the hydroxy group that forms a hydrogen bond with Asp69 is missing in Asp69Ala. In the mutants of His95Ala and Tyr96Ala, the aromatic system of generated molecules is extended to occupy the position of the original residue, forming stronger π-π interaction with Tyr96 and His95, respectively. However, these interactions are weaker in the wild-type protein due to the close distance between these two residues. Additionally, the salt bridges with Asp12 are reserved in the Asp69Ala and His95Ala mutation systems. Therefore, the single-point mutations of key residues significantly affect the chemical structures of molecules generated by DiffGui. Although the generated ligands for the mutants exhibit relatively higher docking scores, their QED, SA, and LogP values demonstrate notable improvements over the reference ligand.

The multi-point mutations exert more profound influences on the generated molecules as they further alter the protein pocket environment. In the Asp12Glu62Ala mutant, the salt bridges with residues at 12 and 62 positions both vanish, whereas the hydrogen bonds with Tyr64, Arg68, and His95 are conserved. The ‘Interact’ mutation system with seven key residues mutated facilitates the production of a molecule with several hydrophobic groups, like isopropyl and isopentyl. This variation not only extinguishes most electrostatic interactions in the complex but also increases the LogP value of the molecule to 5.665, indicating lower binding affinity and higher hydrophobicity of the ligand. The pocket mutation system (‘Pocket-mu’) further decreases the estimated binding affinity (Vina score − 5.730) of the resulting molecule, leading to a loss of specificity in binding with the pocket of KRAS^G12D. In conclusion, the mutation experiments fully testify to the sensitivity of the DiffGui model to the delicate changes within the pocket environment. Although the generated molecules do not bind as tightly as the reference ligand because of its extremely high affinity and the residue mutations, they exhibit higher drug-likeness and synthetic accessibility, which may be attributed to the property label guidance utilized during the generation process.

Discussion

Generating 3D potent molecules inside the protein pockets is of great significance, yet it remains a challenging task. In this study, we propose a novel guided diffusion model, DiffGui, to generate ligand molecules for any given protein target. By integrating bond diffusion and property guidance into the diffusion process, DiffGui enables the simultaneous generation of atoms and bonds in molecules, which exhibit high structural rationality and desirable molecular properties. To incorporate bond diffusion with atom diffusion, we apply distinct noise schedules to atoms and bonds, thus effectively capturing the dependencies between interatomic distances and bond types. Moreover, property labels of molecules are injected into the atomic features, transforming the training process into a blend of conditional and unconditional modeling frameworks, and guiding the inference procedure to yield molecules with anticipated attributes.

Experimental results validate that DiffGui attains SOTA performance on the PDBbind dataset and competitive results on the CrossDocked dataset. It greatly improves the quality of generated molecules, which more closely resemble the reference molecules in terms of the distributions of bond length, bond angle, dihedral angle, and ring percentage. Besides, we can conclude that DiffGui excels at generating novel and diverse molecules that bind more tightly to disease-relevant targets while preserving preferable drug-likeness. Through the adoption of specialized sampling algorithms, DiffGui is capable of performing lead optimization via fragment growing and scaffold hopping strategies, highlighting the versatility and applicability of our method for downstream drug design tasks. Furthermore, the effectiveness of DiffGui has also been validated by wet-lab experiments. Case studies on wild-type and mutated KRAS proteins indicate that DiffGui can not only reproduce the favorable interaction patterns presented in the reference complex, but also detect subtle variations in the protein environment. In summary, DiffGui deeply comprehends the geometric constraints and molecular interactions in the protein-ligand complexes and possesses enhanced generalization capability for new targets.

In future work, we aim to develop target-aware molecular generation techniques based on fragments^59,60, which represent more reliable and synthesizable molecular sub-structures. In addition, we will delve into more sophisticated noise schedules and guidance strategies to further improve the performance of deep generative models. The intricate dynamics of the protein-ligand complex, along with other key molecular properties such as pharmacokinetic/pharmacodynamic profile, toxicity, and metabolism, will also be thoroughly considered. Overall, our objective is to greatly boost the success rate and efficiency of drug discovery and development with the assistance of AI technologies.

Methods

Task definition

Let p denote the protein pocket and x denote the 3D ligand. A ligand molecule with $N$ atoms can be represented as ${{\boldsymbol{x}}}={\left\{{a}_{i},{r}_{i},{b}_{ij}\right\}}_{i,j=1}^{N}$, where ${a}_{i}\in \{{0,1}\}^{{N}_{a}}$ is the atom types, ${r}_{i}\in {{\mathbb{R}}}^{3}$ is the atom coordinates, and ${b}_{{ij}}\in \{{0,1}\}^{{N}_{b}}$ is the chemical bonds. We select ten atom types, including nine real atom types (C, N, O, S, P, F, Cl, Br, and I) and one dummy absorbing type. In addition, we identify five chemical bond types, consisting of four real bond types (single, double, triple, and aromatic bonds) and one dummy absorbing type, which also indicates no bond⁴⁶. In this paper, we denote the molecular properties as ${{\boldsymbol{c}}}\in {{\mathbb{R}}}^{{N}_{c}}$ and focus on five specific properties, namely binding affinity, QED, SA, LogP, and TPSA. Let superscript $t$ represent the latent variables at timestep $t\left(t={{\mathrm{0,1}}},\ldots,T\right)$ and ${{{\boldsymbol{x}}}}^{0}={{\boldsymbol{x}}}$. In a word, the task of conditional molecular generation here is to produce a series of x given p and c.

Overview of DiffGui model

Unlike the pure diffusion model³⁶, DiffGui is a conditional guided diffusion model, where the protein pocket and desired properties guide the molecule generation process. Thus, we aim to model the ${p}_{\theta }\left({{\boldsymbol{x}}}| {{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$ to determine the distribution of ligands that can bind to any given protein pocket while possessing the desired properties. Formally, DiffGui is a latent variable model represented as ${p}_{\theta }\left({{{\boldsymbol{x}}}}^{0}{{\rm{| }}}{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)=\int {p}_{\theta }\left({{{\boldsymbol{x}}}}^{0:{{\rm{T}}}}\right){{\rm{d}}}{{{\boldsymbol{x}}}}^{1:{{\rm{T}}}}$, where ${{{\boldsymbol{x}}}}^{t}$ for $t=1,\ldots,T$ is a sequence of latent variables with the same dimensionality as the data ${{{\boldsymbol{x}}}}^{0} \sim p\left({{{\boldsymbol{x}}}}^{0}| {{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$. As shown in Fig. 1, the proposed DiffGui framework consists of a forward diffusion process and a reverse generative process, both defined as Markov chains. The forward process (Eq. 1) progressively perturbs the data into a stationary distribution, while the reverse process (Eq. 2) gradually denoises the samples back towards the data distribution with a network parameterized by $\theta$:

$$q\left({{{\boldsymbol{x}}}}^{1:T}{{\rm{| }}}{{{\boldsymbol{x}}}}^{0},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)={\prod }_{t=1}^{T}q\left({{{\boldsymbol{x}}}}^{t}{{\rm{| }}}{{{\boldsymbol{x}}}}^{t-1},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$$

(1)

$${p}_{\theta }\left({{{\boldsymbol{x}}}}^{0:T-1}{{\rm{| }}}{{{\boldsymbol{x}}}}^{T},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)={\prod }_{t=1}^{T}{p}_{\theta }\left({{{\boldsymbol{x}}}}^{t-1}{{\rm{| }}}{{{\boldsymbol{x}}}}^{t},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$$

(2)

Since our goal is to produce 3D molecules inside the protein pocket, the model needs to generate continuous atom coordinates, discrete atom and bond types, while preserving SE(3)-equivariance throughout the entire generative process. In the following sections, we will elaborate on how we construct the diffusion process, parameterize the generative process, and implement the classifier-free guidance of molecular properties.

Molecular diffusion process

Building on recent progress in learning continuous atom coordinates and discrete atom or bond types with diffusion models^33,46, we employ a Gaussian distribution ${{\mathcal{N}}}$ to model continuous atom coordinates and a categorical distribution ${{\mathcal{C}}}$ to model discrete atom or bond types. The forward diffusion process is formulated as follows:

$$q({r}_{i}^{t}|{r}_{i}^{t-1},{{\boldsymbol{p}}},{{\boldsymbol{c}}})={{\mathcal{N}}}\left({r}_{i}^{t} \Big|\sqrt{1-{\beta }^{t}}{r}_{i}^{t-1},{\beta }^{t}{{\rm{I}}}\right)$$

(3)

$$q({a}_{i}^{t}|{a}_{i}^{t-1},{{\boldsymbol{p}}},{{\boldsymbol{c}}})={{\mathcal{C}}}({a}_{i}^{t}|(1-{\beta }^{t}){a}_{i}^{t-1}+{\beta }^{t}{{\mathbb{I}}}_{k})$$

(4)

$$q({b}_{ij}^{t}|{b}_{ij}^{t-1},{{\boldsymbol{p}}},{{\boldsymbol{c}}})={{\mathcal{C}}}({b}_{ij}^{t}|(1-{\beta }^{t}){b}_{ij}^{t-1}+{\beta }^{t}{{\mathbb{I}}}_{{k}^{{{{\prime} }}}})$$

(5)

where ${\beta }^{t}\in \left[{\mathrm{0,1}}\right]$ is the pre-defined noise scaling schedule, ${{\rm{I}}}\in {{\mathbb{R}}}^{3\times 3}$ is the identity matrix, and ${{\mathbb{I}}}_{k}$ represents a one-hot vector with a one at the k-th position and zeros elsewhere. For the atom coordinates, we gradually add scaled standard Gaussian noise. For the atom or bond types, we increase the probability mass on the k-th or k’-th type, ensuring that these types are gradually perturbed toward the desired types during the forward process. We refer to it as the absorbing type because it functions by gradually assimilating all atom or bond types into this specific category⁴⁶.

Denoting ${\alpha }^{t}=1-{\beta }^{t}$ and ${\bar{\alpha }}^{t}={\prod }_{s=1}^{t}{\alpha }^{s}$, a desirable feature of the diffusion process is the ability to calculate the noisy data distribution $q\left({{{\boldsymbol{x}}}}^{t}| {{{\boldsymbol{x}}}}^{0},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$ of timestep $t$ in closed-form:

$$q({r}_{i}^{t}|{{{\boldsymbol{x}}}}^{0},{{\boldsymbol{p}}},{{\boldsymbol{c}}})={{\mathcal{N}}}\left({r}_{i}^{t} \Big |\sqrt{{\bar{\alpha }}^{t}}{r}_{i}^{0},\left(1-{\bar{\alpha }}^{t}\right){{\rm{I}}}\right)$$

(6)

$$q({a}_{i}^{t}|{{{\boldsymbol{x}}}}^{0},{{\boldsymbol{p}}},{{\boldsymbol{c}}})={{\mathcal{C}}}\left({a}_{i}^{t} \Big |{\bar{\alpha }}^{t}{a}_{i}^{t-1}+\left(1-{\bar{\alpha }}^{t}\right){{\mathbb{I}}}_{k}\right)$$

(7)

$$q({b}_{ij}^{t}|{{{\boldsymbol{x}}}}^{0},{{\boldsymbol{p}}},{{\boldsymbol{c}}})={{\mathcal{C}}}\left({b}_{ij}^{t} \Big |{\bar{\alpha }}^{t}{b}_{ij}^{t-1}+\left(1-{\bar{\alpha }}^{t}\right){{\mathbb{I}}}_{{k}^{{{{\prime} }}}}\right)$$

(8)

As $t\to T$, we get $q\left({r}_{i}^{t}| {{{\boldsymbol{x}}}}^{0},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right){{\mathscr{\to }}}{{\mathcal{N}}}(0,{{\rm{I}}})$, $q\left({a}_{i}^{t}| {{{\boldsymbol{x}}}}^{0},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)\to {{\mathbb{I}}}_{k}$, and $q\left({b}_{{ij}}^{t}| {{{\boldsymbol{x}}}}^{0},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)\to {{\mathbb{I}}}_{{k}^{{\prime} }}$ according to Eqs. 6–8. This suggests that the atom coordinates approximately approach the standard Gaussian distribution for large $T$, while the atom and bond types place all probability mass on the absorbing types when $t=T$. These distributions, known as prior distributions, will serve as the initial distributions for the reverse process.

Since bond types in molecules are closely related to atom distances and atom types, applying the same noise schedule to bond types as to atom types and positions may lead to inconsistencies in the noised data distribution. Hence, we assign different ${\beta }^{t}$ values for atoms (types and positions) and bond types, ensuring that the information level ${\bar{\alpha }}^{t}$ of bond types decays to zero much faster than that of atoms during the diffusion process. In the first stage, the atoms are only marginally perturbed, and the model pays more attention to disrupt the bond types. In the second stage, almost all real bonds have been removed, and the model concentrates solely on the perturbation of atoms. This approach allows the model to avoid learning bond types when atom distances have obviously deviated from the canonical bond lengths.

Parameterization of molecular generative process

The generative process, conversely, aims to reconstruct the original molecule ${{{\boldsymbol{x}}}}^{0}$ from the initial noise ${{{\boldsymbol{x}}}}^{T}$. To achieve this, we approximate the reverse distribution using a neural network parameterized by $\theta$:

$${p}_{\theta }({r}_{i}^{t-1}|{{{\boldsymbol{x}}}}^{t},{{\boldsymbol{p}}},{{\boldsymbol{c}}})={{\mathcal{N}}}({r}_{i}^{t-1}|{\mu }_{\theta }({{{\boldsymbol{x}}}}^{t},t,{{\boldsymbol{p}}},{{\boldsymbol{c}}}),{\beta }^{t}{{\rm{I}}})$$

(9)

$${p}_{\theta }({a}_{i}^{t-1}|{{{\boldsymbol{x}}}}^{t},{{\boldsymbol{p}}},{{\boldsymbol{c}}})={{\mathcal{C}}}({a}_{i}^{t-1}|{a}_{\theta }({{{\boldsymbol{x}}}}^{t},t,{{\boldsymbol{p}}},{{\boldsymbol{c}}}))$$

(10)

$${p}_{\theta }({b}_{ij}^{t-1}|{{{\boldsymbol{x}}}}^{t},{{\boldsymbol{p}}},{{\boldsymbol{c}}})={{\mathcal{C}}}({b}_{ij}^{t-1}|{b}_{\theta }({{{\boldsymbol{x}}}}^{t},t,{{\boldsymbol{p}}},{{\boldsymbol{c}}}))$$

(11)

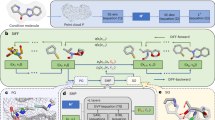
where ${\mu }_{\theta },{a}_{\theta }$ and ${b}_{\theta }$ are all neural networks. An essential characteristic that a neural network should possess for modeling 3D molecules is E(3)-equivariance, i.e., the network’s outputs should be equivariant under any 3D transformation, such as rotation, translation, and reflection. There exist different ways to parameterize ${\mu }_{\theta },{a}_{\theta }$ and ${b}_{\theta }$, and in this case, we choose to predict ${{{\boldsymbol{x}}}}^{t}$ by the above neural networks. Drawing inspiration from MolDiff⁴⁶ that utilized an E(3)-equivariant network to update atom and bond representations through message passing algorithms, we propose modeling the intricate interactions between ligand and protein atoms using an SE(3)-equivariant GNN:

$${\left\{{\hat{r}}_{i}^{t-1},{\hat{a}}_{i}^{t-1},{\hat{b}}_{{ij}}^{t-1}\right\}}_{i,j}={\phi }_{\theta }\left({{{\boldsymbol{x}}}}^{t},t,{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)={\phi }_{\theta }\left({\left\{{r}_{i}^{t},{a}_{i}^{t},{b}_{{ij}}^{t}\right\}}_{i,j},t,{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$$

(12)

Formally, given an input protein-ligand complex $\left\{{{\boldsymbol{p}}},{{\boldsymbol{x}}}\right\}={\left\{{a}_{i},{r}_{i},{b}_{{ij}}\right\}}_{i,j=1}^{N}$ (we overload the notation $N$ to denote the number of atoms in the protein-ligand complex and omit timestep $t$ for simplicity), we construct a complete graph in which vertices represent the atoms and all vertices are connected. Let ${v}_{i}\in {{\mathbb{R}}}^{d}$ and ${e}_{{ij}}\in {{\mathbb{R}}}^{{d}^{{\prime} }}$ denote the hidden representations for vertex $i$ and edge $\left\langle i,j\right\rangle$, respectively. The input vertex features comprise one-hot encodings of atom types, while the input edge features are one-hot encodings of bond types. The updates for the vectors ${v}_{i},{e}_{{ij}}$, and the coordinates ${r}_{i}$ are then defined as follows:

$${\widetilde{e}}_{{ij}}\leftarrow {\phi }_{d}\left({e}_{{ij}},\parallel {r}_{i}-{r}_{j}{\parallel }_{2}\right)$$

(13)

$${v}_{i}\leftarrow {{\rm{Linear}}}\left({v}_{i}\right)+{\sum }_{j}{\phi }_{v}\left({v}_{j},{\widetilde{e}}_{{ij}},t\right)$$

(14)

$${e}_{{ij}}\leftarrow {\sum }_{k}{\phi }_{e}\left({v}_{k},{\widetilde{e}}_{{ki}},t\right) +{\sum }_{k}{\phi }_{e}\left({v}_{k},{\widetilde{e}}_{{jk}},t\right)+{{\rm{Linear}}}\left({v}_{i}\right) \\ +{{\rm{Linear}}}\left({v}_{j}\right)+{{\rm{Linear}}}\left({\widetilde{e}}_{{ij}}\right)$$

(15)

$${r}_{i}\leftarrow {r}_{i}+{\sum }_{j}{\phi }_{r}\left({v}_{i},{v}_{j},{\widetilde{e}}_{{ij}},t\right)\frac{{r}_{i}-{r}_{j}}{\parallel {r}_{i}-{r}_{j}{\parallel }_{2}^{2}}\cdot {{{\rm{M}}}}_{{\mbox{ligand}}}$$

(16)

where Linear$\left(\cdot \right)$ represents linear transformations of the inputs, and ${\phi }_{d},{\phi }_{v},{\phi }_{e},{\phi }_{r}$ are neural networks composed of different multilayer perceptrons (MLPs). ${{{\rm{M}}}}_{{\mbox{ligand}}}$ is the ligand mask, which ensures that the coordinates of protein atoms are not updated. The final atom features ${v}_{i}$ and bond features ${e}_{{ij}}$ are fed into a multi-layer perceptron and a softmax function to obtain ${\hat{a}}_{i}$ and ${\hat{b}}_{{ij}}$, respectively. The main difference between our proposed model and MolDiff lies in our introduction of the protein pocket framework, which deviates from the unconditional molecular generation used in MolDiff. In the generative process, we keep protein-related information fixed to enable the pocket-conditioned molecular generation.

Classifier-free guidance of molecular properties

Guided sampling has emerged as a critical strategy in the development of molecular diffusion models that are capable of generating samples adhering to desired properties ${{\boldsymbol{c}}}$. In this work, we adopt classifier-free guidance⁴⁷ to explicitly incorporate conditional signals. Distinct from classifier guidance⁴⁸, which necessitates the inclusion of an additional classifier, classifier-free guidance streamlines the model architecture by directly integrating guided signals into the training phase, thereby offering enhanced control and flexibility.

Formally, DiffGui consists of an unconditional model ${\phi }_{\theta }\left({{{\boldsymbol{x}}}}^{t},t,{{\boldsymbol{p}}},\oslash \right)$ and a property-conditional model ${\phi }_{\theta }\left({{{\boldsymbol{x}}}}^{t},t,{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$. On one hand, the unconditional model is trained on 3D structures of protein-ligand complexes without property labels. On the other hand, the property-conditional model has access to both molecular properties and the corresponding protein-ligand complex ${{{\boldsymbol{x}}}}^{t}$ at each timestep $t$. During the reverse generative process, we utilize a hyperparameter $\gamma$ to modulate the strength of classifier-free guidance from the conditional model, so that

$${\widetilde{{{\boldsymbol{x}}}}}^{t-1}=(1+\gamma ){\phi }_{\theta }\left({{{\boldsymbol{x}}}}^{t},t,{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)-\gamma {\phi }_{\theta }\left({{{\boldsymbol{x}}}}^{t},t,{{\boldsymbol{p}}},{{\oslash }}\right)$$

(17)

Training

In the training stage, we add noise to the data and train the neural network to recover ${{{\boldsymbol{x}}}}^{t-1}$ from ${{{\boldsymbol{x}}}}^{t}$ by optimizing the predicted distributions ${p}_{\theta }\left({{{\boldsymbol{x}}}}^{t-1}| {{{\boldsymbol{x}}}}^{t},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$ to approximate the true posterior $q\left({{{\boldsymbol{x}}}}^{t-1}| {{{\boldsymbol{x}}}}^{0},{{{\boldsymbol{x}}}}^{t},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$, which can be derived from Eqs. 3–8. The loss functions are defined as follows:

$${L}^{t-1}={L}_{{\mbox{pos}}}^{t-1}+{\lambda }_{1}{L}_{{\mbox{atom}}}^{t-1}+{\lambda }_{2}{L}_{{\mbox{bond}}}^{t-1}$$

(18)

$${L}_{{\mbox{pos}}}^{t-1}=\frac{1}{N}{\sum }_{i}{\parallel r}_{i}^{t-1}{\begin{array}{c}-{\mu }_{\theta }{\left({{{\boldsymbol{x}}}}^{t},t,{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)}_{i}\end{array}\parallel }_{2}^{2}$$

(19)

$${L}_{{\mbox{atom}}}^{t-1}=\frac{1}{N} {\sum }_{i}{D}_{{\mbox{KL}}}\left[q\left({a}_{i}^{t-1}{{\rm{| }}}{{{\boldsymbol{x}}}}^{0},{{{\boldsymbol{x}}}}^{t},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)\parallel {p}_{\theta }\left({a}_{i}^{t-1}{{\rm{| }}}{{{\boldsymbol{x}}}}^{t},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)\right]$$

(20)

$${L}_{{\mbox{bond}}}^{t-1}=\frac{1}{N}{\sum }_{i}{D}_{{\mbox{KL}}}\left[q\left({b}_{{ij}}^{t-1}\left|{{{\boldsymbol{x}}}}^{0},{{{\boldsymbol{x}}}}^{t},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right|\parallel {p}_{\theta }\left({b}_{{ij}}^{t-1}{{\rm{| }}}{{{\boldsymbol{x}}}}^{t},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)\right)\right]$$

(21)

where ${\lambda }_{1}$ and ${\lambda }_{2}$ are pre-defined constants. We randomly sample a timestep $t$ and optimize the neural networks by minimizing the total loss ${L}^{t-1}$. Supplementary Algorithm 1 describes the training process with classifier-free guidance in detail.

Sampling

To generate new molecules, we first sample ${{{\boldsymbol{x}}}}^{T}$ from the prior distributions $p\left({{{\boldsymbol{x}}}}^{T}\right)$ and then iteratively sample from ${p}_{\theta }\left({{{\boldsymbol{x}}}}^{t-1}| {{{\boldsymbol{x}}}}^{t},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$ to gradually remove noise. The prior distribution $p\left({{{\boldsymbol{x}}}}^{T}\right)$ is the standard Gaussian distribution ${{{\mathcal{N}}}}\left(0,{{\rm{I}}}\right)$ for atom positions, along with the categorical distributions for atom and bond types, where all probability mass is assigned to the absorbing type. Supplementary Algorithm 2 describes the sampling process with classifier-free guidance in detail.

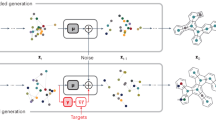
Two novel sampling methodologies (fragment denoising and fragment conditioning) are proposed to perform lead optimization based on known fragments. Fragment denoising (Eqs. 22 and 23) first diffuses the fixed fragment ${{{\boldsymbol{x}}}}_{f}^{0}$ at each step to obtain the hidden information ${{{\boldsymbol{x}}}}_{f}^{t}$, which is then combined with the rest of the ligand ${{{\boldsymbol{x}}}}_{r}^{t}$ to accomplish one-step denoising. In the next denoising step, the denoised fragment part ${{{\boldsymbol{x}}}}_{f}^{t-1}$ is discarded and the corresponding information is retained through a step of forward diffusion. The final molecule is produced by denoising from timestep 1 to 0. Fragment conditioning (Eq. 24) consistently inputs the fixed fragment ${{{\boldsymbol{x}}}}_{f}^{0}$ at each step as context, which also includes information of protein pocket and molecular properties. The final molecule is created by denoising the fixed fragment ${{{\boldsymbol{x}}}}_{f}^{0}$ and the denoised remaining part ${{{\boldsymbol{x}}}}_{r}^{t}$ at the last step.

$$q\left({{{\boldsymbol{x}}}}_{f}^{t}{{\rm{| }}}{{{\boldsymbol{x}}}}_{f}^{0},{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)={{\mathcal{N}}}\left({{{\boldsymbol{x}}}}_{f}^{t}{{\rm{| }}}\sqrt{{\bar{\alpha }}^{t}}{{{\boldsymbol{x}}}}_{f}^{0},\left(1-{\bar{\alpha }}^{t}\right){{\rm{I}}}\right)$$

(22)

$${{{\boldsymbol{x}}}}_{f}^{t-1},{{{\boldsymbol{x}}}}_{r}^{t-1}={\phi }_{\theta }\left({{{\boldsymbol{x}}}}_{f}^{t},{{{\boldsymbol{x}}}}_{r}^{t},t,{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$$

(23)

$${{{\boldsymbol{x}}}}_{f}^{t-1},{{{\boldsymbol{x}}}}_{r}^{t-1}={\phi }_{\theta }\left({{{\boldsymbol{x}}}}_{f}^{0},{{{\boldsymbol{x}}}}_{r}^{t},t,{{\boldsymbol{p}}},{{\boldsymbol{c}}}\right)$$

(24)

Datasets

We utilize the PDBbind dataset for training/testing and the CrossDocked dataset only for testing. The PDBbind dataset^61,62 is a collection of experimentally determined three-dimensional structures of biomolecular complexes archived in Protein Data Bank (PDB), accompanied by binding affinity data (K_d, K_i or IC₅₀). The current 2020 version provides 23,496 biomolecular complexes, of which 19,443 are protein-ligand complexes. For this dataset, we employ 17.3 K complexes for training, 1.8 K complexes for validation and 0.1 K complexes for testing. The CrossDocked dataset⁶³ originally contains 22.5 million poses of ligands docked into multiple similar binding pockets across the PDB. Following the previous work²⁵, we refine the dataset by choosing binding poses with root mean square deviation (RMSD) less than 1.0 Å and split the refined data based on a threshold of less than 30% protein sequence identity. This results in 100,000 protein-ligand pairs for the training set and 100 pairs for the test set. We do not train DiffGui on the CrossDocked dataset due to the absence of affinity data; instead, we only evaluate it on the CrossDocked test set. To ensure a fair comparison, we retrain the baseline models on the PDBbind dataset when evaluating them on this dataset. And we compare DiffGui with the original baselines (trained on the CrossDocked dataset) to assess the generalization capability of our approach. We sample 100 molecules for each protein in the test set to perform evaluation.

Evaluation metrics

We adopt a wide range of metrics to evaluate the quality of generated molecules: (1) Atom Stability refers to the proportion of atoms that possess the correct valencies. (2) Molecular Stability refers to the proportion of molecules in which all constituent atoms are stable. (3) PB-validity is computed using the PoseBusters tool⁶⁴ to check whether the generated molecular conformations have reasonable geometries, including standard bond lengths, appropriate bond angles, and the absence of steric clashes. (4) RDKit-validity measures the proportion of generated molecules that pass the basic test of RDKit program. (5) Novelty is the ratio of generated molecules that are not present in the training dataset. (6) Uniqueness represents the ratio of distinct molecules within all generated molecules. (7) Similarity is computed by comparing the Morgan-2 fingerprints of generated molecules and reference ligands. (8) Interaction Similarity represents the similarity of protein-ligand interaction fingerprints. (9) Binding Free Energy is calculated by the MMGBSA method⁵⁵. (10) Docking Score is estimated by the AutoDock Vina⁵⁴ program, which reports three types of scores - Vina Score, Vina Min, and Vina Dock. Vina Score represents the score of the directly generated ligand pose. Vina Min computes the score after local energy minimization, and Vina Dock provides the best possible score after redocking. (11) Jensen-Shannon (JS) divergence measures the similarity between the generated and reference distributions of bond lengths, bond angles, and dihedral angles. (12) RMSD is the root mean square deviation of heavy atoms between aligned conformations. (13) QED stands for quantitative estimation of drug-likeness combining multiple molecular properties. (14) SA signifies the synthetic accessibility that measures the difficulty of synthesizing organic molecules. (15) LogP is the octanol-water partition coefficient that assesses a compound’s lipophilicity, and it indicates how well the compound dissolves in fats compared to water. (16) TPSA is the abbreviation of topological polar surface area, which predicts the molecule’s ability to interact with biological membranes and its overall bioavailability. The JS divergence and RMSD are defined as follows:

$${{\rm{JS}}}({P|}|Q)=\frac{1}{2}{{D}_{{\mbox{KL}}}}({P|}|M)+\frac{1}{2}{{D}_{{\mbox{KL}}}}({Q|}|M)$$

(25)

$${{\rm{RMSD}}}\left(R,\widetilde{R}\right)={\min }_{\Phi }\sqrt{\left(\frac{1}{n}{\sum }_{i=1}^{n}{{||}\Phi ({R}_{i})-{\widetilde{R}}_{i}{||}}^{2}\right)}$$

(26)

where P and Q are two probability distributions, M (M = 1/2(P + Q)) is a mixture distribution of P and Q, $n$ is the number of heavy atoms, Φ is an alignment function that aligns two conformations by rotation and translation, $R$ and $\widetilde{R}$ are generated conformation and optimized/predicted conformation, respectively.

Baselines

We compare our proposed method DiffGui with the following molecular generation methods: (1) ResGen³⁰, an autoregressive generative model built on the principle of parallel multiscale modeling; (2) PocketFlow³¹, a structure-based autoregressive framework with chemical knowledge explicitly considered; (3) GCDM³², a geometry-complete diffusion model for 3D molecule generation; (4) TargetDiff³³, an initial attempt to produce target-aware 3D molecules using the diffusion model; (5) DiffSBDD³⁴, a diffusion-based framework to generate novel ligands by an inpainting-based sampling approach; (6) PMDM³⁵, a pocket-aware generative method that incorporates a dual diffusion strategy and the cross-attention mechanism.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.