Introduction

The quest for crystalline solids with ultralow thermal conductivity (κ) is crucial for applications in thermal insulation1,2 and energy-efficient technologies3,4. Achieving ultralow κ requires a thorough understanding of the underlying mechanisms of thermal transport at the atomic level. In the kinetic theory5, insulating materials with low phonon group velocity, wide phonon linewidth, and small heat capacity usually have low κ. Following this principle, several strategies have been employed to suppress thermal transport, including complex crystal structures6,7, anharmonic lattice dynamics8,9, and atomic rattling effects10,11.

Complex materials with large unit cells, weak chemical bonding, heavy elements, and rattling phonon modes, such as clathrates12,13, chalcogenides14,15, tetrahedrites16,17, and skutterudites18,19 are good thermal insulators. For instance, ultralow thermal conductivity of 0.2 Wm−1K−1 is witnessed in the complex crystalline materials CsAg5Te314,20 and Cs3Bi2I921 at room temperature. However, the pursuit of structural complexity inevitably introduces significant coherence contribution to κ, arising from wave-like tunneling of densely packed adjacent phonons, as suggested by the unified thermal transport theory proposed by Simoncelli et al.22 and Isaeva et al.23. This leads to a notable enhancement in the thermal transport, with plateaus observed above room temperature in the thermal conductivities of CsAg5Te3 and Cs3Bi2I9, or even an increasing trend in argyrodites24,25,26.

Alternatively, searching for strong anharmonic effect in simple crystalline solids is another way to achieve ultralow-κ materials. For example, the primitive cells of CuI27, InTe28, AgCrSe229, GeSe30, TlSe31, AgI32, Tl3VSe433, and Cs2SnI634 contain no more than 10 atoms, and they exhibit ultralow κ at room temperature. These materials have strong anharmonic phonon vibration modes caused by rattling atoms10,35,36, long-range pair interactions37,38,39, ferroelectric instability-induced phonon softening30,40, and metastable intrinsic defect geometries2, which effectively suppress particle-like phonon propagation. Due to their simple crystal structures, the wave-like tunneling effects in these materials are relatively weak. Our recent work reported that AgTlI2 with a simple crystal structure has an ultralow thermal conductivity of 0.25 Wm−1K−1 at 300 K41.

These insights motivate a structure-informed approach to the discovery of thermal insulators. While previous efforts have predominantly focused on lattice complexity and strong anharmonic effects, an implicit and often underappreciated factor is the presence of weak chemical bonding6,42. Weak bonding typically results in reduced phonon group velocities, which inherently suppress the particle-like phonon propagation. Moreover, low phonon group velocities lead to the reduced velocity matrix elements of coherent modes, thereby diminishing the contribution of wave-like tunneling to thermal transport. For instance, materials such as AgI32, Cs3Bi2I921, and Cs2SnI634, characterized by soft lattice and low elastic moduli, display both strong anharmonic phonon behavior and intrinsically low sound velocities, resulting in ultralow lattice thermal conductivities. This dual suppression of particle-like and wave-like phonon transports underscores the necessity of considering weak bonding as a synergistic strategy alongside anharmonicity for discovering high-performance thermal insulators.

Herein, we synthesized a crystalline solid AgTl2I3 that exhibits an ultralow κ of 0.21 Wm−1K−1 at 300 K, which further decreases to 0.17 Wm−1K−1 at 523 K. To reveal the microscopic mechanisms of the suppressed thermal transport in AgTl2I3, we performed experimental measurements, first-principles anharmonic lattice dynamics calculations, molecular dynamics simulations based on a machine learning neuroevolution potential (NEP)43, and chemical bonding analysis. By incorporating temperature renormalization effects, our study successfully rationalizes the experimentally observed ultralow thermal conductivity of AgTl2I3, offering a robust theoretical basis for understanding the microscopic origin of its thermal insulating properties. Structural and chemical bond analysis reveals that the face-sharing Ag-I polyhedral crystal structure enables extended antibonding states, leading to weak bonding and strong lattice anharmonicity. Theoretical anharmonicity parameters and experimentally measured atomic thermal vibrations indicate that the rattling motion of Ag atoms dominates the thermal insulation. Additionally, this unique crystal structure and weak bonding result in an exceptionally low phonon group velocity, which is experimentally confirmed by further measurement of the sound velocities associated with acoustic phonons near the Brillouin zone center. The face-shared Ag-I polyhedral crystal structure and weakened chemical bonding give rise to strong anharmonicity and low phonon group velocity, thereby suppressing both particle-like propagation and wave-like tunneling in phonon transport.

Results and discussion

Crystal structure and thermal conductivity

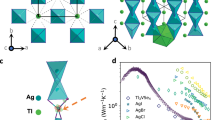
AgTl2I3 crystallizes in the \(R\overline{3}\) space group with a unit cell containing 18 atoms (Fig. 1a). Rietveld refinement of the high-resolution powder X-ray diffraction (PXRD) pattern confirms that the synthesized polycrystalline sample (Fig. 1b) adopts the \(R\overline{3}\) phase and verifies that the sample purity is high, with only trace amounts of the TlI impurities (less than 1%). AgTl2I3 can be described as a framework composed of anionic [Ag3I8]5− and cationic [Tl6I]5+ units. In the anionic [Ag3I8]5−, two Ag+ ions (Ag1) adopt a tetrahedral geometry (Ag1-I), which interconnect via face-sharing with a third Ag+ (Ag2) residing in an octahedron environment (Ag2-I). Meanwhile, the Tl+ cations are coordinated by eight nearest I− neighbors at distances ranging from 3.39 to 3.78 Å, forming a distorted Tl-I octahedron. The Ag-Ag distance (3.00 Å) is notably longer than that in metallic Ag (2.88 Å)44,45, suggesting weak Ag-Ag interactions. The Coulombic repulsion between Ag1 and Ag2 causes an elongation of the Ag-I bonds46, resulting in two inequivalent bond lengths (2.75 and 2.84 Å) of Ag1-I. Meanwhile, the octahedron Ag2 center forms a uniform and longer bond (3.08 Å) with I atoms due to the relatively high coordination number. The polyhedral crystal structure of the cationic [Ag3I8]5− unit creates a flexible structural environment42,47, facilitating rattling-like thermal vibration of Ag atoms. This is supported by the large experimental atomic displacement parameter of Ag atoms from Rietveld refinements (Table S1). The underlying weak bonding characteristics play a crucial role in determining the lattice dynamics and thermal transport properties of AgTl2I3.

Fig. 1: Crystal structure and thermal conductivity of AgTl2I3.
figure 1

a Crystal structure of AgTl2I3 visualized using VESTA84 and distinct coordination environments of Ag1, Ag2, and Tl atoms. b Rietveld refinements of the AgTl2I3 powder sample at 300 K. c Temperature-dependent thermal conductivity κ of AgTl2I3 compared to those of dense thermal insulators14,20,21,24,25,33,34,39,41,48,85,86,87. The inset shows the values at 300 K.

Full size image

The thermal conductivity of the sintered polycrystal sample AgTl2I3, ranging from 100 to 523 K, is shown in Fig. 1c. The thermal conductivities of the sample were measured during heating and cooling cycles using PPMS and LFA. As shown in Fig. S1, the data exhibit excellent repeatability across different instruments and cycles, validating the reliability of the experimental results. AgTl2I3 exhibits an ultralow thermal conductivity of 0.21 Wm−1K−1 at room temperature, which is lower than that of AgTlI241 and Cs3Bi2I6Cl348. Its thermal conductivity is comparable to the values observed in CsAg5Te314,20 and Cs3Bi2I921, positioning it among the materials with the lowest thermal conductivities at room temperature. The anharmonicity parameter (σ) of AgTl2I3 falls within the strongly anharmonic regime (Fig. S2), indicating its intrinsic low thermal conductivity. Additionally, the thermal conductivity of AgTl2I3 continues to decrease with increasing temperature, reaching an even lower value of 0.17 Wm−1K−1 at 523 K. This behavior contrasts sharply with materials having complex crystal structures, such as CsAg5Te3, Cs3Bi2I9, and argyrodites24,25,26, which typically show a plateau or even an increase in thermal conductivity above room temperature due to the wave-like phonon tunneling effect. The continuous decrease in κ of AgTl2I3 over a broad temperature range suggests that both phonon particle-like propagation and wave-like tunneling are effectively suppressed.

Anharmonic lattice dynamics and dual-channel thermal transport

To understand the microscopic phonon transport mechanism in AgTl2I3, it is essential to accurately describe its anharmonic lattice dynamics, including the phonon frequency and linewidth, which are particularly important for such a strongly anharmonic material8,41,49,50. To this end, we consider the temperature-dependent phonon frequency renormalization51,52,53 and the phonon linewidth calculation up to the four-phonon scattering54,55. Figures 2a and S4 show the renormalized phonon dispersions calculated using the self-consistent phonon (SCPH) theory56,57 from 100 to 600 K, compared with the harmonic phonon dispersions at 0 K obtained from the small displacement method (SDM). This phonon frequency renormalization alters the phonon scattering phase space, resulting in smaller phonon linewidths, particularly for the low-frequency phonons that undergo substantial hardening, as shown in Fig. 2b. Significant differences, on the order of magnitude, are observed in the phonon linewidths in the low-frequency region around 1 THz, underlining the critical role of phonon frequency renormalization. Additionally, the frequency-dependent phonon linewidth distribution reveals that the phonon modes exhibit wave-like tunneling starting from approximately 1 THz, as determined by the Wigner criterion58.

Fig. 2: Anharmonic phonon renormalization and dual-channel thermal transport in AgTl2I3.
figure 2

a Phonon dispersions of AgTl2I3 at 300 K calculated using the SCPH method. The harmonic phonon dispersions at 0 K (black dotted lines) calculated by the small displacement method (SDM) are plotted for comparison. b Phonon linewidths (including three- and four-phonon scatterings) of AgTl2I3 at 300 K calculated using perturbation theory (PT) and phonon frequencies obtained via SDM and SCPH schemes. The solid line represents the phonon linewidth equal to the corresponding phonon frequency. The dashed line represents the Wigner limit defined as the average interband spacing58. c Average lattice thermal conductivity of AgTl2I3 calculated using the unified thermal transport theory with different sets of phonon properties, alongside the results obtained from homogeneous nonequilibrium molecular dynamics (HNEMD) simulations. Our experimental thermal conductivity data are also shown for comparison.

Full size image

Anharmonic renormalization significantly impacts phonon frequencies and linewidths, which in turn play a critical role in the thermal conductivity. Since AgTl2I3 is an insulator with a large electronic band gap (Fig. S5), heat transports primarily through lattice vibrations; thus, the following discussion focuses on the lattice thermal conductivity (κL). We integrated the phonon frequencies (with and without temperature renormalization) and linewidths into the unified thermal transport theory22, and calculated the thermal conductivities (Fig. 2c). Additionally, we have also computed the thermal conductivity of AgTl2I3 using HNEMD simulations based on a machine-learning neuroevolution potential (NEP) (Fig. S6), which accounts for all-order phonon scattering processes. The HNEMD result was found to be lower than the thermal conductivity calculated from the unified thermal transport theory, likely due to the high-order phonon scatterings. Nevertheless, both results show reasonable agreement with the experimental data across a wide temperature range. In contrast, calculations based on harmonic force constants significantly underestimate the experimental lattice thermal conductivity. This result underscores the importance of temperature-dependent phonon properties on the thermal transport of AgTl2I3.

Further insights into the microscopic phonon transport mechanisms are provided by the spectral lattice thermal conductivity, as shown in Fig. 3 and S8. Particle-like propagation is predominantly observed in the low-frequency region, which primarily consists of acoustic phonons with relatively high group velocities. In contrast, wave-like phonon tunneling contributes across the entire phonon frequency range (Fig. 3a). As the temperature increases from 300 K to 600 K, a general enhancement of phonon scattering is observed (Fig. S9), leading to a significant suppression of particle-like propagation, while the contribution of wave-like phonon tunneling to thermal transport in AgTl2I3 becomes increasingly prominent (Fig. 3a and b). This shift is driven by the broadening of phonon linewidths, which enhances phonon coherence and facilitates wave-like tunneling processes, particularly in the high-frequency region (>1.5 THz) (Fig. 3c, d). However, our analysis shows that particle-like propagation remains the dominant heat transport mechanism across the entire temperature range studied; it is seen that the wave-like tunneling approaches but does not exceed the particle-like contribution at 600 K (Fig. 2c). This result indicates that wave-like phonon tunneling in AgTl2I3 is less significant despite increased coherence at elevated temperatures, highlighting the overall low efficiency of the phonon transport channels.

Fig. 3: Spectral decomposition and spatial visualization of dual-channel thermal transport in AgTl2I3.
figure 3

The spectral and cumulative particle-like phonon propagation (\({\kappa }_{{{{\rm{L}}}}}^{{{{\rm{p}}}}}\)) and wave-like interband tunneling (\({\kappa }_{{{{\rm{L}}}}}^{{{{\rm{c}}}}}\)) contributions to the lattice thermal conductivity along the x axis at (a) 300 and (b) 600 K. Three-dimensional visualization model of the contributions to the wave-like interband tunneling thermal conductivity along the x axis at (c) 300 and (d) 600 K.

Full size image

The above results suggest that phonon modes below 1.5 THz dominate thermal transport in AgTl2I3, and a deeper understanding of these modes helps unravel the mystery of its strong thermal insulation. Figure 2a shows the phonon dispersion with atomic vibration contribution resolution, indicating that the low-frequency modes in AgTl2I3 are mainly dominated by Tl and Ag atoms. The tetrahedron and octahedron composed of Ag1 and Ag2 share faces with the polyhedron centered on Tl (Fig. 1a), leading to a soft lattice46. Second-order force constants reveal that the strongest interaction in AgTl2I3 occurs between Ag2 and I2 (2.89 eV/Å2), as indicated by the overlap of charge clouds [Fig. 4a]. However, this force constant is much lower than those of the Bi-I bond of 4.77 eV/Å2 in Cs3Bi2I921 and 5.0 eV/Å2 in Cs3Bi2I6Cl348. The weak bonding and soft lattice lead to large thermal vibrations of Ag atoms (Table S2). The Tl-I bonds are weaker than Ag-I due to the longer bond length, and the thermal vibration of Tl atoms primarily contributes to the low-frequency phonon modes below 2.0 THz (Fig. 2a). Although the isotropic atomic displacement parameter of Tl atoms (Uiso) (Tables S1) is smaller than those of Ag atoms and typical rattlers in clathrates59 or skutterudites60,61,62,63 (Fig. S11), it is comparable to that of rattling Tl in TlSe31, indicating that Tl atoms are important for the scattering of low-frequency phonons. This weakly bonded structure plays a critical role in suppressing the thermal transport. Since the phonon group velocity (vg) is proportional to \(\sqrt{{k}/{M}}\), where k is the bond strength and M is the atomic mass5, the weak chemical bonds and large atomic masses are expected to lead to low vg in AgTl2I3. Figures S12 and S13, respectively, show the calculated phonon dispersions and frequency-dependent group velocities of typical thermal insulating materials at 300 K. It is found that the highest phonon frequency of AgTl2I3 is lower than that of most of them. Figure 4b presents the phonon group velocities calculated for AgTl2I3, which are relatively low compared to typical thermal insulating materials, further supporting its observed ultralow thermal conductivity. This is also consistent with the experimentally measured low sound velocities of AgTl2I3, which are 1.138 and 2.169 km/s for the transverse and longitudinal modes, respectively (see Tables S4 and S5). However, it is important to note that the sound velocities in Table S5 reflect only phonon behavior near the Brillouin zone center. To address this, we compared the phonon group velocities of AgTl2I3 across the entire Brillouin zone with those of Cs2SnI6, Cs3Bi2I6Cl3, and Cs3Bi2I9 as shown in Fig. S14. While low-frequency group velocities are similar, AgTl2I3 exhibits significantly lower group velocities in the mid- and high-frequency regions. The suppression of group velocities, particularly above 2 THz, results in a minimal contribution from high-frequency phonons to thermal transport and is directly linked to the weak chemical bonding network.

Fig. 4: Bonding stiffness, charge distribution, and phonon group velocities of AgTl2I3.
figure 4

a The harmonic interatomic force constants (IFCs) for the nearest neighbor atom pairs in AgTl2I3. The inset shows the total charge density of AgTl2I3, where an isosurface of the charge density has been visualized at 0.051 e/Bohr3. b Calculation of the frequency-dependent phonon group velocities of AgTl2I3 and comparison with the maximum of the acoustic phonon group velocities of typical thermal insulation materials at 300 K. The experimentally measured longitudinal (vL) and transverse (vT) sound velocities of AgTl2I3 are also marked for comparison.

Full size image

Chemical bonding analysis

To shed light on the quantum-chemical mechanisms underlying weak bonding in AgTl2I3, we performed the crystal orbital Hamiltonian population (COHP)64 calculations based on the DFT wavefunctions to analyze pairwise atomic interactions. This method decomposes the electronic energy of bands into pairwise orbital contributions, enabling the classification of interactions as bonding, antibonding, or nonbonding states. As shown in Fig. 5a–c, all cation-anion pairs in AgTl2I3 exhibit extended antibonding states below the Fermi level (Ef), which arise from the interaction between the 4d orbital of Ag, the 6s orbital of Tl, and the 5p orbital of I. Figure 5d further illustrates the antibonding states of Ag/Tl-I pairs, visualizing the bonding interaction between Ag (4d)/Tl (6s) and I (5p) atoms. These extended antibonding states suggest that atomic coordination weakens the lattice strength by disrupting the interference of quantum mechanical wavefunctions between orbitals from different pairs. The formation of such s-p/p-d antibonding states at the top of the valence band is a common feature in many metal chalcogenides and halides, and it is a key characteristic of thermal insulating materials21,39,48,65.

Fig. 5: Orbital interaction and antibonding analysis of AgTl2I3.
figure 5

Projected crystal orbital Hamilton population (-pCOHP) and (PDOS) analysis of (a) Ag1-I2/I3, b Ag2-I3, and (c) Tl-I1/I2/I3 orbital interactions in AgTl2I3. Positive and negative values of -pCOHP indicate bonding and anti-bonding states, respectively. The energy is shifted to the Fermi level at 0 eV. d Schematic of the orbital interaction involving the Tl (6s), Ag (4d), and I (5p) atoms. e Comparison of the maximum antibonding values of -pCOHP and the antibonding range below the Fermi level of AgTl2I3 with those of other thermal insulation materials21,39,48,88,89,90,91,92.

Full size image

We compared the COHP values (including the maximum absolute value and the range of antibonding energy extension) of the strongest antibonding state between Ag(4d) and I(5p) in AgTl2I3 with those in other materials exhibiting ultralow thermal conductivity, as shown in Fig. 5e. The maximum COHP value for the Ag(4d)-I(5p) interaction in AgTl2I3 is significantly higher than those in other materials, and the antibonding state of Ag(4d)-I(5p) exhibits a broader energy extension range. The extended strong antibonding interactions between atomic pairs in AgTl2I3 promote the formation of a soft lattice and weak bonding, which lead to low phonon group velocities. This explains the simultaneous suppression of both particle-like phonon propagation and wave-like interband tunneling. To provide quantitative support for our claims, we performed benchmark comparisons of the antibonding energy range and -pCOHPmax near Ef across representative low-κ crystalline materials as shown in Fig. S15. We find that both a broader antibonding range and larger -pCOHPmax near the Fermi level generally correlate with reduced thermal conductivity, suggesting their potential as effective descriptors for identifying ultralow-κ materials. These metrics distinguish AgTl2I3 from other systems with similar anharmonicity parameters and sound velocities, providing a more robust basis for assessing its strong thermal insulation. Beyond providing fundamental insights into phonon transport suppression, the design strategy based on extended antibonding states may be further leveraged to develop crystalline thermal insulators for practical applications such as thermal barrier coatings and advanced thermal management systems. This strategy may be practically implemented by tailoring extended antibonding states through chemical substitution and structural design. For example, selecting cation-anion pairs with favorable orbital hybridization promotes antibonding interactions6,66. Moreover, creating asymmetric coordination environments, such as an asymmetric tetrahedron or distorted polyhedron, facilitates orbital mixing by breaking inversion symmetry6,67,68. These approaches offer concrete design guidelines for achieving strong lattice anharmonicity and suppressed phonon transport in crystalline materials.

In summary, we synthesized polycrystalline AgTl2I3 with a polyhedron-sharing structure and reported its ultralow κL at room temperature through state-of-the-art experiments and theories. The thermal conductivity is one of the lowest recorded among bulk inorganic crystalline materials. Unlike comparable materials with no further suppression of thermal conductivity above room temperature, the κ value decreases to 0.17 Wm−1K−1 at 523 K. Through crystal structure and chemical bond analysis, we revealed extended antibonding states in the structure, which lead to a softened lattice and weak bonding. These features result in rattling-like thermal vibrations and low phonon group velocities, suppressing both particle-like phonon propagation and wave-like tunneling thermal transports. Our work provides a pathway for exploring materials with ultralow thermal conductivity through the analysis of lattice dynamics and chemical bonding.

Methods

Sample preparation and characterization

The polycrystalline AgTl2I3 sample was prepared using stoichiometric amounts of AgI (powder, 99.9%) and TlI (ball, 99.9%) precursors. The precursors were carefully weighed and placed into a graphite tube, which was then loaded into an evacuated silica tube and sealed under a vacuum of approximately 10−4 Pa. The sealed tube was heated to 773 K over a period of 5 h, maintained at this temperature for 24 h, and then gradually cooled to 473 K within 6 h, where it was held for an additional 48 h. Afterward, the furnace was turned off, allowing the sample to cool naturally to room temperature. The obtained ingot was grinded into fine powder and further sintered via spark plasma sintering (SPS) at 523 K for 5 min under a pressure of 90 MPa. The final sintered pellet achieved a density of 96% of the theoretical density.

High-resolution PXRD data of the synthesized AgTl2I3 powder were measured at 300 K using a Bruker D8 Advance Vario 1 two-circle diffractometer (θ ~ 2θ, Bragg-Brentano mode). The instrument was equipped with Cu Kα1 radiation (λ = 1.5406 Å) and a Johansson-type Ge (111) monochromator. Rietveld refinement was conducted using the JANA202069 crystallographic computing system. The relevant refined results are summarized in Table S1.

Heat capacity and thermal transport measurements

The thermal conductivity (κ) was determined using the formula κ = ρCpd, where ρ is the density, Cp is the isobaric heat capacity, and d is the thermal diffusivity. d of the polycrystalline AgTl2I3 sample was measured from 300 to 523 K using a Netzsch LFA 457 laser flash system under a nitrogen atmosphere. For temperatures below 300 K, κ and Cp were collected by a Quantum Design Physical Property Measurement System (PPMS). Cp measurements above 300 K were conducted from 300 to 523 K using a Netzsch STA 449F3 system (Fig. S1), while ρ was determined via the Archimedes method. The statistical error for the low-temperature thermal conductivities measurements using PPMS is derived from the values of conditional standard deviation, calculated from the fit residuals of a heating pulse and a temperature relaxation curve. For high-temperature measurements using LFA, the statistical error is estimated to be 10%70.

Sound velocity measurements

The longitudinal and transverse sound velocities (vL, vT) of the sintered AgTl2I3 pellet at 300 K were obtained using the ultrasonic pulse-echo method. A small amount of grease was applied to ensure optimal contact between the sample and the piezoelectric transducers. The average sound velocity vave of the sample was calculated from the measured vL and vT using the following formula71 : \({v}_{{{{\rm{ave}}}}}={[\frac{1}{3}(\frac{1}{{{v}_{{{{\rm{L}}}}}}^{3}}+\frac{2}{{{v}_{{{{\rm{T}}}}}}^{3}})]}^{-1/3}\).

Density functional theory calculations

Density functional theory (DFT) calculations were performed using the Vienna Ab initio Simulation Package (VASP)72, employing projector-augmented wave (PAW) pseudopotentials73 and the Perdew-Burke-Ernzerhof revision for solids (PBEsol)74 within the generalized gradient approximation (GGA)75 for the exchange-correlation functional. The valence electron configurations of Tl (5d106s26p1), Ag (4d105s1), and I (5s25p5) were considered. The initial AgTl2I3 structure was fully relaxed until atomic forces were reduced to below 10−4 eV/Å. The plane-wave energy cutoff was set to 520 eV, and Brillouin zone sampling was performed using a Γ-centered Monkhorst-Pack k-point grid of 6 × 6 × 6. The optimized lattice constants of AgTl2I3 were found to be a = b = 10.329 Å and c = 19.421 Å, which are in good agreement with the experimental values shown in Table S1. To calculate the anharmonicity parameters (σ)76 and atomic anisotropic displacement parameters, ab initio molecular dynamics (AIMD) simulations were carried out with a 2  × 2  × 2 supercell (144 atoms) using a plane-wave cutoff of 400 eV and a Γ-centered 1  × 1  × 1 k-point mesh. The energy convergence criterion was set to 10−4 eV, with a time step of 2.0 fs and 10000 simulation steps. For static calculations, a 520 eV energy cutoff and a 10−8 eV convergence criterion were applied, using a 3  × 3  × 3 Γ-centered k-point grid to sample the Brillouin zone of AgTl2I3.

Extraction of interatomic force constants

A total of 70 configurations were randomly selected from AIMD simulations at each temperature to form the training set, and atomic forces were then obtained through static DFT calculations. The atomic displacements and forces were used to fit and extract the second-order interatomic force constants (2nd-IFCs) using the self-consistent phonon (SCPH) theory56,57 implemented in the Hiphive package77. The harmonic (second-order) interatomic force constants (IFCs) at 0 K were calculated using the small displacement method implemented in the Phonopy package78 with a displacement of 0.01 Å. The third- and fourth-order force constants were extracted using the Hiphive package77. The harmonic terms at 0 K were subtracted from the force-displacement data before training the cluster space, ensuring that the anharmonic strengths of the third- and fourth-order IFCs were accurately captured. Based on the convergence test (Fig. S3), we determined that the cutoff distances for the second-order, third-order, and fourth-order IFCs are 8.0, 5.5, and 4.0 Å, respectively.