Introduction

Chiral light-matter interaction is a phenomenon in which the coupling between light and matter is influenced by the handedness, or chirality, of both the light and matter1,2,3. It not only provides a method for sensing and control of enantiomers4,5,6,7, but also supports light polarization control and detection with chiral materials8,9,10. From the perspective of photonic information processing, chiral coupling can induce direction-dependent photon emission, scattering, and absorption. These nonreciprocal characteristics are valuable for developing optical and quantum applications11,12,13,14,15 across various platforms, including cold atoms16,17, superconducting qubits18,19, quantum dots20,21,22, plasmonic meta-atoms23,24, and magnonics25,26,27,28,29,30,31,32,33,34,35. Moreover, chiral light-matter interface is essential for developing complex quantum networks36,37,38,39, facilitating deterministic quantum state transfer40,41, and enabling the simulation of nontrivial quantum many-body systems41,42.

Beyond the mentioned applications and platforms, further exploration of chiral coupling and its control techniques is both necessary and intriguing. Here, we focus on electromagnetic wave control, where perfect absorption has garnered significant interest43,44,45,46,47,48,49,50,51. This is vital for applications like energy harvesting and information storage. Achieving total absorption of incident light, without reflection or transmission, is challenging due to strict parameter requirements, often requiring precise control of phase and amplitude across multiple input fields52,53,54,55,56. In this work, we demonstrate that chiral coupling offers a promising strategy for achieving perfect absorption, reducing the need for complex parameter control and tuning. This approach provides a simpler, potentially more robust path57,58,59 to perfect absorption. Notably, this approach enables unidirectional perfect absorption, where incident fields from the opposite direction remain unabsorbed. Furthermore, this method can be easily extended to achieve bidirectional and multi-band perfect absorption, demonstrating its flexibility for practical applications.

To achieve chiral light-matter interactions, we can utilize spin-momentum-locked photon mode60,61,62,63,64,65,66, while ensuring that the interacting matter possesses spin properties or exhibits circular polarization characteristics1. Spin-momentum locking in photonics refers to the dependence of the transverse spin of the electromagnetic field on its propagation direction57,58. This phenomenon is commonly observed in tightly and transversely confined optical fields, such as those in nanofibers67,68, whispering gallery mode resonators11,69,70, and surface plasmon polariton waveguides58,71,72,73. In this work, we achieve photon-magnon chiral coupling within a waveguide magnonic system, where spoof surface plasmon polaritons (SSPPs) support spin-momentum-locked waveguide modes74,75,76, and ferrimagnetic yttrium iron garnet (YIG) spheres provide the magnon modes (spin collective excitation modes). The handedness of the spin precession, or the polarization of the magnon mode, is determined by the direction of the bias magnetic field. In the chiral coupling scenario, magnons couple with photons propagating in one direction, while backscattering is suppressed. We then employ the magnon-photon critical coupling condition77,78,79 to cancel transmission, resulting in unidirectional perfect absorption. This unidirectionality arises because the photon mode traveling in the opposite direction, with an opposing transverse spin, cannot interact with the magnon, allowing unobstructed transmission.

In our device, the operating frequency can be flexibly controlled by adjusting the external magnetic field. Bidirectional perfect absorption is achieved by introducing two YIG spheres coupled to the waveguide at different positions. Furthermore, integrating additional YIG spheres could enable broadband perfect absorption, enhancing system’s versatility. Our work demonstrates that spin-momentum locked interaction is a promising approach for designing directional optical and quantum devices.

Results

Spin-momentum locked waveguide magnonics and theoretical model

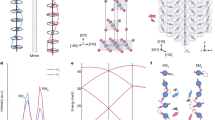
Figure 1a depicts the SSPP waveguide with periodic metallic grooves (period p = 4.1 mm, details see Supplementary Fig. S1). This structure consists of three segments, with Part II (center white dashed box in Fig. 1a) featuring grooves of uniform height h = 7.6 mm that support the SSPP propagating mode. The periodic grooves laterally confine the microwave fields and induce a longitudinal component of the electromagnetic field. This confinement gives rise to a propagating SSPP mode that intrinsically carries transverse spin angular momentum (SAM), ST, over a broad frequency range. The transverse SAM arises from the elliptical rotation of the in-plane magnetic field components, a direct consequence of the broken mirror symmetry and strong transverse confinement71,72,73. Notably, the direction of ST is locked to the propagation direction of the mode, forming a spin-momentum locking relation that underpins the chiral coupling observed in our system, as illustrated in Fig. 1b, c. Figure 1b shows the distribution of microwave magnetic field vectors simulated using the CST Microwave Studio, an electromagnetic simulation software. At the positions marked by red and blue arrows in Fig. 1b, the in-plane magnetic field (hxy) vectors rotate elliptically over time, which is schematically depicted in the top panel of Fig. 1b. The clockwise and counterclockwise polarizations of \({{{\bf{h}}}}_{{{\bf{xy}}}}^{\mp }\) correspond to transverse spins with different orientations. For convenience, we define \({{{\bf{S}}}}_{{{\bf{T}}}}^{-}={S}_{{{\rm{T}}}}^{-}{\overrightarrow{e}}_{z}\) and \({S}_{{{\rm{T}}}}^{-} < 0\), where \({\overrightarrow{e}}_{z}\) is the unit vector in the z direction. Then \({{{\bf{S}}}}_{{{\bf{T}}}}^{+}={S}_{{{\rm{T}}}}^{+}{\overrightarrow{e}}_{z}\) and \({S}_{{{\rm{T}}}}^{+} > 0\). The transverse spin is tied to the wave vector k according to the right-hand rule. Here, we take the top side of the device as an example, as shown in Fig. 1c, where n represents the interface normal, pointing from the device center toward the boundary. It can be found that the rightward-propagating waves produce a negative transverse spin (\({S}_{{{\rm{T}}}}^{-} < 0\)), while the leftward-propagating waves produce a positive transverse spin (\({S}_{{{\rm{T}}}}^{+} > 0\)). Conversely, for the bottom side of the device (insert in Fig. 1d), the situation is reversed due to the symmetry. To quantify the degree of circular polarization and its spatial distribution, we calculate the transverse SAM density of the SSPP waveguide modes under both rightward and leftward microwave excitation, as shown in Fig. 2d.

Fig. 1: Chiral coupling in spin-momentum locked waveguide magnonics.
figure 1

a Schematic of the SSPP waveguide. Part I: the region for momentum matching transition. Part II: the region supporting the propagating SSPP mode. b Distribution of in-plane magnetic filed vectors, where the vectors rotate elliptically at the arrow-marked positions. c Schematic of the transverse spin and spin-momentum locking in the SSPP waveguide. d Dispersion relation of the SSPP mode (solid curve) and the light line (dashed curve). The upper inset shows the polarizations at symmetric points along the y-axis when the microwave is input from Port 1. The bottom insert shows one unit of the SSPP waveguide, with p = 4.1 mm and height h = 7.6 mm. e Measured (solid curve) and simulated (dashed curve) transmission spectra of the SSPP waveguide. f, g Schematic of the chiral coupling between the YIG sphere and the SSPP waveguide.

Full size image
Fig. 2: Tunable chiral couplings in experiments.
figure 2

a–c Transmission spectra measured at three different positions of the YIG sphere (P5, P2, and P1, as marked in d), corresponding to non-chiral, moderate chiral, and perfect chiral coupling, respectively. Rightward and leftward transmission spectra, ∣S21(ω)∣ and ∣S12(ω)∣, are shown as red-dot and blue-dot curves, respectively. Black solid curves represent theoretical fits using Eq. (4). The corresponding absorption spectra, A21 and A12, are plotted by purple- and green-squares, respectively. d Schematic of the YIG sphere position on the SSPP waveguide, overlaid with a color map of the calculated transverse spin angular momentum (SAM) density. e Extracted extrinsic damping rates of the magnon mode, κR and κL, when the YIG sphere is placed at different positions. f Nonreciprocal transmission mapping as a function of magnetic field. The inset shows the isolation ratio (ISO) between ∣S21(ω)∣ and ∣S12(ω)∣.

Full size image

Figure 1d shows the simulated dispersion of the SSPP waveguide mode (solid curve). Within the first Brillouin zone, the dispersion gradually deviates from the light line (dashed curve) and becomes nearly flat as kp/π approaches 1. At the Brillouin zone boundary, the group velocity of the SSPP mode drops to zero at the cutoff frequency fc/2π = 10 GHz. To smoothly load the signal from the device input port to the SSPP mode, we employ a gradient groove design in Part I of the device (left and right white dashed boxes in Fig. 1a), with groove heights varying from 2.6 mm to 7.6 mm, facilitating the momentum transition80 (Supplementary Section I). As shown in Fig. 1e, the measured (solid curve) and simulated (dashed curve) transmission spectra demonstrate low-loss propagation, with transmission coefficients exceeding −3 dB (marked by a horizontal dashed line) throughout the 1–9 GHz band, indicating efficient coupling into the SSPP mode. The Hamiltonian of the SSPP mode can be expressed as

$${H}_{{{\rm{w}}}}/\hslash=\mathop{\sum}\limits_{k}\omega (k){\hat{{p}_{k}}}^{{\dagger} }{p}_{k}+\mathop{\sum}\limits_{k}\omega (k){\hat{{q}_{k}}}^{{\dagger} }{q}_{k},$$
(1)

where ω is the frequency of the traveling photon mode, and k denotes the magnitude of the wave vector. \({\hat{p}}_{k}\,({\hat{p}}_{k}^{{\dagger} })\) and \({\hat{q}}_{k}\,({\hat{q}}_{k}^{{\dagger} })\) represent the annihilation (creation) operators for the rightward and leftward traveling photon modes, respectively, with \(\left[{\hat{p}}_{k},{\hat{p}}_{{k}^{{\prime} }}\right]=\delta (k-{k}^{{\prime} })\) and \(\left[{\hat{q}}_{k},{\hat{q}}_{{k}^{{\prime} }}\right]=\delta (k-{k}^{{\prime} })\).

In the experiment, we study the magnon mode in a YIG sphere (1-mm-diameter), specifically the uniform spin precession mode, also known as the Kittel mode. An external magnetic field B is applied along the  +z axis, as shown in Fig. 1f, g. The magnon mode frequency is given by ωm = γ(B + BA), where γ is the gyromagnetic ratio, and BA represents the anisotropy field in the sphere. The magnon-photon coupling strength \(\tilde{g}(k)\) is

$$\tilde{g}({{\bf{k}}})=-{\mu }_{0}\sqrt{\frac{\gamma {M}_{\rm{s}}{V}_{\rm{s}}}{2\hslash }}[{{{\mathcal{H}}}}_{x}({{\bf{k}}},\rho )-i{{{\mathcal{H}}}}_{y}({{\bf{k}}},\rho )],$$
(2)

where μ0 is the vacuum permeability, Ms and Vs are the saturation magnetization and volume of the YIG sphere, respectively. \({{{\mathcal{H}}}}_{x}({{\bf{k}}},\rho )\) and \({{{\mathcal{H}}}}_{y}({{\bf{k}}},\rho )\) are the x-direction and y-direction magnetic field components of the SSPP waveguide mode at Cartesian coordinate ρ = (X, Y, Z). Notably, the amplitude of the in-plane (xy-plane) magnetic field governs the coupling strength between the magnon and photon modes, whereas the transverse SAM density dictated by \({{{\mathcal{H}}}}_{x}({{\bf{k}}},\rho )\) and \({{{\mathcal{H}}}}_{y}({{\bf{k}}},\rho )\) determines the chirality of the coupled system, as shown in Fig. 2d. This chirality arises from the local phase difference between \({{{\mathcal{H}}}}_{x}\) and \({{{\mathcal{H}}}}_{y}\), which induces elliptical polarization and gives rise to a nonzero transverse SAM. Detailed field distributions of the SSPP waveguide and their influence on magnon-photon coupling can be found in Supplementary Section V. We fix the height Z of the YIG sphere relative to the device plane, as well as its X position at the center of each metallic groove. In this configuration, chiral coupling is fully controlled by moving the YIG sphere along the y-axis. In the presence of chiral coupling, the Hamiltonian for the interaction between the spin-momentum-locked photon mode and magnon mode can be expressed as

$${\hat{H}}_{{{\rm{int}}}}/\hslash=\mathop{\sum}\limits_{k}{g}_{{{\rm{R}}}}(k){\hat{m}}^{{\dagger} }{\hat{p}}_{k}+{\sum}_{k}{g}_{{{\rm{L}}}}(k){\hat{m}}^{{\dagger} }{\hat{q}}_{k}+{{\rm{h.c.}}},$$
(3)

where \({\hat{m}}^{{\dagger} }\) is the magnon creation operator, gR(L) is the coupling strength between the magnon mode and the rightward (leftward)-propagating photon mode, and h.c. denotes the Hermitian conjugate. The total Hamiltonian of the system is given by \(\hat{H}={\hat{H}}_{{{\rm{w}}}}+{\hat{H}}_{{{\rm{m}}}}+{\hat{H}}_{{{\rm{int}}}}\), where \({\hat{H}}_{{{\rm{m}}}}=\hslash {\omega }_{{{\rm{m}}}}{\hat{m}}^{{\dagger} }\hat{m}\). The device is connected to the network analyzer via port 1 and port 2, as shown in Fig. 1a, for spectroscopy measurements. The transmission S21(12) and reflection S11(22) coefficients are derived as (Supplementary Section III)

$${S}_{21(12)}(\omega )=1-\frac{i{\kappa }_{{{\rm{R(L)}}}}}{\omega -{\omega }_{\rm{m}}+i\left({\gamma }_{{{\rm{i}}}}+\frac{{\kappa }_{{{\rm{R}}}}+{\kappa }_{{{\rm{L}}}}}{2}\right)},$$
(4)
$${S}_{11(22)}(\omega )=-\frac{i\sqrt{{\kappa }_{{{\rm{R}}}}{\kappa }_{{{\rm{L}}}}}}{\omega -{\omega }_{\rm{m}}+i\left({\gamma }_{{{\rm{i}}}}+\frac{{\kappa }_{{{\rm{R}}}}+{\kappa }_{{{\rm{L}}}}}{2}\right)},$$
(5)

where γi denotes the intrinsic damping rate of the magnon mode, characterizing its internal losses, and \({\kappa }_{{{\rm{R(L)}}}}=2\pi {g}_{{{\rm{R(L)}}}}^{2}\) represents the extrinsic damping rate associated with the coupling to the rightward (leftward) propagating photon mode. These damping parameters directly determine the spectral linewidths and resonance depths in the transmission and reflection coefficients, as described by Eqs. (4) and (5).

Observation of chirality induced nonreciprocity

To clearly observe the chiral coupling effect in experiment, we use a 1-mm-diameter YIG sphere that precisely overlaps with the high-density region of transverse spin, as indicated by the red and blue regions in Fig. 2d. When the sphere is positioned off-center along the y-axis, the local transverse SAM density ST ≠ 0 induces a directional magnon-photon interaction. For instance, placing the YIG sphere at position P1 (marked in Fig. 2d) and applying an external magnetic field of B = 1167 Gs along the  + z direction leads to chiral coupling. As shown in Fig. 1f, g, the counterclockwise precession of magnetization allows the magnon mode to couple exclusively with rightward-propagating photons (Fig. 1f), while remaining decoupled from the leftward-propagating photons due to their opposite circular polarization (Fig. 1g). This chiral coupling results in the nonreciprocal transmission of the incident field. The measured transmission coefficients ∣S21(ω)∣ and ∣S12(ω)∣ at three typical positions (P5, P2, P1 marked in Fig. 2d) are plotted in Fig. 2a–c. At P5 (the center of the y-axis, Y = 0), the transverse SAM density vanishes (ST = 0), leading to equal transmission amplitudes ∣S21(ω)∣ = ∣S12(ω)∣, as shown in Fig. 2a. This indicates achiral magnon-photon coupling with κR = κL. In contrast, when the YIG sphere is placed at off-center positions such as P2 or P1, where ST ≠ 0, chiral coupling emerges, resulting in nonreciprocal transmission: ∣S21(ω)∣ ≠ ∣S12(ω)∣. At the intermediate position P2, we find κR > κL ≠ 0, where moderate chiral coupling is observed, as depicted in Fig. 2b. We quantify the chirality of the coupling by defining a dimensionless parameter \({{\mathcal{C}}}=({\kappa }_{{{\rm{R}}}}-{\kappa }_{{{\rm{L}}}})/({\kappa }_{{{\rm{R}}}}+{\kappa }_{{{\rm{L}}}})\), which characterizes the degree of asymmetry between the magnon’s coupling to rightward and leftward propagating modes. By moving the YIG sphere along the y-axis, the chirality parameter \({{\mathcal{C}}}\) can be continuously tuned. At position P1, κL is suppressed to zero, resulting in \({{\mathcal{C}}}=1\). In this case, the field incident from the right (i.e., the leftward-propagating wave) is entirely decoupled from the magnon mode, and the transmission remains unity (0 dB), as indicated by the blue-dot curve in Fig. 2c. In contrast, when the incident field is reversed, magnon-photon coupling occurs and ferromagnetic resonance is observed, as shown by the red-dot curve in Fig. 2c. This unidirectional coupling behavior characterized by \(| {{\mathcal{C}}}|=1\), defines the regime of perfect chiral coupling, where the interaction is fully suppressed in one direction while preserved in the other. The black solid curves represent the theoretical results based on Eq. (4). From the fitting, we obtain κR/2π = 1.37 MHz, and κL/2π = 0. Figure 2e presents the extracted extrinsic damping rates of the magnon mode, fitted at various positions of the YIG sphere along the y-axis, illustrating how the coupling asymmetry evolves with position. Notably, the transverse spin of the photon mode exhibits opposite signs on either side of the device with respect to the center at Y = 0, as shown in Fig. 2d. As a result, for positions with Y < 0 (from P1 to P5), we observe κL < κR and hence \({{\mathcal{C}}} > 0\), while for Y > 0 (from P5 to P9), the relation reverses with κL > κR and \({{\mathcal{C}}} < 0\). The chiral coupling-induced nonreciprocal transmission can also be achieved over a wide frequency range by simply sweeping the bias magnetic field, as illustrated by the transmission mappings of ∣S21(ω)∣ and ∣S12(ω)∣ in Fig. 2f. The inset shows the isolation (in decibels) between the rightward and leftward transmission, defined as \(ISO=20{\log }_{10}(| {S}_{21}| /| {S}_{12}| )\).

Realization of unidirectional perfect absorption

Next, we utilize chiral coupling, combined with the magnon-photon critical coupling condition, to achieve unidirectional perfect absorption. Based on Eqs. (4) and (5), we consider the absorption rate A21(12) = 1 − ∣S21(12)∣2 − ∣S11(22)∣2 under both achiral and chiral coupling conditions. For achiral coupling (Fig. 3a), where κR = κL = κ, the maximum absorption rate is achieved at the magnon mode resonance frequency (ω = ωm) with κ = γi. In this scenario, the maximum absorption is \({A}_{\max }=1-2{\gamma }_{{{\rm{i}}}}\kappa /{({\gamma }_{{{\rm{i}}}}+\kappa )}^{2}=50\%\), which represents the theoretical upper limit for a conventional two-port device (Supplementary Section IV). However, in the chiral coupling system, as shown in Fig. 3b, the backscattering is blocked (κL = 0) and the absorption rate \({A}_{21}=1-| {S}_{21}{| }^{2}=1-{[(2{\gamma }_{{{\rm{i}}}}-{\kappa }_{{{\rm{R}}}})/(2{\gamma }_{{{\rm{i}}}}+{\kappa }_{{{\rm{R}}}})]}^{2}\) can reach 100% under the critical coupling condition (κR = 2γi)77,78. Chirality enhances absorption in one direction while suppressing it in the opposite. As shown in the measured absorption spectra in Fig. 2a–c, when κR > κL (\({{\mathcal{C}}} > 0\)), the rightward absorption A21 (Fig. 2b, c) exceeds the reciprocal case shown in Fig. 2a, whereas the leftward absorption A12 is correspondingly reduced. When the system is tuned to the regime of perfect chiral coupling (\({{\mathcal{C}}}=1\) in Fig. 2c), the leftward absorption is zero.

Fig. 3: Realization of unidirectional perfect absorption.
figure 3

a, b Schematics of achiral and chiral couplings in a two-port device. For achiral coupling, the maximum absorption rate is limited to 50%. In contrast, under perfect chiral coupling, the absorption can reach 100% when the critical coupling condition (κ = 2γi) is satisfied. c–e Spectral evolution as the vertical distance (Z) between the YIG sphere and the SSPP waveguide is tuned. The first row shows the S-parameters: transmission coefficients ∣S21(12)(ω)∣ plotted as red (blue) dash dot curves and reflection coefficients ∣S11(22)(ω)∣ as yellow (green) dash dot curves. The second row represents the transmission phase: P21 (red dotted curves) and P12 (blue dotted curves) as functions of frequency. The third row shows the absorption spectra: A21 (red curves) and A12 (blue curves). All measurements are performed under perfect chiral coupling (κL = 0), with the YIG sphere placed at position 1 in Fig. 2d. When the YIG is further brought to Z0 = 0.75 mm (e), the system satisfies the critical coupling condition, and the unidirectional absorption reaches its maximum value.

Full size image

In the following experiment, we fix the YIG sphere at position P1 to ensure perfect chiral coupling (κL = 0 and \({{\mathcal{C}}}=1\)), and finely adjust its vertical distance Z from the device plane to tune κR accordingly, aiming to optimize the rightward absorption A21. The measurements are performed near 6 GHz as a typical example within the tunable range of the magnon mode. This choice is not essential, as the magnon resonance frequency in the YIG sphere can be continuously adjusted via the external magnetic field, allowing the demonstrated unidirectional absorption to be readily extended to other frequency ranges.

Figure 3c–e show the spectral evolution as the YIG sphere is gradually brought closer to the device plane. The first row presents the measured S-parameters. The reflection coefficients ∣S11(ω)∣ (yellow dash dot curves) and ∣S22(ω)∣ (green dash dot curves) remain around −15 dB across the frequency range. The perfect chiral magnon-photon coupling further suppresses the reflected signal at the resonance frequency.

The second and third rows display the transmission phase and absorption for rightward and leftward propagating waves, respectively. As the YIG sphere moves from Z2 to Z0, κR increases, leading to a broadening of the ∣S21(ω)∣ (red dash dot curves) and A21 (red curves) spectra. Correspondingly, ∣S21(ω)∣ decreases at the magnon resonance frequency ω/2π = 6 GHz. When the critical coupling condition is satisfied, i.e., κR/2π = 2γi/2π = 2.4 MHz, a pronounced dip with a π phase shift appears in ∣S21(ω)∣, as shown in Fig. 3e (see Supplementary Section IV for details). At this point, the rightward-propagating microwaves are nearly perfectly absorbed by the magnon mode, with A21 = 99.6% at ωm. In contrast, the reverse transmission amplitude ∣S12(ω)∣ (blue dash dot curves) and the corresponding phase P12 (blue dotted curves) remain unchanged, indicating that the magnon mode remains fully decoupled from the leftward-propagating wave. In addition, several minor absorption peaks can be observed near the Kittel mode frequency in the absorption spectra, which originate from higher-order magnetostatic modes of the YIG sphere. These modes exhibit relatively weak coupling to the waveguide mode and are not optimized for signal absorption, resulting in low absorption amplitudes. Therefore, they are neglected in the context of perfect absorption work. However, considering that these higher-order modes carry additional degrees of freedom such as orbital angular momentum and complex spin textures81, they hold potential value for future exploration in the development of chiral microwave devices.

System tunability and extendibility

Finally, we demonstrate the tunability and extendibility of the system, which includes adjusting the frequency at which perfect absorption occurs and achieving bidirectional perfect absorption. These objectives can be conveniently realized by tuning the bias magnetic field and integrating additional YIG spheres. As shown in Fig. 4a and in the top inset of Fig. 4b, two YIG spheres are placed at symmetric points along the y-axis. For rightward-propagating waves, microwave mode at the lower (upper) point exhibits positive (negative) ST. For leftward propagating waves, the situation reverses. In the experiment, a global bias field (B-field) is applied perpendicularly to the device plane, which saturates the magnetization of the YIG spheres. To independently fine-tune the resonance frequency of the magnon mode in each YIG sphere, we place a small electromagnet coil beneath each sphere as shown in Fig. 4a. The magnetic field direction of the small electromagnet is parallel to the B-field. When the B-field is applied along the  +z direction (Bz > 0), magnon mode 1 of frequency ω1 in YIG sphere 1 couples to the rightward-propagating waves but not to the leftward propagating waves. This yields ∣S21(ω1)∣ < 1 and ∣S12(ω1)∣ = 1 at the resonance frequency ω = ω1. For magnon mode 2 in YIG sphere 2, the situation is reversed, such that at its resonance frequency ω = ω2, ∣S21(ω2)∣ = 1 and ∣S12(ω2)∣ < 1. The measured spectra of ∣S21(ω)∣ and ∣S12(ω)∣ are shown in Fig. 4b as the red and blue curves, respectively. Under critical coupling conditions (top inset of Fig. 4c), unidirectional perfect absorption occurs for both left- and right-incident fields, at two distinct frequencies, ω1 and ω2. This could refer to multi-color perfect absorption. By tuning the small coil magnet to have ω1 = ω2, we achieve bidirectional perfect absorption, as shown in Fig. 4c. Regardless of which port the incident field enters from, it can be approximately 99% absorbed around 6 GHz. To achieve perfect absorption over a broader frequency range, additional YIG spheres can be integrated and tuned to cover a continuous frequency band. Additionally, the absorption direction of each YIG sphere can be controlled by the orientation of the external magnetic field. For example, reversing the B-field to the  −z direction (Bz < 0) results in a reversal of the directional response, effectively swapping the behaviors shown in Fig. 4b, c. Further details are provided in Supplementary Section II.

Fig. 4: Multi-color and bidirectional perfect absorptions.
figure 4

a Schematic diagram of the experimental setup. Two YIG spheres are integrated at different positions along the SSPP waveguide and subjected to a common vertical bias magnetic field (B-field). The magnon mode frequencies of the two YIG spheres are independently tuned via local magnetic field adjustments (B + δB1(2)) using two separate coils. b, c Evolution of the measured transmission and absorption spectra when the magnon mode frequency of YIG 2 is tuned. Red and blue curves correspond to rightward and leftward propagating microwaves, respectively. The top inset schematically illustrates the transverse spin directions of the SSPP waveguide modes at the locations of the two YIG spheres for each propagation direction. All spectra are measured under conditions of perfect chiral coupling and critical coupling for both YIG spheres.

Full size image

Discussions

In this work, we achieve chiral coupling between microwaves and magnon modes using a coupled SSPP-YIG system. Building upon the enhanced magnon-photon coupling established in SSPP-magnon hybrid systems82, our work further explores and utilizes the microwave spin degree of freedom inherent in the SSPP waveguide. In this hybrid system, the magnons couple solely with microwaves propagating in one direction, while the reflection channel is completely closed. Furthermore, by leveraging the critical coupling condition between the magnon mode and the photon mode, the transmitted field is entirely suppressed through the Fabry-Pérot interference, resulting in unidirectional perfect absorption.

Unlike the chiral bound states formed through three-mode hybridization in cavity magnonic systems83, the chiral photonic state demonstrated in this work originates solely from the surface-propagating photon mode. As a result, it offers a simpler and more flexible approach to realizing chiral magnon-photon coupling over a broad microwave frequency range, without the need for precise control of multiple coupled modes. Owing to the tunability of the magnon mode, the frequency of perfect absorption can be flexibly adjusted by the bias magnetic field. By integrating additional YIG spheres, we demonstrate bidirectional perfect absorption, showcasing system’s extendability. Our work demonstrates the potential of chiral light-matter interactions for developing directional signal processing and energy harvesting devices. It may also provides new ideas to design advanced spin-momentum locking devices.

Methods

Device design

As illustrated in Supplementary Section I, we fabricated the spoof surface plasmon polariton (SSPP) waveguide on a 10 × 2 cm2 RO4003C substrate. The RO4003C substrate has a thickness of 0.813 mm and a dielectric constant of 3.38 ± 0.05, the copper layers are 0.035 mm thick. Below the cutoff frequency 10 GHz, microwaves propagate well in the SSPP waveguide, and the insertion loss is less than 3 dB in the range of 1–9 GHz. In the SSPP waveguide, the nonzero transverse spin (ST) is primarily concentrated within an area of 1.6 × 1.6 mm2. To ensure good spatial mode overlap and polarization matching between the magnon and the chiral photon mode, a YIG sphere with a diameter of 1 mm is placed to cover the high-ST region. The bias magnetic field applied to the YIG sphere is aligned with the direction of ST. In the experiment to demonstrate system tunability and extendibility, two 1 mm-diameter YIG spheres are glued to the end of a displacement cantilever and adjusted accurately close to the planar device through a three-dimensional displacement motor. Two small electromagnetic coils are positioned underneath the YIG spheres, locally adjusting the magnetic field at each YIG sphere’s position.

Measurement setup

All measurements were conducted at room temperature. The end of the SSPP device are connected to a vector network analyzer (Keysight E5080B) to obtain the scattering parameters of the waveguide magnonic system. The excitation power is maintained at  −5 dBm throughout all measurements to ensure the magnon mode operates within its linear frequency response regime.