Introduction

In the broad spectrum of electromagnetic waves, thermal radiation holds an important and unique role. It is generated by any object with a temperature above absolute zero, casting a glow across the infrared horizon. This radiation is typically viewed as the incoherent byproduct of thermal oscillations. However, the advent of photonic engineering in nanostructured surfaces (also known as metasurfaces) has revolutionized our ability to tailor thermal emission1,2,3,4, endowing them with properties once exclusive to laser sources: coherence, directionality, polarization and even wavefront control5,6. In turn, these advances have propelled thermal emitters to the forefront of technological innovation, with applications spanning from thermal imaging7,8, sensing9,10, camouflage11 to thermo-photovoltaics12,13,14.

The quest to generate coherent thermal emission has been a particularly important challenge in the past two decades. The key to achieving coherent thermal emission lies in coupling broadband thermal fluctuations to tailored optical resonances supported by photonic structures, thereby guiding the desired spectral components into free space radiation. Traditional approaches rely on surface phonon polaritons (SPhPs)3,15,16,17 or localized surface plasmonic resonances18,19,20,21,22, which are either spectrally limited (e.g., Reststrahlen bands) or suffer from high losses that hinder temporal coherence. In recent years, all-dielectric metasurfaces23,24 have shown high potential for photonic engineering, particularly in the realization of high-Q resonances. The long-range interactions across all-dielectric metasurfaces promotes the generation of nonlocal (spatially extended) quasi-bound states, such as quasi-bound states in the continuum (quasi-BICs)25,26,27 and quasi-guided modes (quasi-GMs)28,29,30, which have been at the basis of nonlocal metasurfaces31. These states have been exploited for various photonic applications, including the demonstration of highly coherent thermal sources32,33. In particular, quasi-GMs as a special type of guided mode resonances (GMRs), induced by the folding of the first Brillouin zone (FBZ), have been harnessed to enable narrowband thermal emission spanning a small range of spatial k components, thereby achieving high temporal and spatial coherence in the radiation output34.

In parallel, controlling the polarization state of thermal emission is another appealing quest for practical applications. However, most metasurface-based thermal emitters exhibit only linear polarization response. Enabling chiral responses for thermal emission holds great promise for applications in imaging35,36, biosensing37,38, and the detection of chiral molecules39,40. In planar photonics, chiral responses have been realized using various metasurfaces, which have been widely applied in quantum41 or perovskite42 emission. However, these are mainly limited to extrinsic chiral responses, corresponding to oblique-angle emission obeying inherent symmetries in terms of how light is distributed in space6. Breaking structural symmetry to impart chiral responses at normal incidence is associated with intrinsic chiral responses43,44,45. For thermal emitters, normal emission from planar structures is particularly attractive, as it ensures manufacturing compatibility and guarantees the radiation efficiency of such miniature integrated light sources. Recently, researchers have demonstrated spin-selective emission based on two-dimensional planar metallic structures46,47, but with limited coherence due to material loss. High-Q resonant dielectric metasurfaces provide an alternative solution for complete control over polarization of thermal emission, while preserving high spatial and temporal coherence5,6. Keeping the high temporal coherence as a precondition, chiral thermal emissions experimentally realized to date are mainly based on two sets of dielectric elliptical disk arrays5. Nevertheless, how to simultaneously control temporal, spatial and spin coherences using simpler geometries remains largely unexplored.

Another critical aspect in the practical applications of engineered thermal emissions is the need to use large-scale metasurfaces to generate sufficient radiation, given that most reported thermal emission features from metasurfaces are inherently weak. However, high-Q resonances in all-dielectric metasurfaces are typically embedded within dispersive bands29,48, which exhibit a one-to-one correspondence between the output angle and the emission wavelength. This necessitates the use of pinhole-shaped spatial filters to select the desired spectral component for high-coherence thermal emissions, substantially diminishing the collected power (see the left panel of Fig. 1b). To address this, we recently proposed a 2D omnidirectional flatband to eliminate the dispersive rainbow effect49. Although one can use a mid-infrared (MIR) lens to collect more power without compromising the temporal coherence, it comes at a cost of the deteriorated spatial coherence due to the involvement of a multitude of wavevectors along the flatband (see the middle panel of Fig. 1b). Achieving thermal emissions with both high temporal and spatial coherence, full control of polarization, and sufficient output power to facilitate high signal-to-noise ratios is still a critical challenge.

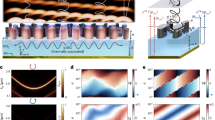
Fig. 1: Thermal emission control based on dispersion engineering in a double-sided corrugated waveguide array.
figure 1

a Illustration of the transition from traditional to metasurface-based thermal emitters, endowing thermal emission with temporal and spatial coherence. The right panel highlights the differences between metallic/local and dielectric/non-local structures in the control of coherence and polarization properties. b The idea of using various dispersion bands and spatial filters for thermal emission extraction. c Schematic representation of our high-coherence thermal emitter with full control of the electromagnetic properties, based on a nonlocal metasurface composed of 1D lattice of Ge waveguides, each with corrugations on both sides. The whole structures is spaced by Al2O3 from a gold mirror. A flatband design along one direction enables the use of 1D spatial filter to collect the emissions over a wide angular range without affecting the temporal coherence, indicated by the red output beam. d Demonstration of the polarization control by simply adjusting the longitudinal spacing of the corrugations, enabling a continuous control over polarization between two circularly polarized singular points.

Full size image

In this work, we demonstrate full control over the polarization of thermal emission using a series of structurally similar designs that differ only in a single geometrical parameter, while simultaneously achieving high temporal and spatial coherence across a wide range of output angles. The key of the design lies in the introduction of periodic corrugations on both sides of each waveguide within the array, where the periodic breaking of translational symmetry folds the guided mode (GM) bands within individual waveguides into the continuum, forming high-Q GMRs. The Q-factors of these GMRs can be tuned by adjusting the corrugation dimensions. The weak but non-vanishing coupling between these high-Q GMRs in the x-direction, which is controlled by the gap between adjacent waveguides, results in a flatband behavior due to the effect of coupled-resonator optical waveguides (CROW)50, a phenomenon well-established in microresonators51. The integration of CROW physics into metasurfaces can give rise to flatband behavior across a much broader range of wavevectors than those reported in 1D gratings52. The enhanced local density of optical states, a characteristic of flatband behavior and often referred to as Van Hove singularities, is recognized for its impact on thermal emissions53. Additionally, strong chiral responses can be enabled at all these wavevectors, a feature that outperforms chiral metasurfaces based on the splitting of a BIC V-point into two circularly polarized C-points in slanted geometries44. Compared to Moiré structure, the geometry is much easier to implement using standard fabrication techniques. Meanwhile, the regular parabolic band is retained along the waveguide direction. Together with the flatband in the orthogonal direction, a saddle-shaped high-Q dispersion band is generated (see the right panel of Fig. 1b). The flatband response allows the use of 1D spatial filters to improve collection efficiency from a large metasurface area without compromising temporal coherence. Since the slot spatial filter only collects a small proportion of the ky wavevector, this approach also preserves the high spatial coherence of thermal emissions. Consequently, our design overcomes the challenge of reconciling high temporal and spatial coherences for thermal emitters with improved power collection. Moreover, by tilting the slot spatial filter relative to the ky direction, one can selectively capture the spectral component of interest. Remarkably, different polarization responses can be achieved by adjusting the longitudinal positions of corrugations along the waveguide direction. By harnessing these features, thermal emission with both high temporal coherence and arbitrary (linear/circular/elliptical) polarization can be generated over a broad range of wavevectors in the momentum space. We experimentally demonstrate thermal emission with arbitrary polarization by fabricating a series of metasurfaces. Our findings reveal that, with this rational design, thermal emission exhibits record-high temporal (Q ~ 304) and spatial (Lc ~ 0.32 mm) coherence, as well as an emission circular dichroism (ECD) of up to 0.91 for circular polarization. Particularly, these characteristics remain unaffected by the output angle of up to 10° along the kx direction, thus enabling the possibility of using low numerical aperture (NA) objectives to collect the radiation. This innovative approach for generating thermal emission with high coherence and tailored polarization properties eliminates the need for complex geometry, multilayer structure fabrication or tilted etching techniques, paving the way for miniaturized, on-chip high-performance thermal light sources in applications such as polarimetric imaging, energy-efficient circular dichroism infrared spectroscopy and sensing, as well as coherent thermal communication.

Results

Figure 1a provides a comprehensive overview of the evolution of thermal emission engineering with metasurfaces over the past decades. Despite long-lasting progress, metal-based metamaterials and local metasurfaces struggle with achieving high spatial and temporal coherence due to their high losses18,46, either dissipative or radiative ones, although relatively broadband thermal emissions at linear18 or circular polarizations46 have been demonstrated. To overcome these limitations and achieve high-coherence thermal emission, it is natural to switch to low-loss all-dielectric metasurfaces. Recent years have witnessed significant success in achieving coherent thermal emissions with various polarizations, including linear32,33 and circular polarizations5,6, as well as wavefront control of the latter, through high-Q quasi-bound states in the past few years. Here, we show that our rational design can shape thermal emission with high temporal, spatial and spin coherence simultaneously, while retaining the same emission characteristics by harnessing the unidirectional flatband design from anisotropic coupling in nonlocal metasurfaces. In Fig. 1c, the yellow area at the bottom represents a sufficiently thick gold layer, which serves as the reflector and, together with the lossy dielectric metasurfaces, provides the source of thermal fluctuations. The top layer employs a high refractive index, low-loss Ge metasurface, which supports a nonlocal high-Q optical resonance. An aluminum oxide (Al2O3) buffer layer with a low refractive index is placed in between, with the goal of critically coupling the resonant mode to free-space radiation, thereby optimizing the emissivity, as well as tailoring the broken out-of-plane symmetry to control the ECD of the emission. When the bottom metal is heated, either by applying a current or placing the whole device in a high-temperature environment, the randomly oriented dipoles related to the thermal excitations in the whole structure will couple into the high-Q modes supported by the upper metasurface. This results in an angle-independent thermal emission along the x-direction, as indicated by the red beam in Fig. 1c. Importantly, our design enables chiral emission over a wide angular range, a feat difficult to achieve with traditional methods that rely on breaking structural symmetry to break the V-point of BIC to achieve high-Q chiral response (C-point), as those methods correspond to a single k-point (i.e., Γ-point) in momentum space43,44. Besides the coherence control and the possibility to use slot spatial filter for improved power collection, Fig. 1d further demonstrates that, by simply adjusting the interspacing (0.5Py-δ) between adjacent corrugations on the opposite side, we can achieve continuous control of the thermal emission polarizations for any states between two opposite spin-polarized singular points on the Poincaré sphere (see Supplementary Fig. 4 for more results of the Stokes parameters’ spectra under different δ values), offering a straightforward but simple approach to polarization state manipulation.

Numerical results

To elucidate the fundamental principles of our structure, we first perform a comprehensive analysis of the band structure evolution. For simplicity, we ignore the gold and Al2O3 layers and assume the Ge metasurfaces are suspended in air. In the absence of corrugations, the original waveguide array extends infinitely in the y-direction and lacks of defined periodicity along this axis. As a result, there is no well-defined FBZ or radiation momentum matching condition in the ky direction, and only GMs located below the light line are supported along ky direction. One typical GM is illustrated by the orange dashed line in Fig. 2a. These modes are characterized by steep dispersion and theoretically infinite Q factors. By periodically perturbing the waveguides, we successfully induce a transition of the GMs along ky direction from bound states to leaky modes that can couple to free-space radiation. This is achieved by precisely tailoring two corrugation arrays on both sides of each waveguide, each with a period of Py and a longitudinal displacement of 0.5Py–δ, as illustrated in the top-right inset of Fig. 2a. This periodic modulation defines a new reciprocal lattice vector and imposes a well-defined FBZ along ky direction. Consequently, the GMs originally located below the light line fold into the radiation continuum, giving rise to GMRs. We proceed to conduct an in-depth analysis using the finite element method (FEM) using the commercial software COMSOL Multiphysics. With the geometric parameters of the structure set as Py = 2460 nm, Px = 3040 nm, w = 970 nm, h = 800 nm, δ = 0, corrugation width L2 = 660 nm and depth L1 = 100 nm, Fig. 2b presents the calculated band structure in both the ΓX and ΓY directions, which exhibits highly anisotropic dispersion band. Along the ΓY direction, the fundamental low-order GM is folded two times in the spectral range of interest and the resulting two branches of GMRs are observed. For clarity, we label these two bands as band A (high-frequency branch) and band B (low-frequency branch), as shown in Fig. 2b. Both bands keep the steep dispersion of the original GMs, ensuring that there are only a few excited modes within a small range of Δk. This effect enables thermal radiation at each frequency to encompass minimal spatial/Fourier components, a key factor to achieve high spatial coherence. A flatband behavior is observed along the ΓX direction. A set of numerical simulations illustrating the dispersion band at different Px can be found in Supplementary Figs. 5 and 8, demonstrating that the lateral coupling efficiency is key to achieve a flatband behavior, which can be explained by the concept of CROW with weak coupling effects50,51. This kind of dispersion band profile, exhibiting a saddle-shaped profile when plotted in three-dimensional (3D) k-space (see Supplementary Fig. 11), is a unique feature of the design, which is distinct from regular two-dimensional (2D) metasurfaces. Although this is barely discernible in Fig. 2b, bands A and B are not degenerate at the Γ point and extend into the ΓX direction. However, the Q-factor of the mode at Γ point on band B becomes infinite (symmetry-protected BIC) due to the preservation of C2 symmetry. For other states on band B, the Q-factor is orders of magnitude larger than those on band A with the same wavevector (see Supplementary Fig. 10). This large difference in the Q-factor between the two bands suggests that the critical coupling condition is only fulfilled for one band. As a result, only thermal emissions from band A can be observed in the far-field spectrum.

Fig. 2: Band structure and Q-factor of GMRs.
figure 2

a A diagram depicting the band folding in the ky direction due to the transition from a 1D lattice of uncoupled waveguides to a periodic structure with period Py. The inset illustrates the evolution of the FBZ from 1D to 2D. b Band structure supported by the periodic structure after the introduction of corrugation array. c Dependence of the Q-factors of band A on ky for different values of L1 (0, 2, 20, and 200 nm) in Fig. 2b, demonstrating an approximately inverse square relationship with respect to the corrugation depth at any wavevector.

Full size image

We further numerically investigate the tunability of Q-factor by L1 for the states on band A, as shown in Fig. 2c. The Q-factor exhibits an inverse square relationship with the corrugation depth L1, which is related with the strength of refractive index modulations. This relationship is maintained at any k point along the band, resulting in GMRs with a nearly constant radiative Q factor (Qrad) across the whole FBZ. In contrast, for traditional quasi-BICs, the Q-factor significantly reduces with ∆k = k-kBIC in the FBZ, confining high-Q resonance modes to a limited k range. Since the Q-factor is tightly correlated with the magnitude of the local electric field in the near-field, this property offers robust field enhancement across the entire band. Consequently, this k-flat and controllable ultra-high Q-factor band opens distinct opportunities for wide-angle spectrally tunable photonic applications.

As an example, we have designed specific structures with a targeted thermal emission wavelength of 5.3 μm. With the thickness of Al2O3 set as t = 590 nm and the geometric parameters of the Ge metasurfaces consistent with those detailed in Fig. 2, we assume L1 = 160 nm for all the subsequent calculations. These geometries are designed to satisfy the critical coupling condition so that narrowband near-unity emissivity is achieved (all material parameters used in our simulations are detailed in the Supplementary Information). According to Kirchhoff’s law of thermal radiation, the emissivity of a thermally balanced object is equal to its absorptivity. Therefore, the emissivity can be characterized by calculating the absorptivity of the structure E(λ) = A(λ) = 1 − R(λ) − T(λ). Given that the gold substrate is thick enough to block light transmission (T(λ) = 0), this equation can be further simplified to E(λ) = A(λ) = 1 − R(λ). Figure 3a illustrates the calculated ECD of the device across different δ values, defined as ECD = (ELCP – ERCP) / (ELCP + ERCP), where ELCP and ERCP represent the left-handed and right-handed circularly polarized (LCP and RCP) emissivity, respectively. Notably, when δ = 0, mirror symmetry guarantees the paired occurrence of LCP and RCP thermal emission, resulting in a net optical helicity of zero and a linearly polarized output. Furthermore, the calculation results reveal that ECD increases with δ, indicating that once the mirror symmetry is broken, the structure emits preferentially LCP or RCP wave, until δ reaches 280 nm, at which point the ECD approaches unity, indicating exclusive LCP or RCP emission. As δ continues to increase, ECD begins to decrease gradually, eventually returning to zero at δ = 0.5 Py due to the recovering of mirror symmetry in the structure. It is significant to observe that reducing δ from 0 results in entirely opposite ECD changes, demonstrating that a continuous adjustment of δ allows for seamless switching between LCP and RCP emission.

Fig. 3: Thermal emission polarization dependence on δ.
figure 3

a Calculated ECD values of the device under different δ conditions. b Far-field radiation polarization patterns of the device for δ values of −280, −140, 0, 140, and 280 nm. c and d Spectral dependence of the LCP and RCP thermal emission on the output angle along x (c) and y (d) directions for δ = 280 nm. The color amplitude indicates the emissivity. e Real part of the Ez for the LCP and RCP emissions at 0° output for δ = 280 nm. f Angular distribution of the emissivity for LCP emission at different wavelengths with respect to the y direction for δ = 280 nm.

Full size image

We selected five representative δ values (−280, −140, 0, 140, and 280 nm) to calculate and plot the far-field polarization states of the respective structure in k-space. The polarization state of the emitted light is described through the framework of Stokes parameters, which encapsulate the intrinsic correlations between the orthogonal components of the electric field. For elliptically polarized light, the electric field vector traces an elliptical path, as illustrated in Fig. 3b. The polarization ellipse is delineated within the Cartesian coordinate system by the x and y components of the electric field, complemented by the orientation angle 0 ≤ ϕ ≤ π and the ellipticity angle −π/4 ≤ χ ≤ π/4. Our findings reveal that at δ = 0, the momentum space exhibits identical linear polarization. Upon increasing or decreasing δ by 140 nm, the far-field polarization transits into elliptically polarized states with opposite chirality, culminating in high-ECD LCP and RCP states at δ = −280/280 nm. These observations are consistent with Fig. 3a. Remarkably, this control is exerted simultaneously over a wide range of wavevectors in any direction within the FBZ, especially at δ = -280/280 nm, where the same chiral emission output can be achieved across a wide range of wavevectors in any direction. This is because the mode originates from a GM and innately inherits its characteristics of angular independence of the polarization. This capability transcends the limitations of traditional chiral quasi-BIC structures requiring breaking the out-of-plane symmetry, as they are constrained to support a single k-point chiral response arising from BIC splitting43,44,54. Our approach demonstrates a significant advantage for practical applications: while it is possible to adjust the emission wavelength through the output angle, it also ensures the robustness of the output spectrum narrow linewidth, the polarization characteristics as well as the ECD.

We calculated and demonstrated the relationship between the emission spectra for different chiral polarization states and the output angle in the y-direction, exemplified for δ = 280 nm in Fig. 3c, d, where the color amplitude signifies the emissivity. The simulated results confirm that the device not only exhibits a large dependence of the emission wavelength on the output angle with respect to the y- direction, but also exclusively emits LCP light over a wide range of output angles, maintaining a stable Q-factor of over 1100 throughout the range. Our further simulation results also indicate that these characteristics exhibit good robustness against manufacturing imperfections (see Supplementary Fig. 15). We also extended the simulation to a broader spectral and angular range (see Supplementary Fig. 7), revealing the emergence of low-ECD modes at longer wavelengths. These unwanted modes can be suppressed using narrowband filters for practical applications. Notably, the ECD remains above 0.8 within the central ±10° range, where polarization purity is most distinguishable. Therefore, we focus on the spectral range of 5.15–5.4 μm and the angular span of ±10°, where the chiral emission features are well preserved. The electric field distribution portrayed in Fig. 3e underscores that an enhanced electric field is present for LCP output, dominated by magnetic dipoles (see Supplementary Fig. 6), while it is decoupled from the RCP output. To quantitatively characterize the spatial coherence of the device along y, which is implied by the steep dispersion for LCP in Fig. 3d, we calculated the spatial angular distribution of the LCP output frequency around 0 and 5°, and the relevant results are presented in Fig. 3f. For an output wavelength of 5.3 μm, which corresponds to normal output, the full width at half maximum (FWHM) of its angular distribution Δθ is merely 0.96°, indicating that the spatial coherence length of the device’s spin output in the normal direction is: Lc = λ/Δθ ≈ 60λ ≈ 0.32 mm»Py. This results significantly surpasses the near-zero spatial coherence length achieved by traditional metallic metasurface-based circularly polarized thermal emission46,47, and nearly three times of the latest results based on all-dielectric localized geometric phase-controlled thermal radiation5. Moreover, for a shorter output wavelength of 5.234 μm, Lc is found to be 1.37 mm. Significantly, thermal emissions across multiple polarization states at different δ values show nearly unchanged results of the spatial coherence (see Supplementary Figs. 9 and 12). Further results indicate (see Supplementary Fig. 13) that if low-loss single-crystal materials are employed in conjunction with low-contrast corrugation depth, the device’s normal emission output Q-factor can reach above 65,000, and Lc can reach the “cm” scale (Lc = 2046λ = 1.078 cm). For the device’s tilted output around 5°, it can even achieve a coherence length of Lc up to 10.63 cm. These features are pivotal for future integrated light sources and high-efficiency thermal emission.

Experimental demonstration

Following our theoretical design, we fabricated a series of metasurfaces with different δ by employing standard nanofabrication techniques, whose details are elaborated in the supplementary information (see Supplementary Fig. 1). The top and xz-cross-sectional scanning electron microscope (SEM) images of the device with δ = 280 nm, are presented in Fig. 4a, b, respectively, showcasing the high precision of our processing techniques. Figure 4c depicts the measurement setup designed to assess the emission performance of the device. To streamline our measurement system, we utilize a commercial heating adapter from Bruker to elevate the device temperature, and its thermal emission was collected by a Fourier transform infrared spectrometer (FTIR) equipped with a mercury-cadmium-telluride (MCT) detector. An aperture was strategically located far from the sample to minimize the collection of environmental radiation and to focus on the device multi-angle output. The chiral emission signal were collected using a quarter-wave plate paired with a rotatable linear polarizer. Furthermore, the heating adapter was integrated with a 3D optical rotation stage to accurately measure the device’s emission output at various angles.

Fig. 4: Experimental demonstration of chiral thermal emission with high coherence at δ = 280 nm.
figure 4

a, b present the top and cross-sectional scanning electron microscope (SEM) images of the fabricated structure, respectively. Both scale bars correspond to 3 μm. c Schematic of the setup used to characterize the thermal emission properties of the structure. Ap Aperture, QWP Quarter-wave plate, LP Linear polarizer, IFO Interferometer, BS Beam splitter, MM Moving mirror. d Measure signals of LCP thermal emission at 0° output for the device at various temperatures (125, 150, 175, and 200 °C), with the dashed line indicating the blackbody thermal emission signal at 125 °C. e Normalized emissivity spectra for two different chirality at four distinct temperatures. f The central emission wavelength and ECD extracted from (e). g, h Measured LCP and RCP emissions supported by the structure in (a) as a function of the output angle in the y- and x -direction, respectively, with color amplitude representing the emissivity.

Full size image

Initially, with the device surface aligned perpendicular to the collection direction, we captured the LCP emission spectra at different temperatures (125, 150, 175, and 200 °C) using the aforementioned setup, as illustrated in Fig. 4d. As expected from Planck’s law of blackbody radiation, the emission intensity increases with temperature. Importantly, this change hardly affects the polarization purity or coherence of the spectrum. A lower emission peak observed in the long-wavelength region of each spectrum is primarily due to the non-zero angle thermal radiation from band B of the device, as the multi-angle thermal emission from the sample was inevitably collected (see Supplementary Fig. 17). A steel plate, coated with candle soot and equal in area to the sample, served as a blackbody reference, with its radiation spectrum at 125 °C represented by the gray dashed line in Fig. 4d. Based on this reference, we normalized the emission intensity of the two chirality of the device at different temperatures. Since blackbody emission represents the theoretical upper limit of thermal radiation at a given temperature, this normalization allows a direct estimation of the absolute emissivity of our structure at the target wavelength. As shown in Fig. 4e, the LCP emission exhibits large emissivity with a narrow output linewidth of 17.5 nm (Q ~ 304) near the wavelength of 5.315 μm, while the RCP emission was almost zero, indicating a significant ellipticity contrast. Importantly, the high-Q characteristic remained stable across temperature variations, representing a two-order of magnitude improvement over traditional metal metamaterial-based linearly/circularly polarized MIR thermal emitters.

In Fig. 4f, the central wavelengths of emissions extracted from Fig. 4e at different temperatures clearly demonstrate the approximate linear control of temperature on the emission wavelength, attributed to the thermo-optic effect of the Ge material55, causing a significant change in the refractive index. This phenomenon is well predicted in our simulations, as shown in Supplementary Fig. 3. Significantly, this provides a means of fine spectral control, where different temperatures correspond to different radiation wavelengths. In practical applications, such as non-dispersive infrared (NDIR) sensing systems, this allows for precise matching to the fingerprint absorption wavelength of the target substance by controlling the temperature, with minimal impact on the spectral linewidth. In addition, we have found that the device’s measured ECD can reach 0.91 and remains largely unaffected by temperature changes. To evaluate the thermal stability, we conducted repeated measurements at 125 °C on the device with δ = 280 nm (see Supplementary Fig. 16). The results show that the central wavelength shifts by less than 1.5 nm across multiple heating cycles, indicating excellent thermal stability of our fabricated structure. In these tests, the ECD varies between 0.891 and 0.92, while the Q-factor ranges from 280 to 304. These uncertainties reflect standard deviations introduced by repeated thermal cycling and long-term measurements, and are represented as error bars in Fig. 4f, capturing typical fluctuations under experimental and environmental conditions. These results highlight that our device provides greater flexibility for the spectral tunability of next-generation single active devices, especially integrated circularly polarized heat sources.

We employed the same angle-resolved setup to measure wide-angle thermal emission across two distinct chirality states of our structure. The dependence of the measured emissivity on the output angle, relative to both the x- and y-direction, is displayed in Fig. 4g, h, respectively. We observed a clear LCP thermal emission toward different directions with respect to the x-direction, characterized by a stable emission at the same central wavelength of 5.315 μm with consistent linewidth. The negligible RCP output is indicative of a high ECD, which is maintained for emission angle up to 10°. The circularly polarized state with high ECD over a large range of wavevectors distinguishes these thermal emitters from quasi-BIC-based counterparts by breaking the out-of-plane symmetry.

In contrast, for inclined output with relative to the y-direction, while the circularly polarized state with high ECD is still observed, a noticeable blue shift of the emission wavelength is evident in Fig. 4h with a slight increase in the output angle. This shift is consistent with the positive slope of the short-wave dispersion band (band A) depicted in Fig. 2b, indicating that each single output frequency encompasses only very few spatial/Fourier components, thereby confirming the nature of ultra-high spatial coherence. It is noteworthy that in actual measurements, as the angle increases, there is a modest decrease in emissivity and a slight broadening of the linewidth. This is primarily attributed to the increased coverage of emission spectral components by the FTIR within the same collection angle after rotating the sample, leading to superimposed state and averaged spectral intensity in the recorded spectrum, as illustrated in the schematic diagram of Supplementary Fig. 17. In practical applications, employing a spatial filter can effectively eliminate emission signals at undesired angles, ensuring the spectral purity of the thermal emission, maintaining a narrow output linewidth, and preserving the polarization performance of the thermal emission signals across different angles.

To experimentally validate the capability of our structure to achieve full polarization control of the thermal emission, we fabricated another four devices with varying δ sizes (140, 0, −140, and −280 nm), as depicted in Fig. 5a–d. The upper panel of these figures present the top-view SEM images of the fabricated structures. To simplify the testing procedure, we utilized two orthogonal linear polarizers to verify the elliptical nature of the thermal radiation. Figure 5a, c, corresponding to δ = 140/−140 nm, show non-zero and distinct emission intensities under different x and y polarizations, indicating their far-field elliptical characteristics rather than purely linear or circular polarization outputs. At δ = 0, the structure’s mirror symmetry results in zero net optical helicity, leading to linear polarization output in the x direction, with negligible emission intensity in the y polarization direction. Finally, for the device with δ = −280 nm, we demonstrated an RCP thermal emission device with a narrow-band and high ECD, opposite to that shown in Fig. 4. These results are largely consistent with our simulation results in Fig. 4a, b. Thus, our findings indicate that by simply adjusting the corrugation spacing δ, continuous regulation between the two singular points on the Poincaré sphere can be achieved.

Fig. 5: Experimental results of the corresponding thermal emission from the structures with varying δ values.
figure 5

a–d The measured emissivity spectra for four fabricated structures with different δ sizes of 140, 0, −140, and −280 nm, illustrated by the top-view SEM images shown in the upper panel. All scale bars correspond to 1 μm. e Comparison of the ECDs, Q-factors, and Lc between our results and those from some reported experimental works.

Full size image

Figure 5e summarizes the experimental Q-factors, ECD, and Lc of typical studies that have achieved linearly polarized18,19,32,33,34,49,56,57,58,59,60,61,62/circularly polarized5,46,47 thermal emission from metasurface-based devices. Here 1D/2D spatial coherence refers to the angular dependence being confined to one/two directions. The spatial coherence of thermal emissions in our structure is actually 1D, as the dispersion band is dispersive only along the y-direction. It is obvious that most studies focus solely on linearly polarized thermal emission, with Q-factors that are significantly lower than our results. Among the circularly polarized thermal emission works listed, not only do they exhibit lower Q-factor and ECD, but they also demonstrate significantly reduced spatial coherence compared to our findings. Furthermore, thermal emission observed in this work remain almost unaffected by the output angle of up to 10° along the x-direction, enabling the use of 1D spatial filters and MIR lenses to collect the radiations, thereby improving output power without affecting the electromagnetics characteristics. This again underscores our results’ excellent alignment with the critical performance metrics of thermal emitters across key aspects including temporal/spatial coherence and polarization control, marking a significant advancement in integrated light sources in the MIR regime.

Discussion

It is important to highlight that, in order to simplify our experiments, all thin films were deposited through electron beam evaporation, a process that introduces significant absorption losses in these amorphous materials, as indicated by the imaginary part k ≈ 5 × 10−4. In comparison to theoretical predictions, the experimentally observed reduction in emission intensity and broadening of the spectral linewidth are attributed not only to the wide angular collection range of the setup (see Supplementary Fig. 17), but more importantly to non-idealities introduced during fabrication. These include increased absorption due to defects generated during thin film growth, and additional scattering losses caused by rough sidewalls resulting from the etching process. Such imperfections lead to a deviation of the fabricated structures from ideal critical coupling conditions, manifested by the broadened linewidths. For practical applications, advanced thin-film deposition methods such as atomic layer deposition (ALD) or molecular beam epitaxy (MBE) could significantly improve material quality. Combined with optimized dry etching process to minimize sidewall roughness, these techniques could effectively reduce absorption and scattering losses, thereby enhancing the coherence of thermal emission. In terms of circular polarization, the anticipated emission Q-factor exceeds 4000, with spatial coherence lengths of Lc = 0.466 mm and Lc = 3.75 mm at normal incidence and a 5° tilted angle, respectively. For the design optimized for linear polarization output, the Q-factor can extend 105, with a spatial coherence length of Lc = 1.078 cm at 0° and reaching the decimeter level (Lc = 1.063 dm) at a 5° tilted angle. These results demonstrate that our design can markedly surpass the limitations of traditional metal/local metasurfaces in terms of coherence and polarization control.

In summary, by integrating arrays of corrugations to both sides of each waveguide within an array, we successful enable the transition from originally confined modes with the dispersion below the light line to GMRs in the continuum. These nonlocal modes feature a saddle-shaped dispersion band, with a k-robust and sustainable ultra-high Q factor across a wide range of wavevectors in the momentum space. By adjusting the longitudinal spacing between adjacent corrugations, we can enable spin-sensitive and selective responses, achieving continuous polarization transitions from LCP to linear polarization to RCP, effectively tracing a closed loop on the Poincaré sphere. This polarization control is effective across a wide angular range of emission directions. Both numerical and experimental results confirm that our planar high-Q nonlocal metasurface design provides extreme coherence and full polarization control of thermal emission over a wide angular range, marking a solid advancement over multi-layer or slanted etching structures that support quasi-BICs with single k-point chiral response. Our special design enables improved emission collection from large-scale metasurfaces (see Supplementary Fig. 14), thereby increasing emission power without sacrificing other properties such as temporal, spatial, and spin coherence—all of which are crucial for high-performance thermal emission devices. In a word, our work has fully addressed the earlier concerns regarding thermal emissions, achieving both high temporal and spatial coherence, full control of polarization, and sufficient output power. These results set a new benchmark for the performances in terms of these attributes. Moreover, our design is readily extendable to other polarization coherent applications like fluorescence, lasers, and nonlinearity. In addition, while our current design strategy is rooted in symmetry analysis and mode engineering with full physical interpretability, future integration with machine learning–assisted design frameworks could further optimize device performance and open new opportunities for advanced thermophotonic applications63.

Methods

Numerical simulations

All numerical simulations were performed based on the FEM using the commercial software of COMSOL Multiphysics. Floquet periodic boundary conditions were implemented in the lateral directions of a unit cell to define the wavevectors, while PML were employed in the z direction to mimic a non-reflecting infinite domain.

Fabrication

First, a 5-nm-thick adhesion layer of Ti, a 100-nm-thick Au film and another 3-nm-Ti were successively deposited onto a Si substrate using electron beam evaporation. After that, two layers of 590-nm-Al2O3 and 800-nm-Ge were deposited onto the sample using the same equipment. Then, the 180-nm-PMMA resist layer was spin coated onto the sample and the designed structure pattern was exposed onto the PMMA layer by electron beam lithography system. After developing, 20-nm-Al2O3 was evaporated onto the sample and the lift-off process was used to transfer the pattern from PMMA to Al2O3 layer. The Al2O3 pattern worked as a mask to obtain the Ge structure in a subsequent inductive coupled plasma-enhanced reaction ion etching process.

Optical measurements

The emissivity of the fabricated samples was measured using a Fourier transform infrared spectrometer (FTIR) (Bruker Vertex 80 V) equipped with a liquid-nitrogen-cooled mercury cadmium telluride (MCT) detector. The emissivity measurements were carried out by loading the sample onto an emission adapter (Bruker, A540) which was employed to heat the sample at different temperatures to induce thermal emissions. Steel plates of the same size blackened by the black soot of candles were used as the standard blackbody reference. Both the blackbody and the fabricated sample were loaded onto the heating plate. When the blackbody and the sample were heated to above 100 °C, the emitted power was sent to the FTIR system and detected by MCT detector. All spectra were acquired using the same FTIR spectrometer with a spectral resolution setting of 2 cm−1, and 15 scans were averaged for each measurement. This offers a good balance between signal-to-noise ratio and acquisition time. For clarity, the data are presented in wavelength units (μm) after conversion from wavenumber (cm−1).