Introduction

Full control over a light beam’s degrees of freedom facilitates the custom tailoring of applications to derive detailed insights about the target system. Polarization shaping, for instance, is instrumental in nanoparticle localization1,2 and quantum entanglement3, while phase or spatial structuring plays a critical role in increasing the channel capacity in communication4 and studies of higher-dimensional entanglement5. In particular, spatial structuring of light in Hermite-Gaussian (HG) and Laguerre-Gaussian (LG) modes, within paraxial approximations, is pivotal for such applications. These modes are typically produced by optical resonators or external spatial mode converters, wherein phase structuring is applied to the fundamental Gaussian mode. Consequently, not only is the generation of these spatial modes crucial, but also the capability to measure and decompose down their distinct properties. With a wide range of applications, substantial efforts have been made to measure and decode the data encoded in these spatial modes6. Building on the extensive efforts to measure and decode spatial modes, traditional techniques for the modal decomposition of arbitrary modes into the LG or HG basis often involve a series of spatial light modulators7,8, a sequence of mode projections to ascertain the relative weights of constituent modes9, Shack Hartman phase front sensor10, or full field measurement via off-axis holography11. However, these configurations tend to be bulky and typically fall short in integration with devices at hand. This is where photonics integrated circuits (PICs) emerge as a transformative solution, offering the potential to miniaturize these systems to the size of a fingertip. The presented approach will aid the implementation of such devices for a compact mode decomposing solution12,13 in the field of imaging and communication.

PICs can be regarded as the optical analog to electronic integrated circuits14,15. With advances in fabrication technology, PICs evolved into controllable and reconfigurable light processors16. One of the main ingredients of most programmable PICs is the integrated version of a Mach-Zehnder interferometer, which consists of tunable phase shifters and directional couplers (on-chip beam-splitters). Each individual Mach-Zehnder interferometer (MZI) can be configured independently by applying an electric signal that, in turn, modifies the optical signal (phase delay) in the waveguides. This paves the way for the design of photonics circuitry capable of performing on-chip computations and manipulations16,17. Such reconfigurable PICs (RPICs) have been utilized, for instance, for signal processing17 and for performing quantum operations as well as unitary transformations18,19,20,21. However, recent developments have shown that RPICs hold great potential for controlling and manipulating free-space optical beams with great flexibility13,22,23,24,25,26, providing an efficient platform for free-space applications. New efficient methods for coupling free-space optical beams into the RPIC27, and new calibration methods allow to spatially resolve information associated with optical modes28,29. These studies offer a wide range of possibilities for combining applications that use free space optical modes1,5,13,30,31 and those that are based on the processing of information in an integrated platform.

In this manuscript, we present an RPIC, referred to as photonic processor, for the decomposition of spatial modes into a basis set spanned by LG modes. This technique provides crucial information regarding both the relative weights and phases of the constituent orthogonal spatial modes contributing to the measured beam. Our study is proving the concept by precisely measuring amplitude and phase of a set of spatial modes at 16 distinct positions distributed in two concentric circles across the transverse plane of the photonic processor. These measured complex amplitudes are then numerically decomposed into the constituting modes. Subsequently, information extracted in the decomposition process enables us to reconstruct the input field at the interface of the photonic processor. It is worth noting that, within the constraints of limited sampling in the transverse plane for our proof-of-concept study, we have successfully decomposed beams that consist of six constituent (azimuthal) modes. This processor marks a significant advancement in integrated photonics for spatial mode sorting or decomposition, particularly in terms of resolving the degeneracy in relative phase differences. Furthermore, the utilization of the silicon-on-insulator (SOI) platform in this investigation enhances its suitability for future applications where the seamless integration of mode generation and detection on a single platform is the ultimate goal.

Results

Mesh architecture and field processing

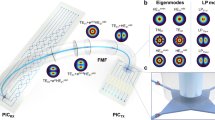
The photonic processor, decomposing spatial modes, is shown in Fig. 1a. It consists of three major building blocks, i.e, the input interface: to couple free-space modes into the chip, the processing unit; i.e., the programmable mesh processing the information, and the output interface consisting of 16 output ports which are used for detecting the light reaching the end of the mesh, eventually allowing for the retrieval of the processed light. The input interface (white circular region in Fig. 1a consists of 16 surface grating couplers (enclosed within white squares) arranged in two concentric rings. These grating couplers allow efficient coupling of free-space light into the chip by routing the light into single-mode waveguides. Each grating coupler (GC) functions as part of an individual pixel, capturing the amplitude and phase of the incoming light across the transverse plane. These pixels are numbered clockwise, starting with the first one on the right, as shown in Fig. 1a. This configuration allows for the light to be sampled at 16 distinct positions in the transverse plane, allowing a detailed spatial analysis of the input signal. After coupling light via the input interface, single-mode waveguides route light into the processing unit. The processing unit consists a collection of MZIs arranged in a binary tree configuration28,32,33. In this configuration, 16 inputs can be fully analyzed in just log2(16) = 428,33, stages. An individual MZI is a fundamental building block of the processing unit and is composed of two directional couplers and two phase shifters. One phase shifter is located before the MZI and one inside the interferometer, as shown in the inset of Fig. 1a. The phase shifters have been realized as TiN heaters, which exhibit intrinsic response times below 100 μs. and can be controlled with a click of a button, providing programability to the photonic processor. The MZIs are arranged in four columns as presented in Fig. 1b, providing full control over the mesh of MZIs to analyze any arbitrary mode33. Once the light has traversed through the mesh, it is outcoupled with the help of GCs designed in the same way as the input GCs. The processed light is further detected using a camera, although on-chip detectors also pose a viable option, which could be integrated for further minituarization.

Fig. 1: Photonic processor architecture and operation.
figure 1

a Optical microscopy image of the photonic circuit highlighting the key components: the input interface for coupling free-space light into the circuit, single processing units featuring phase shifters (PS) and beam splitters (BS), and the output interface for extracting processed information. b Schematic representation of the photonic processor’s operation, illustrating the arrangement of processing units, indicating how light is guided within the mesh.

Full size image

Modal decomposition in our photonic processor involves a two-step process: initially, it entails the measurement of complex amplitudes at the input interface, followed by the decomposition of these measurements into an appropriate basis. The circular arrangement of pixels at the input interface is particularly well suited for a basis with circular symmetry, which led us to select the LG modes as our basis set. The specific pixel arrangement predominantly allows us to explore basis sets that exhibit azimuthal phase variations while keeping the radial index of LG modes fixed. Different pixel arrangements at the input interface could facilitate the use of various mode families for modal decomposition.

This decomposition process is described mathematically by:

$${{{\bf{X}}}}={{{\bf{M}}}}{{{\bf{Y}}}}.$$
(1)

Here, X denotes a 16 × 1 column vector that represents the complex amplitudes measured by the photonic processor. M is a 16 × 9 matrix with each column containing complex amplitudes of the LG0,l mode, with l ranging from  −4 to 4, at each pixel position, and Y is a 9 × 1 vector containing the relative weights and phase relationships of the constituting modes. We employ MATLAB’s linsolve function to solve this linear equation and determine the vector Y. This approach allows for the decomposition of any arbitrary paraxial mode into a linear combination of orthogonal LG0,l modes basis with azimuthal index ranging from  −4 to 4.

To rigorously analyze the decomposition process, it is essential to determine two critical parameters: the maximum azimuthal order that our 16-pixel device can measure and, within this constraint, the number of modes it can distinguish accurately without significant overlap and ambiguity. The principles outlined by the Nyquist theorem are fundamental to this understanding. According to Nyquist, spatially distinct pixels sample a continuously varying complex function of the beam, with the phase variation in the azimuthal direction being particularly significant in our case. The Nyquist criterion states that sampling a signal with frequency ω at a rate of 2ω enables accurate retrieval of the signal’s characteristics. In the context of LG modes, where the azimuthal index l introduces a phase variation of 2lπ, this can be interpreted as l phase oscillations around the beam from 0 to 2π. Applying the Nyquist criterion, our 16-pixel configuration can accurately detect beams with a maximum azimuthal index of  ±8. Beyond this azimuthal order, aliasing and errors are likely to occur, compromising the accuracy of mode detection.

Second important consideration is how many modes the device can accommodate within the available LG basis set without resulting in a non-zero overlap integral. This is crucial for accurately distinguishing the constituent modes present in the beam as measured by the device within the allowed number of modes. Here, experimental factors also play a signinficant role, as the core area of an LG mode increases with index, our pixel arrangement is not suited to efficiently couple higher-order modes into the GCs. Considering these constraints, we set our device for 9 modes with azimutal index spaning from  −4 to 4. The overlap integral among these modes is detailed in the Supplementary note 2.

An essential step in the modal decomposition process is the accurate construction of the basis matrix corresponding to the chosen spatial mode set. For decomposition in the LG basis, this involves generating mode profiles using a well-defined beam waist parameter. The beam waist of the fundamental Gaussian mode determines the spatial scaling of all higher-order LG modes, as they share a common radial scaling parameter. Therefore, selecting an appropriate beam waist that reflects the experimental conditions at the input interface is crucial. In our setup, a collimated beam is focused onto the input interface using a lens, which allows us to estimate the beam waist at the sampling plane effectively. Once this fundamental waist is set, all higher-order modes exhibit consistent relative scaling and shape. This alignment ensures that the theoretically computed complex amplitudes at each sampling point closely match the experimentally retrieved values, enabling accurate basis matrix construction for reliable and precise modal decomposition.

Measurement of complex amplitudes

To facilitate photonic processor to accurately measure phase and amplitude, it is essential to calibrate on-chip elements of every MZI mesh, which includes any phase offset in the phase shifters (due to imperfection in design) in the MZIs, splitting ratios of the beam splitters, and voltage-to-phase relationship of the on-chip heaters used as phase shifters. This is done by implementing a general-purpose calibration protocol that was established in ref. 28. For phase and amplitude reference, a circularly polarized Gaussian beam of 2 mm diameter is illuminated the input interface as shown in Fig. 1b. The circular polarization ensures a homogeneous coupling efficiency for all grating couplers, independent of their specific rotational orientation28. Through several acquisition stages, intensity maps are recorded, and a least-squares fitting routine optimizes the unknown mesh parameters. The calibration process provides the transmission matrix of the mesh28, which is later used for the measurement of any unknown beam distribution29. After calibrating the photonic mesh, the phase and amplitude of an unknown beam are measured by directing it onto the chip’s input interface, which feeds into the calibrated MZIs mesh. The light is manipulated and interfered within this mesh, creating a pattern dependent on the unknown properties. The output intensities are recorded for various phase shifter settings, creating a dataset that, through a reconstruction algorithm using the calibrated transmission matrix, solves the inverse problem to deduce the beam’s amplitude and phase at each input coupler.

For the experimental implementation, a continuous wave laser with a Gaussian intensity profile at 1570 nm is used; the GCs of the input interface work ideally at normal incidence, achieving optimal coupling. To tailor the beam into arbitrary beam distributions, a spatial light modulator (SLM) is employed, using a complex amplitude modulation method34 to create specific mode holograms. Once generated, these modes are weakly focused using a 300 mm focal length lens, ensuring optimal overlap of the input beam with the chip’s input interface. A more detailed experimental setup is presented in the Supplementary note 1.

To illustrate the decomposition process a simple HG0,1 mode is generated using the SLM. The theoretical intensity profile of the generated field is depicted in Fig. 2a. The created modes are then projected onto the photonic processor and analyzed using the measurement algorithm29. The relative position of the pixels, serving as sampling points, is overlaid on Fig. 2a. The overlaid pixels represent the theoretical amplitude and phase, with the color coding indicating the phase at each pixel position, and the relative sizes reflecting the beam’s amplitude at those points. The measured phase and amplitude, for such a beam distribution, are displayed in Fig. 2b. The measured amplitude oscillates from maximum to minimum and vice versa, consistent with the intensity profile of the mode, while the measured phase values have a π phase jump between two lobes of the input mode.

Fig. 2: Modal decomposition with relative phase resolution.
figure 2

Each row corresponds to one input. The first column shows the theoretical intensity profile generated by the SLM, overlaid with points representing the pixel positions, where color indicates phase and diameter represents relative amplitude. The subsequent columns show the measured phase and amplitude, the modal decomposition, and the final reconstructed beam. a–d A HG0,1 input mode. The beam is decomposed in the LG basis, with LG0,1 and LG0,−1 contributions of equal amplitude and phase. e–h A HG1,0 input mode with mixture of LG0,1 and LG0,−1 with π phase difference and equal amplitude.

Full size image

Using the measured amplitudes and phases at the pixel positions, the complex values containing relative strength and phase at pixel positions are determined by using Eq (1) in Matlab’s linsolve function with a suitable basis matrix M. Figure 2c illustrates the decomposition of the measured mode into the LG basis. In this bar plot, the height of each bar represents the relative weight, normalized with respect to the highest mode contribution of a constituting mode. The color of each bar indicates the mode’s phase value. Figure 2c indicates contributions from LG0,1 and LG0,-1 with relative phase difference of −0.0129π. To reconstruct the mode detected by the photonic processor, the complex weights extracted in the decomposition process, which include amplitude and phase for each mode, are multiplied with the two dimensional function representing the corresponding mode. This is mathematically represented as a summation: \(\mathop{\sum }_{i=-4}^{4}{C}_{i}\cdot {{{{\rm{LG}}}}}_{0,i}\), where Ci contains computed relative amplitude and phase of the constituting modes. The decomposed values recreate the expected mode structure at the input interface with a slight beam orientation due to a small relative phase difference, as shown in Fig. 2d, closely matching the generated mode. To demonstrate the ability of the photonic processor in resolving phase degeneracy, we used the orthogonal HG1,0 mode with an overlaid pixel distribution containing the expected amplitude and phase as shown in Fig. 2e. The measurement procedure was repeated, with the amplitude and phase displayed in Fig. 2f. The analysis of the resulting data once again reveals the presence of the LG0,1 and LG0,-1 modes. However, this time they exhibit a relative phase difference of 0.96π, as distinctly shown in Fig. 2g. The relative phase difference between these two orthogonal modes is 0.97π, which is close to the expected phase shift of π. This highlights a significant capability of the processor.

A pivotal objective for the photonic processor is its deployment in scenarios characterized by modes generated with disparate relative weights. To assess its capabilities, a superposition of LG0,−3, and LG0,3 modes was generated with no relative phase and varying relative weights. Demonstrated in the first column of Fig. 3 with pixel distribution, mode combinations of LG0,−3, and LG0,3 were theoretically calculated with relative weight factors of (0.3, 0.7), (0.4, 0.6), (0.5, 0.5), (0.6, 0.4), and (0.7, 0.3). When normalized to the strongest mode in each scenario, these allocations adjust to (0.42, 1), (0.66, 1), (1, 1), (1, 0.66), and (1, 0.42), respectively. For each generated mode, amplitude and phase are measured as shown in the second column of Fig. 3. Subsequent to complex amplitude retrieval for each configuration, modal decomposition was executed. This measurement leads to the normalized bar plots shown in the third column of Fig. 3. The constituent modes were measured to be LG0,−3 and LG0,3 with no relative phase and varying relative contribution of (0.36, 1), (0.61, 1), (1, 0.98), (1, 0.59), and (1, 0.34). The results of modal decomposition align well with the input conditions for beam generation, showing a good match between the reconstructed beam profile in Fig. 3 column 4 with the input beams. However, our measurement process unveiled an inability to differentiate scenarios where one of the modes’ contribution is smaller than 15%, thereby providing us a criteria to exclude any mode with less than a 15% share of contribution in our modal decomposition method. This observation also serves as a good point to highlight potential errors that can occur in such measurements. In these measurements, we assumed that the SLM generated higher order modes with similar diffraction efficiency. Since we are only generating modes within a range of l = ±4, this assumption is reasonable. However, minor errors can originate as a result of limited resolution of SLM and its effect on the diffraction efficiency, which can be attributed to small deviation in above measured results from the expected values. For additional information on error estimation, please see Supplementary note 3.

Fig. 3: Modal decomposition with relative amplitude resolution.
figure 3

Superposition of LG0,−3, and LG0,3 modes. a–d Beam with a relative mixture of (0.42, 1). e–h (0.66, 1). i–l (1, 1). m–p (1, 0.66). q–t (1, 0.42). Column 1 shows the target field from the SLM with overlaid sampling points; column 2 displays the measured amplitude and phase; column 3 presents the modal decomposition; and column 4 shows the reconstructed beam.

Full size image

The scenarios discussed so far have involved mixed modes with equal and opposite azimuthal indices, creating an optimal setting for the concentric circular arrangement of pixels. Nevertheless, practical applications often necessitate the utilization of other modes spanning various azimuthal indices. Such variations lead to different beam waists for each orthogonal mode at the input lens’s focal plane, affecting the intensity of each mode at the pixel positions at the photonic circuit’s input interface. Now, the effectiveness of the method was tested in situations where beams consisted of two or more modes with different weightings. A combination of LG0,-1, and LG0,2 is initially selected with a relative phase of zero and a weight combination of (0.6, 0.4) as shown in Fig. 4a. After normalizing these weights to the maximum mode contribution, the weight combination adjusts to (1, 0.66). Following the measurement of phase and amplitude, the beams are decomposed. The results are depicted in Fig. 4c. The decomposition results normalized to strongest mode reveal a weight 1 for LG0,−1, and 0.52 for LG0,2, along with a certain relative phase among these modes. This relative phase can be explained to originate from the mode order-dependent Gouy phase. Although no phase delay between the constituent modes was introduced initially, the dependence of the gained Gouy phase on the order of the mode leads to differing phase delays upon arrival at the sensor. Since Gouy phase varies with order of the beam, both constituting mode acquire different phase and the measurement results with a relative phase difference. Notably, the modal weight deviates from the expected value of 0.6. This discrepancy can be attributed to differing intensity values at the pixel positions for the two modes. However, the reconstructed mode shown in Fig. 4d, derived from the modal decomposition, corresponds well with the input illumination. To further clarify, we adjusted the mode contributions to (0.4, 0.6) for LG0,−1, and LG0,2 as illustrated in Fig. 4e. The decomposition of the measured complex amplitudes resulted in a relative weight of (0.7, 1) and a relative phase difference. These results also slightly deviates from the expected modal weight of (0.66, 1). Such slight changes in modal weights for both input beams confirm the relative intensity variations for the constituting modes at the pixel positions. Expanding on these results, further measurements were conducted to test how many modes can be distinguished by the photonic device present in a beam. For this purpose, a mode distribution was realized, with mode contributions ranging from LG0,−3 to LG0,3, excluding the fundamental LG0,0 mode, all having equal weight and no relative phase as shown in Fig. 4i. The decomposition of the measured complex amplitudes, depicted in Fig. 4j, and analyzed in the basis set in Fig. 4k, demonstrates the photonic processor’s ability to distinguish separate modes accumulating different relative phases upon focusing. Figure 4k also shows that the relative strength of the modes decreases at the pixel positions as the mode order increases. This variation leads to deviations in the reconstructed beam as compared to the input, illustrated in Fig. 4l. These results underscore two additional strengths of the device presented in the manuscript: its capability to distinguish mode contributions with different weightings and relative phases across variable azimuthal indices, and its ability to measure the Gouy phase at the focal plane. The device also demonstrates its capabilities in analyzing and decomposing a mixed mode beam with up to six constituting modes, showcasing its potential for complex mode analysis.

Fig. 4: Number of mode resolving capability of the photonic processor.
figure 4

a–d Reconstruction of the beam with a mixture of LG0,−1, and LG0,2, with relative weights of 0.6 and 0.4, respectively. e–h Reconstruction of the beam with a mixture of LG0,−1 and LG0,2, with relative weights of 0.4 and 0.6, respectively. i–l Reconstruction of the beam for l ranging from −3 to 3, excluding LG0,0.

Full size image

The measurements presented above confirm the ability of the RPIC to decompose modes carrying both circular polarization and azimuthal indices. Crucially, the local orientation of the grating couplers (GCs) introduces an additional degree of freedom that enables discrimination of any polarization in the circular basis. This capability arises from the polarization-dependent geometric phase imparted by the locally oriented GCs, as described in ref. 28.

To demonstrate simultaneous decomposition of polarization, we performed measurements using linearly polarized Gaussian beams oriented along the x- and y-axes. In the first case, an x-polarized beam was measured, as shown in Fig. 5a. The complex amplitude of the beam was then decomposed into a full basis that includes both polarization and azimuthal mode information, illustrated in Fig. 5b. The results reveal that the beam is composed of the zeroth-order azimuthal mode with right- and left-circularly polarized components having no relative phase difference.

Fig. 5: Polarization resolving capability of the photonic processor.
figure 5

a, b Decomposition of X-polarized Gaussian beam in circular basis, c, d Decomposition of Y-polarized Gaussian beam in circular basis.

Full size image

Next, we performed a similar decomposition on a simulated y-polarized beam in Gaussian mode, whose complex amplitude is shown in Fig. 5c. The mode decomposition indicates contributions from right and left circularly polarized components with a π phase difference, consistent with the expected y-polarization. These observations underscore the additional functionality of the current photonic processor design, which can decompose both the spatial and polarization content of an input beam. The ability to perform single measurements is particularly beneficial for characterizing vector beams, as conventional detection schemes would require multiple polarization projections for complete detection.

Discussion

Comparison with existing techniques

To illustrate performance and potential applications of our on-chip mode-decomposition device in comparison with free space techniques7,35,36, such as Shack–Hartmann sensors, mode-sorting approaches using spatial light modulators (SLMs), and off-axis holography, a comparative Table 1 is prepared.

Table 1 Comparison of on-chip device with alternative techniques
Full size table

First, because the device is fabricated on a silicon platform, it can be readily integrated with current silicon-based technologies. This integration offers a compact footprint and facilitates the combination of the mode analyzer with other functionalities on a single chip. Moreover, our approach is intrinsically polarization-sensitive, enabling the decomposition of vector beams (i.e., beams with spatially varying polarization states). This is particularly useful for analyzing vector beams where orthogonal combination of azimuthal and polarization degree of freedom is used.

One notable limitation of the current implementation is that it resolves nine modes. Although this is fewer than what is achievable in some of the free-space techniques, the fundamental design of our platform allows for scalability. With further optimization, future generations could increase the number of resolvable modes while retaining the benefits of on-chip integration.

Table 1 provides a comparative summary of various techniques in terms of their capabilities for mode resolution, polarization discrimination, scalability with potential for on-chip integration, and data acquisition time. For comparison, we reference works from other groups that have demonstrated these techniques using either free-space or fiber-based modes. While the exact number of resolvable modes is not always explicitly stated in these studies, it is important to note that this capability largely depends on the specific hardware employed in each implementation.

In this study, we introduced and experimentally validated a photonic processor designed for decomposing broad range of spatial mode into the LG basis. The selection of the LG basis is influenced by the arrangement of sampling points at the input interface. By leveraging the reconfigurability of the processor, a calibration for on-chip MZIs is implemented, allowing for the precise measurement of the phase and amplitude for the mode under study. The measured complex amplitudes form a 16 × 1 vector, which is computationally decomposed into the LG basis with an azimuthal index ranging from –4 to 4. This device measures the relative weight and phase of different constituting modes. It represents a step forward toward on-chip mode sorters13 or spatial mode decomposition methods. For instance, we demonstrated the processor’s ability to overcome the degeneracy in the mode decomposition of HG01 and HG10 modes, where the distinction arises from the relative phase information. Additionally, it can distinguish any modes with varying azimuthal index in LG mode family, even those that are superposition of up to six orthogonal modes. The input interface, designed to sample the incoming beam, offers the added advantage of enabling polarization decomposition into circular polarization basis, paving the way for full vector beam analysis. The current processor’s limitations, primarily due to the design of the 16-pixel input interface arranged in two concentric circles, restrict the resolution of modes with radial components. Extending this processor to fiber mode decomposition for optical communication requires increasing the number of input pixels and optimizing their spatial arrangement to capture both radial and azimuthal field variations. However, these constraints can be addressed in future designs with more pixels arranged in various configurations. With the recent demonstration of programmable photonic circuits capable of spatially sorting orthogonal modes to identify independent communication channels13, and our approach of performing full modal decomposition via complex amplitude retrieval, new opportunities can emerge for implementing such platforms in optical communication systems. The use of a silicon-on-insulator (SOI) platform makes our approach inherently scalable and compatible with existing technologies. Moreover, leveraging a reconfigurable platform for generating spatial modes26, combined with complete modal decomposition on the detection side, could play a critical role in high-resolution microscopy, where structured illumination and mode analysis are essential.

Methods

SOI platform

The reconfigurable architecture for performing the mode analysis is based on a 220 nm thick layer SOI platform. Vertical surface grating couplers are arranged radially in two concentric circles of radii 200 μm and 220 μm. Each grating coupler is phase-matched to transverse electric polarization and has an alternating orientation of  ±45° with respect to the radial direction. The single-mode waveguides, used to route the light, have a width of 500 nm. Each MZI is composed of two directional couplers with a length of 40 μm and a spacing of 300 nm. To reconfigure each MZI, two TiN heaters are integrated over the waveguide. The heating introduces a change in the refractive index of the waveguide to modulate the phase of the propagating mode, providing a tuning parameter to control the output of the MZI.

Measurement procedure

The data acquisition process is carried out in four sequential stages. In the first stage, the phase shifters of the first eight Mach-Zehnder Interferometers (MZIs)—those directly connected to the input grating couplers (GCs)—are tuned using linearly spaced electrical power values. Fifteen voltage levels are applied, corresponding to electrical powers that span an approximate phase range of 0 to 2π for each phase shifter. To maintain consistent power consumption during each stage, the subsequent MZIs are driven in opposite directions: while the phase shifters in one MZI ramp from minimum to maximum voltage, the next one ramps in the opposite direction. This approach provides improved thermal management across the chip, with a maximum power consumption of ~580 mW. Although each phase shifter operates as a standard thermo-optic device with intrinsic response times below 100 μs, we introduce an additional delay of a few milliseconds after each voltage to allow the platform to reach thermal equilibrium and ensure stable operation. To fully sample all possible configurations for each MZI, a total of 225 V combinations are measured. During each stage, the phase shifters in the non-active (passive) MZIs are held at constant voltage values. The complete data acquisition process takes ~2 min.