Introduction

In recent years, substantial theoretical1,2,3,4 and experimental5,6 progress has been achieved in understanding emergent behavior of isolated quantum systems out of equilibrium. In this context, non-equilibrium many-body systems can be investigated by measuring quantum dynamics after a quench7, namely after a change of the Hamiltonian parameters that is much faster than the typical energy scales in the system—which is routinely performed in AMO (atomic, molecular, and optical) systems.

Although quench dynamics are extremely complex in general, one would expect that macroscopic observables, after a short time, become insensitive to the microscopic details8. In particular, in the vicinity of a phase transition, the dynamics should give rise to universal critical behavior which leads to scale-invariant spatio-temporal correlations with universal exponents9. Notably, we show that non-equilibrium critical phenomena can emerge in the context of quench dynamics in one-dimensional systems with long-range interactions. In general, universal non-equilibrium phenomena are relevant far beyond the scope of AMO and condensed matter physics, including chemistry, biology, and even sociology10. Examples ranging from glassy transitions seen in polymers, colloidal gels, and spin glasses11 to symmetry-breaking transitions in the Universe after the ‘Big Bang’12 all exhibit non-equilibrium critical behavior.

The unprecedented degree of control over quantum systems in platforms such as trapped ions13,14, ultracold atoms15,16, nitrogen-vacancy centers17, superconducting circuits18,19 and others20,21,22 has made it possible to probe fundamental questions about non-equilibrium many-body physics including prethermalization23,24, many-body localization25,26, discrete time crystals17,27, and dynamical phase transitions5,6. For example, universal scaling around non-thermal fixed points has been observed with Bose-Einstein condensates that exhibit self-similar behavior; these observations are however, not related to an underlying critical behavior28,29,30,31,32. In contrast, the work reported here is fundamentally tied to the existence of a phase transition and extends the remarkably rich domain of critical phenomena in equilibrium to far-from-equilibrium dynamics.

In this work, we investigate the critical behavior in the vicinity of a dynamical phase transition in quench dynamics. An immediate challenge is that a quantum quench generically leads to thermalization33, thus the resulting critical behavior is effectively thermal34,35. While this is the case in a quench from a gapped initial state, a quench from a gapless state (e.g., the critical point of the Hamiltonian) could lead to genuinely non-thermal critical behavior9,36,37,38 (see the schematic picture in Fig. 1a). We attribute these features to the behavior of the soft mode35. Specifically, we find that a generic quench from a gapped initial state excites this mode and heats it up, resulting in effective thermal behavior. In contrast, a critical-to-critical quench leads to overheating of the soft mode, giving rise to novel non-equilibrium critical behavior.

Fig. 1: Critical quench dynamics.
figure 1

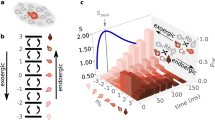
a Disorder-to-order phase transitions emerge even in the non-equilibrium setting of quench dynamics, and exhibit critical behavior at the transition. The ordered and disordered phases are shown in thick and thin lines, respectively, and the arrows indicate a quench to the critical point. While a quench from a gapped initial state (top panel) to the critical point (red circles) generically leads to effective thermal behavior, a quench from a gapless state (bottom panel), corresponding to a distinct critical point, gives rise to non-equilibrium criticality. b Ground-state phase diagram with Ising interaction along x or y direction. \({{{\mathcal{J}}}}{\gamma }^{x,y}/{B}^{z}\) is the ratio of the Kac-normalized effective interaction strength \({{{\mathcal{J}}}}{\gamma }^{x,y}\) to the transverse field strength Bz (see text). The phase boundary is shown in gray dashed lines, with red and green circles indicating the critical points where the quenches are performed. c The experimental sequence starting with all spins initialized along \({\left\vert \downarrow \right\rangle }_{z}\). The first quench is applied with interactions along the x direction, and the evolution is measured by projecting the spins along x. For the second quench, both the interaction and measurement bases are switched from x to y direction. In the double-quench experiment, the second quench is applied after evolving under the first quench, but no measurement is performed before the second quench. The curved lines illustrate the long-range interaction among all the spins where the opacity reflects interaction strengths that weaken with distance.

Full size image

Results

We probe the post-quench dynamics of a transverse-field Ising chain with tunable power-law interactions. The Hamiltonian of the model is represented as (ℏ = 1):

$$H=-{\sum}_{i < j}^{N}\,{J}_{ij}({\gamma }^{x}{\sigma }_{i}^{x}{\sigma }_{j}^{x}+{\gamma }^{\,y}{\sigma }_{i}^{y}{\sigma }_{j}^{y})+{B}^{z}{\sum}_{i}^{N}{\sigma }_{i}^{z},$$
(1)

where \({\sigma }_{i}^{x,y,z}\) are the Pauli matrices acting on the i’th spin. Jij is the interaction strength between ions i and j, Bz is the global transverse magnetic field and N is the number of spins. The coefficients (γ x, γ y) ∈ [0, 1], and only one of them is non-zero during a single quench (Methods). The interaction strength falls off approximately following a power-law of the form Jij ~ J/∣i − j∣p, where J > 0 is the effective interaction strength and p represents the range of interaction13. The exponent p was tuned to be at 0.89 for all the experiments and all system sizes (Methods). We note that, for large system sizes, the interaction matrix elements deviate from a simple power-law behavior and exhibit faster decay at longer distances (see Supplementary Information (SI), Sec. VII.B). In order to maintain a well-defined thermodynamic limit, here onwards, we refer to the interaction after it is Kac-normalized as \({{{\mathcal{J}}}}=\frac{1}{N-1}{\sum }_{i,j}\,{J}_{ij}\)39. We encode the quantum spins in the ground state hyperfine manifold of the 171Yb+ ions, where \({\left\vert \downarrow \right\rangle }_{z}\equiv {| }^{2}{S}_{1/2},F=0,{m}_{F}=0\left.\right\rangle\) and \({\left\vert \uparrow \right\rangle }_{z}\equiv {| }^{2}{S}_{1/2},F=1,{m}_{F}=0\left.\right\rangle\), and we perform high-fidelity state preparation and site-resolved detection using state-dependent fluorescence (Methods)40.

The transverse-field Ising model exhibits a ground-state phase transition from a disordered paramagnet to a magnetically ordered state. As the ratio of Kac-normalized effective interaction field (\({{{\mathcal{J}}}}{\gamma }^{x}\)) to the transverse magnetic field (Bz) is varied across the critical point \({{{\mathcal{J}}}}{\gamma }^{x}/{B}^{z}=1\), the average in-plane magnetization (\(\left\langle {\sigma }^{x}\right\rangle\)) changes from zero (disordered phase) to a non-zero value (ordered phase) in a second-order phase transition (Fig. 1a). By performing quenches to various values of \({{{\mathcal{J}}}}{\gamma }^{x}/{B}^{z}\), we identify the critical point of this phase transition and observe the characteristic divergent fluctuations. We report that, after a single quench from a gapped initial state, the critical behavior and exponents are effectively thermal; see Fig. 1a (top panel). In contrast, the scenario in Fig. 1a (bottom panel) involves preparing a critical initial state, which is experimentally challenging. Instead, we show that a sequence of quenches to multiple critical points (Fig. 1b) achieves the same objective and leads to non-equilibrium critical behavior.

We begin with a single quench sequence where all the spins are initialized in the \({\left\vert \downarrow \downarrow ...\downarrow \right\rangle }_{z}\) state, which is the gapped ground state of the initial Hamiltonian in the absence of the Ising interaction (SI Sec. III). Then the spin system is evolved after an interaction quench of the form Eq. (1), in which γx = 1, γy = 0 (Fig. 1a). We measure the total spin \({S}_{x}={\sum }_{i}^{N}{\sigma }_{i}^{x}/2\) projected along the direction of interaction (here along x) and calculate the net correlator defined as

$$\left\langle {C}_{x}^{2}\right\rangle=\left\langle {S}_{x}^{2}\right\rangle -{\left\langle {S}_{x}\right\rangle }^{2}.$$
(2)

We characterize the dynamics through the net correlator since the Ising symmetry of the Hamiltonian and the initial state implies that the average magnetization along the x direction remains zero at all times. The definition of \(\left\langle {C}_{x}^{2}\right\rangle\) further removes any bias of the average magnetization due to imperfect single-qubit rotations in the experiment. In the Supplementary Fig. 1, we report the post-quench evolution of \(\left\langle {C}_{x}^{2}\right\rangle /{N}^{2}\) with 10 ions. The observed net correlator increases in amplitude and exhibits slower dynamics as Bz is swept from larger to smaller values, consistent with numerical simulation that includes the decoherence effects of the experiment. This behavior hints at a continuous dynamical phase transition3.

Equilibrium phase transitions are commonly identified by defining an order parameter that acquires a nonzero value as the system transitions from the disordered to the ordered phase. Analogous to equilibrium phases, one may consider the in-plane magnetization to identify a dynamical phase transition. Using a mean-field analysis to compute the long-time average of the magnetization, we can identify \({B}_{c}^{z}/{{{\mathcal{J}}}}=1\) as the dynamical critical point of the disorder-to-order phase transition, which coincides with the ground-state critical point (SI Secs. III & V). While magnetization remains zero for our chosen initial state, we instead consider the temporal maximum of the net correlator, \({{{{\mathcal{M}}}}}^{2}={\max }_{t}\left[\left\langle {C}_{x}^{2}\right\rangle /{N}^{2}\right]\), as a proxy for the order parameter; the maximum is chosen to find a large signal in spite of decoherence.

In Fig. 2, we show \({{{{\mathcal{M}}}}}^{2}\) as a function of the scaled magnetic field strength \({B}^{z}/{{{\mathcal{J}}}}\). While there is no sharp transition for finite system sizes (N = 10, 15, 20), the order parameter clearly shows an inflection point around \({B}^{z}/{{{\mathcal{J}}}} \sim 1\) and a peak at small Bz, indicating the onset of ordering. Notably, the observed order parameter qualitatively follows the mean-field prediction in the ordered phase, \({{{{\mathcal{M}}}}}^{2}\propto ({B}^{z}/{{{\mathcal{J}}}})(1-{B}^{z}/{{{\mathcal{J}}}})\); see the dashed line in Fig. 2. Moreover, one can even capture the finite-size corrections by considering fluctuations at finite system sizes. The solid lines in Fig. 2 depict the function describing the finite-size corrected order parameter, which has the critical point and an overall scale as fit parameters. The inferred critical values are well in agreement with the mean-field prediction (SI Secs. IV.A & IV.C). Having identified the dynamical critical point, the immediate questions are: What is the nature of the critical behavior at the phase transition, and does it genuinely go beyond the equilibrium paradigm?

Fig. 2: Phase transition from order parameter.
figure 2

We report scaled maximum net correlator \({{{{\mathcal{M}}}}}^{2}={\max }_{t}[\langle {C}_{x}^{2}\rangle /{N}^{2}]\) as a function of \({B}^{z}/{{{\mathcal{J}}}}\) for system sizes N = 10, 15, 20. The solid lines are obtained by fitting the experimental data to the finite size corrected order parameter (Eq. (28) of SI), which has the critical point as a fit parameter. The extracted values are 0.83 (19), 0.88 (6), 1.01 (9), respectively for N = 10, 15, 20; the difference from the predicted critical point \({B}^{z}/{{{\mathcal{J}}}}=1\) is due to finite-size effects and experimental imperfections. For simplicity, we use the predicted critical value for studies in Figs. 3, 4. The dashed line represents the mean-field solution with an inflection point at \({B}^{z}/{{{\mathcal{J}}}}=1\). For the comparison of the experimental data against decoherence-free numerical simulation, see Supplementary Fig. 2. The error bars are statistical fluctuations around the mean value.

Full size image

As a first step toward answering these questions, we experimentally scale up the single quench experiment to system sizes up to N = 50 ions and observe the net correlator which, at the critical point, characterizes critical fluctuations. As we calibrate the quench Hamiltonian parameters to be at the (mean-field) critical point for all the system sizes, within our experimental uncertainty, we see that the fluctuations grow and evolve more slowly with increasing system size, indicating an emergent universal critical behavior (Fig. 3a). We identify similar behavior by a numerical simulation of the quench dynamics with experimental spin-spin coupling parameters for system sizes up to N = 25 (Supplementary Fig. 3), the maximum number of spins that can be simulated using available computational resources. Such critical behavior leads to scaling relations which are independent of microscopic length/time scales41. Using scaling analysis, we find the net correlator satisfies the functional form given by9

$$\left\langle {C}_{x}^{2}\right\rangle={N}^{1+{\alpha }_{1}}f\left(\frac{{{{\mathcal{J}}}}{t}_{1}}{{N}^{{\zeta }_{1}}}\right),$$
(3)

where the exponent α1 characterizes the amplitude scaling of fluctuations with system size and ζ1 describes the dynamical scaling. We verify that the scaling relation and the experimentally-obtained exponents α1 = 0.42 (14), and ζ1 = 0.19 (8) (see Fig. 3b), are consistent with the results of the exact simulation (see Supplementary Fig. 3). The procedure to determine exponents that yield the best collapse of the data is detailed in the SI Sec. VIII. Remarkably, the above exponents are also consistent with mean-field exponents at the thermal phase transition9α1 = 1/2, ζ1 = 1/4 (SI Sec. IV.B). Additionally, we fit the maximum amplitude of fluctuations against \({N}^{{\alpha }_{1}}\) to obtain the exponent α1 = 0.50(4) (see the inset of Fig. 3b) which is in excellent agreement with that of thermal equilibrium. Indeed, it is expected that the latter procedure leads to a more precise exponent α1 since the dynamical features are more susceptible to decoherence. Note that the numerically obtained exponents do not account for decoherence due to the limitations of numerical methods for the system sizes considered here (Methods).

Fig. 3: Unscaled (a) and scaled (b) fluctuations after a single quench.
figure 3

a We report experimental critical fluctuations with system sizes up to N = 50 ions. We obtain the critical scaling exponents (α1, ζ1) by optimizing the weighted Euclidean distance between each of the curves to get the best collapse for the experimental (b) data [see main text for details]. We observe remarkable similarity between the exponents found in the experiment and simulations (see Supplementary Fig. 3), highlighting the universality of the exponents despite experimental imperfections as well as finite-size effects. Comparing the decoherence-free numerical simulation in Supplementary Fig. 3 with the experimental data, we note that the fluctuations in the experiment are reduced due to decoherence and imperfect detection fidelity; however, as we can see from the scaled data, the scaling collapse is still observed for all the system sizes. In the inset b, we find consistent scaling exponents by fitting the maximum values of the fluctuation (dots) to a power-law fit to \({N}^{{\alpha }_{1}}\) (solid lines). Although this method does not capture the full evolution, we get excellent agreement of exponents for both the simulation and the experiment. The data points from numerical simulation (in green) do not account for decoherence, resulting in higher peak values as compared to the experimental values (see Supplementary Fig. 3). In Supplementary Fig. 3b, we present numerical simulations of critical dynamics for N = 10 and 15, incorporating decoherence effects. The error bars of the experimental data are statistical fluctuations around the mean value.

Full size image

An effective thermal critical behavior is to be expected in quench dynamics if a phase transition exists34,35, but this typically requires higher dimensions or, in this case, long-range interactions. The emergence of the thermal critical exponents does not mean that the system has thermalized. In fact, long-range interacting systems often exhibit prethermalization for a long window in time24,42,43. Instead, the thermal exponents should be attributed to the effective thermalization of the soft mode35. This can be understood through a Holstein-Primakoff transformation that maps spins to bosonic variables, \({\sigma }_{i}^{x}\to \frac{1}{\sqrt{N}}({a}_{i}+{a}_{i}^{{{\dagger}} })\), a mapping that is valid near a fully polarized state along the z direction. The lowest energy excitation of the system corresponds to a collective excitation of a bosonic mode, characterized by the operator a ≡ ∑iai, which becomes gapless (softens) at the phase transition. The total spin can be then described as \({S}_{x}\to \sqrt{N}x\) where x ~ a + a† may be interpreted as the position operator of a harmonic oscillator with a characteristic frequency Ω which vanishes at the phase transition. Applying the equipartition theorem, \({\lim }_{t\to \infty }{\Omega }^{2}{\langle {x}^{2}\rangle }_{t} \sim {T}_{{{{\rm{eff}}}}}\) at long times, we find that the gapless mode is described by a finite effective temperature (SI Secs. IV.A & V.A). In fact, identifying 〈x2〉 ~ Nα and Ω ~ N−ζ, the equipartition theorem reveals that the effective temperature obeys the scaling relation Teff ~ Nα−2ζ. Now, with α → α1 = 1/2 and ζ → ζ1 = 1/4, the effective temperature becomes a constant independent of system size, consistent with thermal equilibrium behavior. Finally, we note that while the description of the soft mode in terms of the spin operators takes a more complicated form due to the experimental interaction matrix, our scaling analysis remains valid (see SI Secs. V & VI).

To break away from the effective thermalization, we now consider the scenario in Fig. 1a. (bottom panel) where the initial state is gapless (i.e., critical) itself. However, realizing such a scheme in experiment can be challenging as it requires high-fidelity adiabatic preparation of the non-trivial critical state prior to the quench. In this work, we instead modify this scheme by applying a sequence of critical quenches. While the resulting critical behavior from multiple quenches is not quantum in nature, due to the over-heating of the soft mode, the prethermalization of our quantum system is crucial to evade thermalization and hence identify genuinely non-equilibrium behavior44.

Experimentally, we first perform a single quench (γ x = 1, γ y = 0) to a critical point and evolve until the fluctuations reach their first maxima. Then we switch the interaction from the x to the y-direction (Fig. 1c) to apply a second quench, i.e. we make γ x = 0, γ y = 1 (Methods). The intermediate evolution after the single quench brings the system to a critical state when the second quench is applied. Upon the second quench, the dominant fluctuations form along the y-direction and in Fig. 4a, we show the unscaled fluctuations (\(\langle {C}_{y}^{2}\rangle /N\)) for system sizes up to 50 ions. These fluctuations also obey the scaling relation in Eq. (3), but with the replacement \({C}_{x}^{2}\to {C}_{y}^{2}\), t1 → t2 (time after the latest quench) and with a new set of exponents α2 and ζ2 identifying a new universal critical behavior. We find the optimal collapse for α2 = 0.63(33) and ζ2 = 0.10(17) (Fig. 4b). We verify that exact numerical simulation results in very similar critical exponents (Supplementary Fig. 4). Notably, these exponents are also in good agreement with the analytical values α2 = 3/4 and ζ2 = 1/8 obtained for the infinite-range LMG model (see SI Sec. IV.D), underscoring the universal character of the observed critical behavior. Finally, we remark that the effective temperature now scales as \({T}_{{{{\rm{eff}}}}} \sim {N}^{{\alpha }_{2}-2{\zeta }_{2}}\), which shows a nontrivial scaling with system size, underscoring a dramatic departure from equilibrium critical behavior. Such non-equilibrium criticality generally emerges upon a quench from a gapless state, and can be attributed to the over-heating of the soft mode9,36,37,38 (see SI Sec. IV).

Fig. 4: Unscaled (a) and scaled (b) fluctuations after a double quench.
figure 4

a We plot the unscaled fluctuations along y direction at the predicted critical points for system sizes of N = 10--50 ions. The second quench is applied when the fluctuations following the first quench reach their maxima and the time t2 is counted after the second quench. b We apply the same scaling collapse technique as for the single quench to find the best scaling exponents (α2, ζ2) for the experimental data. See Supplementary Fig. 4 for numerical simulations of the data. We observe that the critical fluctuations do not monotonically grow for increasing system sizes, as would be expected from the scaling relations. This effect can be attributed to the imperfect switching time between the first and second quench; a nearly perfect collapse can be reproduced numerically using the precise switch times (SI Sec. VII.D). We also report exponents found by a power-law fit of the maximum fluctuations which agree more closely with the analytical prediction (Inset b.). While determining the experimental critical exponents, we have excluded 50 ion data (gray) [see main text for details]. The error bars of the experimental data are statistical fluctuation around the mean value.

Full size image

Experimental decoherence causes the observed fluctuations to be damped for both single and double quenches. We see that the unscaled 50 ion fluctuations after the double quench are significantly damped (Fig. 3a). The major sources of decoherence, which scale with the system size, remain within acceptable thresholds for system sizes N < 50, but these errors start to dominate for N ≥ 50 (“Methods”). This effect is more adverse for the double-quench sequence than the single-quench, since the former involves longer evolution under two quenches. For completeness, we have included all the 50 ion data in Fig. 4a, c, but excluded it in determining the best collapse exponent. Fitting the maximum amplitudes of the fluctuations to \({N}^{{\alpha }_{2}}\) yields exponent α2 = 0.69(9), with tighter error bounds (Inset Fig. 4c). Errors in identifying the peak fluctuation result in erroneous switch time between the two quenches, contributing to imperfect exponents. This effect can be reproduced in the simulation with exact experimental parameters, and correction for such errors in further simulations results in exponents that are well in agreement with the analytically predicted non-equilibrium values (SI Sec. VII.D).

Discussion

In this work, we have demonstrated the ability to identify, both numerically and experimentally, the dynamical critical point of a disorder-to-order phase transition in a 1D transverse-field Ising model. We have observed the non-equilibrium critical behavior upon single and double quenches with up to 50 ions and extracted the universal scaling exponents, which agree with the predictions of numerical simulation of up to 25 spins. A high level of experimental control was achieved by realizing self-similar interaction matrices across different system sizes, which is essential for experimentally identifying and characterizing the critical points of a phase transition. While the decay of experimental spin-spin interactions deviates from the exact power-law models with p < 1 (see SI Sec. VII.B), the resulting universal critical behavior follows the latter models closely, a feature that is also reflected in the spin-spin correlation function (see SI Sec. VII.C). Furthermore, we theoretically predict that the observed double-quench critical scaling is only the first in an infinite hierarchy of universal critical behaviors that emerge in a sequence of multiple quenches (SI Sec. IV.D), an exciting direction to investigate in the future. Future work could also explore extensions of our spin-based trapped-ion simulator to non-equilibrium dynamics that include other degrees of freedom, such as phonons45.

Methods

State preparation and readout

The quantum simulator used in this experiment is based on 171Yb+ ions trapped in all three directions in a 3-layer Paul trap46 with transverse center of mass (COM) mode frequencies ranging from νCOM= (4.64–4.73) MHz and axial COM mode frequencies ranging from νx= (0.23–0.53) MHz depending on system size (N = 10 − 50), with axial frequency being lowered to accommodate more ions in a linear chain. Before each experimental cycle, the ions are Doppler cooled in all three directions by a 369.5 nm laser beam, 10 MHz red-detuned from the 2S1/2 to 2P1/2 transition. We use the same laser to optically pump all the ions to initialize them in the low-energy hyperfine qubit state, \(\left\vert {\downarrow }_{z}\right\rangle {\equiv }^{2}{S}_{1/2}\left\vert F=0,{m}_{F}=0\right\rangle\) with  >99 % fidelity. In addition to Doppler cooling, we apply the resolved sideband cooling method to bring the ions to their motional ground state with  > 90 % fidelity. After the Hamiltonian evolution, we apply global π/2 rotations using composite BB1 pulses to project the spin along the x or y direction of the Bloch sphere from the z direction. We then measure the magnetization of each spin using a state-dependent fluorescence by applying a beam resonant with the \({\phantom{1}}^{2}S_{1/2}{\left|F=1\right\rangle}\Longleftrightarrow ^{2}F_{1/2}{\left|F=0\right\rangle}\) transition. The ions scatter photons if they are projected in the \(\left\vert {\uparrow }_{z}\right\rangle\) state, and appear bright, while in \(\left\vert {\downarrow }_{z}\right\rangle\) state, the number of scattered photons is negligible and the ions appear dark. A finite-conjugate NA = 0.4 objective lens system (total magnification of 70×) collects scattered 369.5 nm photons and images them onto an EMCCD camera, which allows us to perform site-resolved magnetization and correlation measurements with average fidelity of 97 %. No state preparation and measurement (SPAM) correction has been applied to data presented in this work. More details of this experimental apparatus can be found in our previous works13,27,47.

Generating XX and YY type Ising interaction

The global spin-spin interaction in the trapped ion system in consideration is generated by applying a spin-dependent force via non-copropagating 355 nm pulsed laser beams that uniformly illuminate the ion chain. The pair of beams has a relative wavevector difference along the transverse motional direction of the ions. These beams are controlled by acousto-optic modulators which impart beatnote frequencies at νCOM ± μ, and phases (ϕb, ϕr), respectively, where μ is the symmetric detuning from the COM mode ( ≈ 56 kHz). These two tones respectively drive the blue (BSB) and red (RSB) sideband transitions, which, following the Mølmer-Sørensen (MS) protocol48, generate an effective Hamiltonian

$$\begin{array}{rc}H=\mathop{\sum }_{i=1}^{N}{\sum }_{m=1}^{N}\frac{{\eta }_{i,m}{\Omega }_{i}}{2}&\left[{a}_{m}{e}^{\iota {\delta }_{m}t}{e}^{i{\phi }_{M}}+\right.\\ &\left.{a}_{m}^{{\dagger} }{e}^{-\iota {\delta }_{m}t}{e}^{-i{\phi }_{M}}\right]{\sigma }_{i}^{{\phi }_{s}},\end{array}$$
(4)

where ηi,m is the Lamb-Dicke parameter for ion i and mode m, Ωi is the Rabi frequency at ion i, \({a}_{m}^{{{\dagger}} },{a}_{m}\) are the creation and annihilation operators of motional quanta for mth motional mode, δm = μ − νm is the MS detuning from the mth motional mode frequency νm. \({\sigma }_{i}^{{\phi }_{s}}=\cos {\phi }_{s}{\sigma }_{i}^{x}+\sin {\phi }_{s}{\sigma }_{i}^{y}\), where the spin-phase is \({\phi }_{s}=\frac{{\phi }_{b}+{\phi }_{r}+\pi }{2}\) and the motional-phase is \({\phi }_{M}=\frac{{\phi }_{b}-{\phi }_{r}}{2}\) for the phase-sensitive realization of the MS scheme49. The unitary time evolution operator under this Hamiltonian (U(t) ~ e−ιHt) can be found by taking the Magnus expansion, which after appropriate approximation, leads to an effective Hamiltonian13

$$H={\sum}_{i,j}\,{J}_{ij}{\sigma }_{i}^{{\phi }_{s}}{\sigma }_{j}^{{\phi }_{s}}.$$
(5)

In the far detuned limit (δm ≫ ηΩ), where the virtual couplings to the phonon modes are sufficiently suppressed, the analytical form of the Ising coupling between ions i and j is given by13

$${J}_{ij}={\Omega }^{2}{\nu }_{R}{\sum}_{m}\frac{{b}_{im}{b}_{jm}}{{\mu }^{2}-{\nu }_{m}^{2}}\approx \frac{J}{| i-j{| }^{p}},$$
(6)

where νR = hδk2/(8π2M) is the recoil frequency, and bim is the eigenvector matrix element of the i-th ion’s participation in the m-th motional mode (∑i∣bim∣2 = ∑m∣bim∣2 = 1), M is the mass of the single ion. J is the effective interaction strength obtained by a power-law fit of the interaction matrix elements, and J/2π ranges within (0.25 to 0.4) kHz in the experiment for different system sizes. If we set ϕr = 0, ϕb = π, then ϕM = π/2 and ϕs = π, which makes the Hamiltonian of Eq. (5) an effective σxσx interaction. We can change this phase by changing the input waveform to the acousto-optic-modulator. Similarly, we set ϕr = 0, ϕb = 0 to obtain an effective σyσy interaction. In the double quench experiment, we switch these waveform phases to switch between interactions along different Bloch sphere directions.

We further apply a common offset of 2Bz to the frequencies of BSB and RSB tones which in the rotating frame of the qubit, results in an effective transverse field term \({B}^{z}{\sum }_{i}^{N}{\sigma }_{i}^{z}\) in the Hamiltonian of Eq. (5)13. The magnetic field strength Bz is chosen such that Bz ≪ δm for the rotating frame approximation to be valid.

The approximate power law exponent can be theoretically tuned within the range 0 < p < 3. However, in this experiment, we kept the exponent  ≈0.89 for all the system sizes by tuning the axial trap frequency (νx) and motional detuning (μ). We also note that the experimental interaction matrix deviates from a pure power-law decay to an exponential decay at large distances, especially for large system sizes (SI Sec. VIII). In principle, one can tune this exponent by changing only the detuning (μ) (see Eq. (6)), but changing the axial trap frequency (νx) for different system sizes results in more self-consistent scaling of the exact spin-spin coupling matrix50. We remark that maintaining a self-similar interaction matrix can also be achieved with individual optical control over all the ions51, but it is beyond the scope of this experimental setup, which features global optical control.

Experimental error sources

One of the main challenges in scaling up the system size is to maintain the fidelity of the quantum simulation experiments. Among various sources of decoherence in the trapped-ion platform, such as stray magnetic and electric fields, mode frequency drifts, off-resonant motional excitation, spontaneous emission, and additional spin-motion coupling that causes the evolution to depart from ideal simulation13. One such important source, which becomes significant in the large system size limit, is the off-resonant excitation of the motional modes causing residual spin-motion entanglement50,52. In order to trap longer linear chains while maintaining the same interaction profile, we need to operate at a lower axial confinement which can become as low as  ~200 Hz for N = 40–50. At such low axial confinement, the trapped ions are more susceptible to electric field noise and background collisions53. The conventional laser cooling methods start to become inefficient in cooling the ions to their motional ground states, and as a result, errors due to phonon evolution get introduced in the Hamiltonian evolution. To the lowest order, such an error can be modelled as an effective bit flip error during measurement50. Additional cooling methods such as EIT (electromagnetically induced transparency) cooling54 and sympathetic cooling53 would be useful in mitigating the effects of such errors.

Another source of bit-flip error is imperfect detection. Off-resonant pumping from the detection beam limits our detection fidelity to about 98 %. When a large number of ions are trapped in a linear chain, ions near the center of the chain are closer together than the ones at the edges. A random bit-flip error can be introduced due to leakage of light from neighbouring ions, which might cause a dark ion to appear bright and vice versa. More details about various noise sources in this apparatus can be found in previous works47,50,55.

Modeling decoherence

To account for the most relevant source of experimental dissipation, we consider an effective model that incorporates bit-flip errors in the dynamics. In this model, the density matrix evolves in time under the Lindblad master equation as

$$\frac{d\rho }{dt}=-i[H,\rho ]+\kappa \mathop{\sum }_{i=1}^{N}({\sigma }_{i}^{x}\rho {\sigma }_{i}^{x}-\rho ),$$
(7)

where the single bit-flip rate κ is chosen such that the numerically obtained net correlators \(\langle {C}_{x}^{2}\rangle\) best fit the experimental data. For simplicity, we have chosen the bit-flip rate to be uniform across the chain. In the simulations, we numerically calculate the dynamics under Eq. (7) using experimental Hamiltonian parameters and the best-fit value of \(\kappa /{{{\mathcal{J}}}}\) for a given \({B}^{z}/{{{\mathcal{J}}}}\). For N = 10, we find the best fit at \({B}^{z}/{{{\mathcal{J}}}}=\left[0.21,0.50,0.87,1.00,1.50,1.93\right]\) to be \(\kappa /{{{\mathcal{J}}}}=\left[0.057,0.036,0.089,0.085,0.067,0.045\right]\), respectively. For N = 15, and \({B}^{z}/{{{\mathcal{J}}}}=1\), we have \(\kappa /{{{\mathcal{J}}}}=0.024\). In Supplementary Fig. 1, we present the experimentally observed dynamics (represented by dots) of the net correlator after a single quench along with their numerical simulation (represented by solid lines) with 10 and 15 ions. In the subfigure a (10 ions), different colors indicate different values of the quench parameter \({B}^{z}/{{{\mathcal{J}}}}\). In subfigure b, we show the quench to \({B}^{z}/{{{\mathcal{J}}}}=1\) for N = 10 and 15. As shown in Supplementary Fig. 1, the numerical simulations show good agreement with the experimental data, capturing the damping rate as well as the frequency of the underdamped oscillations. The numerical results for 10 ions are obtained under the exact time evolution of the Lindblad master equation using QuTiP’s implementation56. Simulations for systems with 15 ions are obtained using the Monte Carlo wave function method57. This method can, in principle, be used to simulate larger system sizes. However, optimizing the decoherence rate in order to fit the experimental data requires a large number of these simulations, thus limiting our ability to simulate larger system sizes.

Jackknife error estimation

In the experiments reported in this work, we repeat the experiment and measurement sequence 400 times to reduce the quantum projection noise. To estimate the standard errors of the two-body correlators, we have implemented a Jackknife resampling technique58. In this method, we construct a distribution of net correlators by randomly sampling 399 experimental runs, each time leaving out only one run. We then calculate the variance of the distribution, which corresponds to the standard error of the net correlator.