Introduction

As global cooling progressed through the Cenozoic1, Arctic ice sheets began developing in the late Miocene2, and large Northern Hemisphere ice sheets first emerged at the onset of the Pleistocene (~2.6-million-year age; Ma), marking Earth’s shift from a unipolar to a bipolar ice-sheet regime. Since then, Earth’s climate has been characterized by periodical glacial-interglacial cycles. The alignment of glacial cycles with astronomical periodicities leads to linking these climate cycles to variations in Earth’s orbital geometry and axial inclination3,4 that cause the insolation received on Earth to fluctuate at the frequency of obliquity (~1/41 kyr−1), precession (~1/19 and 1/23 kyr−1), and eccentricity (~1/100 and ~1/400 kyr−1)5. Obliquity alters the latitudinal distribution of insolation and seasonal contrast; precession affects the timing and intensity of seasons relative to Earth’s position in its elliptical orbit; and eccentricity influences the Earth–Sun distance, modulating the total insolation received by Earth5. However, during the period after the Mid-Pleistocene Transition (MPT) (~800–1200 ka), the glacial-interglacial cycles display a dominant ~100-kyr cyclicities, no astronomical parameter could directly produce such strong ~100-kyr oscillations6. This is because precession and obliquity cannot directly generate periodicities at ~100-kyr band, and eccentricity’s effect on total insolation is too weak to explain the strong ~100-kyr glacial power4,6,7, despite eccentricity can produce ~100-kyr cycles. Amplitude mismatch between ~100 kyr cycles in eccentricity and climate, and the absence of the 405-kyr power in benthic foraminiferal oxygen isotope (δ18O)6,8, complicate the understanding of the ~100-kyr glacial cycles.

Before the MPT, glacial cycles were directly attributed to obliquity due to dominant ~40-kyr cyclicities, though interpretations for the dominance remain diverse9,10. This idea was extended to explain the post-MPT ~100-kyr glacial cycles as a quantum of 2–3 obliquity cycles11,12,13. Indeed, convincing evidence confirms obliquity’s role in late Pleistocene glacial terminations11,12,14,15. However, the precession and obliquity phases of glacial terminations based on 230Th-dated speleothem chronology16 reveal that late Pleistocene glacial terminations have a closer relationship with precession than obliquity15. This finding supports interpreting ~100-kyr cycles as a quantum of 4–6 precession cycles16,17 or a result of a beat between the main precessional frequencies18. The research on the morphology of deglaciation/termination of glacial cycles further unveils that precession has more influence on deglacial onset, while obliquity is more important for attainment of peak interglacial conditions and glacial inception19. Despite these phase analyses confirm the role of astronomical forcing in driving glacial cycles, the mechanism behind dominant ~100-kyr power remains unclear. A comparison based on spectral analysis suggests that variations in inclination of Earth’s orbital plane could explain late Pleistocene ~100-kyr cycles20. However, this is contested as an artifact of spectral methods17, because unlike inclination’s singular ~100-kyr peak, glacial cycles exhibit variable ~80–120 kyr periodicities16,21.

In contrast to the external astronomical origin, late Pleistocene ~100-kyr glacial cycles were thought as the self-sustained oscillation driven by internal climate feedbacks6,8,22,23,24,25. However, the solely internal mechanisms produce arbitrary phase, conflicting with the observed phase-locking between ~100-kyr cycles of eccentricity and climate6,8. Thus, the plausible explanation for the late-Pleistocene ~100-kyr glacial cycle lies on the models that express these cycles as a nonlinear interaction between orbitally forced response (precession and obliquity) and the internal dynamics of atmosphere, oceans, ice sheets and lithosphere6,24,25,26. This nonlinearity invokes a set of internal feedbacks to channel some of the system’s potential power into the ~100-kyr band6,27. It is accepted that the ~100-kyr glacial cycles were phase-locked to eccentricity over the last 1.2 Ma6,8,28, thus, the key to decoding the strong ~100-kyr glacial cycles depends on finding out the power source that amplifies the ~100-kyr spectral power. Both nonlinear response to precession and obliquity can produce ~100-kyr cycles18,27,29,30,31, potentially amplifying ~100-kyr glacial power. Thus, confirming a potential link between the strong ~100-kyr glacial power and eccentricity-modulated precession or obliquity is pivotal to understanding glacial cycles. In this regard, analyzing the spectral power ratio relationship among the ~100-kyr cycles, precession, and obliquity components could provide clues.

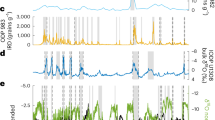
The spectral power ratio relationship solely based on benthic δ18O lack statistical significance because the reverse relationship between the ~21-kyr and ~100-kyr power ratios in δ18O is masked by a nearly antiphase relationship between the ~41-kyr and ~100-kyr power ratio over the last 800 ka (Fig. S1D, F, G), which obscures the roles of precession and obliquity in amplifying ~100-kyr power. Nevertheless, as mentioned above, given that the ~100-kyr glacial cycles were closely related to internal processes6,8,22,23,24,25,32,33, the 100-kyr cycles across climate components should be highly correlated with each other6,22,34 through a series of positive and negative feedbacks22,23,35,36, despite potential time lags or leads between the forcing and the climate feedback37. For example, the expansion and retreat of Pleistocene ice sheets could perturbate sea level and atmospheric-oceanic circulations via meltwater pulses6,16,35,36,38,39,40 and reshape Earth’s energy budget through albedo feedback. Consequently, the spectral power ratio relationship between precession/obliquity and the ~100-kyr components, preserved in ice volume or δ18O, should be projected onto other climate archives that are significantly affected by ice sheets. We therefore examine the spectral power ratio relationship among various coeval paleoclimate proxies, including benthic δ18O, to explore the ~100-kyr glacial cycles. The spectral power ratio serves as a proxy for estimating spectral strength or variance within a specific frequency band (see Methods).

Given the shift from dominant ~40-kyr to ~100-kyr glacial cycles after the MPT and the current availability of high-resolution paleoclimate data, here, we statistically analyze spectral power ratio relationship among the ~21-kyr, ~41-kyr, and ~100-kyr components within datasets across 57 globally distributed paleoclimate archives (including ocean, loess, ice core, and other archives) from 33 sites (Fig. 1; Table S1). These continuous records span pre-MPT (1200–2700 ka), MPT (800–1200 ka), and post-MPT (0–800 ka) intervals, all with robust age models (Table S1) and a high temporal resolution of at least a 2-kyr sampling rate. The ~100-kyr power ratios display persistent negative correlation with ~~21-kyr power ratios across these three intervals, while no relationship with ~41-kyr power ratios. Notably, strong/amplified ~100-kyr climate cycles also occurred before the Pleistocene, such as during the Pliocene, Miocene, and Oligocene27,41,42,43. To test whether these earlier ~100-kyr climate cycles share a similar mechanism with those of the past 800 ka, we extend the analysis to the Eocene–Oligocene Transition (EOT; ~34 Ma), when the Antarctic ice sheet began to develop, by exploring the phase relationship between ice volume/benthic δ18O and benthic δ13C44,45. It turns out that ~100-kyr climate cycles were periodically amplified, coinciding with δ18O/ice volume–δ13C phase coupling, which recurred at ~2.4-Myr eccentricity maxima (before 7.5 Ma) and minima (after 4 Ma).

Fig. 1: Geographic distribution of the collected paleoclimate datasets at 33 sites.
figure 1

The detailed information can be found in Table S1. Group sites 14 and 18 display the locations of multiple datasets used to compose the δ18O stack of Chinese speleothem16 and the Ocean heat content (OHC) stack of Indo-Pacific Warm Pool (IPWP)83.

Full size image

Results

The power decomposition analysis (PDA)46 (see Methods) was used to quantitatively estimate the spectral strength at frequencies corresponding to precession, obliquity, and ~100-kyr bands in paleoclimate records. Figure 2 presents the summarized PDA results for the collected 57 datasets, each based on their original age models, while detailed PDA results are shown in Figs. S2–S5. For comparisons, the overall power ratios of the ~100-kyr, ~41-kyr, and ~21-kyr cycles are shown using box whisker plots (Fig. 2A–C). To ensure significance, only PDA results with spectral power exceeding the 90% significance level at ~1/21 kyr−1, ~1/41 kyr−1, and ~1/100 kyr−1 were included. Detailed spectral estimations of these datasets are provided in Figs. S6–S9.

Fig. 2: The overall power ratios and their correlations across the pre-Mid-Pleistocene Transition (MPT) (1200–2700 ka), MPT (800–1200 ka), and post-MPT (0–800 ka) intervals.
figure 2

A Spectral power ratios at ~100-kyr frequency band for the paleoclimate archives over periods spanning 0–800 ka (in blue), 800–1200 ka (in teal green), and 1200–2700 ka (in vermilion), with power ratios whose corresponding spectral power below 90% confidence level (CL) being removed. B Same as in (A) but for the power ratio at ~21-kyr frequency band. C same as in (A) but for the power ratio at ~41-kyr frequency band. The box whisker plots are used to display the calculated evolutionary power ratios, and the median values are regarded as a criterion to assess the overall variance of ~21-kyr, ~41-kyr and ~100-kyr cycles in records. D, F, H, correlation between median values of the extracted ~100-kyr evolutionary power ratios and those of the extracted ~21-kyr evolutionary power ratios. E, G, I, correlation between median values of the extracted ~100-kyr evolutionary power ratios and those of the extracted ~41-kyr evolutionary power ratios. Trend line and correlation coefficient (r) are shown for each scatter plot. The absence of box-whisker plots for the intervals of 800–1200 ka and 1200–2700 kyr, compared to the interval of 0–800 ka, is due to either the absence of datasets during the corresponding time interval or the datasets being too short to effectively identify the ~100-kyr cycles.

Full size image

Post-MPT ~100-kyr power ratios exceed those of the pre-MPT interval in all datasets, while the opposite trend occurs for ~41-kyr power ratios. These shifts align with the transition from dominant ~41-kyr to ~100-kyr glacial cycles, confirming glacial influence on these records (Fig. 2A, C). Most paleoclimate records over the past ~800 ka show an inverse correlation between the ~100-kyr and ~21-kyr power ratios (Fig. 2A, B), a relationship that persists during and before the MPT (Fig. 2A, B). In contrast, the ~100-kyr power ratio shows no significant correlation with the ~41-kyr power ratio (Fig. 2A, C). Further analysis using the median power ratio values for the ~21-kyr, ~41-kyr, and ~100-kyr bands, represented by the horizontal lines in the box whisker plots, confirms a consistent negative correlation between the ~100-kyr and ~21-kyr power ratios (Fig. 2D, F, H), and no correlation between the ~100-kyr and ~41-kyr power ratios (Fig. 2E, G, I). Heterogeneity in dataset length, age models, and orbital tuning do not influence these relationship (Fig. S10C–F). Additionally, adjusting the frequency bandwidth setting in the PDA does not alter these relationships among the ~21-kyr, ~41-kyr, and ~100-kyr power ratios (Fig. S11).

Discussion

Role of obliquity and precession in 100-kyr climate cycles

In the late Pleistocene, the diminished ~41-kyr ice volume response, coinciding with increased ~100-kyr variability47 (Fig. S1), suggests a nonlinear transfer of obliquity power into ~100-kyr cycles48,49. Thus, the ~100-kyr glacial cycles have been interpreted as arising from 2 to 3 obliquity cycles9,11,12,13,49, frequency modulation of obliquity30,31, or self-sustained oscillations phase-locked to every second or third obliquity cycles24,50. Over the past 2700 ka, the characteristic periodicity of obliquity is centered around ~41 kyr5. If the amplified ~100-kyr glacial power resulted from nonlinear responses to obliquity, a correlation between the ~41-kyr and ~100-kyr power ratios would be expected, as these nonlinearities transfer power from ~41-kyr to the ~100-kyr band. However, our statistical results show no such correlation, suggesting that the amplified ~100-kyr glacial power likely does not originate from obliquity33, although obliquity does play a role in pacing deglaciation timing11,12,15,19,51.

The non-obliquity origin of ~100-kyr glacial power aligns with simulations showing that ~100-kyr glacial cycles persist under a fixed obliquity setting (in which insolation shows no obliquity variations) but nearly vanish without eccentricity/precession-driven insolation variations28,33. Moreover, late Pleistocene glacial cycles do not follow strict integer multiples of obliquity duration15,16, as predicted by the obliquity skipping hypothesis9,11,50. Instead, the declining obliquity expression in ice volume in the late Pleistocene reflects a shift in climate sensitivity from obliquity in the early Pleistocene9,49 to eccentricity/precession in the late Pleistocene6,52,53. This shift in sensitivity could be attributed to the gradual southward extension of large northern ice sheets13,15,53, as precession primarily affects daily insolation at low to mid-latitudes.

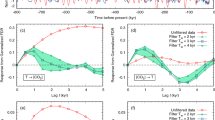
Our analysis of 57 paleoclimate archives reveals persistent negative correlations between ~21-kyr and ~100-kyr power ratios (Fig. 2A, B, D). Could this imply a precessional origin for the ~100-kyr glacial power? An asymmetric (rectified) climate response to precession can transfer variance from precession to its modulator (eccentricity), thereafter amplifying power at the ~100-kyr band6,27,54. However, several factors argue against this mechanism: (1) Even with an extreme threshold setting (extremely asymmetrical response), the resulting ~100-kyr power from this nonlinearity accounts for less than 20% of the spectral variance (Fig. 3J), far below the ~20–50% variance observed in late Pleistocene climate (Fig. 4H). (2) This nonlinearity also amplifies the ~405-kyr power6,27 (Fig. 3), which is absent in δ18O/ice volume, a phenomenon known as the ‘400-kyr problem’6,28. Despite the frequency modulation of ~100-kyr glacial cycles by the ~413-kyr eccentricity has been proposed to explain the absence of the ~405-kyr power in climate28,55, it lacks a clear physical process28. Furthermore, the spectral variance of the ~405-kyr component in the insolation curve is as weak as that of the ~100-kyr band, each contributing less than 1%. Thus, even if all power at the ~405-kyr band were transferred to the ~100-kyr band, their combined intensity still fails to match the observed amplitudes of ~100-kyr cycles.

Fig. 3: Power ratio relationship between ~20-kyr and ~100-kyr components in linear and nonlinear threshold systems.
figure 3

A 1E1T-1P curve over the past 34 Ma, generated by normalizing and averaging variations in eccentricity (E), tilt (T), and reversed precession (P) based on La04 solution74. B, C The ~20-kyr and ~100-kyr spectral power ratios of the 1E1T-P datasets, displaying an in-phase correlation between them. D 0E0T-1P curve over the past 34 Ma, with the weight of E, T, P being 0, 0, and -1, based on La04 solution74. E the clipped/rectified 0E0T-1P with a threshold setting of 0. F, G The ~20-kyr and ~100-kyr spectral power ratios of the clipped 0E0T-1P, exhibiting a nearly anti-phase correlation between them. H, I The 2π-MTM spectra of 0E0T-1P and the clipped 0E0T-1P. The clipping effect can amplify the ~100-kyr power ratio in the datasets, and induce prominent 405-kyr component, which is absent in the marine benthic δ18O and ice volume curve. J the relationship between threshold used to clip the 0E0T−1P curve, and the resulting ~100-kyr power ratios in the corresponding clipped 0E0T-1P curves. The precession parameter poses a negative effect on the strength of northern hemisphere summer insolation; thus, a more negative threshold value indicates a stronger threshold effect. With the increase in threshold (more negative), the ~100-kyr power ratio increases, whereas an upper limitation exists (<0.2).

Full size image
Fig. 4: The coupling between marine benthic δ13C and δ18O/ice volume on the ~100-kyr timescale leads to the ~100-kyr climate cycles.
figure 4

A The sea level equivalent relative to present (m) of the Antarctic and Northern Hemispheric (NH) ice sheets, estimated based on benthic δ18O stack of Westerhold et al.44,45. B The statistically reconstructed 500-kyr mean global mean surface temperatures (GMST) estimated from benthic δ18O stack following Westerhold et al. (with 50 and 95% credible intervals)44,84. C Soil carbonate δ13C data from Pakistan Siwalik61, and equid δ13C data from North America60, act as an indicator reflecting expansion of C4 plants in low and high latitudes, respectively. D Sedimentary accumulation rate (SAR) at Huaitoutala section, NE Tibetan Plateau, indicating tectonic uplift events62. E The uplifting rate of Panama Isthmus relative to sea level64. F Eccentricity parameter based on La04 astronomical solution (in black)74 and the ~2.4-myr filter (in blue). G The evolutionary correlation coefficient between δ13C stack44 and eccentricity (in vermilion)74; and that between δ18O stack44 and eccentricity (in blue); and that between the reversed sea-level equivalent44,45 and eccentricity (in teal green) on the ~100-kyr timescale. The sliding window was set as 1000 kyr. H The evolutionary correlation coefficient between benthic δ18O and δ13C stack44 on the ~100-kyr timescale (the dashed line in blue), and it’s absolute value (the solid line in blue); the evolutionary correlation coefficient between the reversed sea-level equivalent44,45 and δ13C stack44 on the ~100-kyr timescale (the dashed line in teal green), and it’s absolute value (the solid line in teal green); the evolutionary ~100-kyr power ratio of benthic δ18O stack (in black)44. I The evolutionary ~100-kyr power ratio of mean daily insolation on 21 June at 65°N, calculated based on La04 solution74.

Full size image

Alternatively, the intrinsic link between precession and eccentricity may transfer precessional spectral power to the ~100-kyr bands, as all eccentricity periods are related to precessional ones through the heterodyne mechanism5. This nonlinear resonance between the two main precessional frequencies produces a beat at the ~100 kyr, potentially amplifying the ~100-kyr glacial power7,18,56 despite the physical significance of this resonance remains uncertain6. Besides, the self-sustained oscillations phase-locked to 4–6 precession cycles may also channel precessional power into ~100-kyr band24,50. Consequently, regardless of the exact physical mechanism, the persistent negative correlation between ~21-kyr and ~100-kyr power ratios suggests a potential link between eccentricity-modulated precession and ~100-kyr climate cycles33, which favors the persistent influence of eccentricity and precession on the glacial cycles15,51,52,53,57.

Internal carbon cycles driving the 100-kyr climate cycles

As precession is modulated by eccentricity, the ~100-kyr power ratio in eccentricity is expected to covary with the precession power ratio (Fig. 3B, C). Thus, the observed negative correlation between ~21-kyr (assuming it represents precession) and ~100-kyr power ratios in climates essentially reflects the anticorrelation between ~100-kyr power in eccentricity and climate8 (Fig. 4H, I). This anticorrelation was previously hypothesized to arise from the inhibition of ~100-kyr glacial cycles by strong eccentricity-modulated precession forcing8,21. That is, when eccentricity-related ~100-kyr power is weak, precession forcing is weak or moderate over the entire 100-kyr cycle, allowing more time for ice sheets to grow, thereby extending the glacial cycles to the ~100-kyr periodicities. This explanation implies that the ~100-kyr glacial cycles should be phase-locked to eccentricity over the past 5 Ma. However, between ~1.2 and 3.5 Ma, ~100-kyr glacial power was also amplified8 (Fig. 4H), yet neither δ18O nor ice volume was phase-locked to eccentricity (the late Pliocene-early Pleistocene 100-ka problem)32,34 (Fig. 4G). Additional internal feedback mechanism must be involved to explain both the anticorrelation between ~100-kyr power in eccentricity and climate, and the origin of ~100-kyr climate cycles.

Despite the lack of phase-locking to eccentricity during ~1.2–3.5 Ma, benthic δ18O/ice volume remained phase-locked to benthic δ13C at the ~100-kyr timescale32 (Fig. 4H). Similarly, between ~9 and 12.8 Ma, strong ~100-kyr glacial cycles occurred without phase-locking to eccentricity in either δ18O/ice volume or δ13C, yet δ18O/ice volume remained phase-locked to δ13C (Fig. 4G, H). This suggests that ~100-kyr glacial cycles may arise from stochastic oscillations internal to the climate system, particularly involving the carbon cycle and its associated feedbacks22,23,32. Supporting evidence includes the observed phase lags of ice volume behind atmospheric CO2, which is in phase with eccentricity over the past ~400 ka23.

Actually, the ~100-kyr power ratios in benthic δ18O/ice volume show periodical amplification since 34 Ma (Antarctic glaciation onset), not just within the past ~5 Ma (Fig. 4H, I). This intensification of ~100-kyr power consistently occurs when δ18O/ice volume and δ13C are phase-coupled (either in-phase or antiphase) (Fig. 4H). Phase coupling is estimated using both cross spectra (Fig. S12) and evolutionary correlation analysis (see Methods). The correlation coefficient between the ~100-kyr power ratio in δ18O and the absolute evolutionary correlation between δ18O and δ13C are 0.56 (Fig. 4H). Moreover, the former lags behind the later by 46 kyr (Fig. S13), and the eccentricity–δ18O correlation lags eccentricity–δ13C correlation by 61 kyr at the ~100-kyr timescale (Figs. 4G; S13). These observations indicate that the strong ~100-kyr glacial cycles during the past 800 ka arose from the same mechanism as those before ~800 ka and are closely linked to global carbon cycles22,23,32.

Further investigation of the δ18O/ice volume–δ13C coupling at the ~100-kyr timescale reveals an in-phase relationship before 7.5 Ma, shifting to a reversed (antiphase) relationship after 4 Ma (Fig. 4F, H; Fig. S12). This phenomenon has been previously reported through cross spectral analysis41,58,59. The reversed δ18O/ice volume–δ13C phase coupling before and after ~4–7.5 Ma (termed the transition interval) is closely linked to several major environmental changes, including the expansion of C3 to C4 plants60,61 (Fig. 4C), the uplifting of Tibetan Plateau62 (Fig. 4D), the gradual closure of the Panama Isthmus63,64 (Fig. 4E), and the formation of Arctic ice sheets2. These events shifted the boundary conditions, affecting the carbon–climate coupling by perturbing the balance of influence between low-latitude and high-latitude continental carbon reservoirs on carbon cycles59. For example, the closure of the Panama Isthmus enhanced moistures transport to high latitudes, contributing to the formation of permanent Arctic ice sheets63. This transition marked a shift in global climate from the earlier unipolar into the later bipolar ice-sheet regime as early as ~4.5–7.3 Ma2,63 (Fig. 4A).

Before the transition, Earth’s climate was relatively warm and characterized by a unipolar ice-sheet regime (Fig. 4A, B). Perturbations in low-latitude continental carbon reservoirs, which are sensitive to tropical weathering, were hypothesized to dominate the global carbon cycle59. Eccentricity controls the seasonality and the total amount of insolation received on Earth. Thus, during ~100-kyr eccentricity maxima, enhanced insolation and warmer conditions facilitate chemical weathering65. Moreover, increased seasonality leads to climates instability and the shrinkage of continental carbon reservoirs59, which along with the rapid releases of permafrost carbon as a positive feedback to warming66 causes the rapid release of isotopically depleted carbon (12C) into the ocean-atmosphere system58,67. These processes lead to negative excursions in benthic δ13C and a negative correlation with eccentricity (Fig. 4G). Simultaneously, the warmer temperature results in more negative benthic δ18O (Fig. 4G). This causes an in-phase δ18O/ice volume–δ13C coupling at the ~100-kyr timescale (Fig. 4H). This feedback mode is termed the ‘Hyperthermal Style’58. In contrast, after the transition, global temperatures cool, and a permanent Arctic ice sheet exists (Fig. 4A, B). The expansion and contraction of Arctic biomes dominate the carbon cycle58,59. During eccentricity minima, colder and drier conditions caused the contraction of high-latitude vegetation68 and the subsequent shrinkage of high-latitude 12C-enriched continental carbon reservoir, releasing 12C into the ocean and triggering negative δ13C excursion58 (positive correlation between δ13C and eccentricity; Fig. 4G). Meanwhile, polar ice sheet expansion raised benthic δ18O values, producing an anti-phase δ18O/ice volume– δ13correlation (Fig. 4H), termed as the ‘Glacial Style’58.

Our results further reveal that the δ18O/ice volume–δ13C coupling recurred periodically at ~2.4-myr eccentricity maxima (before 7.5 Ma) or minima (after 4 Ma) (Fig. 4F, H). The ~2.4-myr long eccentricity modulates the amplitude of ~100-kyr eccentricity and thereby also influences Earth’s temperature. Eccentricity-scale negative excursions of δ13C are associated with cooling (low eccentricity) under the ‘Glacial Style’ and warming (high eccentricity) under the ‘Hyperthermal Style’58. Thus, we hypothesize that the temperature variation caused by ~2.4-myr eccentricity affects the balance between low- and high-latitude continental carbon reservoirs in regulating carbon cycles. Spectral analysis of the absolute δ18O/ice volume–δ13C correlation displays a distinct ~2.4-myr peak (Fig. S13), supporting this hypothesis. In the ‘Hyperthermal Style’ regime, the low-latitude carbon reservoir dominates the carbon cycles59; the warmth during ~2.4-myr eccentricity maxima facilitate the ‘Hyperthermal Style’58, causing in-phase δ18O/ice volume–δ13C coupling and amplification of ~100-kyr climate cycles (Fig. 4H). Conversely, during ~2.4-myr eccentricity minima, cooling transiently enhances the role of high-latitude continental carbon reservoirs, resulting in an in-phase δ¹³C–eccentricity correlation (as continental carbon reservoir shrinks during eccentricity minima)9, in contrast to periods where low-latitude carbon reservoirs prevail (as continental carbon reservoir expands during eccentricity minima)59. Consequently, during ~2.4-Myr eccentricity minima in the ‘Hyperthermal Style’ regime, δ13C and eccentricity decouple (Fig. 4G). This decoupling disrupts δ18O/ice volume–δ13C coupling (Fig. 4H) and suppresses ~100-kyr climate cycles. In the ‘Glacial Style’ regime, expansion and contraction of high-latitude biomes dominate the carbon cycles and are more sensitive to cold conditions58,59. The ~2.4-myr eccentricity nodes promote this ‘Glacial Style’, causing an anti-phase δ18O/ice volume–δ13C coupling and transferring ~100-kyr signals in carbon cycles to δ18O/ice volume, enhancing ~100-kyr climatic power. Conversely, this ‘Glacial Style’ is disrupted during ~2.4-myr eccentricity maxima (Fig. 4H), as warmer conditions enhance the influence of low-latitude carbon reservoir. Given that low- and high-latitude terrestrial carbon reservoirs respond oppositely to eccentricity59, their simultaneous influence leads to δ13C–eccentricity decoupling, disrupting δ18O/ice volume–δ13C coupling and weakening ~100-kyr climate cycles.

Whether under the ‘Hyperthermal Style’ or ‘Glacial Style’ regime, the ~2.4-myr eccentricity-modulated competition between low- and high-latitude continental carbon reservoirs for dominance in regulating carbon cycles governs the δ18O/ice volume–δ13C coupling, occurring at either ~2.4-myr eccentricity maxima or minima (Fig. 4H). This periodic coupling transmits the internal carbon cycle oscillations into the δ18O/ice volume, inducing strong ~100-kyr climate cycles. Thus, the internal carbon cycles and its ~2.4-myr eccentricity-modulated phase coupling with benthic δ18O/ice volume explain not only the strong ~100-kyr climate cycles of the past ~800 ka but also those since 34 Ma. In this regard, nearly all aspects of the ~100-kyr glacial cycles can be reconciled: (1) The absence of the a ~405-kyr signal in glacial cycles over the last 800 ka is plausible because deep-water δ13C lacks ~405-kyr signals since 1.6 Ma69; (2) Given that the δ18O/ice volume–δ13C phase coupling occurred only at ~2.4-myr eccentricity node in the ‘Glacial Style’ regime (Fig. 4F, H, I), the anticorrelation between ~100-kyr power ratios in eccentricity and climate over the past 5 Ma8 becomes reasonable. This also explains the negative correlation between ~21-kyr and ~100-kyr power ratios (Fig. 2), as eccentricity modulates precession; (3) This anticorrelation accounts for the ~100-kyr power mismatch at Marine Isotope Stage (MIS) 118, because the ~2.4-Myr eccentricity reached a minimum during this interval, which preconditioned the phase coupling between δ18O/ice volume and δ13C, and thereby amplified the ~100-kyr climate cycles (Fig. 4).

Nevertheless, further quantitative estimations are needed to assess the contributions of different carbon reservoirs to carbon cycles in response to the eccentricity-induced temperature changes. This is crucial because the relative importance of different carbon reservoir differs under varying boundary conditions, which underpins the competition hypothesis between low- and high-latitude terrestrial carbon reservoirs. Besides, the ocean ventilation can also trigger excursion in benthic δ13C, and produce opposite δ18O/ice volume–δ13C phase relationships before and after the transition, similar with the competition mode between low- and high-latitude terrestrial carbon reservoirs59. This is because in the Pleistocene, sluggish ocean ventilation during cold intervals (positive excursion of benthic δ18O) suppressed CO2 outgassing from the ocean, leading to negative benthic δ13C excursion70. In contrast, during the much warmer Miocene, vigorous marine ventilation during astronomically-forced cold intervals (positive excursion of benthic δ18O) enhanced CO2 release from the ocean71, resulting in positive excursion of benthic δ13C.

Implications for the MPT and future climate cycles

Between ~800 and 1200 ka, glacial cycles gradually shifted from dominant ~40-kyr to ~100-kyr periodicities, known as the Mid-Pleistocene Transition72. Given that the ~40-kyr signals persisted even after the MPT47,73 (Fig. S1), understanding this transition hinges on explaining why strong ~100-kyr glacial power began to emerge around 1.2 Ma. Based on our results and hypothesis, this shift can be attributed to the ~2.4-myr eccentricity-modulated phase coupling between benthic δ18O/ice volume and δ13C. This is because, around 1.2 Ma, benthic δ18O/ice volume began to exhibit a negative coupling with δ13C, coinciding with the onset of decline in ~2.4-myr eccentricity (and amplitude of ~100-kyr eccentricity) (Fig. 4), which amplifies the ~100-kyr climate cycles. This suggest that ~100-kyr climate cycles may originate from internal carbon cycle dynamics, offering a new perspective on the MPT.

Building on this idea, we infer that future glacial/climate cycles will likely remain dominated by ~100-kyr periodicities, but only if Earth remains in its current bipolar regime, where the ‘Glacial Style’ governs the phase coupling between benthic δ18O/ice volume and δ13C. This is because both ~2.4-Myr eccentricity and eccentricity amplitude are projected to remain below their average levels over the next 400 kyr74 which favors the phase coupling between δ18O/ice volume and δ13C, therefore amplifying the ~100-kyr climate cycles. However, ongoing anthropogenic CO2 emissions, persistent global warming, and Arctic ice loss may shift Earth toward a unipolar regime. In such a scenario, the δ18O/ice volume–δ13C phase coupling would transition to a ‘Hyperthermal Style’ regime, in which ~100-kyr climate cycles occur only during intervals of high eccentricity amplitude.

Methods

Extracting precession, obliquity and ~100-kyr spectral power ratios

To detect long-term evolution of changes in the spectral strength (or variance) of precession, obliquity, and ~100-kyr cycles in the collected climate archives, the evolutionary spectral power ratios at the precession, obliquity, and ~100-kyr bands to the total spectral power of the climate datasets were estimated. The estimation includes three steps. (1) Initially, the evolutionary power spectra of the datasets were calculated using the 2π multi-taper method (MTM)75 with a sliding time window76 (such as Fig. S1B). For the paleoclimate datasets spanning 0–800 ka, 800–1200 ka, and 1200–2700 ka, the sliding windows were set at 500 kyr, 200 kyr, and 500 kyr, respectively. (2) Then, the time-dependent amplitude modulations (power) at these three frequency bands were quantitatively calculated by integrating the evolutionary power at corresponding frequency bands46,76. (3) Thereafter, to facilitate comparisons among different paleoclimate datasets, the integrated evolutionary spectral power at each specific band was normalized by the total evolutionary power (integrated from 0 to the Nyquist frequency) to get the evolution spectral power ratio. This is because the unit of different kind of paleoclimate proxies is different. Over the last 2700 ka, the fundamental frequencies for precession and obliquity are 1/21 kyr-1 and 1/41 kyr-15,74. Thus, during the power integrating process, the frequency bands for the precession, obliquity, and ~100-kyr components were set to 1/18–1/26 kyr−1, 1/33.4–1/50.3 kyr-1, and 1/77–1/175 kyr-1, respectively.

Two software tools can be used to calculate the spectral power ratios: (1) the integratePower function in R package Astrochron76,77, and (2) the Power Decomposition Analysis (PDA) function in Acycle software46,78. The integratePower function processes both spectrograms (time-frequency or evolutionary spectra) and single spectra. Thus, for estimating the overall spectral power ratios of spectific frequenct bands in the clipped 0E0T-P series, we used integratePower function (e.g., Fig. 3J). Nevertheless, integratePower causes windows loss when estimating the evolutionary spectral power ratios, an issue resolved by the PDA function. Therefore, we used the PDA to calculate the evolutionary spectral power ratios for the 57 collected paleoclimate datasets.

Robustness estimation for the spectral power ratio results

Extracting evolutionary spectral power ratios is a non-stationary method and is relatively insensitive to age models because slight variations in the age model do not influence the long-term evolution trend of the spectral power ratio at a specific frequency. As a test, the evolution spectral power ratios at the precession and obliquity frequency bands for three different benthic δ18O stacks were examined (Fig. S1D, F, G). These stacks include the LR04 stack with LR04 age model79, the LR04 stack with LR10 age model8, and the Prob_stack80, (Fig. S1D, F). The LR04 age model was established by tuning the δ18O stack to a target derived from an ice sheet model driven by 65°N summer insolation79. The LR10 age model was based on the average sedimentation rate between tie points, independent of orbital forcing assumptions8. The Prob_stack, compiled from 180 globally distributed benthic δ18O records and developed using a profile hidden Markov model, is more representative than the LR04 stack80. Nevertheless, the Prob_stack adopted the LR04 age model as an initial condition during the stacking process, thereby inheriting the LR04 age model.

The calculated spectral power ratios of these stacks all show similar evolution trends, which also align with those acquired through the ENOF method (Fig. S1C, E)52. The ENOF is a nonstationary method and employed to estimate the temporal amplitude of precession and obliquity in the benthic δ18O over the last 2700 ka52. Therefore, the PDA method is also suitable for non-stationary analysis and can be regarded as an alternative to the ENOF method.

Heterogeneity in dataset length, age models, and orbital tuning may distort PDA results, potentially altering the spectral power ratio correlations. To mitigate these impacts, only PDA results from paleoclimate archives longer than 600 kyr over the past 800 ka were considered (Fig. S10C). Additionally, archives subjected to orbital tuning were separately assessed (Fig. S10D). To further reduce the effects of orbital tuning, datasets primarily constrained by the LR04 age model79 (Fig. S10E, F; Table S2) were tuned to the LR10 age model8. The LR10 age model is independent of orbital tuning. Across all scenarios, the ~21-kyr power ratios negatively correlate with ~100-kyr power ratios, with no observed relationship between the ~41-kyr and ~100-kyr power ratios (Fig. S10). Additionally, the frequency bandwidth setting for the PDA does not influence the relationship among the ~21-kyr, ~41-kyr, and ~100-kyr power ratios (Fig. S11).

Phase coupling estimation between benthic δ13C and δ18O/ice volume

To obtain the phase relationship between benthic δ13C and δ18O/ice volume at the ~100-kyr timescale, the ~100-kyr components were initially extracted from benthic δ13C and δ18O/ice volume using a Gaussian bandpass filter81 with frequency bands setting of ~1/77–1/175 kyr-1. The Cross-Wavelet Transform (XWT)82, based on these filters was then estimated using the MATLAB Cross Wavelet and Wavelet Coherence Toolbox. To further quantitatively estimate their coupling relationship, The evolutionary correlation coefficient between the ~100-kyr filters of benthic δ13C and δ18O/ice volume was calculated with a 1000-kyr sliding windows. A correlation coefficient above 0.5 or below -0.5 indicates in-phase or antiphase coupling, respectively. To keep the consistency between δ18O and ice volume, the sea-level equivalents44,45 were reversed before these calculations.

Lead-lag relationship analysis

Lead-lag analysis was used to estimate the lead/lag relationship between two datasets, reference x and target y series. When target y lags behind reference x, then a positive lag value will be return, which means that reference x occurred earlier than y. The lead-lag relationship analysis was realized using Acycle software78.