Introduction

Advancing high-performance energy storage technology is critical for sustainability and energy equality1. Among these technologies, supercapacitors, store energy through ion electrosorption on the surface of the electrode material. Unlike batteries, this mechanism enables a rapid response to potential changes, thereby allowing high power density2. High surface area carbons are particularly advantageous for capacitive energy storage and extensive efforts have been dedicated to optimizing surface area, electrical conductivity and pore architecture. A critical metric for supercapacitor performance is the volumetric energy density (Wh L−1), which is becoming increasingly relevant as demand for compact and portable electronic devices increases3. Volumetric energy density is intrinsically linked to the electrode density, volumetric capacitance and voltage window. However, due to the inherently low packing density of high surface area carbons, the volumetric energy density of typical carbon-based and commercial supercapacitors is <10 Wh L−14,5, far below even the first-generation lead-acid batteries (50-90 Wh L−1)6.

The graphene and reduced graphene oxide (rGO) family of materials have attracted tremendous interest in supercapacitor applications due to their tunable properties and design flexibility in terms of heteroatom doping, morphology engineering and chemical modification7,8,9. The prevailing consensus is that re-stacking or aggregation of graphene sheets is a suboptimal design strategy4, as the strong inter-planar π-π interactions render these interlayer spaces largely inaccessible to ions. Consequently, research has been directed towards harnessing the high surface area and abundant ion transport channels inherent in randomly assembled 3D graphene sheet structures10,11. While these structures deliver impressive gravimetric energy density (Wh kg−1) at the material level, this is achieved at the great compromise of volumetric performance. Recognizing the need for volumetrically-efficient performance, recent efforts have shifted to engineering dense graphene architectures that preserve ion transport pathways. Notable examples include microhole-arrayed graphene (45.4 Wh L−1)12, multi-nucleus assembled graphene microspheres (83.2 Wh L−1)13, graphene microspheres (83.4 Wh L−1)14, graphene-GO laminates (88.1 Wh L−1)15, and a spark-induced disordered graphene (94.2 Wh L−1)16. Collectively, these findings emphasize that graphene-based materials hold immense promise for volumetrically-efficient supercapacitors.

Despite progress, challenges remain in developing dense graphene electrodes that can be fabricated by methods closer to industrial needs while being compatible with organic electrolytes (typically ammonium salts in acetonitrile), given their preferred choice in industrial supercapacitors on the market17. While neat ionic liquids outperform organic electrolytes in terms of energy density by extending the voltage window and delivering a higher capacitance, as in the studies above, relatively few studies report competitive volumetric energy densities in organic electrolytes. Noteworthy examples include a high-density carbonized chlorobenzene (31.4 Wh L−1)18 and a dense graphene structure (36.5 Wh L−1)19.

In this work, we design a graphene structure tailored to deliver volumetrically-efficient capacitive energy storage. By integrating nano- and meso-scale features of graphene in micron-sized particles, we demonstrate that a multiscale structure, benefiting from each scale20, enhances ion accessibility, transport kinetics, energy storage capacity and long-term stability. A two-step rapid thermal treatment of a graphite oxide (GtO) precursor produces curved and tangled turbostratic crystallites interwoven into disordered domains, yielding multiscale rGO (M-rGO).

Defying the conventional understanding that crystalline domains are inactive in capacitive energy storage, we report an operando electrochemical interlayer expansion (e-IE) process. Here, both organic ammonium electrolytes (e.g. TEABF4 in acetonitrile) and ionic liquids (such as EMIMBF4) are surprisingly able to enter the curved graphene galleries in M-rGO, resulting in a 3-fold increase in capacitance without significant volume expansion of the electrodes. The e-IE process is generic to various electrolytes and organically optimizes pore dimensions to match those of the electrolyte ions. Combined with nanoconfinement effects, a phenomenon which maximizes charge accumulation21,22 and is known to deliver anomalously high capacitance23, and partial charge transfer during ion insertion/ de-insertion, we achieve among the highest BET surface-area-normalized capacitances in literature15,24, reaching 85 µF cm-2 in organic electrolyte and 135 µF cm-2 in ionic liquid electrolyte. Additionally, curvature effects alongside shortened ion diffusion pathways play a role in accelerating ion transport and enabling excellent rate capability at a high specific current of up to 200 A g−1.

Nevertheless, this raises a critical question – if graphene interlayers possess this potential, why is graphite, predominantly composed of highly ordered crystallites, ineffective for double-layer energy storage? Even at high potentials aimed at promoting ion intercalation, graphite shows low capacitance, poor cyclability and excessive electrolyte decomposition and exfoliation25,26,27,28. The weaker π-π interactions between graphene sheets in multi-layer graphene are enriched with a high density of “reactive energetic hotspots” on their edge and basal planes. These hotspots, including functional groups and defects29 significantly enhance ion insertion and de-insertion kinetics within crystalline domains by reducing the energy barriers associated with diffusion30,31.

We fabricate pouch cells (3 × 5 cm stacks) that achieve some of the highest reported volumetric energy densities in organic electrolytes, reaching up to 49.2 Wh L−1 at the stack-level, along with a power density of 69.2 kW L−1 (at 9.6 Wh L−1). To benchmark with state-of-the-art literature, we also evaluated devices employing neat ionic liquid (EMIMBF4). Thanks to an extended voltage window of 4 V and a high volumetric capacitance of 280 F cm-3, these pouches deliver a volumetric energy density of 99.5 Wh L−1. High volumetric energy and power densities in both organic and ionic liquid electrolytes highlights the powerful role of multiscaling to manipulate active sites, energy storage mechanisms and ion transport.

Results

Multiscaling disordered graphene with curved crystallites

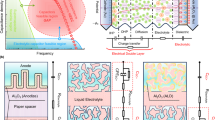
Figure 1A schematically illustrates the key distinctions between multiscale particulate graphene and conventional disordered and lamellar structures. The disordered rGO (D-rGO) network consists of randomly arranged, interconnected 3D porous sheets that facilitate short ion diffusion pathways but suffer from low electrode density due to excessive void volume. In such structures, capacitive energy storage relies on ion electrosorption within the porous network. In contrast, the densely packed lamellar structure, comprised of horizontally stacked 2D graphene sheets exhibits tortuous ion diffusion pathways and poor ion accessibility, limiting charge storage kinetics and capacitance. M-rGO addresses these shortcomings by integrating randomly oriented graphene sheets with abundant nanoscale curved crystallites. The disordered domains serve as ion reservoirs and are ‘transport highways’, while the crystallites contribute significantly to charge storage, creating a structure that is ideally suited to high energy and power density.

Fig. 1: Schematic highlighting the differences between lamellar, disordered and multiscale graphene with morphological characterization of M-rGO.
figure 1

A Conceptual schematic illustrating the differences in structure in terms of density, ion transport and the BET-surface area normalized capacitance. B HR-TEM micrographs of M-rGO showing numerous curved graphene crystallites. C SEM micrograph of M-rGO particles.

Full size image

M-rGO synthesis follows a two-step thermal treatment of particulate graphite oxide (GtO) powder (depicted in Fig. S1, Supporting Information). In the first step, GtO is introduced into a preheated tubular furnace at 700 °C by using suction for conveying the particles across the heated zone of the furnace, and the product is captured in a fine mesh. The suction level is adjusted to maintain a steady flow and a dwell time of ~2 ± 1 s. The rapid heating rate triggers an exothermic removal of oxygen function groups, generating internal pressures sufficient to overcome the van der Waals interactions that stack sheets together, resulting in exfoliated disordered graphene (D-rGO) with a high surface area32,33. Utilizing GtO as the precursor enables the formation of wrinkled and corrugated harmonica-like structures while preserving the original micron-scale particle size (Fig. S2, Supporting Information). In the second step, degassed D-rGO is loaded into an inert airlock chamber at the end of a pre-heated tubular furnace at 700 °C in a nickel crucible (schematically depicted in Fig. S1, Supporting Information). Given that the insertion of the crucible into the heating element with a rod takes ~2 s, D-rGO experiences a temperature rise estimated at ~350 °C s−1 The step is carried out under a continuous flow of N2 gas (at 3.6 NI min−1) for a total dwell time of 12 min, followed by quenching in the inert airlock. The aim of the second treatment step is to restore sp² hybridization and promote the growth of graphene crystallites.

High-resolution transmission electron microscopy (HR-TEM) confirms the formation of crystallites in M-rGO (Fig. 1B). Unlike the predominantly disordered nature of D-rGO (Fig. S3, Supporting Information), M-rGO exhibits an abundance of distinctly tangled curved graphene crystallites interwoven within disordered sheets. A distribution in the degree of crystallinity and interlayer spacings is observed, ranging from highly ordered domains turbostratic structures, to amorphous domains. Supplemental micrographs to further highlight these features are presented in Figs. S4 and S5, Supporting Information. In some instances, crystallites exceed 15 layers, with interlayer spacing ranging from 0.336 nm in the most ordered crystallites, to 0.351 nm or more in the expanded curved domains. To enhance processability and simplify electrode assembly, M-rGO powders are finally subject to gentle roll-milling. Scanning Electron Microscopy (SEM) micrographs (Fig. 1C) reveal a dense, platelet-like morphology with minor wrinkling and lateral dimensions of 5–15 µm. Unless otherwise noted, all characterizations are performed on non-roll-milled samples to capture the material’s intrinsic microstructure.

X-ray Diffraction (XRD) patterns (Fig. 2A) confirm the effective reduction of GtO to D-rGO after the first thermal treatment, indicated by the appearance of the (002) reflection at 23.76°, corresponding to d002 = 0.374 nm. The second thermal treatment shifts this reflection to 26.27° (d002 = 0.339 nm) and suggests enhanced structural ordering. The asymmetric peak profile suggests coexisting domains with varying degrees of order. Peak deconvolution34 reveals the presence of disordered carbon (D), turbostratically-stacked graphene (T), and graphitic domains (G). The broad and predominantly disordered D-rGO structure evolves into sharper turbostratic and graphitic peaks in M-rGO. These findings align with HR-TEM characterizations, confirming that the two-step thermal process is essential for crystallite growth. A time-dependent study further elucidates the structural evolution during the second thermal step (Fig. S6, Supporting Information), revealing that the transition from disordered to ordered structures occurs most rapidly in the first 6 min and plateaus after 12 min.

Fig. 2: Physicochemical differences between D-rGO and M-rGO and the fabrication process for the pouch cell prototypes used throughout this study.
figure 2

A The XRD patterns of D-rGO and M-rGO showing the (002) reflection with disordered (D), turbostratic (T) and graphitic (G) components. B Deconvoluted Raman spectra of D-rGO and C) M-rGO. D N2 adsorption-desorption isotherms and corresponding pore size distributions (in the inset). E Pouch cell assembly procedure from large area electrode fabrication to calendering and device assembly, with cross-sectional SEM of the electrode.

Full size image

We infer that crystallite formation is the combined result of the rapid and violent exfoliation into few-layer sheets loosely bound to each other in the first treatment step, with the rapid temperature rise in the second treatment step. A rapid rise in temperature is understood to induce structural stresses along defect lines, predominantly along non-hexagonal defects. This facilitates reordering of the graphene basal plane, driving self-alignment of disordered regions into ordered graphene structures34,35,36. However, the distinctive curved and tangled turbostratic crystallites are formed by the presence of these thin, few-layer sheets, which, in an attempt to minimize the total free energy and stabilize the structure, experience drastically higher surface diffusion and heat transfer at this scale37,38. Additionally, the first thermal treatment step ensures the absorbed thermal energy is effectively transferred to the carbon lattice in the second step, rather than on the desorption of oxygen functionalities. Unlike refs. 34,35,36,39, where the emphasis is on achieving a highly-ordered, graphitized carbon by employing temperatures > 2000 °C, our approach prioritizes a microstructure for superior ion accessibility and transport. Hence our choice of a relatively low thermal treatment temperature (700 °C) to curtail excessive defect healing effects that would otherwise drive graphitization. Supplementary Table 1 provides a comparative analysis of the carbon crystallite types observed in graphene materials and other carbons, contextualizing our findings and bringing our discovery into perspective.

Defects and disorder inherent in D-rGO play a key role in seeding crystallite formation and growth40. These features can be probed by Raman spectroscopy, which reveals information on defects, disorder and crystallinity41. The spectra of D-rGO (Fig. 2B) and M-rGO (Fig. 2C) are deconvoluted into first-order modes of D, D’, D”, D* and G bands, and second-order modes of G*, 2D, D + D’ and 2D’ bands42. Both spectra are characterized by a distinct graphitic (G band) at ~1585 cm−1, corresponding to in-plane vibrations of sp2 carbons, and a D band at ~1345 cm−1 arising from sp3-related structural disorder and defects in the carbon lattice. The intensity ratio of the D to G band (ID/IG) from the fitted peaks provides an insight into the degree and nature of structural disorder. The initial thermal exfoliation introduces significant lattice defects, reflected by ID/IG ratio of 1.15 ± 0.03. Following the second treatment step, this ratio decreases to 0.94 ± 0.02, indicating increased crystallite size and an improvement in the structural lattice ordering. For both samples, a D” band at ~1500 cm−1 confirms the presence of an amorphous carbon phase, while the D* band located at ~1200 cm−1, arises from sp2-sp3 bonds42,43,44. The second-order region, characterized by overlapping modes and low I2D/IG ratios suggests a multi-layer bulk material45. The position of the 2D band is 2690 cm−1 for D-rGO and 2703 cm−1 for M-rGO, suggesting a higher fraction of sp2 carbons in M-rGO42. Furthermore, the lower FWHM of the G band in M-rGO compared to D-rGO (90 vs. 116 cm−1) confirms a more ordered, though predominantly turbostratic structure (monolayer graphene is ~24 cm−1)46,47.

X-ray Photoelectron Spectroscopy (XPS) analysis reveals a reduction in the oxygen content from 45.2 at% in GtO to 9.6 at% in D-rGO and 6.4 at% in M-rGO (Fig. S7, Supporting Information). Deconvoluted C1s spectra shows an increase in sp2 C = C bonding from 24.2 at% (D-rGO) to 42.9 at% (M-rGO), congruent with an increase in bulk powder conductivity from 51.3 to 231.5 S cm−1, and consistent with the formation of turbostratic structures and reduced defect concentration from observations in HR-TEM, XRD and Raman analysis. N₂ adsorption-desorption isotherms (Fig. 2D) highlight the effects of thermal treatment on porosity and surface area. We note that BET surface area is measured on roll-milled powders, reflecting final materials that are employed in the devices. D-rGO exhibits a BET surface area of 245 m²/g, which decreases to 179 m²/g for M-rGO following the second treatment. Both display a Type IV profile, indicating micropores and narrow slit-shaped mesopores. A reduced hysteresis for M-rGO suggests mesopore narrowing, while negligible change at p/p₀ <0.01 indicates minimal difference in micropore volume. Pore size distribution (in the inset) shows that D-rGO predominantly contains mesopores (15–30 Å) and micropores (~6 Å), whereas M-rGO exhibits a smaller mesopore population, suggesting that crystallite growth occurs at their expense.

To fabricate electrodes, M-rGO powder is formulated into an ink with a minimal binder content (5 wt%) and tape cast onto an aluminium current collector. The resulting large area coatings (Fig. 2E) are cut into 3×5 cm electrodes and calendered to enhance particle adhesion and minimize interparticle voids. At maximum compression, the electrodes achieved a final density of 1.42 ± 0.04 g cm-3 approaching that of graphite electrodes (~1.5 g cm-3)48. For material-level performance studies, we use an intermediate electrode areal mass loading of 1.90 ± 0.1 mg cm-2 at a thickness of 13.3 µm (averaged over 10 measurements), while optimized device configurations employ more practical loadings of 6.1 mg cm-2. The dense electrodes are assembled into pouch cell prototypes for comprehensive electrochemical testing throughout this study.

Operando electrochemical interlayer expansion (e-IE)

The interlayers of curved graphene crystallites are narrower than the diameter of organic electrolyte ions and would therefore typically remains inaccessible for EDL formation. To access these latent capacitive sites, we apply an operando electrochemical interlayer expansion (e-IE) protocol by providing the necessary electrochemical driving force for TEA+ and BF4- ions to separate the van der Waals-bonded graphene layers. This is achieved by incrementally expanding the voltage window in successive galvanostatic charge/ discharge (GCD) cycles (Fig. 3A) at 0.05 A g−1. Up to 2.7 V, a typical linear increase in gravimetric capacitance is observed, delivering 44 ± 2 F g−1. However, at voltage windows exceeding 2.7 V, the linear voltage—capacitance relationship no longer holds, delivering 231 ± 8 F g−1 at 3.8 V. Upon returning to the operating window of 2.7 V, the device delivers 153 ± 4 F g−1, a hysteresis of 247%, over a 3-fold increase in capacitance. In contrast, a device that was subject to e-IE at a higher rate (0.5 A g−1) delivered a lower capacitance of 121 ± 6 F g−1 after e-IE (for a fair comparison, at 0.05 A g−1) (Fig. S8, Supporting Information). While true equilibrium ion configurations require prolonged charging times49, sufficiently low rates reach the limiting capacitance, that is, where the maximum number of capacitive sites are being utilized for a given potential, ultimately accessing more capacitive sites during e-IE. We hypothesize that such a regime decouples kinetic limitations, allowing ions to penetrate into deeper or more sterically hindered (bottleneck) sites50,51 in the first insertion, before moving to the subsequent voltage window. Conversely, a higher specific current limits the extent of ion insertion and interlayer expansion, leading to a reduced post e-IE capacitance. Other considerations are outlined in Supplementary Note 1. In addition, we compare four different categories of carbon materials, which includes a typical highly disordered activated carbon (YP-50F), D-rGO, M-rGO and graphite, subjected to the same e-IE process and measured the efficacy of the hysteresis. YP-50F shows no hysteresis, and graphite, the most crystalline of the materials, shows only modest hysteresis. D-rGO demonstrates an intermediate degree of hysteresis. These experiments affirm that the size, quality and structure of crystalline domains, as demonstrated in M-rGO, is critical for the interlayer expansion process to work effectively (Fig. S9, Supporting Information).

Fig. 3: Materials-level electrochemical performance of M-rGO pouch cell devices before and after carrying out e-IE.
figure 3

A Incremental increases in the potential window for M-rGO up to 3.8 V as part of the e-IE protocol to facilitate ion access into graphene interlayers, exhibiting hysteresis upon returning the standard operating voltage. The symmetric pouch cell devices are cycled at 0.05 A g−1, with an areal loading of 1.9 mg cm−2, 1.2 M TEABF4 in acetonitrile as the electrolyte and Celgard 2400 separator. B CV curves at 50 mV s−1 and (C) GCD curves at 0.2 A g−1 before and after carrying out e-IE. D Nyquist plot before and after e-IE at 2.7 V. E CV curves at higher scan rates 200–800 mV s−1 and rate capability up to 200 A g−1 in the inset. F Cation size-dependence on interlayer expansion at an ion concentration of 1.2 M in acetonitrile. The error bar represents the standard deviation of the average capacitance over 3 measurements. G Electrode height change for different cation sizes. The error bar represents the standard deviation of the average measured height dilation over 10 measurements. H The evolution of the Warburg coefficient with voltage increment and the frequency response at 2.7 V (inset); (I) Dunn’s method to distinguish the CEDL and the CPS at scan rates 2 – 200 mV s−1. The experiments are conducted using three cells to confirm reproducibility and are carried out at room temperature.

Full size image

Cyclic voltammetry (CV) curves assist in visualizing the increases in capacitance before and after applying the e-IE protocol, which can be confirmed by the increase in the enclosed area of the curves in Fig. 3B. The CV profiles show typical capacitive rectangular profiles, with a minor distortion in the range of 1.5 – 2.7 V which is also noted in the galvanostatic charge/ discharge (GCD) curves in Fig. 3C. The (reversible) distortion observed in our CV curves in the range 1.5–2.7 V following e-IE suggests ion-pore matching and a possible partial charge transfer arising from ion insertion/ de-insertion52. Electrochemical Impedance Spectroscopy (EIS) is employed to probe the electron conduction and dynamic ion migration process within the porous carbon. The Nyquist plots of M-rGO devices before and after applying the e-IE process in Fig. 3D demonstrates low resistance of the pouch cell devices, with an equivalent series resistance (ESR) of 0.62 Ω cm2 and 0.80 Ω cm2 before and after, which is >10 times lower compared to similar graphene-based devices12,15. Additionally, the higher slope in the high-to-medium frequency range after e-IE indicates that the interlayer expansion alters the microenvironment within the graphene structure and facilitate more rapid ion diffusion. The low ESR and rapid ion transport in the M-rGO structure translates to a high rate capability. Selected CV curves (Fig. 3E) up to 800 mV s−1 (and up to 1,500 mV s−1 in Fig. S10, Supporting Information), demonstrating the ability to maintain a nearly rectangular shape even at charge/ discharge cycles lasting seconds, while in the inset of the same figure, the device delivers 119 ± 5 F g−1 at a high specific current of 200 A g−1.

We studied ammonium cations of different sizes, specifically (in descending order of the molecular diameter calculated from the van der Waals volumes): THABF453, TBABF454, EMIMBF455, TEABF454, TEMABF454 and SBPBF456 in acetonitrile, and we subject to the same e-IE protocol at 0.05 A g−1. In Fig. 3F, there is an inverse linear relationship between cation diameter and capacitance, decreasing from 53 F g−1 for the smallest ion, SBP+ (0.646 nm ionic diameter) to 31 F g−1 for the largest ion, THA⁺ (0.936 nm ionic diameter). This is consistent with the fact that smaller cations (stripped of their solvation sheath) can more densely populate pores57. However, following e-IE, larger cations demonstrated a greater hysteresis, from 131% for SBP⁺ and a maximum of 249% for TBA⁺, while this trend was reversed for THA⁺ (155%). Electrode dilation is also characterized for each respective electrolyte system (see Supplementary Note 2). From Fig. 3G, electrode dilation exhibits a monotonic increase with cation size, ranging from 9.1 ± 1.1% for SBPBF4 to 14.1 ± 0.8% for EMIMBF4, before sharply rising to 20.4 ± 2.1% for TBABF4, and 58.1 ± 7.1% for the largest cation, THABF4. This trend suggests that increasing cation diameters impose greater strain upon insertion. According to the Lifshitz theory, the van der Waals attraction between graphene sheets is inversely proportional to the cube of interlayer distance58. For M-rGO, the inflection point in the relationship marks the threshold of structural stability of ion insertion. To support this interpretation, micrographs of the disassembled electrodes in Fig. S11 (Supporting Information) show that TBA+ induces moderate exfoliation, while THA+ causes significant exfoliation and particle fracturing, to the extent that few-layer sheets are visible, while this is not the case for smaller cations. This indicates that the pronounced strain associated with bulky cation insertion sufficiently weakens the van der Waals attraction between sheets and makes them vulnerable to exfoliation. This aligns with the use of larger ammonium cations as graphite exfoliation agents59. This structural degradation provides a plausible explanation for the observed decrease in capacitance hysteresis following e-IE for THA+, causing a loss in the number of high-capacitive sites. These results highlight the delicate design trade-off in electrolyte selection. While smaller cations exhibit limited accessibility to curved graphitic domains, larger cations can compromise structural integrity. In contrast, anion size plays a less significant role on capacitance hysteresis as shown in Fig. S12 (Supporting Information).

Electrochemical processes in electrodes post e-IE

To track the micro- and nanoscale structural evolution of M-rGO during the e-IE process, we conducted global dilatometry measurements complemented by SEM, XRD and EIS. Operando dilatometry reveals minimal electrode height changes up to the onset of interlayer expansion at ~3.0 V, reaching a total dilation of 11.2 ± 0.8% post e-IE, and significantly lower than D-rGO (Fig. S13, Supporting Information). We note that all volumetric capacitances reported in this work account for this dilation. To confirm ion insertion into the interlayers, we conducted ex-situ XRD at different voltage intervals (Fig. S14, Supporting Information). The (002) peaks remain unchanged until ~3.0 V, after which they broaden, shift to lower 2θ values and a new peak (00ℓ) emerges at ~16.6°, indicating the formation of a disordered intercalation compound with periodicity along the c-axis60. This structural change is consistent with dilatometry results and electrochemical characterizations, where a sharp electrode height change coincides with increasing capacitance. Moreover, the ex-situ XRD patterns reveal that following e-IE, the energy barrier for subsequent ion insertion into the curved interlayers is reduced and occurs within the operating voltage window of the device.

These changes can be effectively captured by differences in electrochemical behavior. To understand how the energy storage microenvironment evolves during and after the e-IE, EIS was performed at different voltages and the Warburg coefficient (σ) is summarized in Fig. 3H. The Warburg coefficient σ (Ω s-0.5) can be extracted by fitting the gradient of the real part of impedance (Z’) against the angular frequency ω-0.5 in the frequency range 1–10 Hz. It decreases from 0.234 to 0.198 Ω s-0.5 until 2.7 V, before dropping sharply to 0.062 Ω s-0.5 following interlayer expansion—indicating an improvement in the ion diffusion by a factor of ~3. Frequency response analysis, spanning a hierarchy of time scales61, provides key insights into charge storage and ion transport. High frequency components correspond to electrolyte transport in macropores, while lower frequencies are associated with more kinetically limited processes such as desolvation effects and ion penetration into smaller and deeper pores62. The curves in the inset of Fig. 3H show a significant increase in low-frequency (<1 Hz) capacitance provides further evidence that ion insertion results in the generation of new energy storage sites into the smaller and deeper interlayers of M-rGO. Meanwhile, the convergence of the curves at ~3 Hz suggests the charge storage capacity in the meso- to macroscale remain largely unaffected. These findings offer electrochemical evidence that interlayer expansion alters the microenvironment within M-rGO and underscores the advantages of this multiscale design approach. The diverse atomic-scale environment within M-rGO each contribute uniquely to ion dynamics and capacitive energy storage.

The significance of the curved turbostratic graphene crystallites in capacitive energy storage is exemplified by the high BET surface area-normalized capacitance (85.5 µF cm-2) of M-rGO. It greatly exceeds typical activated carbons, which are <10 µF cm-263,64, and notably surpasses the limits of EDL capacitance (5−25 µF cm-2)63 and some other relevant reports15,24. Made possible by the labile nature of the turbostratic curved graphene crystallites, ion insertion into the galleries imposes a highly-confined microenvironment on the host ions, strategically enabling partial charge transfer related to ion insertion/de-insertion. Hence, the large increase in capacitance can be explained by the merging of confinement effects with a partial Faradaic component to the energy storage mechanism, phenomena known to result in an anomalous increase in capacitance, discussed at length in refs. 21,52. Moreover, there is a distinct gap in the type of materials that can reap both of these benefits. To quantify the Faradic-like contribution, we employ Dunn’s method. It relies on the relationship i = k1ν + k2ν1/265 to distinguish the current contribution from CEDL (k1ν) and CPS (k2ν1/2). Figure 3I summarizes the respective contributions at scan rates 2 – 200 mV s−1. According to this method, Faradaic-like capacitance originating from the insertion of ions into size-matching graphene galleries is estimated to contribute ~32% of total capacitance at 2 mV s−1 and ~27% at 200 mV s−1, indicating the rapid and kinetically favorable ion insertion phenomena. However, it is important to acknowledge the nuance and continuum in the transition between EDL capacitance (CEDL) and Faradaic-like processes (CPS) under confinement effects52.

We attribute the excellent rate capability to the multi-scale nature of our material. Disordered graphene sheets act as ion reservoirs and transport highways, while the curved crystallite domains, discretely populated on the graphene sheets with sizes <100 nm according to the HR-TEM, offer high-capacitance sites. Curvature effects are known to play a significant role in accelerating ion transport kinetics. Density functional theory calculations have shown that curvature effects could easily shave off 0.1 eV66 from the diffusion activation energies, and our performance analysis of rate capability and power density in prototype devices provide inferential evidence to this role. As nanosizing shortens the ion diffusion length (λ) while curvature effects influence diffusion (D), the diffusion time (τ) can be significantly reduced according to τ = λ2/Di20. Further analysis in Fig. S15 (Supporting Information) reveals that for M-rGO devices, rate performance is primarily governed by the electrode’s electronic conductivity, with diffusion limitations playing a secondary role. However, at higher active material loadings, diffusion limitations become more pronounced (but still secondary) through the thick electrodes. From a practical standpoint, further improvements in rate capability and power density can be achieved with the addition of conductive agents to promote more effective electron percolation through the electrode. Ion diffusion limitation can be further mitigated by more precisely controlling crystallite size and the number of graphene layers or enhancing ion conduction through the intraparticle porosity, which becomes increasingly constrained in thicker electrodes. This can be feasibly achieved by engineering low-tortuosity electrode architectures such as in ref. 67 or decreasing particle size by employing precursors of smaller particle size.

Pouch-cell device performance

Long-term Galvanostatic Charge Discharge (GCD) cycling tests are conducted at a fast rate of 10 A g−1 where Ohmic drop considerations are non-trivial (Fig. 4A). The M-rGO device that was subject to e-IE attained a high volumetric capacitance of 169 F cm-3 (138 F g−1) and a capacitance retention of 91% over 50,000 cycles with TEABF4, with an average Coulombic efficiency (CE) of 99.7% (see Supplementary Note 3). The ex-situ XRD patterns of the cycled electrodes in Fig. S14 (Supporting Information) attest to the stability and structural integrity of the curved crystallites, confirming sustained ion insertion even after 50,000 cycles. Given the broad applicability of M-rGO to different electrolyte systems, we chose to demonstrate cycling performance with SBPBF4 electrolyte owing to its ability to operate at higher voltage windows68, demonstrating stability up to 3.4 V in our study. At this extended voltage window, this device delivered 175 F cm-3 (142 F g−1) with an average CE of 99.3% and a capacitance retention of 93% over 50,000 cycles. In contrast, without e-IE, the device delivered 48 F cm-3. Owing to the lower gravimetric performance (81 F g−1) and significant electrode swelling, D-rGO initially delivers 60 F cm-3, with poorer retention of 64% and an average CE of 98.1% over the same cycle number. As a control, we also tested YP-50F, which exhibited the lowest volumetric capacitance of 41 F cm-3, given its low electrode density (0.47 g cm-3), but an excellent retention of 94%. We note that all the volumetric capacitances reported in this work considers the maximum, equilibrium electrode dilation.

Fig. 4: Device-level electrochemical performance.
figure 4

A Long-term cycling at 10 A g−1 for symmetrical pouch cells with an areal loading of 1.9 mg cm-2, cycled at room temperature, over 50,000 cycles. The experiments are conducted at room temperature using three cells to confirm reproducibility. B Aggressive voltage float tests at 2.7 V of TEABF4 and SBPBF4 devices as further illustrates the longevity of the M-rGO devices over a 240 h testing period. The voltage float test is carried out once at room temperature. C Rate capability of cells with organic and ionic electrolyte at a practical active material loading of 6.1 mg cm-2. The experiments are conducted using three cells to confirm reproducibility and are carried out at room temperature.

Full size image

A complementary assessment for supercapacitor lifespan involves holding the cell at the nominal voltage and periodically measuring the cell’s state-of-health, given the accelerated degradation at higher voltages69 (Supplementary Note 4). As real-world supercapacitors are often necessarily held at a constant nominal voltage over long periods of time17, voltage float and GCD cycling tests are used cooperatively to assess device longevity and serve as a better reflection of end-use applications70. Results in Fig. 4B illustrate the excellent capacitance retention and low ESR rise over 240 h (10 days) of voltage float, held at 2.7 V for devices assembled with TEABF4 electrolyte and at 3.4 V for devices with the SBPBF4 electrolytes. With a capacitance retention >90% and an ESR increase of <12% for both devices, this result is comparable to commercial products71, further exemplifying the stability of M-rGO devices.

Translating high volumetric capacitance to device-level energy and power density requires the optimization of the volumetric fraction of active material in the device configuration. While our primary objective is to assess the material-level performance, it is equally important to demonstrate the industrial applicability of our pouch cell devices by fabricating electrodes with areal mass loadings comparable to commercial devices5. Increasing the thickness (and areal loading) can enhance energy and power density by increasing the volumetric fraction of active material in the device, but this must be delicately balanced to maintain rate performance, as thicker electrodes suffer from slower ion transport and lower capacitance. To investigate this trade-off, we tested the performance of our devices at areal loadings 1.9, 3.8, 6.1 and 7.6 mg cm-2 in Fig. S16 (Supporting Information). A loading of 6.1 mg cm-2 yields the maximum volumetric energy density for our system, as higher loadings display lower gravimetric capacitance and a greater resistance to calendering, delivering a lower volumetric capacitance. Hence, we assemble optimized devices at an areal loading of 6.1 mg cm-2, employing a thin 9 µm separator, 17 µm current collector and a coating thickness of 42.5 µm (averaged over 10 measurements), translating to a 66% volume fraction of active materials in the stack. To ensure fair benchmarking, consistent with literature, energy and power densities are reported based on the dried stack volume and weight and include the current collector, separator and active material film70.

Rate capability tests (Fig. 4C) validate that even at higher areal loadings, M-rGO is able to deliver 114 F g−1 and 120 F g−1 in TEABF4 and SBPBF4, respectively, at a high specific current of 100 A g−1. To maximize energy density, a majority of studies employ ionic liquids due to their extended voltage window (≥4 V) and higher attainable capacitances. For a direct and fair comparison with literature12,13,14,15,16, we conducted additional tests with pure EMIMBF4, which also underwent the e-IE process (see Fig. S17, Supporting Information), delivering 229 F g−1 (or 280 F cm-3) at 0.2 A g−1.

The Ragone plot of the optimized configuration in Fig. S18 (Supporting Information) highlights the volumetric energy density achievable in EMIMBF4, delivering 99.5 Wh L−1 with a power density of 17.7 kW L−1 (at 9.8 Wh L−1), firmly positioning these pouch cells among the highest reported in terms of volumetric performance12,13,14,15,16 in ionic liquids. Moreover, given the positive effect and possibility of increasing the operating temperature with ionic liquids, we have shown a modest increase in the capacitance when operating at 45 °C to 236 F g−1 (290 F cm-3), which translates to an energy density of 104.1 Wh L−1. To address the distinct need for power density in realistic supercapacitor devices, more readily achievable with organic electrolytes, we further illustrate the significance of M-rGO achieving 49.2 Wh L−1 and a power density of 69.2 kW L−1 (at 9.6 Wh L−1), which also rank among the highest in their class18,19. Supplementary Table S2 and Table S3 provide further details on the cell configuration, electrolyte, mass loadings and volume fraction of active material of the studies we used for comparison.

Multiscale graphene imparts cycling stability

To elucidate the mechanisms underlying the long-term stability of M-rGO, a comprehensive post-testing analysis was conducted (see Supplementary Note 5). In the absence of the e-IE protocol, the M-rGO electrodes displayed a thick, compact film enveloping the particles, observable in Fig. 5A, B. Similarly, the D-rGO electrodes, which also underwent e-IE, exhibited inhomogeneous film deposits on the electrode surface in Fig. 5D, E. In sharp contrast, M-rGO electrodes that underwent e-IE (Fig. 5G, H) displayed no significant or observable film-like deposits.

Fig. 5: The effect of ageing on the surface morphology of the electrodes.
figure 5

A, B SEM micrographs of M-rGO without e-IE and C) the separator surface; (D, E) SEM micrographs of D-rGO with e-IE and (F) the separator surface; (G, H) SEM micrographs of M-rGO with e-IE and (I) the separator surface.

Full size image

Dilatometry results indicate that the cells without e-IE failed to fully stabilize, with electrode height continuing to increase up to 19.7 ± 1.1% (Fig. S19, Supplementary Information). We infer that the continual degradation of electrolyte and deposition of thick film deposits is responsible. Separator surface analysis provides additional insight. Without e-IE, electrodes experienced continual film dissolution and precipitation during ageing, resulting in substantial deposits on the separator surface (Fig. 5C). Conversely, M-rGO and D-rGO subject to e-IE exhibited markedly reduced filming, with only sporadic thin deposits observed (Fig. 5F, I). These findings highlight the dynamic nature of these films and provides further evidence on the stabilizing effect of the second thermal treatment and the implementation of the e-IE protocol.

To evaluate the elemental composition of the degradation by-products and surface films, surface XPS elemental analysis was conducted on the electrodes before and after ageing. While initially showing elevated levels of fluorine, boron and nitrogen, the composition of M-rGO with e-IE stabilized after ageing, which is in sharp contrast to electrodes without e-IE, which exhibited more severe degradation. This is in good agreement with the SEM analysis, as the M-rGO electrodes with e-IE showed thinner SEI-like deposits. Deconvolution of the N1s peak reveals the predominantly polymeric nature of these films in electrodes without e-IE (Fig. S20, Supporting Information), likely as a result of electrolyte polymerization72. The appearance of a small RC loop in the Nyquist plot of the aged cell without e-IE (Fig. S21, Supporting Information) can be attributed to charge resistance arising from the formation of a passive layer73. Moreover, the ion transport-inhibiting effects of the film are captured by the Warburg coefficient, which was almost ~10 times greater for the cell without e-IE (0.654 Ω s-0.5) compared to the one with e-IE (0.068 Ω s-0.5). To further probe the impact of electrolyte decomposition on performance, cells were cycled at a specific current of 10 A g−1 with a severely restricted volume of electrolyte close to critical electrolyte-to-volume ratios, further discussed in Fig. S22 (Supporting Information). In this scenario, electrodes without e-IE experienced a rapid capacitance decay, most notably in the first 50 cycles, with a retention of only 78% over 3000 cycles, while those that were subject to e-IE showed a retention of 96% over the same cycle number. The more rapid decline in capacitance suggests that parasitic side-reactions are actively consuming ions, reducing their availability over successive cycles, an effect which is significantly more pronounced under restricted electrolyte conditions. This stark disparity in cycling performance under a restricted electrolyte volume supports our interpretation that continuous electrolyte consumption and consequently, film formation and build-up are the primary mechanism of degradation for M-rGO devices, and underscore the critical role of e-IE in stabilizing the electrode-electrolyte interphase for enhanced long-term performance.

It is clear that the presence of these non-ionically conductive and insulating interphase films is detrimental to EDL formation and consequently, the performance of supercapacitors. However, the SEI-like films observed on the M-rGO devices subjected to the e-IE protocol, analogous to those found in battery systems where SEI films are formed during the initial cycles through sacrificial electrolyte decomposition, serving to protect the electrode from further decomposition during prolonged operation74. The e-IE process appears to induce the formation of an initial but stable SEI-like layer which mitigates subsequent electrolyte decomposition. This stabilization effect enables excellent performance under harsh voltage float and GCD conditions and even under restricted electrolyte volumes.

In contrast, the protective effect of e-IE is less pronounced in D-rGO electrodes. The discrepancy is likely due to the higher surface area and pronounced height dilation and sheet exfoliation, which increase the electrode-electrolyte contact area, amplifying and exacerbating electrolyte degradation75. The superior stability of M-rGO can be attributed to its reduced dimensional scale from the high fraction of turbostratic graphene interlayers, incorporated in larger micron-scale M-rGO particles.

Discussion

Multiscaling active materials in energy storage applications is an effective way to reap the benefits of each scale. In this work, we demonstrate that a two-step thermal treatment populates an otherwise disordered graphene network with curved and tangled graphene crystallites. In so doing, the micron-sized particles are comprised of macro-meso-scale channels for rapid ion transport through the disordered structure, while the highly confined curved graphene crystallites possess superior energy storage capability. A simple and rapid operando electrochemical interlayer expansion (e-IE) ensures that a maximum number of capacitive sites within the structure are active in energy storage. The low resistance and rapid ion transport enable us to showcase among the highest reported volumetric energy densities for an all-carbon EDLC, delivering up to 99.5 Wh L−1 in ionic liquids and 49.2 Wh L−1 in organic electrolytes. Long-term stability is noted even under aggressive testing conditions. This is revealed to be a result of the combined effects of controlled interphase deposition during the e-IE process and the reduced dimensionality of multiscale graphene to minimize the electrode-electrolyte contact area.

Methods

Thermal treatments

A commercially-available graphite oxide (Sixth Element Inc.) paste was dried at 70 °C for 16 h and then ground into a fine powder using a blade-style grinder with a stainless steel chopping blade (Breville Coffee and Spice Grinder BCG200BSS). To remove any large aggregates/ particulates, the powder was passed through a sieve with mesh size of 200 μm. To minimize physisorption of water, the powder is kept at 80 °C for 2 h before the thermal treatment. A tube furnace (Across International) was pre-heated to 700 °C in an air atmosphere. Small amounts of powder (~20–30 mg) are introduced into the unheated part of the tube in the loading end, and a suction on the product end of the furnace pulls the GtO powder through the heating element, causing a flash thermal shock to remove the oxygen functional groups and induce exfoliation. The suction is controlled to give the material an estimated residence time of ~2 s in the heating element. The exfoliation is audible by a loud popping sound.

In the second thermal step, the tube furnace is fitted with a custom airlock chamber with gloves and a steel rod to bring samples in and out of the heating element. The airlock is fed with a continuous flow of N2 at a rate of 3.6 NI min−1, and fitted with steel wool at the end. About 2.5 g of D-rGO is placed in a large, long nickel crucible (dried at 100 °C for 1 h prior to the experiment), and held in the airlock chamber under N2 flow for 30 min. Then, it is loaded into the heating element and held at a pre-determined period of time for 2, 4, 6, 12 and 30 min, before removing from the heated area and quenched back to room temperature in the airlock chamber for 10 min. This is depicted in Fig. S1, Supporting Information. The powder is gently roll milled in a jar roll mill for 20 min with zirconia balls at a ball to powder ratio of 20 and a rotation speed of 500 rpm (MRC Laboratory Instruments) to aid with processability into inks and electrode coatings. Unless otherwise stated, material-level analysis is carried out on non-roll-milled samples.

Fabrication and testing of pouch cells

The powders are processed into aqueous inks with deionized water, composed of 95 wt% active material and 5 wt% CMC binder (Sigma Aldrich), while the YP-50F (Kuraray Inc) inks were composed of 90 wt% active material, 5 wt% acetylene black (Thermo Fisher Scientific) and 5 wt% CMC (Sigma Aldrich). The inks are stirred in a vacuum mixer (MSK-SFM−16, MTI Corporation, USA) at 600 rpm for 90 min at half vacuum setting, at room temperature and tape cast on a single side of electrochemical-grade aluminium (current collector thickness is 17 µm) with a doctor blade at different gaps to obtain different areal loadings and vacuum dried at 80 °C overnight. They were then cut into 3 × 5 cm electrodes and calendered under maximum compression (at minimum gap setting of ~0 mm) at room temperature and a speed of 0.5 cm s−1 (MSK-HRP-02, MTI Corporation, USA). The electrodes are passed through the calendering machine twice. Aluminium tabs were welded onto the electrodes and assembled into single layer pouch cell devices with a Celgard 2400 separator (4 × 6 cm piece at a thickness of 25 µm) for all material-level studies. For optimization of stack-level performance, ultra-thin polypropylene separator was utilized (Acem Energy, PE single-layer wet-process separator at a thickness of 9 µm). The stacks were dried at 120 °C in a vacuum oven for ~120 h and were immediately transferred to the glovebox (MBraun, Ar atmosphere) with oxygen and moisture content of <0.1 ppm. The pouches were injected with a total of 280 µL 1.2 M TEABF4 in acetonitrile (Watson International Limited, <10 ppm H2O), gradually, at increasing vacuum before final vacuum sealing at -95 kPa. The higher loading electrodes (6.1 mg cm-2) are filled with 320 µL 1.2 M TEABF4 in acetonitrile (Watson International Limited, <10 ppm H2O), 1.2 M SBPBF4 (Watson International Limited <10 ppm H2O) and neat EMIMBF4 electrolyte (Sigma Aldrich, electrochemical grade). These electrochemical-grade electrolytes are used without further purification. Other tested salts include TBABF4 (electrochemical analysis grade, >99% Sigma Aldrich) TEMABF4 (AK Scientific, Inc.) and THABF4 (Sigma Aldrich, >97%) in acetonitrile (Sigma Aldrich, 99.8%, anhydrous). The salts are dried overnight at 40 °C and the solvent is used without further purification. The pouches are rested for 1 h at 40 °C (in an environmental chamber with convection) and then at room temperature (~25 °C) overnight (~16 h) before testing to ensure full wetting of the electrodes. Neat ionic liquid electrolyte cells are rested for 6 h at 40 °C (in an environmental chamber with convection) and then at room temperature (~25 °C) for >2 days before testing to ensure full wetting of the electrodes. All electrochemical testing is carried out in pouch cell format. Galvanostatic charge/ discharge, CV and EIS were performed on EC-Lab (Biologic, France), while long-term galvanostatic charge/ discharge cycling tests were performed on CT-4008 (Neware, China). For e-IE experiments, the potential cutoff is 3.8 V for organic electrolytes and 4.5 V for ionic electrolytes. All other electrochemical tests are carried out at a potential cutoff of 2.7 V for TEABF4, 3.4 V for SBPBF4 and 4.0 V for neat EMIMBF4. EIS (potentiostatic mode) is measured over frequencies 0.01 Hz to 1 MHz under sinusoidal signal, recording 6 points per decade of frequency at 10 mV amplitude at a quasi-stationary potential. All electrochemical tests are conducted using three cells to confirm reproducibility at room temperature unless otherwise stated. A higher temperature ionic electrolyte pouch cell is tested at 45 °C (in an environmental chamber with convection).

Characterization

XRD measurements were conducted in D8 Advance (Bruker, Germany) with CuKα = 1.54184 Å. Powder samples are placed in a low signal silicon wafer holder while electrodes are secured flush with the silicon wafer holders. Ex-situ analysis of the cycled electrodes was carried out by disassembling the pouch cells at different voltages in an Ar-filled glovebox, and washed three times with acetonitrile. It is dried and transferred to a sample holder for XRD analysis, with brief exposure to the atmosphere (<120 min). The chemical states were investigated by XPS, performed on a Thermo Scientific Nexsa Surface Analysis System, employing monochromatic Al Kα X-rays (1486.6 eV) at 72 W (6 mA and 12 kV, 400 × 250 µm2 spot). Ex-situ analysis of the cycled electrodes was carried out by disassembling the pouch cells at the nominal voltage (2.7 V) in an Ar-filled glovebox, and washed three times with acetonitrile. Samples are dried and transferred to a sample holder (and transfer shuttle) under vacuum for XPS analysis so as to avoid exposure to the atmosphere. Data processing was carried out using Avantage software and the energy calibration was referenced to the main line of C 1 s at 284.8 eV. A Renishaw Confocal micro-Raman Spectrometer fitted with a thermoelectrically cooled CCD camera in the 100–3500 cm1 wavenumber range was used to record the Raman spectra using argon gas laser to produce an excitation beam at 514 nm wavelength working at 10 % power. The SEM images were obtained with Varios (ThermoFisher Scientific). Separators were coated with iridium using a Cressington 208HRD sputter coat, with a thickness of 2 nm. The graphene powders and electrodes were not coated. Secondary electron images were collected at an acceleration voltage of 5 kV and a working distance of 4 mm. Ex-situ analysis of the cycled electrodes was carried out by disassembling the pouch cells at the nominal voltage (2.7 V) in an Ar-filled glovebox, and washed three times with acetonitrile. They were dried and transferred to a sample holder for SEM analysis, with brief exposure to the atmosphere (<15 min) when loading into the SEM. The samples were dispersed in ethanol and tip sonicated in preparation for transmission electron microscopy (TEM), and deposited on carbon grids. Images were collected on a FEI Technai G2 T20 TWIN TEM at 200 kV. N2 adsorption-desorption experiments were performed on a BET NOVA Touch instrument using nitrogen gas at 77 K. The specific surface area (SSA) was obtained using the Brunauer–Emmett–Teller (BET) multi-point SSA. The operando electrode dilatometry experiments were carried out by measuring the change in pouch device height using a digital micrometer (Mitutoyo) at different voltage ranges or cycle numbers. The error bar represents the standard deviation of the average measured height dilation over 10 measurements at random spots on the pouch. To evaluate the bulk conductivity, 25 mg of powdered samples were individually loaded into the 1.0 cm internal diameter acrylic cylinder flanged between two copper plungers. The setup includes a manual press for adjusting the powder height in the cylinder, which is measured using a digital Vernier calliper at each compression step, along with a Keithley four-point probe with a 100 mA source current to measure the resistance.

Calculations

Capacitance

The following formula was used obtain the gravimetric capacitance of a single electrode (C) from its GCD curve:

$$C\,=\frac{2I\varDelta t}{m\varDelta V}$$
(1)

Where I is the constant discharge current, ∆t is the discharge time, m is the mass loading of the electrode and V is the voltage window. We note that the capacitance is evaluated on an electrode-level. The capacitance was also evaluated from CV curves using the following equation:

$$C\,=\frac{1}{2({V}_{t}-{V}_{0})\nu }{\int }_{{V}_{0}}^{{V}_{1}}\left|{I}_{m}(V)\right|{dV}$$
(2)

Where Im is the current density (A/g) and V0 and V1 are the lower and upper potential limits of the voltage window. The surface-area normalized capacitance CA (µF cm-2) was calculated based on the BET surface area:

$${{{{\rm{C}}}}}_{A}=\frac{{{{\rm{C}}}}}{{{{{\rm{A}}}}}_{{BET}}}$$
(3)

Volumetric capacitance (Cvol) is calculated according to the formula:

$${C}_{{vol}}=C\times \rho$$
(4)

Where ρ is the bulk density of the electrode active materials.

The gravimetric energy density (Eg) in Wh/kg and volumetric energy density (Evol) in Wh/L of two electrodes is given by:

$${E}_{g}=\frac{1}{3.6}\cdot \frac{1}{8}\,C\varDelta {V}^{2}$$
(5)
$${E}_{{vol}}=\frac{1}{3.6}\cdot \frac{1}{8}{C}_{{vol}}\varDelta {V}^{2}$$
(6)

The gravimetric power density (Pg) and volumetric power density (Pvol) of electrode films can be obtained from:

$${P}_{g}=\frac{{E}_{g}}{\Delta t}$$
(7)
$${P}_{{vol}}=\frac{{E}_{{vol}}}{\Delta t}$$
(8)

Where ∆t is the discharge time. The gravimetric energy density and volumetric energy density of the entire device stack are calculated by formulas:

$${E}_{{wt}-{stack}}={E}_{{wt}}\times {f}_{{wt}}$$
(9)
$${E}_{{vol}-{stack}}={E}_{{vol}}\times {f}_{{vol}}$$
(10)

Where fwt and fvol are the mass and volume fraction of the electrodes in the entire device stack. The stack of an entire device includes active materials, electrode films, current collectors and separators.

Dunn’s method24 allows to differentiate CEDL and the diffusion-controlled processes CPS. At a given fixed potential, the current density (i) from the CVs can be expressed the combination of two terms:

$$i={k}_{1}v+{k}_{2}{v}^{0.5}$$
(11)

Where \({{{{\rm{k}}}}}_{1}v\) accounts for the current density contributed from the EDL capacitive effects while the second term \({{{{\rm{k}}}}}_{2}{v}^{0.5}\) is associated with the pseudocapacitive reactions. Dividing by \({v}^{0.5}\) on both sides of the equation yields:

$$i{v}^{-0.5}={k}_{1}{v}^{0.5}+{k}_{2}$$
(12)

Therefore, reading i from the CVs at a series of scan rates and then plotting \(i{v}^{-0.5}\) vs \({v}^{0.5}\), a linear fitting line with a slope of k1 and a y-intercept of k2 can be obtained.

The bulk electrical conductivity (σ) is calculated using the following equation:

$$\rho=R\frac{A}{h},\sigma=\frac{h}{{RA}}$$
(13)

Where, R = ohmic resistance (Ω), ρ = resistivity (Ω m), h = height of sample in the acrylic cylinder (m), A = piston ground area (m2), σ = conductivity (S m−1).