Probing stress and magnetism at high pressures with two-dimensional quantum sensors

Abstract

Pressure serves as a fundamental tuning parameter capable of drastically modifying all properties of matter. The advent of diamond anvil cells (DACs) has enabled a compact and tabletop platform for generating extreme pressure conditions in laboratory settings. However, the limited spatial dimensions and ultrahigh pressures within these environments present significant challenges for conventional spectroscopy techniques. In this work, we integrate optical spin defects within a thin layer of two-dimensional (2D) materials directly into the high-pressure chamber, enabling an in situ quantum sensing platform for mapping local stress and magnetic environments up to 3.5 GPa. Compared to nitrogen-vacancy (NV) centers embedded in diamond anvils, our 2D sensors exhibit around three times stronger response to local stress and provide nanoscale proximity to the target sample in heterogeneous devices. We showcase the versatility of our approach by imaging both stress gradients within the high-pressure chamber and a pressure-driven magnetic phase transition in a room-temperature self-intercalated van der Waals ferromagnet, Cr_1+δTe₂. Our work demonstrates an integrated quantum sensing device for high-pressure experiments, offering potential applications in probing pressure-induced phenomena such as superconductivity, magnetism, and mechanical deformation.

Introduction

A key requirement for developing modern integrated quantum-sensing devices is the seamless incorporation of sensors into existing toolsets. In high-pressure science, the recently introduced nitrogen-vacancy (NV) centers in diamond anvil cells (DAC) serve as a compelling demonstration, enabling in situ characterization of stress and magnetism under extreme pressures for various applications in materials science and geology^{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}. However, limitations remain across different implementations: NV layers implanted beneath the culet of the diamond anvil are located outside the sample chamber, restricting proximity to the target. In contrast, nanodiamonds placed inside the chamber offer closer access to the sample. Yet, in this geometry, the random positions and crystalline orientations of individual nanodiamond particles hinder their suitability for widefield imaging.

To address these challenges, we propose the negatively charged boron-vacancy (${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$) centers in layered hexagonal boron nitride (hBN) as an alternative high-pressure sensing platform inside DACs. ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ Centers together with a few other recently discovered spin defects in van der Waals materials present a brand-new angle to construct quantum sensing devices^{17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38}. In principle, the atomic-thin structure of the host materials can enable the 2D sensors to be placed sub-nanometers away from the target samples, facilitating the imaging of interfacial phenomena with unprecedented sensitivity and resolution. Moreover, 2D sensors can be easily integrated with other 2D devices through three-dimensional heterogeneous integration, allowing the large-scale manufacture of next-generation microelectronics.

In this work, we present three main results. First, by transferring a thin (~ 100 nm) film of hBN containing ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ centers directly onto the culet of the diamond anvil (Fig. 1), we systematically characterize the electronic spin properties of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ with pressure up to 3.5 GPa. The pressure-induced spin energy shift of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ is measured to be (2π) × (43 ± 7) MHz/GPa, in good agreement with first-principles calculation³⁹, yet significantly different from a previous experiment where weights are placed directly onto the hBN⁴⁰. Notably, the pressure response of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ is around three times larger than that of NV centers in diamond, highlighting its potential as an in situ pressure and stress sensor. Second, we use ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ sensors to directly map out the stress distribution and gradient inside the high-pressure chamber. Using sodium chloride (NaCl) as the pressure-transmitting medium, we find that the stress environment becomes less uniform at around 2 GPa, consistent with previous studies^41,42,43. Finally, we demonstrate the magnetic field imaging capability of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ in a heterogeneous device by investigating the pressure-tuned magnetism in a room-temperature self-intercalated van der Waals ferromagnet, Cr_1+δTe₂. A transition from ferromagnetic to non-magnetic behavior occurs around 0.5 GPa, which can be explained by a decrease in the exchange interaction.

Fig. 1: Experimental platform for high-pressure quantum sensing using ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ defects in hBN.

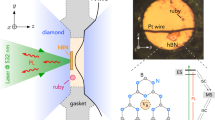
a Top: Schematic of the hBN layer with ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ defects used for stress and magnetism sensing. Bottom: Energy-level diagram of the ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ spin triplet ground state, showing Zeeman splitting induced by a magnetic field and energy shifts caused by in-plane stress components. The dual sensing capabilities enable simultaneous characterization of stress and magnetic fields. b Cr;'oss-sectional schematic of the DAC, illustrating the positioning of the hBN flake containing ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ defects on the culet, the platinum wire for microwave delivery, and the ruby microsphere for pressure calibration. The inset (top left) provides an expanded view of the DAC configuration and sample chamber alignment.

Results

Experimental platform

We choose to work with isotopically purified h¹⁰B¹⁵N to minimize the nuclear spin noise and achieve the optimal ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ spin properties^44,45,46,47. An ensemble of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ is created via a neutron irradiation process (see “Methods”). A ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ center harbors an electronic spin triplet ground state $| {m}_{s}=0,\,\pm 1\left.\right\rangle$, which can be optically initialized and read out at room temperature. In the absence of any external perturbations, the $| {m}_{s}=\pm 1\left.\right\rangle$ states are degenerate and separated from $| {m}_{s}=0\left.\right\rangle$ by a zero-field splitting (ZFS), D_gs = (2π) × 3.48 GHz (Fig. 1a). An applied external magnetic field lifts the degeneracy between $| {m}_{s}=\pm 1\left.\right\rangle$ through Zeeman splitting, while hydrostatic pressure induces a global energy shift of the ZFS, allowing ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ to simultaneously probe the local magnetic and pressure environment.

In our experiment, we use a miniature Pasternak DAC⁴⁸ with two opposing anvils (400μm culet diameter) compressing a stainless steel gasket (Fig. 1b). To integrate ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ sensors into the DAC, we directly transfer a thin h¹⁰B¹⁵N flake with thickness  ~ 100 nm onto the culet of a anvil (Fig. 1b). A coherent microwave field is delivered using a 50 μm width platinum foil across the culet to control the ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ spin states. The sample chamber is packed with NaCl pressure-transmitting medium to provide a hydrostatic environment. A ruby microsphere is loaded on the opposite side of the foil as a standard pressure calibrant.

${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ under pressure

We begin by probing the ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ spin states under pressure via optically detected magnetic resonance (ODMR) spectroscopy: by sweeping the frequency of the applied microwave field while detecting the fluorescence signal ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$, we observe a fluorescence drop when the microwave is in resonance with one of the ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ spin transitions. We apply a small external magnetic field B_ext = 84 G along the loading axis of the DAC (i.e., the out-of-plane direction of hBN) to lift the degeneracy between $| {m}_{s}=\pm 1\left.\right\rangle$ sublevels. The results are shown in Fig. 2a. At 0 GPa, two groups of electronic spin transitions are observed symmetrically around D_gs = (2π) × 3.48 GHz, corresponding to $| {m}_{s}=0\left.\right\rangle \leftrightarrow | {m}_{s}=\pm 1\left.\right\rangle$. Each electronic spin transition further exhibits four hyperfine resonances with a coupling strength of A_zz = (2π) × 65.5 MHz, attributed to the hyperfine interaction between the ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ spin and three nearby ¹⁵N nuclei^26,44,49.

Fig. 2: ODMR spectra of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ defects under varying pressures.

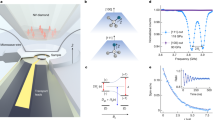
a Top: A representative ODMR spectrum at 0 GPa, with the shaded area indicating a fit to the spectrum using a sum of 8 Lorentzian functions. Error bars represent 1 s.d. accounting statistical uncertainties. Bottom: A waterfall plot demonstrating a global shift in resonance frequencies with increasing (blue) and decreasing (red) pressure, reflecting the ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ sensitivity to lattice strain. b Extracted center frequencies of the ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ spin transitions as a function of pressure, independently calibrated using ruby R2 fluorescence shifts. Data points for two iterations are shown: pressurization for Sample 1 (blue circles) and Sample 2 (yellow circles), and depressurization for Sample 1 (red circles). A linear fit (blue dashed line) of the two rounds of measurements yields a pressure susceptibility of (2π) × (43 ± 7) MHz/GPa. This susceptibility is consistent with a theoretical prediction (green) but significantly deviates from a previous experiments (purple). Shaded regions denote one standard deviation of fits. Inset: Hyperfine splitting increases with pressure, yielding a susceptibility of (2π) × (0.5 ± 0.2) MHz/GPa. Error bars represent 1 s.d. accounting fitting error.

As pressure increases (Fig. 2a), the ODMR resonances exhibit a systematic shift to higher frequencies. This upward shift can be intuitively understood as a consequence of pressure-induced compression of the ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ electronic spin wavefunction, leading to enhanced spin-spin interactions. However, the ODMR contrast decreases with increasing pressure, eventually vanishing at approximately 3.5 GPa. Upon depressurization, the resonant peaks return to their original positions, and the contrast is fully restored to its initial levels. The reduced contrast may be due to the quasi-hydrostatic nature of the NaCl pressure medium at higher pressures, which could lead to symmetry-breaking stress that alters the inter-system crossing rates of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$. Employing a more hydrostatic pressure medium, such as Argon or Neon gas, may help to extend the pressure limit of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ sensors^50,51,52. Similar behavior has been observed for NV centers in a single-crystal diamond chip, where the ODMR contrast vanishes at around 15 GPa with NaCl pressure medium, while the contrast persists up to 60 GPa when switching to Ne gas medium¹.

We fit the measured ODMR curves to a sum of eight Lorentzian functions to extract the ZFS at different pressures calibrated by ruby fluorescence (Fig. 2b). The results includes two samples and three experimental iterations: pressurization for sample S1 (blue) and S2 (yellow), and depressurization for S1 (red). A linear fit across all datasets yields a pressure susceptibility of h = (2π) × (43 ± 7) MHz/GPa, around three times larger than that of NV centers in diamond^1,7,53. For hyperfine coupling strength A_zz, we also observe a pressure dependence of (2π) × (0.5 ± 0.2) MHz/GPa (Fig. 2b Inset).

In situ mapping of stress distribution

To quantitatively interpret the large pressure dependence of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ ZFS, let us first analyze the stress field interaction in ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$. Since each individual ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ resides within a single layer of the hBN crystal, out-of-plane ($\hat{z}$) distortions are expected to have only a minimal effect on the in-plane lattice structure that hosts the defect’s spin density³⁹. As a result, the spin state of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ couples strongly to in-plane stress components σ_xx and σ_yy, while remaining insensitive to out-of-plane stress σ_zz (Fig.  3a). The ground state Hamiltonian of the ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ electronic degree of freedom can be then expressed as:

$${{{{\mathcal{H}}}}}_{{{{\rm{gs}}}}}={D}_{{{{\rm{gs}}}}}{S}_{z}^{2}+\gamma {B}_{{{{\rm{ext}}}}}{S}_{z}+h\frac{{\sigma }_{xx}+{\sigma }_{yy}}{2}{S}_{z}^{2}+{h}^{{\prime} }\frac{{\sigma }_{xx}-{\sigma }_{yy}}{2}\left({S}_{x}^{2}-{S}_{y}^{2}\right),$$

(1)

where D_gs = (2π) × 3.48 GHz is the ZFS, γ = (2π) × 2.8 MHz/G is the spin gyromagnetic ratio, B_ext is the external magnetic field, and S is the electronic spin-1 operator. h, ${h}^{{\prime} }$, σ_xx and σ_yy describe the stress coupling coefficients and the lateral stress components along $\hat{x}$ and $\hat{y}$, respectively.

Fig. 3: Spatial profiles of stress gradients within the high-pressure chamber.

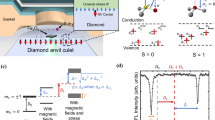
a A schematic illustrating the layered atomic structure of hBN. This structure enables ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ to function as an in-plane hydrostatic pressure sensor by coupling strongly to lateral stress components while remaining insensitive to out-of-plane stress. b A fluorescence scanning image of the hBN flake in the DAC under pressure, with a linecut direction marked by the blue arrow for stress profiling. c Measured lateral stress profile along the linecut shown in (b) for varying pressures, including pressurization (blue) and depressurization (red). At low pressure, the stress distribution is uniform, but as pressure increases beyond 1 GPa, significant stress gradients develop due to the non-hydrostaticity of the solid NaCl pressure medium and slight misalignments of the diamond anvils. Error bars represent 1 s.d. accounting fitting error.

Due to the presence of a pressure-transmitting medium and the fact that diamond surfaces exhibit poor adhesion to layered materials, the stress environment within the sample chamber approximates the hydrostatic condition, i.e. σ_xx ≈ σ_yy ≈ σ_zz. Indeed, previous studies on 2D materials such as WS₂ and graphene in diamond anvil cells have shown that when placed directly on diamond surfaces, these materials experience minimal strain-induced Raman splitting, indicating a predominantly hydrostatic environment^54,55,56. In this case, the last term in Eqn. (1) vanishes, and one only needs to consider the term, $h\frac{{\sigma }_{xx}+{\sigma }_{yy}}{2}{S}_{z}^{2}$, which leads to an overall energy shift of the ZFS. From the measured pressure susceptibility, we obtain h = (2π) × (43 ± 7) MHz/GPa, in good agreement with the previous ab initio calculation of h_th = (2π) × 39.2 MHz/GPa³⁹. Notably, this value is around 25 times smaller than the result obtained from an earlier experiment, which attributed the large temperature-dependent ZFS shift to effective stress from thermal distortion of the hBN lattice⁴⁰. However, our recent work demonstrates that the temperature-dependent ZFS change of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ arises from local spin-phonon interactions, rather than lattice distortion⁵⁷. Consequently, the results here represent the first direct measurement of the stress response of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ centers.

Having characterized the stress susceptibility of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ centers, we now harness ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ sensors to perform in situ imaging of the stress distribution within the high-pressure chamber (Fig. 3b). Figure 3c shows the measured lateral stress profile across  ~15 μm region at various pressures. At 0 GPa, the stress is uniform, reflecting the minimal applied pressure after sealing the sample chamber. As the pressure increases, a spatial gradient emerges in the stress profile and becomes markedly pronounced above 1 GPa. This spatial stress gradient may result from a slight misalignment of the opposing diamond anvils or a decrease in the hydrostaticity of the NaCl medium at higher pressures⁴².

A few remarks are in order. First, the stress sensitivity of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ sensors is estimated to be ${\eta }_{{{{\rm{p}}}}}\approx 0.2\,{{{\rm{GPa}}}}\,{{{{\rm{Hz}}}}}^{-\frac{1}{2}}$ (see Supplementary Materials). While the present ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ sensitivity is still a few times lower than that of state-of-the-art NV centers, ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ centers offer a distinct advantage: they are directly integrated into the sample chamber. In contrast, NV centers are embedded within the diamond anvil, so one must rely on the assumption of stress continuity to infer the stress environment inside the sample chamber². Although NV centers in nanodiamonds or microdiamonds can also be introduced directly into the sample chamber and brought into close contact with the target material, their spatial distribution and orientation are often difficult to control with precision. Second, the observed lateral stress gradient is larger than the previous measurement using NV centers across similar lateral distance², presumably due to the fact that previous work uses a more hydrostatic pressure medium, 16:3:1 methanol/ethanol/water solution, than NaCl. However, since the NV centers are embedded beneath the diamond surface, the solid-liquid interface could potentially redistribute the stress before they reached the sensor plane. One can imagine future work to integrate both ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ and NV centers together to co-image and benchmark the stress environment across the chamber-diamond interface. Indeed, several recent work demonstrate the use of hybrid NV-${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ system for sensing applications^58,59. Lastly, the primary factor limiting the sensitivity of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ sensors is their relatively weak fluorescence intensity. Efforts to enhance the fluorescence yield, such as by applying symmetry-breaking strain^60,61,62,63 or coupling ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ centers to nanocavities^64,65,66, could substantially improve their sensitivity. While integrating such approaches into high-pressure environments remains a longer-term goal, their development suggests potential future pathways for improving ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ sensor performance.

Imaging pressure-driven magnetism in a heterogeneous device

To showcase the versatility of our 2D quantum sensors, we next investigate the pressure-driven magnetic phase transition in a heterogeneous device consisting of a hBN sensing layer and a thin flake of self-intercalated van der Waals magnet, Cr_1+δTe₂. Similar to the stress case, we estimate a magnetic sensitivity of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ to be around ${\eta }_{{{{\rm{B}}}}}\approx 3.1\,{{{\rm{G}}}}\,{{{{\rm{Hz}}}}}^{-\frac{1}{2}}$ at pressure around 0.6 GPa (see Supplementary Materials).

The recent development of van der Waals magnets has opened new avenues for advanced spintronics and quantum technologies^{67,68,69,70,71}. Among a wide range of 2D magnets, transition metal telluride compounds exhibit robust ferromagnetism in ambient conditions, providing a reliable platform for practical device integration^37,72,73,74. Here we synthesize Cr_1+δTe₂ nanoflakes via a chemical vapor deposition process, where the Cr atoms are self-intercalated into the van der Waals gap between 1T-CrTe₂ layers^75,76. Transmission electron microscopy (TEM) studies indicate that the primary phase corresponds to δ ≈ 0.5 (see “Methods”). The thickness of the nanoflakes ranges from 50 − 100 nm, with Curie temperature T_c > 330K. The heterostructure assembly begins with transferring a Cr_1+δTe₂ nanoflake (lateral dimension  ~ 5 μm) on top of the hBN sensing layer, followed by placing the device onto the culet of a diamond anvil (Fig. 4a). To minimize the oxidation of Cr_1+δTe₂, all assembly steps of the DAC are carried out in a nitrogen-filled glove box.

Fig. 4: Investigation of pressure-induced magnetic transitions in self-intercalated Cr_1+δTe₂ using ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ defects.

a A schematic of the DAC assembly, illustrating the heterostructure including Cr_1+δTe₂ sample on top of a hBN flake, and a cross-sectional view of the crystal structure. b Spatial profile of stray magnetic fields across Cr_1+δTe₂ at 0 GPa, 0.62 GPa, and 0.13 GPa. Insets show theoretical expectations of the stray field detected by a ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ located adjacent to a magnetic sample. Error bars represent 1 s.d. accounting fitting error. c Evolution of the maximum stray magnetic field difference as a function of pressure, with data showing pressurization (blue) and depressurization (red) cycles. The maximum field is determined by calculating the stray field difference between the two edges of the sample during the pressurization process. For depressurization, it is calculated based on the difference between the stray field at the center of the sample and that at a distant point. Inset: A two-dimensional scan of the stray field around Cr_1+δTe₂ sample at 0.13 GPa. Error bars represent 1 s.d. accounting fitting error.

We directly characterize the spatial dependence of the stray magnetic fields across the Cr_1+δTe₂ nanoflake at various pressures. All the magnetism measurement are carried out at room temperature, with an external magnetic field B_ext ≈ 84 G aligned along the out-of-plane ($\hat{z}$) axis of hBN. This field suppresses the spin mixing between $| {m}_{s}=\pm 1\left.\right\rangle$ sublevels induced by local electric fields or stress anisotropy, ensuring that the measured ODMR splitting faithfully reflects the local magnetic field signals. Before pressurization (P ~ 0 GPa), the stray field exhibits a characteristic spatial dependence as the measurement location scans across the sample (Fig. 4b). The field initially increases, peaking at one edge, and then reverses polarity upon crossing the sample, eventually reaching a pronounced negative value at the opposite edge. This phenomena is consistent with the expectation that the initial magnetization is oriented in-plane. As the pressure increases above 0.5 GPa, the stray field vanishes, indicating a transition to a non-magnetic state.

Notably, during the depressurization process, a significant stray magnetic field re-emerges when the pressure drops below 0.5 GPa. However, the spatial distribution of this restored stray field differs markedly from the initial configuration. In particular, the measured magnetic field exhibits a pronounced reduction across the sample, suggesting that the recovered magnetization is largely aligned out-of-plane and oriented opposite to the external field. We also perform a two-dimensional confocal scan of the stray field near the sample (Fig. 4c), where a large portion of the sample area exhibits a negative field. Figure 4c illustrates the evolution of the maximum stray magnetic field as a function of pressure during both pressurization and depressurization, where a pressure-driven magnetic transition at around 0.5 GPa is apparent. This transition in Cr_1+δTe₂ can be explained by pressure-induced reduction in atomic spacing that alters the overlap of orbitals and weakens the ferromagnetic exchange interaction strength, agreeing with density functional theory predictions (see Methods)^77,78.

Outlook

Looking forward, our work opens the door to a few intriguing directions. On the application front, the close proximity of our 2D sensors and their demonstrated ability to simultaneously image stress and magnetism under high-pressure conditions enable the exploration of a wide range of pressure-induced phenomena. These include superconductivity and magnetism in materials science, as well as mechanical deformation and paleomagnetism in geology. For instance, one can integrate ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ sensors with the recently discovered thin-film nickelate superconductors to spatially correlate filamentary superconductivity (probed through Meissner repulsion) and local stress environment with sub-micrometer resolution^79,80. On the scientific front, an open question remains as to how the pressure limit of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ sensors can be further extended. Insights from NV centers suggest that replacing NaCl with a more hydrostatic pressure-transmitting medium, such as Daphne oil or noble gases, could substantially enhance the pressure operation limit^1,42. Additionally, from a theoretical perspective, modeling the inter-system crossing and spin properties of ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ centers under various stress configurations promises to yield valuable insights.

During the completion of this work, we became aware of a complementary work exploring ${{{{\rm{V}}}}}_{{{{\rm{B}}}}}^{-}$ in DAC to image pressure-induced magnetism of CrTe₂ in a heterogeneous device⁸¹.

Methods

DAC sample preparation

In our experiment, we use a miniature Pasternak DAC⁴⁸ to apply pressure. The cell body and backing plates are made of beryllium copper (BeCu). Between the two backing plates are two type IIa diamond anvils with a 400 μm culet diameter, compressing a stainless steel gasket. The gasket is preindented to 18 GPa and laser drilled a hole with a diameter of 133 μm. The sample chamber is insulated with a mixture of boron nitride (BN) powder and epoxy. Sodium chloride (NaCl) pressure medium is loaded to provide a quasi-hydrostatic environment. The hBN flake and Cr_1+δTe₂ magnet is picked up using polydimethylsiloxane (PDMS), and transferred then stacked onto a diamond anvil. A platinum wire of 50 μm in width is placed across the heterostrucure are to deliver microwave drive for ODMR measurements.

hBN sample preparation

To grow the h¹⁰B¹⁵N crystals, a mixture of 48.1 wt% chromium (99.99%), 48.1 wt% nickel (99.9%), and 3.8 wt% boron-10 enriched (98% B-10, 99.99%) pieces were loaded into an alumina crucible (98%) and covered before being loaded into a horizontal alumina (98%) furnace. The tube was vacuumed to  <80 microtorr using a rotary vein pump. Then the tube was purged twice with N₂ and argon (99.9999%) to 500 torr, then evcuated back to  <80 microtorr. Finally, the tube was filled to 90% (approximately 780 torr) ¹⁵N₂ (98% enriched, 99.9999%) and complimented to 850 torr with H₂ (99.9999%) before being closed up- and downstream of the tube. The furnace was brought to 1550 C at 200 C/h then left to dwell for 24 h at that temperature. This step was followed with a slow cool at 1 C/h to 1500 C. The furnace was then cooled at 50 C/h to 1350 C followed by 100 C/h to room temperature.

The sample boule was unloaded and removed from the alumina crucible. Heat-release tape was used to exfoliate the crystals from the surface of the boule. After heating the tape to 135 C, acetone (99%) was used to remove the free-standing crystals. The resulting free-standing crystals were mounted between 2 1-inch square quartz plates and pressed under aluminum foil. These samples were irradiated at Ohio State University under fluences of 1.4 × 10¹⁶ (1-h) neutrons per square centimeter.

Cr_1+δTe₂ synthesis and characterization

Chromium telluride Cr_1+δTe₂ nanoplates/nanoflakes were grown using a chemical vapor deposition method in a three-zone quartz tube furnace^75,76,82. CrCl₃ (Alfa Aesar, purity of 99.9%) and Te (Alfa Aesar, purity of 99.999%) powders were used as precursors, each placed in a separate alumina boat within a smaller-diameter quartz tube. The Te boat and CrCl₃ boat were positioned in the center of zone 1 and zone 2, respectively. Several SiO₂ (300 nm)/Si substrates were placed downstream from zone 2 to zone 3. The temperatures of zones 1, 2, and 3 were set to be at 500 C, 750 C, and 750 C, respectively. A carrier gas mixture consisting of 1% H₂ and 99% Ar was supplied at a flow rate of 25 sccm, and the pressure was maintained at 50 Torr during the heat-up process. As soon as the target temperatures were reached, the system was pumped down, and the furnace was turned off and cooled down to room temperature gradually.

TEM studies were conducted using 120 kV JEOL JEM 1400plus. Supplementary Fig. 1a is a low-magnification TEM image of a chromium telluride nanoplate. Selected area electron diffraction (SAED) patterns were collected along [001] and [112] zone axes, which are shown in Supplementary Fig. 1b and c, respectively. The main diffraction spots in both patterns can be indexed by the structure of Cr_1+δTe₂ with δ ≈ 0.5.

The thickness of the Cr_1+δTe₂ sample is determined using atomic force microscopy (AFM). Supplementary Fig. 2 presents a 2D deflection scan obtained via AFM, along with a linecut measurement across the sample. Although the exact thickness of the flake studied in the DAC was not directly measured, the thickness of several other similar flakes from the same synthesis batch was calibrated. These measurements reveal a thickness range of 50100 nm.

First-principles calculations

Density functional theory (DFT) calculations are carried out using the projected augmented wave method^83,84 as implemented in the Vienna Ab initio Simulation Package. The Perdew-Burke-Ernzerhof⁸⁵ of the generalized gradient approximation is adopted for the exchange-correlation functional. Here, we focus on the calculation of CrTe₂ instead of Cr_1+δTe₂ to reduce computational complexity. An energy cutoff of 500 eV was set, and 18 × 18 × 8 k-point mesh was used to sample the entire Brillouin zone. Structural optimization is performed until the forces on all atoms are below 0.01 eV/Å, and the energy criterion for convergence in the self-consistent field calculation is set to 10⁻⁶ eV. The DFT+U approach^86,87 is employed to account for the on-site Coulomb interaction in the Cr 3d orbitals, with U values of 5 eV and 6 eV being considered. The exchange constant J is calculated as a function of applied pressure. Specifically, J is determined by calculating the energy difference between the ferromagnetic (Supplementary Fig. 3a) and antiferromagnetic (Supplementary Fig. 3b) configurations using a 2 × 2 × 1 extended structure, following the method described in⁸⁸. The calculated J values, as shown in Supplementary Fig. 3c, show a trend where increasing pressure results in a reduction in the exchange constant. In the mean field approximation, the Curie temperature T_C is proportional to the exchange coupling constant J. Therefore, the pressure dependence of J in Supplementary Fig. 3c suggests that the T_C of the system is suppressed by increasing pressure.