Introduction

The control of wave propagation lies at the foundation of numerous applications, for which acoustic metamaterials hold immense potential1,2. They are engineered structures, often a lattice of subwavelength resonators3,4. Their collective action endows the bulk material with unusual effective properties such as a negative mass density and/or a negative modulus5,6,7,8. These properties, typically not found in nature, unlock novel wave phenomena9,10,11, including the ability to stop wave propagation in specific frequency ranges called band gaps (BG). Unlike those derived from Bragg scattering12, these BG stem from the hybridization of local resonances with free-space dispersion. Crucially, they are independent of wavelength, allowing for compact and practical metamaterial designs.

Following their success in optics13 and acoustics14, metamaterials have sparked interest in haptics15,16,17. Unlike soft matter damping designed to isolate haptic motor arrays18, metamaterials can operate on stiff, non-dissipative panels such as glass screens. Compared to control and geometric methods19,20,21, they are robust, versatile, and effective at confining elastic waves for the rendering of localized vibrotactile feedback. However, once manufactured, these passive structures possess fixed properties and spatial arrangements that limit their use, whether in haptics or other fields.

To address these issues, researchers have introduced active unit cells22, supporting functions ranging from loss compensation in non-Hermitian metamaterials23 to BG tuning24. Piezoelectric transducers, favored for their adjustable stiffness through shunting, are widely used to activate these cells. They can alter band structure by making variable junctions25,26, reconfigure waveguides27,28, and steer wavefronts29,30. These dynamic systems are best suited for real-time31, low-amplitude, and high-frequency applications, typically in the kHz to MHz ranges.

Electromagnetic actuation offers complementary capabilities. It often involves moving an extraneous permanent magnet to remotely toggle the effective modulus between positive and negative32, or selectively activate resonators for outlining waveguides33,34, albeit with a 300 ms latency per cell. Alternatively, electromagnetic actuation can be distributed within each unit cell by embedding energized coils. They can set bistable or tristable resonators in distinct states, thus controlling BG35,36, phase changes37, and polarization38. This approach also achieves low-frequency BG under 100 Hz via continuously variable stiffness adjustments39.

By enabling real-time reconfiguration of waveguides, active metamaterials could be the key to developing a multi-touch, programmable vibration-based display on rigid surfaces, a major goal of haptic research40. Human touch is exquisitely sensitive to rapid transients and low-frequency vibrations up to about 1 kHz41,42, requiring deep subwavelength unit cells the size of a finger pad. However, current active unit cells do not meet haptic needs. Electromagnetic-based cells are not configured for real-time response, while piezoelectric-based cells operate at excessively high frequencies. Additionally, existing active unit cells can only control a single global vibration source, such as ambient noise, rather than multiple stimuli.

To overcome these limitations, we introduce a novel type of active acoustic metamaterial. It consists of dual-state unit cells made from off-the-shelf electromagnetic linear resonant actuators (LRAs), commonly found in smartphones and game controllers. Both theoretical and experimental results show that a 1D array of LRAs induces a self-tuned, deep subwavelength BG, within touch-relevant frequencies. We report a method to tailor acceleration fields in real-time, enabling the spatial encoding of binary words and time-varying patterns. We demonstrate its relevance for tactile perception. This work opens up new avenues for responsive multi-touch haptic displays, mechanical computing, and overall democratizes active metamaterials through a low-cost, non-expert approach.

Results

Dual-state active unit cell

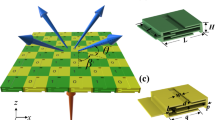
An off-the-shelf LRA with a square footprint of 10 × 10 × 4 mm3 (VLV101040A, Vybronics) was chosen to make subwavelength unit cells that tile the plane, as shown in Fig. 1a. This resonant actuator, illustrated in Fig.  1d, consists of a mass attached to a spiral flexure spring, which restricted oscillations to the z-axis. Requisite active elements are already embedded inside typical LRAs, including a neodymium magnet attached to the moving mass and a coil fixed to the casing. When an alternating current is applied to the coil, the Lorentz force causes the mass to oscillate, generating transverse waves in the base that produce vivid vibrotactile sensations. This was termed the “actuator state”, as schematized in Fig. 1b. On the other hand, if the coil is left disconnected, i.e., in an open circuit, no current can establish and the unit cell remains a passive resonator. This will further be referred to as the “resonator state”. The possibility of a third state that would allow unimpeded vibration propagation was also investigated. This involved shorting the coil to induce eddy current damping in an attempt to nullify resonances. However, it proved insufficient, achieving only a 10% reduction in quality factor (see Supplementary Fig. 1c).

Fig. 1: Overview of the dual-state active acoustic metamaterial.
figure 1

a Schematic of a 2D tactile display made from a square tessellation of dual-state unit cells. Cells in a resonator state (blank) form a metamaterial, insulating cells in an actuator state (colored). The resulting vibration patterns can be reconfigured in real time. A reduced linear array of 11 unit cells is outlined in black. b Equivalent electromechanical model in both states: the “actuator state” and the “resonator state''. Mechanical and electrical energy fluxes are overlaid (dissipative effects are discarded). The electrical circuit consists of a resistance Ra, an electromotive force ea, and an inductance La. The mechanical system includes a moving mass m and a spring K. c Schematic of the linear array of 11 unit cells made with LRAs. d Exploded view of an off-the-shelf LRA with, from top to bottom, a FR-4 substrate (SU), a voice coil (CL), a flexure spring (FL), a moving mass with a neodymium magnet (MM), and a steel casing (SC). e Impulse response of a single LRA measured using a laser interferometer. Both the gain and phase, averaged over 50 trials, are well approximated by a second-order model with minimal damping. f Top view of the prototype with embedded electronics.

Full size image

The dynamic response of a unit cell, central to BG formation, was assessed experimentally (see Methods). As shown in Fig. 1e, the results are in excellent agreement with a second-order linear time-invariant model (\(\forall \,f\in \,\left.\right]0,500\left.\right]\,{{{{\rm{Hz}}}}},\,{{{{\rm{RMSE}}}}}=70\,{{{{\rm{nm}}}}}\cdot \,{{{{{\rm{V}}}}}}^{-1}\), see Supplementary Section 1.1). The moving mass, m = 1.57 g, combined with a compliant spring, K = 3.08 N · mm−1, gave a natural frequency f0 = ω0/2π = 223 Hz. The DC gain, G, was evaluated at 217 nm V−1. The high quality factor, Q = 1/2 ζ = 19.8, achieved through frictionless guiding and minimal damping, is ideal for making a resonant acoustic metamaterial. For simplicity, the close-packed square lattice was reduced to a linear arrangement, as illustrated in Fig. 1c. As depicted in Fig. 1f, a prototype was manufactured with an array of 11 LRAs. They were glued under an elongated printed circuit board (PCB) substrate for seamless integration of driving electronics and sensors (see Section “Methods”).

Deep subwavelength band gap

Acoustic metamaterials are usually fine-tuned through time-consuming finite element analysis (FEA). Instead, an array of low-loss resonators provides a closed-form solution, enabling analytical optimization and a deeper understanding of the underlying physics. To unveil the band structure, the metamaterial was modeled as an infinite series of Timoshenko–Ehrenfest beams of length L, as shown in Fig. 2a. Assuming homogeneity and isotropy, the material properties were derived using an effective medium approximation, blending the attributes of the PCB substrate and LRAs, obtained from bending tests (see Supplementary Fig. 2). Each junction was described by a virtual stiffness, K*, representing the reaction force of an LRA (see Supplementary Fig. 3a). Due to its periodic symmetry, the problem was reduced to a single segment with both continuity and Floquet–Bloch boundary conditions (see Supplementary Section 2.4). It yielded the theoretical dispersion diagrams in Fig. 2b, revealing a complete BG wherein only an evanescent field established.

Fig. 2: Band gap analysis.
figure 2

a Metamaterial as an infinite series of Timoshenko–Ehrenfest beams with springs K* at each junction to capture the resonant action of LRAs. b Dispersion graphs with complete band gaps (BG) for various linear densities ρS (constant EI). Real and imaginary parts of the Bloch wavenumber yield propagating and evanescent modes, respectively. Results fall within the human vibrotactile threshold, defined for a given frequency as the minimum perceivable peak-to-peak vibration amplitude. Reproduced from refs. 42,43. c Left-hand side transmission coefficient relative to the central unit cell, n = 6. d Transmission coefficient against distance from the vibration source. e Frequency shift of the attenuation peaks. f Variations in transmission coefficients for n = 2, where blue and green hues represent levels of flexure tension relative to the reference δx = 0 mm. g Frequency-averaged variations in transmission coefficients, given as the RMSE, against distance from the vibration source.

Full size image

The BG width, η, defined in Fig. 2b, follows an inverse power-law with linear density, ρS, expressed as η = 18.4 (ρS)−0.86 (see Supplementary Fig. 3b), where ρ and S are the effective density and cross-sectional area, respectively. While the flexural rigidity, EI, increases free-space phase velocity and reshapes dispersion curves (see Supplementary Fig. 3c), it has no effect on η when ρS remains constant. Thus, for material properties and dimensions relevant to manufacturing, local inertia governs BG width. Using a standard 1.6 mm thick PCB substrate yields effective beam properties that result in a theoretical BG from 223 to 284 Hz, aligning with the range of peak vibrotactile sensitivity mediated by Pacinian corpuscles42,43, as shown in Fig. 2b.

Experimental validation involved measuring the transmission coefficient, T, between two unit cells (see Methods). Given the symmetry of our prototype, T was derived relative to the central unit cell (n = 6) as \({{{{\rm{T}}}}}=20\log (| {\Gamma }_{n}| /| {\Gamma }_{6}| )\), where Γn is the Fourier transform of the transverse acceleration of the nth unit cell, with n ∈ [1, 11]. Left-hand side transmission coefficients, for n ∈ [1, 5], are presented in Fig. 2c, revealing a BG between 163 and 284 Hz. Right-hand side results are analogous, ranging from 163 to 290 Hz (see Supplementary Fig. 5a). Minor discrepancies likely stem from part-to-part variations in LRAs and an unforeseen imbalance introduced by the tensioning mechanism (see Supplementary Movie 1). For consistency, averaged values of 163 and 287 Hz are used throughout this paper.

The model predicted the upper boundary within 1% accuracy but overestimated the lower boundary by 37%. Such gap arises from the finite number of unit cells, in contrast with the infinite array assumption. An empirical correction (see Supplementary Fig. 4) indicates that 36 unit cells would be enough to match theory within 1%. An attenuation peak of  −13.2 dB at 205 Hz was recorded just five unit cells away from the vibration source, validating our approach even well below the infinite lattice assumption. As shown in Fig. 2c, the peaks, labeled Pn, are shifted towards higher frequencies as more unit cells are involved. This blueshift is linearly correlated to the transmission coefficient (Pearson correlation coefficient r = −0.94, p < 10−3), as shown in Fig. 2e. In fact, the attenuation gradually established with the number of unit cells recruited. As it better approximates the theoretical infinite model, the attenuation converges towards a maxima for f → f0. A convergence error of only 8% was measured at P1, five unit cells away from the source. Within the BG, Floquet–Bloch’s theorem predicts that vibration amplitude decays exponentially with the number of unit cells (see Supplementary Section 2.4). It followed piecewise linear functions instead ( ∀  f ∈ {205, 240, 275} Hz,  R2 > 0.95), as shown in Fig. 2d. This may be attributed to the small set of unit cells considered. Nonetheless, assuming a smooth decay, the transmission coefficient would still approach zero asymptotically, in line with Floquet–Bloch’s predictions. These linear fits failed to intercept the unity transmission coefficient, indicating nonlinearity near the vibration source.

Our acoustic metamaterial is subjected to flexural waves with a free-space wavelength, λ0 = 166 mm at 205 Hz, as estimated using FEA (see Supplementary Section 2.6). In turn, the dimensionless ratio, ϕ = λ0 /L ≈ 17, indicates exceptional subwavelength capabilities. Consequently, this metamaterial can hinder the propagation of elastic waves with wavelengths 17 times larger than a single unit cell. This is a testament to the effectiveness of leveraging prior industrial efforts directed towards the optimization of resonators for mobile applications.

Invariance by changes in boundary impedance

Spurious wave reflections at the extremities of a beam create standing waves and, ipso facto, destructive interference that could mislead BG analyses. To mitigate these effects, a common strategy in numerical simulations is to terminate edges with perfectly matched layers that provide near-zero reflection44,45. However, this solution is not easily implemented in practice. As an alternative, previous transmission measurements were replicated at varying levels of boundary impedance. This was achieved by suspending the metamaterial on flexures, whose stiffness was adjusted via a tensioning motion δx (see Methods, Supplementary Fig. 6 and Movie 1).

Variations in transmission coefficients are presented in Fig. 2f, at five levels of boundary impedance, each obtained by 2 mm increments from the reference signal taken at δx = 0 mm. Results are given for n = 2 (see Supplementary Fig. 5b for the remaining values of n). The BG is the only frequency range that remained mostly unaffected by changes in boundary conditions. As shown in Fig. 2g, the RMSE with respect to the reference, δx = 0 mm, is one to two orders of magnitude lower within the BG than outside of it. Furthermore, the RMSE outside the BG increases with the distance from the vibration source, showing significant edge effects otherwise barely seen within the BG. This provides further evidence that the extraordinary attenuation qualities are intrinsic to the resonant acoustic metamaterial rather than an artifact of suitably designed boundaries.

Spatially localized acceleration field

To maximize energy efficiency and produce vivid stimuli, LRAs set electronically in an actuator state must be driven with a carrier close to resonance. In turn, the carrier frequency naturally falls within the BG of a metamaterial made from remaining LRAs in a resonator state. It is, in that sense, self-tuned. By strategically arranging unit cells in both states, vibrations can be confined in localized areas. However, sufficient spacing must be introduced between activated unit cells to minimize crosstalk.

This was investigated by driving two unit cells with a sinusoidal carrier and increasing their separation, Δx, in 10 mm increments up to 100 mm, as illustrated in Fig. 3b. The RMS acceleration profiles along the metamaterial were interpolated by cubic splines, as shown in Fig. 3a. Within the BG, adjacent sources induced a unique vibration spot. To create distinct spots, they had to be separated by at least 60 mm. This is evident from the inflection point in the acceleration gradient, as shown in Fig. 3d. To achieve the sharpest vibration spots, characterized by the highest gradient, Δx should be maximized. In practice, this was limited by wave reflections when LRAs were activated close to the extremities. This effect was particularly pronounced beyond the BG, at 370 Hz, where destructive interference led to a minimal acceleration, even near vibration sources. Further insights into the attenuation qualities were gained by analyzing a larger number of unit cells than in the previous experiment. This corroborates the exponential decay of evanescent waves predicted by Floquet–Bloch theory (∀ f ∈ {205, 240, 275} Hz,  RMSE ≤ 5.9%), as depicted in Fig. 3c.

Fig. 3: High-speed reconfiguration.
figure 3

a Interpolated RMS acceleration field for two unit cells actuated. b Schematic of the experiment with two unit cells driven by sine waves. c Exponential increase in attenuation with the distance between sources. d Maximum gradient of the acceleration field. The inflection point marks the transition from crosstalk between both sources to distinct vibration spots. e Steady-state RMS acceleration with actuation of LRA n = 1, then commuted to LRA n = 6, for a 205 Hz carrier. Here, the unit cells are arranged from right to left, matching standard binary notation with the least significant bit on the rightmost side. f Rising and falling edges recorded during the electronic commutation of LRAs n = 6 and n = 1, respectively. The dotted line represents the exponential envelope of the LRA settling. g Steady-state RMS acceleration for 3-bit binary numbers counted from 0 to 7 in 25 ms intervals. h Decoding sequence with binarization using thresholds optimized for each carrier. i Decoding success rate as a function of the time delay between each word.

Full size image

High-speed reconfiguration

Our active acoustic metamaterial was specifically designed for dynamic reconfiguration. This was exemplified by electronically switching the powered unit cell from the distal one to the central one, corresponding to n = 1 and n = 6, respectively, as illustrated in Fig. 3e. The transient acceleration during both rising and falling edges is shown in Fig. 3f. The falling edge was followed by an exponential decay with a time constant τ = 22 ms, slightly overestimated by 14% by the second-order model, 1/ζ ω0 = 25 ms. The rising edge established even faster due to the forced response. These results support the use of electromagnetic actuation in combination with MOSFET-based commutation to enable swift reconfiguration. In fact, the limiting factor is the lack of damping, rather than electronics. However, increasing damping could inhibit the resonant BG.

The ability to rapidly shape vibration patterns holds potential for information storage and transmission, which can be quantified by the bandwidth. It was explored by encoding binary words spatially in the wavefield. Limiting them to 3 bits, n ∈ {1, 6, 11}, ensured they were sufficiently spaced apart with Δx = 50 mm. Although slightly less than the previously defined threshold, it effectively reduced crosstalk between each bit while maintaining compactness. The steady-state RMS acceleration for 3-bit binary numbers counted from 0 to 7 at 25 ms intervals is given in Fig. 3g (see Supplementary Movie 2). These patterns can be simply deciphered by thresholding the histogram of RMS acceleration. For each carrier, an optimal threshold can be found numerically, as shown in Fig. 3h. The decoding success rates are given in Fig. 3i. Outside the BG, it remained close to chance level, independent of the delay, as uncontrolled propagation blurred the binary words. Nonetheless, an exact retrieval is possible for carriers within the BG, provided that a minimum delay of 25 ms is respected between each word. This confirms previous observations on the time required to settle a logic state. Despite using electromagnetic unit cells, our metamaterial achieved a reconfiguration time comparable to that of piezoelectric metalenses (13 ms)31. As a result, it can emulate a lossless vibratory display with a 120 bit s−1 rate at a 50 mm spatial resolution.

Application to localized vibrotactile feedback

To evaluate the potential to convey tactile information, we devised a perceptual matching task (see Section “Methods”). Participants were asked to distinguish between seven different vibration patterns, corresponding to the binary conversion of integers from one to seven. Confusion matrices averaged across participants are given in Fig. 4a for two sinusoidal carriers, 205  Hz and 370 Hz, within and beyond the BG, respectively. A two-way repeated measures ANOVA revealed significant effects of both the vibration pattern (F(6, 98) = 4.6,  p < 10−3) and the carrier frequency (F(1, 98) = 119.9,  p < 10−5). This strongly indicates that the perception of local stimuli was mediated by the BG. These findings are consistent with the acceleration fields depicted in Fig. 3g. The interaction term between pattern and frequency significantly impacted the success rate (F(6, 98) = 6.5,  p < 10−5). To further explore this effect, the data were segregated based on the number of simultaneously activated LRAs and a two-way repeated measures ANOVA was conducted. A post-hoc Tukey–Kramer test revealed that an activation of one or two LRAs yielded similar success rates, both in (p = 0.71) and out (p = 1.00) of the BG, as shown in Fig. 4b. Despite the lack of statistical significance (p = 0.13 and p = 0.20), a notable contrast was observed when all three LRAs were activated. In that case, the BG had a negligible effect on perception as participants seemed to confuse multiple vibration points with vibration spread. The increased variance in success rate illustrates this confusion. The mislocalization of tactile stimuli may have also been caused by a funneling illusion, as described by von Békésy46,47.

Fig. 4: Perceptual experiment.
figure 4

a Confusion matrices from the perception of localized vibration patterns that encode binary representations of integers from one to seven. Results averaged across all participants. b Average success rate of the matching task, either aggregated or categorized by the number of LRAs activated simultaneously. Error bars represent one standard deviation. The dotted line represents a chance threshold of 1/7.

Full size image

Overall, participants could accurately perceive tactile messages spatially encoded on three bits with a success rate of 81%. Interestingly, the viscoelastic skin tissues in contact with the acoustic metamaterial did not alter its operational principles, as it still greatly enhanced the perception of local stimuli. However, for frequencies beyond its operating range, the success rate dropped to a mere 34%, highlighting the inherent limitations in rendering localized haptics on conventional continuous media.

Wavefield control along a pre-defined path

Our metamaterial goes beyond discrete reconfiguration through 3-bit binary words. It supports complex transitions, such as the continuous movement of a vibration spot along a prescribed path. This was achieved by driving unit cells with overlapping windowed signals. Specifically, a sinusoidal carrier, windowed by a zero-order Slepian sequence, was employed. It minimized spectral leakage, limiting high-frequency artifacts that could otherwise extend beyond the BG (see Supplementary Fig. 7). Overlapping adjacent signals by 80% was found empirically to ensure smooth, continuous travel of the acceleration field. This led to the simultaneous activation of up to five unit cells, as shown in Fig. 5a.

Fig. 5: Wavefield guiding along spatiotemporal paths.
figure 5

a Activation sequence of LRAs supplied with Slepian-windowed carrier signals. Up to five LRAs were activated simultaneously. b Recorded acceleration field following a linear spatiotemporal reference path represented by the dashed line. c Evolution of the vibration spot for various path speeds, and corresponding linear fits. d Spatiotemporal vibration maps for frequencies below, inside, and above the band gap. The top row was obtained by bilinear interpolation of the RMS acceleration, and the bottom row by Otsu’s binarization. e Sinusoidal reference path sweeping the metamaterial lengthwise at 3 Hz. f Metrics for assessing path-following effectiveness. Lower values indicate better performance.

Full size image

An experiment was conducted aiming at continuously guiding a vibration spot along a linear reference path. The Slepian sequence was timed accordingly. The RMS acceleration field was interpolated to compensate for the limited spatial resolution of the sensor array. This resulted in the spatiotemporal vibration maps depicted in Fig. 5b, d, which were further processed as images. Path-following was evaluated using two complementary metrics. The first metric, M1, counts the number of trails (white blobs in Fig. 5d) left by the vibration sources as they moved through time and space. These trails were obtained by binarizing vibration maps using Otsu’s threshold. A single continuous trail indicates good localization. The second metric, M2 (see definition in Supplementary Section 3.3), quantifies the deviation of the vibration field from the reference path. The best performance, with a single trail and minimal deviation, was achieved for carrier frequencies within the BG, as shown in Fig. 5f and the central panel of Fig. 5d.

We tested path-following at reference velocities \({\dot{x}}_{r}\) up to 300 mm s−1 (see Supplementary Movie 3). As demonstrated in Fig. 5c, this was reliably achieved across all velocities with a 205 Hz sine carrier (\(\forall \,{\dot{x}}_{r}\in \{100,150,\ldots,300\}\,{{{{\rm{mm}}}}}\cdot {{{{{\rm{s}}}}}}^{-1},\,{R}^{2} > 0.94\)). This capacity extends to sinusoidal paths, as shown in Fig. 5e (see Supplementary Movie 4). While vibrations are well-localized, amplitude increases near extremities, likely due to rigid body dynamics of the suspended beam. Adjusting LRA driving voltages selectively could mitigate this effect. Overall, the proposed metamaterial enables continuous steering of low-frequency vibration spots in both time and space. This holds great promise for rendering compelling sensations of tactual apparent motion48.

Discussion

This work tackled the issue of invariant acoustic properties in passive structures by introducing a new type of active metamaterial. It consists of a series of dual-state unit cells, either resonators when left disconnected or vibration sources when powered. Conveniently, these unit cells can be made from off-the-shelf LRAs, commonly found in smartphones. They create a self-tuned metamaterial with a BG that intrinsically includes the optimal actuation carrier frequency. A major strength of this approach is its potential to create acoustic metamaterials with minimal knowledge, serving as a turnkey solution for haptic designers.

Comprehensive theoretical and experimental studies of a 1D prototype revealed a BG from 163 to 287 Hz, with a peak attenuation of 13.2 dB at 205 Hz after five unit cells. This effect remained robust regardless of boundary conditions. A bespoke controller supports real-time reconfiguration of the metamaterial in under 25 ms. This enables dynamic shaping of vibration patterns with a bandwidth of about 120 bit s−1. A closed-loop system with a proportional-derivative or lead-lag compensator could further reduce response time, albeit at the cost of simplicity and reliability. In addition, the unit cells exhibited deep subwavelength behavior by stopping wave propagation at wavelengths 17 times their size. This paves the way for compact, rigid, and non-dissipative materials that mediate vibrotactile feedback.

The spatial resolution of 50 mm, while already relevant to haptic uses, could be improved by making LRAs with a greater quality factor or operating at higher frequencies. Even so, the layout can be reconfigured in finer, 10 mm increments to accommodate diverse hand and finger morphologies. The number of unit cells, presently set to 11, can be adjusted to meet the desired coverage area and application complexity. Extending this approach to 2D, as illustrated in Fig. 1a, would require minimal adjustments. A similar model could be derived for plates, maintaining symmetry and isotropy. While plates exhibit slightly greater bending stiffness than beams by a factor 1/(1 − ν2), this should not affect the BG, primarily governed by local resonances and inertia. In 2D, square LRAs are best arranged in a square lattice, whereas circular LRAs would form a close-packed hexagonal lattice. A notable challenge in 2D is the increased electronic complexity needed to drive numerous electromagnetic actuators.

A perceptual experiment demonstrated that human subjects were able to retrieve 3-bit spatially ingrained messages on a prototype 110 mm. Its ability to steer vibration along a smooth spatiotemporal path also offers a promising solution for creating compelling illusions of apparent motions. Since it follows the Perkins Brailler layout49, this work has direct translational applications as a live communication device for the visually impaired.

Beyond tactile applications in multi-touch refreshable displays, this work has broader implications for mechanical computing50,51. With Boolean logic readily emulated through mechanical metamaterials52, our approach provides spatial storage of elastic energy bits with dynamic allocation. Given that localized waves within the BG can be modulated in both amplitude and frequency, this system even extends beyond binary computation into analog processing. Inspired by phononic analog computing, such as neuromorphic dispersion for image recognition53,54, we foresee the emergence of haptic computing, where reactive metasurfaces could dynamically process and deliver feedback in response to user input.

Methods

Prototype

An acoustic metamaterial was manufactured with an array of 11 LRAs (VLV101040A, Vybronics). These LRAs have a coil resistance Ra = 7.0 Ω and an inductance La = 64 μH, measured at 205 Hz. They were glued on an elongated PCB with a thin layer of cyanoacrylate adhesive (454, Loctite), resulting in a rigid bond that effectively transmitted vibrations. Both extremities of the metamaterial were suspended by flexures cut in a 100 μm-thick polyimide film (Kapton, DuPont). A pop-up structure was designed within this rigid-flex assembly to provide adjustable tensioning of the flexures via a linear motion δx (see Supplementary Fig. 6). Manual setting is demonstrated in Supplementary Movie 1. This allowed the study of dispersive effects due to changes in boundary stiffness, which increased monotonically with flexure tension. These flexures also created efficient routing paths for electrical signals (~40 traces), avoiding undesired stiffness from cables. The device was mounted on a 1.3 kg brass block fitted with rubber feet that filtered out external disturbances. The prototype is illustrated in Fig. 1f.

Vibration generation

The embedded control unit is a 32-bit microcontroller board (Teensy 4.0, PRJC) running at 1.0 GHz. The LRAs were driven in open-loop through H-bridge MOSFET drivers (DRV8837, Texas Instruments), fed by pulse-width-modulated signals coded on 10 bits. To meet the stringent timing requirements, output waveforms were generated offline and stored in look-up tables. The entire device was powered through USB with 5 V, lowered down to 2.5 V with a buck converter (Okami OKL, Murata) in order to supply the LRAs. A large bank of decoupling capacitors covered the transient current intakes from the actuators. A simplified control scheme and the PCB layout are given in Supplementary Fig. 8. For the characterization of the BG, the central unit cell was set to an actuator state and supplied with a linear chirp from DC to 500 Hz, while the remaining cells were left in a resonator state. To avoid any undesired distortions that may be caused by the digital signal generation, a 16-bit analog signal output from an acquisition card (USB-6343, National Instruments) was used instead, but only for the purpose of this analysis. The signal was then fed to a class-D amplifier (TPA3112D1, Texas Instruments).

Full-field vibrometry

To provide real-time, full-field vibrometry, the prototype was fitted with 11 analog accelerometers (ADXL335, Analog Devices), each centered to its corresponding LRA. Only their z-axes were connected, followed by first-order low-pass RC filters with a 500 Hz cut-off (fc = 1/2πRC). The acceleration field along the beam was recorded at a sensitivity of 300 mV ⋅ g−1 and sampled with a 12-bit analog-to-digital converter at 10 kHz. A maximum delay of only 4 μs was measured between successive analog input readings, thus providing the excellent synchronicity required for the transient analysis of active reconfigurations. To maintain synchronicity during the experiments, data were stored on a 1 MB RAM buffer rather than directly exported through USB.

Impulse response of a unit cell

A 1 ms square pulse of 2.28 ± 0.03 V was fed to an LRA through a MOSFET, and repeated 50 times. This circuit was designed to disconnect the coil immediately after pulsing, which prevented the occurrence of undesirable eddy current damping. The LRA was mechanically grounded. Its casing was removed to provide access for the beam of a 632.8 nm HeNe laser interferometer (LSV-2500-NG, SIOS) pointing towards the moving mass, as illustrated in Fig. 1e. Data were digitized on 16 bits at a sampling rate of 100 kHz by an acquisition card (PCI-6121, National Instruments), followed by a zero-lag, two-pole Butterworth low-pass filter with a 1 kHz cut-off. It gave a noise floor of 18 nm RMS, sufficient to resolve minute vibrations. This setup added a 0.57 ms delay, rectified before model fitting (see Supplementary Section 1.1).

Participants and protocol

Eight volunteers (5 males, 3 females) aged 25.1 ± 2.8 (mean ± std) participated in this experiment. The study was conducted with the approval of Sorbonne University Ethics Committee (CER-2021-078), and the participants gave their written informed consent. They were instructed to place their fingertips on the acoustic metamaterial at the three specific locations indicated in Fig. 4a. Their fingers were covered, and they wore noise-canceling headphones to prevent any visual or auditory cues. Flexures were tensioned to δx = 10 mm. The experiment consisted in a matching task in which participants had to recognize localized vibrations patterns, corresponding to the binary conversion of integers from one to seven. Each spatial pattern was randomly repeated 20 times and was displayed with sinusoidal signals at either 205 or 370 Hz. Each tactile stimulus lasted 5 s, and the participants had to give an answer within the next 5 s. The vibration amplitude was kept constant. A total of 140 trials were presented in 2 blocks, separated by a 5 min break.