Introduction

Skyrmions are quasiparticles endowed with non-trivial yet stable topological spin textures that are localized in three dimensions (3D), and are immune to continuous deformations1,2. Arranging a continuous vector field on a sphere in a parametric space yields a wide variety of topological skyrmionic textures. In this form, skyrmions emerge in many physical systems, including nucleons1, Bose-Einstein condensates3,4, liquid crystals5, plasmonic systems6,7, water waves8,9,10, and magnetics11,12. The latter particularly benefits from the localization and stability of skyrmions—key ingredients for enabling future high-density, low-energy information storage and transfer technologies13. Despite their rich topology in 3D space, the realizations of skyrmions to date have been mostly restricted to “baby-skyrmions”—whirls of spin configurations in a two-dimensional (2D) plane3,14,15. Realizing 3D skyrmions unlocks a vast domain of topological structures whose unique features may not only help increase the density of magnetic-memory storage16, but may even lead to new phases of matter17. The search for physical systems to host such 3D topological configurations has been challenging4, and only recently have realizations emerged in fluid chiral ferromagnets18, Bose-Einstein condensates19, and ferroelectric materials20. In contrast to their well-studied 2D counterparts, the burgeoning study of 3D skyrmions is still witnessing rapid developments21.

Another recently explored platform for realizing skyrmions is that of optical waves, which is motivated by the potential for topologically structured electromagnetic fields to bring forth new applications, ranging from high-resolution imaging22 to secure and resilient quantum communications23. The first realizations of optical skyrmions were also restricted to 2D configurations, whereby topological structures are imprinted onto surface-bound evanescent fields in plasmonic systems6,7,22, and in freely propagating monochromatic fields at particular axial planes24,25,26. Such 2D optical skyrmions are not 3D-localized and are inherently static in space. Similar restrictions apply to hopfions in a monochromatic field contained within the focal volume of a lens27,28. In general, monochromatic light is restricted in the spectral domain to a flat 2D surface spanned by the transverse momentum. This contrasts with the original setting for skyrmions in which the spin texture is applied to a closed surface embedded in a 3D space1. Reaching this milestone in optics, therefore, necessitates adding the time dimension, which would allow for fully localizing the skyrmion and transporting it along the propagation axis. However, trivially adding the temporal dimension merely stretches the monochromatic 2D skyrmions in time (so-called skyrmion tubes16). This still leaves two potential pathways for realizing 3D optical skyrmions: producing the closed surface in space-time or in momentum-energy space. The former has been recently attempted in the microwave domain29. In this work, we aim instead at the latter, which enables temporal modulation at optical frequencies.

Nevertheless, a fundamental challenge remains for momentum-energy-space skyrmions, stemming from the need to imprint the skyrmionic texture on a closed spectral surface. As a point of reference, a conventional pulsed optical beam occupies a 3D volume in momentum-energy space. Restriction to an open 2D curved surface embedded in 3D momentum-energy space requires that each wavelength be in a one-to-one association with radial transverse momentum (Fig. 1b). The difficulty is further compounded when considering closed spectral surfaces, whereupon a two-to-one association is needed instead (Fig. 1c, d panel (i)). Efficiently carving out an open or closed spectral surface without spectral filtering in momentum-energy space, and imprinting an arbitrary skyrmionic texture on these surfaces, remains an outstanding challenge in optics. Therefore, producing optical skyrmionic structures with non-trivial 3D-localized topology requires exploiting spatiotemporally non-separable pulsed optical fields30,31, as proposed theoretically in ref. 32.

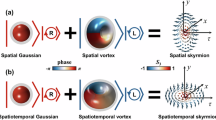
Fig. 1: Ultrafast ST merons in momentum-energy space.
figure 1

a The polarization texture of a meron covers half the unit sphere in parameter space. For their implementations in physical space, the spin configuration is typically mapped from the parameter space onto the \({{\mathbb{R}}}^{2}\) base space via stereographic projection. b An ST meron is constructed by mapping the meron polarization structure from the parameter space onto a 2D spectral surface \({{{\mathcal{S}}}}({k}_{x},{k}_{y},\omega )\) embedded in the 3D momentum-energy \({{\mathbb{R}}}^{3}\) space of an optical wave packet. c The polarization texture of an ST meron implemented on an open, dual-branch spectral surface in the form of a two-sheet paraboloid. d The polarization texture of an ST meron implemented on a closed spectral surface in the form of a spinning-top. The plots in c and d show (i) the 3D Stokes vector distribution in momentum-energy space and (ii) in physical space (x, y, z = 0, τ); (iii) the intensity isosurface I(x, y, z = 0; τ) = 0.1; (iv) a 2D slice of the 3D Stokes vector distribution n(x, y = 0, z = 0; τ) and (v–vii) its projections nx, ny and nz. The arrows in a indicate the Stokes vector orientation, and the arrows in b–d indicate the components of the Stokes vector. The colormaps on the spectral surface \({{{\mathcal{S}}}}({k}_{x},{k}_{y},\omega )\) in b, c(i), and d(i) represent the distribution of frequencies ω. Stokes vectors in physical space shown in c(ii–vi) and d(ii–vi) are constructed under the assumption of narrowband paraxial fields.

Full size image

This challenge has been addressed only very recently in the context of synthesizing propagation-invariant pulsed beams known as space-time wave packets (STWPs)30. However, only simple spectral surfaces in the form of paraboloids of revolution have been realized to date, which lack any polarization texture33,34. Unlocking the potential for topological skyrmionic structures in optics requires more sophisticated control over such spectral surfaces in momentum-energy space, ideally extending to never-before-realized closed spectral surfaces on whose entirety a prescribed polarization texture can be imprinted. Using this platform allows for 3D skyrmions to inherit some of the unique attributes of STWPs, including self-healing35, long-distance diffraction-free propagation36, and dispersion-free propagation in dispersive media37.

Here, we present 3D-localized optical skyrmionic polarization texture imprinted onto open and closed 2D spectral surfaces embedded in the 3D momentum-energy space of an ultrafast pulsed optical beam. Following the proposal in ref. 32, we realize merons (half-skyrmions) that have been of particular interest in the context of momentum-energy space by virtue of their direct link to Berry curvature38,39 (Fig. 1a). We refer to this class of skyrmionic structures as space-time (ST) merons henceforth. An optical structure of this kind is localized in space and time and is endowed with topological stability over propagation at a controllable group velocity. These characteristics are produced by virtue of judicious coupling introduced between the spatial and temporal degrees of freedom of the optical field, which reduces the dimensionality of its spatiotemporal spectrum30. The meron polarization texture on these curved 2D spectral surfaces (Fig. 1b) yields non-trivial 3D topological structures in space-time, whether using open (Fig. 1c) or closed (Fig. 1d) spatiotemporal spectral surfaces. To achieve these goals, we take two decisive steps that build upon previous experimental progress for synthesizing propagation-invariant STWPs30,33. First, we introduce a synthesis methodology to produce closed spectral surfaces via a novel two-to-one conformal coordinate transformation. Second, we have designed and fabricated a record-size birefringent dielectric metasurface consisting of  ~109 nanofins, which serve as a symmetry-breaking device that introduces the target meron structure in momentum-energy space. ST merons synthesized via this methodology inherit some of the unique propagation characteristics of the underlying scalar STWP structure, such as transport at controllable group velocity40, anomalous refraction behavior at interfaces41, and self-healing35. Thus, by modifying the geometry and topology of polarization distribution in momentum-energy space, the propagation dynamics of skyrmionic structures can be tuned in space-time, thereby opening a path for novel topological refraction phenomena42, and novel information channels based on global topological features, potentially offering high-speed optical communication with greater resilience to noise and perturbations23,43, and topological light-matter interactions using photonic quasiparticles44.

Results

Theory of space-time merons in momentum-energy space

Skyrmions are represented by a continuous three-component unit vector field n(r) = (nx(r), ny(r), nz(r)) on a unit two-sphere parameter space; where r = (x, y, z) and x2 + y2 + z2 = 1. These configurations are distinguished by a non-zero topological Skyrmion number N14, which quantifies the number of times n(r) wraps around the unit sphere. Merons, or half-skyrmions, carry a skyrmion number \(N=\pm \frac{1}{2}\), indicating that n(r) covers only half the unit sphere, from the north pole to the equator (Fig. 1a). The meron texture is explicitly given in polar coordinates by: \({{{\bf{n}}}}(\rho,\phi )\,=\,\frac{1}{\sqrt{{\zeta }^{2}+{\Delta }^{2}}}\left\{\rho \cos (\phi+\gamma ),\rho \sin (\phi+\gamma ),\Delta \right\}\); where \(\rho \,=\,\sqrt{{x}^{2}+{y}^{2}},\quad \phi=\arg (x+iy)\), the parameter Δ specifies the meron radius, and the helicity γ ∈ ( − π, π] determines the chirality of the spin texture, which gives rise to a classification of merons into Néel-type (γ = 0) and Bloch-type (γ = ±π/2)14. Previous experimental realizations of optical skyrmions have relied on one of three strategies for mapping the vector n(r) to physical quantities45: (1) mapping n(r) to the normalized electric field vector6; (2) mapping n(r) to time-averaged spin vector7,22; and (3) mapping n(r) to the normalized Stokes vector in paraxial optical fields24,25,27,46. Whereas the first and second approaches all three field components and are thus associated with non-paraxial fields (for example, surface plasmon polaritons), we make use of the third approach, which is more suitable for transportable beams in paraxial optics. All these demonstrations were realized by mapping the 3D vector field n(r) from the parameter space to a flat 2D surface disk in \({{\mathbb{R}}}^{2}\) as a base space (real space), via a Hopf mapping (hopfions) or a stereographic projection (2D skyrmions)14; see Fig. 1a.

In contrast, here we make use of a curved 2D spectral surface \({{{\mathcal{S}}}}({k}_{x},{k}_{y},\omega )\) as a base space in the \({{\mathbb{R}}}^{3}\) momentum-energy domain of a pulsed optical field in narrowband paraxial regime (Fig. 1b–d); where kx and ky are the transverse components of the wave vector, and ω is the temporal frequency. We map the meron texture from the hemisphere in parameter space to the Stokes vector on \({{{\mathcal{S}}}}({k}_{x},{k}_{y},\omega )\), such that \({{{\bf{n}}}}({{{\bf{r}}}})\,=\,\left({s}_{1}({{{\bf{r}}}}),{s}_{2}({{{\bf{r}}}}),{s}_{3}({{{\bf{r}}}})\right)\); here s1, s2, and s3 are normalized Stokes parameters. Scalar optical fields restricted to simple 2D spectral surfaces are known as STWPs30,47, whose characteristics are useful for a variety of applications30,31. First, note that a one-to-one relation enforced between the transverse radial wave number \({k}_{r}\,=\,\sqrt{{k}_{x}^{2}\,+\,{k}_{y}^{2}}\) and the temporal frequency ω leads to diffraction-free propagation30, thus potentially enabling the transportation of localized topological structures over extended distances47. Moreover, when the space-time coupling takes the form of a paraboloid \(\frac{\Omega ({k}_{r})}{{\omega }_{{{{\rm{o}}}}}}\,\approx \,\frac{{k}_{r}^{2}}{2{k}_{{{{\rm{o}}}}}^{2}(1-c/\widetilde{v})}\) (Fig. 1b), the optical wave packet travels rigidly at a controllable group-velocity \(\widetilde{v}\) in linear optical media32,33; here ωo is a carrier frequency, \({k}_{{{{\rm{o}}}}}\,=\,\frac{{\omega }_{{{{\rm{o}}}}}}{c}\) is the associated wave number, c is the speed of light in vacuum, and Ω = ω − ωo (Fig. 1b). The spatiotemporal spectrum of an azimuthally symmetric STWP can be represented by \(\widetilde{E}({k}_{r},\Omega )\,=\,\widetilde{E}({k}_{r})\delta (\Omega -\Omega ({k}_{r}))\), where \(\widetilde{E}({k}_{r})\) is the spatial spectrum, and the delta function is relaxed in practice and replaced with a narrowband spectral function33. After incorporating the meron polarization texture, the spatiotemporal spectrum of such ST merons in the circular polarization basis is: \(\widetilde{{{{\bf{E}}}}}({k}_{r},{\phi }_{k},\Omega )\,=\widetilde{E}({k}_{r},\Omega ){[\sin \frac{\theta ({k}_{r})}{2},-{e}^{i\chi ({\phi }_{k})}\cos \frac{\theta ({k}_{r})}{2}]}^{{{{\rm{T}}}}}\); here, “T” is the transpose operation, \(\theta \left({k}_{r}\right)\,=\,\pi -\arccos \frac{\kappa }{\sqrt{{k}_{r}^{2}+{\kappa }^{2}}}\), \(\chi \left({\phi }_{k}\right)\,=\,{\phi }_{k}+\gamma -\pi\), and \({\phi }_{k}\,=\,\arg ({k}_{x}+i{k}_{y})\) (see Supplementary Note I), and we set γ = π/2 to produce a Bloch-type topological structure. The vectorial field profile in physical space takes the form \({{{\bf{E}}}}(r,z;\tau )\,\propto \,\iint \,d{k}_{r}d\Omega \,\,\,{k}_{r}\widetilde{{{{\bf{E}}}}}({k}_{r},\Omega ){J}_{0}({k}_{r}r){e}^{-i\Omega \tau }\,=\,{{{\bf{E}}}}(r,0;\tau )\), where J0( ⋅ ) is the 0th-order Bessel function of the first kind33, and \(\tau \,=\,t-z/\widetilde{v}\) is a time frame moving at the group velocity \(\widetilde{v}\).

Using the single-branched paraboloidal spectral surface as a building block, we construct complex surface geometries by modifying the space-time coupling function Ω(kr). We consider two such spectral structures: an open-surface double-branched paraboloid \(\Omega ({k}_{r})\,=\,\pm (a{k}_{r}^{2}+b)\), (Fig. 1c), and a closed-surface spinning-top \(\Omega ({k}_{r})\,=\,\pm (\frac{a}{{k}_{r}}+b)\) (Fig. 1d); where a and b are positive real constants. The meron texture here is the same on both branches of these surfaces in momentum-energy space (Fig. 1c, d, panel (i)). In principle, however, independent spin profiles could be prescribed on the two branches to explore other skyrmionic structures. The structure of the ST merons in physical space E(x, y, z; τ) is calculated via a 3D Fourier transform (at z = 0). First, the 3D structure of the unit vector n(x, y, z; τ) for both ST merons reveals non-trivial Stokes vector distributions localized in the 3D space-time volume of the wave packet; see Fig. 1c, d, panel (ii). This is in striking contrast with the spectral distributions in momentum-energy space, where the Stokes vector is distributed over only the surface \({{{\mathcal{S}}}}({k}_{x},{k}_{y},\omega )\). The 3D plots of the intensity isosurface I = 0.1 (after normalizing the intensity to unity) in panel (iii), reveal that the ST meron corresponding to the closed spectral surface is more localized (Fig. 1d), whereas the open-surface ST meron shows the characteristic X-shaped structure of free-space STWPs (Fig. 1c)30,47. To clearly visualize the spatiotemporal structure of the polarization texture in physical space, we plot the Stokes vector n(x, y = 0, z = 0; τ) in panel (iv), and the projections nx, ny, and nz in panels (v–vii) in the 2D space-time plane (x, τ). These plots reveal a swerve of the Stokes vector in the ST meron on a spatial scale smaller than the beam size, and on a shorter temporal scale than the pulse width, corresponding to the sub-wavelength spatial features of 2D skyrmions in evanescent fields22.

Experimental setup

The key to successfully synthesizing ST merons in momentum-energy space is twofold: sculpting a spectral surface \({{{\mathcal{S}}}}({k}_{x},{k}_{y},\Omega )\) through introducing a space-time coupling Ω(kr) into a pulsed optical field, and exercising high efficiency, point-by-point control over the polarization profile on this spectral surface. This task is particularly challenging in the case of a closed spectral surface. Our strategy for synthesizing ST merons from a generic optical pulse follows the four-stage scheme illustrated in Fig. 2a, comprising: (1) spectral analysis; (2) spectral transformation; (3) coordinate transformation; and (4) spin-texture implementation. To construct a prescribed spectral surface, the first step is to spatially resolve the incoming spectrum (spectral analysis). At this point, the field is endowed with linear spatial chirp x1(Ω), whereby the frequencies are arranged in a fixed sequence along the x1 axis (inset I). Realization of a prescribed spectral surface (such as that in Fig. 1b) requires arranging the frequencies in a particular sequence x1(Ω) → x2(Ω) (spectral transformation). Moreover, achieving double-branched open or closed spectral surfaces (Fig. 1c, d) necessitates a two-to-one spectral mapping  ±x1 → x2, thereby re-positioning two spectral lines at two distinct locations at the input to one location at the output, which is in contrast to previous realizations of optical conformal mappings that have all been one-to-one. The result is two precisely overlapped spatially resolved spectra with opposite chirp rates x2(∣Ω∣) that were initially contiguous (inset II). The last step for constructing the spectral surface \({{{\mathcal{S}}}}({k}_{x},{k}_{y},\Omega )\) is the coordinate transformation that maps the rectilinear chirp x2(∣Ω∣) into a radial chirp r(∣Ω∣); i.e., lines corresponding to different wavelengths at the input are converted into circles at the output plane (inset III). Finally, imprinting the meron polarization texture onto the radially resolved spectrum generates the ST meron in momentum-energy space (inset IV).

Fig. 2: Schematic of the experimental setup to synthesize and characterize ST merons.
figure 2

a Evolution of the field structure through four stages of the ST meron synthesis system. b Experimental setup for synthesizing and characterizing ST merons. In the first stage, the spectral components of an incoming ultrafast pulse are spatially separated via a pair of chirped volume Bragg gratings (CBGs) to introduce a linear spatial chirp x1(Ω) (inset I in a). In the second stage, a two-to-one spectral transformation ∣x1∣ → x2 implemented via a pair of spatial light modulators (SLMs) maps a pair of spectral lines at the transverse positions  ± x1 to the same transverse position x2, producing two spatially overlapping spectra x2(∣Ω∣) (inset II in b). A conformal coordinate transformation stage (implemented by a pair of phase plates PP1 and PP2) transforms the linear chirp into a radial chirp r(∣Ω∣) (inset III in a). A birefringent metasurface then imparts the target Stokes vector n(r(Ω)) to the radially spread spectrum (inset IV in a). The spatiotemporal structure of the ST meron is characterized in the spectral domain (after the 4f-system comprising lenses L1 and L2) via spectral Stokes polarimetry, and in real space (after the Fourier-transforming lens L3) by performing spatiotemporally resolved Stokes polarimetry. c Surface profilometry micrographs of the central part of the phase plates (PP1 and PP2). d Scanning electron microscope (SEM) micrographs of the birefringent dielectric metasurface at different spatial scales. HWP half-wave plate, QWP quarter-wave plate, PP phase plate, CCD charge-coupled device, LP linear polarizer, BS beam splitter.

Full size image

The setup for synthesizing ST merons from a generic optical pulse is depicted in Fig. 2b. Starting with linearly polarized pulses from a mode-locked Ti:Sapphire laser of width 100 fs, central wavelength λo ≈800 nm, bandwidth Δλ ≈10 nm, and beam width  ≈3 mm, the spectrum is spatially resolved (spectral analysis) via a pair of chirped volume Bragg gratings (CBGs)48. The first CBG spatially spreads the spectrum (spatial chirp) of the obliquely incident pulse, but simultaneously stretches the pulse in time (temporal chirp). A second identical but reversed-orientation CBG eliminates the temporal chirp while doubling the spatial chirp (see Methods)33.

The second stage comprises a pair of spatial light modulators (SLMs) that impart two phase distributions to implement an afocal conformal spatial transformation from the input plane x1 to the output plane x2 = f(x1)49,50. Because the spectrum is spatially resolved at its input plane x1(Ω), such a spatial transformation corresponds to a spectral transformation. This mapping modifies three aspects of the resolved spectrum. First, it pre-compensates for unwanted scaling that occurs in a subsequent stage (coordinate transformation). Second, it enables the realization of any prescribed spectral structure in real time by tuning the transformation function f(x1). Third, it allows us to implement a two-to-one spectral mapping x2(∣Ω∣), thus producing the surfaces in Fig. 1c, d. To perform this mapping, two phase distributions are concatenated on the first SLM to map the two halves of the input field in the input plane onto the same spatial domain in the output plane f(∣x1∣), and the two phase patterns at the output plane are interleaved on the second SLM (Supplementary Note II.B). Consequently, each position in the output plane is now associated with two wavelengths, i.e., x2(Ω) = x2(−Ω), whereas each position in the input plane was associated with one wavelength x1(Ω). This is a key attribute needed for constructing two-branched spectral surfaces in momentum-energy space.

In the third stage (coordinate transformation), a pair of phase plates implements another conformal mapping in the form of a log-polar coordinate transformation that maps each vertical line at its input plane into a circle at its output49,51. Restricting the implementation of such a coordinate transformation to two phase plates (rather than three or more) necessitates exponentiating the radial coordinate at the output plane49, which is pre-compensated by introducing the logarithmic scaling in the preceding spectral transformation stage, as discussed above. The conjunction of spectral and spatial transformations produces two spatially overlapping spectra that are spread radially with oppositely signed radial chirps r(∣Ω∣); see Supplementary Note II.C. Success in producing closed spectral surfaces in momentum-energy space is hindered by an intrinsic feature of the log-polar coordinate transformation; namely, a singularity at the center of the second phase distribution that leads to a null at the center of the spatiotemporal spectrum at kr = 0. Minimizing the singularity region while remaining in the paraxial regime necessitates fabricating large-area phase plates (14 × 14 mm2 here), which are produced using an analog photolithographic process52 (Fig. 2c and Supplementary Note II.C).

Lastly, realizing the meron polarization texture requires a wavefront shaping platform that imparts a point-by-point birefringent response. Dielectric metasurfaces are an ideal candidate for this task by virtue of their sub-wavelength resolution, compact footprint, and highly efficient polarization-dependent modulation of the phase and amplitude at each point in an optical field by utilizing form birefringence, while operating away from resonances to mitigate errors arising from fabrication inaccuracies53,54,55. We introduce the metasurface at this point in the synthesis procedure to impart to the incident linearly polarized, spatially resolved double-spectrum a spatially varying polarization profile corresponding to the polarization texture of a meron. The large area of the phase plates used in the coordinate transformation stage necessitates, in turn, fabricating a record-size metasurface comprising  ≈ 109 unit cells of 520 × 520 nm2 area each, containing an 800-nm-tall nanofin of TiO2 on a SiO2 substrate. The geometry of each meta-atom in the metasurface is tuned to achieve form birefringence (Fig. 2d). We adopt a phase-retrieval-like algorithm53,54,56,57 to realize the requisite far-field complex amplitude profiles for two orthogonal polarization components58, which yields the requisite parameters of each unit cell. The metasurface was produced via standard planar fabrication processes (see Methods), and the measured spatially resolved Stokes parameters confirm that it imparts the target polarization texture (Supplementary Fig. S11). Finally, a Fourier-transforming lens converts this double-valued spatially resolved spectrum endowed with polarization texture from momentum-energy space (kx, ky, ω) to physical space spanned by (x, y, z; τ).

Measurement results

We carried out the measurements for the two ST merons in Fig. 1c, d: the open-surface ST meron with a spatiotemporal spectrum comprising oppositely oriented paraboloids of revolution (Fig. 3), and the closed-surface ST meron with the spectrum that takes the shape of a spinning-top (Fig. 4). Switching between these two spectral surfaces and modifying their parameters requires only changing the SLM phase distributions in the spectral transformation stage.

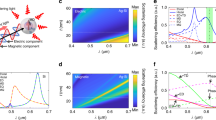
Fig. 3: Characterizing an ST meron whose polarization distribution is imprinted on a two-sheet paraboloid spectral surface.
figure 3

a Measured (top row) and calculated (bottom row) spectral Stokes parameters s(kx, ky) in (kx, ky)-space (integrated over all temporal frequencies ω). b A plot of the Stokes vector distribution (arrows) reconstructed from the measurements in (a), overlaid with the measured spectral intensity profile I(kx, ky) measurements (colormap). c Cross-sectional plots of b at different iso-frequency planes corresponding to λ = 795.95, 795.8, and 795.65 nm. d Measured Stokes vector n(kx, ky, λ) (arrows) plotted in the 3D spatiotemporal spectral domain (momentum-energy space), plotted over the ST spectral surface overlaid with the measured spectral intensity profile I(kx, ky). e Spatiotemporal Stokes parameters (s0, s1, s2, s3) at a fixed axial plane z = 0, where s0 corresponds to the total intensity. The panels are plotted in the (x, τ) plane corresponding to y = 0. The first row presents the measurements and the second row the corresponding theoretical predictions. In d the measured temporal bandwidth is Δλ ≈0.8 nm, and the spatial bandwidth is Δkr ≈0.18 rad/mm; in e the measured pulse width at the beam center is Δτ ≈6 ps, and the beam size at the pulse center is Δx ≈56 μm.

Full size image
Fig. 4: Characterization of an ST meron whose polarization texture is imprinted on a spinning-top spectral surface.
figure 4

a Measured (top row) and calculated (bottom row) spectral Stokes parameters s(kx, ky) in (kx, ky)-space. b A plot of the Stokes vector (arrows) reconstructed from the measurements in a, overlaid with the measured spectral intensity profile I(kx, ky) measurements (colormap). c Cross-sectional plots of b at different iso-frequency planes corresponding to λ = 795.95, 795.8, and 795.65 nm. d Measured Stokes vector n(kx, ky, λ) (arrows) plotted in the 3D spatiotemporal spectral domain (momentum-energy space), plotted over the ST spectral surface overlaid with the measured spectral intensity profile I(kx, ky). e Spatiotemporal Stokes parameters (s0, s1, s2, s3) at a fixed axial plane z = 0, where s0 corresponds to the total intensity. The panels are plotted in the (x, τ) plane corresponding to y = 0. The first row presents the measurements and the second row the corresponding theoretical predictions. In d the measured temporal bandwidth is Δλ ≈ 0.8 nm, and the spatial bandwidth is Δkr ≈0.17 rad/mm; in e the measured pulse width at the beam center is Δτ ≈6.6 ps, and the beam size at the pulse center is Δx ≈63 μm.

Full size image

We first characterize the polarization texture of ST merons in momentum space (kx, ky) by spatially resolved Stokes polarimetry carried out before the Fourier-transforming lens L3 in Fig. 2b, which reveals the momentum-space Stokes parameters si(kx, ky), i = 1, 2, 3 (Figs. 3a, 4a). From these measurements, we construct the polarization distribution n(kx, ky) for two ST merons (arrows in Figs. 3b, 4b) and plot them overlaying the measured spectral intensity I(kx, ky) (colormap in Figs. 3b, 4b). From these measurements, we extract Skyrmion numbers of N = 0.41 and N = 0.42 for the open- and closed-surface ST merons, respectively, which are close to the target value of N = 0.416 (see Supplementary Note III.C). An additional measurement of the correlation between the radial wave number \({k}_{r}\,=\,\sqrt{{k}_{x}^{2}+{k}_{y}^{2}}\) and the temporal frequency ω allows us to isolate the wavelength dependence of these Stokes parameters (Figs. 3c, 4c), thereby enabling the reconstruction of the ST meron polarization structure over the entire spectral surface (Figs. 3d, 4d); see Supplementary Note III.

In addition, we have characterized the polarization texture of the ST merons in physical space by measuring the spatiotemporally resolved Stokes parameters after the Fourier-transforming lens L3 via linear interferometry (Fig. 2b). The ST meron synthesis setup is placed in one arm of a Mach-Zehnder interferometer, and the initial 100-fs pulses are employed as a reference that traverses an optical delay line τ placed in the other interferometer arm. The visibility of the spatially resolved interference fringes recorded by a camera placed in the common path helps reconstruct the spatiotemporal intensity profile of the ST meron at a fixed relative delay τ40. Sweeping the delay line τ thus yields the full spatiotemporally resolved intensity profile I(x, y, z; τ) at the observation plane z = 0 (Figs. 3e, 4e, s0(x; τ)). The visibility of the interference fringes is maximized only after projecting the combined light fields onto one polarization state. Therefore, by repeating the procedure for different polarization components, we retrieve the spatiotemporally resolved Stokes parameters sj(x, y, z = 0; τ) for the ST merons, j = 1, 2, 3. (Figs. 3e, 4e). We plot the 2D intensity profiles and the Stokes parameters in the (x, τ)-plane corresponding to y = 0 for clarity, as we have done in Fig. 1c, d, without loss of crucial information. These measurements are in good agreement with the theoretical predictions plotted in Figs. 3e, 4e (second row), corresponding to s1, s2, and s3. The measured spatiotemporal evolution of polarization texture is observed within a localized region of  ≈ 6 ps temporal width and  ≈60 μm transverse spatial width. It is clear that ST merons with an identical topological polarization structure in momentum-energy space (produced by the metasurface) can be endowed with distinct spatiotemporal polarization configurations in physical space by virtue of the modified spectral surface (Figs. 3d, 4d). This suggests that ST merons may enable on-demand modulation of the spatial distribution of Stokes vector at ultrafast speeds within a localized transverse space, which may be useful for optical sensing and data storage applications45. Note that the spatiotemporal profile of the open-surface ST meron is X-shaped, as it is characteristic of STWPs in free space (Fig. 3e), and that of the closed-surface ST meron is circularly symmetric with respect to space and time, which is characteristic of closed spatiotemporal spectral supports (Fig. 4e), as recently verified for the restricted-dimensional case of light sheets37.

Discussion

We have synthesized optical ST merons in which the polarization texture is imprinted on open and closed 2D spatiotemporal spectral surfaces embedded in the 3D momentum-energy space of a pulsed optical beam, and have observed the associated 3D polarization texture in space-time. The experimental setup presented enables synthesizing ST merons with open and closed spectral surfaces with high efficiency and dynamic tunability, which is yet to be achieved via nonlocal or periodic structures32,59. Our work paves the way for a new class of ultrafast photonic quasiparticles with rich nanoscale topology that can be exploited in sensing, microscopy, secure information transfer, and light-matter interactions. This work also raises new questions and suggests avenues for further development. First, by providing independent control over the polarization texture associated with the two branches of the spectral surface (which spatially overlap after the spectral transformation stage), other topological quasiparticles besides merons can be readily produced. Introducing the polarization texture at the spectral transformation stage (Fig. 2b), via polarization-insensitive SLMs or phase plates in lieu of polarization-sensitive SLMs, provides access to the entire gamut of polarization textures. Second, further pushing the limits of optical conformal mappings in momentum-energy space or exploiting skyrmion-conversion devices60 may yield more complex spectral surfaces on which the polarization texture is implemented. Of special interest are spectral surfaces that are themselves endowed with non-trivial topological structure, such as tori or nested tori, which can thus give rise to space-time hopfions28,61 and Shankar’s skyrmions19. Third, our methodology can be directly extended to add orbital angular momentum (OAM) to each wavelength, sub-band, or the entire spectrum of the ST meron, which enables the exploration of topological spin-orbit coupling62,63 and the investigation of recently discovered effects, such as optical self-torque64 and time-varying OAM65,66, in the context of optical skyrmions. Fourth, the versatility of optically synthesizing 3D polarization texture may be the basis for transferring this polarization texture from light to matter44,67, thereby exciting topological quasi-particle structures in material systems; for example, by laser-induced magnetization68 for next-generation memory devices and spintronics69. This requires examining the synthesis of the polarization texture directly in 3D physical space rather than momentum-energy space. Fifth, the optical ST merons demonstrated here may potentially be used to excite propagating surface plasmon-polariton waves endowed with skyrmionic texture70, which enables field confinement in the deep sub-wavelength regime, and may enable ultrafast spontaneous emission and few-molecule strong coupling, or give rise to new phenomena such as multiphoton spontaneous emission and forbidden transitions44. Moreover, precise control over the 3D polarization configuration of an optical wave packet has a direct influence on the nonlinear optical effect71.

Additionally, the ST merons developed here raise the prospect of potential coupling to optical fibers and waveguides72. In this respect, closed spectral surfaces in momentum-energy space offer an advantage because they always result in pulsed beams that experience effective normal group-velocity dispersion in free space37. Consequently, such wave packets are dispersion-free in optical fibers in the telecommunications window where the group-velocity dispersion is anomalous. Finally, considering recent demonstrations of using space-time coupled fields for speckle-resistance73 and self-healing after an obstruction35, it is intriguing to determine the degree of topological resilience of optical ST merons against external perturbations in complex media, which has not been conclusively studied yet. Such topological protection against scattering, surface defects, and perturbations is crucial for using optical 3D ST topological quasiparticles as carriers of information in optical communications and beyond.

Methods

Spectral analysis via a chirped Bragg grating (CBG)

We spatially resolve the spectrum by making use of a chirped volume Bragg grating (CBG) whose grating period varies longitudinally. When an optical pulse is incident onto the CBG, each wavelength reflects from a different depth within it, where the Bragg condition is met. Therefore, when the field is incident normally onto the CBG, a group delay is introduced between the different temporal frequencies (temporal chirp), thus yielding a stretched pulse. This property of CBGs is widely used for pulse stretching and compression in high-power chirped pulse amplification systems in light of the high damage threshold, high efficiency, and potential for introducing large temporal chirps. A lesser-known property of CBGs is their ability to introduce a spatial chirp—resolving the spectrum spatially—along with a temporal chirp when the pulse is incident obliquely on a conventional CBG, or incident normally on a so-called rotated CBG (r-CBG) in which the Bragg structure is rotated with respect to the input facet. For our purpose, it is crucial to remove the temporal chirp while retaining the spatial chirp. This is achieved by directing the field emerging from the CBG to an identical CBG placed in a reversed geometry with respect to the first; see Supplementary Note II.A and Supplementary Fig. S3. In our experiment, we made use of a CBG (OptiGrate L1-021) with central Bragg period Λo = 270 nm, spectral chirp rate β = −30 pm/mm, average refractive index of n ≈1.5, and length L = 34 mm. The input beam is incident at an angle ϕ ≈16∘ with respect to the normal to the CBG entrance surface. To eliminate the temporal chirp, we route the output field to the opposite side of the same CBG (rather than using a second CBG). We thus obtain a field in the form of a spatially resolved spectrum with a flat-phase wavefront.

Fabrication of the large-area birefringent metasurface

The birefringent metasurface of 14 × 14 mm2 surface area exploited here represents the largest metasurface for shaping vectorial structured light to date. Such a device was fabricated using a process reliant on electron beam lithography and atomic layer deposition, as shown in Supplementary Fig. S9. The procedure is as follows: a fused silica substrate is first spin-coated with a positive tone electron beam resist (ZEP520A, Zeon SMI) that ultimately defines the height of the nanofins (800 nm). After baking the resist, the desired pillar patterns were written by exposing the resist using electron beam lithography (with an accelerating voltage of 150 kV), then developed in O-Xylene for 60 s. The developed pattern defines the geometry of the individual nanopillars. Afterward, TiO2 was deposited via the atomic layer deposition process (ALD) to conformally fill the developed pattern. The excess layer of TiO2 on top of the device was etched away using reactive ion etching to the original height of the resist. Finally, the resist was removed using a downstream ashing (oxygen radicals) process, leaving the individual TiO2 nanopillars surrounded by air. More details on the design and characterization of the birefringent metasurface are given in Supplementary Note II.D.