Introduction

Strong interactions between single photons enable numerous applications in quantum information processing and simulations1. While photons in a vacuum do not interact with each other, when they are confined in nonlinear optical media, the light–matter interaction results in an effective photon–photon interaction2,3. However, the nonlinearity of conventional materials is negligibly weak at the single-photon power level, making realizing strong nonlinear coupling between single photons extremely hard1.

So far, important nonlinear optical phenomena like second harmonic generation (SHG) or down-conversion (DC) occur only statistically and in the presence of many photons, so a more or less small fraction of photons undergo fusion or fission process. Taking advantage of the resonant interaction between cavity photons and atoms in cavity QED4, using electromagnetically induced transparency5, or collective effects in atomic ensembles6, and applying high-power stimulating fields7 are the common ways to circumvent this difficulty and to bring photon–photon interactions close to the quantum limit. However, an experimental observation of the strong coupling between different photon-number states1,8 in the absence of control fields with many photons, a cornerstone of quantum many-body nonlinear optics, is still elusive.

The development of superconducting quantum circuits (e.g., refs. 9,10,11,12,13,14) brings in new possibilities to tackle this problem. Josephson-junction (JJ)-based artificial atoms have a large dipole moment (not limited by the fine structure constant), which, combined with the small mode volume of superconducting coplanar resonators, allows the very large photon–artificial-atom interactions15,16,17,18,19. The largest reported single-photon–single-qubit interactions have entered the ultrastrong and even deep strong coupling regimes20,21,22,23,24,25,26,27,28,29,30,31,32,33. This remarkable property makes Josephson artificial atoms an ideal effective medium to realize strong nonlinear coupling between single photons34,35,36,37,38,39.

Here, we propose and demonstrate the resonant strong coupling of a two-photon state with a one-photon state in a circuit-QED multimode photonic device. In this system, the ultrastrong light–matter interaction breaks the excitation number conservation and enables higher-order processes via virtual photons, and an external flux bias breaks the parity conservation27,34,40. The combined effect of the two enables the strong one–two-photon coupling.

This strong photon-photon interaction induced by the ultrastrong coupling with an off-resonant artificial atom could also be achieved in very different systems and spectral ranges. The key point is to achieve the ultrastrong coupling regime with a single or a few quantum emitters. Strong and even ultrastrong coupling with few organic molecules coupled to a plasmonic nanocavity have been experimentally demonstrated41. Moreover, recently, ab initio calculations have shown that this regime can be achieved even with a single molecule42. Molecules with inversion symmetry would not prevent the coupling of photon states with the same parity (for example \(\vert 1\rangle \leftrightarrow \vert 3\rangle\)). The significant losses exhibited by plasmonic nanocavities should not prevent the observation of all-optical nonlinearities below the single-photon power level in these nanosystems.

Results

Ultrastrongly-coupled circuit-QED device

We realized a superconducting circuit constituted by a coplanar waveguide resonator embedded with an ultrastrongly-coupled flux qubit11,13,25,26,27,43 to implement a multimode system with its two-photon state of the lowest energy mode strongly coupled to the one-photon state of the second mode (see “Methods” for details). Throughout this work, we refer to the nth mode as the nλ/2-mode. The flux qubit is significantly detuned with respect to the resonant frequencies of the two lowest energy modes of the resonator (dispersive regime), and acts as an effective coupler34,35,36 between the n = 1 and n = 2 modes in the absence of any stimulating fields (Fig. 1c, d). The nonlinear coupling enables two photons in the n = 1 mode to coherently interact with a single-photon in the n = 2 mode, a hallmark of which is a spectrally resolved mode splitting. We experimentally observed this photon–photon quantum Rabi-like splitting, resulting from the spontaneous hybridization of one- and two-photon states. It indicates that our system operates in the single-photon strong nonlinear coupling regime1,8, without involving real qubit excitations or any external driving mechanism. As we show here, within this regime, the SHG and stimulated DC processes can occur even when the input signals provide photons to the resonator with mean photon numbers below one.

Fig. 1: Setup.
figure 1

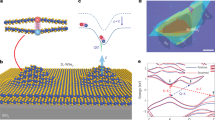
a Schematic of the device. A flux qubit embedded in a λ/2 coplanar waveguide resonator, working as a nonlinear coupler between two modes of the resonator. The dashed cyan lines represent the vacuum current distribution of the n = 1 (λ/2) and n = 2 (λ) modes of the resonator. κout = 3κin, where κin(out) is the loss rate from the input (output) port of the resonator. b Optical image of the flux qubit. c Effective coupling mechanism between the bare states \(\vert 2,0,g\rangle\) and \(\vert 0,1,g\rangle\) via virtual transitions involving intermediate states of the circuit-QED system. Here, the first two entries in the kets denote the number of photons in the first two modes of the resonator, and the third indicates the qubit state (\(\vert g\rangle\) is the ground state). d Scheme of the energy levels at the flux offset corresponding to the minimum gap of the \(\vert 2,0,g\rangle -\vert 0,1,g\rangle\) anticrossing, resulting in an effective coupling between these two states. A key feature of this configuration is that, at the minimum anticrossing gap, all the transitions shown by the arrows have comparable large efficiency, with transition matrix elements ∣X1,0∣ ≃ ∣X+,1∣ ≃ ∣X+,0∣ ~ 1 (see Supplementary Fig. 2). Moreover, the transition energy \({\tilde{\omega }}_{3}\) is almost equal to \(2{\tilde{\omega }}_{1}\), so that the second harmonic generation (with only two initial photons) and degenerate down conversion (with only one initial photon) can occur efficiently at sub-photon input levels.

Full size image

The Hamiltonian of the flux qubit can be written in the basis of two states with persistent currents ± Ip flowing in opposite directions around the qubit loop as (setting ℏ = 1) Hq = −(Δσx + εσz)/2, where σx,z are Pauli matrices, Δ and ε = 2IpδΦext are the tunnel splitting and the energy bias between the two basis states determined by an adjustable external flux bias δΦext. The parameters Δ/2π = 12.3 GHz and Ip = 60 nA are estimated by numerically diagonalizing the three-junction flux qubit Hamiltonian13,43. The resulting transition frequency between the two energy eigenstates \(\vert g\rangle\) and \(\vert e\rangle\) of the flux qubit is \({\omega }_{q}=\sqrt{{\Delta }^{2}+{\varepsilon }^{2}}\). A schematic of the device and the optical image of the flux qubit are shown in Fig. 1.

For the flux qubit ultrastrongly-coupled to the resonantor, the system can be described by a generalized two-mode quantum Rabi Hamiltonian16

$${H}_{s}={H}_{q}+{\sum}_{n=1,2}\left[{\omega }_{n}{a}_{n}^{{{\dagger}} }{a}_{n}+{g}_{n}({a}_{n}^{{{\dagger}} }+{a}_{n}){\sigma }_{z}\right],$$
(1)

where ωn are the resonance frequencies of the n = 1, 2 modes of the resonator, \({a}_{n}^{{{\dagger}} }\) and an are the corresponding creation and annihilation operators, and g1,2 are the coupling strengths of the flux qubit with the n = 1, 2 modes of the resonator.

In Supplementary Fig. 2, we analyze the influence of higher-energy modes, showing that the two-mode approximation is valid. Owing to the inhomogeneous transmission line geometry due to the qubit presence (see Fig. 1b), the higher-mode frequency ω2 is not exactly twice the fundamental resonance frequency ω1. Moreover, because of the contribution of the inductance across the qubit loop (δΦext-dependent) to the total inductance of the resonator, the resonance frequencies ω1,2 of the resonator become V-shaped around the optimal point

$${\omega }_{1,2}(\delta {\Phi }_{{{{\rm{ext}}}}})={\omega }_{1,2}(0)/\sqrt{1-{\beta }_{1,2}\cos (\theta )| \delta {\Phi }_{{{{\rm{ext}}}}}| },$$
(2)

with \(\tan (\theta )=\Delta /\varepsilon\) and β1,2 being constants23. Hereafter, \({\tilde{\omega }}_{j}\) denotes the energy eigenvalues of the Hamiltonian in Eq. (1) with respect to the ground state.

The coupling with the flux qubit determines an effective strong coupling between a single-photon state in mode 2 (\(\vert 0,1,g\rangle\)) and the two-photon state of mode 1 (\(\vert 2,0,g\rangle\)). As shown in Fig. 1c, such a coupling results from higher-order processes involving virtual intermediate transitions enabled by the ultrastrong qubit–resonator interaction29 and, unlike many processes in conventional nonlinear optics, it does not require any external drives. Such an effective interaction can be written as

$${V}_{{{{\rm{eff}}}}}={g}_{{{{\rm{eff}}}}}(\vert \widetilde{0,1}\rangle \langle \widetilde{2,0}\vert+\vert \widetilde{2,0}\rangle \langle \widetilde{0,1}\vert ),$$
(3)

where geff is the nonlinear coupling strength between the two modes (we use \(\vert \widetilde{n,m}\rangle\) to indicate photonic states dressed by the interaction with the qubit at higher excitation energy) and is approximately given by an analytic expression34

$${g}_{{{{\rm{eff}}}}}=\frac{3\sqrt{2}{g}_{1}^{2}{g}_{2}{\omega }_{q}^{2}\sin (2\theta )\cos (\theta )}{4{\omega }_{1}^{4}-5{\omega }_{1}^{2}{\omega }_{q}^{2}+{\omega }_{q}^{4}},$$
(4)

when ω2 ≃ 2ω1. The effective coupling goes to zero for θ = π/2, when the system displays parity symmetry. The effective Hamiltonian in Eq. (3) describes the simultaneous annihilation of two photons in the n = 1 mode and the creation of one-photon in the n = 2 mode as well as the inverse process. The coupling with the flux qubit introduces further Lamb shifts on the resonance frequencies of the resonator. The qubit population is very small at the one–two-photon avoided-level crossing and can be traced out from the dynamics (see Supplementary Fig. 4).

Transmission spectra

The device is placed inside a dilution refrigerator to be cooled down to a temperature of 20 mK. Considering the relevant frequencies (ω1/2π around 5.0 GHz, ω2/2π around 10.0 GHz), the system nearly stays in its ground state at such a low temperature. To see the coupling between the two modes of the resonator, we measured the transmission spectra by applying a weak probe tone with its frequency scanning across the lowest transition energies \({\tilde{\omega }}_{j}\) with j = 1, 3. The spectra are fitted with the numerically calculated excitation energies of the system Hamiltonian Hs. The parameters are determined to be

$${\omega }_{1}/2\pi=5.0/\sqrt{1-{\beta }_{1}\cos (\theta )| \delta {\Phi }_{{{{\rm{ext}}}}}| }\,{{{\rm{GHz}}}},$$
(5a)
$${\omega }_{2}/2\pi=9.7/\sqrt{1-{\beta }_{2}\cos (\theta )| \delta {\Phi }_{{{{\rm{ext}}}}}| }\,{{{\rm{GHz}}}},$$
(5b)
$${g}_{1}/2\pi=2.815\,{{{\rm{GHz}}}},$$
(5c)
$${g}_{2}/2\pi=2.180\,{{{\rm{GHz}}}},$$
(5d)

with \({\beta }_{1}=0.775\,{({\Phi }_{0})}^{-1}\) and \({\beta }_{2}=0.919\,{({\Phi }_{0})}^{-1}\). The coupling strengths

$${g}_{1}/{\omega }_{1}=0.563 > 0.1,$$
(6a)
$${g}_{2}/{\omega }_{2}=0.225 > 0.1$$
(6b)

at the optimal point (δΦext = 0) provide evidence our system is in the multimode ultrastrong coupling regime. Numerical estimates of coupling strengths from circuit quantization qualitatively agree with the fitted values above (see Supplementary Information). Parameters from the fit are used as input for density matrix calculations which are then compared with the measured spectra. Theoretical spectra throughout this work are obtained by using a generalized master equation44,45, where the interaction with the environment takes into account the hybridization of the subsystems due to the ultrastrong coupling (see “Methods” for details).

Figure 2 reports the measured (left) and calculated (right) transmission spectra versus the flux offset. The calculated spectra are proportional to the time derivative of the expectation value of the two-mode field momentum operator:

$$X=i({a}_{1}-{a}_{1}^{{{\dagger}} })+i\sqrt{{\omega }_{2}/{\omega }_{1}}({a}_{2}-{a}_{2}^{{{\dagger}} })$$
(7)

(see Supplemeantary Information for details). Figure 2a shows the lowest energy transition \({\tilde{\omega }}_{1}\) corresponding to the excitation of the state

$$\vert {E}_{1}\rangle \equiv \vert \widetilde{1,0}\rangle \simeq \vert 1,0,g\rangle .$$
(8)

Figure 2b shows the transitions at \({\tilde{\omega }}_{2}\) and \({\tilde{\omega }}_{3}\). When the two-photon resonance frequency of the n = 1 mode of the resonator gets across the single-photon resonance frequency of the n = 2 mode (ω2 ≃ 2ω1), a clear avoided crossing, induced by the effective interaction in Eq. (3), is observed in Fig. 2b, indicating that our system enters the single-photon strong nonlinear coupling regime8 geff > κtot, where κtot is the total loss rate of the resonator. The nonlinear coupling strength geff/2π extracted from the fit is 59 MHz (half the separation between the double peaks at the minimum splitting), which qualitatively agrees with the perturbative result given by Eq. (4) (47 MHz). While for flux offsets outside the two modes resonance condition, the system eigenstates are approximately \(\vert 2,0,g\rangle\) and \(\vert 0,1,g\rangle\); at the anticrossing they are in good approximation their symmetric and antisymmetric superpositions

$$\vert {\psi }_{\pm }\rangle=\vert 2,0,g\rangle \pm \vert 0,1,g\rangle .$$
(9)

Note that outside the avoided-level crossing in Fig. 2b, the spectral line corresponding to the excitation of the two-photon state \(\vert 2,0,g\rangle\) is poorly excited by the weak probe tone. Two-photon contributions get significantly excited only owing to their hybridization with one-photon states at the avoided crossing. The emission of photon pairs under very weak excitation is maximized in this region (see Supplementary Fig. 3). Theoretical calculations accurately reproduce all the spectra in Fig. 2b, thus confirming our interpretation of the data. A peculiar feature of this extreme quantum nonlinear regime is that linear spectra in Fig. 2b are able to evidence quantum nonlinear optical processes.

Fig. 2: Quantum Rabi-like splitting.
figure 2

Quantum Rabi-like splitting between a single-photon and a two-photon Fock state. a Measured and calculated transmission spectra of the one-photon line of the n = 1 mode of the resonator as a function of the flux offset. b Measured and calculated transmission spectra showing the excitation of both the two-photon state of the n = 1 mode and the one-photon state of the n = 2 mode of the resonator. An avoided-level crossing between these two lines is clearly visible. From the fitting, we obtain the Rabi frequency for the one–two-photon coupling geff/2π = 59 MHz, the loss rate due to the input–output ports (κin + κout)/2π = 2.6 MHz, the internal loss rate κint/2π = 10.4 MHz [total loss rate of the resonator κtot/2π = (κin + κout + κint)/2π = 13 MHz], the intrinsic loss rate of the qubit κq/2π = 200 MHz, and the pure dephasing rate of the qubit κq,dep/2π = 200 MHz (the last two have a very weak influence on the calculated spectra).

Full size image

Nonlinear optics below the single-photon power level

To further characterize the nature of the strong nonlinear coupling, we measured the SHG at the single-photon power level by applying a weak signal at ω and monitoring the SHG signal at 2ω. The result is shown in Fig. 3. As expected, the SHG signal shown in Fig. 3a is more intense near the minimum of the avoided-level crossing and for flux offsets where the system is double resonant: \({\tilde{\omega }}_{3}=2{\tilde{\omega }}_{1}\), as confirmed (despite some shift due to some small discrepancy in the fitted energy levels) by the theoretical calculations in Fig. 3b (see Supplementary Information for details). The efficiency

$$\eta \equiv {S}_{21}^{(2\omega )}/{S}_{21}^{(\omega )}$$
(10)

of the SHG signal, shown in Fig. 3a, is about 0.1 at the point where the SHG amplitude is maximum. Such efficiency is achieved with an input corresponding to only 0.25 photons into the resonator, clearly operating in the quantum limit. To the best of our knowledge, SHG in the true (without additional many-photon drives) quantum limit has never been experimentally observed until now46. A theoretical estimate (see Supplementary Fig. 3) shows that the efficiency can approach η = 0.3 for 1.5 input photons. The efficiency can be significantly improved by reducing the internal losses of the resonator and setting the system at the perfect feeding condition so that no output signal at ω is present47. Also, to the best of our knowledge, near-deterministic photon up/down conversion has so far been achieved predominantly using atomic level transitions48. Crucially, our approach has the potentiality to achieve near-deterministic pure photon up/down conversion without involving atomic transitions, thereby avoiding the associated losses.

Fig. 3: Second harmonic generation.
figure 3

a The amplitude of the SHG versus the external flux bias δΦext and the SHG frequency. The efficiency \(\eta \equiv {S}_{21}^{(2\omega )}/{S}_{21}^{(\omega )}\) of the SHG is about 0.1 at the point where the SHG amplitude is maximized (ω1/2π = 4.9 GHz and δΦext = −45 mΦ0), which qualitatively agrees with the theoretical result in Supplementary Fig. 2. b Theoretical calculation corresponding to the plot in (a). c The amplitude of the SHG versus the average photon number \({\overline{n}}_{1}\) in the resonator. The signal frequency applied at the n = 1 mode of the resonator is ω1/2π = 4.9 GHz (at δΦext = −45 mΦ0). The red solid curve is the theoretical fit. The average photon number in (c) is determined by contrasting the experimental data—plotting the maximum second harmonic generation (SHG) amplitude against input power—with the theoretical simulation outlined in Supplementary Eq. (35), as depicted in (c). The power applied in (a and b) corresponds to an average photon number \({\overline{n}}_{1}\simeq 0.25\) in the resonator.

Full size image

Figure 3c shows that the SHG amplitude is thresholdless and starts with a linear dependence on the mean value of input photons \({\bar{n}}_{1}\), while it tends to saturate for higher input powers. It can clearly be distinguished from the noise floor even for the mean number of input photons in the resonator \({\overline{n}}_{1}\) significantly below 1, which is a striking, unprecedented result, made possible via the photonic strong coupling regime shown in Fig. 2b. The mean number of input photons in the resonator is evaluated using a standard input–output relationship49 (see Supplementary Information for details). During the calibration of the photon number, the obtained fitted parameters allowed us to reproduce in very good agreement not only the data in Fig. 3c but also the spectra in Fig. 2 and the interference fringes in Fig. 4. Hence, although there might be a slight deviation from the true photon number, we expect it to be less than 10% of our fitted values. The hybridization between one- and two-photon states at the minimum of the avoided-level crossing gives rise to matrix elements X+,1, X+,0, X1,0 all of the order of unity, which enable observation of the SHG well below the single-photon power level.

Fig. 4: Interference between two probe tones.
figure 4

a, c Gain of the transmitted amplitude of the signal field in the n = 1 (n = 2) mode of the resonator versus the average photon number \({\overline{n}}_{{{{\rm{2(1)}}}}}\) and the phase of the control field in the n = 2 (n = 1) mode of the resonator. The average photon numbers of the signal fields in the resonator’s n = 1 and n = 2 modes are about 0.25 and 0.13, respectively. The frequencies of the probe tones are ω/2π = 4.905 GHz and 2ω/2π (at δΦext = −46 mΦ0). b, d Theoretical calculations corresponding to the plots in (a, c). The gain is defined as the ratio between the output signal amplitude at ω (2ω) when a secondary signal is applied at 2ω (ω), and the output amplitude of the same signal at ω (2ω) in the absence of the secondary signal applied at 2ω (ω). The phase shifts in the experimental data in (a, c) are an artifact due to an electronic delay.

Full size image

A further direct consequence of the achieved photonic strong coupling is the observation of interference between a probe at ω (2ω) and a control tone at 2ω (ω) both at the single-photon power level, resulting in the amplification or suppression of the transmitted amplitude of probe signals50. The amplification and suppression are phase dependent, just as in the case of degenerate parametric amplifiers51,52. The difference is that a much stronger pump tone is not needed here, and we observe these interference phenomena at an incredibly low-power limit (average photon number in the resonator below one). The results are shown in Fig. 4. Changing the phase of the control tones, we can see that the transmitted amplitude of the signal at the n = 2 (n = 1) mode (signal field) is amplified or suppressed periodically with visibility approaching 1. It turns out that the visibility of the interference for the signal at 2ω becomes relevant for higher intensities of the control signal (at ω) (see Fig. 4c, d) with respect to what is observed for the signal at ω (see Fig. 4a, b). Conversely, to obtain a high visibility for interference at ω, it requires a larger probe signal at ω. This difference originates from the fact that the interference at 2ω requires the stimulated conversion of two photons of the control tone. On the contrary, the probe signal at ω receives two photons from the down conversion of photons at 2ω of the control tone. The observed tilting in the experimental data is attributed to a slight change in the phase of the signal when adjusting the output power. These two-tone interference data are well reproduced (except, of course, for the tilting) by numerical calculations based on the generalized master equations including a two-tone interaction term [see Supplementary Eq. (36)], shown in Fig. 4b, d.

We note that this work does not provide any experimental evidence of spontaneous DC. This is a direct consequence of our setup, which selects only coherent signals, with the phase determined by the input signal. This technique allows to filter thermal noise and to allow the detection of very small signals. Spontaneous down conversion is not a coherent signal and it is thus filtered out. However, Fig. 4a provides clear evidence of stimulated DC (phase-dependent amplification of the signal at ω in the presence of a tone at 2ω), which gives rise to a coherent signal that can be detected by our setup. A simple understanding of the phase sensitivity of the signal amplification at ω can be easily obtained considering the standard evolution equation for the linear parametric amplifier in the weak pump limit [see Supplementary Eq. (40)].

Discussion

We experimentally observed an unstimulated strong coupling between a single-photon and a two-photon Fock state. The observed single-photon strong nonlinear coupling is enabled by an embedded-in flux qubit, which, while remaining in its ground state, acts as an effective coupler between two modes of a superconducting coplanar waveguide resonator. The strong coupling between photon states of opposite parity is enabled by the spontaneous mixing of even- and odd-number photon states, which is a unique feature of the generalized quantum Rabi Hamiltonian in the ultrastrong coupling regime27,34.

The counterpart in time-resolved experiments of the quantum Rabi splitting reported here are quantum Rabi oscillations enabling the conversion of a single-photon into two photons and vice versa with a period TR = 2π/geff and with an efficiency that can potentially approach 100%34 (for geff significantly larger than the losses). In contrast to most conventional implementations of nonlinear optics, the regime demonstrated here can reach unit efficiency only using a minimal number of photons and without exciting atomic transitions, which introduce additional losses. For example, in many cases pure dephasing in superconducting artificial atoms is the main source of decoherence.

These results unlock a new regime for photons in quantum nonlinear optics1,8 (coherent interaction between photon multiplets), which has important implications in both fundamental research34 and applications53,54. Examples of direct applications include

  1. (i)

    the realization of deterministic quantum light (single-photon and photon pair) sources as in the cases of traditional spontaneous parametric down conversion but with an unprecedented efficiency (approaching 100%);

  2. (ii)

    an all-optical deterministic controlled-phase gate (\(\vert \widetilde{0,1}\rangle \leftrightarrow -\vert \widetilde{0,1}\rangle\), a geometric phase effect under a full Rabi oscillation (2TR), where the presence or the absence of a photon in mode 1 corresponds to the control qubit).

This two-photon quantum phase gate represents a key element for the realization of a still elusive universal nonlinear optical quantum computing53,54. These controlled quantum Rabi oscillations can be realized by using suitable flux offset pulses to tune the system in and out the minimum of the avoided-level crossing \(\vert \widetilde{0,1}\rangle \leftrightarrow \vert \widetilde{2,0}\rangle\).

Methods

Superconducting circuit device

Our device is a 3 mm × 10 mm chip fabricated on a single crystal sapphire substrate (see Supplementary Fig. 1b). The superconducting coplanar waveguide resonator is defined by patterning a niobium thin film using optical lithography. The flux qubit consists of two identical large JJs and a smaller JJ (with an area ratio α ≈ 0.5) in a loop geometry.

The qubit loop and its connection to the center conductor of the coplanar waveguide resonator are made by electron beam lithography and double-angle evaporation of aluminum. Placing the qubit loop near the antinode of the current distribution for the n = 2 mode of the resonator makes the qubit coupled to the n = 1 mode and the n = 2 mode of the resonator simultaneously (see Fig. 1a).

The values of the Josephson energy EJ/h = 173 GHz, the area ratio α ≈ 0.5 and EJ/EC ≈ 100 of the JJs in the qubit are optimized to ensure the flux qubit working as an effective nonlinear coupler, i.e., both far-away detuned and strongly coupled with the relevant modes of the resonator, and are used to numerically diagonalize the three-junction flux qubit Hamiltonian to estimate the values of Δ and Ip.

The device is coupled to the environment through two capacitors of different sizes (see Fig. 1). One of these input–output ports is used as an input port to excite the device with one or two coherent weak tones, while the other port is used to detect signals. In order to reduce the output through the input port, the size of the output capacitor has been chosen to be larger (≃ 1.7 times) than that of the input one. Notice that the loss rate associated to a capacitive port is proportional to the square of the corresponding capacitance.

Input–output and generalized master equation

The standard quantum optics approach to describe open quantum systems no longer holds in the case of ultrastrong coupling. To properly derive the time evolution of the system and the input–output relations, the interaction term between the system and the environment has to be expressed on the basis of the eigenstates of the system. Moreover, the field input–output relations include anharmonic operators. This problem can be circumvented by expressing the time evolution of the field operators in terms of the generalized master equation, rather than the nonlinear input–output relations (See Supplemeantary Information for details).