Introduction

The major seismic discoveries of the D″ discontinuity1,2,3,4,5, ultra-low velocity zones (ULVZs)6,7,8,9,10,11,12, and prominent low wave velocity anomalies beneath Africa and Pacific13,14,15,16,17,18 in the Earth’s lowermost mantle have facilitated a series of new understandings of dynamics, mineral physics, composition, geochemistry, and evolution history of the Earth19,20,21,22,23,24. As the dynamic processes may change morphological features and seismic properties in the lowermost mantle, studying temporal change of seismic structures in the region would have provided another direct insight on the deep Earth’s dynamics. Seismological efforts have been made in the search of temporal change of seismic properties near the core-mantle boundary (CMB)25,26,27. However, no temporal change of seismic properties was reported in the human time scale so far, possibly limited by availability of suitable seismic data.

Here we perform an extensive search of temporal change through the seismic data and report temporal changes of seismic data sampling the lowermost mantle between a pair of nearly co-located earthquakes occurring on 2000/07/07 and 2009/12/17. We infer temporal changes of seismic properties in the lowermost mantle based on waveform modeling of the seismic data and discuss implications of these discovered temporal changes of seismic properties to the dynamics and mineral physics in the lowermost mantle.

Results

We search possible seismic signal associated with temporal change of seismic structure in the Earth’s lowermost mantle through the seismic data of global earthquake doublets (Methods). An earthquake doublet is two earthquakes occurring at close locations (<1 km) but at different times. The relative seismic signal changes at a station between a doublet are only sensitive to the relative doublet event parameters and temporal change of seismic structure along the seismic ray paths between the occurring times of the doublet28. As the seismic effects of relative doublet event parameters can be accurately accounted for, doublet analysis has been an important tool for detecting temporal changes of seismic structures near the earthquake sources29,30 and in the Earth’s inner core31,32. We find no credible temporal change of seismic waves sampling the lowermost mantle in the seismic data of all identified doublets spanning from 1993 to 2023 (Methods), except in one doublet AI-0009 occurring on 2000/07/07 (event 2000) and 2009/12/17 (event 2009) beneath the Aleutian Islands (i.e., doublet AI-D7 in the Supplementary Data).

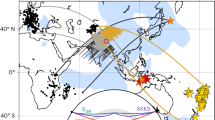
Evident temporal changes are observed between the doublet AI-0009 data of SKS and S-Scd-ScS phases at an epicentral distance of 94.9° recorded at seismic station IU.SDV in Santo Domingo, Venezuela (Fig. 1). SKS is a seismic wave traveling as a shear wave in the mantle and a compressional wave in the Earth’s outer core, while S-Scd-ScS phases are shear waves traveling through the lowermost mantle with S and Scd turning above and in the D″ region respectively and ScS reflected at the CMB (Fig. 1b). We illustrate those temporal changes by superimposing the seismic data between the doublet after corrections for the effect of relative doublet location and origin time. Any mismatch of relative arrival time and shape in those superimposed doublet waveforms reflects the effect of temporal change of seismic structure between the occurring times of the doublet. Superimposed SKS waveform pair recorded by IU.SDV exhibits evident differences in both waveform shape and travel time, with a broader wavelet in event 2009 than in event 2000 and the phase arriving 160 ms earlier in event 2009 than in event 2000 (left panel, Fig. 1c). Superimposed S-Scd-ScS waveform pair recorded by IU.SDV exhibits a misalignment of relative travel time in the radial component with the seismic signals in event 2009 changing from 80 ms earlier in the beginning portion of the wavelet to 30 ms earlier in the middle of the wavelet to no discernable change in the later portion of the wavelet. In contrast, no difference is observed in the transverse components of the doublet data in either waveform shape or travel time (right panel, Fig. 1c). These temporal changes of SKS and S-Scd-ScS phases between the doublet are consistently observed at the frequency bands of good data quality from 0.4 Hz to 2.0 Hz. No other discernible temporal changes of S-wave waveform and travel time are observed between the doublet that can be confidently attributed to temporal change of seismic structure in the lowermost mantle (Fig. 2, Supplementary Information).

Fig. 1: Observed temporal changes of seismic data sampling the Earth’s lowermost mantle between doublet AI-0009 at seismic station IU.SDV.
figure 1

a Superimposed IU.SDV waveforms between doublet AI-0009 (red for event 2000 and blue for event 2009) after the correction for the effect of the relative doublet location and origin time, with the radial and transverse components labeled as R comp. and T comp. respectively, and the temporally changing SKS and S-Scd-ScS phases noted. b Ray paths of SKS (left panel) and S-Scd-ScS (right panel) from doublet AI-0009 (star) to station IU.SDV (triangle), along with associated temporally changing ultra-low velocity zone (ULVZ; orange) and the lowermost mantle (D″; green). The inner core boundary and the core-mantle boundary are labeled as ICB and CMB, respectively. c Superimposed SKS and S-Scd-ScS waveforms in zoom-in time windows marked by dashed lines in panel a. Note the waveform and travel time changes of SKS phases and the travel time shift in the radial component of S-Scd-ScS phases but no travel time change in the transverse component. Waveforms are bandpass filtered from 0.4 Hz to 2.0 Hz.

Full size image
Fig. 2: Waveform alignments of S-wave phases of doublet AI-0009 at other seismic stations except IU.SDV.
figure 2

a Great-circle ray paths (gray lines) from doublet AI-0009 (star) to seismic stations (triangles labeled with station names; seismic stations from the CI network are marked collectively as “CI….” due to their close locations), with those sampling the lowermost 380 km of the mantle marked by thick lines (green for IU.SDV path and black for the other paths) and the SKS entry and exit points at the core-mantle boundary (CMB) marked by dots (orange for IU.SDV path and black for the other paths). The regions of detection and non-detection of ultra-low velocity zones (ULVZs) at the base of the CMB35 are shown as shaded and light blue patches, respectively. b Superimposed S-wave waveforms of doublet AI-0009 after corrections for the effect of relative doublet location and origin time, with the radial and transverse components marked on the left top as R comp. and T comp. respectively, and station names and epicentral distances marked on the left. Waveforms are bandpass filtered from 0.4 Hz to 2.0 Hz and are aligned along the theoretical travel times based on the Preliminary reference Earth model44 (PREM) (Time = 0 s). Because of the data quality, the waveforms with their station names marked with an asterisk are further filtered from 0.5 Hz to 2.0 Hz.

Full size image

The waveform changes observed in the IU.SDV SKS observations and the relative travel time difference observed in the radial S-Scd-ScS waveforms cannot be explained by the relative doublet location and origin time, as those relative differences of source parameters cannot generate different SKS waveform shapes between the events and a relative time difference in the radial components of S-Scd-ScS phases accompanying with no relative travel time difference in the transverse components of the waveforms between the doublet. The observed temporal changes of the seismic data cannot be explained by possible differences of source focal mechanisms between the doublet, as no waveform shape changes are observed in S-Scd-ScS phases. Because SKS and S-Scd-ScS phases have almost identical take-off angles from the seismic sources, any focal mechanism difference between the doublet would generate similar changes of waveshapes between the two phases. Synthetic tests also indicate all possible source mechanisms within the uncertainties of the GCMT solution produce little waveform and travel time differences of the seismic phases between the doublet, further excluding the earthquake sources as the origin of the observed SKS and S-Scd-ScS changes between the doublet (Supplementary Fig. 1). The observed temporal travel time changes of the IU.SDV SKS and S-Scd-ScS phases cannot be caused by clock errors of the station, as no travel time differences are observed in other seismic phases of the station, including the subsequent pulses after SKS arrivals (the phases in a time window of 1435–1441 s on the left panel in Fig. 1c) and the transverse S-Scd-ScS phases. And, the observed temporal changes of IU.SDV observations are not the result of seismic noise. Synthetic analysis shows that random noises in the seismic data at station IU.SDV would generate negligible differences in the waveform and relative travel time of both SKS and radial S-Scd-ScS phases between the doublet (Supplementary Fig. 2). We conclude that the observed IU.SDV waveform and travel time differences between the doublet are caused by temporal changes of seismic structure between the occurring times of the doublet.

The observed IU.SDV temporal change of seismic data cannot be explained by a change of shallow seismic structure between the doublet. Because S-Scd-ScS phases have similar take-off angles from the earthquake source and similar incident angles to the station, a change of shallow structure beneath the station would cause a nearly constant travel time shift in the seismic signals of S-Scd-ScS phases, different from the observed varying arrival time changes from 80 ms in the beginning portion of the wavelet to no discernable change in the later portion of the wavelet. Changes of shallow structure also cannot explain the travel time shift of SKS, as the subsequent energy pulse after SKS exhibits no temporal change between the doublet.

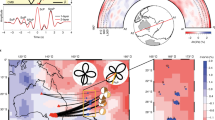
The temporal changes of SKS travel time and waveform at IU.SDV are the result of structural changes in the lowermost mantle between the occurring times of the doublet. In the entry point of the IU.SDV SKS phases at the CMB, several studies have suggested possible presence of ULVZs in the lowermost mantle33,34,35,36. ULVZs are small-scale structures of tens of kilometers high and hundreds to thousands of kilometers wide with very low seismic velocities. ULVZs are proposed to be the regions of partial melt9,34,37 and are the most likely candidate structures in the lowermost mantle that could experience seismically detectable changes in a decadal time scale. We thus suggest a temporal change of a ULVZ near the SKS entry point at the CMB for the explanation of the observed temporal changes of SKS phases in IU.SDV. We should point out that a change of a ULVZ structure near the SKS exit point at the CMB could explain the seismic data equally well, and the modeling results would equally apply to a changing ULVZ near the SKS exit point at the CMB. Because the shape of ULVZ cannot be well constrained with the limited seismic data, we test ULVZs with a simple edge and explore how the change of the simple edge explains the observed temporal changes of SKS waveform and travel time. Our results would depend on the non-uniqueness of the ULVZ geometry we assume, but modeling with this simple geometry allows us to explore the first-order feature and length scale of morphological change of the ULVZ, as those parameters are not significantly dependent on the actual geometry of the ULVZ. Detailed synthetic modeling (Methods) indicates that both a ULVZ with its edge shrinking and a ULVZ with its edge laterally moving could explain the seismic data (Fig. 3a). The length scale of lateral change of ULVZ edge is 16–45 km for a shrinking ULVZ and is 21–27 km for a moving ULVZ. The shrinking ULVZ model could explain the seismic observations slightly better than the moving ULVZ model, but both types of models are acceptable in their synthetic fitting to the doublet observations (Fig. 3a, Supplementary Fig. 3). ULVZ shrinking and moving in both sides of the SKS CMB entry point could explain the seismic data equally well.

Fig. 3: Changing ultra-low velocity zone (ULVZ) and lowermost mantle anisotropy inferred from the observed temporal changes in SKS and S-Scd-ScS phases at IU.SDV.
figure 3

a (Left) Two types of changing ULVZ along the core-mantle boundary (CMB) that explain SKS data: I. shrinking ULVZs (top), and II. moving ULVZs (bottom). An approximate SKS ray path is marked by green arrow. ULVZ edges change from red lines at the occurring time of the earlier event (2000) to blue lines at the occurring time of the later event (2009) between doublet AI-0009, with amounts of lateral change labeled. (Right) Superimposed SKS waveforms of doublet AI-0009, with the top pair for the observations (labeled as Obs.) and the two bottom pairs for synthetics of the two types of ULVZ changing models on the left panel (labeled as Syn. I and Syn. II; synthetics of the two models in each type are indistinguishable and are only plotted for the left model of each type). b (Left) Velocity model of a changing D″ that explains S-Scd-ScS data: SV-wave velocities change with respect to (w.r.t) the Preliminary reference Earth model44 (PREM) (labeled as \(\delta {V}_{{SV}}\)) from red line at the occurring time of event 2000 to blue line at the occurring time of event 2009 between doublet AI-0009, with amounts of SV-wave velocity change labeled. (Right) Superimposed S-Scd-ScS waveforms of doublet AI-0009 (red for event 2000 and blue for event 2009), with the top panel for radial components (labeled as R comp.) and the bottom panel for transverse components (labeled as T comp.). In each panel, the top pair show the observations between the doublet (labeled as Obs.) and the bottom pair shows synthetics of the changing D″ anisotropy shown on the left panel (labeled as Syn.). The radial synthetics are calculated based on the red (for event 2000) and blue (for event 2009) models on the left panel, respectively, while the transverse synthetics are calculated based on the red model on the left panel for both events.

Full size image

The observed temporal change in the radial components of S-Scd-ScS waveforms at station IU.SDV is the result of temporal change of SV-wave velocity in the D″ region between the occurring times of the doublet. As no discernable changes are observed in the transverse components of the S-Scd-ScS phases, the SH-wave velocity should have no changes between the doublet. We thus search the best-fit changed SV-wave velocity model in the lowermost mantle that would explain the observed temporal change in the radial components of the S-Scd-ScS waveforms. Note that the observed early arrival of the SV energy in event 2009 in the beginning portion of the S-Scd-ScS waveforms would require an SV-wave velocity increase in some depths above the CMB (i.e., the top portion of the D″ region), while the no temporal change of ScS phase in the latter portion of the S-Scd-ScS waveforms would require a decrease of SV-wave velocity close to the CMB (i.e., the bottom portion of the D″ region) to offset the effects of the SV-wave velocity increase required by the S-Scd data in the top portion of the D″ region. Detailed synthetic modeling (Methods) shows that the observed temporal change of the radial components of the S-Scd-ScS waveforms can be best explained by an SV-wave velocity change from an increase of 0.10%–0.13% at the D″ discontinuity to 0% at the middle depth of the D″ layer to a decrease of 0.13%–0.18% at the base of the mantle between the occurring times of the doublet (Fig. 3b and Supplementary Fig. 4).

Discussion

The inferred 10s km scales of ULVZ structural change in a decadal time scale indicate two possible geodynamical processes associated with ULVZs in the lowermost mantle. (1) ULVZs possess a very low viscosity and are deformed by the background mantle flow. In this scenario, ULVZs likely have an origin of partial melt, as only a partially molten material would have such a low viscosity to be deformed in such length scales in a decadal time scale. (2) ULVZs are moved by a vigorous localized convection flow in the lowermost mantle. In this scenario, the inferred ~20 km movement of ULVZ in a decadal time scale would suggest that localized mantle flows are orders of magnitude more intense than those in the current generation of geodynamical models23,36.

The inferred change of SV-wave velocity in accompany with the requirement of no SH-wave velocity change in the D″ region suggests that the temporal change occurs on the seismic anisotropy in the region38,39,40. Synthetic tests further confirm that the pair of radial and transverse doublet observations cannot be explained by a change of any isotropic velocity structures (Supplementary Fig. 5). The inferred opposite directions of anisotropy change in the top and lower portions of the D″ region indicate a separate layer circulation in the D″ region. Our results reveal a previously unrecognized flow pattern in the Earth’s lowermost mantle, with localized convective flows deforming or moving ULVZs by tens of kilometers in a decadal time scale and opposite flows circulating in the top and bottom portions of the D″ region in a separate D″ circulation layer (Fig. 4).

Fig. 4: Cartoon illustration of dynamic processes responsible for the inferred decadal changes of seismic structure in the Earth’s lowermost mantle.
figure 4

In a decadal time scale, the ultra-low velocity zones (ULVZs) (yellow piles) are deformed or moved (from dashed red to solid blue) along the core-mantle boundary (CMB) by vigorous localized material flows (black arrows) in the lowermost mantle by tens of kilometers, and a separate layer circulation of opposite flows (green arrows) in the top and bottom portions of the D″ region changes alignments of anisotropic crystals in opposite directions and generates opposite changes of seismic shear wave anisotropy (marked by εSV−SH). Particle motions of SH and SV waves (changing from red to blue), increased/decreased SV-wave velocity, and unchanged SH-wave velocity are shown in the zoom-in panels.

Full size image

Our results call for a new generation of geodynamical and mineral physics models that would account for the discovered vigorous localized lowermost mantle flows related to the ULVZs and internal circulation in the D″ region. The inferred length scales of ULVZ morphological change would place constraints on the viscosity of the ULVZs and the localized mantle flow surrounding the ULVZs. With the inferred km/yr scale of ULVZ morphological change being 4–5 orders of magnitude larger than the cm/yr scale of flow velocity in the current geodynamical models of the Earth’s mantle, our results suggest that the viscosity in the interior or in the lowermost mantle surrounding the ULVZs is about 10−4–10−5 times lower than the values currently perceived in the possible solid materials in the region41. The inferred magnitude and pattern of D″ anisotropy changes would place constraints on the flow pattern, magnitude of deformation, and possible mineral components in the D″ region, as well as the interaction of the region with the rest of the mantle flow.

Methods

Searching temporal change of seismic data

Global doublets are searched in a two-step procedure8,14. In the first step, potential doublets are searched from earthquake pairs (magnitudes ≥ 4.5) that are located within 60 km based on the Preliminary Determination of Epicenters Bulletin (PDE) and have P-wave signal pairs of waveform cross-correlation coefficients (CC) ≥ 0.95 recorded by more than three stations of the Global Seismographic Network (GSN). In the second step, all potential doublets are relocated using a master event algorithm42, and only those with a separating distance ≤ 1.0 km are retained as doublets. The final doublet catalog includes 61 doublets and 62 clusters (multiple repeating earthquakes) spanning from 1993 to 2023 (Supplementary Data, Supplementary Fig. 6). We inspect waveform alignments of seismic phases at global seismic stations of all doublets and search potential temporal changes between the doublets. Only doublet AI-0009 is found to have credible changes in the seismic phase pairs that are related to the Earth’s lowermost mantle (Supplementary Information).

We relocate doublet AI-0009 based on the observed relative travel times of P-wave seismic phases traveling out of the Earth’s core and recorded by the global stations of the GSN and available local networks along azimuths that are not well covered by the GSN stations. The local networks include the GEOFON (GE), the Canadian National Seismograph Network (CN), the Mediterranean Very Broadband Seismographic Network (MN), and the United States National Seismic Network (US). High-quality P-wave phases are used for the doublet relocation, as the P-waves are usually enriched in high-frequency signals and permit high-precision extraction of differential travel time between waveform pairs. As a result, using P-waves provides the best resolution of the relocation results. Only high-quality P-wave observations, with the CC coefficients between the doublet waveforms ≥ 0.95, are selected for doublet relocation. All the selected data are visually inspected. This data selection process yields 27 pairs of P and 4 pairs of pP phase energy for doublet relocation (Supplementary Fig. 7). The relocation result shows that the doublet are located within 0.6 km in the horizontal direction and 0.05 km in depth. The relocation has a minimal root mean square (RMS) travel time residual of 11 ms among the mantle P-wave phases used in the relocation (Supplementary Table 1 and Supplementary Fig. 8).

We study potential temporal changes of seismic phases between the doublets in the broadband seismic data of global seismic stations from the EarthScope Data Management Center43. Data quality is controlled by the CC of waveform pairs between the doublet and final visual inspection. We compute the CCs of the doublet waveforms of S (Sdiff, Sn), sS (sSdiff, sSn), SS, ScS, and SKS phases in a 25-s time window around the predicted signal arrivals based on the Preliminary reference Earth model44 (PREM). The waveform pairs with a CC over 0.95 are selected for final visual inspection. These selection criteria yield 9 pairs of CMB-related S-wave phase pairs, including 6 pairs of ScS, 1 pair of ScS-SKS, 1 pair of SKS and 1 pair of S-Scd-ScS, and 15 pairs of non-CMB S-wave phases (Fig. 2).

All above seismograms are removed with their respective instrument responses, transferred to displacements, and interpolated to a time sample rate of 1000 Hz (0.001 s). P-wave phases are filtered from 0.8 Hz to 2.0 Hz, and S-wave phases are from 0.4 Hz to 2.0 Hz. Due to the data quality, some S-wave phases are further filtered from 0.5 Hz to 2.0 Hz.

Waveform modeling approach

We compute SKS synthetics with a two-dimensional P-SV hybrid method45,46 and radial S-Scd-ScS synthetics with a generalized ray theory (GRT) method47. Synthetics of the two events are computed based on the relative source parameters obtained in the relocation. Since we are only interested in the temporal changes of seismic signal and seismic structure, we define a transfer function as the deconvolution of the observation of event 2000 with the synthetic of model 2000. The transfer function would include the effect of source time function and propagation effects due to the difference of model 2000 from the real seismic structure at the occurring time of event 2000. We obtain doublet synthetics by convolving the synthetics of their respective models with the transfer function. With this processing, event 2000 synthetic is identical with event 2000 observation, and the difference between event 2009 synthetic and event 2000 synthetic can be attributed to the effect of the structure and velocity change of model 2009 from model 2000. Synthetic alignments between the two events can thus be compared to the data alignments between the doublet and be used to study the temporal change of seismic structure between the doublet.

ULVZ change from changing SKS

We set a temporally changing one-sided ULVZ structure near the entry point of SKS at the CMB to model the temporal change of SKS waveform and travel time observed at station IU.SDV between the doublet (top panels, Supplementary Fig. 3). Due to the trade-off between parameters of ULVZ structures45, we fix some basic parameters of ULVZ for model 2000 with the most common values in the literature9,45, with a P-wave velocity decrease of 10%, an S-wave velocity decrease of 30%, a density increase of 20% and a height of 40 km. We parameterize the ULVZ at the time of event 2000 by the epicentral distances of the top and bottom points of the simple edge, i.e., Xtop and Xbottom. Two types of ULVZ change are considered from event 2000 to event 2009: a moving ULVZ and a deforming ULVZ, both represented by a changing Xbottom, i.e., \({{{{\rm{d}}}}X}_{{{{\rm{bottom}}}}}^{09-00}\). Xtop is fixed for a deforming ULVZ while it changes a same distance as Xbottom for a moving ULVZ. We search the best-fit ULVZ location (Xtop and Xbottom) and its associated changing slope (i.e., equivalently \({{{{\rm{d}}}}X}_{{{{\rm{bottom}}}}}^{09-00}\)) that generate synthetic pairs of the two events best fitting the SKS observations (bottom panels, Supplementary Fig. 3a, b for deforming ULVZ and Supplementary Fig. 3c, d for moving ULVZ). Note that we take the half of the inferred \({{{{\rm{d}}}}X}_{{{{\rm{bottom}}}}}^{09-00}\) values of a deforming ULVZ as the inferred length scales of structural change, as both the top and bottom positions would likely change in a dynamical system.

To quantify the SKS waveform fitting between observations and synthetics, we define a fitness index based on the average of CCs of doublet SKS waveforms in two time windows:

$${{{{\rm{Index}}}}}_{{SKS}}=\frac{{{{{\rm{CC}}}}}_{{SKS}}^{{{{\rm{syn}}}}09}-{{{{\rm{CC}}}}}_{{SKS}}^{{obs}00}}{1-{{{{\rm{CC}}}}}_{{SKS}}^{{obs}00}}$$
(1)
$${{{{\rm{CC}}}}}_{{SKS}}^{W}=({{{{\rm{CC}}}}}_{\left[1425,\,1435\right]{{{\rm{s}}}}}^{W}+{{{{\rm{CC}}}}}_{\left[1428,\,1434\right]{{{\rm{s}}}}}^{W})\times 0.5$$
(2)

where \({{{{\rm{CC}}}}}_{\left[{{{{\rm{t}}}}}_{1},{{{{\rm{t}}}}}_{2}\right]{{{\rm{s}}}}}^{W}\) is the CC value between waveform W (“syn09” for the 2009 synthetic and “obs00” for the 2000 observation) and the 2009 observation in the time window between t1 and t2 in seconds (s). A higher SKS index means a better synthetic waveform fit to the observations, with the index being 1 if a 2009 synthetic is identical with the 2009 observation and 0 if a 2009 synthetic is identical with the 2000 observation. Models with an SKS index ≥ 0.70 generate synthetic waveforms fitting the observations reasonably well and are considered as acceptable models (Supplementary Fig. 3).

D″ anisotropy change from changing S-Scd-ScS

We infer temporal changes of SV-wave velocity structure in the D″ region that explain the observed temporal change of radial S-Scd-ScS travel time between the doublet at IU.SDV, based on a series of D″ background velocity models. The D″ background velocity models are parameterized by a D″ discontinuity at the top of the D″ region with a velocity perturbation dVtop with respect to PREM and at a height of Htop above the CMB. In the background D″ models, the SV-wave velocity linearly changes to the value of the PREM at the CMB from the top of the D″ region. We parameterize models of SV-wave velocity temporal change with two parameters: a temporal change of velocity at the top of the D″ region with respect to the background model \({{{\rm{d}}}}{V}_{{{{\rm{top}}}}}^{09-00}\) and a temporal change of velocity at the base of the D″ region (i.e., the CMB) with respect to the background model \({{{\rm{d}}}}{V}_{{{{\rm{CMB}}}}}^{09-00}\). The linear SV-wave velocity gradients in the D″ region are changed accordingly with \({{{\rm{d}}}}{V}_{{{{\rm{top}}}}}^{09-00}\) and \({{{\rm{d}}}}{V}_{{{{\rm{CMB}}}}}^{09-00}\). We search the best-fit background D″ model (dVtop, Htop) and its associated changing \({{{\rm{d}}}}{V}_{{{{\rm{top}}}}}^{09-00}\) and \({{{\rm{d}}}}{V}_{{{{\rm{CMB}}}}}^{09-00}\) from event 2000 to event 2009 that generate synthetic pairs of the two events best fitting the S-Scd-ScS observations (Supplementary Fig. 4).

To quantify the S-Scd-ScS waveform fitting between the observations and synthetics, we define a fitness index based on the CC and L2-norm residuals (the difference between the synthetics and observations) in various time windows:

$${{{{\rm{Index}}}}}_{S-{Scd}-{ScS}}=\sqrt{\frac{{{CC}}_{S-{Scd}-{ScS}}^{{syn}09}-{{CC}}_{S-{Scd}-{ScS}}^{{obs}00}}{1-{{CC}}_{S-{Scd}-{ScS}}^{{obs}00}}\times \left(1-\frac{{L}_{2}^{{syn}09}}{{L}_{2}^{{obs}00}}\right)}$$
(3)
$$\left\{\begin{array}{c}{{{{\rm{CC}}}}}_{S-{Scd}-{ScS}}^{W}={{{{\rm{CC}}}}}_{\left[1465,\,1485\right]{{{\rm{s}}}}}^{W}\\ {{{{\rm{L}}}}}_{2,{S}-{Scd}-{ScS}}^{W}={{{{\rm{L}}}}}_{2,\left[1471,1480\right]{{{\rm{s}}}}}^{W}\end{array}\right.$$
(4)

where \({{{{\rm{L}}}}}_{2,\left[{{{{\rm{t}}}}}_{1},{{{{\rm{t}}}}}_{2}\right]{{{\rm{s}}}}}^{W}\) is the L2-norm residual between waveform W and the 2009 observation in the time window between t1 and t2 in seconds (s). The L2-norm residuals are applied for assessing the fitness of the observed time shifts between the doublet S-Scd-ScS waveforms, and are calculated based on the synthetics and observations that are self-normalized by the respective maximum-minimum amplitudes in the time window of the first portion of the wavelet (1471–1475 s). The index is set to be −1 if \(({{CC}}_{S-{Scd}-{ScS}}^{{syn}09}-{{CC}}_{S-{Scd}-{ScS}}^{{obs}00}) < 0\) or \((1-\frac{{L}_{2}^{{syn}09}}{{L}_{2}^{{obs}00}}) < 0\). A higher S-Scd-ScS index means a better synthetic waveform fit to the observations. Models with an index ≥ 0.75 generate synthetic waveforms fitting the observations reasonably well and are considered as acceptable models (Supplementary Fig. 4).