Introduction

Faults accommodate deformation through a spectrum of slip behaviours ranging from earthquakes to aseismic slip and creep. This variety includes the newly discovered phenomena of low-frequency and slow earthquakes1, whose underlying mechanisms are still debated2,3,4. In this context, laboratory experiments have played a key role in interpreting the inferred fault slip behaviours in terms of dynamic frictional instabilities5,6,7,8. The dependence of friction on sliding velocity, for example, laid the foundation for the rate and state friction (RSF) theory6,7,8, which provides a widely employed physical framework in earthquake dynamics. The fine-tuning of constitutive RSF parameters in numerical simulations and laboratory experiments reproduces the full spectrum of slip behaviour9,10,11 and even determines whether unstable events repeat regularly in time or evolve into deterministic chaos12. These results are obtained without considering complex fault dynamics, which implies that second-order variations of friction can alone lead to strong bifurcations of the dynamic system. In fact, experimental results are commonly portrayed with the relatively simple dynamics of a single-degree-of-freedom spring-slider.

This interpretative framework, built on the frictional properties of rocks, relies on the response of the whole experimental sample, treated as homogeneous, without distinguishing processes occurring at smaller scales. However, several studies show that even minor spatial heterogeneities can have a strong impact on bulk behaviour. Heterogeneities may be found in the form of fault roughness13,14,15,16,17,18, frictional parameters19,20,21, lithology22,23,24,25,26,27, and shear fabrics27,28,29. Fabrics are of particular interest since these characteristic structures found in experimentally deformed samples are also found in natural faults30,31,32,33,34.

A growing body of evidence14,22,25,26,27,28,29,34 suggests that fault zone structures and shear fabrics are central to earthquake dynamics, yet they remain poorly understood even in the laboratory, hidden within sample assemblies and unveiled only after their entire deformation history is completed. Here, we report on deformation experiments to investigate in real time the spontaneous evolution of fault fabrics and their effect on slow laboratory earthquakes. A transparent assembly and a high-speed optical camera were used to capture the evolution of the experimental fault zone in tandem with its macroscopic mechanical behaviour.

In this work, we show a large variety of rupture patterns, suggesting a complexity of dynamic processes in space and time modulated by fault fabric and applied loading rates.

Results

A direct view of fault processes

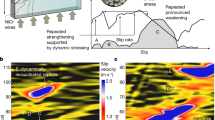
We performed deformation experiments on the biaxial apparatus BRAVA35 using a modified double-direct shear (DDS) configuration, where two simulated fault zones are deformed under controlled conditions (Fig. 1a). In all experiments we maintained a constant normal load of 25 kN (nominal normal stress of 10 MPa) but varied the forcing velocity of the central slider, here called loading point velocity (LPV). Details on the setup and experimental procedure are included in the “Methods” section. Different from a common DDS setup, the central slider (Fig. 1a) is not made of metal but of transparent Plexiglas (polymethyl methacrylate). This assembly allows recording the evolution of the mechanical properties of the material (Fig. 1b) while simultaneously visualising fault zone deformation (Fig. 1c). We studied fault zones composed of montmorillonite clay powder because: (i) it is a relevant rock-forming phyllosilicate typically found in subduction zones associated with shallow slow slip and tectonic fault tremor36,37; (ii) although displaying rate-strengthening behaviour, it is frictionally unstable at laboratory conditions comparable to the natural settings38; and (iii) it has adhesive properties39 that ensure strong coupling at the layer boundary and thus shear deformation internal to the fault zone; (iv) it has a strong poroelastic response when subject to compression40.

Fig. 1: Experimental setup, shear strength evolution, and fault structure development.
figure 1

a Double direct shear arrangement with two fault zones, a transparent central block, and a camera to capture images of the inner fault surface (XY plane). b Friction and average fault surface luminosity during shear deformation at constant LPV = 10 µm/s. c Snapshots of the fault surface luminosity showing spatiotemporal evolution of luminosity during shear. Temporal sequence of snapshots is given in (b). Riedel R1 shears begin to form after the peak stress (grey box in panel (b)). They form first at the bottom (white arrow) and then progressively above as slip accumulates. Higher-stressed areas appear darker. The black arrow indicates subsidiary R-shears forming through lateral extrusion of the sample. Dashed region in VIII: area analysed in Figs. 2 and 3. Video version of panel (c) in Supplementary Movies 1 and 2.

Full size image

On one side of the assembly, a high-speed camera films the light of a uniform light source reflected by the sample-block interface (Fig. 1a), hereafter called for simplicity “fault surface”. We use the reflectivity as a proxy for the fault zone stress as well as a marker of the structures developing in the sample layer38. This is possible thanks to the phenomenon of frustrated total internal reflection, the same that makes a fingerprint appear when pressing a thumb against polished glass. Here, the quantity of light reflected is inversely proportional to the number of clay platelets pressed against the fault surface. Therefore, the luminosity of the fault surface is a function of the poroelastic state of the fault zone, where porosity is a function of the state of stress40. Tests to calibrate the relation between luminosity and fault zone stress state yield a qualitative but strong, inverse, and nonlinear proportionality38 (Supplementary Section SI1). In the following sections, we first document the development of fault structures and then investigate how unstable slip starts and propagates along the fault zone.

Evolution of fault zone structures

Our experiments provide remarkable videos on the development of fault zone structures with shear displacement. For this documentation, we shear the initially homogeneous layer of montmorillonite powder applying a constant normal load of 25 kN and a constant LPV = 10 µm/s to the central slider until the macroscopic friction (apparent friction) achieves a constant value (Fig. 1b). This practice, so-called run-in, is common in rock-deformation experiments and is used to achieve steady state shear strength, i.e., when the fault is considered at macroscopic mechanical equilibrium with the imposed boundary conditions. All of our experiments exhibit consistent behaviour during the run-in, developing a specific structure that forms in a sequential pattern (Fig. 1c).

During shear loading to peak friction conditions (Fig. 1b, frames I–III), there is a progressive increase of stress (darkening) from the top to the bottom of the fault prior to the formation of fault shear fabric structures (Fig. 1c, frames I–III). Only after peak friction, a first structure forms with a local decrease of stress (increase of luminosity, Fig. 1c, white arrow). This feature corresponds to the termination of oblique zones of localised shear, called Riedel41 shear bands (R-shears). They are arcuate in the XY plane (Fig. 1c), with convexity oriented towards the loading point. Progressively, new shear bands form with a rather regular spacing (~5 mm, Fig. 1c III–VIII), populating the experimental fault in the direction of the loading point (positive Y direction). Toward the end of the experiment, the luminosity of the fault is no longer homogeneous but shows persistent local stress minima marking the terminations of the R-shears (Fig. 2a). A remarkable observation is that, after 250 s of shearing (displacement of 2.5 mm), friction has already achieved steady-state conditions (Fig. 1b), but the shear fabric continues to evolve with progressive population of the fault zone with R-shears (frames VI–VIII).

Fig. 2: Structural elements of the experimental fault zone.
figure 2

a Luminosity profile along the dashed region of Fig. 1c (frame VIII), correlated with a sketch of the kinematic cross section (YZ) of the deformed sample (Y = 0 is at the right of panel (a). Dashed lines R1–R9 indicate the position and sequence of formation of the R-shears, sketched below. Lower sub-panels below show a schematic YZ section interpreted from microstructural analysis (see panel (b)) with the following structural elements: upper (BU) and lower (BL) B-shears, R-shears (R), and micro-lithons (ML). Shaded areas above R-shears show relaxed regions of low stress. b Electron back-scattered image of a YZ sample cross-section showing the upper and lower B-shears, R-shears, and micro-lithons. The close-up in the red box shows the S–C fabric43 contained in BU. c Sketch of the structural elements of the deformed sample (XYZ coordinate system is defined in Fig. 1).

Full size image

The geometry and sequential development of the shear fabric elements are clear in both the real-time images (Fig. 1) and the deformed samples recovered after the experiments (Fig. 2b and Supplementary Fig. S3). The R-shears form at ~30° to the shear plane and cut the entire sample layer from one boundary to the other (Fig. 2b). They dip roughly in the same direction of slip, representing shear localisation features that produce “normal” kinematic motion (Fig. 2b). Our images also show a subsidiary set of R-shears that are rarely identified in previous studies. These features form at the lateral edges of the fault zone (Figs. 1 and 2c), joining the first R-shear set at a sharp angle (Fig. 1c, black arrow). Formation of this set is accompanied by the lateral extrusion of material from the assembly.

The R-shears bound low-strain regions referred to as “micro-lithons”42 (ML, Fig. 2), and they correspond to so-called spectator regions. In XY view, they are characterised by an upper (closer to the loading point) bright area and a lower dark area (Fig. 1c), suggesting a gradient in stress distribution between the R-shears (Figs. 1c and 2c). In addition to R-shears, two boundary shear zones form as a consequence of shear localisation: one in proximity of the central slider (upper B-shear, BU) and one in proximity of the lateral forcing block (lower B-shear, BL). These present a well-developed S–C fabric43 (close-up of Fig. 2b) and represent the high-strain zones accommodating shear motion. An important feature is that strain is partitioned between both B-shears after their development, with BL being mostly active close to the older R-shears and BU close to the younger R-shears. This observation and further information on the development of the fault structures are detailed in Supplementary Section SI4.

Slip instabilities

We now explore the influence of shear fabric on the genesis (nucleation), propagation, and arrest of slip instabilities. In this new set of experiments, we repeat the run-in procedure described above to develop the characteristic fault structure. We then vary the LPV between 0.01 and 10 µm/s and observe unstable slip behaviour occurring in stick-slip cycles. These laboratory earthquake events occur only for LPVs below 7.5 µm/s, finding agreement with previous works on slip stability and forcing velocity dependence38,44. The cycles are composed of a “stick” stage, characterised by a nearly linear increase of friction in time, and a “slip” stage, characterised by spontaneous slip accompanied by a quasi-dynamic drop in friction (Fig. 3a). We label these events as “slow” since the bulk slip velocity is not larger than 10 µm/s, as demonstrated in our previous tests38. During slow slip events, the luminosity changes only subtly across the fault surface (variations <1% of the sensitivity range). In fact, the position of the main fault structures as well as the distribution of stress (luminosity) do not vary substantially throughout the stick-slip series (see Supplementary Section SI4). Nevertheless, the slight luminosity change recorded during the friction drops shows a negative correlation with the friction (balloon in Fig. 3a) and clearly illuminates the passage of a rupture front across the fault. Hereby, we define “rupture” as the phenomenological description of the spatial-temporal variation of mechanical attributes (e.g., stress and luminosity) in response to the propagation of an instability. A quick visualisation of the ruptures nucleating and propagating along the shear direction (Y) is shown in Fig. 3c, which depicts the stressing rates (time derivative of luminosity) as a function of time (Fig. 3c). We can immediately see that a plethora of slip phenomena emerges, modulated by the LPV.

Fig. 3: Unstable sliding in laboratory slow slip.
figure 3

a Evolution of friction (black, close-up in (b)) and average luminosity (blue) as a function of time for a range of load point velocities (LPV). Note that the average luminosity is anticorrelated with friction (balloon) but appears nearly invariant throughout the stick-slip series when compared to the variations during run-in (Fig. 1b). c Qualitative stressing rate (inverse of luminosity change rate, dL/dt with dt = 20 ms) in the shear direction restricted to the stripe of Fig. 1c, frame VIII. Red circles indicate the approximate time and location of nucleation.

Full size image

Nearly periodic stick-slip is observed at LPV < 2.5 µm/s with a transition to more complex, aperiodic events, and eventually aseismic slip for higher LPVs. All of the slow slip events present some differences in rupture patterns, but two main groups with specific characteristics emerge (Fig. 3a, and Supplementary Section SI5). The first, “regular” slow slip events, are observed mainly at LPVs ranging between 0.25 and 2.5 µm/s. The second, “irregular” slow slip events, is observed at LPV < 0.25 µm/s. These two categories are of particular interest and are described in detail in the following sections. At LPVs ≧ 2.5 µm/s, the slip behaviour quickly transits to chaotic stick-slip. Chaotic events are irregularly spaced in time, present variable friction drops, overlap in time, and are characterised by complicated rupture patterns (compare regular stick-slip with chaotic stick slip in Fig. 3c). Together with each major rupture propagating in the direction of shear (dark blue traces), numerous smaller events nucleate at other locations and interfere with each other (light red-blue patterns), causing a chaotic stressing rate across the experimental fault (Fig. 3c). The clear fluctuations of friction visible during regular ruptures (t < 613 s, Fig. 3c) disappear when multiple instances nucleate and propagate in short time intervals (interval 616–617 s) or synchronously (interval 626–629 s). At LPV > 10 µm/s chaotic stick-slip quenches to stable sliding. Surprisingly, despite the measured constant friction, luminosity changes reveal that ruptures still continue to nucleate and propagate in the fault zone (Fig. 3c). These ruptures present small stressing rates (lighter colours, Fig. 3c), random propagation patterns, and irregular timing. These features, occurring in concert, mask the existence of instabilities from the mechanical time series to produce what macroscopically appears as aseismic shear motion.

Regular slow slip

Regular slow slip events start at the boundary of the uppermost micro-lithon (Fig. 4c, d), close to the subsidiary R-shear next to R9 (circle in Fig. 4g), where stress heterogeneities are larger. From this region, the rupture front propagates in the X (Fig. 4f) and Y (Fig. 4e) directions. Ruptures propagate as wrinkle-like pulses38 with dimensions smaller than the separation between the Riedel shears (<5 mm, Fig. 4e, f). The width of the wrinkle appears to be proportional to the propagation velocity of the pulse45 (see Supplementary Fig. S4).

Fig. 4: Regular slow slip.
figure 4

a The evolution of friction and average luminosity across three slow slip cycles, with b close-up of the third event. Note that luminosity increases during the entire friction drop. c Qualitative stress change (inverse of luminosity change) along the shear direction with time, with d close-up of the third event. e, f Qualitative stressing rate (inverse of luminosity change rate, dL/dt with dt = 20 ms) in the shear (e) and horizontal (f) directions. g Snapshot of the luminosity at t = 360 s. Dashed regions show locations of the stress rate calculations for panels (e) and (f). Arrows: black arrow, start of the instability; white, change of main rupture direction. Yellow circle: nucleation site. Video version of panels d–f in Supplementary Movies SM3 and 4.

Full size image

We observed a range of rupture speeds depending on propagation direction and shear fabric. For instance, in Fig. 4b the rupture migrates at ~110 mm/s in the X-direction (Fig. 4f), remaining mostly confined within the uppermost micro-lithon (Fig. 5a, frames I–VII, and 5c), above R9. Most of the macroscopic friction drop occurs during this stage (from black to white arrow, Fig. 4b). Note that the slow velocity (7 mm/s), measured along the Y-direction in Fig. 4d, indicates that the rupture propagates mostly as a mode III (anti-plane shear) in its initial stages. The uppermost micro-lithon acts as a preferential channel for mode III ruptures in the majority of slow slip events, not exclusively the regular ones (Supplementary Section SI5). When the rupture encounters the rightmost boundary (Fig. 4f, white arrow, and 5a, frame VII), it overcomes the bounding Riedel and propagates in the shear direction, relieving stress across the entire fault surface. In the meantime, additional minor ruptures propagate within the uppermost micro-lithon (Fig. 4f, blue stripes past the white arrow), contributing to a further local stress drop. Now (Fig. 5a, frames VII–XII), the rupture is faster in the shear (Y) direction (up to v ~ 225 mm/s) than along the X-direction (average v ~ 0) and thus propagates mainly as a mode II (in-plane shear). Our measurements show a range of interesting spatiotemporal complexity, including momentary phases of arrest and deceleration at each local stress maximum within the micro-lithons (Fig. 4e, dashed lines). The final rupture arrest occurs when the front approaches the lowermost boundary of the sample. All of these so-called regular rupture events propagate across the entire fault surface.

Fig. 5: Regular rupture.
figure 5

a Qualitative stress change (inverse of luminosity change) across the experimental fault surface with respect to a reference frame at t = 0, not shown. Same event as Fig. 4b. Each frame is separated by ∆t = 0.1 s (frame I is at t = 0.1), reported with Roman numerals (panel b). Dotted lines indicate the rupture front position in the previous time frame. b Friction curve showing the timing of each frame in (a). c Luminosity with rupture fronts of panel a, dotted in white and nucleation site circled in yellow. d Rupture progression (dark to light) with nucleation site in yellow.

Full size image

Complex ruptures and irregular slow slip

Irregular slow slip events mostly occur at LPVs < 0.25 µm/s. These differ from regular slow slip events by one or more features such as: two-stepped friction drops, partial ruptures (confined ruptures), and/or complex propagation patterns. In three consecutive events occurring at low LPV (100 nm/s, Fig. 6a, c), the first two nucleate at the topmost micro-lithon and do not rupture the entire fault (Fig. 6c), leading to an increase of stress in the unruptured lower half of the sample. This region is then ruptured by a third event nucleating inside of it (Fig. 6d, black arrow). Unlike regular slow slip events, the rupture slowly expands (~14 mm/s, Fig. 6f) from the nucleation site (Fig. 7, frames I–IV) and then accelerates to a much faster propagation speed.

Fig. 6: Irregular slow slip.
figure 6

a The evolution of friction and average luminosity across three irregular slow slip cycles, with b close-up of the third event. Note that luminosity increases only during the first part of the friction drop. c Qualitative stress change (inverse of luminosity change) along the shear direction with time, with d close-up of the third event. e, f Qualitative stressing rate (inverse of luminosity change rate, dL/dt with dt = 20 ms) in the shear (e) and horizontal (f) directions. g Snapshot of the luminosity at t = 130 s. Dashed regions show locations of the stress rate calculations for panels (e) and (f). Arrows: black, start of the third instability; white, the rupture reaches the topmost stressed microlithon; orange, second part of the friction drop not matched by changes in luminosity. Yellow circle: nucleation site. Video version of panels (d–f) in Supplementary Movies SM5 and 6.

Full size image
Fig. 7: Complex rupture.
figure 7

a Qualitative stress change (inverse of luminosity change) across the experimental fault surface with respect to a reference frame at t = 0, not shown. Same event as Fig. 6b. Each frame is separated by ∆t = 0.1 s (frame I is at t = 0.1), reported with Roman numerals (panel b). Dotted lines indicate the rupture front position in the previous time frame. b Friction curve showing the timing of each frame in (a). c Luminosity with rupture fronts of panel a, dotted in white and nucleation site circled in yellow. d Rupture progression (dark to light) with nucleation site in yellow.

Full size image

We observe that the nucleation stage is composed of a small rupture that induces the nucleation of another one in the neighbouring micro-lithon across R3 (Fig. 7, white arrow, frames V–VI). Notably, the event behaves as a wrinkle-like rupture even during the nucleation phase since the stressing rate is restricted to a thin region close to the rupture front (Fig. 6e, f). After the nucleation stage, the rupture expands at faster rates (>50 mm/s, Fig. 6e, f) toward the sides of the fault and reaches the topmost micro-lithon (Fig. 7, frames VI–IX), then rapidly propagates across it from left to right (frames IX–X) and continues to the bottom left (frames X–XII). This rupture shows a clockwise rupture pattern (Fig. 7d), with faster propagation at the boundaries of the fault zone. Again, arrest coincides with a decrease of rupture front speed (Fig. 6d). The rupture event clearly correlates with the first half of the slip event, which is modulated in two steps of roughly equal friction drop (starting at the white and orange arrows in Fig. 6b). Only the first step corresponds to the variation in luminosity recorded at the fault surface. This effect is probably linked to the diachronous rupture of each side of the double-direct shear configuration. This is a common feature of irregular slow slip events observed at low LPVs (<0.25 µm/s). The description of irregular slow slip events applies as well to the main events recorded during chaotic slow slip (Fig. 3b, c).

Discussion

Our experiments qualitatively reveal the state of stress, the development of self-organised structures, and how these control the nucleation, propagation, and arrest of slip instabilities. Here we provide an explanation of this self-organised shear fabric.

Fabric development and spontaneous redistribution of stress on-fault

At the beginning of each experiment, we force the microstructural reorganisation of the fault structure from the initial homogeneity (uniaxially pressed powder) to an optimal shear fabric (localised shear zones). This configuration is reproducible across experiments and consists of the formation of two types of shear bands (Fig. 8a): (i) two boundary (B−) shear zones forming at the fault surface (BU) and close to the lateral block (BL,), and (ii) several Riedel shears (R1–R9), which together bound sigmoidal low strain domains, the micro-lithons (ML). The micro-lithons are consistently ten in number and with rather regular spacing, suggesting that there is a geometrical control between sample dimension (layer thickness, contact area), experimental conditions (run-in velocity and normal load), and optimal stress distribution31,41,46. The regularity of R-shear spacing is probably aided by the small grain size and homogeneity of the initial samples. The shear strain is accommodated mainly by both B-shears and is partitioned between the two through the activity of R-shears (Fig. 8a).

Fig. 8: Schematic of fault structures and slip modes.
figure 8

a Schematic drawing showing the structures developed during shearing of the experimental fault, associated stress state, and main features. b Simplified, representative rupture patterns for both regular and irregular events. c Cross-section showing the possible nucleation within a Riedel shear (R) and subsequent propagation to the boundary shears (BU and BL). ML are the micro-lithons. White and black arrows indicate the shear sense.

Full size image

The formation of each R-shear relieves stress from the micro-lithon it bounds, with the largest stress decrease recorded in its proximity. Immediately after the formation of the R-shear, stress increases inside the micro-lithon close to the previous R-shear (Supplementary Section SI4) producing the small-scale fluctuations of stress in the Y direction (Fig. 2a). This effect recalls the way stress is relieved at asperities when material is plucked out in response to adhesive wear47,48, transferring the strain from the sliding surface to a new, deeper slip zone. In our case, the lower B-shear.

In the fault’s final configuration, the top of the R-shears separates the least stressed regions from neighbouring loci of stress concentration (Fig. 8a). The formation of R-shears seems thus a necessary mechanism that redistributes stress across the fault while boundary shear zones creep to accommodate stable sliding. This effect is of paramount importance in producing heterogeneities that determine the initiation and mode of fault instability49,50. Given the impossibility of forming further R-shears towards the loading point, the last formed micro-lithon is the most stressed region of the fault and presents large stress heterogeneities at its boundaries (Fig. 8a), especially in correspondence with a low stress embayment. This is the area mostly affected by the loading conditions, and that becomes inherently unstable.

Lastly, it is important to point out an important feature. Although a fault zone structure fully populated by R-shears can be reasonably seen as a final state of mechanical equilibrium, the analysis of both time series and footage does not confirm this interpretation. The bulk friction has, in fact, already achieved steady state conditions (Fig. 1b) after the formation of the fifth R-shear, as well as the average luminosity. This means that the continuous evolution of the inner structure of the fault zone throughout the experiment, which is responsible for the spatial reorganisation of stress, leads to a first-order mechanical equilibrium (e.g., macroscopic friction, stress), characterised by the contribution of all points of the fault (i.e., bulk response). This is what is commonly observed with the single observation point (load cell) of the experimental apparatus. However, second-order variations may still evolve with strain within the sample, spontaneously following the fabric development, at a scale smaller than the bulk fault, without requiring further energy dissipation. This has important implications on the rate-dependence of friction, sliding stability, and their relationship with strain and strain rate51,52,53.

Nucleation of slip instabilities

As much as all slow slip events display rather variable rupture patterns (Supplementary Section SI5), most initiate at the highest stress heterogeneity (regular slow slip events, Fig. 8b), located at the bounding R-shear of the uppermost micro-lithon (Figs. 3–5). Irregular events (Fig. 8b) may also originate at smaller stress heterogeneities inside the fault (Fig. 6g). The ruptures thus start in regions where sharp local stress gradients are observed, but the absolute entity of the local stress seems subordinate to the intrinsic instability of the area and memory effects. This is clear since the overall stress state of the fault remains remarkably unchanged across several creep-slip cycles (Supplementary Section SI4) while minor redistribution of stress can disrupt the previous rupture patterns and favour nucleation in other regions (Fig. 6c). For this reason, irregular slip events may emerge as a consequence of incomplete ruptures or overlapping chaotic rupture patterns (Fig. 3c).

In our experiments, most events display no clear distinction between a nucleation and a dynamic phase sensu Ohnaka and Shen54. Instead, different rupture speeds are recorded depending on the direction of the rupture front (slower in the X direction, Fig. 4e, f), while a fictitious nucleation stage may emerge due to a specific choice of directional averaging of the fault luminosity (e.g., Fig. 4d). This highlights the importance of the observation point on the fault (e.g., camera or other sensors), here privileged by the planar view. A distinct, slow nucleation phase is clearly observed only when the instability initiates in more central areas of the fault (irregular events, Fig. 8b). Given the general lack of a distinguishable, systematic nucleation phase, a reliable measure of the nucleation size for use in numerical models55 is unattainable. Neither can nucleation size be calculated theoretically since the

material is rate-strengthening38 and the stress distribution is heterogeneous. Nevertheless, since we observe partitioning of strain between the different shear zones, it is reasonable to assume that slow slip events tend to nucleate away from the B-shear zones, for example, inside the R-shears (Fig. 8c), and we should better document the subsequent emergence of the rupture only when it expands across the BU-shear. In support of this hypothesis, we recorded the formation of plumose structures along R-shears formed in over-consolidated clay experiments (Supplementary Section SI6). These structures indicate the energetic formation of R-shear through fracture-like mechanisms, potentially associated with the nucleation of slip instabilities.

The beginning of slow slip instabilities in our experiments is phenomenologically related to the formation and migration of dilatant waves (increased luminosity) from a source region of stress heterogeneity, such as those forming at elastic bi-material interfaces56,57 and widely known as Schallamach waves58. These are self-healing detachment pulses that start and propagate in a similar manner to what was observed in our experiments. The similarity implies that the instability grows as the local loss of adhesion, which manifests in clay as a region with growing porosity (increased luminosity) and possible detachment of platelets from the central slider. In our tests, the loss of adhesion may be aided by the nucleation of ruptures within the R-shears, which, being at high angle to the B-shears, enhances the stress heterogeneity at the critically stressed sites.

To corroborate this mechanistic interpretation of adhesion loss, we highlight the existence of different regimes at different loading point velocities (LPVs, Fig. 3), as observed in analogue tests on bi-material interfaces56,58. Additionally, it was demonstrated that slow slip self-healing pulses can emerge as a function of stiffness contrast and finite size of the setup at elastic-frictional bi-material interfaces59. Nevertheless, the growth and propagation of slip instabilities is clearly not a simple process acting at the sample-slider interface. Instead, it occurs in a volume inside the sample, independently of the choice of the forcing block material, albeit with small differences in mechanical observables38 (e.g., duration of the slip event).

On a final note, the higher occurrence of irregular events observed at the lowest LPV may indicate the activity of slow processes such as viscous creep, whose effect is otherwise negligible due to the small interseismic time60. This effect likely drives efficient stress transfer and relaxation (foliation flattening, porosity reduction43) and/or enhanced healing (adhesion and cohesion of clay platelets) at the most stressed asperities. It is therefore obvious that LPV strongly shapes the characteristics of slow slip events, but it is not the only factor. We expect that the evolution of fault structures with large strains (not explored in this article) and the change of boundary conditions would impact the dynamics of laboratory earthquakes, as demonstrated in previous literature51,52,53,60.

In our experiments it is difficult to adapt existing models for a number of reasons: (i) deformation occurs in a thin boundary shear zone (<100 µm), which is not a proper bi-material interface, (ii) an important fraction of deformation is accommodated by creep (up to 20% of the LPV during stick stages38), and (iii) instabilities form independently of the stiffness of the central slider38. In this light, the intrinsic elastic properties (bending) of the clay platelets61, the preferred frictional sliding along the S–C foliation38, and the sub-mm stress heterogeneities on the fault zone may play a far more important role in nucleation than the bulk properties of the sample and experimental setup.

Our observations suggest that slip instabilities nucleate within the gouge layer as a result of stress heterogeneity determined by shear fabric evolution. In other words, nucleation of dynamic instabilities is a volumetric process driven by shearing and sensitive to tiny variations of the loading rate. This implies that the macroscopic description of dynamic slip instabilities as retrieved from the single observation point on the load cell in classic rock deformation experiments does not resolve the complex spatial-temporal evolution of sliding at smaller wavelengths. Thus, the macroscopic slip of the whole sample is the result of strain partitioning within the volume.

Propagation, arrest, and quenching of slow slip

Besides nucleation, propagation, and arrest, the rupture pattern is strongly influenced by stress distribution and fault structures. All ruptures tend to be initially confined within the micro-lithons where they originate, with the high-stressed areas acting as barriers17. These barriers are overcome when the macroscopic rupture breaks perpendicular to the ML boundary and especially when it joins the low-stressed fault edges (Fig. 5 frames VI–VII). The same effect of the fault edge on rupture propagation is reported in analogue experiments in plastic faults62. We observe that each jump across the R-shears can be met with some latency and causes a progressive deceleration of the rupture edge (Fig. 4e). This effect is observed especially in the region where the earliest R-shears formed, the same area of the fault where some partial ruptures stop at low LPVs (Fig. 6c). This effect is probably related to the region of strain partitioning between the upper and lower boundary (B-)shear zones (Fig. 8a, Supplementary Section SI4). Here, especially at low LPVs, the rupture may “sink” into the R-shears, dissipating the available elastic energy into distributed permanent deformation.

With increasing LPV, the bulk frictional instability of the experimental fault is quenched towards stable sliding (LPV > 7.5 µm/s, Fig. 3c). This, however, is not related to the disappearance of slow slip instabilities. Slow, pulse-like ruptures continue to nucleate, especially at the large stress heterogeneity where regular events originate (Fig. 3c) and, at the same time, propagate while other subsidiary ruptures still sweep across the fault and nucleate in other locations. The bulk stability recorded in the time series (apparent friction) is then the result of the combined effect of: (i) interfering rupture patterns, (ii) recurrence time smaller than that required for a complete rupture, (iii) inhomogeneous redistribution of stress across cycles, and (iv) different nucleation sites. We argue that the inherent instability of the material is also related to the sample size14,59, which signifies that the embryonal phases of an earthquake (small-scale processes) are severely affected by the role of heterogeneities across different scales. This raises a fundamental problem stemming from the lack of an observational continuum of structures from the laboratory to real faults. We still have little information on how stress and strain partitioning acts in fault domains larger than the laboratory tests and smaller than the resolution of seismological methods48. For example, the fault patch acting as an asperity in nature might vary substantially depending on larger-scale geological features63 irreproducible in the laboratory.

Our observations suggest that macroscopic slip associated with the friction drop is due to strain partitioning between B- and R-shear within the fault zone, characterised by spatial-temporal evolution defining the so-called rupture patterns. Rupture involves the evolution of fabric over the entire gouge layer and is affected by small-scale heterogeneities and fluctuations of the loading velocity. While this does not preclude the interpretation of macroscopic dynamic slip instabilities, it complicates the interpretation of mechanical processes acting at the micro scale.

The complex dynamics of experimental slow slip

Our experiments allowed us to image the dynamics of slow slip in laboratory clay faults. The experimental fault evolves with slip to form a reproducible inner structure composed of localised shear zones and low-strain domains. This structure is in continuous evolution with strain, despite the apparent early achievement of bulk mechanical equilibrium (steady state conditions). This structure represents the self-organisation and redistribution of stress across the fault zone (i.e., the gouge layer), which has important effects on the genesis and propagation of unstable events. At low forcing velocities, slow slip events nucleate due to adhesion loss at local stress heterogeneities, which are not necessarily the largest inside the fault zone. The nucleation stage does not show a characteristic, recognisable length scale, and it is associated with stress heterogeneities in the gouge volume. The slip instability inferred from the mechanical data is indeed associated with the spatial-temporal evolution of a strain pulse. Slip instabilities propagate as self-healing dilatant pulses, causing only minor redistribution of stress across the fault zone, but do introduce memory effects in the regions they sweep through. As a consequence, each slow slip event is different and can follow complex rupture patterns, especially at both low (LPV < 0.25 µm/s) and high (LPV > 2.5 µm/s) loading rates. Even when the fault is macroscopically stable (steady-state apparent friction) at high loading rates, slip pulses continue to nucleate and propagate, but become chaotic and of smaller entity. The dynamics of slow slip appear thus complex even in experimental small faults, questioning whether constitutive laws for earthquake nucleation and frictional instability may represent processes across all scales, which would require proper addressing.

Methods

Deformation experiments

Deformation experiments were carried out in BRAVA35, a bi-triaxial rock deformation apparatus (Fig. 9a) hosted at the HPHT laboratory at the Istituto Nazionale di Geofisica e Vulcanologia (Rome, Italy). The experimental setup consists of a double direct shear sample holder, composed of two lateral forcing blocks compressing two parallel sample layers against a transparent Plexiglas central slider (Fig. 9b). The sample has an initial thickness of 5 mm and is compressed on a nominal squared area of contact of 50 by 50 mm (Fig. 9b). The samples were humidified beforehand at 100% room humidity for 12 h, allowing a thin film of water to be adsorbed on the surface of the platelets. The contact surface between the forcing blocks and the sample is flat. Normal stress and shear motion are controlled by two orthogonal hydraulic pistons (Fig. 9a) and are transferred to the sample by the lateral blocks and the central slider (Fig. 9b), respectively. On one side, a shielded LED lamp provides a homogeneous white light source. On the other hand, a high-speed camera (NAC Memrecam) films the light reflected by the sample-block interface (Fig. 9c). The segment connecting the camera focus and the centre of the sample-block interface has a length of 450 mm and lies on a XZ plane at 36° to the shear plane (XY, Fig. 9c, Supplementary Fig. S2). The Plexiglas slider caused the distortion of the interface. The distortion of the source for each pixel is nonlinear and is a function of its coordinates, Snell’s law, and the positioning of the camera in the experimental setup. The distorted images are linearly stretched in the X–Y directions to obtain a satisfactory correction, which is fully detailed in the Supplementary Section SI2. After the correction, the position of each pixel is deviated from the original by less than 1 mm. Errors in the estimates of rupture velocity are negligible considering the experimental variability. Our video measurements have a temporal resolution of 0.02–0.0067 s and a spatial resolution of ~50 µm and ~130 µm in the shear (S.D.) and horizontal (H.D.) directions, respectively, determined by the angle of view (Fig. 1b).

Fig. 9: Experimental apparatus, setup, and sample assembly.
figure 9

a Side view of the apparatus BRAVA with mounted sample; b top view of the experimental setup in scale; c ensembled double direct shear sample holder. S.D., H.D., and T.D. are the shear, horizontal, and thickness directions, respectively. All figures maintain the original proportions.

Full size image

Video analysis

Video analysis was carried out with a custom MATLAB© code performing simple operations on raster frames (.tif) extracted from the videos, including static and rolling background removal. In the static background removal (Figs. 4c, d, 5a, 6c, d, 7a), the background image corresponds to the first frame of interest of the video and is systematically subtracted from the following frames. The resulting video displays changes in the luminosity of the fault surface (quantified in arbitrary units, a.u.) with respect to the initial frame. The change in reflectivity obtained with static background removal qualitatively shows the stress change on the fault surface. The rolling background removal (Figs. 3c, 4e, f, 6e, f) is operated by subtracting from each frame the frame preceding by a fixed separation of time. The optimal separation for visualisation has been selected by trial and error. The rolling background removal qualitatively indicates the stress change rate on the fault surface, which is the discrete derivative of the stress change. Linear pixel-wise averaging in the X and Y directions was used on selected areas to image the propagation of rupture fronts. This analysis could not provide quantitative results due to the strong non-linearity between luminosity, stress, and poroelastic state of the material (Supplementary Section SI1). Nevertheless, our analysis shows a robust inverse correlation between luminosity and stress, corroborating the results and supporting the discussion.