Mechanistic understanding of nitrate reduction as the dominant production pathway of nitrous oxide in marine oxygen minimum zones

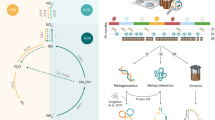
Abstract

Nitrous oxide (N₂O), a potent greenhouse gas and ozone-depleting agent, is produced intensely in oxygen minimum zones (OMZs) predominantly through nitrate reduction $\left({{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}\right)$. However, mechanisms and controls of this pathway remain unclear. Here, we investigate the microbial ecology governing this pathway using experiments and an ecosystem model. We experimentally confirm a critical hypothesis: most ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers do not utilize extracellular nitrite, an intermediate of the pathway. Model results demonstrate that the ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway is compatible with oxygen, and that its response to oxygen is heterogeneous because it is governed by niche partitioning of distinct microbial types and thus may not follow a smooth curve. Lastly, experiments demonstrate that this pathway is sensitive to the type of organic matter, its electron acceptor, in addition to organic matter availability. These findings advance our mechanistic understanding of the primary N₂O production pathway, necessary for predictions of marine N₂O emissions.

Introduction

Nitrous oxide (N₂O) is a potent greenhouse gas and ozone-depleting agent with a global warming potential nearly 300 times that of carbon dioxide (CO₂)¹. The ocean is a major source of N₂O, accounting for ~35% of global natural N₂O emissions², but estimates of the marine N₂O budget are subject to large uncertainties^3,4. These uncertainties are largely attributed to an incomplete mechanistic understanding of the diverse N₂O cycling pathways, and they prevent accurate predictions of global N₂O emissions under climate change.

The most intense sources and sinks of N₂O in the ocean occur within oxygen minimum zones (OMZs)^3,5, typically characterized by an anoxic layer of water sandwiched by oxygenated waters. OMZs accommodate a wide spectrum of O₂ conditions, which support all microbially mediated N₂O cycling processes (Fig. 1a). Although abiotic photochemical N₂O production has been recently discovered⁶, this pathway is restricted to sunlit environments and is only potentially relevant to the smaller portions of OMZ waters that overlap with the euphotic zone. In the dark, subsurface waters that characterize most of the OMZs, N₂O is primarily produced and consumed by a variety of microbial metabolisms (Fig. 1a). Aerobic ammonia-oxidizing organisms produce N₂O through three mechanisms: nitrification^7,8, nitrifier-denitrification, and hybrid formation processes^9,10,11. N₂O is also produced and consumed by anaerobic microorganisms carrying out subsets of the multi-step denitrification pathway: the step-wise reduction of nitrate $\left({{{{\rm{NO}}}}}_{3}^{-}\right)$ to nitrite $\left({{{{\rm{NO}}}}}_{2}^{-}\right)$, nitric oxide (NO), N₂O, and finally dinitrogen gas (N₂)^12,13,14. Here, for simplicity, we refer to microbes performing any part of this denitrification sequence as “denitrifiers”.

Fig. 1: N₂O producing or consuming pathways.

a Known N₂O-producing or consuming pathways. b Microbial functional types producing or consuming N₂O that are distinguished using stable isotope (¹⁵N) incubation experiments and resolved in the ecosystem model. The ${{{\rm{NH}}}}$₃$\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathways include N₂O produced as a byproduct of ammonia oxidation and hybrid formation. AOO stands for ammonia-oxidizing organisms.

Recent work has identified that the predominant pathway of N₂O production in OMZs is from the reduction of ${{{{\rm{NO}}}}}_{3}^{-}$ (${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{NO}}}}}_{2}^{-}\to {{{\rm{NO}}}}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$, and abbreviated as ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$)^15,16,17,18. N₂O produced by denitrifiers in OMZs is one to three orders of magnitude higher than that from ammonia-oxidizing organisms, and the production from ${{{{\rm{NO}}}}}_{3}^{-}$ reduction is one to two orders of magnitude higher than that from ${{{{\rm{NO}}}}}_{2}^{-}$ reduction^16,18,19,20.

Given that ${{{{\rm{NO}}}}}_{3}^{-}$ must first be reduced to ${{{{\rm{NO}}}}}_{2}^{-}$ before being further reduced to N₂O, it seems counterintuitive to observe higher rates of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ than ${{{{\rm{NO}}}}}_{2}^{{{{\rm{\hbox{-}}}}}}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$, assuming most ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers can utilize external ${{{{\rm{NO}}}}}_{2}^{-}$. This assumption is derived from the widespread presence of dissimilatory nitrite reductases in the periplasm of cultured denitrifiers²¹, where ${{{{\rm{NO}}}}}_{2}^{-}$ can be supplied from the extracellular space. Moreover, ${{{{\rm{NO}}}}}_{2}^{-}$ is often exported from the cytoplasm into the periplasm by transporters due to its toxicity at high intracellular concentrations²², making external exchange a likely scenario. However, a previous estuarine study hypothesized that ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers might rarely exchange ${{{{\rm{NO}}}}}_{2}^{-}$ with their extracellular environments¹⁹, which could explain the observed higher rates of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ compared to ${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$. A critical first step to explain the prevalence of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ in OMZs is to experimentally test this hypothesis.

Furthermore, even if most ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers do not exchange ${{{{\rm{NO}}}}}_{2}^{-}$ with the environment, this alone does not explain their dominance over the ${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway. Previous ecological theory and modeling work demonstrated that ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers have a competitive advantage over other denitrifier types in OMZs under dynamic conditions in which organic matter (OM) is sometimes replete and sometimes limiting microbial growth²³. In that model, diverse denitrifying functional types were described using the redox chemistry underlying each metabolism. The model also included a penalty for pathway length, which, together with the redox chemistry, indicated that the competitiveness for OM increased with denitrification pathway length, while that for nitrogen decreased. The different competitive abilities caused a shift of the ${{{{\rm{NO}}}}}_{3}^{-}$-reducing denitrifier community from single-step $\left({{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{NO}}}}}_{2}^{-}\right)$ to multiple-step denitrifiers (${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ and then ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}$) along a gradient of low to high OM:${{{{\rm{NO}}}}}_{3}^{-}$ supply. An intermediate regime, where OM limitation was periodically alleviated due to pulses of OM supply, and where ${{{{\rm{NO}}}}}_{3}^{-}$ was not yet depleted, favored the viability of the intermediate pathway length, ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$. The modeled pulsing of OM realistically mimics the time-varying nature of productivity and sinking OM in the ocean, and so is a more realistic portrayal of in situ conditions, particularly in shallower waters. In contrast, the model did not identify a favorable ecological niche for the ${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway in any conditions. However, this work did not focus on the relative N₂O production pathways along an oxygen gradient, considering the potential contributions of ammonia-oxidizing organisms to N₂O production.

Together, field observations, theoretical frameworks, and ecosystem modeling all point toward the dominance of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers in OMZs. However, critical questions remain. First, do most ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers take advantage of the relatively high ambient ${{{{\rm{NO}}}}}_{2}^{-}$ in OMZs, and if not, why? Second, where are the niche spaces and relative N₂O production rates of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers along an oxygen gradient, particularly when accounting for N₂O production by aerobic ammonia oxidizers? Third, how do the availability and type of OM, a more direct variable affecting this heterotrophic pathway than oxygen, but much less studied, impact the activity of the ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers? Addressing these questions is crucial for understanding the oceanic N₂O budget and predicting N₂O emissions, especially in light of ongoing natural and anthropogenic changes^24,25. Here, we investigate the niche dynamics and environmental controls governing N₂O production from ${{{{\rm{NO}}}}}_{3}^{-}$ using a combination of ¹⁵N stable isotope incubation experiments conducted in Earth’s largest OMZ, the Eastern Tropical North Pacific (ETNP) OMZ, and new analyses from an updated version of the OMZ ecosystem model²³.

Results and discussion

The majority of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers do not utilize ambient ${{{{\rm{NO}}}}}_{2}^{-}$

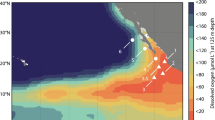
The rates of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ were determined at three stations in the ETNP OMZ using stable isotope (¹⁵N) incubation experiments (Fig. 2a). ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ was the largest N₂O producing pathway compared to previously measured production from ${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ and ${{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathways^18,26 during the same cruise, which is consistent with previous work^16,17. The maximum ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates (2.3–5.7 nM-N₂O d⁻¹) at all three stations were measured in samples collected from the upper layer of the anoxic region (Fig. S1). The maximum rate at the offshore OMZ station PS2 was lower than at the other two stations, but the large error bar associated with the rate at one location (250 m depth) implied that a higher rate there might be possible. Overall, these potential ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates were substantially higher than ${{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ (maximum rate = 0.15 nM-N₂O d⁻¹)²⁶ and ${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates (maximum rate = 0.5 nM-N₂O d⁻¹)¹⁸, which were determined during the same cruise, measured at the same time on the same research vessel.

Fig. 2: Sampling stations (PS1–PS3) investigated in this study and the response of NO₃^– → N₂O rates to unlabeled ¹⁴NO₂^– additions at oxycline and anoxic depths of two stations (PS2, PS3).

a Sampling stations, O₂ concentrations at σ_θ = 26.5 and maximum N₂O concentrations compiled from previous studies^20,47,51. b–e Error bars represent standard errors of linear regression slopes of estimated N₂O concentration accumulation over time. Filled circles indicate rates that are significantly larger than zero, and open circles indicate insignificant rates. An asterisk indicates a significant difference between the two rates in c, based on an unpaired two-tailed Student’s t-test (P < 0.05).

As a first step to explain the prevalence of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway in OMZs, we must determine whether ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers utilize ${{{{\rm{NO}}}}}_{2}^{-}$ from their external environments. Here, we used isotope dilution experiments to test the effect of excess ${{{{\rm{NO}}}}}_{2}^{-}$ on the rate of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$, which was measured by adding a known amount of ¹⁵N-labeled ${{{{\rm{NO}}}}}_{3}^{-}$ and unlabeled ${{{{\rm{NO}}}}}_{2}^{-}$ into natural seawater samples and tracking the accumulation of ¹⁵N in N₂O over time following previous methodology²⁷. If most ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers freely exchange ${{{{\rm{NO}}}}}_{2}^{-}$ with the environment, then adding unlabeled ${{{{\rm{NO}}}}}_{2}^{-}$ will dilute the ¹⁵N-labeled ${{{{\rm{NO}}}}}_{2}^{-}$ pool produced from the reduction of the labeled ${{{{\rm{NO}}}}}_{3}^{-}$. Thus, the fraction of labeled N₂O will be smaller resulting in a lower calculated rate of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ when more unlabeled ${{{{\rm{NO}}}}}_{2}^{-}$ is added. We collected samples from oxycline and anoxic depths at two OMZ stations where in situ ${{{{\rm{NO}}}}}_{2}^{-}$ concentrations were low (0–0.6 µM), so that added ¹⁴${{{{\rm{NO}}}}}_{2}^{-}$ (0.9–17.5 µM) would significantly dilute any ¹⁵${{{{\rm{NO}}}}}_{2}^{-}$ that may have leaked out of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ cells and been re-incorporated.

Overall, the measured ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates at two stations did not have a significant response to additions of unlabeled ${{{{\rm{NO}}}}}_{2}^{-}$ (Fig. 2b–e). This was particularly obvious at both sampled depths of the coastal station PS3 (average 3.8 ± 0.8 nM-N₂O d⁻¹, Fig. 2c, e). At the oxycline depth (90 m) of Station PS2, none of the rates were significantly larger than zero (Fig. 2b). The rate at the anoxic depth (120 m, Fig. 2d) of Station PS2 showed a slightly decreasing trend with increasing ${{{{\rm{NO}}}}}_{2}^{-}$ addition until ${{{{\rm{NO}}}}}_{2}^{-}$ reached 13.2 µM, and then the rate increased again at the highest ${{{{\rm{NO}}}}}_{2}^{-}$ concentration. However, except for the rate measured at 13.2 µM ${{{{\rm{NO}}}}}_{2}^{-}$ (the fourth data point on the plot, which was significantly smaller than the second data point), all the other rates were statistically indistinguishable, suggesting that ${{{{\rm{NO}}}}}_{2}^{-}$ addition also had little effect on ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates in these samples.

Collectively, these results suggest that microbial communities responsible for the rates of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ do not significantly exchange ${{{{\rm{NO}}}}}_{2}^{-}$ with the external environment. Therefore, ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ and ${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ are likely performed by two distinct microbial functional groups in this environment, and we cannot simply assume that the ${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway is just a down-stream reaction step within the overall ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway performed by the same ${{{{\rm{NO}}}}}_{3}^{-}$-reducing microbes. Accordingly, the complex marine N₂O production network (Fig. 1a) can be conceptualized as three separate processes, each tied to a distinct microbial functional group (Fig. 1b), though these functional groups need not map onto taxonomy (for example, each functional group may be composed of multiple taxonomic groups). Thus, in terms of functional groups, N₂O is produced by (1) ${{{{\rm{NO}}}}}_{3}^{-}$-reducing denitrifiers (${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$), (2) ${{{{\rm{NO}}}}}_{2}^{-}$-reducing denitrifiers $\left({{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}\right)$, and (3) ammonia-oxidizing archaea (AOA) during ammonia oxidation, including hybrid formation $\left({{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}\right)$. We assume nitrifier-denitrification (${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ performed by ammonia-oxidizing bacteria, which are rare in OMZs) is negligible, consistent with direct rate measurements in the eastern tropical North Pacific¹⁸. This functional partitioning implies that each N₂O production pathway occupies a distinct ecological niche, and their respective responses to environmental drivers (e.g., oxygen and OM availability) are likely to differ. Rather than treating these responses uniformly, they should be understood in the context of niche partitioning among microbial functional groups.

The ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway is compatible with oxygen

Oxygen is a well-known critical environmental factor that differentially impacts various N₂O cycling pathways^16,28,29. To examine its effects on the ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway, we performed O₂ addition experiments using samples collected from the oxycline and anoxic depths at two stations in the ETNP OMZ. Only two previous studies have experimentally examined the response of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates to O₂ additions, and these experiments showed that the rate was not inhibited by O₂ concentrations up to 7 µM in the ETNP OMZ¹⁷ and 23 µM in the ETSP OMZ¹⁶, respectively. However, both studies only sampled at the oxycline depths, and in one of the studies¹⁷ O₂ concentrations were calculated based on added and in situ O₂ concentration rather than monitored directly within incubation bottles. The calculated O₂ concentration does not always reflect the real O₂ concentration because O₂ diffuses through the bottle cap during sampling and incubation processes³⁰, and microbes consume O₂ rapidly in bottles³¹. Thus, directly measuring O₂ in bottles at multiple data points allows for a more accurate determination of concentration. Here, we used O₂ sensors to monitor O₂ concentration in bottles during incubations, at both oxycline and anoxic depths, and expanded the maximum O₂ addition to ~40 µM. This allowed us to better characterize the response of the ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway as performed by different microbial communities across a broader O₂ range and under more accurate in-bottle conditions.

In general, O₂ additions inhibited ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates in these incubation experiments. We observed inhibition at much lower O₂ concentrations (around 2 µM) compared to previous work, but significant rates were still detected at relatively high O₂ concentrations (Fig. S2). In the oxycline samples, most rates were not detectable (Fig. S2a, b), but significant rates at anoxic depths were detected when O₂ concentrations exceeded 10 µM in incubation bottles (Fig. S2a, c, d).

The effect of O₂ on ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ was also assessed by analyzing how ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates varied across a natural O₂ gradient by plotting measured rates against in situ O₂ concentrations at their respective sampling depths. These rates of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ at different locations represent different microbial communities and distinct environmental conditions besides O₂, such as temperature, salinity, pH, and OM availability. Thus, it is not surprising that distinct ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates were detected from different locations with similar in situ O₂ concentrations (Fig. S3), as previously observed^16,18. We extended the ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rate measurement to samples with in situ O₂ concentrations (200 µM) much higher than those in previous studies (<30 µM). Notably, we detected significant rates (0.04–0.48 nM-N₂O d⁻¹) from samples with in situ O₂ concentrations ranging between 194 and 200 µM at all three sampling stations (Figs. S1 and S3a). These rates are small compared to ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates at anoxic depth, but are comparable to N₂O production rates from ${{{{\rm{N}}}}{{{\rm{H}}}}}_{4}^{+}$ or ${{{{\rm{NO}}}}}_{2}^{-}$^18,26.

Traditionally, the relationship between ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates and O₂ concentration has been modeled as a smooth inhibition curve¹⁷, reflecting an intuitive assumption about O₂ sensitivity. However, our observations show that this relationship rarely follows a smooth pattern (Figs. S2 and S3). Deviations of the measured data points from this expected pattern were often attributed to experimental errors. However, our model analysis below suggests that microbial interactions set by their different resource competitive abilities can indeed lead to such heterogenous responses of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates to O₂ (Fig. 3).

Fig. 3: Schematic of the model and biomass, nutrients, and rates at quasi-equilibrium states from model simulations with different organic matter (OM) and O₂ supply rates.

a Schematic of the virtual chemostat model with diverse microbial types. b Changes of biomass along an increasing OM to O₂ supply ratio. c Changes of percentages along an increasing OM to O₂ supply ratio. Dashed red line indicates the percentage of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ contribution to the total N₂O production rate (where ${{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ contributes the remainder). Dashed gray line indicates the percentage of ${{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ in total ${{{{\rm{N}}}}{{{\rm{H}}}}}_{4}^{+}$ oxidized by ammonia-oxidizing archaea. d Changes of nitrogen-cycling rates along an increasing OM to ${{{{\rm{NO}}}}}_{3}^{-}$ supply ratio. b–d share the same legend shown on the right of (d). AerHet stands for aerobic heterotrophs. In b and c, OM supply rate is 0.3 µM-N per day, O₂ supply rate varies, and ${{{{\rm{NO}}}}}_{3}^{-}$ supply rate is at 1.2 µM per day. In (d), O₂ supply rate is zero, ${{{{\rm{NO}}}}}_{3}^{-}$ supply rate is at 1.2 µM per day, and OM supply rate varies. e–g N₂O concentrations, ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates and ${{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates with different O₂ concentrations, respectively. e–g share the same color bar shown on the right of g, which indicates different OM supply rate in the units of µM-N per day.

Ecological niche of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers

To unravel the mechanisms underlying the observed compatibility of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ with O₂ and the variable O₂ inhibition concentrations observed across different locations, we updated a recently developed ecosystem model²³. In this model, the key metabolisms responsible for nitrogen and O₂ cycling in OMZs are represented as microbial functional types, parameterized using the redox reactions underlying the metabolisms (Fig. 3a). The denitrifiers in particular are described using the thermodynamics of each denitrifier module as well as a pathway length penalty. Here, we modified the model to incorporate the ${{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway (see the “Methods” section) based on empirical relationships, determined using the same experimental methods as we used here to measure N₂O production rates^16,17. Following previous methods^23,32,33, this model does not impose any pre-defined O₂ inhibition term or threshold for microbial processes. Instead, ecological niches emerge from ecological interactions among different microbial functional types and the resources. To mimic the different water layers of the OMZ, constant ${{{{\rm{NO}}}}}_{3}^{-}$, varying O₂ and dynamic OM are supplied into the model (Fig. 3a). Here, we expanded the analysis to include a broader range of O₂ supply rates than in the original model²³. For each supply ratio, results are averaged over time after the system reaches a quasi-equilibrium state, where microbial biomass and nutrient concentration oscillate in a regular repeating pattern due to the periodic supply of OM.

The model successfully reproduces the accumulation of N₂O to hundreds of nanomolar when O₂ is below 1 µM (Figs. 3e and S4a, e). Overall, ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates decrease with increasing O₂ concentration (Fig. 3f) because the fraction of the microbial community operating anaerobically decreases with increasing O₂ supply. However, the apparent O₂ sensitivity of the model solutions—defined here as the relationship between the resulting steady-state O₂ concentration and the ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rate—depends additionally on the OM supply rate. In general, higher OM supply rates enhance the O₂ tolerance of the ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway (Figs. 3f and S4k). Notably, changes in ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates across O₂ and OM supply gradients are not smooth (Figs. 3f and S4k). This is due to complex microbial interactions driven by the confounding impacts of these two modes of control via the different nutrient supply ratios, primarily OM:${{{{\rm{NO}}}}}_{3}^{-}$ and OM:O₂ (Fig. 3b, d). In our model, the ${{{{\rm{NO}}}}}_{3}^{-}$ supply rate is constant, so the change in OM supply rate drives the change in OM:${{{{\rm{NO}}}}}_{3}^{-}$ supply. Meanwhile, both the OM supply rate and the O₂ supply rate together control the OM:O₂ supply.

Consistent with previous findings^23,32, increasing OM:O₂ supply generally shifts the microbial community from exclusively aerobic heterotrophs to the coexistence of aerobic heterotrophs and denitrifiers, and eventually to a denitrifier-only scenario (Fig. 3b), and increasing OM:${{{{\rm{NO}}}}}_{3}^{-}$ supply generally shifts ${{{{\rm{NO}}}}}_{3}^{-}$-reducing denitrifiers from ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{NO}}}}}_{2}^{-}$, to ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ and finally to ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}$ denitrifiers (Fig. 3d). This shift in ${{{{\rm{NO}}}}}_{3}^{-}$-reducing denitrifiers sets niche boundaries of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers in the variable OM and O₂ supply landscape (Figs. 3c and S4k).

However, the dynamics within the microbial community are further complicated by the presence of chemoautotrophic microbes, especially ${{{{\rm{NO}}}}}_{2}^{-}$-oxidizing bacteria (NOB) and AOA (Fig. S4h, i). NOB and AOA disrupt the otherwise smooth increase in aerobic heterotroph biomass (Fig. S4g–i) and O₂ concentration (Fig. S4a). NOB utilize ${{{{\rm{NO}}}}}_{2}^{-}$ produced from ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{NO}}}}}_{2}^{-}$ denitrifiers alone when OM supply and O₂ supply are low, and from both ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{NO}}}}}_{2}^{-}$ denitrifiers and AOA when these supplies are high. At the peripheries of anoxic zones, NOB occupy a unique niche that allows them to efficiently deplete O₂, and competitively restrict the growth of aerobic heterotrophs³³. Both NOB and AOA achieve their highest biomass in this unique niche (Fig. S4). In particular, the high AOA biomass combined with the high N₂O yield (3.2%) due to the low O₂ (0.06 µM) in this unique niche leads to a local peak in ${{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ production (Figs. 3c and S4f). The heterogeneity in the relationship between N₂O production rates and O₂ concentrations in the model, caused by competition and facilitation among different microbial functional groups when O₂ and OM supplies change, mirrors the variabilities in observations. In other words, our model suggests that N₂O production rates should not conform to a smooth inhibition curve. Because our model does not impose fixed O₂ inhibition functions or thresholds for any microbial functional type, these O₂ niches are not pre-specified but arise from the outcome of the competitive and cooperative interactions among the functional types.

To compare the model results with observational data, which typically report O₂ concentration (rather than O₂ supply), we plotted the resulting modeled quasi-equilibrium N₂O concentrations, ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates, and ${{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates against O₂ concentrations (Fig. 3e–g). As in our experiments, modeled ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates decrease with increasing O₂ concentration, but the model predicts significant ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates when the average O₂ concentration is as high as 30 µM (Fig. 3f). The compatibility of the ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway with high O₂ concentrations predicted by the model is consistent with our experiments (Figs. S2 and S3). ${{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates also generally decrease with increasing O₂, yet unlike the denitrifier production, low but non-zero rates were sustained throughout the tested O₂ concentration range (Fig. 3, compare the insert panels f and g) as often observed, which contribute to supersaturated N₂O concentrations in oxygenated ocean (Fig. 3e, insert)^11,29. Since the N₂O yield from ${{{{\rm{N}}}}{{{\rm{H}}}}}_{4}^{+}$ is uncertain and was detected to be more than 20% when O₂ concentration is nearly zero¹⁸, we tested a much higher N₂O yield from ${{{{\rm{N}}}}{{{\rm{H}}}}}_{4}^{+}$ (~60%). Results show that ${{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates are still much lower than ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates because rates of ${{{{\rm{N}}}}{{{\rm{H}}}}}_{4}^{+}$ oxidation, an aerobic process, are low with limited O₂ (Fig. S5). In summary, the model supports a conceptual framework in which ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ and ${{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ co-occur under suboxic conditions, with ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ as the dominant pathway (Fig. 3c, f, g). Under oxic conditions, ${{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ becomes the primary contributor to N₂O production, because it is associated with the aerobic metabolism (ammonia oxidation) (Fig. 3c, g).

The type of OM matters

Despite the important role of OM in regulating the ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway, as indicated by our model results (Fig. 3), the effect of OM on ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ has been less thoroughly investigated experimentally compared to the effect of O₂. In reality, OM is an immensely diverse mixture of thousands of compounds derived from various living or dead particulate OM (POM) sources, with a wide range of turnover rates³⁴. OM with distinct structures and properties may affect the ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway differently. However, despite recent analytical advances in the field^35,36,37,38, identifying chemical structures of OM remains challenging.

Here, we used a simplified but practical approach to test the effect of OM type without specifically characterizing its chemical composition. We collected naturally occurring POM samples in different size fractions from different depths, and measured their carbon concentrations and their nitrogen to carbon ratios. We added these natural POM samples and commercially available casamino acids to samples collected from different depths and measured the rates of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ (Fig. 4) compared to control samples without OM additions. At Station PS2, OM that was larger than 2 µm collected from 100 m stimulated ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates the most in samples from both oxycline and anoxic depths (Fig. 4a, c). At Station PS3, the OM that increased the rates the most was from 55 m and was larger than 2 µm (Fig. 4d). OM from the same depths but in a smaller size fraction (0.4–2 µm) or OM from most other depths did not stimulate N₂O production rates (Fig. 4b, d). Neither carbon concentration nor nitrogen-to-carbon ratio has a clear effect on ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates in most samples, even though the rate measured for samples from the anoxic depth at Station PS3 showed a positive relationship with C concentration (Fig. S6). At both stations, rates at anoxic depths were more stimulated by OM additions than those at oxycline depths (Fig. 4), which might be due to lower in situ OM availability at greater depths.

Fig. 4: The response of NO₃^–→N₂O rates to organic matter (OM) additions in samples collected from oxycline (90 m, 3.7 µM O₂ at Station PS2 and 40 m, 5 µM O₂ at Station PS3) and anoxic depths (120 m at Station PS2 and 60 m at Station PS3).

a–d OM types, except for the casamino acid, are labeled by their collection depth and size fractions (0.4: 0.4–2 µm, 2.0: >2 µm or bulk: >0.4 µm). Error bars represent standard errors of linear regression slopes of estimated N₂O concentration accumulation over time. Filled bars indicate rates that are significantly larger than zero, and open bars indicate insignificant rates. The asterisk indicates that a rate is significantly different from the control based on an unpaired two-tailed Student’s T-test (P < 0.05).

Interestingly, the type of OM that most strongly stimulated ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates at both stations (OM from 100 m and 55 m in Fig. 4) originated from the deep chlorophyll maximum (Fig. S1 in Sun et al. (2021)³¹), a subsurface layer where specific phytoplankton accumulate due to their adaptation to low light and low oxygen conditions. OM from these depths is likely of “highest quality”—freshly produced by phytoplankton and thus is the most familiar and preferred OM of heterotrophic microbes. However, this OM is not necessarily the most labile or consists of the most carbon, as indicated by the nitrogen-to-carbon ratio and the carbon concentrations (Fig. S6). In a previous study examining the effect of OM on nitrogen loss via denitrification (${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}$) and anammox, the OM that stimulated nitrogen loss rates the most was not the OM with the highest nitrogen to carbon ratio or more carbon, but the OM collected in situ³⁹. The authors hypothesized that local in situ OM was more beneficial to microbes, consistent with our hypothesis, suggesting that microbial communities are adapted to metabolize the types of OM they are regularly exposed to in their environment. In addition, OM produced by phytoplankton may serve more than just as a carbon source for heterotrophic microbes. OM could also support mutualistic relationships by providing essential micronutrients⁴⁰. It is noteworthy that OM from the same depths but in the smaller size fraction (0.4–2 µm) did not stimulate the ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ rates (Fig. 4). This size fraction likely consisted of mainly live picophytoplankton cells, implied by the known cell size of the dominant phytoplankton at these depths and the strong green coloration of these samples (Fig. S7). These results support the hypothesis that OM produced by phytoplankton or derived from the degradation of their dead cells is preferred by ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers. We did not differentiate OM larger than 2 µm, but a recent study on N₂O production in oxygenated estuary-coastal ocean waters showed that OM particle size influenced N₂O production pathways: ${{{{\rm{NH}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ dominated N₂O production in smaller particles while ${{{{\rm{NO}}}}}_{{{{\rm{x}}}}}^{-}$ (${{{{\rm{NO}}}}}_{3}^{-}$ and ${{{{\rm{NO}}}}}_{2}^{-}$)→N₂O dominated in larger ones⁴¹. In the oxic seawater, larger OM-contained particles are more likely to create anoxic microenvironments than smaller particles^42,43, which could be a main reason for the detection of denitrification-derived N₂O in large particles.

Remaining challenges for understanding the N₂O cycle

This study employs microbial ecology to mechanistically explore the dominance of the ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway in OMZ N₂O production and its responses to oxygen and OM availability and different types of OM. Our results show that ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers are compatible with low but non-zero oxygen concentrations and are favored by dynamically supplied, freshly produced OM. These experimental findings, together with model results, suggest that the oxic–anoxic interface represents a key ecological niche for ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers.

However, many challenges remain in fully understanding the N₂O cycle in OMZs. First, while our modeling framework parameterizes most microbial functional types using their underlying redox chemistry, we relies on an empirical relationship to describe N₂O production from AOA due to the lack of a stoichiometric description of these complex pathways. In addition, a pure AOA culture with a marine origin was demonstrated to produce O₂ and cycle N₂O anaerobically^44,45. New research shows that AOA can also produce N₂O via a novel pathway involving nitroxyl dimerization, although it remains unclear how important this pathway would be in the ocean⁴⁶. These findings and unknowns highlight the need to better understand the multiple, potentially overlapping pathways by which AOA produce N₂O. This remains a major area for future research.

Second, we still lack an explanation for the small, yet nonnegligible ${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ pathway, which is competitively excluded in our model by the other functional types. Specifically, ${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ denitrifiers are typically outcompeted by ${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}$ denitrifiers when ${{{{\rm{NO}}}}}_{2}^{-}$ is limiting, and by NOB when O₂ is present. We hypothesize that ${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ can be sustained when ${{{{\rm{NO}}}}}_{2}^{-}$ limitation is alleviated, which is likely to be the case in the anoxic core of OMZs where ${{{{\rm{NO}}}}}_{2}^{-}$ accumulates. Incorporating our microbial functional types in more complex higher-dimensional models (i.e., 3D and eddy-resolving)⁵ will allow the simulation of the interplay among microbial and physical processes⁴⁷ that could lead to ${{{{\rm{NO}}}}}_{2}^{-}$ accumulation that cannot be captured by our simple 0-D model.

Third, our study highlights that different types of OM may differentially affect N₂O production. Although characterizing OM composition across different ocean layers and linking OM types to specific microbial processes remains challenging, recent advances in high-resolution molecular techniques and in situ biogeochemical measurements offer promising approaches to address this knowledge gap. In summary, advancing our understanding of marine N₂O cycling will require a multidisciplinary approach that integrates experimental methods, mechanistic modeling, and theoretical analyses, with each informing and refining the others.

Methods

Sampling and stable isotope incubation experiments

We measured the rate of ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$ using stable isotope (¹⁵N) incubation experiments, following established protocols²⁷. Samples were collected from three stations within the oxygen-deficient zone of the Eastern Tropical North Pacific on R/V Sally Ride (SR1805) during March and April 2018 (Fig. 2a). Water was collected from 10 different depths using 30 L Niskin bottles, equipped with a Seabird CTD (conductivity, temperature, depth, and oxygen with a SBE 43 sensor), and transferred into 60 mL glass serum vials for ${{{{\rm{NO}}}}}_{3}^{-}$ reduction and N₂O production measurements. Oxygen concentrations from the SBE sensor were corrected by STOX sensors⁴⁸.

For the manipulation experiments, two depths corresponding to the oxycline and upper anoxic zone were selected. These included three experimental setups: (1) for O₂ sensitivity experiments, in which varying amounts of air-equilibrated seawater (0, 0.2, 0.5, 1, 2, 5, 8, 12, 20 mL) from the same Niskin bottle were added into He-purged vials to achieve O₂ concentrations ranging from 10 nM to 40 µM. Oxygen levels were monitored in duplicate bottles per treatment using optical sensor spots (PyroScience). (2) ${{{{\rm{NO}}}}}_{2}^{-}$ addition experiments, in which five treatments of ¹⁵${{{{\rm{NO}}}}}_{3}^{-}$ were amended with different amounts of unlabeled natural-abundance ${{{{\rm{NO}}}}}_{2}^{-}$ to reach final concentrations of 0.9, 4.4, 6.5, 13.2, 17.5 µM ${{{{\rm{NO}}}}}_{2}^{-}$.

(3) OM addition experiments, in which naturally occurring POM was collected using in situ pumps (McLane; for surface waters, a Husky 307, Graco was used) at selected depths and filtered onto two size classes (0.4 µm Millipore membrane filters, 2 µm Sterlitech Polycarbonate filters), with a 53 µm prefilter to exclude grazers. Depths for OM collection were selected based on water column features, such as mixed layer depths (50 m at PS2, 15 m at PS3) and the deep chlorophyll maximum (100 m at PS1 and 55 m at PS3), for incubations conducted at the same stations. POM collected with in situ pumps represents a mixture of suspended and sinking particles. OM stock solutions were prepared by rinsing the filtered OM with sterile seawater into serum bottles, autoclaved for 20 min, and subsequently purged with He for 20 min. A 0.1 mL aliquot of the concentrated OM stocks was added to each incubation vial, and casamino acids (2.4 µM final concentration) were used as an additional labile OM treatment. To assess the quality and quantity of the collected particles, 40 mL of the OM stocks were filtered onto pre-combusted GF/F filters, dried and stored frozen until analysis. In the laboratory, total carbon, nitrogen, and biomass δ¹³C and δ¹⁵N were analyzed on a Vario ISOTOPE Select elemental analyzer (Elementar Isoprime). An in-house aminocaproic acid standard (ACROS) and the USGS 40 L-glutamic acid standard were used for measurement calibration.

All serum bottles were amended with ¹⁵N-${{{{\rm{NO}}}}}_{3}^{-}$ to achieve a final concentration of 3 µM, incubated in the dark at 12 °C, and duplicate vials were terminated after 12 and 24 h by adding 200 µL of saturated ZnCl₂. One bottle from each treatment was immediately killed to serve as the t0 and killed control. N₂O production rates were determined by analyzing the production of ⁴⁵N₂O and ⁴⁶N₂O using a custom-built gas chromatography isotope ratio mass spectrometer, as described by Frey et al. (2022)²⁶. ¹⁵${{{{\rm{NO}}}}}_{2}^{-}$ production from ¹⁵${{{{\rm{NO}}}}}_{3}^{-}$ incubations was assessed using the azide method⁴⁹. Rates were calculated from the slope of the linear regression of ¹⁵N production over time and were corrected for the fraction of the N pool initially labeled in the nitrate pool.

Statistical tests

Unpaired two-tailed Student’s T-test (significance indicated by P < 0.05, Graphpad) was used to test if the slopes of the linear regressions were significantly different from zero for all experimental data and to test if two rates were significantly different from each other in Fig. 2b–e and Fig. 4. T, P, n and df are presented to their corresponding experimental data in an Excel file in Github (https://github.com/xinsun12/ChemostatModel_clean_N2O).

An ecosystem model with microbial functional types producing and consuming N₂O

We performed analyses on N₂O production pathways and related microbial functional types using a microbial ecosystem model (Fig. 3a). We describe microbial functional types in the model based on their unique redox chemistry following previous protocols^23,32. In summary, we use half reactions to describe the oxidation of the electron donor, the reduction of the electron acceptor, and the biomass synthesis. We included the same microbial functional types as our previous work. These microbes are two autotrophic nitrifier types (ammonia-oxidizing organisms, AOO and nitrite-oxidizing organisms, NOO), an autotrophic anaerobic ammonia-oxidizing bacteria type (anammox bacteria), an aerobic heterotrophic type, and six types of heterotrophic denitrifiers (${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{NO}}}}}_{2}^{-}$, ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$, ${{{{\rm{NO}}}}}_{3}^{-}\to {{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}\to$N₂, ${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}$, ${{{{\rm{NO}}}}}_{2}^{-}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}\to {{{{\rm{N}}}}}_{2}$, and ${{{{\rm{N}}}}}_{2}{{{\rm{O}}}}\to {{{{\rm{N}}}}}_{2}$).

In the current model, updated from our recent framework²³, we implemented the production of N₂O by AOO. Since the redox chemistry underlying the N₂O production from AOO is highly complicated, and the stoichiometry of these reactions has not been fully resolved¹¹, we used the measured N₂O produced from AOO per nitrite produced from ammonia to represent N₂O production from AOO^16,17.

$${{\rm{Rate}}}\; {{\rm{of}}}\ {{{{\rm{N}}}}{{{\rm{H}}}}}_{4}^{+}\to {{{{\rm{N}}}}}_{2}{{{\rm{O}}}}=\frac{1}{1+\frac{1}{\left(\frac{0.2}{{O}_{2}}+0.08\right)\%}}\times {{\rm{rate}}}\; {{\rm{of}}}\ {{{{\rm{N}}}}{{{\rm{H}}}}}_{4}^{+}\to {{{{\rm{N}}}}{{{\rm{O}}}}}_{2}^{-}$$

(1)

We chose to use this empirical equation (Eq. (1)) because it was determined using the same experimental methods as we used here to measure N₂O production rates.