Introduction

Caveolae are nanoscale invaginations of the plasma membrane which form a characteristic and abundant feature of the plasma membrane in many mammalian cell types1. A typical caveola shape can be described as a 50–80 nm diameter, nearly spherical bulb connected to the plasma membrane by a narrow neck1.

Since their discovery more than 70 years ago2,3 caveolae have remained a focus of cell biological research due to the constantly emerging insights into their multiple functions in cell physiology4,5 and the deepening understanding of the molecules and molecular complexes involved in caveola formation and dynamics6,7,8. To date, much of the focus on the mechanisms governing caveola membrane shape, formation, and disassembly has been on the protein content of these surface domains, but we have known for a long time that lipids are critical in moderating caveolar structure and function9,10,11. Yet, despite a wealth of phenomenological knowledge, the physical mechanisms governing caveola shaping by the critical constituents of caveolae, through the co-function of proteins and lipids, remain elusive. The present work aims to propose such a mechanism by accounting for the recent breakthrough in the structural biology of caveola-forming proteins along with the state-of-the-art information on the conformations of caveolar membranes and the role of lipids in caveola biogenesis.

Since detailed reviews are already available on the structure and function of caveolae6,7,12, we present only a sketch of the recently emerged experimental data relevant to the proposed model.

The major protein families responsible for caveola formations in mammalian cells are the integral membrane proteins, caveolins, the peripheral filamentous proteins, cavins, and the dynamin family protein EHD21,6,13,14. The caveolin and cavin self-assemble on the membrane surface into a dense two-layer complex. EHD2 forms ring-like oligomers decorating the rims of the caveolin-cavin coats.

Crucial for elucidating the mechanism of caveola formation is to understand the role of each of the proposed structural components. An insight into this issue was provided by experiments on a bacterial system that lacks endogenous caveolin proteins or intracellular trafficking and, hence, provides a simplified model system to understand membrane sculpting by caveolins15,16. The expression of a wide range of recombinant caveolins in Escherichia coli resulted in the formation of membrane-enclosed vesicles, termed h-caveolae, derived from the cytoplasmic membrane15. The curvature, size, and caveolin density of h-caveolae were similar to those of native caveolae15. Similar observations were made through the expression and insertion of caveolin in a Leishmania-based cell-free expression system17. This suggests that caveolins must be the primary factor in the mechanism of caveola shaping, with cavins and EHD2 playing assisting and regulatory roles. Consistent with this, some invertebrate species were shown to possess caveolin-dependent membrane invaginations in the absence of cavin proteins6,18. The major data was accumulated for the most ubiquitous member of the caveolin family, CAV1, referred to below simply as caveolin, for brevity.

Another important question is about the oligomerisation state in which caveolin generates membrane curvature during caveolar biogenesis. Along the pathway of caveola formation, caveolin undergoes sequential stages of oligomerisation, starting with monomers, which are followed by higher-order oligomers. Caveolin monomers are synthesized in the ER19,20 and then transported to the Golgi complex in a COPII-dependent process20. The cavin monomers assemble in the 8S oligomeric complexes in the late Golgi complex21. The 8S complexes are then transported to the plasma membrane, forming higher-order 70S complexes with cavin proteins characteristic of mature caveolae22.

It was previously hypothesized22 and predicted by numerical simulations23 that caveolin monomers alone22,24 or in complex with cholesterol23 can bend membranes, implying that they can drive caveola shaping. Alternatively, the curvature was assumed to emerge after the 8S complex formation7. An experimental discrimination between the different possibilities was again offered by the bacterial system, in which disease-associated mutations that blocked 8S oligomer formation15,16, as shown directly by cryoEM25, blocked also curvature driven by caveolin15. This provided direct evidence that the caveolin 8S complex, rather than a caveolin monomer, serves as a minimal functional unit of the membrane curvature generation. This was indirectly supported by the results obtained on mammalian cell systems, showing that mutant caveolin with impaired protomer-protomer interaction exhibits reduced plasma membrane association and accumulates in the Golgi complex21,26,27.

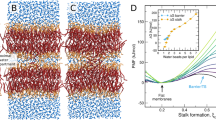
The ability of caveolin 8S complexes to form the caveolar bulbs must be determined by their structure and the mode of interaction with the membrane matrix. According to the recent experimental advance, a caveolin 8S complex consists of 11 copies of the protein assembled into a tightly packed flat (but see refs. 28,29) disc of about 14 nm diameter and 3 nm thickness30,31. One of the planes and the outer rim of a caveolin disc are hydrophobic, whereas the second plane is hydrophilic and contains a protruding β-barrel in the middle30,31. This structure suggests a particular character of the caveolin disks’ association with the plasma membrane. It has been predicted6,7,30,31,32 and confirmed by molecular dynamic simulations33 that a caveolin disc embeds into the cytosolic membrane leaflet such that its flat hydrophobic plane comes into contact with the bottom surface of the extracellular membrane leaflet, and this insertion displaces 250 lipid molecules on the cytosolic leaflet (Fig. 1).

Fig. 1: Description of the model. Yellow rectangles represent caveolin disks.
figure 1

The part/s of the distal monolayer contacting the hydrophobic plane/s of the disc/s (monolayer I) is/are shown in red color. The monolayer fragment/s that do not contact the disc plane/s (monolayers II and III) is/are shown in dark blue colour. A The reference state preceding the relaxation of the system. The dashed lines represent the monolayer neutral planes. B A decrease of the number of lipid molecules contacting the disc leads to the area stretching of the monolayer I. C Relaxation of the monolayer I stretching that leads to tilt and splay in the monolayers I and II. The axes \({{{\rm{x}}}}_{{{\rm{I}}}}\) and \({{{\rm{x}}}}_{{{\rm{II}}},{{\rm{III}}}}\) are chosen to describe, respectively, the monolayer I and the monolayers II and III; (D) Kinking of the membrane profile, which generates the tilt and splay in the monolayer III but results in an overall relaxation of the system’s elastic energy. E Membrane with multiple disks. Notations: \({{{\rm{\phi }}}}_{{{\rm{B}}}}\) and \({{\rm{\varphi }}}\) in (C–E) are, respectively, the boundary tilt and kink angles; \({{\rm{R}}}\) and \({{\rm{L}}}/2\) in (E) represent, respectively, the disc radius and the half-distance between adjacent disks determined along the system’s mid plane; the dashed lines in (E) show the boundaries of the building block defined as the system and at the same time represent the radius of the effective curvature, \({{{\rm{\rho }}}}_{{{\rm{eff}}}}=\frac{1}{{{{\rm{J}}}}_{{{\rm{eff}}}}}\).

Full size image

The activity of caveolins and the accessory proteins in caveola biogenesis in mammalian cells is significantly affected and modulated by the membrane lipids, with a special role played by cholesterol in mammalian cells6,20,34. Depletion of cholesterol from the plasma membrane leads to caveolar instability and flattening of the caveolar invaginations9,35. Yet, the generation of h-caveolae in sterol-free E.coli15, obviously, does not require cholesterol. Therefore, at least some of the probably multiple roles of cholesterol in caveolar biogenesis can be played by other lipids.

Caveolae generated by caveolins, with or without (h-caveolae) cavins, have peculiar configurations. While initially the shapes of caveolar bulbs were regarded as smoothly rounded, high-resolution EM imaging revealed the bulb profiles to have a faceted appearance15,16,36. The size of the facets closely aligns with the known size of caveolin disks which suggests that the facets are paved by the disks30,36 whereas the caveolin-free membrane gaps between the flat facets must be kinked to generate the overall closed membrane configuration (but see refs. 28,29).

The outlined experimental information and qualitative ideas on the caveolin disks driving caveola formation and the faceted appearance of caveolar bulbs pose a challenge to understanding the physical mechanism behind all this phenomenological knowledge. The outstanding specific questions are about the forces responsible for the membrane kinking at the vertices of the faceted caveolar profiles, resulting in the overall curved shapes of the caveolar surfaces, and the mechanism by which lipids, and particularly cholesterol, influence caveola formation and disassembly.

Here we propose a model addressing these questions. The central hypothesis of our model is that the interaction energy of the extracellular membrane leaflet with the hydrophobic plane of a caveolin disc differs from that with the cytoplasmic leaflet. We show that the difference in these energies drives the generation of elastic stresses and strains within the membrane monolayers, which, in turn, favor the membrane kinking in the vicinity of the disc boundary and, hence, result in an overall curved faceted membrane configuration. We predict that these elastic stresses drive enrichment of the extracellular leaflets of caveolar membranes in lipids having effective molecular shapes of truncated cones and thus characterized by a strongly negative intrinsic molecular curvature such as cholesterol37 and diacylglycerols (DAG)38. We demonstrate that such lipids facilitate the concentration of the caveolin disks in the membrane plane into dense domains and enhance the emerging curvature of caveolar membranes. We discuss the major points of difference between the present and the alternative28,39 models of membrane shaping by caveolin 8S complexes.

Results

Qualitative essence of the model

To qualitatively explain the central idea of the model, we start by considering the effect of embedding a single disc into one of the membrane monolayers of an initially flat lipid bilayer. We discuss the factors leading to the kinking of the membrane profile along the edge of the disc, which can be seen as the generation of an overall membrane curvature. Further, we qualitatively consider the curved membrane configurations resulting from the insertion of multiple disks into the same monolayer and discuss the effective interaction between the disks, expected to be mediated by the monolayer elastic stresses. We qualitatively discuss the expected impact of lipids with negative intrinsic molecular curvature, such as cholesterol and DAG, on the membrane shaping by the inserted caveolin disks.

Membrane with a single caveolin disc

The membrane monolayer harboring a caveolin disc will be referred to below as the proximal monolayer, whereas the second monolayer will be called the distal one. We assume that the hydrophobic plane of the disc reaches the bilayer’s midplane and, therefore, contacts the hydrophobic plane of the distal monolayer (Fig. 1A). The fragment of the distal monolayer contacting the disc will be referred to as the monolayer I. The rest of the distal monolayer will be called the monolayer II. The part of the proximal monolayer flanking the disc will be referred to as the monolayer III (Fig. 1A).

Our major assumption is that the contact between the distal and the proximal monolayers along the bilayer mid-plane is energetically more favorable than the contact between the distal monolayer and the hydrophobic plane of a caveolin disc. We will denote the former and latter contact energies related to one lipid molecule by, respectively, \({\varepsilon }_{L}\) and \({\varepsilon }_{P}\). The origin and driving force of all the effects considered below is the contact energy difference,

$$\Delta \varepsilon={\varepsilon }_{P}-{\varepsilon }_{L},$$
(1)

which is assumed to be positive, \(\Delta \varepsilon > 0\). In the following, we will refer to ∆ε as the differential contact energy.

The chief idea of our model is that the differential contact energy, ∆ε, causes the generation of elastic deformations and stresses within the membrane monolayers, which, in turn, drive the kinking of the membrane profile at the disc’s edge. To explain the model intuitively, we decompose the kinking process into sequential steps.

In the first step, the caveolin disc of the area, Ap, is inserted into the initially flat membrane, but the system is kept flat, and the distal monolayer remains intact (Fig. 1A). We denote by No the number of lipid molecules found at this stage in the monolayer I, so that the in-plane area per lipid molecule, a, in this monolayer is \({a}_{0}=\frac{{A}_{p}}{{N}_{0}}\). Here and in the following, the area per lipid molecule, a, is determined at a special intra-monolayer plane referred to as the neutral plane for which the deformations of stretching are energetically decoupled from the deformations of bending40,41 and, hence, of the deformation of the splay of the lipid hydrocarbon chains42,43 (see below). The neutral plane lies, approximately, along the interface between the polar and hydrophobic moieties of a lipid monolayer (Fig. 1A)38,40,44.

At the second step, because of the positive differential contact energy, \(\Delta \varepsilon > 0\) (Eq.1), the system tends to reduce the number of lipid molecules in the monolayer I. This can be achieved by shifting a number of lipid molecules, ∆N, from the monolayer I into the monolayer II (Fig. 1B). As a result of such shifting, the hydrophobic plane of the disc, Ap, turns out to be contacted by a smaller number, N0-∆N, of lipid molecules, meaning that the monolayer I undergoes stretching (Fig. 1B). The in-plane area per one lipid molecule in the monolayer I increases and becomes, \(a={a}_{0}+\Delta a\), with the area increment approximately equal \(\Delta a\approx {a}_{0}\frac{\Delta N}{{N}_{0}}\). The monolayer stretching is associated with an elastic energy45,46, which is determined by the extent of deformation, \(\frac{\Delta a}{{a}_{0}}\), and the monolayer rigidity for stretching characterized by the stretching modulus, Γ45,46.

The stretching energy accumulated at the second step can be partially or almost fully released at the third step in which the lipid molecules located at the boundary between the monolayers I and II (i.e., along the edge line of the caveolin disc) tilt towards the center of the disc (Fig. 1C). This tilting enables the neutral plane of the monolayer I to contract and, hence, the lipid stretching, ∆a, to relax while keeping the same reduced number of lipid molecules, N0-∆N, in the monolayer I. We will quantify the extent of this tilt by the angle, \({\phi }_{B}\), referred to below as the boundary tilt (Fig. 1C).

The larger \({\phi }_{B}\) the more efficient the relaxation of the monolayer stretching and the reduction of the stretching energy. Yet, lipid tilting requires an alternative energy cost. Being induced at the boundary between the monolayers I and II the lipid tilt propagates47,48 into each of these monolayers, its value decreasing with the distance from the boundary (Fig. 1C). The tilt variation along the monolayer surface gives rise to the splay deformation, whose essence is the relative spreading of the lipid polar heads and the ends of the hydrocarbon chains42,43,48 (Fig. 1C). The splay is conventionally defined as positive if the lipid heads are spread compared to the chain ends and as negative otherwise42,43. The monolayer tilt and splay are associated with elastic energies, which are determined by the extent of each deformation and the related rigidity characterized by the elastic modulus \({\kappa }_{t}\) for tilt and κ for splay42,43,48,49.

Generally, the outcome of the second and third steps is a combination of stretching of the monolayer I and the tilt-splay in the monolayers I and II. Yet, the relative extent of these deformations is set by the relationships between their rigidities. The dominant deformation is the one for which the membrane monolayer has the least rigidity. Lipid monolayers are considerably less rigid for the tilt-splay deformation than for the area stretching. Indeed, the monolayer stretching modulus, Γ, is of the order of a few hundred \(\frac{{{\rm{mN}}}}{m}\)45,46, whereas the tilt modulus, \({\kappa }_{t}\), is in the range of a few tens \(\frac{{{\rm{mN}}}}{m}\)43,48,49,50, and the splay modulus, κ ≈ 4 10−20 Joule51,52,53 related to the square of the monolayer thickness h ≈ 2nm is of the order of \(\frac{\kappa }{{h}^{2}}\approx 10\) \(\frac{{{\rm{mN}}}}{m}\). Therefore, the leading deformation resulting from the second and third steps must be that of the tilt-splay, while the monolayer stretching in the monolayer I must be negligibly small. In other words, the tilt-splay deformation at the third step must result in, practically, complete relaxation of the area stretching so that the latter will be neglected.

At the fourth step, we allow the system to deviate from the flat state by developing a kink of the membrane midplane at the disc’s edge (Fig. 1D) in case this can relax the tilt-splay energy. We quantify the extent of the kink by the kink angle, φ (Fig. 1D). A simple geometrical consideration shows that for the monolayer II, the kinking reduces its tilt at the boundary with the monolayer I from \({\phi }_{B}\) to \({\phi }_{B}-\varphi\) (Fig. 1D).

At the same time, the kinking results in the generation of the tilt-splay deformation in the monolayer III with the tilt at the boundary with the disc equal to the kink angle, φ. As a result, the kinking of the membrane profile reduces the elastic energy accumulated in monolayer II but generates some elastic energy in monolayer III. Yet, as we show by the calculations (see SI), the kinking enables a reduction of the overall elastic energy of the system and is, therefore, energetically favorable.

Taken together, the major idea of the model is that the differential contact energy, \(\Delta \varepsilon\) (Eq. 1), favors a kinking of the membrane profile at the edge of the inserted caveolin disc (Fig. 1D).

In the following sections, we quantitatively analyze the dependence of the kink angle, \(\varphi\), on the differential contact energy, \(\Delta \varepsilon\), by using the models of the membrane tilt and splay elasticity.

Membrane with multiple caveolin disks

To grasp the qualitative essence of the membrane shape generated by multiple caveolin disks, we can consider it to be composed of elementary units, each unit represented by a bilayer fragment containing a single disc flanked by lipid bilayer fragments and having a kinked profile as discussed above (Fig. 1D). Putting such units side-by-side as mosaic elements with a smooth transition between their tilt and shape profiles provides an overall curved configuration (Fig. 1E). The effective curvature of the membrane, \({J}_{{eff}}\), is set by the kink angle, \(\varphi\), and the effective arc length, which is equal to the sum of the disc radius and the half-distance, L/2, between the edges of the neighboring disks (Fig. 1E).

There must be a cross-talk between adjacent disks mediated by an interplay between the elastic stresses generated in the membrane matrix by each of them. This interplay is expected to affect the values of the kink, \(\varphi\), and boundary tilt, \({\phi }_{B}\), angles at every disc, making them dependent on the inter-disc distance, L. Moreover, the elastic stress interplay must mediate an effective interaction between the disks.

In the following sections, we will derive the quantitative relationships relating the geometrical parameters of the system and the effective interaction between the disks to the inter-disc distance by using the model for the tilt and splay elasticity of lipid monolayers42,43,48.

Effects of conical lipids

In the above reasoning, we implicitly assumed the membrane monolayers to be homogeneous all over the monolayer areas. This consideration did not account for a possible interplay between the monolayer stresses induced by the insertion of the caveolin disks and a, generally, inhomogeneous distribution along the monolayer planes of lipid species modulating the monolayer elastic properties. For mammalian caveolae, the most essential lipid of this kind is cholesterol, which, as already mentioned, has a remarkable impact on the caveola morphology and stability9,20,35,54,55. As far as the lipid monolayer elasticity is concerned, a distinctive feature of cholesterol is the effective molecular shape of an inverted cone exhibited in mixed monolayers37. This effective shape of cholesterol can be described by the molecular intrinsic curvature, \(\zeta\), which has a strongly negative value in the range between\(-\frac{1}{2.3}{{\mbox{nm}}}^{-1}\) and \(-\frac{1}{2.9}{{\mbox{nm}}}^{-1}\)37. Besides cholesterol, the same type of an effective molecular shape and, hence, a strongly negative intrinsic curvature characterize such lipids and dioleoylphosphatidylethanolamine44 and diacylglyceroles (DAG), the latter having the intrinsic curvatures close to -1 \({{\mbox{nm}}}^{-1}\)38,56. In the following we refer to lipids with a strongly negative intrinsic curvature as the conical lipids or simply cones.

The presence of cones in the lipid monolayer regions subjected to negative lipid splay decreases the related elastic energy42,43, the effect being proportional to the cones’ surface concentration57. In the monolayer I of our system, the hydrocarbon chains of lipid molecules are spread compared to the polar heads, so that the splay is negative. In monolayers II and III, the heads are spread relatively to the chain ends and, hence, the splay is positive (Fig. 1C–E). Hence, enrichment of the monolayer I and depletion of the monolayers II and III in cones are expected to reduce the monolayer elastic energy and enhance the membrane kinking driven by the difference in the contact energies, \(\Delta \varepsilon\).

In the following, we quantitatively account for the interplay between the membrane stresses and the cones’ surface concentration, resulting in the partitioning of the cones between the plasma membrane (which plays the role of a lipid reservoir) and different monolayers of the system. We analyze the impact of the cones’ partitioning on the extent of the overall membrane curvature and the effective interaction between the embedded caveolin disks.

Main definitions and equations

Description of the system

We consider a lipid bilayer with caveolin disks of radius R inserted into its proximal monolayer, the edges of the disks and separated by a distance L along the bilayer midplane (Fig. 1E). We assume, for simplicity, that the bilayer consists of two types of lipids, the basic lipid and the cones. The local molar ratio of the cones in a monolayer will be denoted by c so that the molar ratio of the basic lipid is 1-c. Each monolayer of the bilayer can freely exchange the lipid material with an external reservoir consisting of the same components. The molar ratio of the cones in the reservoir is \({c}_{0}\). The reservoir is a prototype of the plasma membrane to which real caveolae are connected.

For technical simplicity, we consider the two-dimensional version of the model in which a bilayer’s configuration is described by the two-dimensional profile of its mid-surface (Fig. 1) and is uniform in the third direction. We expect the model predictions to retain their qualitative validity also for realistic three-dimensional configurations.

The bilayer with the inserted disks can be considered as built up of structural blocks (Fig. 1E). Each such block consists of half of a caveolin disc of length R covered by the monolayer I, and the bilayer fragment of length L/2, consisting of the monolayers II and III and extending halfway to the adjacent disc (Fig. 1E). The structural block will be referred to below as the system, for brevity. The point on the system’s midplane separating the disc and bilayer parts (Fig. 1E) will be called the internal boundary of the system. The external boundaries of the system are the points on the mid-plane representing the interface between the system and the adjacent structural blocks.

In the following, the physical values of the monolayers I, II, and III of the system will be denoted by the corresponding index. The relationships in which no indices are used apply to any of the three monolayers.

Each monolayer of the system is described by its neutral plane, which is parallel to the system’s midplane and separated from it by a distance, h, approximately equal to the monolayer thickness (Fig. 1A). Each monolayer is characterized at every point of its neutral plane by the tilt vector, \(\vec{t}\), and splay, \(\bar{J}\), of the constituent lipid molecules. A detailed introduction of the notions of tilt and splay is presented and discussed in refs. 42,43,47,48. In brief, the lipid tilt, \(\vec{t}\), quantifies the deviation of the unit vector, \(\vec{n}\), describing the orientation of the lipid hydrocarbon chains from the unit normal, \(\vec{N}\), of the monolayer neutral monolayer plane (Fig. 1C). For the 2D model considered here, we choose the x-axis directed along the neutral as indicted in (Fig. 1C). For small angles, \(\phi\), between \(\vec{n}\) and \(\vec{N}\), the projection of the tilt vector to the x-axis is equal \(t=\phi\) if \(\vec{n}\) slants away from \(\vec{N}\) in the direction of the x-axis (Fig. 1C) and, \(t=-\phi\), for the opposite direction of the slanting. The lipid splay, \(\bar{J}\), quantifies the variation of the lipid chain orientation along the monolayer neutral plane and is determined as the sum of the divergence of the tilt, \({{\mbox{div}}}\vec{t}\), and the mean curvature of the monolayer neutral plane, J42,43,47,48. As we will explain below, in the 2D model considered here, the curvature can be neglected so that all three monolayers of the system will be regarded as flat, J = 0, in which case the splay is equal to, \(\bar{J}=\frac{d\phi }{{dx}}\), with x being the coordinate along the monolayer x-axis.

The physical state of each of the system’s monolayers is characterized by the distribution along the monolayer neutral plane of the lipid tilt angle, \(\phi (x)\), the splay, \(\frac{d\phi (x)}{{dx}}\), and the cones’ concentration, \(c(x)\).

The system’s mid-plane profile sharply turns at the internal boundary. This turn will be described by the kink angle, \(\varphi\) (Fig. 1D, E). In addition, we define the boundary tilt angle, \({\phi }_{B}\), as illustrated in (Fig. 1D, E). The values of \({\phi }_{B}\) and \(\varphi\) set the tilt angles in the three monolayers at the internal boundary of the system,

$${\phi }_{I}=-{\phi }_{B},{\phi }_{{II}}={\phi }_{B}-\varphi,{\phi }_{{II}}=\varphi .$$
(2)

At the external boundaries of the system, all the tilt angles must vanish,

$${\phi }_{I}={\phi }_{{II}}={\phi }_{{III}}=0,$$
(3)

to guarantee a smooth transition to the adjacent structural blocks.

Energy of the system

Our goal is to find the equilibrium configuration of the system corresponding to the minimum of the system’s energy, F. The energy will be computed with respect to the initial state in which the system is flat, so that the kink angle vanishes, \(\varphi=0\), and there is no tilt-splay all along each of the three monolayers, which also means that the boundary tilt angle vanishes \({\phi }_{B}=0\) (Fig. 1A). The cones’ concentration, c, in the initial state is homogeneous in each monolayer and equal to that in the reservoir, \({c}_{0}\).

We consider the energy F to consist of the change of the differential contact energy, \({F}_{{cont}}\), the monolayer elastic energies of the emerging tilt and splay, \({F}_{{el}}\), and the energy of the cones’ repartitioning between the system’s monolayers and the reservoir, \({F}_{c}\), so that

$$F={F}_{{cont}}+{\sum}_{i}{F}_{{el}}^{i}+{\sum}_{i}{F}_{c}^{i}.$$
(4)

Here and below, the index “i” becomes I, II, or III depending on the system’s monolayer in mind. The meaning of \({\Sigma }_{i}\) in (Eq.4) is the summation of the contributions by the three monolayers of the system.

The change in the differential contact energy, \({F}_{{cont}}\), is proportional to the variation in the number of lipid molecules contacting the hydrophobic plane of the caveolin disk (monolayer I), \(\Delta N\), which results from the emerging tilt deformation. For small boundary tilt angles, \({\phi }_{B} < 1\), it can be expressed as

$${F}_{{cont}}=-\frac{h\cdot D}{a}\Delta \varepsilon {\phi }_{B}.$$
(5)

In (Eq. 5) and below the multiplier D is used to convert the energies provided by the two-dimensional model and, thus, related to the unit length of the axis pointing in the third direction, into the energies related to a caveolin disc and having the regular units. Therefore, the value of D will be taken equal to the size of a caveolin disc, D = 2R. The area per lipid molecule on the monolayer neutral plane, a, and the monolayer thickness, h, will be assumed constant because of the effective non-stretchability of the monolayer.

To determine the energy of tilt and splay in each monolayer of the system, we will use the elastic model introduced and developed in refs. 42,43 and recently summarized in detail in the Supplementary Material of47. This energy is related to the unit area of the monolayer neutral plane for small deformations, \(\phi < 1\) and \(\frac{d\phi }{{dx}}h < 1\), is given by

$${f}_{{el}}=\frac{1}{2}\kappa {\left(\frac{d\phi }{{dx}}\right)}^{2}-\kappa \frac{d\phi }{{dx}}{J}_{S}+\frac{1}{2}{\kappa }_{t}{\phi }^{2},$$
(6)

where \(\kappa\) is the monolayer splay modulus equivalent to the Helfrich bending modulus, \({\kappa }_{t}\) is the monolayer tilt modulus, and \({J}_{S}\) is the spontaneous splay equivalent to the Helfrich spontaneous curvature42,43. The spontaneous splay, \({J}_{S}\), depends on the intrinsic curvatures of the constituent lipids and the lipid composition58. We use the simplest linear model for this dependence58,59 according to which,

$${J}_{S}=c\cdot \zeta .$$
(7)

where \(\zeta\) is the intrinsic curvature of the cones. The relationship (Eq. 7) implies that the basic lipid has a vanishing intrinsic curvature. The total elastic energy of a monolayer is obtained by integrating \({f}_{{el}}\) over the monolayer area, \(A\), which for the 2D model is reduced to the integration over the linear coordinate, \(x\),

$${F}_{{el}}=D\cdot \int {f}_{{el}}{dx}.$$
(8)

The energy of the cones’ redistribution, \({F}_{c}\), is the consequence of a decrease in the entropy of mixing between the cones and the basic lipid, which accompanies a deviation of the mole fraction of the cones’, \(c\), from that of the reservoir, \({c}_{0}\). Here we assume, for simplicity, that there is no direct interaction either between the cones themselves or between the cones and the basic lipid. This enables us to account for the most generic effects of the conical lipid molecules. The resulting change of the free energy related to the unit area of the monolayer neutral plane can be presented as (see e.g. SI of 60 for derivation and detailed explanations),

$${f}_{c}=\frac{{k}_{B}T}{a}\left[c\cdot {{\mathrm{ln}}}\left(\frac{c}{{c}_{0}}\right)+(1-c){{\mathrm{ln}}}\left(\frac{1-c}{1-{c}_{0}}\right)\right]$$
(9)

where \({k}_{B}T\) is the product of the Boltzmann constant and the absolute temperature, and \(c\) is the cones’ local mole fraction varying along the monolayer’s neutral plane. The relationship (Eq. 9) assumes that the molecular in-plane area, \(a\), of cones is equal to that of the basic lipid, which is another simplifying approximation.

We assume that the deviation of the cones’ molar ratio, \(c\), from its reservoir value, \({c}_{0}\), is small, \(\frac{c-{c}_{0}}{{c}_{0}} < 1\), all over the system and use the first non-vanishing order approximation of (Eq. 9),

$${f}_{c}=\frac{1}{2}\frac{{k}_{B}T}{a}\frac{{\left(c-{c}_{0}\right)}^{2}}{{c}_{0}(1-{c}_{0})}$$
(10)

The total energy of the cones’ repartitioning is given by the integration of \({f}_{c}\) (Eq. 10) over the area of the monolayer neutral plane,

$${F}_{c}=D\cdot \int {f}_{c}(x){dx}$$
(11)

Strategy of analysis

We will start with determining the equilibrium distributions of the tilt angle, \(\phi (x)\), the splay, \(\frac{d\phi (x)}{{dx}}\), and the cones’ concentration, \(c(x)\), along the neutral plane of each monolayer for fixed values of the kink angle, \(\varphi\), and the boundary tilt angle, \({\phi }_{B}\), and a given half-distance between the adjacent disks, \(L/2\). This will be done by deriving the equations of equilibrium for the tilt and cones’ distributions and solving them for each monolayer upon fulfilling the boundary conditions (Eqs. 2, 3) (see SI A). Using the obtained results and (Eqs. 4–11), we will determine the energy of the system as a function of the fixed values, \(F({\phi }_{B},\varphi,L/2)\). Further, for each distance, \(L\), between the caveolin disks, we will seek the values of the kink, \(\varphi\), and boundary tilt, \({\phi }_{B}\), angles minimizing the energy.

Solutions

For each inter-disc distance, \(L\), we describe the equilibrium configuration of the system by the optimal value of the kink angle, \({\varphi }^{*}\) (Fig. 1D, E), determining the system’s shape, the optimal value of the boundary tilt angle, \({\phi }_{B}^{*}\) (Fig. 1D), characterizing the extent of the tilt and splay deformations in the system, and the optimal distribution of the cones’ mole fractions, \(c\), in the system’s monolayers. In addition, we determine the membrane-mediated force acting between the disks, which will allow us to predict whether the assembly of caveolin disks into caveolar coats can occur spontaneously or requires the action of additional forces counteracting the membrane-mediated ones. The full details of the computations are presented in (SI A). Below, we present only the results of this analysis.

Length scales

To simplify the presentation of further results (SI A), we define the combinations of the system’s parameters which set the energy and length scales of the system.

The energy scale is

$${\sigma=\sigma }_{0}\sqrt{1-\frac{\kappa }{{k}_{B}T}{\zeta }^{2}a{c}_{0}(1-{c}_{0})}$$
(12)

where,

$${\sigma }_{0}=\frac{a}{h}\sqrt{\kappa {\kappa }_{t}}$$
(13)

is the basic energy scale corresponding to a homogeneous monolayer with no cones’ repartitioning.

The length scale, whose meaning is a characteristic decay length of the splay and tilt deformations, is,

$$\lambda={\lambda }_{0}\sqrt{1-\frac{\kappa }{{k}_{B}T}{\zeta }^{2}a{c}_{0}(1-{c}_{0})},$$
(14)

where,

$${\lambda }_{0}=\sqrt{\frac{\kappa }{{\kappa }_{t}}},$$
(15)

is the basic length scale of a homogeneous monolayer.

The reported values of the monolayer splay (bending) modulus, \(\kappa\), determined for monolayers of different lipid compositions53,61, various membrane charges62, and diverse cholesterol contents63,64,65 vary in a wide range between less than \({10k}_{B}T\) and about \({30k}_{B}T\). The reported values of the tilt modulus, \({\kappa }_{t}\), are in the range \(10-60\frac{{mN}}{m}\)43,48,49,50. Since \(h\approx 2\,{nm}\), and \(a\approx 0.7\,{{nm}}^{2}\), the basic energy scale \({\sigma }_{0}\) (Eq. 13) is in the range about 2–20 \({k}_{B}T\), and the basic length scale, \({\lambda }_{0}\), has values within the approximate range of 1–3 nm. The actual energy (Eq. 12) and length (Eq. 14) scales can be strongly reduced compared to their basic values due to cones’ redistribution.

Configurations of the system

The optimal shape of the system for a given inter-disc distance, \(L\), is set by the optimal kink angle, which is given by (see SIA)

$${\varphi }^{*}=\frac{1}{2}\frac{\Delta \varepsilon }{\sigma }\frac{1}{\left[\coth (\rho )+\frac{1}{2}\cdot \coth ({{\mbox{l}}})\right]},$$
(16)

while the optimal boundary tilt angle is

$${\phi }_{B}^{*}=2{\varphi }^{*},$$
(17)

where σ is the energy scale (Eq. 12), and \({{\mbox{l}}}=\frac{L}{2\lambda }\) and \(\rho=\frac{R}{\lambda }\) are, respectively, the half-distance between adjacent caveolin disks and the disc radius, both normalized by the length scale (Eq. 14).

The dependence of the optimal kink angle, \({\varphi }^{*}\), on the inter-disc distance, \(L\), for different values of the cones’ mole fraction, \({c}_{0}\), is presented in (Fig. 2a).

Fig. 2: The dependences of the optimal geometrical parameters of the system on the inter-disc distance, L, for different values of the mole fraction of cones in the reservoir, c0.
figure 2

a The kink angle, \(\varphi\); b The effective curvature, \({J}_{{eff}}\). The dot at each curve indicates the distance of a maximal effective curvature. Parameters used for all curves: \(\zeta=1/2.5\,n{m}^{-1}\), \(\kappa=10{k}_{B}T\), \({\kappa }_{t}=10{k}_{B}T/n{m}^{2}\), \(\Delta \varepsilon=1{k}_{B}T\), \(R=7\,{nm}\), \(h=2\,{nm}\), \(a=0.7\,n{m}^{2}\).

Full size image

The resulting effective curvature of the faceted system’s profile can be determined as

$${J}_{{eff}}=\frac{1}{\lambda }\frac{{\varphi }^{*}}{(\rho+{{\mbox{l}}})}$$
(18)

The dependence of \({J}_{{eff}}\) on the inter-disc distance, L, for different \({c}_{0}\) is presented in (Fig. 2b).

These results (Fig. 2) show that both the optimal kink angle, \({\varphi }^{*}\), and the corresponding effective curvature of the system, \({J}_{{eff}}\), increase with rising cones’ mole fraction, \({c}_{0}\). This means that the presence of cones is predicted to boost the membrane kinking and increase the effective membrane curvature generated by the caveolin disks.

A remarkable feature of our results is that the effective curvature, \({J}_{{eff}}\), reaches a maximal value, \({J}_{{eff}}^{*}\), for a certain inter-disc distance, \({L}^{*}\), which, therefore, is the most favorable in terms of the curvature generation. The representative dependences of \({J}_{{eff}}^{*}\) and \({L}^{*}\) on the cones’ mole fraction, \({c}_{0}\), for typical values of the basic elastic parameters are presented in (Fig. 3).

Fig. 3: The optimal conditions for the curvature generation for different mole ratios of cone-like lipid molecules, c0.
figure 3

a The optimal inter-disc distance, \({L}^{*}\), at which the effective curvature adopts a maximal value (b)The maximal effective curvature \({J}_{{eff}}^{*}\). The parameter values used: \(\zeta=1/2.5\,n{m}^{-1}\), \(\kappa=10{k}_{B}T\), \({\kappa }_{t}=10\) \({k}_{B}T/n{m}^{2}\), \(\Delta \varepsilon=1{k}_{B}T\), \(R=7\,{nm}\), \(h=2\,{nm}\), \(a=0.7n{m}^{2}\).

Full size image

Based on the observations of faceted caveolae15,16,36, the distances between the flat facets, \(L\), are in the range of a few nanometers, while the effective caveolar radii are nearly \(30{{\mbox{nm}}}\). According to our model predictions (Fig. 3a), such distances are optimal for curvature generation. Another conclusion of our results (Fig. 3b) is that for a modest value of the differential contact energy \(\Delta \varepsilon=1{k}_{B}T\), the observed 30 nm radii of caveolar membranes correspond to biologically feasible values of the cholesterol mole fraction, \({c}_{0}\), in the range of 20–30%. In case of the differential contact energy, \(\Delta \varepsilon\), larger than \(1{k}_{B}T\), lower cholesterol mole fractions would be required for generation of the observed curvatures.

The distributions of the cones’ mole fraction, \(c\), in the system’s monolayers (see SIA, Eqs. A12, A16, A20)) are illustrated in (Fig. 4). The monolayer I contacting the hydrophobic face of the caveolin disc is enriched in, while the monolayers II and III bridging the adjacent disks are depleted from the cones. The major enrichment and depletion are concentrated near the disc boundary.

Fig. 4: Distribution of cones across the system for different values of the background mole fraction, c0.
figure 4

The values of the boundary tilt \({\phi }_{B}\) and kink \(\varphi\) angles correspond to the energy minimum. The solid lines describe the area of the monolayer \(I\), the dashed lines describe the monolayers \({II}\) and \({III}\). The parameter values used for all curves: \(\kappa=10{k}_{B}T\), \({\kappa }_{t}=10{k}_{B}T\), \(\zeta=1/2.5\,n{m}^{-1}\), \(\Delta \varepsilon=1{k}_{B}T\), \(L=2\,{nm}\), \(R=7\,{nm}\), \(h=2\,{nm}\), \(a=0.7\,{{nm}}^{2}\).

Full size image

Membrane-mediated interaction between the caveolin disks

The dependence of the system’s energy on the inter-disc distance is given by (see SI A)

$${F}^{*}=-\frac{1}{2}\frac{h}{a}\frac{{(\Delta \varepsilon )}^{2}}{\sigma }\frac{1}{\left[\frac{\cosh (\rho )}{\sinh (\rho )}+\frac{1}{2}\cdot \frac{\cosh \left({{\mbox{l}}}\right)}{\sinh \left({{\mbox{l}}}\right)}\right]}.$$
(19)

The membrane-mediated repulsive force acting between the adjacent caveolin disks, \({{\mathscr{F}}}\), corresponding to the energy (Eq. 19) is given by

$${{\mathscr{F}}}=-\frac{1}{\lambda }\frac{d{F}^{\ast }}{d{{\mbox{l}}}}=\frac{1}{4}\frac{h}{a}\frac{{(\Delta \varepsilon )}^{2}}{\lambda \sigma }\frac{1}{{\left[\frac{\cosh (\rho )}{\sinh (\rho )}\sinh ({{\mbox{l}}})+\frac{1}{2}\cdot \cosh ({{\mbox{l}}})\right]}^{2}}.$$
(20)

The dependencies of the energy and force on the inter-disc distance, \(L\), are presented in (Fig. 5).

Fig. 5: The membrane-mediated interaction between the caveolin disks.
figure 5

The energy of the system (a) and the corresponding repulsive force between adjacent disks (b) as functions of the inter-disc distance, \(L\), for different mole fractions of cone-like lipids in the reservoir, \({c}_{0}\). Parameters used for all curves: \(\zeta=1/2.5\) \(n{m}^{-1}\), \(\kappa=10{k}_{B}T\), \({\kappa }_{t}=10\) \({k}_{B}T/n{m}^{2}\), \(\Delta \varepsilon=1{k}_{B}T\), \(R=7\,{nm}\), \(h=2\,{nm}\), \(a=0.7n{m}^{2}\), \(D=14\,{nm}\).

Full size image

The energy \({F}^{*}\) (Fig. 5a) is negative, which is a result of an overall relaxation of the energy of the initial state due to the emerging tilt, splay and kink deformations in the system’s monolayers, as qualitatively discussed above. The most efficient relaxation is reached for the inter-disc distances exceeding the length scale, \(L\gg \lambda\). Increase of the cones’ mole fraction, \({c}_{0}\), results in a deeper energy relaxation due to a reduction of the energy cost of the splay deformation (Fig. 5a).

The membrane-mediated force between the disks, \({{\mathscr{F}}}\), is repulsive for all inter-disc distances (Fig. 5b). The predicted repulsive force is, practically, zero for large inter-disc distances and starts to grow when the distance becomes comparable to or smaller than the length scale, \(L\le \lambda\). Since \(\lambda\) decreases with a growing mole fraction of the cones, \({c}_{0}\) (Eq. 14), a rise in the cones’ concentration is predicted to reduce the distance to which the disks can approach each other without any significant membrane-mediated resistance.

To get a sense of the characteristic magnitude of the membrane-mediated repulsive force between the caveolin disks, \({{\mathscr{F}}}\), we estimate its value for an experimentally relevant distance of \(L=2{{\mbox{nm}}}\). According to (Fig. 5b), the force is \({{\mathscr{F}}}{{\mathscr{\approx }}}1\frac{{k}_{B}T}{{nm}}=4{pN}\). This is a biologically feasible force, which can be developed, for example, by just a couple of molecular motors66.

Discussion

The mechanisms by which the caveolin-based protein complexes sculpt the 50-80 nm large caveolar bulbs have remained elusive despite a long history of the field spanning many decades67. While the major ideas behind the mechanisms of membrane shaping by proteins have been elaborated67,68,69, the shapes of caveolae pose an additional challenge related to their faceted appearance15,16,30,36. Whereas cavins can control the caveolar shaping either through their binding to caveolins within a two-layer structure12 or due to the electrostatic interactions mediated by the cavin disordered domains70, the primary role must be played by caveolins which have been shown to generate the caveola-like structures if expressed in otherwise caveola-free bacterial membranes lacking cavins15. The previously proposed mechanism by which a caveolin molecule alone could produce local membrane curvature was based on a computationally discovered binding between the caveolin molecules shallowly embedded into one membrane leaflet and the molecules of cholesterol constituting a considerable part of the membrane lipid composition23,71. Yet a shallow embedding of caveolin needed for the membrane curvature generation72 does not comply with the experimental findings6,7 since an ensemble of such caveolin-cholesterol molecular complexes should be expected to generate smooth rather than faceted membrane profiles. Moreover, caveolin generates caveola-like membrane invaginations when expressed in cholesterol-free E.coli15.

The recent structural data on caveolin assembly and arrangement within membranes made the phenomenon of membrane curving by caveolins even more puzzling and suggested that it is driven by a mechanism different from all those considered previously30. Caveolin was discovered to oligomerize into flat disks of about 14 nm diameter inserted into one membrane leaflet up to the interface with the second leaflet. As mentioned in the Introduction, these disc-like caveolin oligomers, rather than monomeres, appear to be responsible for the curvature generation. It feels counterintuitive that such large disc-like particles lying flat on the membrane plane can drive membrane curvature.

Here, we proposed a mechanism to explain this phenomenon. The central hypothesis of the model is that the contact energy of lipid molecules of one membrane leaflet with the hydrophobic plane of a caveolin disc embedded into the second leaflet is larger than the energy of the contact between the two leaflets. We showed by modeling that such differential contact interaction results in the generation of the tilt-splay deformations of the lipid monolayers in the vicinity of a caveolin disc, as confirmed by numerical simulations33. These deformations drive the kinking of the membrane profile along the boundaries of the inserted caveolin disks, and, hence, an overall membrane bending. In addition, our model accounted for an enhancing effect on this bending produced by conical lipids such as cholesterol and DAG characterized by a strongly negative intrinsic curvature.

Model predictions

Our model led to several predictions, some of which confirm the existing experimental knowledge, while others await experimental verification.

First, the proposed bending-by-kinking mode of membrane curvature generation results in a faceted rather than smoothly curved membrane profile, which is in accord with experimental observations of caveolar shapes15,16,36. Importantly, according to our model, caveolin molecules must be located on the flat facets of caveolae as suggested in refs. 6,7,30,31,32.

Second, using the geometrical parameters of cell caveolae and the established values of the elastic moduli of lipid monolayers, we concluded that the differential contact energy per lipid molecule of the order of \({1k}_{B}T\) is sufficient to explain the observations. The differential contact energy for caveolin 8S complexes in lipid was neither measured nor computed and represents, therefore, a prediction of our model. Yet, evaluation of the analogous energy for lipid domains in a regular lipid environment provided values in the range \(0.1-1\frac{{k}_{B}T}{{{nm}}^{2}}\)73,74,75,76, which supports the feasibility of our prediction.

The third prediction of our model is that the membrane stresses generated by the caveolin disc insertion result in a repulsive interaction between the disks. This means that an attractive force, \({{{\mathscr{F}}}}_{{att}}\), which was not a part of the present analysis, must act between the caveolin disks to overcome this membrane-mediated repulsion and concentrate the disks in the membrane plane into domains with an experimentally observed high density of caveolin. There are different possible origins of such an attractive force. One is an effective interaction mediated by inter-disc connections through cavin molecules in vertebrate cells. Another is non-specific Van-der-Waals interaction77.

The model predicts that the induced effective membrane curvature, \({J}_{{eff}}\), non-monotonously depends on the distance, \(L\), between the adjacent cavin disks (Fig. 2b). The curvature vanishes for zero, \(L=0\), and infinite, \(L\to \infty\), separations, and reaches a maximal value, \({J}_{{eff}}^{*}\), for an optimal distance, \({L}^{*}\), which is in the range of a few nanometers for a characteristic mole ratio of cholesterol, \({c}_{0}=0.3\) and the typical values of the monolayer elastic parameters. This means that the most efficient curvature generation occurs if the attractive force, \({{{\mathscr{F}}}}_{{att}}\), has such character and distance dependence that it brings the caveolin disks to a separation \({L}^{*}\) but not closer than that. The characteristic value of the attractive force needed to bring the caveolin disks to about 2 nm separation is predicted to have a value of a few pN. In case of Van-der-Waals interaction between disks, according to a rough estimation, such force corresponds to Hamaker constant \({A}_{{Ham}}\) of a few tens of zeptojoules (zJ), which is feasible for interaction through a hydrophobic medium77. If the attractive interaction between caveolin disks is provided by binding of the cavin proteins70, relevant for the efficiency of the curvature generation is the length of a cavin-mediated bond between the disks, determined by the detailed structure of the cavin-caveolin complex. This bond length must be in the nanometer range.

An essential prediction of the model relates to the effects and distribution of conical lipids and, specifically of cholesterol. Generally, the model predicts a substantial enhancement by the cones of the caveolar membrane shaping by caveolin disks and provides a mechanistic background to all the observed effects of cholesterol on caveola formation described in the Introduction. Specifically, an increase in the background cholesterol mole fraction, \({c}_{0}\), is predicted to boost the effective membrane curvature, \({J}_{{eff}}\), generated by the disks (Fig. 3b) which agrees with the observations55. Further, an increase of \({c}_{0}\) is predicted to reduce the membrane-mediated repulsive force between the disks at large and intermediate separations and, hence, to alleviate the requirement on the strength of an attractive force needed for a sufficient concentration of the caveolin disc in the membrane plane and generation of relevant membrane curvatures. This may explain why cholesterol was required for the assembly and stabilization of 70S caveolin complexes20 as well as the observed caveolar instability and flattening upon cholesterol depletion from the plasma membrane9,35. It has to be emphasized that, within the proposed mechanism, the effects of cholesterol are of mechanical rather than chemical origin and are related to the negative intrinsic curvature, \(\zeta\), of cholesterol molecules37. Therefore, similar effects on the membrane shaping by caveolin disks can be produced by other conical lipids with strongly negative intrinsic curvatures such as, e.g., diacylglycerols78. Interestingly, specific diacylglycerol species were shown to be enriched in h-caveolae generated in E.coli (Walser 2012) and our model would predict a role for these or related lipids in membrane sculpting by caveolin in that system.

Model assumptions

The goal of this work was to propose the basic principles underlying the mechanism of caveola shaping by the disc-like caveolin complexes and to present them in a most straightforward and technically simple way. The presented model was not intended to explicitly account for the whole phenomenology of caveolar biogenesis described to date in literature. Below, we list and discuss some of the specific limitations of the model.

One limitation is the two- rather than three-dimensional character of the model. This consideration substantially simplified the analysis, allowing us to obtain analytical and easily understandable relationships between the geometrical features of the system and the experimentally relevant parameters such as the cholesterol mole fraction, \({c}_{0}\). Yet a shortcoming of this simplification is that a comparison between the predicted membrane conformations and the ones observed in experiments can have only a semi-quantitative meaning.

In our computations, we assumed a vanishing geometrical curvature of the bilayer fragments flanking the disc part and consisting of the monolayers II and III. This can be justified a posteriori based on the obtained results. The bilayer curvature would be generated if there were an asymmetry between the monolayers II and III. This asymmetry can be a consequence of a difference between the monolayers in either the deformations of tilt-splay, or the cones’ concentration. According to the obtained results, in the energetically optimal state of the system, both the tilt-splay and the cholesterol concentration are equal in the monolayers II and III and, hence, there is no asymmetry between the leaflets.

We used simplifying assumptions concerning the membrane lipid composition. We considered the membrane as consisting of two lipid species, one (the basic lipid) with a vanishing and the second (cones) with a strongly negative molecular intrinsic curvature, \(\zeta\). In reality, a cell plasma membrane contains a variety of lipid species with different non-vanishing intrinsic curvatures, all of which would exhibit some extent of redistribution within the system according to the same mechanism as considered above for cones. Consideration of the redistribution of additional lipids would predict even larger effective curvatures generated by caveolin disks. Further, we assumed the basic lipids and the cones to form ideal mixtures without direct interactions between the components. To keep the consideration as simple as possible and avoid additional unknown parameters, we did not include in the model the possible effects of the proposed direct interactions between cholesterol and caveolin33,39,79,80,81.

The model does not specify the interaction between the lipid molecules and the caveolin disks. While particular chemical interactions between lipids and the caveolar coat proteins have been proposed79,80,81 our model describes them by a general parameter of the difference in contact energies, \(\Delta \varepsilon\), whose value was assumed to have an order of \(1{k}_{B}T\). Verification of this assumption requires detailed quantitative information on the energies of lipid-caveolin interactions that is currently unavailable.

We did not consider the influence on the membrane shape of potential local perturbation of membrane thickness that might be caused by caveolin disks, similar to the effects seen with many integral proteins and protein complexes. This assumption is based on both structural30,31 and simulation33 data, which do not indicate any significant membrane thickness perturbation, suggesting that such effects are likely negligible or vanishing.

Finally, we did not include in our analysis the effects of membrane tension, which are expected to have a significant impact on the membrane curvature. A discussion of this important topic will be presented in a separate article.

Previously suggested mechanisms

Our model was preceded by two proposals of possible mechanisms of caveola shaping by caveolin. As mentioned in the Introduction, initially, the ability to generate membrane curvature was attributed to caveolin monomers22,24 and their complexes with cholesterol23, which was supported by numerical simulations. In light of the data obtained in the bacterial system15, this mechanism does not appear to play a leading role in the caveola biogenesis since caveola formation requires caveolin oligomerization.

A mechanism of caveola shaping by caveolin 8S complexes was suggested in refs. 28,29 based on all-atom simulations. The simulations predicted a conical rather than a flat configuration of caveolin 8S complexes and the volcano-like shape of the membrane scaffolded by the caveolin cone28,29,39. A curved configuration of the 8S complex was also obtained in simulations in ref. 39. Following this model, 8S complexes must be expected to be located on sharp peaks rather than flat regions of the caveolar membrane profiles. The current experimental data support a flat rather than cone-like configuration of the 8S caveolin complex, raising uncertainty about the validity of the cone-like model.

In contrast to the previous models, the mechanism of curvature generation by caveolin suggested here employs the 8S complex rather than monomeric caveolin, and assumes the 8S complex conformation to be a flat disc with all parameters corresponding to those measured experimentally. Our model computationally predicts the impact of a membrane-embedded disc on membrane curvature.

Methods

Python was used for computations and figure generation.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.