Introduction

Inhomogeneously broadened resonance lines are characterized by the possibility to excite selectively a narrow part of the spectrum by applying monochromatic radiation. This leads to the appearance of “spectral holes", which were first observed by Feher in the spin resonance line of an ensemble of donors in silicon1. Spectral hole burning (SHB) has since then been an important tool in Electron Paramagnetic Resonance (EPR) spectroscopy, forming, for instance, the basis for all-microwave hyperfine spectroscopy2,3. In the optical domain, SHB has been a cornerstone of REI-doped crystals spectroscopy, particularly helpful for resolving the hyperfine structure below the inhomogeneous linewidth4,5,6.

Besides spectroscopy, SHB is also useful to prepare a desired absorption profile into the REI ensemble line, by transfering part of the population into auxiliary storage levels in a frequency-selective manner. The storage levels are usually the REI nuclear spin hyperfine levels7, or more rarely the spin states of neighboring nuclei of the host crystal8. The spectral preparation constitutes the first step of many information processing protocols that rely on REI ensembles, both classical (pattern recognition9, filtering10, spectral analysis11) and quantum (photon storage12,13,14,15). In these applications, the lifetime of the hole/anti-hole (H/AH) pattern can be a limiting factor and has therefore been a focus of recent studies16. Lifetimes of days or weeks have been reported by optically pumping hyperfine levels of non-paramagnetic REI systems, such as Eu3+: YSO17. Shorter lifetimes have also been observed in paramagnetic Kramers REIs; with lifetimes ranging from a few seconds to a minute reported for optically pumped electronic and hyperfine transitions of Nd3+ and 167Er3+ doped YSO, respectively18,19, and a lifetime of 50 s observed in microwave-pumped Er3+ doped YSO20. We note that Er3+ is a particularly interesting REI for applications, owing to its 1.5 μm optical transition in the c-band telecom window. Here, we report hole lifetimes as long as one week in Er3+: CaWO4 at 10 mK by pumping at microwave frequency on the paramagnetic transition, and using the spin states of neighboring 183W nuclei of the host crystal as auxiliary levels.

Results

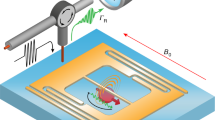
The unit cell of scheelite is depicted in Fig. 1a. It has a tetragonal symmetry, with two axes (a, b) equivalent under a 90° rotation around the c axis. Er3+ ions substitute for Ca2+, as is often the case for REIs in scheelite. Er3+ is a Kramers doublet, and at low temperatures only the lowest-energy doublet is populated, so that Er3+ ions behave as an effective electron spin S = 1/2, with energy levels denoted as \(\vert {\downarrow }_{S}\rangle\) (ground state) and \(\vert {\uparrow }_{S}\rangle\) (excited state). Note that we will only consider the Er3+ isotopes which have a zero nuclear spin. Owing to the S4 symmetry of this site, Er3+: CaWO4 has a gyromagnetic tensor γ that is diagonal along the crystalline a, b, c axes, with γ∣∣/2π = −17.45 GHz/T, and γ⊥/2π = −117.3 GHz/T, depending on whether the magnetic field is applied parallel or perpendicular to the c axis21. Most atoms in the scheelite lattice have zero nuclear spin, apart from tungsten, whose 14%-abundant isotope 183W has a nuclear spin I = 1/2 with a gyromagnetic ratio γW/2π = 1.77394 MHz/T22.

Fig. 1: Principle of the experiment.
figure 1

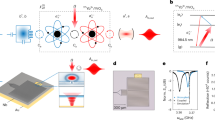
a Schematic of the scheelite unit cell, showing an Er3+ ion (purple) substituting for a Ca2+ ion (blue). When the magnetic field B0 is applied along the c axis, nearest neighbor 183W nuclei belong to two sets of four sites with identical hyperfine coupling, which we call Type I (in green), and Type II (in red). b Schematic of the setup. A niobium lumped-element resonator is deposited on top of a CaWO4 sample, and probed in microwave reflectometry. c Energy levels of an Er3+ electron spin of frequency ωS with levels \(\left\vert {\downarrow }_{S}\right\rangle\) (ground state) and \(\left\vert {\uparrow }_{S}\right\rangle\) (excited state), coupled to a nuclear spin of frequency ωI and levels \(\left\vert {\uparrow }_{I}\right\rangle\) (ground state) and \(\left\vert {\downarrow }_{I}\right\rangle\) (excited state). EPR-allowed transitions (noted a) are at frequency ωS ± A/2, and EPR-forbidden transitions (noted f) at ωS ± ωI. Irradiation at ωp can be resonant with all four possible transitions of spin packets with different spin frequency ωS due to inhomogeneous broadening, resulting in a characteristic Hole/Anti-hole pattern in the spin density ρ(ω). d Blue dots: measured resonator internal losses κi as a function of magnetic field B0, showing a peak when the Er3+ ions are resonant with ω0. Solid black line is a Lorentzian fit, yielding the inhomogeneous linewidth 0.62 mT translating in a frequency Γ/2π = 10.9 MHz. Inset: reflection coefficient S11(ω) away from (red dots) and at (orange) the Er3+ resonance, with Lorentzian fits.

Full size image

The measurements are conducted at 10 mK, by microwave reflectometry on a superconducting resonator (resonance frequency ω0/2π = 7.839 GHz) patterned directly on top of a scheelite crystal (see Fig. 1b), with an erbium concentration of 3 ppb measured by CW EPR23. The resonator consists of a finger capacitor in parallel with a μm-wide wire, acting as the inductance, and oriented approximately along the crystalline c axis. A magnetic field B0 (of magnitude B0) is applied in the plane of the resonator, approximately along the crystalline c axis. Measuring the reflection coefficient S11(ω) yields the resonator energy coupling rate κc ∼ 4.9 ⋅ 106 s−1, internal loss rate κi ∼ 3 ⋅ 105 s−1, which corresponds to a total linewidth κ = κc + κi ∼ 2π ⋅ 0.8 ⋅ 106 rad ⋅ s−1. The presence of the Er3+ ions manifests itself as an increase in κi(B0) when the spin resonance frequency ωS = ∣γ ⋅ B0∣ is resonant with ω0 (see Fig. 1); the measured peak width of 0.62 mT translates into an inhomogeneous linewidth Γ/2π = 10.9 MHz. The inhomogeneous broadening is due to the electrostatic and magnetic local environment of each Er3+ ion which varies throughout the crystal24,25,26. In the following, B0 is fixed at the center of the spin resonance, with the coils in persistent mode for increased stability (see Methods). The spin density ρ(ω) (spectral distribution) is obtained by measuring the reflection coefficient S11(ω) with a vector network analyzer (VNA) (see Methods). Note that since Γ ≫ κ and a scanning range of 100 kHz is chosen for measuring SHB, the equilibrium density ρ0 can be considered constant across the entire probing range. Moreover, most experiments reported here are conducted at temperatures T satisfying kT ≪ ℏωS such that at thermal equilibrium, only \(\vert {\downarrow }_{S}\rangle\) is populated significantly.

SHB in our sample arises because of the magnetic dipolar interaction between each Er3+ ion and the 183W nuclear spins surrounding it. At microwave frequency and millikelvin temperature, a two-level approximation is sufficient to describe the system dynamics, although a more complete model (see Methods) is useful to describe quantitatively the SHB spectra. Consider, for simplicity, the coupling of one Er3+ spin (operator S) to one 183W nuclear spin (operator I), described in the secular approximation by the Hamiltonian H = ωSSz + ωIIz + Sz(AIz + BIx). Here, ωI = −γW B0 is the 183W Larmor frequency, and A (resp. B) is the isotropic (resp., anisotropic) component of the hyperfine interaction. In the limit where ∣ωI∣ ≫ A, B, the energy eigenstates are close to the uncoupled states \(\vert {\downarrow }_{S}{\uparrow }_{I}\rangle,\vert {\downarrow }_{S}{\downarrow }_{I}\rangle,\vert {\uparrow }_{S}{\uparrow }_{I}\rangle,\vert {\uparrow }_{S}{\downarrow }_{I}\rangle\) (in increasing energy order). The nuclear-spin-conserving transitions \(\vert {\downarrow }_{S}{\uparrow }_{I}\rangle \leftrightarrow \vert {\uparrow }_{S}{\uparrow }_{I}\rangle\) and \(\vert {\downarrow }_{S}{\downarrow }_{I}\rangle \leftrightarrow \vert {\uparrow }_{S}{\downarrow }_{I}\rangle\) at respectively ωS + A/2 and ωS − A/2 are EPR-allowed with 〈↓S↑I∣Sx∣↑S↑I〉 ≈ 〈↓S↓I∣Sx∣↑S↓I〉 ≈ 1/2. Due to a slight electron-spin-state-dependent mixing of the nuclear spin states caused by the BSzIx term, the forbidden transitions \(\vert {\downarrow }_{S}{\uparrow }_{I}\rangle \leftrightarrow \vert {\uparrow }_{S}{\downarrow }_{I}\rangle\) and \(\vert {\downarrow }_{S}{\downarrow }_{I}\rangle \leftrightarrow \vert {\uparrow }_{S}{\uparrow }_{I}\rangle\), at respective frequencies ωH = ωS − ωI and ωL = ωS + ωI, can also be weakly driven since ∣〈↓S↑I∣Sx∣↑S↓I〉∣ ≈ ∣〈↓S↓I∣Sx∣↑S↑I〉∣ ≈ ∣B/(4ωI)∣. SHB relies on relaxation pathways of the electron-nuclear spin system. At low temperature, electron-spin relaxation occurs via spontaneous emission of phonons through the direct process, and of microwave photons through the Purcell effect27. The measurements reported here were performed at a microwave power (-106 dBm at sample input) large enough to excite a large number of Er3+ ion spins in the bulk of the crystal. The average radiative rate of these ions, located at ∼100 μm from the inductance, is negligible compared to their non-radiative rate dominated by the direct phonon emission process26, in contrast with recent detection of single-Er3+ spins, which were very close (∼100 nm) to the inductance28. Therefore, one can assume an identical non-radiative relaxation rate for all the ions, measured to be Γ1 ≈ 5 s−1 in the conditions of our experiment23. Because of the nuclear-electron-spin mixing, electron spin relaxation with nuclear-spin-flipping is moreover also possible via the forbidden transitions, at a much lower rate \({\Gamma }_{1x}\approx {\Gamma }_{1}{B}^{2}/(4{\omega }_{I}^{2})\).

SHB occurs by applying a strong pump tone at frequency ωp, of duration much longer than the characteristic electronic relaxation times \({\Gamma }_{1}^{-1}\) and \({\Gamma }_{1x}^{-1}\). Due to inhomogeneous broadening, the pump is resonant with each of the 4 transitions for 4 different spin packets (see Fig. 1). When the pump is resonant with a forbidden transition (say, \(\vert {\downarrow }_{S}{\uparrow }_{I}\rangle \leftrightarrow \vert {\uparrow }_{S}{\downarrow }_{I}\rangle\), occurring when ωp = ωH), it drives this transition, which is rapidly followed by electron spin relaxation into the ↓S↓I state. This transfers spin population of this packet from ωp − ∣ωI∣ + A/2 into ωp − ∣ωI∣ − A/2 (see Fig. 1c). When the pump is resonant with an allowed transition (say, \(\vert {\downarrow }_{S}{\uparrow }_{I}\rangle \leftrightarrow \vert {\uparrow }_{S}{\uparrow }_{I}\rangle\), when ωp = ωS + A/2), the system will cycle many times on the allowed transition, until one cross-relaxation event happens into the state \(\vert {\downarrow }_{S}{\downarrow }_{I}\rangle\), which transfers population from ωp into ωp − A. Summing up all 4 spin packets yields a predicted H/AH pattern shown in Fig. 1c. Once a H/AH pattern has been burned by a strong pump at ωp, it can be probed with a much weaker ( ∼60 dB less) probe tone of varying frequency; it can also be washed out by sweeping the frequency of a strong pump tone, enabling to effectively reset the spin density.

We record SHB spectra with the following pulse sequence. We first use high-power scans to reset the spin density to its equilibrium value, ρ0(ω), probed by weak scans as a reference. We then apply a 120 s-long microwave pulse at frequency ωp with intermediate power for burning spectral holes. We finally measure the resulting spin density ρ1(ω) with low-power scans. The experiments are repeated ten times and averaged. One difficulty is that the complete SHB pattern does not fit inside the narrow linewidth of our resonator, where ρ(ω) can be measured. So, we chose to record and erase subsequently 3 spectra around the line frequency center ω0 after applying a pump at respectively ω0 + ωI (red forbidden transition pumping), ω0 − ωI (blue forbidden transition pumping), and ω0 (allowed transition pumping).

Relative density changes ρ1(ω)/ρ0(ω) of order 0.5–1.3 are observed, as shown in Fig. 2 for the 3 pump frequencies. Consider first the forbidden transition spectrum. We focus on the red-sideband (Fig. 2a), since the blue-sideband spectrum is a mirror image as expected. We first note that the frequency difference between the pump and the center of the hole of 795 kHz is close to the unperturbed 183W Larmor frequency, ∣ωI∣/2π = 794 kHz, confirming that the SHB occurs by storage in 183W nuclear spin states. Two sets of H/AH patterns can be identified in the spectrum, marked by green (resp. red) arrows. From comparison to computed dipolar magnetic couplings, we identify the green set with the largest isotropic hyperfine coupling ∣AI∣/2π ∼ 35 kHz as arising from the four 183W nuclear spins located on the (ab) plane-parallel square surrounding the Er3+ site (Type I in Fig. 1a). The red and gray sets of shallower peaks/dips are respectively attributed to the Types II and III 183W nuclear spins contribution (see Fig. 1a), with ∣AII∣/2π,  ∣AIII∣/2π ∼ 15–20 kHz. At the center of the spectrum, a narrow 2 kHz-wide hole flanked with two narrow side anti-holes is observed, which we attribute to the numerous weakly-coupled nuclear spins located outside of the unit cell. The ∼ 2-kHz hole linewidth is much larger than the 5 Hz homogeneous linewidth estimated from Hahn-echo measurements23,26, likely because of a combination of power-broadening, magnetic field drift and spectral diffusion over the 2 min needed to burn the spectral hole. A simulation reproduces the observations satisfyingly (see Fig. 2 and Methods), the smaller measured modulation amplitude may be linked to magnetic field drifts during the pumping sequence. Note that the agreement was obtained by adjusting the values of Type I and Type II spins hyperfine constants to the data (see Methods); the fitted values differ from the pure dipolar contribution, likely pointing to the existence of a non-zero Fermi contact interaction, as already observed by Mims in Ce3+: CaWO429.

Fig. 2: Spectral hole burning.
figure 2

Measured (blue solid line) and simulated (black solid line) spin density ρ1(ω) normalized to the unperturbed spin density ρ0(ω). Each sequence starts with a repetitive high power (∼ −96 dBm) reset scan with a range of 4 MHz centered at ω0, followed by a lower power (∼ −156 dBm) reference scan with a range of 100 kHz yielding ρ0(ω), a pumping step at single frequency ωp (power -106 dBm), and a measurement scan yielding ρ1(ω). The entire sequence is repeated for ten times. The pump frequency ωp/2π is ω0/2π − 795  kHz (a), ω0/2π + 795 kHz (b) and ω0 (c). Green, red, and gray arrows point respectively to H/AH structure due to Types I–III 183W nuclear spins.

Full size image

The resonant spectrum shows a central hole, flanked with two broad and shallow anti-holes peaking at ∼ 17 kHz. Those are attributed to the Types II–III 183W spin. The two Type I 183W anti-holes expected at  ±35 kHz are not visible, due to their low B value when B0 is well aligned with the c axis. This is confirmed by the simulations, which indeed predict un-measurably small values for the Type I anti-holes in the resonant spectrum (see Fig. 2). Slightly mis-aligned SHB spectra are shown in Methods, for comparison.

We now study the case when the pump consists of pairs of short microwave pulses at ω0, separated by a delay τ, and repeated a large number of times N (see Fig. 3). A qualitative understanding can be obtained by considering the power spectrum of a pair of pump pulses, which is proportional to \({\cos }^{2}[2\pi (\omega -{\omega }_{0})/\tau ]\) and vanishes at all frequencies \({\tilde{\omega }}_{k}={\omega }_{0}+\pi (2k+1)/\tau\), k being an integer (see Fig. 3b). Consequently, all Er3+ ions except those at these frequencies have a finite probability to be excited and finally cross-relax with a 183W nuclear spin flipping, as explained above. This leads to a progressive population build-up at \({\tilde{\omega }}_{k}\), and a corresponding depletion of all other frequencies, forming an effective spectral grating30. This accumulated grating measured as a change in spin density resulting from the pulse pair pumping is shown in Fig. 3c in a narrow frequency range around ω0, with the reflection coefficient S11(ω) shown on a larger scale in Fig. 3a. Both show the expected modulation.

Fig. 3: Two-pulse pumping and accumulated echo.
figure 3

Pumping consists of two consecutive pulses of frequency ω0 and duration 1 μs, separated by a delay τ, and repeated N times after a waiting time 200 ms. a Measured reflection coefficient without (orange line) and with (blue line) two-pulse pumping. b Computed spectral power density of the two pulses; it goes to zero at frequencies \({\tilde{\omega }}_{k}\) (see text). c Measured Er3+ density ρ1(ω) after two-pulse pumping, renormalized to the reference density ρ0(ω). It shows a periodic pattern of anti-holes at frequencies \({\tilde{\omega }}_{k}\). d, e The blue line is the measured average value of the I quadrature following a microwave pulse (purple part) at ωp, after a periodic grating was generated by two-pulse pumping with τ = 50 μs (d) and τ = 100 μs (e). f First-echo amplitude Ae as a function of N. green (pink) dots are measurements (simulations). g The blue line is the measured average value of the I quadrature following three consecutive microwave pulses (purple) at ω0, after a periodic grating was generated by two-pulse pumping with τ = 200 μs. The inset is a zoom on the three generated echoes.

Full size image

The spectral grating in the spin density can also be probed in the time domain, by measuring the spin response following a short excitation probe pulse. As shown in Fig. 3d, e, a series of echoes are observed, at times jτ (j positive integer), with alternating phases, and an overall decaying amplitude Ae,j. Such accumulated echoes were also observed in optics31; they form the basis for the generation of atomic frequency combs12. The echo emission is readily understood by the fact that the Free-Induction Decay emission from a spin ensemble is the Fourier Transform of the spin density, so that the periodic modulation in the frequency domain corresponds to a delay-line effect in the time domain. The emission of several echoes is related to the grating harmonics; the echo train is well-reproduced by a simple computation of the measured spin density Fast Fourier Transform (see Methods). The progressive buildup of the modulation is studied in Fig. 3f, in which we plot the amplitude of the first accumulated echo Ae as a function of the number of pump pairs of pulses. A plateau is reached after N ∼ 2 ⋅ 104. A similar buildup dynamics is seen in the simulations, indicating that they capture the main features of the pumping mechanism. We finally show in Fig. 3g that the delay-line effect also works when several input pulses are present, similar to atomic frequency comb memories12.

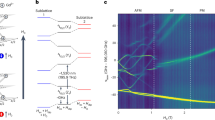
We now measure the lifetime of the holes imprinted in the spin density. We show here results for the accumulated echoes (similar results were obtained for the hole burning, see Methods). A pumping sequence consisting of N = 18,000 pairs of pulses separated by τ = 100 μs is applied to the spins, with a waiting time tw = 0.2 s. The resulting spin population is probed by blocks of five pulses separated by 0.2 s, with a separation Δt between the blocks. The echo amplitude Ae, averaged within each block, is shown as a function of the time t elapsed since the end of the pumping sequence in Fig. 4a. Echoes are still measurable after 6 days of waiting time.

Fig. 4: Temperature dependence of accumulated echo.
figure 4

A periodic grating is generated by two-pulse pumping with τ = 100 μs and N = 18,000, following a reset by VNA scan. It is probed by repeating blocks of five pulses, with a waiting time Δt in-between. a Red circles show the measured first accumulated echo amplitude Ae averaged over the five pulses of block j, as a function of the delay t = jΔt following the grating generation, at 10 mK. Blue circles show the rescaled echo amplitude. The solid line is a fit by a sum of two exponentially decaying functions, yielding τ1 = 8.4 h and τ2 = 841.9 h for rescaled data. b Rescaled measured echo amplitude as a function of t, at various sample temperatures. Δt = 1 h for 10 mK, Δt = 10 min for T = 52 and 94 mK, Δt = 1 min for T = 185 mK, and Δt = 30 s for T = 233 mK. c Measured time constants τ1 (blue circles) and τ2 (light blue circles) as a function of the sample temperature, T. Fitting the data between 50 and 220 mK with the Orbach formula yields Γ1x = 0.002 s−1 (τ1, dark blue dashed line) and 0.03 s−1 (τ2, light blue dashed line). The orange dash-dot line shows ∼ T−9 scaling, as expected for the Raman process.

Full size image

In these measurements, the probe pulses themselves have an impact on the spin density modulation by exciting the erbium ions and enabling cross-relaxation, artificially accelerating the decay. We calibrate this spurious effect by recording the echo amplitude as a function of the number of probe pulses in the same conditions of pumping and probing, but without any waiting time between the pulses. The echo decay at 10 mK, rescaled by this reference curve, is shown in Fig. 4a (see Methods). The long-time decay is considerably slowed down compared to the non-rescaled data, indicating that the probe pulse impact was actually the dominant source of decay, despite the low rate of probing (five pulses every Δt = 60 min). The measurements are repeated at various sample temperatures, and the rescaled echo decay curves are shown in Fig. 4b. All curves display a non-exponential decay, which we phenomenologically fit by a sum of 2 exponentials, \({A}_{1}{{{{\rm{e}}}}}^{-t/{\tau }_{1}}+{A}_{2}{{{{\rm{e}}}}}^{-t/{\tau }_{2}}\), with τ1 (τ2) the short (long) time constant. The time constants τ1 and τ2 are shown as a function of the temperature T in Fig. 4c. A strong dependence is observed, with both time constants sharply decreasing when the temperature is increased, τ2 in particular changing by three orders of magnitude between 10 and 200 mK. Remarkably, at 10 mK, τ2 reaches one month.

Discussion

We now discuss these results in view of three possible mechanisms that can contribute to the accumulated echo signal decay. The first is the direct relaxation of the nuclear spins involved in the spectral holes, by a \(\vert {\downarrow }_{S}{\uparrow }_{I}\rangle \leftrightarrow \vert {\downarrow }_{S}{\downarrow }_{I}\rangle\) transition. The rate at which this occurs has no reason to be temperature-dependent in the explored temperature and magnetic field range, and our measurements therefore show that for spins near an Er3+ ion, it is at most 3 ⋅ 10−7s−1, more than 6 orders of magnitude lower than the intra-183W bath flip-flop rate estimated to be  ≈ 1 s−1 32. Low relaxation rates are indeed expected for nuclei close to a paramagnetic impurity, because the latter produces a magnetic field gradient which detunes these spins from the bath frequency thus slowing down their energy exchange. This so-called frozen core effect33 has been observed in numerous systems, including donors in silicon34,35, and Nitrogen-Vacancy centers in diamond36; our results show that it is quite pronounced in REI-doped CaWO4, with a quasi-infinite lifetime for some of the proximal nuclear spins which appear to be completely decoupled from the homonuclear spin bath, likely favored by the low gyromagnetic ratio of 183W nuclei and their low density in scheelite.

A second mechanism is nuclear spin relaxation occurring via the electron spin excited state, either resonantly or virtually, analogous to Orbach or Raman electron spin relaxation processes. The Orbach rate should be given by \(\sim {\Gamma }_{1x}/({{{{\rm{e}}}}}^{\frac{\hslash {\omega }_{0}}{{k}_{B}T}}-1)\), whereas the Raman rate should scale like T9 as in Kramers doublets. These rates, moreover, depend on the nuclear spin location with respect to the erbium ion, via the cross-relaxation rate. Fitting the Orbach formula to τ1(T) (resp., τ2(T)) measurements between 50 and 220 mK with B as only fitting parameter yields reasonable agreement and values of B/2π = 32 kHz (resp., B/2π = 124 kHz) close to the expected values for nearest-neighbor 183W nuclei. Therefore, it is likely that the Orbach process is the dominant source of echo decay above 50 mK, whereas the Raman process does not seem to match the observations (see Fig. 4). The two-exponential decay may then originate from the inhomogeneity of the nuclear-spin environment around the Er3+ ions, due to the 14% natural abundance of 183W. The decay times measured at 10 mK deviate from the Orbach prediction, indicating either that the sample effective temperature is somewhat higher than the cryostat base temperature (which is quite possible), or that a third mechanism is limiting the hole lifetime.

This third mechanism may be spectral diffusion of the Er3+ spin transition37. Whereas the echo amplitude is insensitive to a global B0 drift occurring during the waiting time, a drift of the frequency of each ion, uncorrelated with the others, leads to echo decay. This is in contrast to recording the hole area in the frequency domain, which is often insensitive to possible spectral diffusion of the optical line or laser in optical hole burning measurements17. Spectral diffusion is known to occur in paramagnetic systems, caused, for instance, by the change in local magnetic field due to spin-flips and flip-flops of surrounding paramagnetic impurities38. Usual methods to measure spectral diffusion involve a stimulated echo sequence37,39,40, and they probe the drifts on a typical timescale of sub-millisecond to seconds; little is known, however, about possible spectral diffusion at longer time scales. In that regard, the existence of two time scales might represent several different erbium populations, some with faster spectral diffusion due to their proximity to fluctuating paramagnetic impurities for instance, and some with much slower spectral diffusion. Note that our results imply that the spin frequency of most Er3+ ions drifts by much less than 10 kHz (1 ppm relative frequency change) with respect to the center of the line over one month duration at 10 mK; to our knowledge, such an exceedingly weak spectral diffusion has never been reported.

Our results show that in ultra-pure scheelite crystals at millikelvin temperatures, nuclear spins around a paramagnetic impurity are completely frozen; in these conditions, the lifetime of spectral holes can be a good probe for spectral diffusion over very long time scales, which is found to be exceedingly weak at the lowest reachable temperature of 10 mK. It would be interesting to investigate whether these properties pertain to other crystals and paramagnetic impurities. In principle, similar results could also be obtained in scheelite by replacing the microwave pumping by an optical pumping on the Er3+ 1.5 μm transition, which would then open the door to optical storage applications of these ultra-long hole lifetimes. More generally, our measurements suggest that millikelvin temperatures are an interesting and overlooked regime for REI applications, particularly in quantum storage. On that topic, we first note that much greater modulations of the spin density than the one demonstrated here would be required for building an atomic-frequency comb usable for quantum memory, as well as a larger ensemble cooperativity. Assuming these can be achieved, the long hole lifetime would be beneficial for implementing quantum storage protocols in the microwave41,42 or the optical domain43,44.

Methods

Sample

The CaWO4 crystal used in this experiment originates from a boule grown by the Czochralski method from CaCO3 (99.95% purity) and WO3 (99.9% purity). The erbium ion replacing calcium has a doping concentration of 3.1 ± 0.2 ppb, measured from continuous-wave EPR spectroscopy23. A sample was cut in a rectangular slab shape (9 × 4 × 0.5 mm), with the surface approximately in the (bc) crystallographic plane, and the c axis approximately parallel to its long edge. Due to imprecision in dicing the CaWO4 boule, the exact crystallographic c axis deviates slightly from the sample plane, which is characterized by the angle β0. The projection of c axis in plane is defined as \({c}^{{\prime} }\), see Supplementary Fig. 1a.

On top of this substrate, a lumped-element LC resonator, with an inductive wire in the middle and interdigitated capacitor fingers on both sides, was fabricated by sputtering 50  nm of niobium and patterning the film by electron-beam lithography and reactive ion etching. The sample is placed in a 3D copper cavity with a single microwave antenna and an SMA port used both for the excitation and the readout in reflection. The top and bottom capacitor pads are shaped as parallel fingers in an effort to improve the resonator resilience to an applied residual magnetic field perpendicular to the metallic film.

As shown in Supplementary Fig. 1b, in the (yz) resonator plane, the z axis is defined along the direction of the inductive wire, with the y axis perpendicular to it, while the x axis is perpendicular to the plane. Notably, due to the lack of a method to determine the small angle between the projection of the c axis on the (yz) plane (denoted as the \({c}^{{\prime} }\) axis) and the y axis, we assumed this angle to be zero for simplicity, given that this small residual angle has a negligible impact on any of the results presented in the article. Based on the \(y \sim {c}^{{\prime} }\) assumption, the y axis makes a small angle β0 with the crystalline c-axis, while the (yz) plane forms β0 with the crystalline (bc) plane.

Experimental setup

The complete setup schematic is shown in Supplementary Fig. 2.

Room-temperature setup

The room-temperature setup contains two sets of instruments: (i) a VNA for frequency domain measurements, (ii) a microwave source, an arbitrary waveform generator (AWG) and an acquisition card for pulsed time-domain measurements. Two slow switches are used to allow the switching between the sets of VNA spectrum and spin-echo measurements.

The pulses used to drive the spins are generated by mixing a pair of in-phase (I) and quadrature (Q) signals from the AWG with the local oscillator (LO) at the spin resonator frequency ω0 from a microwave source.

The demodulation of the output of the signal is achieved by a second I/Q mixer with the same LO. Then the I and Q signals are amplified and digitized by an acquisition card.

Low-temperature setup

The spin excitation pulses at the input of the dilution unit are filtered and attenuated to minimize the thermal noise. They are directed, through a circulator, to the antenna of the 3D cavity containing the spin resonator. The reflected and output signals on this antenna are routed to room temperature through a Josephson Traveling Wave Parametric Amplifier (TWPA), a double-junction circulator for isolation and a HEMT amplifier.

Magnetic field alignment and stabilization

A 1T/1T/1T 3-axis superconducting vector magnet provides the static magnetic field B0 for this experiment. The alignment of the magnetic field occurs through a two-step process. First, we align the field in the sample plane (yz) by applying a minor field strength of 50 mT while minimizing the resonator losses and frequency shift relative to the zero-field values. Second, we ascertain the direction of the crystallographic c axis projection on the sample plane, defined as θ = 0° (axis \({c}^{{\prime} }\) in Supplementary Fig. 3), by measuring the erbium spectroscopic ensemble line using a Hahn-echo sequence for various θ angles within the (yz) plane23, see Supplementary Fig. 3. Due to the anisotropy of the gyromagnetic tensor, we use a in-plane angle θ and a small fixed out-of-plane angle β0 coming from misalignment of substrate dicing to express the center of the ensemble line \({B}_{0}^{peak}\) as

$${B}_{0}^{peak}=\hslash {\omega }_{0}/\sqrt{{\gamma }_{\parallel }^{2}{\cos }^{2}\theta {\cos }^{2}{\beta }_{0}+{\gamma }_{\perp }^{2}(1-{\cos }^{2}\theta {\cos }^{2}{\beta }_{0})}.$$
(1)

At each angle, we scan the total field B0 by simultaneously adjusting the current in all three coils to maintain the same angle. After the field B0 is well-aligned with \({c}^{{\prime} }\) axis, a small additional out-of-plane field δB⊥ can be introduced to adjust the total field closer to the actual c-axis orientation. However, this adjustment comes at the expense of increased internal loss in the resonator, as well as decreased signal-to-noise ratio. The misalignment angle can be obtained from \(\beta \sim \arctan (\delta {B}_{\perp }/{B}_{0})\).

Since the out-of-plane field significantly affects both the resonator internal loss and the frequency, it is more meaningful to use the effective gyromagnetic ratio \({\gamma }_{{{{\rm{eff}}}}}\equiv {\omega }_{0}/{B}_{0}^{peak}\), to quantify how well the total field aligns with the c-axis. For each value of δB⊥, we obtained the γeff from the measured center of the spin ensemble line \({B}_{0}^{peak}\) and resonator frequency ω0, as shown in Supplementary Fig. 4. When δB⊥ = 7.4 mT, γeff reaches its minimum, corresponding to an alignment angle of β = 0.95°, which is similar to the β0 extracted in Supplementary Fig. 3. However, at this same point, the resonator’s internal loss has increased by a factor of 30 compared to the case of δB⊥ = 0.

In the SHB measurements (Fig. 2 in the main text), better alignment with actual c axis provides a more symmetric and straightforward condition for studying the system’s hyperfine structure. Therefore, we choose δB⊥ = 6 mT, as it still allows for a decent signal-to-noise ratio. In the accumulated echo measurements (Figs. 3, 4 in the main text), we set δB⊥ = 0 and keep B0 within the sample plane.

The stability of the magnetic field is determined by the operational mode (either current supplied or persistent mode) of the three superconducting coils within the vector magnet, as well as their associated current sources. In the spectroscopy data (Fig. 1) presented in the main text, we utilize the current supplied mode alongside a commercial current source (Four-Quadrant Power Supply Model 4Q06125PS from AMI). Conversely, the SHB and accumulated echo data depicted in Figs. 2, 3, and 4 necessitate a better stability (with less than 10 kHz variation) over long periods of time. Therefore we place all three coils in persistent mode to minimize the noise.

Estimation of spin density

In this section, we derive the expression for estimating the ratio of spin density between the reference and hole burning spectra from the measured reflection coefficient S11.

The reflection coefficient of the spin-resonator system is

$${S}_{11}=1-\frac{i{\kappa }_{c}}{(\omega -{\omega }_{0})+i({\kappa }_{c}+{\kappa }_{i})/2-W(\omega )},$$
(2)

with \(W(\omega )={g}_{ens}^{2}\int\frac{\rho ({\omega }^{{\prime} })d{\omega }^{{\prime} }}{\omega -{\omega }^{{\prime} }+i{\Gamma }_{2}/2}\), \({g}_{ens}=\sqrt{\int{g}^{2}\rho (g)dg}\) being the ensemble coupling constant, and Γ2 the spin homogeneous linewidth. In the limit where Γ2 is small compared to all characteristic couplings of the system, it can be shown that \(\rho (\omega )=-Im[W]/(\pi {g}_{ens}^{2})\)45.

In the limits ω ~ ωs and ω ~ ω0, the reflection coefficient simplifies to:

$${S}_{11}=1-\frac{2{\kappa }_{c}}{{\kappa }_{i}+{\kappa }_{c}}+i\frac{4{\kappa }_{c}}{{({\kappa }_{c}+{\kappa }_{i})}^{2}}W(\omega ).$$
(3)

We develop ∣S11∣2, keeping only first order terms in W(ω), and get

$$| {S}_{11}{| }^{2} \sim {\left(\frac{{\kappa }_{i}-{\kappa }_{c}}{{\kappa }_{i}+{\kappa }_{c}}\right)}^{2}+\frac{4{\kappa }_{c}({\kappa }_{i}-{\kappa }_{c})Im[W(\omega )]}{{({\kappa }_{i}+{\kappa }_{c})}^{3}}.$$
(4)

Finally, the spin density for probe frequencies closed to the resonance can be obtained from

$$\rho (\omega )\propto Im[W](\omega )=\frac{{({\kappa }_{i}+{\kappa }_{c})}^{3}}{4{\kappa }_{c}({\kappa }_{i}-{\kappa }_{c})}\left[| {S}_{11}(\omega ){| }^{2}-{\left(\frac{{\kappa }_{i}-{\kappa }_{c}}{{\kappa }_{i}+{\kappa }_{c}}\right)}^{2}\right].$$
(5)

This leads to the ratio of spin densities between the hole-burning condition (ρ1) and reference condition (ρ0) as follows:

$$\frac{{\rho }_{1}(\omega )}{{\rho }_{0}(\omega )}=\frac{| {S}_{11}^{(1)}(\omega ){| }^{2}-{\left(\frac{{\kappa }_{i}-{\kappa }_{c}}{{\kappa }_{i}+{\kappa }_{c}}\right)}^{2}}{| {S}_{11}^{(0)}(\omega ){| }^{2}-{\left(\frac{{\kappa }_{i}-{\kappa }_{c}}{{\kappa }_{i}+{\kappa }_{c}}\right)}^{2}}.$$
(6)

Note that κi and κc are intrinsic resonator internal loss and external coupling rate when spins are detuned from resonance ω0. In the accumulated echo measurements, κi ~ 2.7 ⋅ 105 s−1, while in the hole burning measurements, κi ~ 9.7 ⋅ 106 s−1 due to the applied out-of-plane magnetic field.

Spin density reset

Given the long lifetime of the holes imprinted in the spin density, originating from dynamical polarization of nuclear spins in our system, it is crucial to reset the spin density to its equilibrium value. This ensures the removal of the imprinted spectrum pattern from the previous measurement, guaranteeing that each new measurement starts under the same conditions. The reset process can be achieved by sweeping the pump tone with a strong power across a wide frequency range (at least ten times larger than the scanning range of interest for observing holes). Specifically, we use VNA scan for the reset with a chosen power of −71 dBm at the sample input and a range of 5 MHz centered at ω0. The process contains 24 VNA scans, each lasting 10 s with a step size of 0.5 kHz.

To illustrate the efficacy of the reset process, we use low-power VNA scans (∼ −131 dBm at the sample input) to investigate the reflection within the range of interest under various senarios. We first obtain a spectrum to establish a baseline. Subsequently, a hole is created at ω0 with resonant drive, resulting in a noticeable modification of the spectrum due to the change of spin density. Finally, following the application of the reset process mentioned above, we acquire another spectrum for comparison with the baseline and the spectrum featuring the hole, which demonstrates the erasure of the hole pattern in the spectrum, as shown in Supplementary Fig. 5.

Probe-pulse-induced depolarization and signal rescaling

We now discuss the backaction of the excitation pulses used to retrieve the accumulated echo signal in the time domain from the periodic modulation of the spin density. Due to cross-relaxation, the pulse applied to the spin ensemble can create depolarization of nuclear spins, which reduces the modulation depth of the grating and therefore affects the measured echo amplitude over time. As a result, the corresponding observed decay time constant becomes shorter than its intrinsic value.

To study the impact of the pulse-induced decay, we measure the echo amplitude as a function of number pulses under identical conditions of pumping (N = 18,000 pairs of pulses separated by τ = 100 μs) and probing, but without any extra waiting time between the pulses. Supplementary Fig. 6 shows the measured average amplitude of the first echo that appears after the excitation pulse, plotted as a function of the number of pulses applied to the system. This observed pulse-induced decay curve can serve as a reference for calibrating measurements where a waiting time is introduced between probing pulses.

Fitting the measured data to a triple exponential function and rescaling its starting point (no pulse applied) to one provides a scaling factor for the actual measurements with varying number of probing pulses and different waiting times between two adjacent pulses.

SHB spectra with misalignment of crystalline c-axis

In addition to the SHB spectra presented in the main text, where the magnetic field B0 is aligned with the crystal c-axis, we have also recorded the spectra under a slight misalignment, where B0 is in the sample plane but misaligned with the actual c-axis. The same measurement sequence is applied to obtain the 3 spectra for a pump applied at respectively ω0 + ωI (forbidden transition pumping, on the red sideband), ω0 − ωI (forbidden transition pumping, on the blue sideband), and ω0 (allowed transition pumping). The relative spin density change, ρ1(ω)/ρ0(ω), is plotted in Supplementary Fig. 7 for the 3 pump frequencies. More complex spectra are observed, because the mis-alignment breaks the magnetic equivalence between Type I (or II or III) sites.

Decay of hole and spin density modulation spectra

As a complementary measurement of the decay of the accumulated echo obtained in the time domain in the main text, it is also of interest to demonstrate the time evolution of the spectra of both the hole and the periodically modulated pattern. In this measurement, the system is reset, followed by the creation of a hole via the lower forbidden transition using the same protocol as in Supplementary Fig. 7. The spectrum is then probed every five hours, as depicted in Supplementary Fig. 8, showing the temporal spectral decay featuring a slow fading characteristic. It’s noteworthy that, in contrast to rapid pulsed measurements, frequency domain scanning operates at a slower pace with more averaging for noise reduction and thus induces stronger decay due to cross-relaxation.

Regarding the spin density modulation, after resetting the system, the grating is created using a similar approach in Supplementary Fig. 6, with a different delay time (τ = 50 μs). The probing is performed in the frequency domain with a VNA instead of accumulated echo measurements in the time domain. Supplementary Fig. 9a show the time evolution of the grating pattern up to 80 h. The separation of two adjacent peaks is 20 kHz as expected from 1/τ given the chosen τ = 50 μs. Supplementary Fig. 9b, c show the Fourier analysis for the measured periodic pattern. The amplitude of the 20 kHz peak, obtained from fast Fourier transform (FFT), decays but remains non-zero 80 h after the creation. The time dependence of FFT phase reveals frequency fluctuations, demonstrating high frequency stability throughout the entire measurement duration. This indicates that the frequency drift due to global magnetic field drift and spectral diffusion over several days is ∼ 5 kHz, and the corresponding field fluctuation is less than 0.3 μT.

Echo efficiency

After creating the grating, the echo efficiency relative to the input pulse can be measured by sending a non-saturated pulse (attenuated by 40 dB at the input) and monitoring the intensity of the echo output from the grating. Supplementary Fig. 10 shows an efficiency of 4 × 10−5 in our setup and protocol used for the accumulated echo experiments. This low efficiency arises from two main factors. First, the finite density modulation of our method, which can be optimized during the preparation stage. Second, the low cooperativity, resulting from both the low quality factor of the resonator and the low erbium concentration (3 ppb) in the substrate. By using a resonator with a lower coupling rate and a sample with a higher Er doping concentration, the efficiency can be significantly improved.

Simulation of SHB and accumulated echo

System Hamiltonian

The system we consider is a single Er3+ ion with zero-nuclear-spin isotope doped in CaWO4. The Hamiltonian that describes the subspace of the ground 4I15/2 multiplet (S4 point symmetry) is given by

$${H}_{Er}={H}_{cf}+{H}_{Z},$$
(7)

where Hcf is the reduced crystal-field Hamiltonian

$${H}_{cf}= {\alpha }_{J}{B}_{2}^{0}{O}_{2}^{0}+{\beta }_{J}\left({B}_{4}^{0}{O}_{4}^{0}+{B}_{4}^{4}{O}_{4}^{4}+{B}_{4}^{-4}{O}_{4}^{-4}\right)\\ +{\gamma }_{J}\left({B}_{6}^{0}{O}_{6}^{0}+{B}_{6}^{4}{O}_{6}^{4}+{B}_{6}^{-4}{O}_{6}^{-4}\right),$$
(8)

and therein \({O}_{l}^{m}\) are the Stevens equivalent operators, αJ, βJ, γJ are the Stevens coefficients in the Cartesian system of coordinates with the z-axis parallel to the c-axis46, and \({B}_{l}^{m}\) are the crystal-field parameters47. HZ = g J μ B J ⋅ B0 is the Zeeman interaction, where J = 15/2, gJ = 6/5 is the Landé factor of Er3+, and μB is Bohr magneton. The lowest two energy levels of the Er3+ ion under the magnetic field B0 can be effectively described by means of a spin-1/2 S Hamiltonian

$${H}_{eff}={\mu }_{B}{{{{\bf{B}}}}}_{{{{\bf{0}}}}}\cdot {{{\bf{g}}}}\cdot {{{\bf{S}}}},$$
(9)

where the anisotropic g-factor tensor g has a diagonal form in the crystal frame, with g⊥ = gaa = gbb = 8.38 and g∥ = gcc = 1.247 21. Due to the J = 15/2 multiplet structure, the dipole moment in the \(\vert {\uparrow }_{S}/{\downarrow }_{S}\rangle\) states computed from the full crystal field theory deviates significantly from the simple Kramers doublet expectation. Therefore, we always adopt the expectation values of J instead of S in later computations.

The CaWO4 bath consists of 183W nuclear spin bath (Il = 1/2 and a total of Ns spins) with a natural concentration pn = 0.145. The Hamiltonian of the bath is given by

$${H}_{n}={g}_{n}{\mu }_{n}{\sum }_{l=1}^{{N}_{s}}{{{{\bf{B}}}}}_{{{{\bf{0}}}}}\cdot {{{{\bf{I}}}}}_{l},$$
(10)

where gn is the g-factor of 183W nuclear spins and μn is the nuclear magneton. To simplify the computation for hole burning and accumulated echo, we disregard the internal dipolar interaction among nuclear spins and focus solely on a nuclear spin bath that does not interact with each other. The dipolar hyperfine interaction is assumed as

$${H}_{int}={\sum }_{l=1}^{{N}_{s}}{{{\bf{J}}}}\cdot {{\mathbb{A}}}_{l}\cdot {{{{\bf{I}}}}}_{l},$$
(11)

where \({{\mathbb{A}}}_{l}=\frac{\mu }{4\pi {r}_{l}^{3}}{g}_{J}{\mu }_{B}{g}_{n}{\mu }_{n}\left(1-3{{{{\bf{r}}}}}_{l}{{{{\bf{r}}}}}_{l}/{r}_{l}^{2}\right)\), and therein μ is the vacuum permeability, and rl is the displacement between the lth 183W nuclear spin and central spin.

The external magnetic field B0 is applied along c-axis. As the energy gap between the first-excited states \(\vert \Uparrow \rangle\) and ground states \(\vert \Downarrow \rangle\) of the electron is much stronger than the interaction from the bath, the Hamiltonian for Er3+ ion doped in the CaWO4 bath can effectively be described by a pure dephasing model

$$H\approx \left\vert \Uparrow \right\rangle \left\langle \Uparrow \right\vert \otimes {H}_{\Uparrow }+\left\vert \Downarrow \right\rangle \left\langle \Downarrow \right\vert \otimes {H}_{\Downarrow }$$
(12)

with the central-spin-conditional bath Hamiltonian

$${H}_{k}={\omega }_{0,k}+{H}_{n}+{\left\langle {J}_{z}\right\rangle }_{k}{\sum }_{l=1}^{{N}_{s}}\left({A}_{l}^{xz}{I}_{l,x}+{A}_{l}^{yz}{I}_{l,y}+{A}_{l}^{zz}{I}_{l,z}\right),$$
(13)

where the subscript \(k=\Uparrow \left(\Downarrow \right)\) refers to the first-excited (ground) subspace. ω0,k is the corresponding electronic level, and \({\langle \, {J}_{z}\rangle }_{k}\) is the expectation value of electronic spin. The energy gap of the two levels, ω0 = ω0,⇑ − ω0,⇓, is referred to as the frequency of resonant transition. Il,x, Il,y, and Il,z are the three components of the vector \({{{\bf{z}}}}\cdot {{\mathbb{A}}}_{l}\) with according hyperfine interaction coefficient \({A}_{l}^{xz}\), \({A}_{l}^{yz}\), and \({A}_{l}^{zz}\). Since the interaction between bath spins can be omitted, the Hamiltonian H can be rewritten as \({H}_{k}={\omega }_{0,k}+{\sum }_{l=1}^{{N}_{s}}{H}_{l,k}\). Furthermore, due to the z-axis symmetry, the Hamiltonian (13) can also be transformed into

$${H}_{k}={\omega }_{0,k}+{\sum }_{l=1}^{{N}_{s}}\left[\left({\omega }_{I}+{\left\langle \, {J}_{z}\right\rangle }_{k}{A}_{l}\right){I}_{l,\tilde{z}}+{\left\langle \, {J}_{z}\right\rangle }_{k}{B}_{l}{I}_{l,\tilde{x}}\right],$$
(14)

where \({\omega }_{I}={g}_{n}{\mu }_{n}\vert {{{{\bf{B}}}}}_{0\vert}\) is a gyromagnetic ratio of 183W nuclear spin. The operators \({I}_{l,\tilde{x}}\) and \({I}_{l,\tilde{z}}\) are in the frame whose strength \({A}_{l}={A}_{l}^{zz}\) and \({B}_{l}=\sqrt{{({A}_{l}^{xz})}^{2}+{({A}_{l}^{yz})}^{2}}\), respectively, refer to the isotropic and anisotropic component of the hyperfine interaction of lth nuclear spin. Moreover, we can also introduce \({\eta }_{l,k}={\langle {J}_{z}\rangle }_{k}{B}_{l}/({\gamma }_{W}+{\langle {J}_{z}\rangle }_{k}{A}_{l})\) as a mixing angle that quantify these two isotropic and anisotropic hyperfine interactions.

With the help of exact diagonalization (ED), the energy spectrum of a nuclear spin bath with Ns spins can be formally written as

$$H\approx {\sum }_{j=1}^{{2}^{{N}_{s}}}\left({\varepsilon }_{{e}_{j}}\left\vert {e}_{j}\right\rangle \left\langle {e}_{j}\right\vert+{\varepsilon }_{{g}_{j}}\left\vert {g}_{j}\right\rangle \left\langle {g}_{j}\right\vert \right),$$
(15)

where \({\varepsilon }_{{e}_{j}}\) and \({\varepsilon }_{{g}_{j}}\) (\(\vert {e}_{j}\rangle\) and \(\vert {g}_{j}\rangle\)) are the system eigenenergies (eigenstates) with \(j=1,\cdots \,,{2}^{{N}_{s}}\). Each system eigenstate \(\vert {e}_{j}\rangle\) (\(\vert {g}_{j}\rangle\)) is a series multiplication of each single nuclear-spin state \(\vert {I}_{l}^{\Uparrow }\rangle\) (\(\vert {I}_{l}^{\Downarrow }\rangle\)) with l = 1, ⋯  , Ns, coupled with electronic state \(\vert \Uparrow \rangle\) (\(\vert \Downarrow \rangle\)), i.e., \(\vert {e}_{j}\rangle = \vert \Uparrow \rangle \otimes \vert {I}_{1}^{\Uparrow }\rangle \otimes \cdots \otimes \vert {I}_{{N}_{s}}^{\Uparrow }\rangle\) (\(\vert {g}_{j}\rangle=\vert \Downarrow \rangle \otimes \vert {I}_{1}^{\Downarrow }\rangle \otimes \cdots \otimes \vert {I}_{{N}_{s}}^{\Downarrow }\rangle\)). Here \(\vert {I}_{l}^{k}\rangle=\vert {\downarrow }_{l}^{k}\rangle\) or \(\vert {\uparrow }_{l}^{k}\rangle\) stands for the eigenstate of lth nuclear-spin Hamiltonian Hl,k with ωl,k/2 or  − ωl,k/2 eigenenergy and therein k = ⇑ or ⇓. (ωl,k is the according transition frequency of lth nuclear spin.) And the nuclear-spin eigenstates obey the relations \({{\vert} \langle {\uparrow }_{l}^{\Uparrow }\vert {\uparrow }_{l}^{\Downarrow }\rangle \vert }^{2}={{\vert} \langle {\downarrow }_{l}^{\Uparrow }\vert {\downarrow }_{l}^{\Downarrow }\rangle \vert }^{2}={\uplambda }_{l}\approx 1\) and \({\vert \langle {\uparrow }_{l}^{\Uparrow }\vert {\downarrow }_{l}^{\Downarrow }\rangle \vert }^{2}={\vert \langle {\downarrow }_{l}^{\Uparrow }\vert {\uparrow }_{l}^{\Downarrow }\rangle \vert }^{2}={\xi }_{l} \; \ll \; {\uplambda }_{l}\).

Therefore, if we consider the transition matrix component \(\left\langle {e}_{i}\right\vert \, {J}_{x}\vert {g}_{j}\rangle\) for \(i,j=1,\cdots \,,{2}^{{N}_{s}}\), the process of multi-nuclear-spin-flipping can almost be neglected, since the transition probability for n-spin-flipping process is effectively proportional to ξ n−1. For later hole-burning and accumulated echo computations, we only take into consideration processes involving at most one nuclear-spin flip (spin-conversed).

Generation of H and AH

We investigate the spectrum hole burning by means of continuous-wave pumping to alter the probabilities distribution of energy spectrum and thus generate the hole and anti-hole burning in transition spectrum. The corresponding pumping process is described by the driven Hamiltonian

$${H}_{pump}={\sum }_{i,j=1}^{{2}^{{N}_{s}}}{\Omega }_{p}\left\langle {e}_{i}\right\vert \, {J}_{x}\left\vert {g}_{j}\right\rangle {e}^{-i{\omega }_{p}t}\left\vert {e}_{i}\right\rangle \left\langle {g}_{j}\right\vert+H.c.,$$
(16)

where Ωp and ωp are, respectively, the pumping amplitude and frequency. H.c. stands for the hermitian conjugate of the Hamiltonian.

Our focus is on the evolution of probability distribution for each level under the continuous pumping process. Specifically, we extract the diagonal component of density matrix and redefine a new \({2}^{{N}_{s}+1}\) dimensional vector \(\vec{\rho }={[{\rho }_{{e}_{1}},\cdots,{\rho }_{{e}_{{2}^{{N}_{s}}}},{\rho }_{{g}_{1}},\cdots,{\rho }_{{g}_{{2}^{{N}_{s}}}}]}^{T}\), which is spanned in Cartesius basis that denoted \(\{\vert {e}_{1}\rangle,\cdots \,,\vert {e}_{{2}^{{N}_{s}}}\rangle,\vert {g}_{1}\rangle,\cdots \,,\vert {g}_{{2}^{{N}_{s}}}\rangle \}\). The components of \(\vec{\rho }\), i.e., \({\rho }_{{e}_{i}}\) and \({\rho }_{{g}_{j}}\) are respectively the probabilities for the eigenstates \(\vert {e}_{i}\rangle\) and \(\vert {g}_{j}\rangle\). And the pumping rate equations between the transition \(\vert {e}_{i}\rangle\) and \(\vert {g}_{j}\rangle\) can be written as

$$\left\{\begin{array}{c}{\dot{\rho }}_{{e}_{i}}=-{\tilde{\Omega }}_{i}{\rho }_{{e}_{i}}+{\sum}_{j}{\Omega }_{ij}{\rho }_{{g}_{j}},\\ {\dot{\rho }}_{{g}_{j}}=-{\tilde{\Omega }}_{j}{\rho }_{{g}_{j}}+{\sum}_{i}{\Omega }_{ij}{\rho }_{{e}_{i}},\end{array}\right.\left(i,j=1,2,\cdots \,,{2}^{{N}_{s}}\right),$$
(17)

where \({\tilde{\Omega }}_{i\left(j\right)}={\sum }_{j\left(i\right)}{\Omega }_{ij}\), and therein the pumping rate Ωij, which is based on the Fermi golden rule, is given by

$${\Omega }_{ij}=2{\Omega }_{p}^{2}{\left\vert \left\langle {e}_{i}\right\vert \, {J}_{x}\left\vert {g}_{j}\right\rangle \right\vert }^{2}\frac{{\Gamma }_{2}}{\left({\Delta }_{ij}^{2}+{\Gamma }_{2}^{2}\right)}.$$
(18)

There is a broadening with a Lorentz distribution, and the half-width at half-maximum (HWHM) Γ2 stems from T2 = 30 ms. \({\Delta }_{ij}={\varepsilon }_{{e}_{i}}- {\varepsilon }_{{g}_{j}}- {\omega }_{p}+\delta\), and therein δ is the random central spin detuning and admits the Gaussian distribution \(\delta \sim \frac{\exp (-\frac{{\delta }^{2}}{2{\Gamma }^{2}})}{\Gamma \sqrt{2\uppi }}\) with spin broadening linewidth Γ/2π = 10.9 MHz. This linewidth is much larger than the linewidth of the resonant cavity (around 1 MHz). Thus, we assume that it obeys a uniform distribution in our simulation.

Moreover, if we also consider the electronic relaxation process, which induces the transition from \(\vert {e}_{i}\rangle\) to \(\vert {g}_{j}\rangle\), the Eq. (17) is revised to

$$\left\{\begin{array}{l}{\dot{\rho }}_{{e}_{i}}=-{\tilde{\Lambda }}_{i}{\rho }_{{e}_{i}}+{\sum}_{j}{\Omega }_{ij}{\rho }_{{g}_{j}},\quad \\ {\dot{\rho }}_{{g}_{j}}=-{\tilde{\Omega }}_{j}{\rho }_{{g}_{j}}+{\sum}_{i}{\Lambda }_{ij}{\rho }_{{e}_{i}},\quad \end{array}\right.\left(i,j=1,2,\cdots \,,{2}^{{N}_{s}}\right),$$
(19)

where \({\tilde{\Lambda }}_{i}={\sum }_{j}{\Lambda }_{ij}\) with Λij = Ωij + Γij. Therein, \({\Gamma }_{ij}\approx {\bar{\Gamma }}_{1}| \langle {e}_{i}| \,{J}_{x}| {g}_{j}\rangle {| }^{2}{\delta }_{ij}\) is the rate of relaxation process, where \({\bar{\Gamma }}_{1}\) is determined by \({\bar{\Gamma }}_{1}| \langle {e}_{i}| \, {J}_{x}| {g}_{i}\rangle {| }^{2}\approx 1/{T}_{1}=5\) s−1, which is based on the fact that all the matrix components of the resonant transition are almost the same, i.e., ∣〈ei∣Jx∣gi〉∣2 ≈ ∣〈ej∣ Jx∣gj〉∣2.

The rate equation of Eq. (19) can be reformulated as

$$\frac{{{{\rm{d}}}}\vec{\rho }}{{{{\rm{d}}}}t}=M\vec{\rho },$$
(20)

where M is a \({2}^{{N}_{s}+1}\) dimension transition matrix with its non-zero components giving by

$$\left\{\begin{array}{l}\left\langle {e}_{i}\right\vert M\left\vert {e}_{i}\right\rangle=-{\tilde{\Lambda }}_{i},\left\langle {e}_{i}\right\vert M\left\vert {g}_{j}\right\rangle={\Omega }_{ij},\quad \\ \left\langle {g}_{j}\right\vert M\left\vert {e}_{i}\right\rangle={\Lambda }_{ij},\left\langle {g}_{j}\right\vert M\left\vert {g}_{j}\right\rangle=-{\tilde{\Omega }}_{j},\quad \end{array}\right.\left(i,j=1,2,\cdots \,,{2}^{{N}_{s}}\right).$$
(21)

At time t, the probability distribution \(\vec{\rho }\) can be obtained via the following evolution

$$\vec{\rho }={e}^{Mt}\vec{{\rho }_{0}},$$
(22)

where the initial state \(\vec{{\rho }_{0}}\) is usually set as the thermal state \(\vec{{\rho }_{0}}={[0,\cdots,0,1/{2}^{{N}_{s}},\cdots,1/{2}^{{N}_{s}}]}^{T}\). The changes from \(\vec{{\rho }_{0}}\) to \(\vec{\rho }\) form the basis for generating a H and AH. After the pumping process around 120 s, the T1 relaxation process will still alter the probability distribution (denoted by \(\vec{{\rho }^{{\prime} }}\)), the components of which are given by

$${\rho }_{{e}_{j}}^{{\prime} }=0,{\rho }_{{g}_{j}}^{{\prime} }={\rho }_{{g}_{j}}+{\rho }_{{e}_{j}}$$
(23)

Accordingly, we present the results of hole burning via the relative spin density change ρ1(ω)/ρ0(ω) in Fig. 2 of the main text, where the spin density is defined as

$${\rho }_{1}\left(\omega \right)=\frac{1}{{{{\mathcal{N}}}}}\int{{{\rm{d}}}}\delta {\sum }_{j=1}^{{2}^{{N}_{s}}}\frac{{\Gamma }_{2}{\left\vert \left\langle {e}_{j}\right\vert \, {J}_{x}\left\vert {g}_{j}\right\rangle \right\vert }^{2}{\rho }_{{g}_{j}}^{{\prime} }\left(\delta \right)}{\pi \left[{\left({\varepsilon }_{{e}_{j}}-{\varepsilon }_{{g}_{j}}+\delta -\omega \right)}^{2}+{\Gamma }_{2}^{2}\right]},$$
(24)

where only the no-spin-flipping transition is considered since it contributes most of the spectrum in the probe process. Γ2 is the corresponding HWHM, which characterizes small broadening of single electronic spin that contributes to the homogeneous broadening of spin ensemble. Compared with the experimental spectrum resolution, the small broadening for each spectrum contribution can be regarded as a delta function and can be treated discretely in the simulation. \({{{\mathcal{N}}}}\) is the normalization factor, and here we emphasize that \({\rho }_{{g}_{j}}^{{\prime} }\) is a function of δ. Meanwhile, we can also define the reference spin density \({\rho }_{0}\left(\omega \right)\) by substituting \({\rho }_{{g}_{j}}^{{\prime} }\) from Eq. (24) into \({{\rho }_{0}}_{{g}_{j}}\) to observe how much the probabilities have been altered.

The simulation results, which are compared with the experimental ones, are shown in Fig. 2 in the main text. In the experiments, three pumping frequencies ωp = ωL, ωH, and ω0 were used to, respectively, induce the lower forbidden (ωL = ω0 − ωI), higher forbidden (ωH = ω0 + ωI), and resonant transitions ω0/2π = 7.808 GHz, where ωI is 183W nuclear spin Zeeman frequency. The experiments were conducted with the external magnetic field primarily applied along c-axis, with a slight bias of about 1 mT in b-axis, i.e., B0 = (0, 1, 450) mT, which leads to \({\langle {J}_{z}\rangle }_{\Uparrow }=0.3\) and \({\langle {J}_{z}\rangle }_{\Downarrow }=-0.7\). However, it always indicates a symmetric result \({\langle {S}_{z}\rangle }_{\Uparrow }\approx 0.5\) and \({\langle {S}_{z}\rangle }_{\Downarrow }\approx -0.5\) obtained from the spin-1/2 Hamiltonian (9). The inconsistent results obtained from the above two calculation methods might be the reason that Heff can only successfully capture the transition frequency between the ground Kramers doublets but not the eigenstates and therefore leads to different values of dipole moment.

The simulation results are based on an ensemble average of 500 different nuclear spin spatial configurations (Ns = 8), which provide results that are almost in agreement with the experimental data. In the following, we will discuss more detail about how we obtained the simulation results.

The transition spectrum for ωL and ωH pumping situations shows symmetric results about the central frequency ω0. For each Ns-spin bath, the lower (higher) forbidden transition pumping can theoretically generate Ns holes located at ωl,hole = ωL + ωl,⇑ (ωH − ωl,⇑) and Ns anti-holes located at ωl,anti−hole = ωL + ωl,⇓ (ωH − ωl,⇓) in the transition spectrum, where l = 1, ⋯  , Ns. The experimental result (red curve) in Fig. 2a, b in the main text shows an obvious 40 kHz-interval hole and anti-hole pair, the central frequency of which is about  − ( + )15 kHz deviated from ω0. In fact, whatever is the hyperfine strength of the several nuclear spins nearby the central spin. The same absolute value \(\vert {\langle {S}_{z}\rangle }_{\Uparrow }\vert=\vert {\langle {S}_{z}\rangle }_{\Downarrow }\vert\) from the Heff can always give a symmetric hole or anti-hole distribution without an extra deviation from ω0. Therefore, only the full crystal-field approach in some extent can be adopted to effectively describe the deviation between central position of the hole and anti-hole pair and resonant transition ω0. The hyperfine strength of nuclear spins on the first shell (nearest four, Type I) is much larger than that of other spins, making it more likely that they are involved in this hole and anti-hole pair. To obtain agreement with the experimental data, we need to tune the hyperfine strength of Type I spins, instead of using the dipolar approximation for hyperfine interaction, which is not applicable when considering nuclear spins located near the central spin (see Supplementary Table I). However, the main hole and anti-hole near the central frequency ω0 are the compound-spin results of the relatively distant nuclear-spin dynamics.

As for the ω0 driven situation, there is one hole at the central frequency ωl,hole = ω0 and 2Ns symmetric anti-holes at the frequency ωl,anti−hole = ω0 ± ωl,⇓ ∓ ωl,⇑. Among them, simulation shows that the nuclear spins on the second shell (next-nearest, Type II) contribute the most to the spectrum. Here, we also tune the hyperfine strength of Type II spins in order to obtain the results that agree with the experimental data.

Nevertheless, there may be several reasons for the slight inconsistency between the experimental and simulation results. First, the oversimplified model used: although the simulation we have considered above can provide the position of the holes and anti-holes, it cannot precisely predict their depth or height since it only considers the ensemble average of eight-nuclear-spin bath. Second, unknown free parameters, such as pumping amplitude Ωp or the hyperfine strength of nuclear spins on the first and second shells, were used to tune the simulation. These parameters may have different values in the experimental setup, leading to discrepancies between the simulation and experimental results. Further studies may require a more accurate model and a better understanding of the experimental parameters.

Model of polarization transfer and generation of accumulated echo

In the preceding section, we discussed the probability distribution of the system energy spectrum, which is modulated by continuous-wave pumping and results in the H and AH burning in the transition spectrum. However, instead of relying solely on continuous-wave pumping, we also conducted experiments using a series of pulse sequences as a polarization generator. This approach creates a modulated spin density and a grating in the transition spectrum. In this section, we demonstrate the generation of the grating through simulations.

Similar to the hole burning scheme, the system is initially located at the electronic ground state \({\hat{\rho }}_{0}=1/{2}^{{N}_{s}}{\sum }_{j=1}^{{2}^{{N}_{s}}}\vert {g}_{j}\rangle \langle {g}_{j}\vert\). The polarization generator used in this experiment, denoted as π/2-τ-π/2, consists of a two non-selective microwave (m.w.) pulses separated by a time interval τ. In the rotating frame, which rotates in the right-hand sense with frequency ω0 about the z-axis of the laboratory frame, the π/2 pulse is assumed to cause the electron spin to flip with the angle π/2 along the direction of m.w. field (x -axis), with frequency ω1 and duration tp, such that ω1tp = π/2. In our simulation, we set ω1/2π = 0.25 MHz and tp = 1 μs, which effectively induces only the nuclear-spin resonant transition but not the lower (higher) forbidden transition, due to the fact that ωI > ω1.

For each resonant transition \(\vert {e}_{j}\rangle \leftrightarrow \vert {g}_{j}\rangle\), the presence of a large electronic-spin broadening δ can cause the precession axis to tilt from ϕ = 0 (x-axis) into \({\phi }_{j}=\arctan ((\delta+{\varepsilon }_{{e}_{j}}-{\varepsilon }_{{g}_{j}})/{\omega }_{1})\) in the x-z plane, with a frequency \({\omega }_{eff,j}=\sqrt{{(\delta+{\varepsilon }_{{e}_{j}}-{\varepsilon }_{{g}_{j}})}^{2}+{\omega }_{1}^{2}}\). The matrix form of π/2 pulse in the subspace \(\{\vert {e}_{j}\rangle,\vert {g}_{j}\rangle \}\) is defined as \({R}_{j}=\cos {\theta }_{j}{\mathbb{I}}- i\sin {\theta }_{j}({\sigma }_{z}\sin {\phi }_{j}+ {\sigma }_{x}\cos {\phi }_{j})\), where θj = ωeff, jtp/2, \({\mathbb{I}}\) is the identity matrix, and σi (i = x, y, z) are Pauli matrix components. Therefore, π/2 pulse for the whole system is expressed as \({R}^{\pi /2}={R}_{1}\otimes \cdots \otimes {R}_{{2}^{{N}_{s}}}\).

In the experiments, the system undergoes a series of polarization generators with a total sequence number N. Before the nth sequence, the initial density matrix is denoted by \({\hat{\rho }}_{0,n}\), with \({\hat{\rho }}_{0,1}={\hat{\rho }}_{0}\) when n = 1. After each π/2-τ-π/2 polarization generator, the density matrix is modified into

$${\hat{\rho }}_{1,n}={R}^{\pi /2}{U}_{\tau }{R}^{\pi /2}{\hat{\rho }}_{0,n}{R}^{-\pi /2}{U}_{\tau }^{{{\dagger}} }{R}^{-\pi /2},$$
(25)

where Uτ is the free-evolution operator of the Hamiltonian, and † refers to Hermitian conjugate. There is a time interval between each two polarization generator sequences, during which the relaxation and decoherence processes cause the density matrix becoming \({\hat{\rho }}_{2,n}={\sum }_{j=1}^{{2}^{{N}_{s}}}{p}_{n,j}\vert {g}_{j}\rangle \langle {g}_{j}\vert\) with

$${p}_{n,j}=\left\langle {g}_{j}\right\vert {\hat{\rho }}_{1,n}\left\vert {g}_{j}\right\rangle+\mathop{\sum }_{i=1}^{{2}^{{N}_{s}}}{\left\vert \left\langle {g}_{j}\right\vert {\sigma }_{x}\left\vert {e}_{i}\right\rangle \right\vert }^{2}\left\langle {e}_{i}\right\vert {\hat{\rho }}_{1,n}\left\vert {e}_{i}\right\rangle .$$
(26)

After each sequence of polarization generators, the density matrix of the system changes, with \({\hat{\rho }}_{0,n+1}={\hat{\rho }}_{2,n}\). The final probability distribution is represented by \({\hat{\rho }}_{2,N}\) after N sequences of polarization generators, which can form periodical modulated holes and anti-holes in the transition spectrum, as shown in Supplementary Fig. 11a. By increasing the sequence number N, deeper holes and higher anti-holes can be obtained in the spectrum. The nearest interval between the two anti-holes is related to the time interval τ in the polarization generator, specifically Δω = 2π/τ.

Once a grating has been created in the transition spectrum, we can use a π/2-τ sequence to detect the accumulated echo or the distribution of \({\hat{\rho }}_{2,N}\) with the help of transforming the polarization into coherence. After the probe process, the density matrix of the system is defined as

$${\hat{\rho }}_{{{{\rm{e}}}}}={U}_{\tau }{R}_{x}^{\pi /2}{\hat{\rho }}_{2,N}{R}_{x}^{\pi /2{{\dagger}} }{U}_{\tau }^{{{\dagger}} },$$
(27)

where the off-diagonal term corresponds to the coherence of the system

$${A}_{{{{\rm{e}}}}}\left(t,N\right)=\mathop{\sum }_{j=1}^{{2}^{{N}_{s}}}{p}_{N,j}{e}^{it\left({\varepsilon }_{{e}_{j}}-{\varepsilon }_{{g}_{j}}\right)}.$$
(28)

The simulation results are displayed in Supplementary Fig. 11b, where the echo signals are visible when t ≈ nτ (n is the positive integer). The amplitudes for each echo decrease over time. As more sequences of pulse are performed on the system, the corresponding echo signals become amplified. In addition, Fig. 3f in the main text is referred to as the comparison between the experimental and simulation results for each sequence N, which are in almost agreement.