Introduction

Understanding the interaction between slow slip and regular earthquakes is key to advancing our knowledge of earthquake nucleation processes e.g., refs. 1,2. While some studies suggest that slow slip events (SSEs) may trigger large earthquakes by modifying local stress conditions e.g., refs. 3,4,5,6, others propose that SSEs relieve accumulated stress and reduce the likelihood of large events7,8. Simulations of SSEs9 indicate that recurrence intervals of long- and short-term SSEs may shorten prior to a major earthquake. However, a global catalog comparison of SSEs and nearby seismicity does not reveal a consistent correlation between slow slip and subsequent earthquake activity10. These contrasting interpretations may arise from limited observation period, low detection resolution, or the inherently variable behavior of slow slip phenomena. To date, compelling evidence of ubiquitous precursory slow slip remains limited.

In this study, we examine aseismic slip behavior in eastern Taiwan using two complementary indicators: repeating earthquake sequences (RESs) and earthquake swarms. Repeating earthquakes, which reflect localized fault creep, are sensitive to variations in aseismic loading e.g., ref. 6. Earthquake swarms, meanwhile, often indicate transient aseismic slip and/or fluid overpressure, and are highly sensitive to subtle changes in stress and pore pressure e.g., refs. 11,12,13. Laboratory and theoretical studies show that changes in pore pressure can reduce effective normal stress, promoting a spectrum of slip modes including slow and fast earthquakes14,15,16. Taiwan provides an exceptional natural laboratory to investigate these processes due to its rapid tectonic deformation, frequent large earthquakes, and dense seismic instrumentation. Here, we explore the interaction between aseismic and seismic slip preceding the April 3, 2024 Mw7.3 Hualien earthquake.

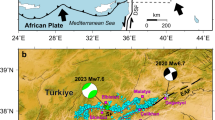
Taiwan is one of the most seismically active regions globally, especially along the active Longitudinal Valley (LV) suture zone in eastern Taiwan. This zone, resulting from the collision between the Luzon Arc on the Philippine Sea Plate and the continental crust of the Eurasian Plate, hosts two parallel, head-to-head fault structures with opposing dips: the east-dipping Longitudinal Valley Fault (LVF) to the east and the west-dipping Central Range Fault (CRF) to the west e.g., refs. 17,18,19. Since 2000, these fault systems have produced 13 M ≥ 6 events (Table S1), revealing complex interaction patterns, including (1) simultaneous ruptures or delayed triggering during sequences of M7 events e.g., refs. 20,21 and (2) out-of-phase occurrences of M ≥ 6 events due to the stress shadow effect22. Among these, two events exceeded magnitude 7.0, as shown by numbers 10 and 11 in Fig. 1 and Table S1 of the supplementary material.

Fig. 1: Tectonic setting, major earthquakes, and repeating events.
figure 1

a Simplified tectonic setting of Taiwan. Tectonic units from west to east are the Coastal Plain (CP), the Western Foothills (WF), the Hsuehshan Range (HR), the Central Range (CeR) and the Coastal Range (CoR). The black rectangle marks the area shown in (b). b Distribution of Mw ≥ 6 mainshocks in eastern Taiwan since 2000, with their focal mechanisms and aftershocks within 1 month shown by correspondingly colored circles. Number on the top of the focal mechanisms corresponds to the ID number with mainshock information listed in Table S1. The red thick line indicates the surface trace of the Longitudinal Valley fault (LVF) with a strike of approximately N30°E. Repeating earthquake sequences (RESs) updated to 2024 are denoted by brown diamonds, highlighting the creeping LVF in the south from near the surface to a depth of 25 km and the creeping Central Range fault (CRF) in the north at depths of 10-25 km. c, d Cross-sections A-A’ and B-B’ within a zone of 25 km width (gray dashed bracket in b) showing the approximate fault geometry of the east-dipping LVF and west-dipping CRF. The background color represents the Vp/Vs ratio27. Blue-shaded bars indicate the first-order fault geometry of the CRF and LVF.

Full size image

The April 3, 2024 Mw7.3 Hualien earthquake likely nucleated on the LVF23, as inferred from the alignment of the earlier stage of aftershocks (see Movie S1 of the supplementary material). This event was followed by two M6-7 and 25 M5-6 aftershocks within a month, which reveal conjugate ruptures on both the northern LVF and CRF24(purple circles in Fig. 1b). In contrast, the September 18, 2022 Mw7.0 Guanshan-Chihshang earthquake sequence initiated on the southern CRF and triggered aftershocks on both the CRF and the creeping segment of LVF, the Chihshang Fault (marked by light purple circles in Fig. 1b, d)21,22,25. The seismicity, aftershocks, and slow slips along both creeping and locked segments of the LVF and CRF present a unique opportunity to improve understanding of fault interactions via aseismic slip and the role of aseismic slip in earthquake cycles.

In this study, we compile a 24-yr catalog of RESs and earthquake swarms to assess the spatiotemporal association between slow slip indicators and regional seismicity, and further, investigate aseismic slip evolution leading up to the 2024 Mw7.3 Hualien mainshock. In the following sections, we (1) quantify the aseismic slip rate variations using RESs data, (2) analyze swarm migration and dynamics, (3) identify GNSS-observed slow slip episodes, and (4) evaluate seismicity rate changes preceding the mainshock. Finally, we use Coulomb stress modeling to explore how these aseismic processes may have contributed to triggering the 2024 Mw7.3 event.

Results

Aseismic slip rates from repeating earthquakes

RESs involve groups of events characterized by nearly identical waveforms, magnitudes, and locations, representing repeated ruptures of the same fault patches. Their short recurrence intervals imply rapid loading from surrounding aseismic slip, making them effective indicators of fault creep and interseismic deformation rates26,27,28,29. In eastern Taiwan, RESs have been documented along the creeping segments of the LVF and CRF30,31,32,33,34. We updated the previously established RESs catalog30 from 2000–2011 to 2012–2024, to include events through May 2024. The RES detection approach is described in Methods.

The updated RESs catalog contains 649 events across 148 sequences from January 1, 2012–April 18, 2024, with magnitudes ranging from 2.0 to 5.1. Merging this with the January 1, 2000 through December 31, 2011 RES catalog30, the integrated dataset comprises 1499 RES events in the 148 sequences. Each sequence includes 3–34 events. As shown by diamonds in Fig. 1, these events cluster into two spatial groups: in the northern LV (north of 23.6°N), RESs occur on the west-dipping CRF, while in the southern LV (south of 23.6°N), they cluster along the east-dipping LVF.

Using the scaling relationships developed for creeping sections in eastern Taiwan30, the slip for each repeating event can be obtained using the scaling relationship between the slip estimate (d) and seismic moment (Mo) as logd = − 1.21 + 0.11 logMo and logd = − 1.96 + 0.14 logMo for the LVF and CRF, respectively (see Methods for how these scaling laws were inferred). Slip histories from multiple RESs were then combined to estimate the spatiotemporal variations in aseismic slip driving the repeating events. The regional cumulative slip was calculated in one-day increments by measuring the change in slip between consecutive days. To ensure that the calculation window exceeded the length of any data gaps but remained shorter than the targeted recurrence pattern, we applied a 180-day averaging window. This smoothing reduces short-term variability and enables a more robust determination of the slip-rate time series30.

Figure 2 presents the temporal distribution of RESs events and the corresponding aseismic slip rate, while Fig. S1 in the supplementary material visualizes the along-strike spatiotemporal evolution of M ≥ 2 seismicity density and RESs-derived aseismic slip. We systematically tested the sensitivity of the computed slip rate to different averaging windows (Fig. S1b–c). Shorter averaging windows yield higher temporal resolution but are prone to noise when below the RESs inter-event time (mean: 15 days; maximum: 127 days). Longer windows increase reliability but may introduce time lags30. Near-zero slip rates using 1-month time window (Fig. S1b–c ) typically reflect gaps in RESs detection.

Fig. 2: Repeating earthquake sequences (RESs) derived aseismic slip rates in eastern Taiwan.
figure 2

Magnitude distribution (top), occurrence rate, and slip rate (bottom) of RESs since 2000 for (a) northern Longitudinal Valley (LV) on the Central Range fault (CRF) and (b) southern LV on the Longitudinal Valley fault (LVF). Cumulative RESs events and the derived slip rates are denoted by black and dark red lines, respectively. Using a moving window analysis, the RESs slip rate is calculated as the average value within a 3-month window before and after each plotted point. The plotted value is updated daily, advancing forward in time. Vertical red dashed lines indicate the occurrence time of Mw ≥ 6 events with the ID number corresponding to Table S1. Black arrows and black dashed lines mark the significant change of the RESs occurrence rate. The occurrence rate averaged over each sub-period is indicated by the number.

Full size image

In the southern LV area where RESs are widely distributed along the east-dipping LVF, from near surface to 30 km (Fig. 1d), the highest aseismic slip rate peak occurred shortly after the 2003 Mw6.8 Chihshang earthquake, coinciding with a sharp increase in RES activity. Following the Mw6.8 mainshock, the RESs occurrence rate tripled from 13.7 to 41.6 events per year, which persisted for 6 years. In the northern LV where the RESs mainly occurred on the west-dipping CRF below the depth of 10 km, the RESs occurrence rate is generally higher than in the southern LV; The small fluctuations in aseismic slip rate tend to show annual variation30. The most pronounced CRF aseismic slip acceleration followed the April 18, 2019 Mw6.1 event, with RESs activity increasing from 33.3 to 45.8 events/year.

Not all large earthquakes in eastern Taiwan influence aseismic slip as captured by RESs. Along the northern CRF, where more than five M ≥ 6 earthquakes occurred during the study period, the RESs-inferred aseismic slip rate remains relatively stable. This may reflect the fact that RESs tend to occur at depths of 10–25 km, whereas most large earthquakes ruptured shallower parts of the fault (<10 km). Only RESs located in close proximity to mainshock hypocenters (e.g., Number 6 in Fig. 1) show evidence of stress-driven acceleration in aseismic slip.

Aseismic slip behavior from earthquake swarms

Aseismic slip can also manifest through earthquake swarms, clusters of earthquakes lacking a clear mainshock and a typical aftershock decay pattern. These swarms are generally associated with fluid intrusions and elevated pore pressure e.g., refs. 35,36,37, which can induce fault unclamping and promote slow slip38,39. A previous study in Taiwan26 analyzed 153 M ≥ 3 swarm sequences (4726 events) and their relationship with 59 M ≥ 6 earthquakes, finding limited evidence of precursory swarms. Instead, swarms more often followed large earthquakes. As demonstrated by the previous study26, a significantly higher proportion of swarm events followed M ≥ 6 earthquakes when the separation distance was less than 10 km, highlighting a spatial dependence in post-mainshock swarm triggering.

To build a more comprehensive swarm catalog, we applied a composite clustering method26 that integrates multiple declustering algorithms. Swarm sequences were identified from events with M ≥ 2.0, consistent with the estimated magnitude of completeness (Mc) for this region (see Methods for details). From January 1, 2000 to April 30, 2024, we identified 15 swarm sequences comprising 4109 events with magnitude ranging from M2.0 to 5.9 (Table S2 and Fig. S2). Of these, 82% of the swarm events (in 10 sequences) occurred in the northern LV (Fig. S2a), coinciding with the aftershock zone of the 2024 Mw7.3 Hualien earthquake and along the west-dipping CRF (Fig. 1b, c, Fig. S2c). These northern swarms are spatially associated with high Vp/Vs zones (cross-section in Fig. S2b–c), suggesting a fluid-saturated environment. In addition, the composite method yields a declustered earthquake catalog that excludes mainshock-aftershock sequences and swarm-like clusters, which is used for background seismicity analyses.

The longest swarm sequence (Sequence 9) occurred from April 18 to August 18, 2021, comprising 796 events, including nine 6 > M ≥ 5 earthquakes (Fig. 3). Approximately 2 months after the first event, 86% of swarm events occurred at depths shallower than 15 km, ultimately reaching regions of high Vp/Vs ratio and low Vp and Vs27. The swarms mainly spanned depths of 5–22 km, partially overlapping with RESs depths (13–22 km, green squares in Fig. S11). This swarm sequence demonstrated bilateral migration, with 69% of events propagating upward and 31% downward. Compared to the vertical direction, northward migration was less pronounced (Fig. 3a, b and Movie S2).

Fig. 3: Spatiotemporal evolution and diffusion characteristics of the 2021 earthquake swarm.
figure 3

a Spatial distribution of the swarm sequence from April 18 to August 18, 2021. Circles represent swarm events, with color indicating the time elapsed since the beginning of the sequence and size proportional to magnitude. Stars indicate events with magnitude greater than 5.0. The first event of the swarm sequence is denoted by white circle. Green squares denote repeating earthquake events that occurred within a ± 0.5-year window relative to the swarm onset (total time window: 1 year). b Along-strike distribution of swarm and repeating earthquake events. The along-strike distance is defined between points p and p’, corresponding to the start and end of the pink line in Fig. 1b. c Across-strike distribution of swarm and repeating earthquake events. d Magnitude-time plot of the swarm events, showing the temporal occurrence and relative size of earthquakes within the sequence. e Time-space evolution of the swarm sequence. (see Supplemental Movie S2 for animated view of event sequence). The black solid line indicates the best-fit synthetic diffusion curve (D = 5.4 ± 1.1 m2/s) determined by the majority of the 90th percentile distance points (pink squares) obtained each day, following \(r=\sqrt{4\pi {Dt}}\), where r is the distance (km) from the first event, t is the elapsed time (days), and D is the diffusivity (m2/s) with uncertainty denoted by one standard deviation (dashed lines).

Full size image

To quantify the swarm’s migration, we applied a diffusion model to the swarm triggering front. Assuming constant permeability and pore pressure conditions, the hydraulic diffusivity (D) was estimated by fitting the diffusion equation \(r=\sqrt{4{{{\rm{\pi }}}}{Dt}}\), where r is the distance from the first event in a swarm sequence to the triggering front, t is the elapsed time from the start of diffusion, and D is the hydraulic diffusivity28. The best-fit curve was selected to span the majority of 90th percentile distance points (pink squares in Fig. 3e) obtained every 20 earthquakes29. The minimum RMS misfit between the observed and predicted triggering front is obtained using moving time bins containing 20 events, with 10 events overlapping between consecutive bins.

A sensitivity test was performed by sequentially removing early data points (the first 1 to 20 pink squares in Fig. 3e). In other words, the first time we removed the first point (90th percentile obtained using the first 20 events) to measure D1, the second time we removed the initial two points for D2, and the third time D3 for removing three points, and finally, D20 for removing the first 20 points at the earlier stage of the sequence. This yielded a distribution of diffusivity estimates (D1 to D20), from which we computed the mean and standard deviation. For Seq. 9, the mean hydraulic diffusivity was approximately 5.4 m²/s, with standard deviation of 1.1 m²/s, indicating rapid fluid migration from the mid-crust.

Key parameters for each swarm sequence in northern LV area are listed in Table S2, including onset time, duration, sequence duration, number of M ≥ 5 events, seismic moment (maximum and cumulative), b-value, mean diffusivity (D), and standard deviation (SD). Notably, a new swarm initiated 19 days after the 2024 Mw7.3 mainshock on April 22, was excluded from this study due to the catalog cutoff at April 30, 2024. We found that across all swarm sequences, the cumulative moment scales positively with both maximum event size and swarm duration, but inversely with b-value. All sequences except Seq. 1 had b-values < 0.91. This pattern can be explained by the tendency for sequences with a larger maximum event to also include a higher proportion of relatively large events, resulting in lower b-values. Such sequences, often led by relatively large events (e.g., M > 5), tend to persist for longer durations and release greater cumulative seismic moment.

Migration was observed in all swarm sequences but showed no consistent directivity (Figs. S3–S11). High D values were generally associated with greater uncertainty, suggesting that diffusivity estimates exceeding ~10 m²/s should be treated with caution. In contrast, focused swarms (e.g., Seqs. 8 and 9) featured more events and yielded lower diffusivity standard deviations, providing more reliable estimates.

Spatiotemporal association between swarm versus repeating earthquakes

We examined the temporal relationship between swarm sequences and deeper aseismic slip using the RESs time series. Figure 4c compares individual swarm timelines with the evolving aseismic slip rate. To assess potential triggering or causal relationship, we aligned all swarms by their onset (time = 0) and stacked the surrounding aseismic slip rate histories across a ± 180-day window (Fig. 4b). We found that 6 out of 9 swarm sequences were preceded by an increase in aseismic slip rate, suggesting a possible causal link between deep aseismic slip and the initiation of swarm activity. Exceptions include Seqs. 4-6, where no clear precursory acceleration was observed.

Fig. 4: Spatiotemporal association between repeating earthquake sequences (RESs) and earthquake swarms.
figure 4

a Distribution of RESs and earthquake swarms in the northern LV area. The ten different colors represent the ten sequences. Brown diamonds indicate RESs, while the circles represent the earthquake swarms and are color coded by the index of earthquake swarm sequence. Red stars indicate the M6+ event since 2000. b Aseismic slip rate changes 180 days before and during the swarm period. Color corresponds to different swarm sequences in (a). Gray vertical line marks the timing of the first event of each earthquake swarm. Horizontal dashed lines indicate the mean value of slip rate 180 days before and during the swarm onset. c Time evolution of earthquake swarms (colored circles) and the RESs derived average aseismic slip rate. Here, the aseismic slip rate from the RESs in the close-up area (gray box in (a)) is slightly smaller than the one for RESs slip rate in Fig. 2a. The number next to the circles in (b) and (c) denotes the swarm sequence identification. Black stars and vertical dashed lines denote the times of the M6+ events in (a). Start and end of the along-strike distance is denoted by p and p′, corresponding to the start and end of the pink line in Fig. 1b.

Full size image

To test the robustness of the temporal relationship between the changes in aseismic slip rate and swarm activity, we performed a sensitivity analysis by calculating the average aseismic slip rate before (dpre) and after (dpost) each swarm onset across sliding time windows of 1 to 12 months. The difference (df = dpost - dpre) quantifies whether slip rate accelerated before or after the swarm onset. A negative df indicates precursory acceleration, while a positive df suggests slip increase following the swarm. Despite some variability across time windows, Seqs. 3, 4, 5, and 6 consistently exhibited negative df values, while Seqs. 2, 7, and 9 showed positive df (Fig. S12). Most consistent results were obtained using 3- to 6-month averaging windows, which revealed precursory acceleration in 6 of 9 cases, supporting the hypothesis that increased aseismic slip often precedes swarm activity. Seqs. 2 and 9 show the strongest temporal and spatial alignment between swarms and RESs (i.e., relatively large number of repeating events are activated in the close neighborhood of swarm events, indicated by green squares vs. colored circles in Figs. S4 and S11), with significant slip rate changes near swarm onsets (Fig. S12).

To further examine the spatiotemporal relationship between RESs accelerations, swarms, and M\(\ge\)6 events, we plotted separation distance against time difference between each pair of phenomena in Fig. S13. Here, the aseismic slip acceleration is defined by the peak in RESs-derived slip rate history in Fig. 4c. (1) Swarm vs. RESs acceleration (Fig. S13a): Spatial separations range from 10 to 50 km, with time differences generally <0.4 yr. However, smaller spatial separation does not consistently correspond to shorter interaction times, suggesting different underlying mechanisms. (2) Swarm vs. M\(\ge\)6 events (Fig. S13b): A positive correlation is observed, as that closer swarm-mainshock pairs tend to occur with shorter separation times. The closest pairing (27 km) corresponds to a long-duration swarm and short time lag. (3) RESs acceleration vs. M ≥ 6 events (Fig. S13c): No clear trend is observed, despite spatial separations of 5–40 km and time lags <0.35 yr. These results indicate that while swarms and M ≥ 6 events exhibit possible triggering relationships, RESs accelerations appear more loosely coupled with subsequent large earthquakes. Further statistical examination is needed to confirm and strengthen these correlations and interpretations.

Geodetic observation during the swarm sequences

To quantify crustal deformation associated with the swarm sequences, particularly after 2019 where RESs-derived slip rate began to accelerate (Fig. 2a), we analyzed GNSS data pre-processed by the Taiwan geodetic model at the Institute of Earth Science, Academia Sinica, Taiwan (https://tgm.earth.sinica.edu.tw/). To detect the transient deformation, we selected 11 GNSS stations (Fig. 5 and Fig. S14) and processed the time series data by correcting long-term linear trends, seasonal periodic motions, local Mw ≥ 6 coseismic offsets and related post-seismic deformation (the GNSS processing methodology is detailed in the Methods section).

Fig. 5: Global Navigation Satellite Systems (GNSS) data and earthquake swarms.
figure 5

a Distribution of the selected 11 GNSS stations (triangles) and the swarm sequences in 2019 (red dots) and 2021 (black dots). Stars indicate the Mw ≥ 5.5 events since 2019. b, c (Top) N and E components of the processed GNSS signals, color coded by different stations shown in (a). Black curve represents the moving median of 1-month data. Vertical lines denote the occurrence time of the Mw ≥ 5.5 events since 2019. (Bottom) Magnitude-time plot with cumulative number of swarm events. The red, black, and grey dots in the bottom panel indicate the 2019 swarm sequence, 2021 swarm sequence, and background seismicity, respectively. Blue lines indicate the cumulative number of swarm events. Orange-shaded bars indicate the swarm period.

Full size image

The corrected time series reveals transient deformation patterns coinciding with swarm activity (Fig. 5b, c). The 2019 swarm (denoted by red dots in Fig. 5a and lower panel of Fig. 5b, c), occurred approximately four months after the Mw 6.1 earthquake and ~30 km to its south, is found to produce ~10 mm of eastward and southward displacement at stations FLNM and DNFU. During the 2021 swarm sequence (denoted by black dots in Fig. 5a and lower panel of Fig. 5b, c) particularly between Mw 5.9 and Mw 5.5 events, gradual eastward displacements of ~15 mm were observed at stations YENL, SOFN, <10 mm at TUNM and HUAL, and up to ~20 mm at NDHU. We interpret these displacements as primarily reflecting a combination of post-seismic and aseismic deformation, rather than coseismic slip from the Mw 5.9 event at the depth of 15 km and its afterslip. This interpretation is supported by the fact that most seismicity between the Mw5.9 and Mw5.5 events was concentrated around 10 km depth (Fig. 3b, c), a depth unlikely to generate measurable surface displacements. Moreover, the GNSS displacement time series during this interval can be well modeled by a post-seismic exponential decay function without requiring a co-seismic step (Fig. S15).

To interpret the observed transient deformation, we performed a forward modeling assuming a west-dipping fault plane as the primary rupture surface. Due to the limited number of GNSS stations (only two or three) showing significant displacements near the swarm epicenters, the fault geometry was constrained simply using the locations and focal mechanisms of M ≥ 5 swarm earthquakes. The dip and rake angles were fine-tuned to better fit the observations (see Table S3). Assuming that the observed transient deformation is solely tied to slip associated with the swarm events, we approximated the imposed fault slip based on the total seismic moment released during each sequence. For the 2019 swarm, this corresponds to ~2 cm of slip across a 15 × 20 km area. For the 2021 swarm (time period between Mw 5.9 and Mw 5.5 event), we consider two fault segments based on the depth distribution of swarm events: ~5 cm of slip on the shallow segment (40 × 10 km area) and ~4 cm on the deeper segment (40 × 18 km area), as illustrated by the blue vectors in Fig. S16.

The forward modeling results show that for the 2019 swarm, the predicted displacements account for only about half of the observed surface motion (red and black arrows in Fig. S16), suggesting a significant contribution from additional aseismic slip. In contrast, the predicted displacements for the 2021 swarm are slightly larger than the observations. These discrepancies may arise from simplifications in fault geometry and limited GNSS station coverage. A denser GNSS network and more detailed fault modeling will be necessary to better constrain the aseismic slip contributions.

Interplay of seismic and aseismic slip episodes in northern LV

In the region surrounding the active swarms (grey box in Fig. 4a), intense aseismic slip episodes were observed following the April 18, 2019, M6.1 earthquake. This is indicated by a sharp increase in the occurrence rate of RESs at the time of this M6.1 event (Fig. 2a), followed four months later by the onset of the 2019 swarm on August 2, 2019 (Seq. 8). Figure 6 summarizes the temporal evolution from 2019 to 2024, including swarm activity, RESs-derived aseismic slip rate, GNSS displacements corrected using monthly averages, and seismicity parameters.

Fig. 6: Seismic, aseismic, and Global Navigation Satellite Systems (GNSS) time series in northern Longitudinal Valley (LV).
figure 6

a Temporal distribution of earthquake swarm events. b Repeating earthquake sequences (RESs) derived seismic slip rate color coded with various averaging window. c Cumulative number of RESs events. Colored dashed lines show the estimated occurrence rate, with numbers representing the computed rate values. d Cumulative moment of RESs events. Colored dashed lines show the estimated moment rate, with numbers representing the computed moment rate values. e The corrected 1-month moving average (removing co-seismic effect and linear trend) GNSS time series of YENL, TUNM, and SOFN stations (E component) in the north and DNFY and FLUM (N component) in the south of the study area. The time series are from events in the close-up area northern LV area (gray box in Fig. 4a) since 2019 when the RESs derived aseismic slip accelerated. Vertical red dashed lines indicate the times of five M6+ events in the study area, while grey lines indicate two M6+ events occurred in the south LV area. f–h Temporal distribution of occurrence rate of seismicity, a- and b- values using original earthquake catalog. Shallow seismicity (≤ 15 km) and deep seismicity (\( > \) 15 km) are indicated by dark blue and light blue, respectively. i Occurrence rate of declustered seismicity. The shaded orange area marks the time span of the 2019 and 2021 swarms. Numbered arrows denote different stages of seismic and aseismic slip behavior. The time history of seismic and aseismic behavior was determined using a centered 30-day averaging window, in steps of one day, consistent with the daily resolution of GNSS data. Seismicity and swarm events are counted as the number per day. Daily seismicity rate and a- and b-values are calculated using a moving window approach, in which a ± 15-day window is centered on each day. Estimates are only shown for windows containing more than 100 events to ensure statistical robustness.

Full size image

In April 2019, an M6.1 earthquake occurred at the depth of 20 km in the northern part of the study area, spatially close to a cluster of deep RESs. These RESs responded with a notable acceleration in slip rate (first red dashed line in Fig. 6). Approximately 3.5 months later, a separate swarm sequence occurred to the south (first orange peak in Fig. 6a), accompanied by a discernible increase in the RESs activity, which is visible in the monthly average slip rate (green curve in Fig. 6b), along with ~10 mm of gradual displacement recorded at nearby GNSS stations (blue circles in Fig. 6e). Given the considerable spatial separation between the swarms, RESs, and the 2019 M6.1 event, we infer the presence of two distinct aseismic slip episodes: (1) a deep slip event at depths greater than 15 km in the north, where deep, widely distributed RESs aligned along the mountain strike responded to the nearby 2019 M6.1 event, leading to significant acceleration of aseismic slip rate; and (2) shallower slip episodes in the south, where aseismic slip was detected by nearby GNSS stations during the shallow swarm sequence.

In contrast, the prolonged 2021 swarm sequence from April 17 to August 29, spanned a broad depth range from ~24 km to near the surface and overlapped substantially with RESs (Fig. S11), yet occurred independently of any major earthquake. This episode marked the onset of the most consequential aseismic–seismic coupling observed in the 24-year record that may have initiated a sequence of fault processes that ultimately led to the 2024 Mw7.3 Hualien earthquake. This swarm-RESs coupling, and its potential connection to the 2024 Mw7.3 earthquake, requires detailed examination. The spatiotemporal evolution of this activity can be divided into four stages:

Stage 1 (April-August, 2021): Acceleration of aseismic slip and swarm activity. The intense earthquake swarm lasted from April 17 to August 29, initiated near 14 km depth and exhibited multiple waves of activity. During the first two months (first spike for 2021, Fig. 6a), swarm events clustered at depths of 15–20 km and migrated upward and northward. At the same time, the RESs-derived aseismic slip rate at 15–25 km depth began to accelerate, a trend most evident in the monthly average (green line in Fig. 6b). Increases in RESs’ moment rate and occurrence rate are also observed during this interval (Fig. 6b–d). In the later half of the sequence (second spike for 2021 in Fig. 6a), the swarm activity intensified at shallower depths, accompanied by a renewed rise in the RESs-derived slip rate. This indicates that deep aseismic deformation persisted while shallow brittle failure became more pronounced. Concurrently, GNSS stations near swarm zone recorded transient horizontal displacements (Fig. 6e).

Notably, the swarm period is marked by a sharp increase in shallow seismicity (≤15 km), reflected in both a greater number of events and elevated a- and b-values (Fig. 6f–h, dark blue). In contrast, the declustered background seismicity (Fig. 6i) shows no comparable change, indicating that the observed acceleration in shallow seismicity was driven primarily by the swarm itself rather than by background seismic processes. Over the full four-month period, the shallow seismicity rate increased from 4.39 to 10.75 events/day, while the deep seismicity rate remained steady at ~4 events/day (Fig. S17). The simultaneous acceleration of swarm activity, enhanced RESs-derived slip rate, and transient surface deformation suggest an aseismic slip episode that likely accompanied by fluid migration and activated both brittle and aseismic slip along multiple depth levels of CRF.

Stage 2 (September, 2021 to late-2022): Cascade-like M6+ events. After the 2021 swarm, both the RESs-derived slip rate and overall seismicity declined until late 2022. During this period, however, a sequence of large earthquakes occurred, including the March 22 M6.7 event in southern LV (number 7 in Fig. 1), the June 20 M6.1 event in northern LV (event 8 in Fig. 1), and September 17 -18 M6.5 and M7.0 events in southern LV (events 9 and 10 in Fig. 1). During this period, earthquake occurrence in southern LV increased significantly. In contrast, the northern LV experienced a pronounced decline in seismicity, with the shallow rate dropping from 10.75 to 2.51 events/day and the deep seismicity rate also dropped from 3.79 to 2.46 events/day (Fig. S17). Stage 2 is therefore characterized by a cascade of seismic slip events occurring primarily outside the swarm zone.

Stage 3 (2023 to 2024): Gradually accelerated seismic and aseismic slip rates. Beginning in October 2022, the RESs-derived slip rate slightly increased, as shown in the long-period trends (6-month averaging windows in Fig. 6b), and continued until a few months prior to the April M7.3 event. While the annual number of repeating earthquakes remained nearly constant (~45 events/year, Fig. 6c), their seismic moment rate increased from ~1.3–1.4 × 10¹⁵ to 2.2  × 10¹⁵ N-m/day (Fig. 6d). This pattern indicates a larger slip per event, consistent with progressive deep fault creep and mechanical weakening at depths greater than 15 km.

Meanwhile, background seismicity from both original and declustered earthquake activities intensified, particularly at shallow depths when compared to earlier time periods. As shown by Fig. 6f–h, seismicity rate, a- and b-values increased notably in the shallow crust following the cascade of M6+ events. The rising a-value reflects an overall increase in seismic activity, while the increasing b-value suggests a greater proportion of smaller events. This pattern is consistent with Fig. S17, which shows a rise in the occurrence rate of shallow earthquakes from 2.51 to 8.37 events/day across 2023, while seismicity at greater depths shows a relatively minor increase, from 2.46 to 5.05 events/day. The declustered catalog further reveals that both shallow and deep seismicity began a gradual, slight rise roughly one year before the mainshock.

To reconcile (1) the observed increase in deep aseismic slip and RESs moment rate, (2) the rise in seismicity rate in both declustered and original earthquake catalogs, and (3) the elevated a- and b-values in the shallow crust one year before the mainshock, we propose a depth-dependent fault evolution model. At greater depths (>15 km), the CRF appears to undergo progressive aseismic slip, likely accompanied by upward fluid migration. This deep process may have weakened the overlying crust and promote more small events on both the LVF and CRF. The concurrent rise in shallow seismicity and elevated a- and b-values suggests a brittle response within a more heterogeneous and a possibly fluid-rich environment. These patterns suggest that deep slow slip and shallow brittle failure have operated as coupled processes along the CRF, which may represent an intermediate stage in the preparatory phase leading to large earthquake nucleation. However, given that aseismic slip signals are resolved only at monthly timescales, it remains difficult to establish a direct temporal link between aseismic and seismic slip in the final month preceding the mainshock.

Stage 4 (2024 April to May): M7.3 event and renewed shallow swarm activity. The April 3, 2024 M7.3 mainshock, with a hypocenter depth of 21 km, was followed by a sequence of aftershocks aligned along the steeply east-dipping LVF until April 22. At that time, a new shallow swarm was initiated at shallow depths above 11 km on the gently west-dipping CRF (Fig. S18). This post-mainshock sequence included 5 M6+ events while two of them overlapped spatially with the 2021 swarm, likely representing a recurrence of swarm activity on the same structural segment. Because the RESs catalog ends shortly after the mainshock, the evolution of deeper aseismic slip following the mainshock remains unconstrained and requires further monitoring.

In summary, we propose that since 2019, the CRF has been progressively activated through both RESs and swarm activity. As illustrated by the conceptual model in Fig. 7, the mid-2021 swarm sequence initiated at ~14 km depth, partially overlapping with the creeping segment of the CRF characterized by abundant RESs, and subsequently migrated upward to ~5 km and downward to ~ 20 km. During this period, deep aseismic slip remained elevated, suggesting that a propagating fluid pressure perturbation may have driven both the swarm and RESs activity observed in Stage 1. Significant aseismic slip likely contributed to the triggering of fluid-assisted earthquake swarms, with upward fluid migration potentially weakening the fault at shallow depths. However, the 2022 M6.1 event in Stage 2, located ~30 km south of the swarm zone and opposite the migration direction, implies that fluid migration alone cannot fully explain its occurrence. In Stage 3, seismicity intensified along a broader extent of the fault, especially at shallow depths, and was followed by the 2024 M7.3 mainshock on the east-dipping LVF and renewed swarms on the west-dipping CRF. The recurrence of CRF swarm activity after the mainshock highlights the need to evaluate how prior aseismic slip and earlier seismic events may have jointly loaded this segment. The following Coulomb stress models assess whether the observed sequence of seismic and aseismic slip episodes collectively promoted failure on the M7.3 rupture plane.

Fig. 7: Conceptual model of seismic–aseismic slip interplay.
figure 7

Red and blue lines indicate different fault behaviors of Central Range fault. Purple, orange, and yellow dashed lines outline the distribution of the 2019, 2021, and 2024 swarms, respectively, while the black dashed line outlines the distribution of the RESs. The bilateral fluid migration pattern during the 2021 swarm is denoted by arrows. The background color indicates the Vp/Vs ratio28. The east-dipping black line next to the 2024 M7.3 mainshock represents the assumed rupture plane approximated by the aftershock evolution revealed in Movie S1.

Full size image

Stress triggering models

To establish whether the sequential seismic and aseismic slip episodes can be explained by static stress triggering, we applied a series of Coulomb stress models and focused on the role of aseismic slip on the M6+ events at Stages 2–4. The fault models used for individual aseismic and seismic slip events are described in Methods “Fault models for static stress computation” and listed in Table S4. The stress evolution at successive rupture sites is illustrated by sequential plots of the Coulomb stress change in Figs. S19–S22.

As shown in Fig. S19, cumulative slip from the majority of 2021 swarm sequence at depths shallower than 11 km (shallow aseismic slip episodes) resulted in a 10 kPa increase in Coulomb stress on the 2022 M6.1 rupture, while the aseismic slip from RESs at deeper portion of the fault contributed an additional 6 kPa stress change. This suggests that the M6.1 event may have been triggered by aseismic slip episodes in 2021. Both the shallow and deeper aseismic slip however, induced a negative stress change on the fault segment that later hosted the April 22, 2022 M6.7 event.

The stress changes associated with major seismic events (the 2022 March 22 M6.7, 2022 June 20 M6.1, 2022 September 18 M7.0, and 2024 April 3 M7.3 events) were also examined by evaluating the stress changes induced by preceding ruptures (Figs. S20–S22). The results indicate that the major earthquakes in 2022 can be largely explained by stress change from previous M6+ events. Specifically, the 2022 March 22 M6.7 event produced a 10 kPa stress increase on the fault segment that later hosted the 2022 June 20 M6.1 event. This M6.1 event later contributed a 2 kPa stress increase on the fault of the subsequent M7.0 event. However, the September 18 M7.0 event resulted in a −3 kPa stress change on the fault segment hosting the 2024 M7.3 event. This suggests that the M7.0 event alone does not fully account for the occurrence of the M7.3 mainshock.

Instead, the combined effect of both aseismic and seismic events likely played a crucial role in the stress triggering of the 2024 M7.3 event. This interpretation is supported by the cumulative Coulomb stress increase of up to 30 kPa at the eventual rupture location, resulting from deep aseismic episodes in 2021 and three major M6+ ruptures in 2022 (Fig. S23). Notably, a stress change on the order of 10 kPa is commonly considered sufficient to influence fault failure timing in tectonically loaded systems40,41,42. Therefore, a cumulative 30 kPa increase represents a substantially elevated stress state, capable of significantly advancing the timing of a large earthquake. In addition to fault weakening due to upward fluid migration, this level of stress accumulation from both slow and fast slip along the CRF likely contributed to the enhanced seismicity and RESs activity observed during Stage 3, ultimately facilitating nucleation of the April 3, 2024 Mw7.3 mainshock.

Discussion

Controlling factors of fast diffusivity

During the 2021 swarm, rapid pore-pressure diffusion from approximately 22 km to the near-surface is required to explain the inferred diffusivity of 5.4 m2/s. In addition to the stress increments induced by the aseismic slips that can trigger earthquakes, the increase in pore pressure can also destabilize pre-existing fractures within the fluid-saturated zone, thereby generating earthquakes. The presence of a high pore pressure environment in the shallow CRF may play an important role in modulating earthquake cycles in eastern Taiwan.

As summarized in Table S2, the estimated diffusivities for Seqs. 1 to 9 range from 2.1 m2/s to 31.0 m²/s. Higher diffusivities (D > 10 m²/s) in Seqs. 1, 6, and 7 are associated with large uncertainties, as indicated by coefficient of variation between 41–57%. Earthquake locations may initially be scattered during the first several days before becoming concentrated along clustered strands or confined within the triggering front, which reveals a clear migration pattern. This dispersion in early stages contributes to relatively large uncertainty in the D estimates. However, the D uncertainty may also come from the earthquake location (4.6 ± 3.9 km at depth43). Despite the simplified approximation of the diffusion rates, which captures the majority of triggering fronts (represented by the 90th percentile distance points in one-day bins), the space-time evolution of swarm events (Figs. S3–S11) still exhibits a visible migration trend with D higher than a few m2/s.

Figure S24 summarizes the scaling of swarm diffusivity and duration using swarm data from northeast Japan and this study. The swarms in northeast Japan and the northeast LV area in Taiwan follow a negative correlation described in a power law of duration \(\propto {D}^{-0.5}\). This suggests that swarms lasted longer when they migrated slowly with limited spatial extension, a trend commonly observed in various tectonic settings e.g., ref. 29. The diffusion rates measured in this study are relatively high compared with those observed in other natural swarms, such as 0.008–1.5 m²/s from multiple swarms triggered by the M9.0 Tohoku earthquake in northeast Japan29, 0.09–0.12 m²/s from the long-lived earthquake swarm preceding the M7.7 Noto earthquake44,45, and ~1 m²/s from natural swarms in the Long Valley caldera in California. Before the M7.7 Noto earthquake, several intermittent seismic activities were observed, with rapid hypocenter migration with high diffusivity (101–102 m2/s)44. This migration can be explained by a combined effect from aseismic slip induced stresses and rapid fluid flow in a highly permeable environment.

The diffusion rate inferred in this study is higher than most swarm observations in various tectonic settings (references in the previous paragraph) but lower than the rates of 3–90 m2/s from injection-induced swarms in Soultzsous-Forets, France, and 15–2300 m2/s from volcanic activity in Fagradalsfjall46. The upper limit for pore pressure diffusion in seismogenic fractures is estimated at 10 m2/s47. Several mechanisms have been proposed to explain fast diffusivity, including sudden increases in permeability, low viscosity of pore fluids, highly pressurized pore fluids, stress transfer, and aseismic slip e.g., refs. 28,29,38,46,48,49,50,51,52,53. Although crustal permeability, fluid viscosity, and pore pressure are difficult to estimate in this study, the concurrent acceleration of aseismic slip rate from RESs and geodetic signal of slow slip suggests that the fast migration requires not only fluid movement but also the involvement of aseismic slip that triggers seismicity.

Another key parameter for distinguishing fluid-assisted from slip driven swarms is migration velocity11. By analyzing global migrating swarm sequences, two different behavioral regimes were previously proposed: (1) slow slip driven sequences - migration velocities up to several tens of kilometers per day (2) fluid-induced sequences – migration velocities of hundreds of meters per day. The northern LV swarms were plotted against global data11 (Fig. S25). While two downward-migrated sequences fall within the slow-slip regime, most upward-migrated sequences lie near the boundary between the two regimes, suggesting contribution from both mechanisms. A significant portion of slow slip, supported by deep-seated repeating earthquakes, must be considered in facilitating fluid-induced processes, which likely contributed to the fast propagation of swarm events in this study.

Origin of the fluid

The northern LV area is a collision-subduction transition zone where the westernmost Philippine Sea Plate subducts beneath the Eurasian Plate. Numerous earthquakes occur along a west-dipping seismogenic zone (CRF), extending to a depth of ~25 km. The CRF serves as a lithological boundary, separating the metamorphic belt to the west from the deformed accretionary wedge to the east. It delineates the exhumed metamorphic rocks beneath the Central Range from the sedimentary formations and volcaniclastic rocks beneath the Coastal Range e.g., ref. 54. Most repeating events and earthquake swarms are aligned along the west-dipping CRF, suggesting that the two aseismic phenomena are spatially connected and temporally correlated. The swarm-prone area within the shallow CRF is believed to be fluid-saturated, as indicated by high Vp/Vs shown in Fig. 7.

Some events within the swarm sequences exhibit long duration, low-frequency energy (<5 Hz), referred to as low-frequency earthquake swarms, which are believed to result from fluid movement through the damage zone55,56,57. During the active swarm sequences in mid-2021, a significant number of low frequency earthquake swarms were identified58, suggesting the presence of a fluid-rich body at depths of less than 11 km beneath the Longitudinal Valley. This interpretation is supported by observations of high Vp/Vs, low Vp and Vs, low resistivity59,60, and low Qp and low Qs61. The presence of fluid around the shallow CRF coincides with the location of swarm events in the study area and may be linked to the accreted forearc materials of the PSP and/or the fractured sediments along the LV suture62. Given that the high Vp/Vs body is adjacent to the exhumed Yuli Belt (i.e., high-pressure metamorphic rocks), these fluids may have also been released during the exhumation, leading to a dynamic, tectonic-hydrothermal fluid system located at shallow depths that could facilitate aseismic slip63,64,65,66,67,68,69,70,71. In addition to fluid-induced aseismic slip episodes, it is also possible that deeper aseismic slip pulses modify pore fluid pressure, thereby promoting fluid movement.

In summary, the suture zone in eastern Taiwan, formed by arc–continent collision between the Eurasian and Philippine Sea plates, generates frequent large earthquakes and aseismic slip, posing a major seismic hazard. From 2000 to 2024, this region hosted 13 M6+ events, including the April 3, 2024 Mw7.3 Hualien earthquake. Using repeating earthquake sequences (RESs) and swarm catalogs, we investigated aseismic slip preceding these events. Most swarms occurred in the northern Longitudinal Valley, within the 2024 epicentral area, and six of the nine sequences coincided with accelerating aseismic slip detected by deeper RESs on the west-dipping Central Range fault (CRF).

A notable mid-2021 episode featured a four-month swarm that began at ~14 km depth, migrated upward to ~5 km and downward to ~20 km, and was accompanied by 10–20 mm GNSS displacements. The swarm displayed bilateral migration with rapid diffusivity (~5.2 m²/s), consistent with combined effects of overpressured fluids and deep aseismic slip. This episode was followed by a cascade of M6+ earthquakes in 2022 and renewed increases in slip and seismicity in 2023. The acceleration cannot be explained solely by afterslip of the nearby M6.1 event, suggesting progressive CRF activation through coupled swarm and RES activity.

Stress modeling shows that aseismic and seismic slips during 2021–2022 added up to ~30 kPa positive Coulomb stress on the eventual rupture. Together with fluid-driven weakening of the CRF, these processes likely promoted shallow seismicity and facilitated nucleation of the 2024 mainshock. These results highlight the role of aseismic slip and fluids in earthquake triggering and hazard assessment in Taiwan.

Methods

Earthquake catalog

We analyzed seismicity in the area bounded by latitudes 22.6°–23.4° and longitudes 120.8°–122° from January 2000 to April 2024 using data from the Central Weather Administration (CWA) in Taiwan. Crustal earthquakes with depths shallower than 50 km were selected, corresponding to the average Moho depth in eastern Taiwan (Wang et al., 2010). To ensure statistical robustness in the temporal distribution of earthquakes, we applied the maximum likelihood estimation method72 to determine the minimum magnitude of completeness (Mc), which was estimated to be 2.0. Consequently, a minimum magnitude threshold of 2.0 was adopted for the seismicity analyses. The final catalog comprises 133,627 events with magnitudes ranging from 2.0 to 7.3.

Repeating Earthquake identification

Using the published repeating earthquake waveform procedure30 for events from 2000 to the end of 2011, the repeating earthquake catalog was updated from 2012 to the end of April 2024. The same procedure30,32 was followed to identify repeating earthquakes using two criteria: (1) a cross-correlation coefficient (CCC) higher than 0.9 at more than three stations and (2) a small differential S-P time (dSmP) that ensures more than 50% source overlap. By assuming 3 MPa stress drop, Vp = 4.0 km/s, and Vp/Vs = 1.78, the threshold of dSmP ≤ 0.02 s is used for ML ≥ 2.5 events, while dSmP ≤ 0.01 s is used for ML < 2.5 events.

The seismogram records used in this study were selected from the seismic stations operated by the Taiwan Seismological and Geophysical Data Management System (GDMS). GDMS was established through a collaboration between the Central Weather Administration (CWA) and the Institute of Earth Sciences, Academia Sinica (IESAS). Vertical component seismograms from 50,934 M ≥ 2 earthquakes in the CWA hypocenter catalog for the period January 1, 2012 to April 30, 2024 were used. All earthquake pairs with separation distances of less than 20 km were initially selected. The time window for each event included 3 s before the P-wave arrival and 57 s afterwards.

Slip estimate for individual repeating events

Assuming that the cumulative slip of repeating earthquakes reflects tectonic loading over a single seismic cycle and can be approximated using GPS-derived interseismic slip rates73, as previously adopted in studies30,32,34. We combined these geodetically constrained slip rates with the cumulative seismic moment release of each sequence to estimate the average rupture area for individual repeating events, as defined in Eqs. 3 and 4. The seismic moment (Mo) was calculated using catalog magnitude (ML) data converted to moment magnitude (Mw)74, and then to Mo using the empirical formulation75:

$${M}_{W}=\left(0.91\pm 0.03\right){M}_{L}+\left(-0.07\pm 0.15\right).$$
(1)
$$\log {M}_{o}=1.5\left({M}_{W}+10.73\right).$$
(2)

The rupture area A and seismic moment release rate (\(\widetilde{{M}_{0}}\)) for each repeating sequence can be computed using Eq. 3, and slip for each event in the same sequence is inferred using Eq. 4.

$$\dot{\widetilde{{M}_{0}}}=\frac{\sum {M}_{0}}{{T}_{i}}=\mu A\dot{\widetilde{d}.}$$
(3)
$$d=\frac{{M}_{0}}{\mu A}$$
(4)

\({T}_{i}\) is the total duration of the sequence, \(\mu\) is the shear modulus, and \(\dot{\widetilde{d}}\) is the interseismic slip rate. By applying this framework, a previous study established empirical scaling relationships between slip and seismic moment for different regions30. In the southern Longitudinal Valley (LV), the repeating earthquake sequences (RESs) yielded a best-fit relation of log d = –1.21 + 0.11 log Mo, while in the northern LV, the corresponding scaling was log d = –1.96 + 0.14 log Mo. These regional differences reflect variations in fault structure, interseismic loading, and RES depth, and highlight the importance of local calibration in slip moment scaling analyses.

Earthquake swarm identification

To distinguish earthquake swarms from mainshock-aftershock sequences, the swarm sequence is expected to exhibit high seismicity density without a dominant mainshock. In more swarm-like clusters, a higher proportion of background seismicity is typically observed. A previous study26 proposed a composite declustering method that mitigates uncertainties associated with arbitrary parameter choices in individual models. Following their approach, we applied three declustering methods: the Epidemic-Type Aftershock Sequence (ETAS) model76, the nearest-neighbor method (NN13)77, and the interaction-zone method (Re85)78, which links earthquakes based on spatial and temporal proximity.

The identification of earthquake swarms requires the determination of density rate anomalies (δμ0). To do so, the density rate (μ0) of the declustered seismicity is first estimated to represent the background rate as

$${\mu }_{0}\left(x,y,t\right)={\sum }_{i}{\omega }_{i}{e}^{-\sqrt{\frac{{\left(x-{x}_{i}\right)}^{2}{+\left(y-{y}_{i}\right)}^{2}}{l}}}{e}^{-\frac{\left|t-{t}_{i}\right|}{T}}\times \frac{1}{2\pi {l}^{2}{\alpha }_{i}},$$
(5)

where ω denotes the earthquake probability of the background event, l denotes a spatial smoothing parameter, and T indicates the temporal smoothing parameter. \({{t}}_{i}\) represents the occurrence time of an earthquake in the catalog. The scaling parameter αi is defined as

$${\alpha }_{i}=2T\,-T\left({e}^{-\frac{{t}_{s}-{t}_{i}}{T}}-{e}^{-\frac{{t}_{e}-{t}_{i}}{T}}\right),$$
(6)

where ts and te are the starting and ending times of the input catalog. The procedure was followed for estimating the stacked density rate (μ0stack) using three different declustering algorithms26. The same parameter settings for the declustering algorithms were maintained, but the smoothing parameters for the density rate (Eq. 1) were modified from T = 15 days and l = 30 km to T = 5 days and l = 3 km, in consideration of the different magnitude cutoffs. The chosen cutoff magnitude was 3.0 for all of Taiwan26, but here M2.0 is used to obtain a more complete swarm catalog in eastern Taiwan.

To identify density rate anomalies (δμ0), the local rate change of μ0stack in each swarm was estimated as δ(t) = {(μ0stack(t) - μ0average(t))/μ0average(t)}x100, where μ0average(t) is the averaged μ0(x,y,t) within a 3 km radius of each event, with the average μ0average being computed over a two-year window centered on time t (Fig. S26a). As shown by Fig. S26b, the resulting number of clusters is found to decrease smoothly with increasing threshold on δ. To discriminate between swarm-like and aftershock-like clusters, the latter type is expected to have greater magnitudes. Thus, in Fig. S26c, the number of clusters with a maximum magnitude greater than 6 is plotted against δ threshold. The number of M\(\ge \,\)6 clusters decreases from 13 to 0 when δ changes from −20 to 15, while the corresponding number of total clusters decreases from 140 to 27. To retain more swarm-like clusters while excluding all the aftershock-like clusters, the optimal δ was chosen as 15 in this study.

GNSS data processing and analysis procedures

The Taiwan Continuous GNSS Array is operated by the Institute of Earth Sciences, Academia Sinica (IESAS), the Central Weather Administration (CWA), the Geological Survey and Mining Management Agency (GSMMA), and the Ministry of the Interior (MOI). GNSS position time series for stations across Taiwan are available for download from the Taiwan Geodetic Model (TGM) website (https://tgm.earth.sinica.edu.tw/TseriesList). GNSS data are processed using GipsyX/RTGx software79, incorporating final orbit and clock parameters from Caltech Jet Propulsion Laboratory (JPL) for precise satellite positioning. To mitigate atmospheric errors, we apply an ionosphere-free linear combination technique80, which integrates multiple frequency observations to reduce ionospheric effects. Tropospheric delays are corrected using the Vienna Mapping Function81. Ocean tide loading effects are removed using the FES2004 model82, which accounts for deformations caused by Earth-ocean gravitational interactions. The daily coordinate time series are processed in the International Terrestrial Reference Frame 2014 (ITRF14) and then transformed into a local NEU (north, east, up) coordinate system.

To analyze these GNSS time series, we first apply least-squares regression to model and remove long-term linear trends, annual and semi-annual seasonal signals, instrumental offsets, and coseismic displacements. For earthquakes showing clear co-seismic offsets, we further correct for postseismic deformation by fitting an exponential decay function of the form:

$$\Delta \left(t\right)=A{e}^{-t/{{{\rm{\tau }}}}},$$
(7)

where \(\Delta\)(t) presents the time-dependent postseismic displacement, A is the initial postseismic amplitude, t is time since the mainshock, and τ is the characteristic decay timescale. Only magnitude greater than 6.0 events in this study area (listed in Tables S1 and S5) are assumed to generate postseismic deformation considered in this correction. For smaller events, we evaluate the significance of potential postseismic effects by comparing the root-mean-square (RMS) misfits between models with and without exponential decay term. If the difference is less than 10% of the mean observational uncertainty, we consider the postseismic effect negligible and did not apply postseismic correction.

The modeling is guided by visual inspection to ensure that the fitting exponential decay captures the observed relaxation at each station. The estimated postseismic decay constants (τ) and their uncertainties are summarized in Table S5. Residual time series are computed by subtracting the full regression model (including postseismic terms) from the raw observations. The original and corrected GNSS time series are shown in Fig. S14 and Fig. 5, respectively.

Fault models for static stress computation

To better understand whether the sequential seismic and aseismic slip episodes can also be explained by static stress triggering, a series of computations of Coulomb stress change was conducted. The source model and receiver fault assumptions are listed in Table S4. The apparent 2021 slow slip episodes comprised two segments: one illuminated by the shallow swarm activity (5–15 km) and the other by the deeper RESs (15–25 km). The fault geometry along the northern CRF was approximated by the averaged strike, dip, and rake from the M5+ events, while the fault length and width were approximated by the spatial distribution of both the swarm and RES activity. Similarly, the aftershock distribution and published source model were adopted for parameterizing the three mainshocks in 2022. The fault areas of the M6.1 June 20, 2022, M6.7 March 22, 2022, and M7.0 September 18, 2022 events are represented by the spatial distribution of the aftershocks that occurred in the month following each mainshock, while their fault orientations were derived from the focal mechanisms of the mainshocks.