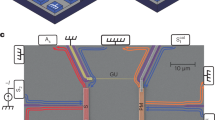
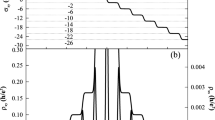
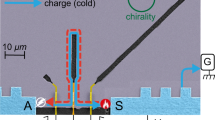
Abstract
Considering a range of candidate quantum phases of matter, half-integer thermal conductance is believed to be an unambiguous evidence of non-Abelian states. It has been long known that such half-integer values arise due to the presence of Majorana edge modes, representing a significant step towards topological quantum computing. Here, we challenge this prevailing notion by presenting a comprehensive theoretical and experimental study where half-integer two-terminal thermal conductance plateau is realized employing integer quantum Hall states. Our proposed setup features a confined geometry of bilayer graphene, interfacing distinct particle and hole-like integer quantum Hall edges. Each segment of the device exhibits full charge and thermal equilibration. Our approach is amenable to generalization to other quantum Hall platforms, and may give rise to other values of fractional quantized transport. Our study demonstrates that the observation of robust non-integer values of thermal conductance can arise as a manifestation of mundane equilibration dynamics as opposed to underlying non-trivial topology.
Similar content being viewed by others
Data availability
Source data are provided with this paper. All other data that support the findings of this study are available from the corresponding authors upon request.
References
Kane, C. L. & Fisher, M. P. Thermal transport in a Luttinger liquid. Phys. Rev. Lett. 76, 3192–3195 (1996).
Kane, C. L. & Fisher, M. P. A. Quantized thermal transport in the fractional quantum hall effect. Phys. Rev. B Condens. Matter 55, 15832–15837 (1997).
Greiner, A., Reggiani, L., Kuhn, T. & Varani, L. Thermal conductivity and Lorenz number for one-dimensional ballistic transport. Phys. Rev. Lett. 78, 1114–1117 (1997).
Jezouin, S. et al. Quantum limit of heat flow across a single electronic channel. Science 342, 601–604 (2013).
Banerjee, M. et al. Observed quantization of anyonic heat flow. Nature 545, 75–79 (2017).
Srivastav, S. K. et al. Universal quantized thermal conductance in graphene. Sci. Adv. 5, eaaw5798 (2019).
Srivastav, S. K. et al. Vanishing thermal equilibration for hole-conjugate fractional quantum hall states in graphene. Phys. Rev. Lett. 126, 216803 (2021).
Srivastav, S. K. et al. Determination of topological edge quantum numbers of fractional quantum hall phases by thermal conductance measurements. Nat. Commun. 13, 5185 (2022).
Ma, K. K. W., Peterson, M. R., Scarola, V. W. & Yang, K. Fractional quantum hall effect at the filling factor ν = 5/2. In Encyclopedia of Condensed Matter Physics, 324–365 (Elsevier, 2024).
Matsuda, Y., Shibauchi, T. & Kee, H.-Y. Kitaev quantum spin liquids. Rev. Mod. Phys. 97, 045003 (2025).
Moore, G. & Read, N. Nonabelions in the fractional quantum hall effect. Nucl. Phys. B 360, 362 – 396 (1991).
Banerjee, M. et al. Observation of half-integer thermal Hall conductance. Nature 559, 205–210 (2018).
Paul, A. K., Tiwari, P., Melcer, R., Umansky, V. & Heiblum, M. Topological thermal hall conductance of even-denominator fractional states. Phys. Rev. Lett. 133, 076601 (2024).
Abanin, D. A. & Levitov, L. S. Quantized transport in graphene p-n junctions in a magnetic field. Science 317, 641–643 (2007).
Williams, J. R., Dicarlo, L. & Marcus, C. M. Quantum Hall effect in a gate-controlled p-n junction of graphene. Science 317, 638–641 (2007).
Özyilmaz, B. et al. Electronic transport and quantum Hall effect in bipolar graphene p-n-p junctions. Phys. Rev. Lett. 99, 166804 (2007).
Zimmermann, K. et al. Tunable transmission of quantum hall edge channels with full degeneracy lifting in split-gated graphene devices. Nat. Commun. 8, 14983 (2017).
Pandey, P. et al. Half-quantized hall plateaus in the confined geometry of graphene. arXiv:2410.03896 (2024).
Ji, W. & Wen, X.-G. \(\frac{1}{2}({e}^{2}/h)\) conductance plateau without 1d chiral majorana fermions. Phys. Rev. Lett. 120, 107002 (2018).
Kayyalha, M. et al. Absence of evidence for chiral majorana modes in quantum anomalous Hall-superconductor devices. Science 367, 64–67 (2020).
Uday, A., Lippertz, G., Bhujel, B., Taskin, A. A. & Ando, Y. Non-Majorana origin of the half-integer conductance quantization elucidated by multiterminal superconductor–quantum anomalous hall insulator heterostructure. Phys. Rev. B 111, 035440 (2025).
Nakamura, J., Liang, S., Gardner, G. C. & Manfra, M. J. Half-integer conductance plateau at the ν = 2/3 fractional quantum hall state in a quantum point contact. Phys. Rev. Lett. 130, 076205 (2023).
Fauzi, M. H., Nakagawara, K., Hashimoto, K., Shibata, N. & Hirayama, Y. Synthesizing 2h/e2 resistance plateau at the first Landau level confined in a quantum point contact. Commun. Phys. 6, (2023).
McCann, E. & Fal’ko, V. I. Landau-level degeneracy and quantum hall effect in a graphite bilayer. Phys. Rev. Lett. 96, 086805 (2006).
McCann, E. & Koshino, M. The electronic properties of bilayer graphene. Rep. Prog. Phys. 76, 056503 (2013).
Maher, P. et al. Bilayer graphene. tunable fractional quantum hall phases in bilayer graphene. Science 345, 61–64 (2014).
Li, J., Tupikov, Y., Watanabe, K., Taniguchi, T. & Zhu, J. Effective Landau level diagram of bilayer graphene. Phys. Rev. Lett. 120, 047701 (2018).
Kumar, R. et al. Absence of heat flow in ν = 0 quantum Hall ferromagnet in bilayer graphene. Nat. Phys. 20, 1941–1947 (2024).
Matsuo, S. et al. Edge mixing dynamics in graphene p-n junctions in the quantum hall regime. Nat. Commun. 6, 8066 (2015).
Paul, A. K. et al. Interplay of filling fraction and coherence in symmetry broken graphene p-n junction. Commun. Phys. 3 (2020).
Maher, P. et al. Evidence for a spin phase transition at charge neutrality in bilayer graphene. Nat. Phys. 9, 154–158 (2013).
Wei, D. S. et al. Mach-Zehnder interferometry using spin- and valley-polarized quantum hall edge states in graphene. Sci. Adv. 3, e1700600 (2017).
Jo, M. et al. Quantum Hall valley splitters and a tunable Mach-Zehnder interferometer in graphene. Phys. Rev. Lett. 126, 146803 (2021).
Manna, S., Das, A., Goldstein, M. & Gefen, Y. Full classification of transport on an equilibrated 5/2 edge via shot noise. Phys. Rev. Lett. 132, 136502 (2024).
Manna, S., Das, A., Gefen, Y. & Goldstein, M. Shot noise as a diagnostic in the ν = 2/3 fractional quantum hall edge zoo. Low. Temp. Phys. 50, 1113–1122 (2024).
Manna, S., Das, A., Gefen, Y. & Goldstein, M. Multiple mechanisms for emerging conductance plateaus in fractional quantum hall states. Phys. Rev. Lett. 134, 256503 (2025).
Manna, S. & Das, A. Experimentally motivated order of length scales affect shot noise. Phys. Rev. B 112, 195128 (2025).
Amet, F., Williams, J. R., Watanabe, K., Taniguchi, T. & Goldhaber-Gordon, D. Selective equilibration of spin-polarized quantum hall edge states in graphene. Phys. Rev. Lett. 112, 196601 (2014).
Long, W., Sun, Q. -f & Wang, J. Disorder-induced enhancement of transport through graphene p-n junctions. Phys. Rev. Lett. 101, 166806 (2008).
Li, J. & Shen, S.-Q. Disorder effects in the quantum Hall effect of graphene p − n junctions. Phys. Rev. B 78, 205308 (2008).
Berg, E., Oreg, Y., Kim, E.-A. & von Oppen, F. Fractional charges on an integer quantum hall edge. Phys. Rev. Lett. 102, 236402 (2009).
Bid, A. et al. Observation of neutral modes in the fractional quantum hall regime. Nature 466, 585–590 (2010).
Kumar, R. et al. Observation of ballistic upstream modes at fractional quantum hall edges of graphene. Nat. Commun. 13, https://www.nature.com/articles/s41467-021-27805-4 (2022).
Kumar, R. et al. Electrical noise spectroscopy of magnons in a quantum hall ferromagnet. Nat. Commun. 15, https://www.nature.com/articles/s41467-024-49446-z (2024).
Wang, J., Meir, Y. & Gefen, Y. Edge reconstruction in the ν=2/3 fractional quantum hall state. Phys. Rev. Lett. 111, 246803 (2013).
Moore, J. E. & Haldane, F. D. M. Edge excitations of the ν= spin-singlet quantum hall state. Phys. Rev. B 55, 7818–7823 (1997).
Zhang, G., Gornyi, I. & Gefen, Y. Landscapes of an out-of-equilibrium anyonic sea. Phys. Rev. Lett. 134, 096303 (2025).
Zhang, G. et al. Measuring statistics-induced entanglement entropy with a hong–ou–mandel interferometer. Nat. Commun. 15, 3428 (2024).
Bartolomei, H. et al. Fractional statistics in anyon collisions. Science 368, 173–177 (2020).
Han, C., Park, J., Gefen, Y. & Sim, H.-S. Topological vacuum bubbles by anyon braiding. Nat. Commun. 7, 11131 (2016).
Rosenow, B., Levkivskyi, I. P. & Halperin, B. I. Current correlations from a mesoscopic anyon collider. Phys. Rev. Lett. 116, 156802 (2016).
Głodzik, S. & Sedlmayr, N. Quantized thermal Hall conductance and the topological phase diagram of a superconducting bismuth bilayer. Phys. Rev. B 108, 184502 (2023).
Karmakar, S., Ratnakar, A. & Das, S. Elevated Hall responses as indicators of edge reconstruction. arXiv preprint arXiv: 2505.08746 https://arxiv.org/abs/2505.08746 (2025).
Pizzocchero, F. et al. The hot pick-up technique for batch assembly of van der Waals heterostructures. Nat. Commun. 7,https://doi.org/10.1038/ncomms11894 (2016).
Acknowledgements
The authors thank Prof. Moty Heiblum for critical comments on the manuscript. U.R. and S.M. thank Arup Kumar Paul for useful discussions. We thank the International Centre for Theoretical Sciences (ICTS) for participating in the program - Condensed Matter meets Quantum Information (code: ICTS/COMQUI2023/9), where the collaboration was initiated. S.M. was supported by the Weizmann Institute of Science, Israel Deans fellowship through Feinberg Graduate School and the senior postdoctoral fellowship. Y.G. was supported by the InfoSys Chair, IISc, Bangalore. S.M. and Y. G. were also supported by the Minerva Foundation and grant no 2022391 from the United States–Israel Binational Science Foundation (BSF), Jerusalem, Israel. Ankur Das was supported by IISER, Tirupati Startup grant and ANRF/ECRG/2024/001172/PMS. M.G. has been supported by the Israel Science Foundation (ISF) and the Directorate for Defense Research and Development (DDR&D) through Grant No. 3427/21, the ISF Grant No. 1113/23, and the US-Israel Binational Science Foundation (BSF) through Grant No. 2020072. A.D. thanks the Department of Science and Technology (DST) and Science and Engineering Research Board (SERB), India, for financial support (SP/SERB-22-0387), (DST/NM/TUE/QM-5/2019), and also acknowledges funding through the Intensification of Research in High Priority Areas programme of the Science and Engineering Research Board (Grant No. IPA/2020/000034). A.D. also thanks CEFIPRA project SP/IFCP-22-0005. Growing the hBN crystals received support from the Japan Society for the Promotion of Science (KAKENHI grant nos. 19H05790, 20H00354 and 21H05233) to K.W. and T.T. The authors gratefully acknowledge the use of Blender (https://www.blender.org/) and Inkscape (https://inkscape.org/)—both free and open- source software—for the creation and refinement of figures presented in this work.
Author information
Authors and Affiliations
Contributions
K.W. and T.T. synthesized the hBN crystals. U.R. contributed to device fabrication, measurement, data acquisition, and analysis. S.C. contributed to the measurement. S.M., Ankur D., M.G., and Y.G. contributed to the development of theory, analysis and data interpretation. A.D. contributed in designing the experiment, data interpretation, and analysis. All the authors contributed to writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Roy, U., Manna, S., Chakraborty, S. et al. Half-integer thermal conductance in integer quantum Hall states. Nat Commun (2026). https://doi.org/10.1038/s41467-026-69659-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-026-69659-8