Predominance of non-adiabatic effects in zero-point renormalization of the electronic band gap

Abstract

Electronic and optical properties of materials are affected by atomic motion through the electron–phonon interaction: not only band gaps change with temperature, but even at absolute zero temperature, zero-point motion causes band-gap renormalization. We present a large-scale first-principles evaluation of the zero-point renormalization of band edges beyond the adiabatic approximation. For materials with light elements, the band gap renormalization is often larger than 0.3 eV, and up to 0.7 eV. This effect cannot be ignored if accurate band gaps are sought. For infrared-active materials, global agreement with available experimental data is obtained only when non-adiabatic effects are taken into account. They even dominate zero-point renormalization for many materials, as shown by a generalized Fröhlich model that includes multiple phonon branches, anisotropic and degenerate electronic extrema, whose range of validity is established by comparison with first-principles results.

Introduction

The electronic band gap is arguably the most important characteristic of semiconductors and insulators. It determines optical and luminescent thresholds, but is also a prerequisite for characterizing band offsets at interfaces and deep electronic levels created by defects¹. However, accurate band gap computation is a challenging task. Indeed, the vast majority of first-principles calculations relies on Kohn–Sham Density-Functional Theory (KS-DFT), valid for ground state properties², that delivers a theoretically unjustified value of the band gap in the standard approach, even with exact KS potential^3,4,5.

The breakthrough came from many-body perturbation theory, with the so-called GW approximation, first non-self-consistent (G₀W₀) by Hybertsen and Louie in 1986⁶, then twenty years later self-consistent (GW)⁷ and further improved by accurate vertex corrections from electron-hole excitations (GWeh)⁸. The latter methodology, at the forefront for band-gap computations, delivers a 2–10% accuracy, usually overestimating the experimental band gap. GWeh calculations are computationally very demanding, typically about two orders of magnitude more than G₀W₀, itself two orders of magnitude more time-consuming than KS-DFT calculations, roughly speaking.

Despite being state-of-the-art, such studies ignored completely the electron–phonon interaction. The electron–phonon interaction drives most of the temperature dependence of the electronic structure of semiconductors and insulators, but also yields a zero-point motion gap modification at T = 0 K, often termed zero-point renormalization of the gap (ZPR_g) for historical reasons.

The ZPR_g had been examined 40 years ago, by Allen, Heine and Cardona (AHC)^9,10 who clarified the early theories by Fan¹¹ and Antoncik¹². Their approach is, like the GW approximation, rooted in many-body perturbation theory, where, at the lowest order, two diagrams contribute, see Fig. 1, the so-called “Fan” diagram, with two 1st-order electron–phonon vertices and the “Debye–Waller” diagram, with one 2nd-order electron–phonon vertex. In the context of semi-empirical calculations, the AHC method was applied to Si and Ge, introducing the adiabatic approximation, in which the phonon frequencies are neglected with respect to electronic eigenenergy differences and replaced by a small but non-vanishing imaginary broadening¹⁰. It was later extended without caution to GaAs and a few other III–V semiconductors^13,14.

Fig. 1: Lowest-order diagrams for the contribution of the electron–phonon interaction to the zero-point renormalization of the gap ZPR_g.

a Fan diagram, with two first-order screened electron–phonon vertices; b Debye-Waller diagram, with one second-order screened electron–phonon interaction vertex.

In this work, we present first-principles AHC ZPR_g calculations beyond the adiabatic approximation, for 30 materials. Comparing with experimental band gaps, we show that adding ZPR_g improves the GWeh first-principles band gap, and moreover, that the ZPR_g has the same order of magnitude as the G₀W₀ to GWeh correction for half of the materials (typically materials with light atoms, e.g., O, N ...) on which GWeh has been tested. Hence, the GWeh level of sophistication misses its target for many materials with light atoms, if the ZPR_g is not taken into account. By including it, the theoretical agreement with direct measurements of experimental ZPR_g is improved. This also demonstrates the crucial importance of phonon dynamics to reach this level of accuracy.

Indeed, first-principles calculations of the ZPR_g using the AHC theory are very challenging, and only started one decade ago, on a case-by-case basis^{15,16,17,18,19,20,21,22,23,24,25} (see the Supplementary Note 3), usually relying on the adiabatic approximation, and without comparison with experimental data. An approach to the ZPR_g, alternative to the AHC one, relies on computations of the band gap at fixed, distorted geometries, for large supercells^{18,26,27,28,29,30,31,32,33} (see and the Supplementary Note 3). As the adiabatic approximation is inherent in this approach, we denote it as ASC, for “adiabatic supercell”. A recent publication by Karsai, Engel, Kresse and Flage-Larsen³⁴, hereafter referred to as KEKF, presents ASC ZPR_g based on DFT values, as well as based on G₀W₀ values for 18 semiconductors, with experimental comparison for 9 of them. Both AHC and ASC methodologies have been recently reviewed³⁵.

Although the adiabatic approximation had already been criticized by Poncé et al. in 2015²⁴ (Supplementary Note 5) as causing an unphysical divergence of the adiabatic AHC expression for infrared-active materials with vanishing imaginary broadening, thus invalidating all adiabatic AHC calculations except for non-infrared-active materials, the full consequences of the adiabatic approximation have not yet been recognized for ASC. We will show that the non-adiabatic AHC approach outperforms the ASC approach, so that the predictions arising from the mechanism by which the ASC approach bypasses the adiabatic AHC divergence problem for infrared-active materials are questionable. This is made clear by a generalized Fröhlich model with a few physical parameters, that can be determined either from first principles or from experimental data.

Although the full electronic and phonon band structures do not enter in this model, and the Debye-Waller diagram is ignored, for many materials it accounts for more than half the ZPR_g of the full first-principles non-adiabatic AHC ZPR_g. As this model depends crucially on non-adiabatic effects, it demonstrates the failure of the adiabatic hypothesis, be it for the AHC or the ASC approach.

By the same token, we also show the domain of validity and accuracy of model Fröhlich large-polaron calculations based on the continuum hypothesis, that have been the subject of decades of research^{36,37,38,39,40,41,42}. Such model Fröhlich Hamiltonian captures well the ZPR for about half of the materials in our list, characterized by their strong infrared activity, while it becomes less and less adequate for decreasing ionicity. In the present context, the Fröhlich large-polaron model provides an intuitive picture of the physics of the ZPR_g.

Results

Zero-point renormalization: experiment vs. first principles

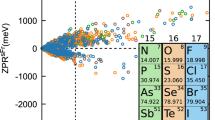
Figure 2 compares first-principles ZPR_g with experimental values. As described in the “Methods” section, and in Supplementary Note 2, the correction due to zero-point motion effect on the lattice parameter, ZPR${}_{{\rm{g}}}^{{\rm{lat}}}$, has been added to fixed volume results from both non-adiabatic AHC (present calculations) and ASC methodologies³⁴. While for a few materials experimental ZPR_g values are well established, within 5-10%, globally, experimental uncertainty is larger, and can hardly be claimed to be better than 25% for the majority of materials, see Supplementary Note 1. This will be our tolerance.

Fig. 2: Absolute values of first-principles band gap renormalization ZPR_g compared with experimental ones.

Blue full circles: present calculations, using non-adiabatic AHC, based on KS-DFT ingredients; red empty triangles: adiabatic supercell KS-DFT results ³⁴. Dashed lines: limits at which the smallest of both ZPR is 25% smaller than the largest one (note that the scales are logarithmic). For consistency, the computed lattice ZPR${}_{{\rm{g}}}^{{\rm{lat}}}$ were added to both ASC and AHC. The majority of non-adiabatic AHC-based results fall within the 25% limits, while this is not the case for ASC-based ones. See numerical values in Supplementary Table II.

Let us focus first on the ASC-based results. For the 16 materials present in both KEKF and the experimental set described in the Supplementary Table I, the ASC vs. experimental discrepancy is more than 25% for more than half of the materials (KEKF KS-DFT ASC calculations are based on GGA-PBE, except for Si, Ge, GaAs, and CdSe, where the PBE0 hybrid functional has been used, thus the better score of Ge and GaAs for ASC calculations than for AHC calculations might be partly explained by this different KS-DFT functional). There is a global trend to underestimation by ASC, although CdTe is overestimated.

By contrast, the non-adiabatic AHC ZPR_g (blue full circles) and experimental ZPR_g agree with each other within 25% for 16 out of the 18 materials. The outliers are CdTe with a 43% overestimation by AHC, and GaP with a 33% underestimation. For none of these the discrepancy is a factor of two or larger. On the contrary, in the ASC approach, several materials show underestimation of the ZPR_g by more than a factor of 2. The materials showing such large underestimation (CdS, ZnO, SiC) are all quite ionic, while more covalent materials (C, Si, Ge, AlSb, AlAs) are better described.

Therefore, Fig. 2 clearly shows that the non-adiabatic AHC approach performs significantly better than the ASC approach. AHC ZPR_g and ASC ZPR_g also differ by more than a factor of two for TiO₂ and MgO (see Supplementary Note 3), although no experimental ZPR_g is available for these materials to our knowledge.

We now examine band gaps. Figure 3 presents the ratio between first-principles band gaps and corresponding experimental values, for 12 materials. The best first-principles values at fixed equilibrium atomic position, from GWeh⁸, are represented, as well as their non-adiabatic AHC ZPR corrected values.

Fig. 3: Ratio between first-principles band gaps and experimental ones⁶⁴.

First-principles results without electron–phonon interaction⁸ are based on G₀W₀ (diamonds) or on GWeh (squares). Blue full circles are the GWeh results to which AHC ZPR_g and lattice ZPR${}_{{\rm{g}}}^{{\rm{lat}}}$ have been added, while empty red circles are the GWeh results to which only AHC ZPR_g was added. GWeh usually overshoots, while adding the electron–phonon interaction gives better global agreement. See numerical values in Supplementary Table III.

For GWeh without ZPR_g, a 4% agreement is obtained only for two materials (CdS and GaN). There is indeed a clear, albeit small, tendency of GWeh to overestimate the band gap value, except for the 3 materials containing shallow core d-electrons (ZnO, ZnS, and CdS) that are underestimated. By contrast, if the non-adiabatic AHC ZPR_g is added to the GWeh data (blue dots), a 4% agreement is obtained for 9 out of the 12 materials (8 if ZPR${}_{{\rm{g}}}^{{\rm{lat}}}$ is not included).

For ZnO and ZnS, with a final 10–12% underestimation, and CdS with a 5% underestimation, we question the GWeh ability to produce accurate fixed-geometry band gaps at the level obtained for the other materials, due to the presence of rather localized 3d electrons in Zn and 4d electrons in CdS.

As a final lesson from Fig. 3, we note that for 4 out of the 12 materials (SiC, AlP, C, and BN), the ZPR_g is similar in size to the G₀W₀ to GWeh correction, and it is a significant fraction of it also for Si, GaN and MgO. As mentioned earlier, GWeh calculations are much more time-consuming than G₀W₀ calculations, possibly even more time-consuming than ZPR calculations (although we have not attempted to make a fair comparison). Thus, for materials containing light elements, first row and likely second row (e.g., AlP) in the periodic table, GWeh calculations miss their target if not accompanied by ZPR_g calculations. Variance and accuracy of G₀W₀ calculations is discussed in the litterature⁴³.

Supplementary Table V gathers our full set of ZPR results, beyond those present in the ASC or experimental sets. It also includes 10 oxides, while the experimental set only includes three materials containing oxygen (ZnO, MgO, and SrTiO₃), and there are none in KEKF ASC set. The ZPR_g of the band gap for materials containing light elements (O or lighter) is between −157 meV (ZnO) and −699 meV (BeO), while, relatively to the experimental band gap, it ranges from −4.6% (ZnO) to −10.8% (TiO₂). This can hardly be ignored in accurate calculations of the gap.

Generalized Fröhlich model

We now come back to the physics from which the ZPR_g originates, and explain our earlier observation that the ASC describes reasonably well the more covalent materials, but can fail badly for ionic materials. We argue that, for many polar materials, the ZPR_g is dominated by the diverging electron–phonon interaction between zone-center LO phonons and electrons close to the band edges, and the slow (non-adiabatic) response of the latter: the effects due to comparatively fast phonons are crucial. This was already the message from Fröhlich³⁶ and Feynman³⁷, decades ago, initiating large-polaron studies. However, large-scale assessment of the adequacy of Fröhlich model for real materials is lacking. Indeed, the available flavors of Fröhlich model, based on continuum (macroscopic) electrostatic interactions, do not cover altogether degenerate and anisotropic electronic band extrema or are restricted to only one phonon branch, unlike most real materials^44,45,46,47.

In this respect, we introduce now a generalized Fröhlich model, gFr, whose form is deduced from first-principles equations in the long-wavelength limit (continuum approximation), see Supplementary Note 5. Such model covers all situations and still uses as input only long-wavelength parameters, that can be determined either from first principles (Supplementary Note 6) or from experiment (Supplementary Note 7). We then find the corresponding ZPR_g from perturbation theory at the lowest order, evaluate it for our set of materials, and compares its results to the ZPR_g obtained from full first-principles computations. The corresponding Hamiltonian writes (see Supplementary Note 5 for detailed explanations):

$${\hat{H}}^{{\rm{gFr}}}={\hat{H}}_{{\rm{el}}}^{{\rm{gFr}}}+{\hat{H}}_{{\rm{ph}}}^{{\rm{gFr}}}+{\hat{H}}_{{\rm{EPI}}}^{{\rm{gFr}}},$$

(1)

with (i) an electronic part

$${\hat{H}}_{{\rm{el}}}^{{\rm{gFr}}}= \mathop {\sum}\limits_{{\bf{k}}n}\frac{{k}^{2}}{2{m}_{n}^{* }(\hat{{\bf{k}}})}{\hat{c}}_{{\bf{k}}n}^{+}{\hat{c}}_{{\bf{k}}n},$$

(2)

that includes direction-dependent effective masses ${m}_{n}^{* }(\hat{{\bf{k}}})$, governed by so-called Luttinger parameters in case of degeneracy, electronic creation and annihilation operators, ${\hat{c}}_{{\bf{k}}n}^{+}$ and ${\hat{c}}_{{\bf{k}}n}$, with k the electron wavevector and n the band index, (ii) the multi-branch phonon part,

$${\hat{H}}_{{\rm{ph}}}^{{\rm{gFr}}}= \mathop {\sum}\limits_{{\bf{q}}j}{\omega }_{j0}(\hat{{\bf{q}}}){\hat{a}}_{{\bf{q}}j}^{+}{\hat{a}}_{{\bf{q}}j},$$

(3)

with direction-dependent phonon frequencies ${\omega }_{j0}(\hat{{\bf{q}}})$, phonon creation and annihilation operators, ${\hat{a}}_{{\bf{q}}j}^{+}$ and ${\hat{a}}_{{\bf{q}}j}$, with q the phonon wavevector and j the branch index, and finally (iii) the electron–phonon interaction part

$${\hat{H}}_{{\rm{EPI}}}^{{\rm{gFr}}}= \mathop {\sum}\limits_{{\bf{q}}j,{\bf{k}}n^{\prime} n}{g}^{{\rm{gFr}}}({\bf{q}}j,{\bf{k}}n^{\prime} n){\hat{c}}_{{\bf{k}}+{\bf{q}}n^{\prime} }^{+}{\hat{c}}_{{\bf{k}}n}({\hat{a}}_{{\bf{q}}j}+{\hat{a}}_{-{\bf{q}}j}^{+}).$$

(4)

The k and q sums run over the Brillouin zone. The sum over n and $n^{\prime}$ runs only over the bands that connect to the degenerate extremum, renumbered from 1 to n_deg. The generalized Fröhlich electron–phonon interaction^48,49 is

$$\begin{array}{ll}{g}^{{\rm{gFr}}}({\bf{q}}j,{\bf{k}}n^{\prime} n)=\displaystyle\frac{i}{q}\,\frac{4\pi }{{\Omega }_{0}}\left(\right.\frac{1}{2{\omega }_{j0}(\hat{{\bf{q}}}){V}_{{\rm{BvK}}}}{\left)\right.}^{1/2}\frac{\hat{{\bf{q}}}.{{\bf{p}}}_{j}(\hat{{\bf{q}}})}{{\epsilon }^{\infty }(\hat{{\bf{q}}})}\\ \times \, \mathop {\sum}\limits_{m}{s}_{n^{\prime} m}(\hat{{\bf{k}}}^{\prime} ){({s}_{nm}(\hat{{\bf{k}}}))}^{* }.\end{array}$$

(5)

This expression depends on the directions $\hat{{\bf{k}}}$, $\hat{{\bf{q}}}$, and $\hat{{\bf{k}}}^{\prime}$ (${\bf{k}}^{\prime} ={\bf{k}}+{\bf{q}}$), but not explicitly on their norm (hence only long-wavelength parameters are used), except for the $\frac{1}{q}$ factor. The electron–phonon part also depends only on few quantities: the Born effective charges (entering the mode-polarity vectors p_j), the macroscopic dielectric tensor ϵ^∞, and the phonon frequencies ω_j0, the primitive cell volume Ω₀, the Born-von Karman normalization volume V_BvK corresponding to the k and q samplings. The s tensors are symmetry-dependent unitary matrices, similar to spherical harmonics. Equations (1)–(5) define our generalized Fröhlich Hamiltonian. Although we will focus on its T = 0 properties within perturbation theory, such Hamiltonian could be studied for many different purposes (non-zero T, mobility, optical responses ...), like the original Fröhlich model, for representative materials using first-principles or experimental parameters.

The conduction band ZPR${}_{{\rm{c}}}^{{\rm{gFr}}}$ can be obtained with a perturbation treatment (Supplementary Note 5), giving

$$\begin{array}{lll}{{\rm{ZPR}}}_{{\rm{c}}}^{{\rm{gFr}}}\,=\,-\displaystyle \mathop {\sum}\limits_{jn}\frac{1}{\sqrt{2}{\Omega }_{0}{n}_{{\rm{deg}}}}{\int}_{4\pi }d\hat{{\bf{q}}}\left(\right.{m}_{n}^{* }(\hat{{\bf{q}}}){\left)\right.}^{1/2}\\ \,\times \,\left(\right.{\omega }_{j0}(\hat{{\bf{q}}}){\left)\right.}^{-3/2}\displaystyle\left(\frac{\hat{{\bf{q}}}.{{\bf{p}}}_{j}(\hat{{\bf{q}}})}{{\epsilon }^{\infty }(\hat{{\bf{q}}})}\right)^{2}.\end{array}$$

(6)

A similar expression exists for the valence band ZPR${}_{{\rm{v}}}^{{\rm{gFr}}}$. The few material parameters needed in Eq. (6) can be obtained from experimental measurements, but are most easily computed from first principles, using density-functional perturbation theory with calculations only at q = Γ (e.g., no phonon band structure calculation). Eq. (6) can be evaluated for all band extrema in our set of materials, irrespective of whether the extrema are located at Γ or other points in the Brillouin Zone (e.g., X for the valence band of many oxides, with anisotropic effective mass), whether they are degenerate (e.g., the three-fold degeneracy of the top of the valence band of many III–V or II–VI compounds), and irrespective of the number of phonon branches (e.g., 3 different LO frequencies for TiO₂, moreover varying with the direction along which q → 0).

Figure 4 compares the band gap ZPR from the first-principles non-adiabatic AHC methodology and from the generalized Fröhlich model. The 30 materials can be grouped into five sets, based on their ionicity: 11 materials containing oxygen, rather ionic, for which the Born effective charges and the ZPR are quite large, 6 materials containing chalcogenides, also rather ionic, 4 materials containing nitrogen and 5 III-V materials, less ionic, and 4 materials from group-IV elements, non-ionic, except SiC.

Fig. 4: Zero-point renormalization of the band gap: comparison between first-principles AHC values and generalized Fröhlich model.

See Eq. (6). Data for 27 materials are represented. Non-ionic group IV materials are omitted. The markers identify materials of similar ionicity: oxides (purple circles), other II–VI materials containing S, Se, or Te (yellow squares), nitrides (green diamonds), other III-V materials, containing P, As, or Sb (dark blue triangles), and group IV material SiC (light blue hexagon). Dashed lines: limits at which the smallest of both ZPR is 25% smaller than the largest one. Dotted lines: limits at which the Fröhlich model ZPR misses, respectively, 50% and 67% of the AHC values (note that the scales are logarithmic). See numerical values in Supplementary Table V.

For oxygen-based materials, the ZPR ranges from 150 meV to 700 meV, and the gFr model captures this very well, with less than 25% error, with only one exception, BeO. The chalcogenide materials are also reasonably well described by the gFr model, capturing at least two-third of the ZPR. Globally their ZPR is smaller (note the logarithmic scale).

For the nitride materials and for SiC, the gFr captures about 50% of the quite large ZPR (between 176 meV and 406 meV). The adequacy of the gFr model decreases still with the III–V materials and the three non-ionic IV materials. In the latter case, the vanishing Born effective charges result in a null ZPR within the gFr model (these three materials are omitted from Fig. 4).

For the oxides and chalcogenides, the ZPR is thus dominated by the zone-center parameters (including the phonon frequencies), and the physics corresponds to the one of the large-polaron picture³⁷, namely, the slow electron motion is correlated to a phonon cloud that dynamically adjusts to it. This physics is completely absent from the ASC approach. Even for nitrides, the gFr describes a significant fraction of the ZPR.

A perfect agreement between the non-adiabatic AHC first-principles ZPR and the generalized Fröhlich model ZPR is not expected. Indeed, differences can arise from different effects: lack of dominance of the Fröhlich electron–phonon interaction in some regions of the Brillouin Zone, departure from parabolicity of the electronic structure (obviously, the electronic structure must be periodic so that the parabolic behavior does not extend to infinity), interband contributions, phonon band dispersion, incomplete cancellation between the Debye–Waller and the acoustic phonon mode contribution.

It is actually surprising to see that for so many materials, the generalized Fröhlich model matches largely the first-principles AHC results. Anyhow, as a conclusion for this section, for a large number of materials, we have validated, a posteriori and from first principles, the relevance of large-polaron research based on Fröhlich model despite the numerous approximations on which it relies.

Discussion

We focus on the mechanism by which the AHC divergence of the ZPR in the adiabatic case for infrared-active materials²⁴ is avoided, either using the ASC methodology or using the non-adiabatic AHC methodology. As Fröhlich and Feynman have cautioned us^36,37, and already mentioned briefly in previous sections, the dynamics of the “slow” electron is crucial in this electron–phonon problem.

In the ASC approach, the bypass of this divergence can be understood as follows, see Fig. 5a. Consider a long-wavelength fluctuation of the atomic positions, frozen in time. At large but finite wavelength, the potential is periodically lowered in some regions of space and increased in some other regions of space, in an oscillatory manner with periodicity ΔL ∝ 1/q, where q is the small wavevector of the fluctuation, see Fig. 5a “LO phonon potential” part. Without such long-wavelength potential, the electron at the minimum of the conduction band has a Bloch type wavefunction, with an envelope phase factor characterized by the wavevector k_c multiplying a lattice-periodic function. Its density is lattice periodic. With such long-wavelength potential, as a function of the amplitude of the atomic displacements, the corresponding electronic eigenenergy changes first quadratically (as the average of the lowering and increase of potential for this Bloch wavefunction forbids a linear behavior except in case of degeneracy), but for larger amplitudes, it behaves linearly, as the electron localizes in the lowered potential region and the minimum of the potential is linear in the amplitude of the atomic displacements. This is referred to as “nonquadratic coupling”³². A wavepacket is formed, by combining Bloch wavefunctions with similar lattice periodic functions but slightly different wavevectors (k_c, k_c + q, k_c − q, etc), coming from a small interval of energy Δϵ⁰ ∝ q² ∝ 1/(ΔL)², see Fig. 5a “Wavefunction” part. This nonquadratic effect is actually illustrated in Fig. 4 of ref. ²³ (see the frozen-phonon eigenvalues), as well as in Fig. 2 of ref. ³².

Fig. 5: Schema of the long-wave phonon-induced potential and corresponding electronic wavefunction.

Real part (oscillating with lattice periodicity) and envelope are represented. a Adiabatic case, b non-adiabatic, time-dependent case. In the non-adiabatic case, the electron does not have the time to adjust to the change of potential, see text.

By contrast, in the time-dependent case, as illustrated in Fig. 5b, the wavepacket will require a characteristic time Δτ, to form or to displace. This will be given by the Heisenberg uncertainty relation, Δϵ⁰Δτ ≳ $\hbar$, hence Δτ ≳ $\hbar$/Δϵ⁰ ∝ ΔL². For long wavelengths, the characteristic time diverges. As soon as Δτ is larger than the phonon characteristic time τ_ph ~ 1/ω_LO, the “slow” electron will lag behind the phonon, and the static or adiabatic picture described above is no longer valid.

In all adiabatic approaches, either AHC or ASC, the electron is always supposed to have the time to adjust to the change of potential, in contradiction with the time-energy uncertainty principle. Furthermore, the adiabatic AHC approach only considers the quadratic region for the above-mentioned dependence of eigenvalues with respect to amplitudes of displacements. This results in a diverging term²⁴. At variance with the AHC case, the ASC approach samples a whole set of amplitudes, including the onset of the asymptotic linear regime, in which case the divergence does not build up. However, this ASC picture does not capture the real physical mechanism that prevents the divergence to occur, the impossibility for the electron to follow the phonon dynamics, that we have highlighted above. By contrast, such physical mechanism is present both in the non-adiabatic AHC approach and in the (generalized) Fröhlich model: the “slow” electron does not follow adiabatically (instantaneously) the atomic motion. The divergence of the adiabatic AHC is indeed avoided in the non-adiabatic picture by taking into account the non-zero phonon frequencies.

Thus, the ASC avoids the adiabatic AHC divergence for the wrong reason, which explains its poor predictive capability for the more ionic materials emphasized by Fig. 2. To be clear, we do not pretend the nonquadratic effects are all absent, but the non-adiabatic effects have precedence, at least for materials with significant infrared activity, and the nonquadratic localization effects will be observed only if the electrons have the time to physically react. The shortcomings of the ASC approach are further developed in the Supplementary Discussion. As a consequence of such understanding, all the results obtained for strongly infrared-active materials using the adiabatic frozen-phonon supercell methodology should be questioned.

For non-infrared-active materials, the physical picture that we have outlined, namely the inability of slow electrons to follow the dynamics of fast phonons, is still present, but does not play such a crucial role: the electron–phonon interaction by itself does not diverge in the long-wavelength limit as compared to the infrared-active electron–phonon interaction, see Eq. (5), only the denominator of the Fan self-energy diverges, which nevertheless results in an integrable ZPR²⁴. In such case, neglecting non-adiabatic effects, as in the ASC approach, is only one among many approximations done to obtain the ZPR.

Beyond the discovery of the predominance of non-adiabatic effects in the zero-point renormalization of the band gap for many materials, in the present large-scale first-principles study of this effect, we have established that electron–phonon interaction diminishes the band gap by 5% to 10% for materials containing light atoms like N or O (up to 0.7 eV for BeO), a decrease that cannot be ignored in accurate calculations of the gap. Our methodology, the non-adiabatic Allen-Heine-Cardona approach, has been validated by showing that, for nearly all materials for which experimental data exists, it achieves quantitative agreement (within 25%) for this property.

We have also shown that most of the discrepancies with respect to experimental data of the (arguably) best available methodology for the first-principles band-gap computation, denoted GWeh, originate from the first-principles zero-point renormalization: after including it, the average overestimation from GWeh nearly vanishes. There are some exceptions, materials in which transition metals are present, for which the addition of zero-point renormalization worsens the agreement of the band gap. For the latter materials, we believe that the GWeh approach is not accurate enough.

Methods

First-principles electronic and phonon band structures

Calculations have been performed using ABINIT⁵⁰ with norm-conserving pseudopotentials and a plane-wave basis set. Supplementary Table I provides calculation parameters: plane-wave kinetic cut-off energy, electronic wavevector sampling in the BZ, and largest phonon wavevector sampling in the BZ. For most of the materials, the GGA-PBE exchange-correlation functional⁵¹ has been used and the pseudopotentials have been taken from the PseudoDojo project⁵². For diamond, BN-zb, and AlN-wz, results reported here come from a previously published work²⁴, where the LDA has been used, with other types of pseudopotentials.

The calculations have been performed at the theoretical optimized lattice parameter, except for Ge for which the gap closes at such parameter, for GaP, as at such parameter the conduction band presents unphysical quasi-degenerate valleys, and for TiO₂, as the GGA-PBE predicted structure is unstable⁵³. For these, we have used the experimental lattice parameter. The case of SrTiO₃ is specific and will be explained later.

Density-functional perturbation theory^54,55,56 has been used for the phonon frequencies, dielectric tensors, Born effective charges, effective masses, and electron–phonon matrix elements.

First-principles calculations of zero-point renormalization

We first detail the method used for the AHC calculations. In the many-body perturbation theory approach, an electronic self-energy Σ appears due to the electron–phonon interaction, with Fan and Debye–Waller contributions at the lowest order of perturbation³⁵:

$${\Sigma }_{{\bf{k}}n}(\omega )={\Sigma }_{{\bf{k}}n}^{{\rm{Fan}}}(\omega )+{\Sigma }_{{\bf{k}}n}^{{\rm{DW}}}.$$

(7)

The Hartree atomic unit system is used throughout ($\hbar$ = m_e = e = 1). An electronic state is characterized by k, its wavevector, and n, its band index, ω being the frequency. These two contributions correspond to the two diagrams presented in Fig. 1.

Approximating the electronic Green’s function by its non-interacting KS-DFT counterpart without electron–phonon interaction, gives the standard result for the T = 0 K retarded Fan self-energy³⁵:

$$\begin{array}{l}\displaystyle\mathop{\sum }\limits_{{\bf{k}}n}^{{\rm{Fan}}}(\omega )=\frac{1}{{N}_{{\bf{q}}}}\displaystyle\mathop{\sum }\limits_{{\bf{q}}j}^{{\rm{BZ}}}\mathop{\sum }\limits_{n^{\prime} }| \left\langle {\bf{k}}+{\bf{q}}{n}^{\prime}\right|{H}_{{\bf{q}}j}^{(1)}\left|{\bf{k}}n\right\rangle {| }^{2}\times \\\displaystyle \left[\frac{1-{f}_{{\bf{k}}+{\bf{q}}n^{\prime} }}{\omega -{\varepsilon }_{{\bf{k}}+{\bf{q}}{n}^{\prime}}-{\omega }_{{\bf{q}}j}+i\eta }+\frac{{f}_{{\bf{k}}+{\bf{q}}n^{\prime} }}{\omega -{\varepsilon }_{{\bf{k}}+{\bf{q}}n^{\prime} }+{\omega }_{{\bf{q}}j}+i\eta }\right].\\ \end{array}$$

(8)

In this expression, contributions from phonon modes with harmonic phonon energy ω_qj are summed for all branches j, and wavevectors q, in the entire Brillouin Zone (BZ). The limit for infinite number N_q of wavevectors (homogeneous sampling) is implied. Contributions from transitions to electronic states $\left\langle {\bf{k}}+{\bf{q}}n^{\prime} \right|$ with KS-DFT electron energy ${\varepsilon }_{{\bf{k}}+{\bf{q}}n^{\prime} }$ and occupation number ${f}_{{\bf{k}}+{\bf{q}}n^{\prime} }$ (1 for valence, 0 for conduction, at T = 0 K) are summed for all bands $n^{\prime}$ (valence and conduction). The ${H}_{{\bf{q}}j}^{(1)}$ is the self-consistent change of potential due to the qj-phonon³⁵. Limit of this expression for vanishing positive η is implied. For the Debye-Waller self-energy, ${\Sigma }_{{\bf{k}}n}^{{\rm{DW}}}$, we refer to the litterature^21,35.

In the non-adiabatic AHC approach, the ZPR is obtained directly from the real part of the self-energy, Eq. (7), evaluated at ω = ε_kn³⁵:

$${{\rm{ZPR}}}_{{\bf{k}}n}^{{\rm{AHC}}}=\Re e{\Sigma }_{{\bf{k}}n}(\omega ={\varepsilon }_{{\bf{k}}n}).$$

(9)

If the adiabatic approximation is made, the phonon frequencies ω_qj are considered small with respect to eigenenergy differences in the denominator of Eq. (8) and are simply dropped, while a finite η, usually 0.1 eV, is kept. With a vanishing η, the adiabatic AHC ZPR at band edges diverges for infrared-active materials, see Supplementary Note 5.

Summing the Fan and Debye-Waller self-energies, and working also with the rigid-ion approximation for the Debye-Waller contribution delivers the non-adiabatic AHC ZPR, given explicitly in Eqs. (16) and (17) of ref. ²⁴. We do not work with the approach called dynamical AHC, also mentioned in this work²⁴. It corresponds to Eq. (166) of ref. ³⁵. Both non-adiabatic and dynamical AHC ZPR flavors were studied e.g., in ref. ²³, but the comparison with the diagrammatic quantum Monte Carlo results for the Fröhlich model, see e.g., Fig. 1 of ref. ²⁵, is clearly in favor of the non-adiabatic AHC approach. Actually, this also constitutes a counter-argument to the claim by Cannuccia and Marini¹⁷, that band theory might not apply to carbon-based nanostructures. The cumulant expansion results for the spectral function²⁵ demonstrates that the dynamical AHC spectral function is unphysical, with only one wrongly placed satellite. The physical content of the present non-adiabatic AHC theory, focusing on the crucial role of the LO phonons, is very different from the physical analysis based on the dynamical AHC theory¹⁷.

The imaginary smearing of the denominator in the ZPR computation is 0.01 eV, except for SiC, where 0.001 eV is used. Other technical details are similar to previous studies by some of ours^24,25.

The dependence of the electronic structure on zero-point lattice parameter corrections is computed from

$${{\rm{ZPR}}}_{{\bf{k}}n}^{{\rm{lat}}}={{\rm{\varepsilon }}}_{{\bf{k}}n}(\{{{\bf{R}}}_{i}^{T = 0}\})-{{\rm{\varepsilon }}}_{{\bf{k}}n}(\{{{\bf{R}}}_{i}^{{\rm{fix}}}\}),$$

(10)

where the lattice parameters $\{{{\bf{R}}}_{i}^{{\rm{fix}}}\}$ minimize the Born-Oppenheimer energy without phonon contribution, while $\{{{\bf{R}}}_{i}^{T = 0}\}$ minimizes the free energy that includes zero-point phonon contributions, see Supplementary Note 2.

At variance with the AHC approach, in the ASC the temperature-dependent average band edges (here written for the bottom of the conduction band) are obtained from

$$\langle {\varepsilon}_{{\rm{c}}}(T)\rangle ={Z}_{I}^{-1}\mathop {\sum}\limits_{m}\exp (-\beta {E}_{m}){\langle {\varepsilon}_{{\rm{c}}}\rangle}_{m},$$

(11)

where β = k_BT (with k_B the Boltzmann constant), T the temperature, Z_I the canonical partition function among the quantum nuclear states m with energies E_m (${Z}_{I}={\sum }_{m}\exp (-\beta {E}_{m})$), and ${\langle {\varepsilon }_{{\rm{c}}}\rangle }_{m}$ the band edge average taken over the corresponding many-body nuclear wavefunction. At zero Kelvin, this gives an instantaneous average of the band edge value over zero-point atomic displacements, computed while the electron is NOT present in the conduction band (or hole in the valence band) thus suppressing all correlations between the phonons and the added (or removed) electron.

Convergence of the calculations

As previously noted^24,25, the sampling of phonon wavevectors in the Brillouin zone is a delicate issue, and has been thoroughly analyzed in Sec. IV.B.2 of ref. ²⁴. In particular, for infrared-active materials treated with the non-adiabatic effects, at the band structure extrema, a ${N}_{{\bf{q}}}^{-1/3}$ convergence of the value is obtained. We have taken advantage of the knowledge acquired²⁴ to accelerate the convergence by three different methodologies. In the first one, we fit the ${N}_{{\bf{q}}}^{-1/3}$ behavior for grids of different sizes, and extrapolate to infinite N_q. In the second one, we estimate the missing contribution to the integral around q = 0, at the lowest order, see Supplementary Methods B, using ingredients similar to those needed for the generalized Fröhlich model, except the effective masses. For ZnO and SrTiO₃, a third correcting scheme, further refining the region around the band edge with an extremely fine grid, is used.

The special case of SrTiO₃

While phonons in most materials in this study are well addressed within the harmonic approximation, this is not the case for SrTiO₃. This material is found in the cubic perovskite structure at room temperature, and undergoes a transition to a tetragonal phase below 150 K, characterized by tilting of the TiO₆ octahedra⁵⁷. Within our first-principles scheme in the adiabatic approximation, the cubic phase remains unstable with respect to tilting of the octahedra. Quantum fluctuations of the atomic positions actually play a critical role in stabilizing the cubic phase at high temperature⁵⁸, as well as suppressing the ferroelectric phase at low temperature^59,60.

Since SrTiO₃ is however a material for which large polaron effects are clearly identified⁴⁶, we decided to study it as well. We addressed the anharmonic stabilization problem using the state-of-the-art TDep methodology⁶¹. We used VASP molecular dynamics to generate 40 configurations in a 2 × 2 × 2 cubic cell of STO at 300 K, producing 20,000 steps with 2 fs per step and sampling the 40 configurations out of the last 5000 steps. Then we computed the forces with ABINIT and performed TDep calculations with the ALAMODE code⁶². Our calculation stabilizes the acoustic phonon branches and yields a phonon band structure in good agreement with experimental data.

Sources of discrepancies between experiment and theory

The anharmonic corrections to phonon frequencies are not the only reasons for potential differences between the experimental ZPR_g and our non-adiabatic AHC ZPR_g values. The following phenomena may also play a role: (1) the rigid-ion approximation^18,21; (2) the nonquadratic behavior of the eigenenergies with collective displacements of the nuclei, in reference to the ASC³²; (3) the reliance on GGA-PBE eigenenergies and eigenfunctions, instead of more accurate (e.g., GW) ones^29,34; (4) self-trapping effects, overcoming the quantum fluctuations, yielding small polarons⁶³. There is still little knowledge about each of these effects when correctly combined to predict the ZPR_g beyond the AHC picture.

As an example, in KEKF³⁴, the difference between the ASC-PBE and the ASC-GW was argued to be only a few meV, but a more careful look at their values show that it is often bigger than 10% of the ASC-PBE. Unfortunately, the convergence of the ASC-GW results with respect to supercell size could not be convincingly achieved by KEKF³⁴. It remains to be seen whether a non-adiabatic AHC treatment based on GW matrix elements would differ by such relative ratio, see the Supplementary Discussion. Altogether, it would be hard to claim more than 25% accuracy with respect to experimental data, from our non-adiabatic AHC ZPR_g calculations. Together with the experimental uncertainties, this explains our choice for the 25% accuracy comparative limit used in Fig. 2.