Introduction

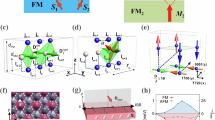
The lack of inversion symmetry at the interface between a heavy metal (HM) and a ferromagnet (FM) induces the antisymmetric exchange interaction so-called Dzyaloshinskii–Moriya interaction (DMI)1,2,3,4. Recently, DMI has been intensively studied in the material combinations possessing perpendicular magnetic anisotropy (PMA) due to their necessities in creating magnetic chiral textures, such as magnetic skyrmions for the new type of racetrack memory device5,6,7,8. Generally, in order to stabilize skyrmions at room temperature, multilayer structures with repetitive stacking of FM/HM bilayer are utilized because multi-stacking of the bilayer unit easily provide the PMA and the sizable DMI at the same time, both of them arising from the same physical origin, i.e., interfacial SOC9,10,11,12,13. In this respect, Co/Pd and Co/Pt interfaces are one of the well-known material combinations providing both the PMA and the DMI originating from interfaces, resulting in stable magnetic skyrmions14,15. With the same manner of such an AB-type multi-stacking structure composed of several nanometer-thick layers, a layer structure with ABC-type repetitive stacking of a few atomic monolayers is interesting system as illustrated in Fig. 1a. An epitome is the [Co/Pd/Pt] superlattice (SL) possessing PMA generated by the bulk-type spin momentum locking due to absence of inversion symmetry in stacking order16. Note that not interfaces but asymmetry of bulk-type band formation in the [Co/Pd/Pt]-SL as illustrated in Fig. 1b is essential to give rise to such a chiral phenomenon, resulting in strong PMA.

Fig. 1: SL structure with symmetry breaking in stacking order.
figure 1

a SLs with AB-type and ABC-type stacking-order, which is composed of nm-thick and sub-nm-thick layers, respectively. b Schematic image of an asymmetric band structure in terms of direction of magnetization in the SL with ABC-stacking order.

Full size image

Such inversion symmetry breaking (ISB) in the SL with ABC-type stacking order would traditionally be accounted for by involving the Rashba model Hamiltonian, \({\mathcal{H}}_R = \alpha _R\left( {{\mathbf{k}} \times {\hat{z}}} \right) \cdot {\mathbf{\sigma}}\), which was initially proposed for a surface, where \(\hat z\) is the direction of inversion-symmetry-breaking-induced potential gradient17. The oddness of the SOC in the k space due to the ISB is shown by the dependence of the Hamiltonian on the linear terms in k, although higher odd-order may in principle also appear. Rashba effect manifests most immediately into a spin-splitting within the k space, and it has been vastly utilized to interpret a number of magnetic phenomena11,18,19,20, in particular those well understood to originate from the ISB, such as the DMI responsible for exotic magnetic textures such as skyrmions and chiral domain walls, and spin–orbit torque. It should be noted that amorphous ferrimagnet GdFeCo exhibits bulk DMI feature, which is independent of interface but due to inhomogeneous distribution of elemental content21. In this context, further study to distinguish DMI interface and bulk origin would be interesting topic.

In this study, we investigate DMI of the [Co/Pd/Pt]-SL arising from bulk spin-momentum locking. First-principles calculations reproduce such DMI enhancement in the SL, showing that the asymmetry of bands around Fermi energy level induced by ISB. The observed behavior of DMI upon increasing the repetitions of the ABC-layer unit in the SL suggests that while the interfacial and bulk DMI co-exist with small N, the enhancement of DMI with larger N can be attributed to the bulk-type asymmetric band formation around the Fermi level.

Results and discussion

DMI of the noncentrosymmetric SLs

Estimation of the magnetocrystalline energy (MCA) and DMI is done by following the steps outlined previously22,23,24. Here, we consider 1–4 [Co/Pt/Pd] units, and anticlockwise rotation of the spin-spiral structures as shown in Fig. 2a–c. The detailed process is explained in the “Method” section. The calculation results are summarized in Fig. 2d and e. The odd terms of the MCA energy (\(E_{{\rm{MCA}}}^{{\rm{odd}}}\)), which quantifies ISB, are summarized in Fig. 2d. This quantity is related to the ISB-induced shift of the band structure along the ky direction due to the magnetization along x direction. We note that \(E_{{\rm{MCA}}}^{{\rm{odd}}}\) increases with the repetition number N of [Co/Pt/Pd] unit layers. The total MCA and \(E_{{\rm{MCA}}}^{{\rm{odd}}}\) in the [Pt/Co/Pd]N increases shown in Fig. 2d, and the total MCA value can be expected to reach 0.043 meV Å−2 obtained for the bulk [Co/Pt/Pd]-SL, i.e. the infinitely periodic system along c direction [Pt/Co/Pt]∞16. When the DMI constants are further extracted by utilizing the polynomial expression of the frozen magnon energy (Eq. 2 in “Method” section), we obtain a DMI energy density (D) value of the asymmetric [Pt/Co/Pd]N structure which increases with N [see Fig. 2e]. Here, we use the unit J m−2 for DMI values of the structures in order to compare with experimental results, shown later in this study. It is important to note that the D value increases with N and converges to the bulk value. Such linear dependence of DMI cannot be simply explained by the interfacial origin. If the increase in DMI with N is fully originated from the interfacial spin–orbit coupling, DMI should be independent of N because the gains in the DMI energy by increasing the number of interfaces are compensated by the volume of Co layers. The detailed mechanism of this result is explained in the following paragraph with anatomy of the k-dependent band structures.

Fig. 2: ISB-related MCA energy and DMI of the [Co/Pt/Pd]-SL.
figure 2

a The side view and b the top view of the model crystal structure of Co/Pt/Pd-based multilayer system. The M direction for the propagation of the spin-spiral wave is indicated by the red arrow in (b). c Anticlockwise rotation of the spin-spiral structures. The calculated N dependence of d the odd term of MCA energies \(E_{{\rm{MCA}}}^{{\rm{odd}}}\) and e the DMI for the [Pt/Co/Pd]N model systems, while those obtained for the bulk system are shown using straight lines. The N dependence of the total MCA energies EMCA of the [Pt/Co/Pd]N model systems and the corresponding bulk value are shown in (d) using dashed lines.

Full size image

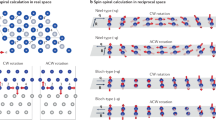
The two-dimensional MCA contour map of [Pt/Co/Pd]1 is shown in Fig. 3a. This map shows the typical characteristic of the MCA in the systems with ISB. Since the in-plane magnetization is oriented along the +x direction, i.e., \({\mathbf{m}} = m_{+{\rm{x}}}{\hat{x}}\), the MCA is asymmetric along the ky axis, which is along the ẑ × m direction, and shows mirror symmetry along kx direction. Similar behavior is obtained for other N. The Fermi surface of [Pt/Co/Pd]1 is visibly shifted towards negative ky as shown by using the red color in Fig. 3b for m+x magnetization, and is shifted symmetrically towards negative ky when the magnetization is along the \(m_{ - {\rm{x}}}\hat x\) direction, as plotted by using the blue color in Fig. 3b. In order to check the band contribution to the Rashba splitting, we plot Fermi surface by switching off the spin–orbit coupling in each atomic layer. Comparing the results shown in Fig. 3d–f, it is visible that switching off SOC in Pt layer alters the shape of the Fermi contour most considerably compared to that in Co and Pd. As the change in the Fermi contour indicates the modification of the band structure around the Fermi level, the result implies the crucial role of Pt bands to the band splitting, which should be attributed to the strong SOC constant of the Pt atom.

Fig. 3: k-dependent MCA energy and Fermi surface in the [Pt/Co/Pd] unit structure.
figure 3

a Two-dimensional (kx, ky) contour map of k-dependent MCA energy and b Fermi surface for different in-plane magnetization directions along +x and –x axes, plotted using respectively red and blue lines, of the [Pt/Co/Pd]1 model system depicted in (c). d–f Fermi surface of the [Pt/Co/Pd]1 model system in the absence of SOC on the Pt1, Co1, and Pd1 layer, respectively.

Full size image

The anatomy of the DMI can be decomposed in a similar fashion. For this purpose, one can extract the DMI using the polynomial expression (Eq. 1 the in “Method” section) from the spiral structures built for several q vectors by switching on/off the SOC of a particular layer. In this work, however, we choose a simpler approach, i.e., by calculating the asymmetry between the energies of spiral structures with q = ±0.25, of which the degeneracy is lifted due to the ISB. When the asymmetric energy in a total structure, which is correlated with DMI and defined here as the energy difference between q = ±0.25 states, are denoted as \(E_{{{\mathbf{q}}} = {\pm 0.25}}^{{\rm{asym}}}\), the contribution of a particular layer L to the asymmetric energy can be given as

$$E_{{{\mathbf{q}} = \pm 0.25}}^{{\rm{asym}}}\left( L \right) = E_{{{\mathbf{q}}} = \pm 0.25}^{{\rm{asym}}}\left( {{{{\mathrm{tot}}}}} \right) - E_{{{\mathbf{q}}} = \pm 0.25}^{{\rm{asym}}}(L_{{{{\mathrm{off}}}}})$$
(1)

where \(E_{{{\mathbf{q}}} = \pm 0.25}^{{\rm{asym}}}({{{\mathrm{tot}}}})\) is the asymmetric energy which includes the contribution of all layers, and \(E_{{{\mathbf{q}}} = \pm 0.25}^{{\rm{asym}}}(L_{{{{\mathrm{off}}}}})\) is the asymmetric energy when the SOC contribution of layer L is switched off. The results are summarized in Fig. 4, clearly showing that, first of all, despite being the carrier of the magnetic moments, Co gives very small contribution to the DMI. In fact, the largest contribution to the asymmetric energy, hence to the DMI, is coming from the neighboring Pt layers, which can be understood to dominate the band around Fermi level, as shown in Fig. 3d–f. It should be noted that for all N, Pd gives smaller and opposite contribution to the DMI, in comparison to Pt. Additionally, the evaluated total \(E_{{\mathbf{q}} \pm 0.25}^{{\rm{asym}}}\) for all N, as plotted in the inset of Fig. 4, shows considerable deviations for all contributions, then, converges to that of the bulk with infinite periodicity. This implies the existence of a non-interfacial origin, but bulk spin-momentum locking25 for the DMI in the considered [Pt/Co/Pd]-SL systems.

Fig. 4: Origin of the N-dependence of DMI in the [Pt/Co/Pd]-SL.
figure 4

The contribution of different atomic layer L to the asymmetric energy between the spiral structures with wave vectors q = ±0.25, \(E_{{\mathbf{q}} = \pm 0.25}^{{\rm{asym}}}\left( L \right)\). The corresponding atomic layer contributions for bulk system, i.e. with N = ∞, are shown with black lines. The sequence of the layers is illustrated. The total asymmetric energy \(E_{\mathbf{q}} = \pm 0.25^{\rm{asym}}\left( {\mathrm{tot}} \right)\) is also shown.

Full size image

Experimental observation of DMI of the noncentrosymmetric SLs

To experimentally confirm the bulk spin-momentum locking for the DMI, the [Co 0.4/Pd 0.4/Pt 0.4 (nm)] SLs, hereafter [Co/Pd/Pt]-SL, was prepared as the noncentrosymmetric SL varying N as explained in the “Method” section [see also Fig. 5a]. The X-ray reflection pattern of the film with N = 5 clearly shows the 1st-Bragg-like peak, implying that the [Co/Pd/Pt] unit structure is well preserved without severe atomic intermixing in spite of such ultra-thin thickness range26,27. All [Co/Pd/Pt]-SLs are confirmed to have PMA as shown in Fig. 5c and d. In Particular, all magnetic hysteresis curves measured with the easy-axis field sweep show squareness of unity and sharp switching properties of the SLs. In case of the hard-axis loops taken with in-plane field sweep, any signal jump in the loops was not observed, showing saturation at higher than 1 T. When N > 2, the saturation field becomes about 2 T. Thus, the films have strong PMA property with good coherency even though they have complexed layer structures.

Fig. 5: Magnetic properties of the [Co/Pd/Pt] SLs.
figure 5

a A layer structure of the Co/Pd/Pt SLs. b XRR measurement result with the Co/Pd/Pt SL with N = 5. Magnetic hysteresis curves with c out-of-plane and d in-plane magnetic fields.

Full size image

In order to estimate the DMI energy of each SL, the measurement based on the extended droplet model was conducted28,29. Figure 6a shows the schematic illustration of the droplet measurement. Since the nucleated magnetic droplet possesses domain wall magnetizations with two opposite radial direction. As illustrated in Fig. 6a, we can consider two domain wall magnetizations (MDW1 and MDW2) with respect to Hx. If we approximate that the two domain wall magnetizations dominate the total domain wall energy under Hx, the total domain wall energy of nucleated magnetic droplet can be obtained from sum of the domain wall energies: σtotal = σDW1(+Hx) + σDW2(−Hx), where σDW1(+Hx) and σDW1(−Hx) are the domain wall energies with respect to Hx. The nucleation field through the relation is as follows: μ0Hn = \(\pi \sigma _{{{{\mathrm{DW}}}},{{{\mathrm{total}}}}}^2t_{{{{\mathrm{FM}}}}}/2\mu _0{\mathbf{M}}_{{{\mathrm{S}}}}pk_{{{\mathrm{B}}}}T\), where tFM is the ferromagnet thickness, μ0MS is the saturation magnetization, p represents the thermal stability factor, kB is the Boltzmann constant, and T denotes temperature30. Therefore, square root of nucleation fields in terms of Hx should follow the blue curve in Fig. 6a. Note that σtotal is proportional to \(\sqrt {H_{{{{\mathrm{n}}}},z}}\) when Hx > HDMI, otherwise σtotal becomes constant. The crossing point of the two linear curves can be defined as DMI-induced effective field (HDMI). Based on this model, the angular dependence of coercivity was measured to obtain \(\sqrt {H_{{{{\mathrm{n}}}},{{{\mathrm{z}}}}}}\) of the SLs as illustrated in inset of Fig. 6(b). In this measurement concept, applied magnetic field can be decomposed into Hx and Hn,z. The detailed measurement scheme is as follows; first of all, the sample is saturated to the +z direction. Then, the magnetic field is swept from the positive to negative field in terms of various polar angles (θ) in order to obtain the θ dependence of switching field (HSW). Considering the measurement time scale (ramping rate ~1 T/min.) is much slower than that of complete switching via domain wall propagation initiated from the nucleation, we can consider the relation of μ0Hn,z = μ0HSWcosθ. The angular dependence of the HSW was obtained from the anomalous Hall effect measurement in terms of θ [see Fig. 6b]. Every SLs shows sharp switching behavior as shown in Fig. 6b. With this approach, we could obtain the quantitative information of DMI by plotting the Hx dependence of \(\sqrt {H_{{{{\mathrm{n}}}},z}}\).

Fig. 6: N-dependent DMI of the [Co/Pd/Pt]-SL.
figure 6

a Illustration of droplet nucleation field profile in terms of in-plane field. b HSW of the [Co/Pd/Pt]-SL with N = 6 measured using anomalous Hall effect in terms of θ. Inset shows the configuration of a device with external field (Hex), components of the Hex (Hx and Hz), and Ms. Solid lines are the fitting results before and after the threshold field. c Normalized \(\sqrt {H_{{\rm{n}},{\rm{z}}}}\) vs. Hx plots in terms of N. The solid lines indicate the fitted lines when Hx < HDMI and HX > HDMI. HDMI values can be obtained from crossing points indicated by the arrows. d D values of the SLs in terms of N. e Ku vs. D plots. The red solid line is the linearly fitted line. The error bars represent standard deviations from the best fit.

Full size image

HDMI values for all N values with each SL are clearly determined with the \(H_{{{\mathrm{x}}}}{{{\mathrm{vs}}}}.\sqrt {H_{{{{\mathrm{n}}}},z}}\) plots as shown in Fig. 6c with arrows. The measured data show that HDMI values of [Co/Pd/Pt]-SLs are N-dependent. Here, D should be discussed for precise discussion with excluding effects of Keff and MS, based on the relation D = μ0MsΔHDMI, where Δ denotes the domain wall width which is determined by the exchange stiffness constant (A) and Keff by Δ = \(\sqrt {A/K_{{{{\mathrm{eff}}}}}}\). In all samples, A = 10 pJ m−1 is assumed since A in ultra-thin Co layers are usually an order of a few (typically 1–15) pJ m−131,32.

Note that difference of DMI between Pt/Co and Co/Pd interfaces in the [Co/Pd/Pt]-SL can also enhance total DMI energy and the value should be larger than other symmetric structures. In other words, the interfacial origin should be also considered to explain our observation.

In order to confirm the characteristics of DMI originating from the interface, the dependence of repetition number (N) was studied in all series of the SLs. Figure 6d shows that the [Co/Pd/Pt]-SL shows N-dependence of DMI. Such increase of DMI in the [Pt/Co/Pd]N is fully consistent with our theoretical works. Especially, DMI of the [Co/Pd/Pt]-SL linearly increases by more than 300% when N increases from 2 to 10. Such behavior cannot be simply explained by the interfacial origin. We should note here that in order to reproduce the calculation results in our experiment, we used the smallest possible thickness of each layer which is about thickness of two atomic monolayers. Our XRR study in Fig. 4 proves well-defined layer structures. One atomic monolayer as shown in our DFT calculation is difficult to have continuous film in reality. Therefore, there should be both the conventional interface and Rashba-type bulk contributions simultaneously for our experimental observation, while the latter is dominant for the calculation especially with larger repetition numbers. Although quantitative comparison between calculation and experimental results is limited in this study, both results manifest that DMI in such an ABC-type structure cannot be explained with conventional approach with interfacial origin, indicating formation of asymmetric band structure. We also note that D has the linear relation with uniaxial magnetic anisotropy (Ku) estimated from the magnetic hysteresis loops shown in Fig. 5c and d as shown in Fig. 6e. Our results suggest that the enhancements of both D and PMA have the same origin in the Rashba SLs, namely the bulk spin-momentum locking16.

Our experimental and theoretical studies demonstrate that the bulk spin-momentum locking in a SL can be made with asymmetric atomic stacking and structural coherency. Especially, the N-dependence of DMI of the [Co/Pd/Pt]-SL is an important phenomenon arising from the band asymmetry. So far, material selection has been limited to several cases for the development of skyrmion-based devices. On the other hand, bulk DMI can be made with such ABC-type material combination within atomic scale, which is larger than interfacial contribution. Hence, our experimental and theoretical findings can provide more options to design chiral magnet for spintronic devices. As a final remark, in two-dimensional system with C3v symmetry, only non-Lifshitz invariant DMI can exist33. Our observation is related to this non-Lifshitz invariant but Lifshitz invariant terms dominate as the SL is three-dimensional object with strong two-dimensional feature inherent from interface. The noncentrosymmetric SL in this sense would invite further study on Lifshitz invariant contribution in DMI.

Methods

Experiment

The [Co/Pd/Pt]-SL were deposited by the UHV magnetron sputtering system. The thickness of magnetic layer (Co) is varied in each SL. The static magnetic properties such as Ms and magnetic anisotropy energy are investigated by the vibrating sample magnetometer (VSM). In order to quantify DMI energy, we used the extended droplet method24,25,26. All the films were patterned into a microstrip with a Hall bar structure by E-beam lithography to prevent the nucleation of domain at the rough microstrip edge. Ti (5 nm)/Au (100 nm) electrodes are defined to make electrical contacts with μm-scale Hall bars by photolithography and lift-off process.

The first principles calculations for MCA and DMI of SLs

Our first-principles DFT calculations are based on the Generalized Gradient Approximation34 as implemented in the Full-Potential Linearized Augmented Plane Wave (FLAPW) code21. The MCA energy EMCA has been defined in our calculation as the energy difference between the in- and out-of-plane magnetization direction, i.e., EMCA = Eip − Eop, where Eip and Eop refer respectively to the total energy of the in- and out-of-plane magnetization. The inclusion of SOC is done via the second variational method21. The in-plane magnetization direction has been chosen to be along the x direction. We found that our calculated MCA energy has converged at a relatively large two-dimensional k-point mesh of 100 × 100. In addition to the total MCA energy, we also virtually decomposed the k-dependent MCA energy into \(E_{{{{\mathrm{MCA}}}}}^{ + k_y}\) and \(E_{{{{\mathrm{MCA}}}}}^{ - k_y}\) in which \(E_{MCA}^{ \pm k_y} = E\left( {m_{{{\mathrm{x}}}}, {\pm k_{{{\mathrm{y}}}}}} \right) - E\left( {m_{{{\mathrm{z}}}}, \pm k_{{{\mathrm{y}}}}} \right)\) and calculated the odd term of the MCA energy \(E_{{{{\mathrm{MCA}}}}}^{odd}\) by following the recipe in our previous work16, as \(E_{{\rm{MCA}}}^{{{{\mathrm{odd}}}}} = E_{{\rm{MCA}}}^{ + k_{\rm{y}}} - E_{{\rm{MCA}}}^{ - k_{\rm{y}}}\). This quantity, despite the fact that it contains no physical meaning, illustrates the physics of Rashba spin–orbit coupling and provides an estimation of the degree of ISB by the shift of the Fermi surface. Comparison with bulk values has been done with a three-dimensional k-point mesh of 75 × 75 × 45 for the bulk [Co/Pt/Pd]-SL16.

The estimation of D values was done by following the steps outlined previously23,24 We start from the ferromagnetic configuration which is found to be the ground state of all model systems at the scalar relativistic approximation, i.e., without the SOC. Next a set of spiral spin structures with wave vectors q = a/λ along the M = (1, 1, 0) direction (see Fig. 3b), where λ is the wavelengths of the spin-spiral structures, are generated by utilizing the generalized Bloch theorem35,36. When the SOC is then included, the spin-spiral structures have been assumed to be the Néel xz out-of-plane rotation type. The frozen magnon energy, E(q), for q = 0, ±0.1, ±0.2, ±0.25 has been fitted with a polynomial expansion;

$$E\left(q \right) = C_0 + C_1{\mathbf{q}} + C_2{\mathbf{q}}^2 + C_3{\mathbf{q}}^3 + C_4{\mathbf{q}}^4$$
(2)

where the odd terms C1 and C3 occur due to the presence of ISB. The DMI discussed in this work is extracted as the antisymmetric exchange stiffness constant C1, i.e., first order in q, or D ≡ C1. Convergence of the calculated DMI has been obtained with a 40 × 40 k−point mesh within the two-dimensional Brillouin zone. As in the case of MCA energy, we have also computed the DMI for the bulk CoPtPd system with the Néel xz out-of-plane rotation type magnetic structures along the M direction, and a three-dimensional 40 × 40 × 20 k-point mesh has been used.