Abstract
In pursuit of scientific discovery, vast collections of unstructured structural and functional images are acquired; however, only an infinitesimally small fraction of this data is rigorously analyzed, with an even smaller fraction ever being published. One method to accelerate scientific discovery is to extract more insight from costly scientific experiments already conducted. Unfortunately, data from scientific experiments tend only to be accessible by the originator who knows the experiments and directives. Moreover, there are no robust methods to search unstructured databases of images to deduce correlations and insight. Here, we develop a machine learning approach to create image similarity projections to search unstructured image databases. To improve these projections, we develop and train a model to include symmetry-aware features. As an exemplar, we use a set of 25,133 piezoresponse force microscopy images collected on diverse materials systems over five years. We demonstrate how this tool can be used for interactive recursive image searching and exploration, highlighting structural similarities at various length scales. This tool justifies continued investment in federated scientific databases with standardized metadata schemas where the combination of filtering and recursive interactive searching can uncover synthesis-structure-property relations. We provide a customizable open-source package (https://github.com/m3-learning/Recursive_Symmetry_Aware_Materials_Microstructure_Explorer) of this interactive tool for researchers to use with their data.
Similar content being viewed by others
Introduction
“Seeing is believing”; thus, imaging is one of the most powerful tools for scientific discovery. While human memory has a tremendous capability to recall images, we cannot associate the images with metadata (e.g., date of data collection, sample properties, or sample processing and provenance, etc.). Instruments of scientific discovery from optical to scanning probe to electron microscopes and spectrometers generate enormous volumes of images containing information about the properties and structure of materials. While advances in optics and electronics have accelerated the resolution, length, and timescales of imaging, the downstream analysis tools have not kept pace. Recently, it has been purported that machine learning can extract and represent underlying physics from large datasets1.
Machine learning, however, is only as good as the objective with which it is trained and thus struggles with unstructured exploratory tasks2. There has been an emergence in machine learning tools to accelerate discoveries from imaging sources3. Most commonly, researchers have trained machine learning models on labeled datasets to identify pre-determined features of significance. For example, convolutional neural networks (CNNs) can be trained to identify imaging modes in electron microscopy [e.g., transmission electron microscopy (TEM) vs. scanning TEM (STEM)]4. However, classification is limited by the requirement that researchers know a piori what features they are looking to discover and have at least a small labeled dataset. Research tasks tend to emphasize unknown discoveries, and thus classification is ill-posed. To extract more information from images, CNNs have been extended using a UNET architecture to segment phases5, and nanoparticles6. Alternatively, autoencoder structures have been leveraged to unmix statistical information from hyperspectral piezoresponse force microscopy7 and current-voltage spectroscopy8. This concept has been extended via the inclusion of rotational invariance to extract the orientation of ferroelectric variants from atomically resolved images9. While autoencoders are powerful in extracting information from imaging data that lies on a narrow distribution, they provide significantly less insight when the data is diverse10.
CNNs are typically constructed of convolutional layers that convolve filters across an image and pooling layers that combine spatial information. During optimization, the weights of the filters are adjusted towards an objective. For classification, the output of the 2-dimensional filters is flattened into a single dimension that eventually predicts the probability that an observed image belongs to a class. When training CNNs as classifiers, the learned filters resemble standard computer vision filters (e.g., edges, lines, etc.)11. CNNs have achieved incredible performance on image classification tasks. For example, it is common for models trained on ImageNet to achieve top-5 accuracy of >98%12. One of the core challenges with materials science datasets is that there are no large, labeled datasets for training. To circumvent the requirement for large databases, in a method called transfer learning13, filters learned on large, labeled datasets from, for example, ImageNet can be used for a new objective where data might be limited. Transfer learning has been used to classify microstructures, structure-property predictions, and much more14,15,16. Transfer learning requires a discrete objective for optimization, which is undefined in exploratory data analysis.
In materials imaging, one of the most pervasive concepts is symmetry, periodicity, and long-range order. The mathematics of CNNs are unable to learn this concept parsimoniously17. The process of convolving filters across an image imposes translational equivariance – meaning that the network can detect if a feature exists and its location. In practice, to make CNNs computational tractable, it is common to add pooling layers that use a region-based summary statistic to reduce the dimensionality of the data. As a result of pooling layers, CNNs are commonly translational invariant, meaning they can detect if a feature exists in an image but cannot determine its precise location. Similarly, if an image were rotated even slightly, the outputs of the filters would change, resulting in a unique trajectory through the network. To combat this, researchers have developed 2D-rotational equivariant18, and 3D-euclidian neural networks19; however, it is still an open question how to learn symmetry parsimoniously.
Despite these inherent limitations, all is not lost. Using over-parameterized models, large datasets, and data augmentation, it is possible to at least approximate symmetry. This means that given enough data, neural networks can be trained to accurately predict symmetry (within the bounds of a dataset) despite having no proper understanding of the concept of symmetry. This is achieved by learning a data-driven discrepancy model that leads to correct narrow-bounded conclusions without any requirement for parsimony. The challenge with learning in this fashion is that if a new example lies on the periphery of the training data distribution, the predictions might be nonsensical. Until neural networks can learn concepts like symmetry parsimoniously, their use in materials microstructures should be restricted to narrow-bounded problems (e.g., binary classification), where subsequent physics-based validation is possible, or there is an expert-in-the-loop. Even when it is impossible to learn underlying mathematical concepts, there can be utility in approximations when the task is untenable for human analysis, and independent validation is possible. For example, neural-network-based suggestive interactive frameworks provide an unprecedented capability to discover complex correlations in large datasets that are impossible to extract without flexible data-driven models.
Imaging and microscopy are ubiquitous in materials science. For example, the study of ferroelectric relies on understanding highly-ordered nanoscale domain structures. Piezoresponse force microscopy (PFM) is a high-throughput technique used to image domain structures in ferroelectrics. In PFM, a conductive cantilever is brought into contact with a surface, and an AC-electrical stimulus is used to measure the local piezoresponse in the lateral and vertical directions. To enhance the signal-to-noise, it is common to measure the response near the cantilever resonance frequency. To mitigate resonant shifts associated with changing tip-surface interactions, dual-frequency resonance tracking (DART) has been implemented by Asylum Research20. This technique uses a dual-frequency excitation with two lock-in amplifiers coupled to a phase-lock loop to measure piezoresponse at two frequencies simultaneously. It is important to characterize the structure, order, and periodicity in these images to understand structure-property relations.
Here, using a database of 25,133 DART-PFM images, we demonstrate how an interactive suggestive neural-network framework can be used to discover correlations in scientific images. To do this, we develop two neural-network-based image feature extractors. The first is based on transfer-learning pretrained image classifiers trained on ImageNet. A second neural-network provides symmetry-aware features. We achieve this by generating 1,000,000 images that belong to the 17-wallpaper group symmetries21. We trained a classifier that achieved >99% testing accuracy with a 60%-training, 20%-validation, 20%-testing split. Following feature extraction, we use manifold learning techniques to create two-dimensional projections that correlate images based on their composition and structure irrespective of the length scale of the images. Correlation of projections to metadata (e.g., filename) demonstrates preservation of trends in experimentalist, experimental timeline, and experimental methods. Through recursive exploration, more nuanced details of the image similarity are revealed. This provides a method for researchers to identify correlations in large unstructured image databases to accelerate scientific observations and discoveries. If coupled with a structured database containing metadata, the combination of filtering and projections would provide insights into synthesis-structure-property relationships. We democratize this tool by releasing all source code under a 3-clause BSD License, a non-restrictive open-source license.
Results and discussion
Data collection, collation, and feature extraction
We extracted 25,133 DART-PFM images acquired from 2013–2019 within the Lane Martin and Ramamoorthy Ramesh Laboratory at the University of California Berkeley7,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195,196,197,198,199,200,201,202,203,204,205,206,207,208,209,210,211,212,213,214,215,216,217,218,219,220,221,222,223,224,225,226,227,228,229,230,231,232,233,234,235,236,237,238,239,240,241,242,243,244,245,246,247,248,249,250,251,252,253,254,255,256,257,258,259,260,261,262,263,264,265,266,267,268,269,270,271,272,273,274,275,276,277,278,279,280,281,282,283,284,285,286,287,288,289,290,291,292,293,294,295,296,297,298,299,300,301,302,303,304,305,306,307,308,309,310,311,312,313,314,315,316. Within this data, there are PFM images of PbZr1−xTixO3, BiFeO3, PbTiO3/SrTiO3 superlattices, and much more. These films were grown at various growth conditions, epitaxial strain, elastic and electrostatic boundary conditions, and substrate orientation. Additionally, within this dataset, there were various stroboscopic switching studies. Associated with these images, we were provided access to the file and sample names and the sample province in the form of handwritten notes.
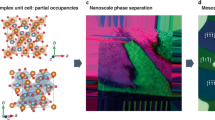
DART-PFM images contain multichannel information, including the topography, two amplitude, and phase channels, and an estimate of the resonance frequency. CNNs for natural-image classification are designed for red-green-blue (RGB) images. To make PFM images compatible with pretrained neural networks, we stacked the topography and one of the amplitude and phase channels to form RGB images. Then, using a pretrained VGG-16 convolutional neural-network317 (Fig. 1a) trained on ImageNet318 (~14 million images and 1,000 object categories), we extracted the 4096 latent features from the layer immediately preceding the classification layer for all stacked PFM images. While these features are tailored to classify natural images, mapping images from other domains to this latent space can produce a manifold where image similarity is preserved.
a VGG-16 architecture pretrained on ImageNet database. The gray area represents the pretrained VGG-16 model. FC3 was determined by training an autoencoder to reduce the dimensionality of the feature vector from 4096 to 512. The gear represents that this is the only layer optimized in the VGG-16 model. b ResNet-34 architecture with symmetry awareness by training it to classify wallpaper group symmetries.
To enhance the latent features, we embedded physics awareness into the latent manifold. In microstructural images such as ferroelectric domain structures, long-range order and symmetry are pervasive concepts. We built a dataset of 1,000,000 images equally distributed amongst the 17-wallpaper group symmetries to include this symmetry awareness. To do this, we sampled various-sized unit cells from the ImageNet dataset and conducted symmetry operations to create images (Supplementary Fig. 1). We provide this dataset available open-source (see data availability). We then trained a ResNet-34 using an ADAM optimizer to predict wallpaper group symmetry (Fig. 1b). We refer to this model as ResNet-34-Symm-Aware. Following training, our model achieved >99% testing accuracy (Supplementary Fig. 2).
It is important to note that despite this model achieving >99% test accuracy on predicting symmetry, it does not actually learn the concept of symmetry. Learning or detecting symmetry parsimoniously from images is not something possible using current machine learning or analytical methods. We do the next best thing; we provide symmetry awareness by training a model to approximate symmetry detection. This symmetry awareness improves the model’s performance but should not be relied upon without validation.
We, once again, extracted the 512 latent features from the layer immediately preceding the classification layer. While these latent features cannot accurately determine symmetry from PFM images, the features they extract are sensitive to the symmetry in images. Since the latent dimensions between these two feature extractors are of different sizes, we reduced the dimensionality of the natural-image features from 4096 to 512 using a dense autoencoder with a single-latent layer (see methods for details). Following training, the latent layers were stacked into a 1024-dimensional feature vector. By including an equal number of regular and symmetry-aware features, we consider both symmetry and non-symmetry-related information approximately equally.
Manifold learning
To further reduce the dimensionality of the latent space to a tenable two-dimensions, we used Uniform Manifold Approximation and Projection (UMAP)319,320. This technique belongs to the class of neighbor graph manifold learning techniques—of which t-distributed stochastic neighbor embedding (t-SNE)321 is the most common. UMAP works by building complexes of simplices that represent topological space. Based on Nerve theorem, it can be shown that all the vital topology of a data manifold can be preserved. For the mathematics to work, the data must be uniformly distributed on a manifold – a condition absent in real data. This can be corrected by defining a Riemannian metric on the manifold that makes this true. Essentially, what this is doing is taking regions of the manifold and distorting the distance metric such that the data maps to a uniformly distributed Euclidean space. Using fuzzy topology and under the assumption that the manifold is locally connected, it is possible to avoid the curse of dimensionality by making the local connectivity distributions independent of the dimensionality. These different representations of the manifold space are combined using a probabilistic fuzzy union of weight edges \(f\left( {\alpha ,\beta } \right) = \alpha + \beta - \alpha \cdot \beta\). This graph is then translated to a low-dimensional manifold by minimizing the cross-entropy \(\mathop {\sum}\limits_{\alpha \in A} {\mu \left( \alpha \right)\log } \left( {\frac{{\mu \left( \alpha \right)}}{{\upsilon \left( \alpha \right)}}} \right) + \left( {1 - \mu \left( \alpha \right)} \right)\log \left( {\frac{{1 - \mu \left( \alpha \right)}}{{1 - \upsilon \left( \alpha \right)}}} \right)\) between these two graphs. In this equation, the first term tries to correctly group local connectivity, where the second term tries to ensure the distance between groups is represented accurately. This can be optimized using stochastic gradient descent with negative sampling. UMAP has significant advantages over t-SNE in that it creates more uniform projections, scales significantly better, and has an adaptable mathematical framework. For this work, we used the original open-source implementation319.
Image similarity search in natural images
To demonstrate this concept, we conduct a toy demonstration using the CAL101 image dataset322. This dataset contains images from 101 distinct categories, each of which contains 40–80 images. Since these images are not symmetry-sensitive, only the VGG-16 network trained on the ImageNet database was used as a feature extractor. We note that the symmetry-aware model resulted in significantly worse results as symmetry is not a good descriptor of natural images (Supplementary Figs. 3–4). Following feature extraction, UMAP was used to project the feature manifold into a 2-dimensional space. We show the resulting UMAP image similarity manifold (Fig. 2, closeup images are provided in Supplementary Figs. 5–7). Looking at this projection, much of the important similarity is preserved. For example, image categories such as people, airplanes, motorcycles, soccer balls, and stop signs are tightly clustered. More interestingly, similar categories, for example, vehicles (bottom—circle, Fig. 2), animals (top—star, Fig. 2), and household furnishing (center left—square, Fig. 2), are grouped. It is important to note that this occurs without any categorical association between the classes, only similarities in the images. This demonstrates that UMAP projections of neural-network features preserve local similarity between images of the same class and more global similarity associated with commonalities amongst classes. The ability of this methodology to preserve global similarity means it is possible to identify similarities between uncorrelated images.
Image similarity search in piezoresponse force microscopy images
Having proven the capability of this approach on natural images, we applied this concept to our database of 25,133 PFM images. We extracted features using both the VGG-16 natural image and ResNet-34 symmetry-aware models. We show the 2D-UMAP projection (Fig. 3) with n_neighbors = 5, min_dist = 0.3, n_components = 2, metric = “correlation”. The projections were relatively insensitive to reasonable hyperparameter choices (Supplementary Figs. 8–10). All 25,133 PFM images are included in this projection (black dots); however, we show only 1000 random images (Fig. 3, additional closeups are provided Supplementary Figs. 11–15). Further details regarding the role of feature extractors on PFM images is discussed in Supplementary Fig. 16.
Similar to the natural images, this projection preserves similarity between the images. For example, there are clusters of (001)-oriented PbZr1-xTixO3 with c/a/c/a domain structures (Fig. 3 green-triangle). These are adjacent to extended clusters of striped-phase BiFeO3 (Fig. 3 blue-square), (111)-oriented PbZr1−xTixO3 (Fig. 3 red-circle). The large section on the top right-hand side of the image shows experiments with tip-induced 180-degree switching (Fig. 3 purple-star), and the bottom shows regions where there was minimal PFM contrast (Fig. 3 yellow-diamond). Such results indicate that the neural-network feature extractor combined with UMAP projections can conduct fuzzy classification and association of microstructures based solely on the images. Furthermore, this method preserves semantic relationships between microstructures despite differences in imagining conditions, magnification, tip, date, acquisition time, etc.
To explore how this approach can preserve image similarity, we conducted studies where a single image was selected (shown with dashed box), and the 9-nearest neighbors in UMAP Euclidean space were selected (Fig. 4). In the example shown in the main text (Additional examples in Supplementary Figs. 17–19), an image of a ~400 nm thick PbZr0.2Ti0.8O3/BaSrRuO3/SmScO3 film with dense c/a/c/a domain structures was selected. Using the VGG-16 model without symmetry awareness as a feature extractor resulted in 9-nearest neighbors, which at first glance appear to have similar structures. Upon closer inspection, it is observed that only 2 of the nearest neighbors are PbZr1−xTixO3 with c/a/c/a domain structures (Fig. 4 green-star), with the rest having a striped BiFeO3 domain structure (Fig. 4 red-x). Conversely, using the combined VGG-16 and ResNet-34-Symm-Aware model as a feature extractor, except one (Fig. 4 red-x) of the 9-nearest neighbors, had a similar PbZr1−xTixO3, c/a/c/a domain structure (Fig. 4 green-star). Furthermore, nearest neighbors 1 and 4 (Fig. 4 diamond) are images obtained from a similarly synthesized film by a different grower. This, and other examples, highlights the importance of including symmetry-awareness to improve image similarity projections of PFM images of ferroelectric domain structures.
Nine (9) next-nearest neighbors in UMAP-projected space near a random piezoresponse force microscopy image for the (a) VGG-16, and (b) ResNet-34-Symm-Aware model. The images determined to be semantically similar are marked with a green-star, and those deemed different are marked with a red x. These images were extracted by finding the nearest neighbors in Euclidian space from a selected image in the UMAP projection. The selected image is marked original. The nearest neighbors are sorted by increasing Euclidean distance from the original randomly selected image.
This technique becomes even more powerful when metadata filters are applied. Here, we filter the data to only those samples grown by Dr. Rujuan Xu. Owing to the narrower distribution of the data, latent space projections automatically cluster similar samples and experiments. For instance, ordered (Fig. 5 green-square) and frustrated (Fig. 5 orange-circle) (111)-oriented, and (001) oriented (Fig. 5 blue-triangle) PbZr1−xTixO3 are clustered close together. Furthermore, experiments such as box-in-a-box (Fig. 5, pink-plus), single-point (Fig. 5 yellow-diamond), and patterned ferroelastic switching (Fig. 5 green-x) are all identified. We once again note that these similarities are identified regardless of image magnification, rotation angle, etc. Furthermore, it is somewhat uncanny how associations between similar yet different classes are preserved. For instance, the ordered, frustrated, and switching studies on (111)-PbZr1−xTixO3 are neighbors. Similarly, all switching type studies are grouped. This demonstrates that sequential searching and projection of images based on metadata filters provides a pathway to discovering correlations in unstructured image databases.
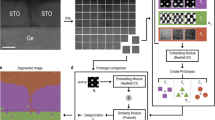
Since image similarity is, by definition, a fuzzy metric, the utility of this approach hinges on interactive human-in-the-loop exploration toward an evolving objective. To provide this interaction, we have created a platform for recursive image exploration of microstructural images. We built a Bokeh dashboard to conduct recursive searching of symmetry-aware projections. The front-facing dashboard has three panels an initial projection, a recursive projection, and a metadata viewer (Fig. 6a). Following neural-network-based feature extraction, UMAP projections of an entire database or a subset of filtered images are visualized. Using the Bokeh server, it is possible to pan and zoom to explore this projection.
Furthermore, it is possible to select specific images individually or in a region of interest (Fig. 6b). Once selected, the software will automatically compute a recursive UMAP projection of the selection. In the example shown, we selected an image from a set of studies where patterns of ferroelectric domains were written (Fig. 6c). The application selects all images within the selection and recomputes the UMAP projection. By narrowing the distribution in the feature space, subsequent UMAP two-dimensional projections refine the similarities identified. In this example (Fig. 6d–e), we show that the new projection captures detailed semantic similarities; in this case, all images with similar focus-ion beam milled regions. We provide additional examples of recursive searching (Supplementary Figs. 20–22). In this tool recursive projections can also be explored interactively. A tooltip can be configured within this module to display metadata associated with an image object (Fig. 6f). We provide a video highlighting (Supplemental Video 1) some of the interactive features of this software package. We have released the software package Recursive_Symmetry_Aware_Materials_Microstructure_Explorer under the open BSD-3-Clause License to democratize this tool for widespread use. In this package, we include trained VGG-16 and ResNet-34-Symm-Aware models. A user can supply their data in RGB format and use the interactive visualization toolkit. We provide an example of this using images scraped from google image search. More information is available at https://recursive-symmetry-aware-materials-microstructure-explorer.readthedocs.io/en/latest/.
Benchmarking
This interactive recursive searching and exploration has to be fast and scalable on conventional workstations to be viable. We conducted benchmarks on a Lambda Labs Workstation with 16 cores, 64 GB of RAM, and two NVIDIA 2080 RTX GPUs. Feature extraction from our entire dataset using both models on a single GPU progressed at ~150 iters/second. Since feature extraction is only required once and deep learning inference is embarrassingly parallel, this only needed 3 min to process the 25,133 DART-PFM images. We tested UMAP speed by conducting UMAP with \({{{\mathcal{O}}}}\left( {2^n} \right)\) from n = 4−19. For \({{{\mathcal{O}}}}\left( {2^{19}} \right)\) the UMAP projection took less than 300 s, and \({{{\mathcal{O}}}}\left( {2^{15}} \right)\) took less than 30 s (Supplementary Fig. 23). We note that it would be rare that more than 500,000 images would be searched without applying metadata filters that reduce the number of images being compared.
In summary, we demonstrate, develop, and democratize a method to interactively and recursively search large unstructured databases of microstructural images. We achieve this by generating a wallpaper group symmetry dataset and training a ResNet-34 model to predict the symmetry. Using this network, combined with a pretrained VGG-16 model, we extract features and create UMAP projections of 25,133 DART-PFM images. We demonstrate that we can enhance the semantic projections of image similarity by including symmetry awareness in the model. We show how recursive searching with the help of metadata filters can elucidate hidden correlations in large unstructured image databases. This toolkit is made openly available under non-restrictive open-source licenses. This work motivates increased sharing of open data and emphasis on data and metadata curation as a pathway to increase the scientific impact of costly experiments and accelerate scientific progress.
Methods
Wallpaper group symmetry dataset
The wallpaper group symmetry dataset was generated using a custom python script. First, this script scraped a random image from the ImageNet dataset. Then, a random swatch in the shape of the primitive unit-cell of variable size was selected. This unit-cell was rotated in euclidian space, and then the symmetry operators were applied to generate an image, which was cropped to a 256 × 256 image.
Training symmetry-aware feature extractor
A ResNet-34 model from Pytorch was downloaded and a classification layer of size 17 was added to the model. We trained our model using the 1,000,000 generated wallpaper group symmetry images with a 60-training/20-validation/20-testing split to predict the wallpaper group symmetry of the image. The model was trained for six (6) epochs on an NVIDIA Titan RTX GPU. The model was optimized using an ADAM optimizer with a learning rate of 3 × 10−5. The learning rate was scheduled using fit-one-cycle. Further details are provided in the Supplemental Materials.
Feature extraction of PFM images
PFM images were constructed into red-green-blue images by stacking the height, first-amplitude, and phase channels from the DART-PFM images. All images were normalized using a min-max scalar applied to each channel. Features were extracted by predicting the latent vector immediately preceding the classification layer in both the VGG-16 and ResNet-34-Symm-Aware models. Following feature extraction, a single-layer dense autoencoder was used to reduce the VGG-16 model from 4096 to 512 features such that it is balanced with the symmetry-aware features. We trained the model for 50 epochs using ADAM, achieving a final loss of 0.07. The manifold of these features was then learned using UMAP as described in the main text. The hyperparameters for UMAP were n_neighbors = 5, min_dist = 0.3, n_components = 2, metric = “correlation”. Further details regarding the computational pipeline and visualization methods are obtainable in the reproducible open-source code made openly available.
Data availability
Wallpaper group symmetry images used for training symmetry-aware feature extractors are available on Zenodo https://www.zenodo.org/deposit/4747082. We note that this dataset is nearly 100 GB21.
Code availability
All software is provided open-source under non-restrictive licenses. Source code and models can be obtained on GitHub https://github.com/m3-learning/Recursive_Symmetry_Aware_Materials_Microstructure_Explorer. Documentation is provided on via a readthedocs website located at https://recursive-symmetry-aware-materials-microstructure-explorer.readthedocs.io/en/latest/.
References
Karniadakis, G. E. et al. Physics-informed machine learning. Nat. Rev. Phys. 3, 422–440 (2021).
Locatello, F. et al. A sober look at the unsupervised learning of disentangled representations and their evaluation. Preprint at https://arxiv.org/abs/2010.14766 (2020).
He, K., Zhang, X., Ren, S. & Sun, J. Deep Residual Learning for Image Recognition. Preprint at https://arxiv.org/abs/1512.03385 (2015).
Weber, G. H., Ophus, C. & Ramakrishnan, L. Automated labeling of electron microscopy images using deep learning. In 2018 IEEE/ACM Machine Learning in HPC Environments (MLHPC) (IEEE, 2018). https://doi.org/10.1109/mlhpc.2018.8638633.
Horwath, J. P., Zakharov, D. N., Mégret, R. & Stach, E. A. Understanding important features of deep learning models for segmentation of high-resolution transmission electron microscopy images. NPJ Comp. Mater. 6, 1–9 (2020).
Groschner, C. K., Choi, C. & Scott, M. C. Machine learning pipeline for segmentation and defect identification from high-resolution transmission electron microscopy data. Microsc. Microanal. 1–8 https://doi.org/10.1017/S1431927621000386 (2021).
Agar, J. C. et al. Revealing ferroelectric switching character using deep recurrent neural networks. Nat. Commun. 10, 4809 (2019).
Holstad, T. S. et al. Application of a long short-term memory for deconvoluting conductance contributions at charged ferroelectric domain walls. NPJ Comp. Mater. 6, 1–7 (2020).
Kalinin, S. V. et al. Unsupervised learning of ferroic variants from atomically resolved STEM images. Preprint at https://arxiv.org/abs/2101.06892 (2021).
Alain, G. & Bengio, Y. What regularized auto-encoders learn from the data-generating distribution. J. Mach. Learn. Res. 15, 3563–3593 (2014).
Yosinski, J., Clune, J., Nguyen, A. & Fuchs, T. Understanding neural networks through deep visualization. Preprint at https://arxiv.org/abs/1506.06579 (2015)
sotabench: Image Classification on ImageNet Benchmark. https://sotabench.com/benchmarks/image-classification-on-imagenet.
Bengio, Y. Deep learning of representations for unsupervised and transfer learning. In Proceedings of ICML Workshop on Unsupervised and Transfer Learning 17–36 (2012).
Li, X. et al. A transfer learning approach for microstructure reconstruction and structure-property predictions. Sci. Rep. 8, 13461 (2018).
Jha, D. et al. Enhancing materials property prediction by leveraging computational and experimental data using deep transfer learning. Nat. Commun. 10, 5316 (2019).
Kitahara, A. R. & Holm, E. A. Microstructure cluster analysis with transfer learning and unsupervised learning. Inter. Mater. Manuf. Innov. 7, 148–156 (2018).
Hinton, G. Talk “What is wrong with convolutional neural nets?” https://www.youtube.com/watch?v=rTawFwUvnLE (2017).
Worrall, D. E., Garbin, S. J., Turmukhambetov, D. & Brostow, G. J. Harmonic networks: Deep translation and rotation equivariance. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 5028–5037 (openaccess.thecvf.com, 2017).
Thomas, N. et al. Tensor field networks: Rotation- and translation-equivariant neural networks for 3D point clouds. Preprint at https://arxiv.org/pdf/1802.08219.pdf (2018).
Rodriguez, B. J., Callahan, C., Kalinin, S. V. & Proksch, R. Dual-frequency resonance-tracking atomic force microscopy. Nanotechnology 18, 475504 (2007).
Guo, Y. & Agar, J. Wallpaper group symmetry dataset based on imageNet. https://doi.org/10.5281/ZENODO.4747082 (2021).
Neumayer, S. M. et al. Piezoresponse amplitude and phase quantified for electromechanical characterization. J. Appl. Phys. 128, 171105 (2020).
Breckenfeld, E., Shah, A. B. & Martin, L. W. Strain evolution in non-stoichiometric heteroepitaxial thin-film perovskites. J. Mater. Chem. C. Mater. Opt. Electron. Devices 1, 8052 (2013).
Karthik, J., Mangalam, R. V. K., Agar, J. C. & Martin, L. W. Large built-in electric fields due to flexoelectricity in compositionally graded ferroelectric thin films. Phys. Rev. B Condens. Matter Mater. Phys. 87, 024111 (2013).
Fletcher, P. C., Mangalam, V. K. R., Martin, L. W. & King, W. P. Field emission from nanometer-scale tips of crystalline PbZrxTi1−xO3. J. Vac. Sci. Technol. B Nanotechnol. Microelectron. 31, 021805 (2013).
Mangalam, R. V. K., Karthik, J., Damodaran, A. R., Agar, J. C. & Martin, L. W. Unexpected crystal and domain structures and properties in compositionally graded PbZr(1−x)Ti(x)O3 thin films. Adv. Mater. 25, 1761–1767 (2013).
Baeumer, C., Rogers, S. P., Xu, R., Martin, L. W. & Shim, M. Tunable carrier type and density in graphene/PbZr0.2Ti0.8O3 hybrid structures through ferroelectric switching. Nano Lett. 13, 1693–1698 (2013).
Breckenfeld, E. et al. Effect of growth induced (non)stoichiometry on interfacial conductance in LaAlO3/SrTiO3. Phys. Rev. Lett. 110, 196804 (2013).
Fletcher, P. C., Mangalam, R. V. K., Martin, L. W. & King, W. P. Pyroelectric electron emission from a thin film of PbZrxTi1−xO3 on a nanofabricated cathode. In 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII) (IEEE, 2013). https://doi.org/10.1109/transducers.2013.6626880.
Lee, S., Apgar, B. A. & Martin, L. W. Strong visible-light absorption and hot-carrier injection in TiO2/SrRuO3Heterostructures. Adv. Energy Mater. 3, 1084–1090 (2013).
Breckenfeld, E., Wilson, R. B. & Martin, L. W. Effect of growth induced (non)stoichiometry on the thermal conductivity, permittivity, and dielectric loss of LaAlO3 films. Appl. Phys. Lett. 103, 082901 (2013).
Huijben, M. et al. Ultrathin limit of exchange bias coupling at oxide multiferroic/ferromagnetic interfaces. Adv. Mater. 25, 4739–4745 (2013).
Apgar, B. A., Lee, S., Schroeder, L. E. & Martin, L. W. Enhanced photoelectrochemical activity in all-oxide heterojunction devices based on correlated “metallic” oxides. Adv. Mater. 25, 6201–6206 (2013).
Rondinelli, J. M. et al. Accelerating functional materials discovery Insights from geological sciences, data-driven approaches, and computational advances. Am. Ceram. Soc. Bull. 92, 14–22 (2013).
Mangalam, R. V. K., Agar, J. C., Damodaran, A. R., Karthik, J. & Martin, L. W. Improved pyroelectric figures of merit in compositionally graded PbZr1−xTixO3 thin films. ACS Appl. Mater. Interfaces 5, 13235–13241 (2013).
Xu, R. et al. Ferroelectric polarization reversal via successive ferroelastic transitions. Nat. Mater. 14, 79–86 (2015).
Martin, L. W., Chu, Y.-H. & Ramesh, R. in Emerging Non-Volatile Memories (eds Hong, Seungbum, Auciello, Orlando, Wouters, Dirk) 103–166 (Springer US, 2014).
Xu, R., Karthik, J., Damodaran, A. R. & Martin, L. W. Stationary domain wall contribution to enhanced ferroelectric susceptibility. Nat. Commun. 5, 3120 (2014).
Spurgeon, S. R. et al. Thickness-dependent crossover from charge- to strain-mediated magnetoelectric coupling in ferromagnetic/piezoelectric oxide heterostructures. ACS Nano 8, 894–903 (2014).
Apgar, B. A. & Martin, L. W. Understanding the competition between epitaxial strain and thermodynamics in TiO2: structural, morphological, and property evolution. Cryst. Growth Des. 14, 1981–1988 (2014).
Gleason, S. L. et al. Magnon spectra and strong spin-lattice coupling in magnetically frustrated MnB2O4(B = Mn,V): Inelastic light-scattering studies. Phys. Rev. B Condens. Matter Mater. Phys. 89, 134402 (2014).
Chen, Z. H., Damodaran, A. R., Xu, R., Lee, S. & Martin, L. W. Effect of “symmetry mismatch” on the domain structure of rhombohedral BiFeO3 thin films. Appl. Phys. Lett. 104, 182908 (2014).
Kozina, M. et al. Measurement of transient atomic displacements in thin films with picosecond and femtometer resolution. Struct. Dyn. 1, 034301 (2014).
Brinks, P. et al. Enhanced thermoelectric power factor of NaxCoO2 Thin films by structural engineering. Adv. Energy Mater. 4, 1301927 (2014).
Lee, J. C. T., Damodaran, A. R., Ramesh, R., Martin, L. W. & Abbamonte, P. X-ray diffraction studies of stripelike ferroelectric domains in thin films of BiFeO3. Phys. Rev. B Condens. Matter Mater. Phys. 89, 214104 (2014).
Winkler, C. R. et al. Real-time observation of local strain effects on nonvolatile ferroelectric memory storage mechanisms. Nano Lett. 14, 3617–3622 (2014).
Zhang, J., Xu, R., Damodaran, A. R., Chen, Z.-H. & Martin, L. W. Understanding order in compositionally graded ferroelectrics: Flexoelectricity, gradient, and depolarization field effects. Phys. Rev. B Condens. Matter Mater. Phys. 89, 224101 (2014).
Agar, J. C. et al. Tuning susceptibility via misfit strain in relaxed morphotropic phase boundary PbZr1−xTixO3 Epitaxial thin films. Adv. Mater. Interfaces 1, 1400098 (2014).
Kesim, M. T., Zhang, J., Alpay, S. P. & Martin, L. W. Enhanced electrocaloric and pyroelectric response from ferroelectric multilayers. Appl. Phys. Lett. 105, 052901 (2014).
Dagdeviren, C. et al. Conformable amplified lead zirconate titanate sensors with enhanced piezoelectric response for cutaneous pressure monitoring. Nat. Commun. 5, 4496 (2014).
Damodaran, A. R., Breckenfeld, E., Chen, Z., Lee, S. & Martin, L. W. Enhancement of ferroelectric Curie temperature in BaTiO3 films via strain-induced defect dipole alignment. Adv. Mater. 26, 6341–6347 (2014).
Breckenfeld, E., Bronn, N., Mason, N. & Martin, L. W. Tunability of conduction at the LaAlO3/SrTiO3 heterointerface: Thickness and compositional studies. Appl. Phys. Lett. 105, 121610 (2014).
Tong, T., Karthik, J., Mangalam, R. V. K., Martin, L. W. & Cahill, D. G. Reduction of the electrocaloric entropy change of ferroelectric PbZr1−xTixO3 epitaxial layers due to an elastocaloric effect. Phys. Rev. B Condens. Matter Mater. Phys. 90, 094116 (2014).
Tong, T., Karthik, J., Martin, L. W. & Cahill, D. G. Secondary effects in wide frequency range measurements of the pyroelectric coefficient of Ba0.6Sr0.4TiO3 and PbZr0.2Ti0.8O3 epitaxial layers. Phys. Rev. B Condens. Matter Mater. Phys. 90, 094116 (2014).
Bhatia, B., Damodaran, A. R., Cho, H., Martin, L. W. & King, W. P. High-frequency thermal-electrical cycles for pyroelectric energy conversion. J. Appl. Phys. 116, 194509 (2014).
Breckenfeld, E., Chen, Z., Damodaran, A. R. & Martin, L. W. Effects of nonequilibrium growth, nonstoichiometry, and film orientation on the metal-to-insulator transition in NdNiO3 thin films. ACS Appl. Mater. Interfaces 6, 22436–22444 (2014).
Haasch, R. T., Breckenfeld, E. & Martin, L. W. Single crystal perovskites analyzed using X-ray photoelectron spectroscopy: 1. SrTiO3 (001). Surf. Sci. Spectra 21, 87–94 (2014).
Haasch, R. T., Breckenfeld, E. & Martin, L. W. Single crystal perovskites analyzed using X-ray photoelectron spectroscopy: 2. YAlO3 (110). Surf. Sci. Spectra 21, 95–102 (2014).
Haasch, R. T., Breckenfeld, E. & Martin, L. W. Single crystal perovskites analyzed using X-ray photoelectron spectroscopy: 3. LaAlO3 (001). Surf. Sci. Spectra 21, 103–111 (2014).
Haasch, R. T., Breckenfeld, E. & Martin, L. W. Single crystal perovskites analyzed using X-ray photoelectron spectroscopy: 4. (LaAlO3)0.3(Sr2TaAlO6)0.7 (001). Surf. Sci. Spectra 21, 112–121 (2014).
Haasch, R. T., Breckenfeld, E. & Martin, L. W. Single crystal perovskites analyzed using X-ray photoelectron spectroscopy: 5. NdGaO3 (110). Surf. Sci. Spectra 21, 122–130 (2014).
Haasch, R. T., Breckenfeld, E. & Martin, L. W. An introduction to single crystal perovskites and single crystal rare-earth scandate perovskites analyzed using X-ray photoelectron spectroscopy. Surf. Sci. Spectra 21, 84–86 (2014).
Haasch, R. T., Martin, L. W. & Breckenfeld, E. Single crystal rare-earth scandate perovskites analyzed using X-ray photoelectron spectroscopy: 1. PrScO3 (110). Surf. Sci. Spectra 21, 131–139 (2014).
Haasch, R. T., Martin, L. W. & Breckenfeld, E. Single crystal rare-earth scandate perovskites analyzed using X-ray photoelectron spectroscopy: 2. NdScO3 (110). Surf. Sci. Spectra 21, 140–148 (2014).
Haasch, R. T., Martin, L. W. & Breckenfeld, E. Single crystal rare-earth scandate perovskites analyzed using X-ray photoelectron spectroscopy: 3. GdScO3 (110). Surf. Sci. Spectra 21, 149–156 (2014).
Haasch, R. T., Martin, L. W. & Breckenfeld, E. Single crystal rare-earth scandate perovskites analyzed using X-ray photoelectron spectroscopy: 4. TbScO3 (110). Surf. Sci. Spectra 21, 157–164 (2014).
Haasch, R. T., Martin, L. W. & Breckenfeld, E. Single crystal rare-earth scandate perovskites analyzed using X-ray photoelectron spectroscopy: 5. DyScO3 (110). Surf. Sci. Spectra 21, 165–172 (2014).
Moyer, J. A., Mangalam, R. V. K. & Martin, L. W. in Epitaxial Growth of Complex Metal Oxides (eds Koster, G., Huijben, M., & Rijnders, G.) 129–172 (Elsevier, 2015).
Baeumer, C. et al. Ferroelectrically driven spatial carrier density modulation in graphene. Nat. Commun. 6, 6136 (2015).
Lee, S. et al. A novel, layered phase in Ti-rich SrTiO3 epitaxial thin films. Adv. Mater. 27, 861–868 (2015).
Moyer, J. A., Lee, S., Schiffer, P. & Martin, L. W. Magnetically disordered phase in epitaxial iron-deficient Fe3O4 thin films. Phys. Rev. B Condens. Matter Mater. Phys. 91, 064413 (2015).
Comes, R. B. et al. Visible light carrier generation in co-doped epitaxial titanate films. Appl. Phys. Lett. 106, 092901 (2015).
Wilson, R. B., Apgar, B. A., Hsieh, W.-P., Martin, L. W. & Cahill, D. G. Thermal conductance of strongly bonded metal-oxide interfaces. Phys. Rev. B Condens. Matter Mater. Phys. 91, 115414 (2015).
Spurgeon, S. R. et al. Polarization screening-induced magnetic phase gradients at complex oxide interfaces. Nat. Commun. 6, 6735 (2015).
Xu, R., Zhang, J., Chen, Z. & Martin, L. W. Orientation-dependent structural phase diagrams and dielectric properties of PbZr1−xTixO3 polydomain thin films. Phys. Rev. B Condens. Matter Mater. Phys. 91, 114106 (2015).
Gaponenko, I., Tückmantel, P., Karthik, J., Martin, L. W. & Paruch, P. Towards reversible control of domain wall conduction in Pb(Zr0.2Ti0.8)O3 thin films. Appl. Phys. Lett. 106, 162902 (2015).
Moyer, J. A., Gao, R., Schiffer, P. & Martin, L. W. Epitaxial growth of highly-crystalline spinel ferrite thin films on perovskite substrates for all-oxide devices. Sci. Rep. 5, 10363 (2015).
Zhang, H.-T., Dedon, L. R., Martin, L. W. & Engel-Herbert, R. Self-regulated growth of LaVO3 thin films by hybrid molecular beam epitaxy. Appl. Phys. Lett. 106, 233102 (2015).
Agar, J. C. et al. Complex evolution of built-in potential in compositionally-graded PbZr(1−x)Ti(x)O3 thin films. ACS Nano 9, 7332–7342 (2015).
Chen, Z. et al. 180° ferroelectric stripe nanodomains in BiFeO3 thin films. Nano Lett. 15, 6506–6513 (2015).
Chen, F. et al. Ultrafast terahertz gating of the polarization and giant nonlinear optical response in BiFeO3 thin films. Adv. Mater. 27, 6371–6375 (2015).
Zhang, J., Agar, J. C. & Martin, L. W. Structural phase diagram and pyroelectric properties of free-standing ferroelectric/non-ferroelectric multilayer heterostructures. J. Appl. Phys. 118, 244101 (2015).
Islam, M. A. et al. Surface chemically switchable ultraviolet luminescence from interfacial two-dimensional electron gas. Nano Lett. 16, 681–687 (2016).
Yadav, A. K. et al. Observation of polar vortices in oxide superlattices. Nature 530, 198–201 (2016).
Jablonski, M. L. et al. Asymmetric response of ferroelastic domain-wall motion under applied bias. ACS Appl. Mater. Interfaces 8, 2935–2941 (2016).
Agar, J. C. et al. Highly mobile ferroelastic domain walls in compositionally graded ferroelectric thin films. Nat. Mater. 15, 549–556 (2016).
Hinnefeld, J. H. et al. Single gate p-n junctions in graphene-ferroelectric devices. Appl. Phys. Lett. 108, 203109 (2016).
Damodaran, A. R. et al. New modalities of strain-control of ferroelectric thin films. J. Phys. Condens. Matter 28, 263001 (2016).
Pandya, S. et al. Strain-induced growth instability and nanoscale surface patterning in perovskite thin films. Sci. Rep. 6, 26075 (2016).
Tselev, A. et al. Microwave a.c. conductivity of domain walls in ferroelectric thin films. Nat. Commun. 7, 11630 (2016).
Gao, R. et al. Interfacial octahedral rotation mismatch control of the symmetry and properties of SrRuO3. ACS Appl. Mater. Interfaces 8, 14871–14878 (2016).
Dedon, L. R. et al. Nonstoichiometry, structure, and properties of BiFeO3 films. Chem. Mater. 28, 5952–5961 (2016).
Agar, J. C. et al. Frontiers in strain-engineered multifunctional ferroic materials. MRS Commun. 6, 151–166 (2016).
Brahlek, M. et al. Mapping growth windows in quaternary perovskite oxide systems by hybrid molecular beam epitaxy. Appl. Phys. Lett. 109, 101903 (2016).
Bhatia, B. et al. High power density pyroelectric energy conversion in nanometer-thick BaTiO3 films. Nanoscale Microscale Thermophys. Eng. 20, 137–146 (2016).
Lu, H. et al. Nanodomain engineering in ferroelectric capacitors with graphene electrodes. Nano Lett. 16, 6460–6466 (2016).
Martin, L. W. & Rappe, A. M. Thin-film ferroelectric materials and their applications. Nat. Rev. Mater. 2, 16087 (2017).
Chen, F. et al. Ultrafast terahertz-field-driven ionic response in ferroelectric BaTiO3. Phys. Rev. B. 94, 180104 (2016).
Chen, Z. et al. Self-assembled, nanostructured, tunable metamaterials via spinodal decomposition. ACS Nano 10, 10237–10244 (2016).
Saremi, S. et al. Enhanced electrical resistivity and properties via ion bombardment of ferroelectric thin films. Adv. Mater. 28, 10750–10756 (2016).
Chen, Y. et al. Pressurizing field-effect transistors of few-layer MoS2 in a Diamond anvil cell. Nano Lett. 17, 194–199 (2017).
Pandya, S. et al. Direct measurement of pyroelectric and electrocaloric effects in thin films. Phys. Rev. Appl. 7, 034025 (2017).
Rogers, S. P., Xu, R., Pandya, S., Martin, L. W. & Shim, M. Slow conductance relaxation in graphene–ferroelectric field-effect transistors. J. Phys. Chem. C. Nanomater. Interfaces 121, 7542–7548 (2017).
Hong, Z. et al. Stability of polar vortex lattice in ferroelectric superlattices. Nano Lett. 17, 2246–2252 (2017).
Damodaran, A. R. et al. Large polarization gradients and temperature-stable responses in compositionally-graded ferroelectrics. Nat. Commun. 8, 14961 (2017).
Angsten, T., Martin, L. W. & Asta, M. Orientation-dependent properties of epitaxially strained perovskite oxide thin films: Insights from first-principles calculations. Phys. Rev. B. 95, 174110 (2017).
Gao, R. et al. Ferroelectricity in Pb1+δZrO3 thin films. Chem. Mater. 29, 6544–6551 (2017).
Damodaran, A. R. et al. Three‐state ferroelastic switching and large electromechanical responses in PbTiO3 thin films. Adv. Mater. 29, 1702069 (2017).
Damodaran, A. R. et al. Phase coexistence and electric-field control of toroidal order in oxide superlattices. Nat. Mater. 16, 1003–1009 (2017).
Chen, Z. et al. Electron accumulation and emergent magnetism in LaMnO3/SrTiO3 heterostructures. Phys. Rev. Lett. 119, 156801 (2017).
Pandya, S. & Martin, L. W. Epitaxy on polycrystalline substrates. Science 358, 587–588 (2017).
Li, Q. et al. Quantification of flexoelectricity in PbTiO3/SrTiO3 superlattice polar vortices using machine learning and phase-field modeling. Nat. Commun. 8, 1468 (2017).
Zhu, Y. et al. Structural imaging of nanoscale phonon transport in ferroelectrics excited by metamaterial-enhanced terahertz fields. Phys. Rev. Mater 1, 060601 (2017).
Khan, A. I. et al. Differential voltage amplification from ferroelectric negative capacitance. Appl. Phys. Lett. 111, 253501 (2017).
Saremi, S., Dasgupta, A., Gao, R. & Martin, L. W. New facets for the role of defects in ceramics. Amer. Cer. Soc. Bull. 97, 16 (2018).
Dasgupta, A. et al. Nonstoichiometry, structure, and properties of Ba1−xTiOy thin films. J. Mater. Chem. C. Mater. Opt. Electron. Devices 6, 10751–10759 (2018).
Shafer, P. et al. Emergent chirality in the electric polarization texture of titanate superlattices. Proc. Natl Acad. Sci. USA 115, 915–920 (2018).
Ievlev, A. V. et al. Chemical phenomena of atomic force microscopy scanning. Anal. Chem. 90, 3475–3481 (2018).
Saremi, S. et al. Electronic transport and ferroelectric switching in ion-bombarded, defect-engineered BiFeO3 thin films. Adv. Mater. Interfaces 5, 1700991 (2018).
Ievlev, A. V. et al. Subtractive fabrication of ferroelectric thin films with precisely controlled thickness. Nanotechnology 29, 155302 (2018).
Xu, R. et al. Reducing coercive-field scaling in ferroelectric thin films via orientation control. ACS Nano 12, 4736–4743 (2018).
Dedon, L. R. et al. Strain-driven nanoscale phase competition near the antipolar–nonpolar phase boundary in Bi0.7La0.3FeO3 thin films. ACS Appl. Mater. Interfaces 10, 14914–14921 (2018).
Pandya, S. et al. Pyroelectric energy conversion with large energy and power density in relaxor ferroelectric thin films. Nat. Mater. 17, 432–438 (2018).
Zheng, L. M. et al. Ambipolar ferromagnetism by electrostatic doping of a manganite. Nat. Commun. 9, 1897 (2018).
Xiao, J. et al. Intrinsic two-dimensional ferroelectricity with dipole locking. Phys. Rev. Lett. 120, 227601 (2018).
Agar, J. C. et al. Machine detection of enhanced electromechanical energy conversion in PbZr0.2Ti0.8O3 Thin films. Adv. Mater. 30, 1800701 (2018).
Nelson, C. T. et al. Phase coexistence of ferroelectric vortices and classical a1/a2 domains in PbTiO3/SrTiO3 superlattices. Microsc. Microanal. 24, 1638–1639 (2018).
Gu, Z. et al. Resonant domain-wall-enhanced tunable microwave ferroelectrics. Nature 560, 622–627 (2018).
Angsten, T., Martin, L. W. & Asta, M. Electronic and polar properties of vanadate compounds stabilized by epitaxial strain. Chem. Mater. 30, 5870–5877 (2018).
Saremi, S. et al. Local control of defects and switching properties in ferroelectric thin films. Phys. Rev. Mater. 2, 084414 (2018).
Lim, J. S. et al. Ultrafast collective oxygen-vacancy flow in Ca-doped BiFeO3. NPG Asia Mater. 10, 943–955 (2018).
Chen, Z. et al. Complex strain evolution of polar and magnetic order in multiferroic BiFeO3 thin films. Nat. Commun. 9, 3764 (2018).
Zhang, S. et al. Band-gap reduction in (BiCrO3)m/(BiFeO3)n superlattices: Designing low-band-gap ferroelectrics. Phys. Rev. Appl. 10, 044004 (2018).
Ievlev, A. V. et al. Nanoscale electrochemical phenomena of polarization switching in ferroelectrics. ACS Appl. Mater. Interfaces 10, 38217–38222 (2018).
Wang, Z. et al. Experimental demonstration of ferroelectric spiking neurons for unsupervised clustering. in 2018 IEEE International Electron Devices Meeting (IEDM) (IEEE, 2018). https://doi.org/10.1109/iedm.2018.8614586.
Pandya, S., Velarde, G., Zhang, L. & Martin, L. W. Pyroelectric and electrocaloric effects in ferroelectric silicon-doped hafnium oxide thin films. Phys. Rev. Mater. 2, 124405 (2018).
Kaspar, T. C. et al. Electronic structure and band alignment of LaMnO3/SrTiO3 polar/nonpolar heterojunctions. Adv. Mater. Interfaces 6, 1801428 (2019).
Shetty, S. et al. Relaxor behavior in ordered lead magnesium niobate (PbMg1/3Nb2/3O3) thin films. Adv. Funct. Mater. 29, 1804258 (2019).
Pandya, S. et al. Understanding the role of ferroelastic domains on the pyroelectric and electrocaloric effects in ferroelectric thin films. Adv. Mater. 31, e1803312 (2019).
Takamura, Y., Leonard, K., Luo, A., Martin, L. W. & Matsumoto, H. Platinum nanoparticle induced nanoionic effects on electrical conduction in strontium cerate and zirconate. J. Solid State Electrochem. 23, 953–963 (2019).
Xu, R. et al. Kinetic control of tunable multi-state switching in ferroelectric thin films. Nat. Commun. 10, 1282 (2019).
Stoica, V. A. et al. Optical creation of a supercrystal with three-dimensional nanoscale periodicity. Nat. Mater. 18, 377–383 (2019).
Das, S. et al. Observation of room-temperature polar skyrmions. Nature 568, 368–372 (2019).
Kim, J. et al. Epitaxial strain control of relaxor ferroelectric phase evolution. Adv. Mater. 31, e1901060 (2019).
Pandya, S. et al. New approach to waste-heat energy harvesting: pyroelectric energy conversion. NPG Asia Mater. 11, 26 (2019).
Nelson, C. T. et al. In situ electric field manipulation of ferroelectric vortices. Microsc. Microanal. 25, 1844–1845 (2019).
Meng, D. et al. Enhanced spontaneous polarization in double perovskite Bi2FeCrO6 films. J. Am. Ceram. Soc. 102, 5234–5242 (2019).
Hsu, S.-L. et al. Emergence of the vortex state in confined ferroelectric heterostructures. Adv. Mater. 31, e1901014 (2019).
Lu, X. et al. Mechanical-force-induced non-local collective ferroelastic switching in epitaxial lead-titanate thin films. Nat. Commun. 10, 3951 (2019).
Velarde, G. et al. Quantifying intrinsic, extrinsic, dielectric, and secondary pyroelectric responses in PbZr1-xTixO3 thin films. ACS Appl. Mater. Interfaces 11, 35146–35154 (2019).
Mei, A. B. et al. Ferroelectric properties of ion-irradiated bismuth ferrite layers grown via molecular-beam epitaxy. APL Mater. 7, 111101 (2019).
Zhang, L. et al. Enhanced pyroelectric properties of Bi1−xLaxFeO3 thin films. APL Mater. 7, 111111 (2019).
Saremi, S., Kim, J., Ghosh, A., Meyers, D. & Martin, L. W. Defect-induced (dis)order in relaxor ferroelectric thin films. Phys. Rev. Lett. 123, 207602 (2019).
Guzelturk, B. et al. Light-induced currents at domain walls in multiferroic BiFeO3. Nano Lett. 20, 145–151 (2020).
Chen, S. et al. Versatile and highly efficient controls of reversible topotactic metal–insulator transitions through proton intercalation. Adv. Funct. Mater. 29, 1907072 (2019).
Gao, R. et al. Designing optimal perovskite structure for high ionic conduction. Adv. Mater. 32, e1905178 (2020).
Neumayer, S. M. et al. To switch or not to switch – a machine learning approach for ferroelectricity. Nanoscale Adv. 2, 2063–2072 (2020).
Wehmeier, L. et al. Phonon-induced near-field resonances in multiferroic BiFeO3 thin films at infrared and THz wavelengths. Appl. Phys. Lett. 116, 071103 (2020).
Taz, H. et al. Integration of amorphous ferromagnetic oxides with multiferroic materials for room temperature magnetoelectric spintronics. Sci. Rep. 10, 3583 (2020).
Lupi, E. et al. Large polarization and susceptibilities in artificial morphotropic phase boundary PbZr1-xTixO3 superlattices. Adv. Electron Mater. 6, 1901395 (2020).
Fernandez, A., Kim, J., Meyers, D., Saremi, S. & Martin, L. W. Finite-size effects in lead scandium tantalate relaxor thin films. Phys. Rev. B. 101, 094102 (2020).
Elangovan, H. et al. Giant superelastic piezoelectricity in flexible ferroelectric BaTiO3 membranes. ACS Nano 14, 5053–5060 (2020).
Barrozo, P. et al. Defect-enhanced polarization switching in the improper ferroelectric LuFeO3. Adv. Mater. 32, e2000508 (2020).
Huang, Y.-L. et al. Manipulating magnetoelectric energy landscape in multiferroics. Nat. Commun. 11, 2836 (2020).
Prasad, B. et al. Ultralow voltage manipulation of ferromagnetism. Adv. Mater. 32, e2001943 (2020).
Kim, J. et al. Ultrahigh capacitive energy density in ion-bombarded relaxor ferroelectric films. Science 369, 81–84 (2020).
Parsonnet, E. et al. Toward intrinsic ferroelectric switching in multiferroic BiFeO3. Phys. Rev. Lett. 125, 067601 (2020).
Acharya, M. et al. Searching for new ferroelectric materials using high-throughput databases: An experimental perspective on BiAlO3 and BiInO3. Chem. Mater. 32, 7274–7283 (2020).
Chen, S. et al. Recent progress on topological structures in ferroic thin films and heterostructures. Adv. Mater. 33, e2000857 (2021).
Chen, A. et al. Couplings of polarization with interfacial deep trap and Schottky interface controlled ferroelectric memristive switching. Adv. Funct. Mater. 30, 2000664 (2020).
Pesquera, D. et al. Beyond substrates: Strain engineering of ferroelectric membranes. Adv. Mater. 32, e2003780 (2020).
Das, S. et al. Local negative permittivity and topological phase transition in polar skyrmions. Nat. Mater. 20, 194–201 (2021).
Shetty, S., Kim, J., Martin, L. W. & Trolier-McKinstry, S. Non-linearity in engineered lead magnesium niobate (PbMg1/3Nb2/3O3) thin films. J. Appl. Phys. 128, 194102 (2020).
Kim, J. et al. Beyond expectation: Advanced materials design, synthesis, and processing to enable novel ferroelectric properties and applications. MRS Adv. 5, 3453–3472 (2020).
Weymann, C. et al. Full control of polarization in ferroelectric thin films using growth temperature to modulate defects. Adv. Electron. Mater. 6, 2000852 (2020).
Das, S. et al. A new era in ferroelectrics. APL Mater. 8, 120902 (2020).
Nguyen, K. X. et al. Transferring orbital angular momentum to an electron beam reveals toroidal and chiral order. Preprint at https://arxiv.org/abs/2012.04134 (2020).
Belhadi, J. et al. Growth mode and strain effect on relaxor ferroelectric domains in epitaxial 0.67Pb(Mg1/3Nb2/3)O3–0.33PbTiO3/SrRuO3 heterostructures. RSC Adv. 11, 1222–1232 (2021).
Velarde, G., Pandya, S., Karthik, J., Pesquera, D. & Martin, L. W. Pyroelectric thin films—Past, present, and future. APL Mater. 9, 010702 (2021).
Meier, D. et al. Translation domains in multiferroics. Phase Transit. 86, 33–52 (2013).
Seidel, J. et al. Domain wall functionality in BiFeO3. Phase Transit. 86, 53–66 (2013).
Wu, S. M. et al. Full electric control of exchange bias. Phys. Rev. Lett. 110, 067202 (2013).
Biswas, A. et al. Selective A- or B-site single termination on surfaces of layered oxide SrLaAlO4. Appl. Phys. Lett. 102, 051603 (2013).
Rayan Serrao, C. et al. Epitaxy-distorted spin-orbit Mott insulator in Sr2IrO4 thin films. Phys. Rev. B Condens. Matter Mater. Phys. 87, 085121 (2013).
Fina, I. et al. Anisotropic magnetoresistance in an antiferromagnetic semiconductor. Nat. Commun. 5, 1–7 (2014).
Lubk, A. et al. Electromechanical coupling among edge dislocations, domain walls, and nanodomains in BiFeO3 revealed by unit-cell-wise strain and polarization maps. Nano Lett. 13, 1410–1415 (2013).
Liu, J. et al. Tuning the electronic properties of Jeff = 1/2 correlated semimetal in epitaxial perovskite SrLrO3. Preprint at https://arxiv.org/abs/1305.1732 (2013).
Guo, R. et al. Non-volatile memory based on the ferroelectric photovoltaic effect. Nat. Commun. 4, 1990 (2013).
Polking, M. J. et al. Controlling localized surface plasmon resonances in GeTe nanoparticles using an amorphous-to-crystalline phase transition. Phys. Rev. Lett. 111, 037401 (2013).
Kim, Y.-M. et al. Atomic structure of surface dielectric dead layer in BiFeO3 thin film. Microsc. Microanal. 19, 1928–1929 (2013).
Gao, P. et al. An in situ TEM study of ferroelastic domain mobility. Microsc. Microanal. 19, 1500–1501 (2013).
Becher, C. et al. Functional ferroic heterostructures with tunable integral symmetry. Nat. Commun. 5, 1–6 (2014).
Chu, J.-H. et al. Possible scale invariant linear magnetoresistance in pyrochlore iridates Bi2Ir2O7. N. J. Phys. 21, 113041 (2019).
Seidel, J. & Ramesh, R. in Functional Metal Oxides (eds Satishchandra B. O., Thirumalai V. V., & Blamire, M. G) 245–265 (Wiley-VCH Verlag GmbH & Co. KGaA, 2013).
Yi, D. et al. Tuning the competition between ferromagnetism and antiferromagnetism in a half-doped manganite through magnetoelectric coupling. Phys. Rev. Lett. 111, 127601 (2013).
Zhang, J. et al. A nanoscale shape memory oxide. Nat. Commun. 4, 2768 (2013).
Kaz, D. M. et al. Bright cathodoluminescent thin films for scanning nano-optical excitation and imaging. ACS Nano 7, 10397–10404 (2013).
Ravichandran, J. et al. Ambipolar transport and magneto-resistance crossover in a Mott insulator, Sr2IrO4. J. Phys. Condens. Matter 28, 505304 (2016).
Ramesh, R., Loganathan, R., Menon, S. S., Baskar, K. & Singh, S. Controlled nucleation and growth of nanostructures by employing surface modified GaN based layers/heterostructures as bottom layer. RSC Adv. 4, 7112 (2014).
Seidel, J. & Ramesh, R. In Mesoscopic Phenomena in Multifunctional Materials (eds Saxena, Avadh, Planes, Antoni) 1–21 (Springer Berlin Heidelberg, 2014).
Schlom, D. G. et al. Elastic strain engineering of ferroic oxides. MRS Bull. 39, 118–130 (2014).
Ravichandran, J. et al. Crossover from incoherent to coherent phonon scattering in epitaxial oxide superlattices. Nat. Mater. 13, 168–172 (2014).
Pravarthana, D. et al. BiFeO3/La0.7Sr0.3MnO3 heterostructures deposited on spark plasma sintered LaAlO3 substrates. Appl. Phys. Lett. 104, 082914 (2014).
Ramesh, R. Electric field control of ferromagnetism using multi-ferroics: the bismuth ferrite story. Philos. Trans. A Math. Phys. Eng. Sci. 372, 20120437 (2014).
Ramesh, R. Electric field control of magnetism using multiferroic bismuth ferrite. J. Jpn. Soc. Powder Powder Metall. 61, S19–S24 (2014).
Marti, X. et al. Room-temperature antiferromagnetic memory resistor. Nat. Mater. 13, 367–374 (2014).
Gao, P. et al. Ferroelastic domain switching dynamics under electrical and mechanical excitations. Nat. Commun. 5, 3801 (2014).
Wang, S. et al. Atomic and electronic structures of lattice mismatched Cu2O/TiO2 interfaces. Appl. Phys. Lett. 104, 211605 (2014).
Liu, H.-J., Liang, W.-I., Chu, Y.-H., Zheng, H. & Ramesh, R. Self-assembled vertical heteroepitaxial nanostructures: from growth to functionalities. MRS Commun. 4, 31–44 (2014).
Schaab, J. et al. Imaging and characterization of conducting ferroelectric domain walls by photoemission electron microscopy. Appl. Phys. Lett. 104, 232904 (2014).
Heron, J. T., Schlom, D. G. & Ramesh, R. Electric field control of magnetism using BiFeO3-based heterostructures. Appl. Phys. Rev. 1, 021303 (2014).
Unguris, J. et al. Simultaneous imaging of the ferromagnetic and ferroelectric structure in multiferroic heterostructures. APL Mater. 2, 076109 (2014).
Seidel, J. et al. Electronic properties of isosymmetric phase boundaries in highly strained Ca-Doped BiFeO3. Adv. Mater. 26, 4376–4380 (2014).
Becher, C. et al. Functional ferroic heterostructures with tunable integral symmetry. Nat. Commun. 5, 4295 (2014).
Singh, S. et al. Induced magnetization in La0.7Sr0.3MnO3/BiFeO3 superlattices. Phys. Rev. Lett. 113, 047204 (2014).
Fina, I. et al. Anisotropic magnetoresistance in an antiferromagnetic semiconductor. Nat. Commun. 5, 4671 (2014).
Gao, W. et al. Room-temperature negative capacitance in a ferroelectric-dielectric superlattice heterostructure. Nano Lett. 14, 5814–5819 (2014).
Kumar, M. H. et al. Lead-free halide perovskite solar cells with high photocurrents realized through vacancy modulation. Adv. Mater. 26, 7122–7127 (2014).
Heron, J. T. et al. Deterministic switching of ferromagnetism at room temperature using an electric field. Nature 516, 370–373 (2014).
Domingo, N. et al. Giant reversible nanoscale piezoresistance at room temperature in Sr2IrO4 thin films. Nanoscale 7, 3453–3459 (2015).
Yan, Z. et al. Growth of high-quality hexagonal ErMnO3 single crystals by the pressurized floating-zone method. J. Cryst. Growth 409, 75–79 (2015).
Lee, Y. et al. Large resistivity modulation in mixed-phase metallic systems. Nat. Commun. 6, 5959 (2015).
Zhou, Z. et al. Probing electric field control of magnetism using ferromagnetic resonance. Nat. Commun. 6, 6082 (2015).
Khan, A. I. et al. Negative capacitance in a ferroelectric capacitor. Nat. Mater. 14, 182–186 (2015).
Polking, M. J., Alivisatos, A. P. & Ramesh, R. Synthesis, physics, and applications of ferroelectric nanomaterials. MRS Commun. 5, 27–44 (2015).
Giovanni, D. et al. Highly spin-polarized carrier dynamics and ultralarge photoinduced magnetization in CH3NH3PbI3 perovskite thin films. Nano Lett. 15, 1553–1558 (2015).
Schaab, J. et al. Ferroelectric domains in the multiferroic phase of ErMnO3 imaged by low-temperature photoemission electron microscopy. J. Phys. Conf. Ser. 592, 012120 (2015).
Khan, A. I., Marti, X., Serrao, C., Ramesh, R. & Salahuddin, S. Voltage-controlled ferroelastic switching in Pb(Zr0.2Ti0.8)O3 thin films. Nano Lett. 15, 2229–2234 (2015).
Liu, X. et al. Probing single magnon excitations in Sr2IrO4 using O K-edge resonant inelastic x-ray scattering. J. Phys. Condens. Matter 27, 202202 (2015).
Zhao, Y. et al. Electric-field control of magnetism in multiferroic heterostructures. In 2015 IEEE Magnetics Conference (INTERMAG) (IEEE, 2015). https://doi.org/10.1109/intmag.2015.7156525.
Zhang, W., Ramesh, R., MacManus-Driscoll, J. L. & Wang, H. Multifunctional, self-assembled oxide nanocomposite thin films and devices. MRS Bull. 40, 736–745 (2015).
Asif Islam, K., Korok, C., Ramamoorthy, R. & Sayeef, S. Understanding negative capacitance dynamics in ferroelectric capacitors. In 2015 Fourth Berkeley Symposium on Energy Efficient Electronic Systems (E3S) (IEEE, 2015). https://doi.org/10.1109/e3s.2015.7336793.
Bakaul, S. R. et al. Single crystal functional oxides on silicon. Nat. Commun. 7, 10547 (2016).
Khan, A. I. et al. Negative capacitance in short-channel FinFETs externally connected to an epitaxial ferroelectric capacitor. IEEE Electron Device Lett. 37, 111–114 (2016).
Manipatruni, S. et al. Scalable energy-efficient magnetoelectric spin-orbit logic. Nature 565, 35–42 (2018).
Schaab, J. et al. Optimization of electronic domain-wall properties by aliovalent cation substitution. Adv. Electron. Mater. 2, 1500195 (2016).
Wang, C. et al. Ferroelastic switching in a layered-perovskite thin film. Nat. Commun. 7, 10636 (2016).
Liu, J. et al. Strain-induced nonsymmorphic symmetry breaking and removal of Dirac semimetallic nodal line in an orthoperovskite iridate. Phys. Rev. B. 93, 085118 (2016).
Liu, Z. Q. et al. Full electroresistance modulation in a mixed-phase metallic alloy. Phys. Rev. Lett. 116, 097203 (2016).
Gao, Y. et al. Dynamic in situ observation of voltage-driven repeatable magnetization reversal at room temperature. Sci. Rep. 6, 23696 (2016).
Ko, C. et al. Ferroelectrically gated atomically thin transition-metal dichalcogenides as nonvolatile memory. Adv. Mater. 28, 2923–2930 (2016).
Clarkson, J. et al. An invisible non-volatile solid-state memory. Preprint at https://arxiv.org/abs/1604.03383 (2016).
Giovanni, D. et al. Tunable room-temperature spin-selective optical Stark effect in solution-processed layered halide perovskites. Sci. Adv. 2, e1600477 (2016).
Yi, D. et al. Atomic-scale control of magnetic anisotropy via novel spin-orbit coupling effect in La2/3Sr1/3MnO3/SrIrO3 superlattices. Proc. Natl Acad. Sci. USA 113, 6397–6402 (2016).
Krupin, O. et al. Ultrafast dynamics of localized magnetic moments in the unconventional Mott insulator Sr2IrO4. J. Phys. Condens. Matter 28, 32LT01 (2016).
Nguyen, K. X. et al. Reconstruction of polarization vortices by diffraction mapping of ferroelectric PbTiO3/SrTiO3 superlattice using a high dynamic range pixelated detector. Microsc. Microanal. 22, 472–473 (2016).
Ramesh, R. Observation of polar vortices in oxide superlattices. Microsc. Microanal. 22, 1246–1247 (2016).
Mundy, J. A. et al. Atomically engineered ferroic layers yield a room-temperature magnetoelectric multiferroic. Nature 537, 523–527 (2016).
Lorenz, M. et al. The 2016 oxide electronic materials and oxide interfaces roadmap. J. Phys. D. Appl. Phys. 49, 433001 (2016).
Ievlev, A. V. et al. Chemical state evolution in ferroelectric films during tip-induced polarization and electroresistive switching. ACS Appl. Mater. Interfaces 8, 29588–29593 (2016).
Gao, T. et al. Electric-field induced reversible switching of the magnetic easy axis in Co/BiFeO3 on SrTiO3. Nano Lett. 17, 2825–2832 (2017).
Kim, J., Ramesh, R. & Kioussis, N. Revealing the hidden structural phases of FeRh. Phys. Rev. B. 94, 180407 (2016).
Bakaul, S. R. et al. High speed epitaxial perovskite memory on flexible substrates. Adv. Mater. 29, 1605699 (2017).
Biswas, A., Yang, C.-H., Ramesh, R. & Jeong, Y. H. Atomically flat single terminated oxide substrate surfaces. Prog. Surf. Sci. 92, 117–141 (2017).
Zheng, G. et al. Epitaxial strain controlled magnetocrystalline anisotropy in ultrathin FeRh/MgO bilayers. AIP Adv. 7, 055914 (2017).
Lu, Z. et al. Electrically induced, non-volatile, metal insulator transition in a ferroelectric-controlled MoS2 transistor. Appl. Phys. Lett. 112, 043107 (2018).
Mundy, J. A. et al. Functional electronic inversion layers at ferroelectric domain walls. Nat. Mater. 16, 622–627 (2017).
Nguyen, K. X. et al. Measuring orbital angular momentum (OAM) and torque transfer from polarization vortices with the electron microscopy pixel array detector. Microsc. Microanal. 23, 1634–1635 (2017).
Chen, D. et al. A strain-driven antiferroelectric-to-ferroelectric phase transition in La-doped BiFeO3 thin films on Si. Nano Lett. 17, 5823–5829 (2017).
Clarkson, J. D. et al. Hidden magnetic states emergent under electric field, in A room temperature composite magnetoelectric multiferroic. Sci. Rep. 7, 15460 (2017).
Nina, B., Ramamoorthy, R. & Pu, Y. Manipulating ferroelectrics through changes in surface and interface properties. ACS Appl. Mater. Interfaces 9, 39736–39746 (2017).
Liu, Z. Q. et al. Electrically reversible cracks in an intermetallic film controlled by an electric field. Nat. Commun. 9, 41 (2018).
Kim, K.-E. et al. Configurable topological textures in strain graded ferroelectric nanoplates. Nat. Commun. 9, 403 (2018).
Campanini, M., Erni, R., Yang, C., Ramesh, R. & Rossell, M. D. Periodic giant polarization gradients in doped BiFeO3 thin films. Nano Lett. 18, 717–724 (2018).
Huang, B.-C. et al. Atomically resolved electronic states and correlated magnetic order at termination engineered complex oxide heterointerfaces. ACS Nano 12, 1089–1095 (2018).
Kim, J.-W. et al. Controlling entangled spin-orbit coupling of 5d states with interfacial heterostructure engineering. Phys. Rev. B. 97, 094426 (2018).
dos Reis, R., Hsu, S.-L., Ophus, C., Ramesh, R. & Ciston, J. Three-dimensional polarization by means of scanning HOLZ-CBED technique. Microsc. Microanal. 24, 178–179 (2018).
Nguyen, K. X. et al. Mapping polarity, toroidal order, and the local energy landscape by 4D-STEM. Microsc. Microanal. 24, 176–177 (2018).
Ramamoorthy, R. Defect engineering using crystal symmetry. Proc. Natl Acad. Sci. USA 115, 9344–9346 (2018).
Das, S. et al. Perspective: Emergent topologies in oxide superlattices. APL Mater. 6, 100901 (2018).
Mei, A. B., Ramesh, R. & Schlom, D. G. Discovery of ordered vortex phase in multiferroic oxide superlattices. Preprint at https://arxiv.org/abs/1810.12895 (2018).
Manipatruni, S. et al. Voltage control of unidirectional anisotropy in ferromagnet-multiferroic system. Sci. Adv. 4, eaat4229 (2018).
Singh-Bhalla, G. et al. Unexpected termination switching and polarity compensation in LaAlO3/SrTiO3 heterostructures. Phys. Rev. Mater. 2, 112001 (2018).
Mundy, J. A. et al. A high-energy density antiferroelectric made by interfacial electrostatic engineering. Preprint at https://arxiv.org/abs/1812.09615 (2018).
Manipatruni, S. et al. Scalable energy-efficient magnetoelectric spin-orbit logic. Nature 565, 35–42 (2019).
Steffes, J. J., Ristau, R. A., Ramesh, R. & Huey, B. D. Thickness scaling of ferroelectricity in BiFeO3 by tomographic atomic force microscopy. Proc. Natl Acad. Sci. USA 116, 2413–2418 (2019).
Yi, D. et al. Tailoring magnetoelectric coupling in BiFeO3/La0.7Sr0.3MnO3 heterostructure through the interface engineering. Adv. Mater. 31, e1806335 (2019).
Spaldin, N. A. & Ramesh, R. Advances in magnetoelectric multiferroics. Nat. Mater. 18, 203–212 (2019).
Ramesh, R., Manipatruni, S. & Young, I. Electric-field control of magnetism. MRS Bull. 44, 288–294 (2019).
Ramesh, R. & Schlom, D. G. Creating emergent phenomena in oxide superlattices. Nat. Rev. Mater. 4, 257–268 (2019).
Doyle, S. et al. Tunable giant exchange bias in an intercalated transition metal dichalcogenide. Preprint at https://arxiv.org/abs/1904.05872 (2019).
Yadav, A. K. et al. Author correction: Spatially resolved steady-state negative capacitance. Nature 568, E13 (2019).
Everhardt, A. S. et al. Tunable charge to spin conversion in strontium iridate thin films. Phys. Rev. Mater. 3, 051201 (2019).
Luo, Q. et al. Nanoelectromechanical switches by controlled switchable cracking. IEEE Electron Device Lett. 40, 1209–1212 (2019).
Lin, C.-C. et al. Experimental demonstration of integrated magneto-electric and spin-orbit building blocks implementing energy-efficient logic. In 2019 IEEE International Electron Devices Meeting (IEDM) (IEEE, 2019). https://doi.org/10.1109/iedm19573.2019.8993620.
Gray, I. et al. Imaging uncompensated moments and exchange-biased emergent ferromagnetism in FeRh thin films. Phys. Rev. Mater. 3, 124407 (2019).
Campanini, M. et al. Imaging and quantification of charged domain walls in BiFeO3. Nanoscale 12, 9186–9193 (2020).
Huang, Y.-L. et al. Unexpected giant microwave conductivity in a nominally silent BiFeO3 domain wall. Adv. Mater. 32, e1905132 (2020).
Cheema, S. S. et al. Publisher correction: enhanced ferroelectricity in ultrathin films grown directly on silicon. Nature 581, E5 (2020).
Shao, Y.-T. et al. Mapping topological dipole textures, chirality, and the potential energy landscape of polar skyrmions using 4D-STEM. Microsc. Microanal. 26, 968–970 (2020).
Ercius, P. et al. The 4D camera—an 87 kHz frame-rate detector for counted 4D-STEM experiments. Microsc. Microanal. 26, 1896–1897 (2020).
Brown, H. et al. An optical sectioning method for 3D reconstruction using 4D-STEM. Microsc. Microanal. 26, 2454–2455 (2020).
Susarla, S. et al. Atomic resolution crystal field splitting mapping in polar vortices oxide superlattices. Microsc. Microanal. 26, 3178–3180 (2020).
Seidel, J. & Ramesh, R. In Domain Walls (eds Meier, D., Seidel, J., Gregg, M., & Rames, R.) 340–350 (Oxford University Press, 2020).
Meier, D., Seidel, J., Gregg, M. & Ramesh, R. Domain Walls (Oxford University Press, 2020).
Kathiresan, M. et al. Optimization of piezoelectric MEMS process on Sr and La co-doped PZT thin films. J. Adv. Dielectr. 2050010 (2020).
Zhang, Y. et al. Deterministic reversal of single magnetic vortex circulation by an electric field. Sci. Bull. (Beijing) 65, 1260–1267 (2020).
Zhang, H. et al. Itinerant ferromagnetism in van der Waals Fe5-xGeTe2 crystals above room temperature. Phys. Rev. B. 102, 064417 (2020).
Nan, T. et al. Electric-field control of spin dynamics during magnetic phase transitions. Sci. Adv. 6, eabd2613 (2020).
Sayed, S. et al. Unified framework for charge-spin interconversion in spin-orbit materials. Phys. Rev. Appl. 15, 054004 (2021).
Fan, S. et al. Site-specific spectroscopic measurement of spin and charge in (LuFeO3)m/(LuFe2O4)1 multiferroic superlattices. Nat. Commun. 11, 5582 (2020).
Miranda, K., Girard-Dias, W., Attias, M., de Souza, W. & Ramos, I. Three dimensional reconstruction by electronmicroscopy in the life sciences: An introduction for cell and tissue biologists. Mol. Reprod. Dev. 82, 530–547 (2015).
Maniv, E. et al. Antiferromagnetic switching driven by the collective dynamics of a coexisting spin glass. Sci. Adv. 7, eabd8452 (2021).
Shao, Y.-T. et al. Emergent chirality in a polar meron to skyrmion phase transition. Preprint at https://arxiv.org/abs/2101.04545 (2021).
Maniv, E. et al. Exchange bias due to coupling between coexisting antiferromagnetic and spin-glass orders. Nat. Phys. https://doi.org/10.1038/s41567-020-01123-w (2021).
Li, Q. et al. Subterahertz collective dynamics of polar vortices. Nature 592, 376–380 (2021).
Steinhardt, R. A. et al. DyFe2O4: A new trigonal rare-earth ferrite grown by molecular-beam epitaxy. APL Mater. 9, 041106 (2021).
Hong, Z. et al. Vortex domain walls in ferroelectrics. Nano Lett. 21, 3533–3539 (2021).
Meisenheimer, P. B. et al. Engineering new limits to magnetostriction through metastability in iron-gallium alloys. Nat. Commun. 12, 2757 (2021).
Ramachandran, K. et al. α-Fe2O3/AmTiO2 heterojunction-based photoanode with improved interfacial charge transport properties for enhanced photoelectrochemical water splitting. J. Mater. Sci.: Mater. Electron. https://doi.org/10.1007/s10854-021-06050-x (2021).
Fertitta, E. et al. Study of disorder in pulsed laser deposited double perovskite oxides by first-principle structure prediction. NPJ Comput. Mater 7, 92 (2021).
Zhang, Z. et al. Epitaxial ferroelectric Hf0.5Zr0.5O2 with metallic pyrochlore oxide electrodes. Adv. Mater. 33, e2006089 (2021).
Tückmantel, P., Gaponenko, I., Caballero, N. & Agar, J. C. Local probe comparison of ferroelectric switching event statistics in the creep and depinning regimes in thin films. Phys. Rev. 126, 117601 (2021).
Ramesh, R. & Martin, L. W. Electric field control of magnetism: multiferroics and magnetoelectrics. Riv. Nuovo Cim. 44, 251–289 (2021).
Gao, R. et al. Correlating surface crystal orientation and gas kinetics in perovskite oxide electrodes. Adv. Mater. 33, e2100977 (2021).
Kim, J. et al. Frequency-dependent suppression of field-induced polarization rotation in relaxor ferroelectric thin films. Matter 4, 2367–2377 (2021).
Simonyan, K. & Zisserman, A. Very deep convolutional networks for large-scale image recognition. Preprint at https://arxiv.org/abs/1409.1556 (2014).
Deng, J. et al. ImageNet: A large-scale hierarchical image database. In 2009 IEEE Conference on Computer Vision and Pattern Recognition (IEEE, 2009). https://doi.org/10.1109/cvpr.2009.5206848.
McInnes, L. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction—umap 0.5 documentation. https://umap-learn.readthedocs.io/en/latest/.
McInnes, L., Healy, J. & Melville, J. UMAP: Uniform manifold approximation and projection for dimension reduction. Preprint at https://arxiv.org/abs/1802.03426 (2018).
Maaten, L. & Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 9, 2579–2605 (2008).
Caltech101. http://www.vision.caltech.edu/Image_Datasets/Caltech101/.
Acknowledgements
T.N.M.N. acknowledges primary support from the Nano/Human Interfaces Presidential Initiative and secondary support from National Science Foundation under grant TRIPODS + X: RES-1839234. Y.G., J.C.A., S.Q., and K.S.F. acknowledge primary support from National Science Foundation under grant TRIPODS + X: RES-1839234. We graciously acknowledge all experimentalists who were involved in collecting the data used in this study. Contributors include Prof. Lane Martin and Ramamoorthy Ramesh. We want to recognize all trainees that took part in collecting this data, including Liv Dedon, Shishir Pandya, Anoop Damodaran, Sahar Saremi, Anoop Damodaran, Zhuhang Chen, Ran Gao, Shang-lin Hsu, Julia Mundy, Arvind Dasgupta, Gabe Velarde, Xiaoyan Lu, Sujit Das, Ajay Yadav, Bhagwati Prasad, James Clarkson, David Pesquera, Jieun Kim, Megha Acharya, Suraj Cheema, Eduardo Lupi, Wenbo Zhao, Lei Zhang, Margaret McCarter, Hongling Hu, and Derek Meyers.
Author information
Authors and Affiliations
Contributions
J.C.A., T.N.M.N., Y.G. and K.S.F. designed and conceived the experiments. T.N.M.N. developed the recursive image similarity methodology, Y.G. created the wallpaper group symmetry dataset and trained the symmetry-aware neural-network. T.N.M.N. and S.Q. developed the software package for distribution. J.C.A. and R.X. provided experimental insights regarding images contained in the database. J.C.A., T.N.M.N., Y.G., S.Q., R.X. and K.S.F. wrote the manuscript. All authors were involved in revising the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nguyen, T.N.M., Guo, Y., Qin, S. et al. Symmetry-aware recursive image similarity exploration for materials microscopy. npj Comput Mater 7, 166 (2021). https://doi.org/10.1038/s41524-021-00637-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-021-00637-y