Introduction

Optoelectronic neuromorphic devices have been actively investigated as a solution to the von Neumann bottleneck of current mainstream computing1,2,3. Their implementations crucially rely on the rapid response of properties of materials to light stimuli. Lasers are essential for achieving practical applications; they are used for ultrafast manipulation of the functional properties of various compounds, such as the excitation of magnons and ferromagnetism4,5,6, insulator-to-metal transition (IMT)7, orbital order transition8, and ferroelectric and magnetic order switching9,10,11. This form of dynamic material manipulation offers the opportunities to control different microscopic degrees of freedom and forms nonequilibrium quantum states with nontrivial properties inaccessible in the static limit, analogous to strain, pressure, chemical doping, electric or magnetic fields. The high sensitivity is governed by strong correlation between electronic states or ferroic orders and structural distortions12,13,14. Interestingly, the IMT arising from the strong coupling of electronic states to lattice vibrations in the THz regime, is strongly sensitive to THz pulse-driven optical phonons.

BaBiO3 is well known for this strong interaction as a charge-ordered insulator with a fully commensurate three-dimensional charge density wave15,16, where dynamical interconversion between large local lattice distortions and charge disproportionation induces anharmonic oxygen vibrations and Cooper pairing17,18. BaBiO3 undergoes a series of structural transitions with increasing temperature19, showing a monoclinic phase at room-temperature and rhombohedral phase transition at ~405 K. This is followed by a rhombohedral-to-cubic transition at ~705 K. The structural distortions from cubic to monoclinic structure (space group C2/m) feature breathing-in and breathing-out distortions combined with tilting distortions of BiO6 octahedra20. The former local distortion produces two inequivalent Bi sites involving a charge disproportionation of the formal Bi4+ in the cubic lattice into Bi3+ and Bi5+, and introduces dynamical Jahn-Teller interconversion between the shallow double-well potential of degenerate O(pπ)-O(pπ) bonds at the Fermi level21. IMT can be realized by locally “undoing” the Jahn-Teller distortion, that is, the anti-Jahn-Teller effect22,23, by modulating the electrical carrier density using an electric field, chemical doping, or pressure7,24. However, all of these processes are too slow to meet the requirements of ultrafast science. A conventional above-gap laser excitation in the visible range would directly modify the electronic degree of freedom and alter the occupation of the states; however, it may also cause undesired dissipation and heating problems due to the high energy of the photons24,25.

Mode-selective vibrational excitation using THz lasers is a promising solution. In particular, nonlinear phononics relies on the resonant optical excitation of infrared (IR) phonons using external light pulses to coherently couple to Raman-active phonons, inducing targeted structural distortions with desirable features, which holds the promise for tailoring properties of quantum materials on the ultrashort femto- or picoseconds timescale26,27. The breathing mode existing in cubic BaBiO3 has been shown as an efficient mode to drive metal-to-insulator transition28. Having determined the most relevant mode, the corresponding IR mode coupled with the breathing mode can then be interpreted in terms of symmetry principles or phonon scattering theory. Both methods require a comprehensive theoretical study of the lattice vibrations of BaBiO3 at finite temperatures. However, the investigation can be difficult because of the prohibitive computational cost of determining higher-order force constants for a system involving complex distortion modes and accounting for temperature-induced anharmonic phonon renormalization. Therefore, the phonon–phonon interaction in monoclinic BaBiO3 and its coupling to the electronic structure have been studied less, and we have addressed this challenging task.

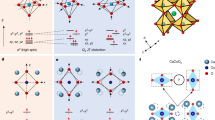
We explored the possibility of suppressing the breathing mode of monoclinic BaBiO3 by exciting a nonlinearly coupled IR phonon, which is expected to drive the IMT. This scheme is depicted schematically in Fig. 1. The breathing mode was modeled to produce an asymmetric double-well energy profile that is characteristic of charge order with two different types of cations, Bi3+(Bi1) and Bi5+(Bi2), at the two energy minima pointing in opposite directions. The goal is to create a single well occupying the central position of the double well, in which the Bi atoms at the local energy minima prefer the Bi4+ valence state. Towards this goal, we utilize the lattice dynamics to select the target mode for excitation. An anharmonic Hamiltonian expanded as a function of amplitudes for the two coupled modes is constructed, based on the first-principles calculations, to determine the coupling constants. Solving the equations of motion numerically for the coupled phonon modes upon the pulse coherently pumps IR mode describes their dynamics. Finally, we show the nonlinear phononic interaction steers the system towards a desirable metallic electronic state according to the time evolution of the calculated band gaps.

Fig. 1: Light-induced insulator-to-metal transition pathway.
figure 1

Schematics of a, b crystal structure, c, d energy profile, and e, f band structure from insulating (left plane) to a metallic (right plane) state under the illumination of a THz pulsed laser as well as displacement patterns associated with the excited breathing (Ag) and pumped Infrared (Bu) phonon modes (middle plane).

Full size image

Results and discussion

Pumped infrared-active phonon selection

Following this pathway for nonlinear phononic modulation of the breathing mode by coherent excitation of a specific IR mode, it is crucial to identify the breathing mode and the strongly coupled IR mode in the monoclinic structure. Therefore, the phonon dispersion should be studied. The ground-state structure belongs to the centrosymmetric 2/m point group with ten atoms in the primitive cell. The 2 × 2 × 2 supercell used for phonon calculations is shown in Fig. 2a. Because of the dynamical instability of the monoclinic phase at 0 K, imaginary frequencies were present near the Y point k = (1/2,1/2,0), as shown by the gray lines in Fig. 2b. The phonon instabilities are associated with the oxygen octahedral rotation. We employed compressive sensing lattice dynamics (CSLD)29,30 and self-consistent ab initio lattice dynamics (SCAILD)31,32 to accurately treat the phonon instabilities and anharmonicity. Considering the requirements of efficient devices capable of working near room temperature, we calculated the phonon properties at 300 K (see Methods section for details). As seen from the blue lines in Fig. 2b, the imaginary phonon softening disappears with increasing temperature, which can be attributed to the anharmonic effects of the lattice vibrations33. To distinguish the breathing mode and the Raman- and IR-active modes, we investigated the irreducible representation, and the calculated phonon eigenfrequencies and symmetries are listed in Table 1. At the zone-center, the optical phonons were classified as \(\Gamma = 7A_g + 5B_g + 6A_u + 9B_u\). The modes of symmetry, Ag and Bg are Raman-active, and Au and Bu are infrared-active. The Ag(25) is a vibrational mode with alternating breathing-in and breathing-out distortions of the BiO6 octahedra, the so-called breathing mode (see Fig. 1). The quadratic-linear coupling between any single infrared-active mode of the quadratic form and the single breathing mode is symmetry-allowed in the monoclinic BaBiO3 according to group theory; it is the lowest-order and dominant nonlinear coupling, and therefore only be considered in the following.

Fig. 2: Phonon spectrums of monoclinic BaBiO3 and energy profiles of the coupled phonons.
figure 2

a Crystal structure of the supercell used for phonon calculations. b Phonon spectrums of monoclinic BaBiO3 at 0 K (gray lines) and 300 K (blue lines). c Calculated total energy as a function of the Ag(25) amplitudes for several values of the Bu(26) mode amplitudes. We plot \(\Delta E = E(Q_{{{\mathrm{R}}}},Q_{{{{\mathrm{IR}}}}}) - E( - 0.82,Q_{{{{\mathrm{IR}}}}})\) for visual purposes. The vertical dash line denotes the minimum of the single-well potential.

Full size image
Table 1 Calculated phonon frequencies (in THz) and their irreducible representation in monoclinic BaBiO3.
Full size table

Next, we identify the IR mode that couples the strongest with the breathing mode. In previous theoretical studies, selection rules based on group theory have been used to select several candidates. The coupling coefficients linking the activated IR and resonant Raman modes can be evaluated by the allowed higher-order anharmonic interaction terms presented in the thermodynamic energy expansion24,34. Here, we consider that the interactions among three phonons resemble three-phonon scattering rates, calculated from second- and third-order force constants, via a perturbative many-body expansion as implemented in the PHONO3PY code35. This treatment has been successfully explored in our earlier study10. With this method, we computed the anharmonic phonon-phonon interaction strengths between all IR modes to the breathing mode, and identified the most effectively pumped IR mode. We focused on the quadratic-linear case and the results are presented in Table 1. The numerical values we obtained for all IR modes vary in the interval [10−12, 10−7] eV, and the magnitude of Bu(26) is of the order of 10−7 eV and larger than that of other IR modes. The frequency of the Bu(26) mode is comparable in value to the Ag(25) mode, making it a suitable candidate for coherently exciting the latter due to the nonlinear phononic coupling. This mode corresponds to the stretching of the BiO6 octahedra (see the displacement pattern in Fig. 1), which is expected to prevent significant structural distortion caused by the breathing mode.

Energy profiles calculations and fitting

As mentioned above, the breathing mode is responsible for the IMT, which is characterized by a double-well shape of the energy profile. Therefore, it is essential to illustrate the response of this energy profile to the strong anharmonic coupling between Bu(26) and Ag(25). In Fig. 2c, the energy profiles exhibiting a double-well potential for Ag(25) mode with amplitudes ranging from −2.2 to 0.7 Å amu1/2, are plotted with respect to different Bu(26) amplitudes. The Ag(25) mode possesses the full symmetry of the 2/m group and by following the atomic displacements of its positive and negative amplitudes we derive the asymmetric energy profile. At room temperature, the system has only an exact ground state with the non-equivalent bond length of the Bi(1)-O and Bi(2)-O bond as 2.32 Å and 2.17 Å, respectively (Fig. 1a), which is consistent with the experimental values36,37. In addition, to compare the oxidation states present in BaBiO3, we analyze the Bader charges38. The Bader charges of Bi3+ and Bi5+ are 1.91 and 2.25 e, with the charge difference being 0.34 e, consistent with the previously calculated one of 0.35 e39. The two potential minima correspond to the valence fluctuations at the two Bi sites [Bi3+(Bi1)Bi5+(Bi2)→Bi5+(Bi1)Bi3+(Bi2)]. Therefore, the right potential well as the initial state is found to be lower than the left potential well. In addition, With increase in the Bu(26) mode amplitude, the depth of the double-well gradually decreases and evolves to a single-well potential with its minimum closer to the intermediate position of the two potential wells. The resulting Ag(25) amplitudes being negative are required to reduce the breathing distortion and bring the structure closer to cubic symmetry. To examine the transition in more detail, we compared the bond lengths in equilibrium structure with that in nonequilibrium energy global minimum structure corresponding to the coupled excited modes, with mode amplitudes Q(Ag(25)) and Q(Bu(26)) being −1.07 and −1.64 Å amu1/2, respectively. A schematic of this structure is presented in Fig. 1b. The Bi(1)-O bond lengths vary from 1.95 to 2.46 Å, and Bi(2)-O bond lengths show a large variation and are around 2.01–2.59 Å. The mean bond lengths are calculated to be 2.21 Å in Bi(1) and 2.28 Å in Bi(2), and they exist between 2.17 and 2.32 Å. Combination with Bader charge analysis, we find that the charges on two Bi sites are 2.13 and 1.97 e, respectively. The values are very similar to the calculated ones in cubic BaBiO3 (2.1 e), which confirms that the valence state of Bi is converted into +4. It is relevant to point out that the latter can be obtained from the equilibrium structure by only a change in the internal atomic coordinates, indicating the possibility of an IMT rather than a transformation of the monoclinic crystal structure to a cubic one.

In contrast, the coupling behaviors of the potential profiles provide essential information to obtain a detailed expression of the system’s energy profiles with respect to the amplitudes of Ag(25) and Bu(26). The fittings were performed using the least-squares fitting method, in which the lowest-order symmetry-allowed nonlinear phonon coupling term that is squared in the IR and linear in the breathing mode is involved. Both the double-well and single-well parabolic energy profiles were used, so that the anharmonic coupling between the two modes can be included to evaluate the formula of the polynomial expression as follows:

$$\begin{array}{l}E(Q_{{{\mathrm{R}}}},Q_{{{{\mathrm{IR}}}}}) = \frac{1}{2}\omega _{{{{\mathrm{IR}}}}}^2Q_{{{{\mathrm{IR}}}}}^2 + \frac{1}{2}\omega _{{{\mathrm{R}}}}^2Q_{{{\mathrm{R}}}}^2 + \frac{1}{3}a_3Q_{{{\mathrm{R}}}}^3 \\ \qquad\qquad \qquad \, + \frac{1}{4}a_4Q_{{{\mathrm{R}}}}^4 + \frac{1}{4}b_4Q_{{{{\mathrm{IR}}}}}^4 + gQ_{{{{\mathrm{IR}}}}}^2Q_{{{\mathrm{R}}}}\end{array}$$
(1)

Here, \(Q_{{{\mathrm{R}}}}\) and \(Q_{{{{\mathrm{IR}}}}}\) are the amplitudes of the Ag(25) and Bu(26) modes, respectively. The calculated values of the coupling coefficients are listed in Table 2.

Table 2 Values of the coefficients of the polynomial determined from a fit to the energy profiles of amplitudes of Ag(25) and Bu(26) modes.
Full size table

Coupled phonons dynamics and electronic state transition

The dynamics equations of \(Q_{{{\mathrm{R}}}}\) and \(Q_{{{{\mathrm{IR}}}}}\) can be obtained by taking the derivatives of Eq. (1) with respect to the amplitudes of the two modes, with the laser field introduced by an external time-dependent driving term of the form \(F(t) = Z^ \ast E_0\sin (\omega t){{{\mathrm{e}}}}^{ - t^{{{\mathrm{2}}}}/(2\tau ^2)}\):

$$\ddot Q_{{{{\mathrm{IR}}}}} + \gamma _{{{{\mathrm{IR}}}}}\dot Q_{{{{\mathrm{IR}}}}} + \omega _{{{{\mathrm{IR}}}}}^2Q_{{{{\mathrm{IR}}}}} = - b_4Q_{{{{\mathrm{IR}}}}}^3 - 2gQ_{{{\mathrm{R}}}}Q_{{{{\mathrm{IR}}}}} + F(t)$$
$$\ddot Q_{{{\mathrm{R}}}} + \gamma _{{{\mathrm{R}}}}\dot Q_{{{\mathrm{R}}}} + \omega _{{{\mathrm{R}}}}^2Q_{{{\mathrm{R}}}} = - a_3Q_{{{\mathrm{R}}}}^2 - a_4Q_{{{\mathrm{R}}}}^3 - gQ_{{{{\mathrm{IR}}}}}^2$$
(2)

where γIR and γR are the corresponding damping constants, approximately 10–20% of the respective phonon frequencies40. Given their closed mode frequency, we keep the damping the same and take them as 1.1 THz. The force pulse has a symmetric pulse shape with a fixed bandwidth of τ = 200 fs and a pump frequency of \(\omega = 1.03\omega _{{{{\mathrm{IR}}}}}\), as used for optical excitation41,42. The mode Born effective charges Z* for IR is calculated as 1.47 e amu−1/2 (ref. 43).

Therefore, we investigated the dynamics of nonlinearly coupled phonons by numerically solving the coupled equations of motion in the presence of an external THz field. As a comparison of the dynamics of the \(Q_{{{\mathrm{R}}}}\) for several values of the peak electric field of the pump pulse presented in Fig. 3a shows, the dynamics in the three cases differ by a large amount. Shown in the insert is the time evolution of the \(Q_{{{{\mathrm{IR}}}}}\) and the pump pulse at a peak amplitude of 12 MV cm−1, where time t = 0 ps is the time of arrival of the pump pulse peak. Under relatively lower peak electric field of the pump (E0 < 9 MV cm−1), the \(Q_{{{\mathrm{R}}}}\) oscillates about the equilibrium position. When the peak electric field reaches E0 ≈ 11 MV cm−1, the \(Q_{{{\mathrm{R}}}}\) exhibits oscillations characteristic with a long-period around a displaced position, then damped oscillation for t > 0.5 ps; however, it eventually relaxes back to its original equilibrium position. For field amplitude of up to 12 MV cm−1, a shorter-period oscillation of \(Q_{{{\mathrm{R}}}}\) about a displaced position is found when the \(Q_{{{{\mathrm{IR}}}}}\) mode is being pumped; hereafter, a steady-state (\(Q_{{{\mathrm{R}}}}\) shifts to a maximum value and no longer drifts) is reached. This behavior is also reflected in the time plots of the mean amplitudes of the IR (open circles) and breathing (filled circles) modes (Fig. 3b), which is the range where the oscillation position is easier to detect. Three different regions showing qualitatively different behaviors were identified. The system remains in the ground state before the optical excitation. The optical excitation initially causes the \(Q_{{{{\mathrm{IR}}}}}\) to displace gently away from its equilibrium position with very low amplitude oscillations due to the combining action of the resonance driven by external pulse and nonlinear phononic coupling with the breathing mode during the duration of the pump pulse, but \(Q_{{{{\mathrm{IR}}}}}\) quickly relaxes to its original position and dies out with time decays. On the other hand, the amplitude of the breathing mode starts with a small displacement from its equilibrium position at the onset of nonlinear coupling at t > −0.5 ps, then quickly increases before entering the stable critical oscillation. Subsequently (\({{t}} \ge {{{\mathrm{1}}}}{{{\mathrm{.2ps}}}}\)), the breathing mode firmly oscillates around a displaced position Q≈1.2 Å amu1/2, close to the single potential minimum (Fig. 2c) at which it can still exist and leaves the system in a metastable state. The critical value corresponds to a maximum displacement of 0.14 Å of O atom, which is almost comparable to those experimentally induced in La1/2Sr3/2MnO4 by available light pulses and is smaller than the theoretically estimated those for LaCuO48,24. Also, the displacement amounts to approximately 6% of the Bi–O distance, below the threshold (~10%) for melting crystals given by the Lindemann instability criterion44,45,46. Thus, the resonant transition of the electronic state in BaBiO3 seems attainable. In particular, the transition time was shown to be of the order of picoseconds, demonstrating that the IMT in BaBiO3 can be optically triggered on the picosecond timescale using ultrafast laser pulses.

Fig. 3: Time-dependent dynamics of the coupled phonons and electronic state, and the mode contributions to electronic state change.
figure 3

a Time evolution of Ag(25) mode nonlinearly coupled to the pumped Bu(26) mode for pumped pulse with a peak electric field of 9, 11, and 12 MV cm−1, respectively. The insert shows the time evolution of the pump pulse as high as 12 MV cm−1 and the corresponding pumped Bu(26) mode. b Time evolutions of the mean amplitudes of Ag(25) and Bu(26) modes at a peak electric field of 12 MV cm−1. The insert shows time dependence of band gap. HSE-calculated band structures for c equilibrium monoclinic BaBiO3 (red dash lines) and coupled excited modes (black lines), as well as d single excited Ag(25) mode (green lines) and single excited Bu(26) mode (light wine lines) with corresponding amplitudes given in parentheses for each mode as (Q(Ag(25)), Q(Bu(26))) in units of Å amu1/2. The Fermi level is set to zero.

Full size image

The time evolution of the band gap with respect to the breathing distortion amplitude shows an IMT, as presented in the inset of Fig. 3b. Initially, the system has a band gap opening of 0.45 eV at the ground state. Then, the band gap lasting ~0.2 ps abruptly collapses, followed by a static zero value with time decays. These results confirm our prediction that suppressing the breathing mode using a THz laser can transform the insulating state of the system into a metallic state.

Mode contributions

To verify the mode contributions to the electronic properties, we compared their band structures using the Heyd-Scuseria-Ernzerhof (HSE) hybrid functional method47 as depicted in Fig. 3c, d. The equilibrium BaBiO3 (dashed red lines) shows an indirect band gap, in good agreement with previous experimental result48. Compared to equilibrium BaBiO3, the band structure of coupled excited modes (solid black lines) shows a closing of band gap as a result of lowering of the energy of the conduction band and raising of the valence band level. It is evident that the nonequilibrium IR mode (light wine lines) itself does not show any pronounced effect on the band structure, whereas the Raman mode (green lines) shifts the valence and conduction band energy levels. The shifts in the energy levels further suggest that the electronic states near the Fermi level are coupled predominantly to the breathing mode and reflect a stronger electron-phonon coupling. A similar situation also exists in PrMnO3 and YBa2Cu3O6.5, where the metallic and superconducting states are much less sensitive to the driven IR mode than the nonequilibrium Raman mode amplitude24,49. This is a general feature of nonlinear phononic coupling, in which the IR only provides a route to achieve them. There are also some other exceptional cases. For example, the IR mode in CaTiO3 and LaTiO3 cooperatively leads to a moderate bandwidth and band gap change34 because they are directly accessed through IR-induced lattice distortion. The detailed studies of the comparison of how the IR modes in these given materials affect their macroscopic properties are almost nonexistent, in particular when the materials under investigation adopt prominently different symmetries and chemical compositions, and are outside the scope of the present work.

In summary, we demonstrated the effect of dynamical lattice distortions induced by nonlinear phononic coupling in the electronic properties of monoclinic BaBiO3. We observed that the dynamic instability disappears at 300 K. We showed that the THz laser with a frequency of 11.71 THz, tuned in resonance with the corresponding IR phonon, drives a coherent breathing mode to negative displacement resulting from a cubic coupling of the latter to the square of the pumped phonon and thereby induces an anti-Jahn-Teller effect, which drives IMT of BaBiO3 of the order of picoseconds. Analysis of the Bader charges and HSE-calculated band structure point to the fact that the Bi valences present a valence of +4 and the system displays a metallic electronic state, similar to the features of cubic BaBiO3. The electronic property is less sensitive to the IR mode and is dominated by the coupling between the breathing vibrations and electronic excitations. Our study paves the way to realize the strong coupling of electrons with the lattice via nonlinear phononics and exploit the dynamic material design near room temperature.

Methods

Density functional calculations

All calculations were carried out based on the density-functional theory (DFT), as implemented in the Vienna ab initio simulation package (VASP)50,51. We used the projector augmented wave (PAW)52 potential with the following electronic configurations: 5s25p66s2 for Ba, 6s26p35d10 for Bi, and 2s22p4 for O. The Perdew-Burke-Ernzerhof of generalized gradient approximation was employed53. The Brillouin zone was sampled using the \(\Gamma\)-centered Monkhorst-Pack k-point mesh of 6 × 6 × 6 for monoclinic unitcell. The energy cutoff was taken as 520 eV and integrations were performed using Gaussian smearing with a width of 0.05 eV. The total energies converged to 10−11 eV and Hellmann-Feynman forces on each atom converged to below 10−8 eV Å−1 for structural relaxation and DFT calculations.

Phonon calculations

A 2 × 2 × 2 supercell with a 2 × 2 × 2 k-point grid was used to calculate the harmonic and anharmonic force constants. The phonon spectrum at 0 K was computed using the finite difference method implemented in the PHONOPY code54. To achieve convergent phonon frequencies and eigenvectors at 300 K, the SCAILD method31,32 was employed. Starting with a 2000-step ab initio molecular dynamics (AIMD) calculation at 300 K, a time step of 1 fs, and the canonical NVT ensemble, the configurations were obtained. The displacements and forces were calculated and fitted to generate the initial force constants. An iterative approach could be adopted. For each iteration, 40 random structures were produced using the full quantum mean square thermal displacement matrix32, which were further used to produce the dataset of displacements and forces as the input to the subsequent CSLD29,30 by performing DFT calculations. The CSLD calculations were performed to swiftly train the harmonic and anharmonic force constants. Convergence was not reached until the 20th iteration, when the fitting error for the force constants became less than 0.02 eV Å−2. The phonon-phonon interaction strength calculations were performed using PHONO3PY code35 with convergent force constants. With quasi-static approximation, the energy profiles were obtained by distorting the equilibrium monoclinic structure along the eigenvectors of the two coupled modes. And for all obtained structures, we kept the cell parameters unchanged and optimized only the internal atomic coordinates in this part of the calculation.

Band structure calculations

Traditional DFT calculations considerably underestimate the band gap; therefore, the HSE hybrid functional47 was used to provide an accurate description of the band structure. Moreover, self-energy-corrected quasi-particle band structure calculations were carried out using the shell DFT-1/2 method55,56 (a variant of DFT-1/2)57, which rectifies the electronic self-interaction error that is prominent in localized valence band states. In BaBiO3, the hole is localized on the O anions; thus, a trimmed O self-energy potential is introduced for all O anions. The outer (rout) and inner (rin) cutoff radii were figured out in a variational way, where rout is constantly 2.1 bohr while rin is ~0.4 bohr. The self-energy potential was treated as an external potential, as included in the O pseudopotential, and self-consistent runs yielded the resulting electronic band structure.

In addition, Bader charge analysis38 and comparison with cubic BaBiO3 were performed to check the valence of Bi in the nonequilibrium structure. The mode effective charge Z* of IR mode calculated from the Born effective charges obtained using density functional perturbation theory and phonon mode eigenvectors was employed to give a quantitative estimate of the response strength of the phonon with respect to the external light43.