Automated design of hybrid halide perovskite monolayers for band gap engineering

Abstract

The recent experimental confirmation of perovskite monolayers has sparked ongoing efforts in their prediction and synthesis, showcasing their flexible tunable band gap and potential in advanced functional devices. Although large-scale computational designs have been successfully performed for inorganic perovskite monolayers, the complexity introduced by organic cations hinders the same approaches applied to the hybrid halide perovskite monolayers. To address this challenge, we have proposed a high-throughput first-principles computational workflow that automates the design of hybrid halide perovskite monolayers. We strategically reduce the complexity of the configurations by analyzing the orientation of cations and the structural symmetry. Over 400 hybrid halide perovskite monolayers have been designed, and their structures and fundamental properties are stored in the database. Correlation analyses show a strong correlation between band gaps and metal-halogen-metal bond angles or metal-halogen bond lengths, consistent with prior studies for bulk and layered perovskites. The underlying physics that the band gap is modulated by the antibonding in the metal-halogen bond makes band gap engineering of hybrid halide perovskite monolayers feasible. Accordingly, initial research on lateral heterojunctions and solar cells has been conducted to explore the potential practical applications of the designed hybrid halide perovskite monolayers. Our study lays the foundation for further exploration of hybrid halide perovskite monolayers and highlights promising opportunities for their potential applications in electronic and optical devices.

Introduction

Emerging perovskite monolayers exhibit unusual physics because of their reduced dimensionality, soft lattice, and diverse surface configurations, offering auspicious prospects for applications in semiconductor devices, solar cells, and light-emitting diodes^1,2,3,4,5,6. Over the past decade, hybrid halide perovskite monolayers (HHPMs), a prominent subclass of monolayer perovskites that include both organic and inorganic components, have been synthesized through solution-based growth or mechanical exfoliation^7,8. Their electronic structures, particularly the band gaps, can be flexibly tuned through surface modification or compositional substitution, rendering them promising candidates for band gap engineering^9,10,11,12. Therefore, it is crucial to urgently design innovative high-performance HHPMs to advance the next generation of electronic and optical devices.

To date, the experimental synthesis of perovskite monolayers remains limited, despite reports indicating the feasibility of synthesizing both hybrid halide and oxide monolayer perovskites^8,13. Fortunately, in silico approaches provide a platform for efficiently designing a wide range of structures and predicting material properties in advance of experiments^14,15. In recent years, high-throughput computational approaches have achieved numerous successes in the field of both monolayer and perovskite materials, as shown in Fig. 1. Computational designs have produced tens of thousands of two-dimensional (2D) materials, which are cataloged in databases like the Materials Cloud 2D Crystal Database (MC2D)^16,17, the Computational 2D Materials Database (C2DB)^18,19, and the 2D Materials Encyclopedia (2DMatPedia)²⁰. Subsequently, high-throughput computational methods have been proposed for screening 2D ferromagnetics²¹, 2D ferroelectrics²², and 2D superconductors²³. At the same time, there have been notable high-throughput computational investigations into various types of perovskites, including bulk hybrid halide perovskites²⁴, organometallic halide perovskites²⁵, inorganic layered perovskites²⁶, and defective perovskites²⁷. Furthermore, recent research has also delved into high-throughput computational studies of inorganic perovskite monolayers^28,29 In addition to high-throughput computational studies, machine learning has emerged as a valuable tool in the field of perovskite design, such as machine leaning for predicting prerovskite solar cells³⁰, data-driven design of MASn_xPb_1−xI₃ perovskites³¹, and accurate machine learning model training for the optical behavior of halide perovskites³². However, there is still a lack of systematic computational design for HHPMs.

Fig. 1: High-throughput computational research on monolayer and peorvskite materials.

High-throughput computational research on HHPMs is still lacking.

The main challenge in designing HHPMs, as opposed to inorganic perovskites, is the large number of atomic configurations resulting from the potential orientations of the organic cations. This presents a global geometry optimization problem involving a molecule on a surface, and several advanced computational techniques have been developed to tackle this challenge. For example, Jung et al. have developed a global optimization protocol for surface molecule adsorbates using an on-the-fly machine learning method³³. Krautgasser et al. have adapted the basin hopping algorithm to explore the global structure of adsorbates on surfaces³⁴. Hörmann et al. introduced an algorithm and software designed to search for the structure of commensurate organic monolayers on inorganic substrates³⁵. These methods are not designed to consider the symmetry and charge distribution of the structure, as they are developed for general purposes. Consequently, the aforementioned approaches fall short in achieving optimal efficiency since they neglect the specific structural features present in the existing HHPMs.

To address the challenges of dimensional oversizing of atomic configurations, we propose an efficient method that reduces the search space for organic cations on inorganic substrates. By analyzing the structure of existing HHPMs from the databases such as the Perovskite Database Project³⁶ and the Experimental Layered Hybrid Halide Perovskite Database³⁷, we observe two facts, namely (i) organic cations exhibit orientation preference, and (ii) HHPMs tend to maintain relatively high symmetry. The former, attributed to the non-neutral charge attraction from substrates, limits the number of possible orientations of organic cations^38,39, and the latter constrains the relative orientations between organic cations in order to form high symmetry^40,41. Therefore, the candidate atomic configurations can be greatly reduced by considering the orientation preference of the organic cations and the crystal symmetry.

In this work, an automated computational workflow was developed for the design of HHPMs and the computation of their fundamental electronic and optical properties. The modular workflow effectively manages dependencies and parallelism and maximizes the utilization of various computational software. Over 400 HHPMs were designed, and their structures and properties were stored in a database for further research and analysis. The investigation reveals a strong correlation between the band gaps of HHPMs and the metal-halogen-metal bond angles or metal-halogen bond lengths, providing a feasible approach to engineer the band gap of HHPMs. Subsequent analysis unveils the physical mechanism underlying the modulation of band gaps, showing that they are influenced by the energy level of the antibonding state in the metal-halogen bond. Additionally, preliminary studies were conducted on the applications of solar cells and lateral heterojunctions to explore the potential of HHPMs in optical and electronic devices.

Results and discussion

Workflow

The design of HHPMs presents complexity due to two primary factors: (i) the multitude of candidate atomic configurations arising from the unrestricted orientation of organic cations, and (ii) the requirement for efficient integration of diverse first-principles computational codes, ensuring a balance between efficiency and accuracy across various systems. To address these challenges, we have developed an automated computational workflow to manage extensive computational processes and to automatically track data provenance.

The proposed automated workflow for designing and calculating HHPMs is depicted in Fig. 2. The workflow requires three inputs, denoted as A, B, and X, which represent organic cations, metal atoms, and halogen atoms, respectively. The workflow comprises three distinct steps: (i) orientation of cations based on their molecular point group and dipole moment, (ii) construction and relaxation of HHPM structures with the reduced chemical formula A₂BX₄, and (iii) calculation of the fundamental properties of the designed HHPMs.

Fig. 2: The schematic diagram of the workflow for designing HHPMs.

The workflow requires three inputs: A, cation; B, metal element; and X, halogen element, and consists of three parts: cation orientation, structure relaxations, and property calculations. The color of the node represents GTO-basis DFT, NAO-basis DFT, PW-basis DFT, or non-DFT process.

Cation orientations

In the first step of the workflow, the optimization, standardization, and orientation of the cations are conducted, expediting the process of structure optimization for the following two reasons.

First, the uncoated metal-halogen framework demonstrates an uneven charge distribution vertically, resulting in an accumulation of a net negative charge on the halogen surface. This net negative charge not only attracts cations but also influences their orientation by compelling them towards their positive charge centers. Consequently, the organic cations align themselves in a preferred orientation vertically, thereby reducing the number of potential atomic configurations. The orientation and charge distributions of the cations are characterized by the molecular dipole moment, which is directed from the positive to the negative charge center. Subsequently, the organic cations are aligned parallel to the molecular dipole moment, pointing away from the metal-halogen substrate. However, in case of nonpolar organic cations displaying a zero molecular dipole moment, their orientation is determined based on their local charge distribution and molecular symmetry.

Second, the symmetry of cations plays a pivotal role in the subsequent steps of the workflow, further reducing the multitude of potential atomic configurations. As a result, precise geometry optimization and symmetry standardization for the cations are carried out to prevent misidentification of symmetry.

Currently, 23 cations are under consideration and listed ordered by the number of atoms in 3a. These cations exhibit diverse molecular point groups, comprising polar groups including C₁, C_s, C_2v, and C_3v, as well as non-polar groups including D_3h and T_d. Detailed structures can be referenced in Supplementary Fig. 1 and in the database.

Relaxations

In the second step of the workflow, the construction, filtration, and relaxation of HHPMs are conducted. Figure 2b illustrates the pristine primitive cell of the assembled PPHMs prior to relaxation. The primitive cell includes two metal atoms, two halogen atoms, and two organic cations positioned on each side of the metal-halogen substrate, indicated by the simplified chemical formula A₂BX₄ (A, organic cations; B, metal atoms; X, halogen atoms). The initial B-X bond length is set as the summation of the atomic radii of the B and X atoms. The cations are placed within voids formed by the surface halogen atoms. While two organic cations on the same side can be individually oriented in-plane, those on opposite sides are arranged with an inversely symmetric distribution to minimize the out-of-plane dipole moment.

Each of the two cations on the same side is individually oriented in the plane, with an angular step of 45^∘ (the smallest angle between the symmetry elements of the metal-halogen substrate) to generate all potential atomic configurations. This angle was thoroughly tested, as it can yield the same results as a smaller angle of 15^∘. Subsequently, structures with symmetric equivalence among the candidate atomic configurations are discarded. An advanced method has been reported for utilizing machine learning to predict the stability of given cation pairs and orientations⁴², which can be used to determine the most stable cation orientations. In contrast to bulk hybrid perovskites, the cations in HHPMs have limited rotational freedom due to the unbalanced charge distribution on the surface above and below the metal-halogen framework. Therefore, our strategy considers all possible configurations within reasonable computational resources.

Following this, the candidate atomic configurations undergo relaxation using a two-step scheme. The coarse relaxation focuses on filtering out extremely unreasonable structures, while the fine relaxation attains the ground state structure. As such, the first relaxation adopts a relatively lower computational precision in comparison to the second relaxation. After the coarse relaxation, the atomic configurations with the lowest energy and 5 meV per atom (i.e. range from 0.15 to 0.47 eV in total, depending on the number of atoms) above the lowest energy are kept for the fine relaxation. This threshold is tested as a safe value to ensure that the ground state is not filtered out.

After the fine relaxation, only the atomic configuration with the lowest energy, identified as the ground state, is selected for property calculations. While studies indicate that atomic configurations in different phases can coexist at room temperature^43,44, our focus exclusively lies on the ground state at zero temperature in this workflow.

Property calculations

In the third step of the workflow, the fundamental properties of the designed HHPMs are calculated. This sub-workflow is carefully structured to optimize parallelism and ensure computational dependencies. The comprehensive computational framework is illustrated in Supplementary Fig. 2. It commences with a test calculation, wherein the spin-polarization and out-of-plane dipole correlation are activated. Subsequent decisions regarding enabling the spin-polarization and/or dipole correlation in the following calculations are based on the results of the test calculation. This approach avoids unnecessary time spent on challenging-to-converge spin-polarization and dipole correlation calculations. For electronic and optical property calculations, the spin-orbital coupling (SOC) is considered for an accurate band gap.

After relaxation, the pristine metal-halogen framework undergoes a distortion to minimize the total energy, as depicted in Fig. 3c. This distortion is linked to the surface cations, which prompt a reduction in crystal symmetry. An analysis is carried out to explore the influence of these cations on crystal symmetry, focusing on the relationship between the layer group of HHPMs, the point group of cations, and the cation angles, as shown in Fig. 3d.

Fig. 3: Structures and symmetries of HHPMs.

a Cations used to construct HHPMs, ordered by number of atoms. b The perfect metal-halogen framework before relaxation. Each side of the unit cell contains two cations. The orientation of the cations is independent. c The relaxed structure of (Butylammonium)₂PbI₄ as an example. d The relationships between layer group of unrelaxed HHPMs, layer group of relaxed HHPMs, point group of cations, and angles between cations. LG layer group, PG point group.

The relationship between the cation type and the structure of HHPMs is a crucial aspect influencing the band gap, as demonstrated in the subsequent section. Understanding this association is essential for comprehending band gap engineering through cation substitution. The layer group p2₁/b11 is common in most HHPMs, except for p1 and p$\bar{1}$. These structures are predominantly contributed by cations with molecular point groups of C_s, T_d, and C_3v. Cations with C₁ symmetry are restricted to forming HHPMs with layer groups of p1 and p$\bar{1}$ due to their lower symmetry. A 90^∘ angle is prevalent in most HHPMs, offering a suitable alignment with the metal-halogen framework. Furthermore, most cations in HHPMs tend to favor an angle that is not 0^∘ or 180^∘, contributing to distort the lattice of the metal-halogen framework.

Band gap distributions

The band gap is a fundamental property that is critical for the applications of HHPMs in electronic or optoelectronic devices, such as field-effect transistors, solar cells, light-emitting diodes, and photodetectors¹. To improve band gap estimations, a variety of exchange-correlation functionals and corrections have been developed, such as hybrid functionals, DFT+U⁴⁵, and self-interaction correction methods⁴⁶. The hybrid Heyd-Scuseria-Ernzerhof 06 (HSE06)⁴⁷ is generally considered to be the most accurate exchange-correlation functional for band gap estimation. However, it is extremely computationally slow, approximately 1000 times slower than generalized gradient approximation (GGA)-type exchange-correlation functionals. Fortunately, the exchange-correlation functional benchmark study shows that the GGA-type functional, high local exchange 16 (HLE16)⁴⁸, has an accuracy close to HSE06, and the metaGGA-type functional, modified Becke-Johnson (mBJ)⁴⁹, has an accuracy even a little better than HSE06⁵⁰. Moreover, both the mBJ, as well as the local mBJ (LMBJ)⁵¹, and the HLE16 are non-hybrid exchange-correlation functionals, so their computational speed is significantly faster than the HSE06 and slightly slower than the GGA-type functional, Perdew-Burke-Ernzerhof (PBE)⁵². In addition to advanced exchange-correlation functionals, the DFT-1/2⁵³ method has also demonstrated excellent accuracy in estimating perovskite band gaps^54,55,56. In order to enhance the accuracy of the band gap results and to systematically compare the effectiveness of various techniques, we conducted band gap calculations using four functionals or methods: (i) PBE, (ii) HLE16, (iii) LMBJ, and (iv) PBE-1/2, which integrates DFT-1/2 with the PBE functional.

Apart from the exchange-functional, the SOC is another crucial factor significantly influencing the estimation of the band gap in perovskites, especially in the case of the presence of Pb element. Studies have demonstrated that SOC typically leads to a reduction in the band gap of Pb-containing halide perovskites^57,58. For this reason, the electronic structures and band gaps are calculated with the inclusion of SOC for all designed HHPMs, even in cases where the SOC influence is negligible. However, calculations without considering the SOC effect are also conducted for comparison purpose.

We have calculated the complete metal-halogen combinations for Pb-, Sn-, Ge-, and Cd-containing HHPMs because of the abundant experimental data on these structures, while for Cu-, Fe-, and Mn-containing HHPMs, only the experimental reported metal-halogen combinations are included. Here we specifically focus on the band gaps of Pb-, Sn-, Ge-, and Cd-containning HHPMs, as the computational data for these systems are more comprehensive. All HHPMs have a band gap and are categorized as semiconductors or insulators. Figure 4a shows the overall distributions of band gaps calculated using different techniques, with and without the inclusion of SOC. Since the band gap is a non-negative quantity and has no upper limit, the distributions of band gap are asymmetric and fit well with lognormal distributions defined by Eq. (1). The mode and mean values are derived by fitting the lognormal distribution function. The band gaps calculated with the PBE functional demonstrate the smallest values, which is consistent with the known tendency of the PBE functional to underestimate band gaps. The band gaps calculated by the PBE-1/2 method show the largest values, and the band gaps of the HLE16 and LMBJ are between those of the PBE and PBE-1/2 methods. Including the SOC results in a decrease of the band gap in all methods, which is the same phenomenon that occurs in bulk perovskite calculations^57,58.

Fig. 4: Band gap distributions and electronic structures.

a Lognormal fitted band gap distributions of total HHPMs. b Metal- and halogen-resolved band gap distributions. c The comparison between the calculated and experimental band gaps. d The element-resolved band structure of (Butylammonium)₂PbI₄. e The total and projected DOS of (Butylammonium)₂PbI₄.

Figure 4b shows the metal- and halogen-resolved band gap distributions. The metal-resolved band gap distributions show an ascending band gap order of Ge < Sn < Pb < Cd, and halogen-resolved show I < Br < Cl < F. This suggests that the band gap can be flexibly tuned over a wide range by substituting metal and halogen atoms. Similar statistical patterns can be observed in the experimental band gaps of layered hybrid halide perovskites³⁷. The SOC exhibits varying degrees of band gap reduction in response to different metal-halogen combinations. As the atomic number of the metal and halogen elements increases, the SOC influence of their combination also increases. The largest influence is observed in the Pb-I combination, where the band gap is decreased by about 1 eV.

To validate the accuracy of the calculated results, a comparison is performed between the calculated and experimental band gaps, as shown in Fig. 4c. The experimental band gap data and their references are presented in Supplementary Table 1^{59,60,61,62,63,64,65,66,67,68,69,70,71,72,73}. Note that the experimental band gaps are obtained from the layered hybrid halide perovskites because of the current paucity of experimental band gap data for PPHMs. Nevertheless, the band gap of the layered structure is considered to be close to that of the PPHMs due to the weak interactions between layers. For both Pb and Sn systems, the PBE-1/2 with SOC (purple filled markers) exhibits the most accurate band gap estimations. The LBMJ with SOC (blue filled markers) and HLE16 with SOC (green filled markers) exhibit slight underestimation of the band gap, while the PBE with SOC (red filled markers) exhibits a significant underestimation of the band gap.

As shown in Table 1, the mean absolute error (MAE) defined as Eq. (2), mean error (ME) defined as Eq. (3), mean absolute percentage error (MAPE) defined as Eq. (4), and mean percentage error (MPE) defined as Eq. (5) are calculated to quantify the error in predicting the band gap for each method. An interesting result emerges that the PBE without SOC is the most accurate method for estimating the band gap for Pb systems, whereas the least accurate for Sn systems. In Pb systems, the influence of SOC is significant. Neglecting SOC can result in an overestimation of the calculated band gap, whereas the PBE functional typically underestimates the band gap. The combination of these two errors tends to offset each other, thereby rendering the PBE the most accurate approach for determining band gaps in Pb systems⁵⁷. In contrast to Pb systems, the influence of SOC on the band gap in Sn systems is found to be less pronounced, exposing the drawback of the PBE functional in underestimating band gaps.

Table 1 Accuracy analysis

The LMBJ and HLE16 functionals demonstrate comparable accuracy in determining the band gap of Pb systems, with an MAE of approximately 0.3 eV. Differently, the HLE16 functional exhibits better accuracy than the LMBJ in estimating the band gap of Sn systems, with an MAE of 0.48 eV. Study have shown that the HSE06 functional coupled with SOC achieves a MAE of 0.43 eV in predicting the band gap of perovskites⁵⁸. Therefore, as alternatives of HSE06 funcitonal, it can be proved that the LMBJ and HLE16 functionals have comparable accuracy to HSE06 for predicting the band gap of perovskites, and even better for some structures. Nevertheless, these functionals, including LMBJ, HLE16, and HSE06, still exhibit some degree of error in estimating the band gap of HHPMs. Surprisingly, the PBE-1/2 demonstrates minimal error for both Pb and Sn systems, especially with an MPE approaching zero.

To further investigate the electronic properties, we calculated the band structures of the designed HHPMs. As a illustrative example, the element-resolved band structure of (Butylammonium)₂PbI₄ calculated by the PBE-1/2 method is shown in Fig. 4d. The electronic states near band edges are predominantly contributed by the metal (Pb) and halogen (I) atoms, while the cation (comprising H, C, and N atoms) contributes to the deeper energy levels. Furthermore, the projected density of states indicates that the valence band maximum (VBM) originates from the Pb s orbital and Sn p orbital, and the conduction band minimum CBM from the Pb p orbital, as shown in Fig. 4e.

On the one hand, the band gap of HHPMs demonstrates a significant correlation with the cation type, since the metal-halogen framework of the initial structures remains consistent for all cations, yet the band gaps vary. On the other hand, the band gap is not determined by the type of cation according to the electronic structure, as the band edges are primarily contributed by the metal and halogen atoms, while the cation plays little role in the band edges. This contradiction is rationalized by introducing the physical picture that the cation indirectly affects the band gap. The cation influences the structure of the metal-halogen framework by Coulomb and van der Waals (vdW) interactions, and the metal-halogen framework determines the band gap. In other words, the cation does affect the band gap, but indirectly. Similar mechanisms that the component indirectly affects the band gap are also found in bulk perovskites^74,75 and layered perovskites⁷⁶.

Band gap engineering

As previously discussed, the band gap of HHPMs is influenced by both the metal-halogen framework and surface cations, either directly or indirectly. However, to enhance the band gap engineering, it is imperative to comprehend the underlying physical mechanisms. To achieve this, various structural parameters have been extracted from atomic structures, including the lattice, bond lengths, insertion depth of cations, and bond angles, to investigate their relationship with band gaps. Given the abundance of computational data and structural variables, a convenient and effective method for identifying the most influential factor is through a correlation analysis. The Pearson correlation coefficient, a commonly used statistical measure, is defined as Eq. (6) and serves as a robust tool for elucidating linear associations between two datasets. This statistical approach facilitates the identification of the most significant variable associated with band gaps among a set of structural variables.

The calculated Pearson correlation coefficients between structural variables and band gaps for the Pb-I and Cd-I systems are illustrated in Fig. 5a, b, respectively. Corresponding correlation coefficients for additional systems can be found in Supplementary Figs. 3 to 12. Notably, distinct correlation patterns are observed among systems featuring various metal atoms, except for the Sn and Ge systems, which demonstrate analogous trends.

Fig. 5: Band gap engineering.

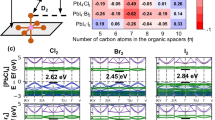
a, b The Pearson correlation coefficients between band gaps and structural parameters for Pb-I and Cd-I systems, respectively. PCC, Pearson correlation coefficients; D_cat, depth of organic cation in metal-halogen substrate; H_cat height of organic cation; ${L}_{{{{\rm{BX}}}}}^{{{{\rm{v}}}}}$, vertical B-X bond length; ${L}_{{{{\rm{BX}}}}}^{{{{\rm{h}}}}}$, horizontal B-X bond length; ∠BXB, B-X-B bond angle; H height of metal-halogen substrate; ∠γ, lattice angle in plane. c The partial charge densities at the CBM and VBM for (Guanidinium)₂PbI₄, (Propylammonium)₂PbI₄, and (Butylammonium)₂CdI₄. d The band gap change versus B-X-B angle for (Propylammonium)₂PbI₄. e The band gap change versus vertical B-X bond length for (Butylammonium)₂CdI₄. f, g The schematic energy level diagrams of (Propylammonium)₂PbI₄ and (Butylammonium)₂CdI₄, respectively. The red arrow indicates the main change in the energy level influenced by the B-X-B bond angle or the vertical B–X bond length, resulting in band gap changes.

In Pb systems, there is a notable correlation between the metal-halogen-metal (B-X-B) bond angles and band gaps (see Fig. 5a and Supplementary Figs. 3 and 4). However, in Sn and Ge systems, the band gap is strongly correlated with the horizontal metal-halogen (B-X) bond lengths (see Supplementary Figs. 7 to 12). It is noteworthy that the behavior of elements within the same group IV is different. Upon further analysis, it becomes apparent that both the horizontal B-X bond length and the B-X-B bond angle influence the band gap through a shared mechanism. Consequently, the subsequent analysis will concentrate on Pb systems firstly rather than Sn and Ge systems.

Differently, in Cd systems, the band gap exhibits significant positive and negative correlations with the vertical and horizontal B-X bond lengths, respectively (see Fig. 5b and Supplementary Figs. 5 and 6). It is important to highlight that the vertical and horizontal B-X bond lengths are interrelated variables in Cd systems, exhibiting a strong negative correlation. Nevertheless, relying solely on correlation analysis cannot definitively determine which variable predominantly influences the band gap in Cd systems.

The band gap, which is defined as the energy level difference between the CBM and VBM, is primarily influenced by the electronic states near the band edges. The band-decomposed charge densities at the CBM and VBM of the compounds (Guanidinium)₂PbI₄, (Propylammonium)₂PbI₄, and (Butylammonium)₂CdI₄ are presented in Fig. 5c to exemplify the electronic structural characteristics near the band edges. In Pb systems, the electronic states are concentrated around the Pb atoms at the CBM and the Pb and I atoms at the VBM. As the B-X-B bond angles decrease, the electronic states change near the B-X-B bond angles, which can be observed by comparing the horizontal I atoms at the CBM of (Guanidinium)₂PbI₄, and (Propylammonium)₂PbI₄. The B-X-B bond angles at the CBM exhibit minimal electronic states, while those at the VBM exhibit numerous electronic states. Consequently, it can be inferred that the B-X-B bond angles at the VBM are of greater significance than the CBM in determining the band gap.

In Cd systems, the electronic states primarily cluster around the Cd and vertical I atoms at the CBM and the I atoms at the VBM. The absence of states near the horizontal I atoms at the CBM and the Cd atoms at the VBM indicates that the horizontal B-X bond does not play a significant role in influencing the band gap. Similarly, the absence of states near the Cd atoms suggests that the vertical B-X bond is also not a critical factor in influencing the band gap. The vertical B-X bond at the CBM stands out as it exhibits numerous states near both the Cd and I atoms. Consequently, the B-X bond at the CBM emerges as the primary factor influencing the band gap in Cd systems. This conclusion is consistent with the strong correlation between the vertical B-X bond length and the band gap in Cd systems. Moreover, the correlation between the horizontal B-X bond lengths and the band gaps is only a side effect of the vertical bond lengths.

Since the influencing variables on the band gap have been identified as the B-X-B bond angle for Pb systems and the vertical B-X bond length for Cd systems, additional band gap calculations were performed by varying the bond lengths or angles to confirm these findings. Modifying either bond angles or lengths is achieved by introducing a slight offset, in range of -0.01 to 0.01 Å, to the halogen atoms. The changes in electronic structure mainly occur in the vicinity of the halogen atom due to the small offset distance applied. In Pb systems, the band gap decreases with the B-X-B bond angle and increases with the offset distance (see Fig. 5d). In Cd systems, the band gap decreases with the vertical B-X bond length as well as the offset distance (see Fig. 5e). Notably, the band gap response to the atomic offset remains linear owing to the small offset distance used. The observed trend in band gap variation is consistent with the previous correlation analysis, as expected.

After a comprehensive description of the band gap engineering laws, it is necessary to explain the basic principles of the physics involved. Since the band gap demonstrates a strong correlation with the B-X-B bond angle for the Pb systems and with the vertical B-X bond length for the Cd systems, attention is focused on the bonding properties of the horizontal B-X bonds for Pb systems and the vertical B-X bonds for Cd systems. To further investigate, we calculated the crystal orbital Hamilton population (COHP) for the horizontal and vertical B-X bonds in Pb and Cd systems, respectively, as shown in Supplementary Figs. 13 and 14. Figure 5f, g show simplified schematic diagrams illustrating the bond orbital energy levels of the Pb and Cd systems, as analyzed from the COHP results.

For Pb systems, as indicated by the charge density analysis, the band gap is primarily determined by the B-X-B bond angles at the VBM. The VBM is characterized by an antibonding state of the metal s and halogen p orbitals. A decrease in the B-X-B bond angle will result in reduced overlap between the halogen p orbital and the metal s orbital due to the distribution of the halogen p orbital resembling a dumbbell shape. This reduction in orbital overlap causes the energy level of the antibonding state to decrease and thus the band gap increases. Consequently, as the B-X-B bond angle decreases, the energy level of the antibonding VBM decreases, leading to a wider band gap.

For Cd systems, the contribution of the CBM to the band gap is more significant than that of the VBM, as evidenced by the band-decomposed charge density analysis. The CBM is characterized by an antibonding state involving metal s and halogen p orbitals. An increase in the vertical B-X bond length reduces the orbital overlap between the metal s and halogen p orbitals, leading to a lower energy level of the CBM and a narrower band gap.

As mentioned above, the correlation analyses for Sn and Ge systems are different from those for Pb systems, while the COHP analyses and bond orbital energy level diagrams are similar to thosed of Pb systems, as shown in Supplementary Figs. 15 to 18. In Sn and Ge systems, the band gap is strongly positively correlated with the horizontal B-X bond length. As the B-X bond length increases, the overlap between the metal s and halogen p orbitals decreases, leading to a decrease in the anti-bonding VBM energy level and an increase in the band gap. While the structural variables affecting the band gap are different for Sn/Ge and Pb systems, the underlying physical mechanisms are similar. This difference in structural variables may be due to the smaller lattice size of Sn and Ge systems compared to Pb systems, which makes the B-X change more pronounced than the B-X-B bond angle change.

It is a well-known law that the band gap is strongly correlated with the B-X-B bond angle in many perovskite materials. For example, the band gap of Sn- or Pb-containing bulk perovskites⁷⁴ increases with the reduction of the B-X-B bond angle. Similar results have already been demonstrated in experiments for metal halide perovskites⁷⁷ and hybrid layered halide perovskites³⁷. Our research has revealed that this correlation between the band gap and the B-X-B bond angle is also applicable to HHPMs. In addition, different patterns have been observed in Cd systems, where the band gap is strongly positively correlated with the vertical B-X bond length. This discrepancy can be attributed to the completely different electronic state characteristics at the band edges in Cd systems. Consequently, it is evident that metal atoms play a key role in the mechanisms involved in the band gap engineering of PPHMs.

Applications

Upon the completion of the workflow calculations, the designed HHPMs were stored in a database, named the Hybrid Halide Perovskite Monolayers Database. The database is well developed and the web-based query client is provided for data sharing and reuse. Figure 6a shows the schematic diagram of this process. Here, two application-focused studies are conducted as representative instances using this database.

Fig. 6: Applications in lateral heterojunctions and solar cells.

a The schematic diagram, from workflow calculations to database and data query. b The band alignment types of semiconductor HHPMs. c The distributions of SLME versus direct allowed band gap. d–g The absorption coefficients versus wavelength for (Guanidinium)₂PbI₄, (Ethanolammonium)₂SnI₄, (Hydroxylammonium)₂GeI₄, and (Phenylmethylammonium)₂CdI₄.

Lateral heterojunctions

Lateral and vertical heterojunctions are specific concepts and configurations in 2D materials due to their ultra thin structure. By constructing heterojunctions, it is possible to obtain more properties that are not present in individual materials. 2D heterojunctions are used in various electronic and optoelectronic devices, such as field effect transistors, resonant tunneling diodes, and light emitting diodes^78,79. Unlike vertical heterojunctions, which are generally bonded by vdW interactions, the lateral heterojunctions are bonded by chemical bonds, and are highly property coalescent and more stable. However, the construction of lateral heterojunctions presents a greater challenge due to the need to account for both lattice mismatch and lateral termination structure. In response to these difficulties, numerous approaches have been devised, such as the utilization of structures sharing identical crystal protocols⁸⁰ and employing the same materials with varying defects⁸¹. The designed HHPMs are suitable for the design of lateral heterojunctions because they share the same metal-halogen structures with small lattice mismatches, and the band gap is effectively modulated by surface cations. It has been confirmed experimentally that lateral heterojunctions formed by 2D perovskites are feasible^82,83.

Figure 6b lists the types of band alignments between semiconductor HHPMs, with the definitions of type I, II, and III alignments given in the legend. It is noteworthy that type I and type II band alignments are predominantly observed, while type III alignments are less common. Subsequently, type I and II lateral heterojunctions have been successfully constructed, owning a consistent electronic structure at the interface. The structures of these heterojunctions can be found in Supplementary Figs. 19 and 21, with the corresponding computed local DOS displayed in Supplementary Figs. 20 and 22. However, the electronic structure of type III heterojunctions remains elusive, as the large energy level difference results in an excessively long transition region. Even with heterojunction lengths exceeding 100 Å and close to 1000 atoms, the electronic properties do not manifest.

Solar cells

The flexibly tunable band gap of the designed HHPMs makes them promising candidates for solar cell applications. However, it is important to recognize that the accuracy of the band gap estimation plays a critical role in determining the accuracy of the predicted performance in solar cell applications. By comparing the calculated band gap with the experimental data, the band gap calculated by the PBE-1/2 method has the best accuracy, so the following optical properties are calculated by the PBE-1/2 method.

We have performed calculations on the frequency dependent dielectric function and used it to determine the spectroscopic limited maximum efficiency (SLME) following Eqs. (7) to (15)⁸⁴. The distribution of calculated SLMEs versus direct allowed band gaps is shown in Fig. 6c. The SLMEs are distributed along the line of the Shockley-Queisser (SQ) limit, which represents the theoretical maximum efficiency versus the direct allowed bandgap. Since the SLME is determined not only by the direct allowed band gap, but also by the absorption spectral characteristics of the materials, the SLMEs cannot reach the SQ limit.

With considering the absorption spectral characteristics, the structure with best band gap not the structure with highest SLME. The SLMEs of the Sn- and Ge-based structures have similar and large values, while the SLMEs of Pb-based structures have lower values. The Cd-based have very low SLMEs, which means they are not suitable for solar cells. For each metal-based structure, the SLME of I-based have largetst LSEM value combination with same metal element.

Then, the absorption coefficients of the HHPMs with the highest SLME for Pb, Sn, Ge, and Cd are shown in Fig. 6d-g, respectively. In comparison to the Sn- and Ge-based HHPMs, the Pb-based HHPMs process a wider band gap, resulting in lower optical absorption within the visible light spectrum. Conversely, the Sn- and Ge-based HHPMs, which have similar and narrower band gaps, exhibit higher optical absorption in the visible light spectrum. Despite Ge-based HHPMs have a slightly larger band gap than Sn-based HHPMs, their optical absorption is greater, leading to a higher SLME value. Cd-based HHPMs have the largest band gap and low absorption coefficient, making them unsuitable for solar cell applications.

In conclusion, we presents systematic research on the material design, band gap engineering, and potential applications of HHPMs. We have developed an efficient computational workflow for systematically designing a large number of HHPMs, addressing challenges related to the orientation of the organic cations. The resulting band gaps demonstrate remarkable tunability, following a lognormal distribution. Our analysis, including the examination of band structure, correlation coefficient, and band-decomposed charge density, reveals that the B-X-B bond angle and the B-X bond length are the primary factors influencing the band gap. Specifically, we find that variations in the B-X-B bond angle or the B-X bond length impact the band gap by altering the orbital overlap of metal s and halogen p orbitals. Additionally, we have stored information on the designed HHPMs and their fundamental properties in a database, which is accessible to other researchers. As a preliminary example, we investigate and highlight the potential applications of HHPMs in lateral heterojunctions and solar cells. This study contributes to a foundational understanding of band gap engineering in HHPMs and provides a comprehensive database of designed HHPMs for further research and applications.

Methods

Workflow implementation

Workflow

The workflow for automating the design of HHPMs is implemented using the computational framework AiiDA (Automated Interactive Infrastructure and Database)^85,86,87. In addition to supporting workflow design, AiiDA provides essential functionalities like data provenance to track data lineage, scheduler control for efficient computation, and plugin interfaces for integration with third-party software. Third-party developed AiiDA plugins are used to invoke DFT codes, including aiida-nwchem⁸⁸, aiida-siesta^89,90, and aiida-vasp⁹¹. The remaining components of the workflow are developed internally.

Atomic modeling

In order to automate the design and calculations of HHPMs, each step of atomic modeling was meticulously implemented through programming languages, thus negating the need for graphical user interfaces. Consequently, the atomic modeling packages ASE (Atomic Simulation Environment)⁹² and Pymatgen (Python Materials Genomics)⁹³ are extensively utilized for atomic modeling, input generation, and output parsing. The Spglib⁹⁴ library was used to identify the layer group, standardize structure, and match symmetry equivalents of HHPMs. The SYVA⁹⁵ code was used to identify the molecular point group and standardize structure of cations. Atomic radius information used for the initial guess of bond lengths is sourced from the Mendeleev⁹⁶ package.

DFT computational details

GTO-basis DFT

The geometry optimization and molecular dipole moment calculations of cations were performed using the GTO-basis DFT implemented in the NWChem (Northwest Computational Chemistry Package)⁹⁷ code. The metaGGA-type exchange-correlation functional r²SCAN⁹⁸ and the basis set 6-311G**⁹⁹ were used in geometry optimizations. The geometry converges with the maximum and root mean square of Cartesian steps smaller than 6 × 10⁻⁵ and 4 × 10⁻⁵ a.u., respectively. The hybrid exchange-correlation functional B3LYP (Becke, 3-parameter, Lee-Yang-Parr)¹⁰⁰ and the basis set def2-TZVPD (valence triple-zeta polarization with diffuse functions)^101,102 were used in molecular dipole moment calculations. The energy precision of optimizer for a line search was set to 5 × 10⁻⁶ eV.

NAO-basis DFT

The structures of HHPMs were relaxed using the NAO-basis DFT implemented in the SIESTA (Spanish Initiative for Electronic Simulations with Thousands of Atoms)⁹⁰ code for a high performance. This is because the NAO basis set is vacuum-free and suitable for low-dimensional structures. The exchange-correlation funcitonal PBE and the basis set double-ζ polarization (DZP) were used. The atomic potential was described by optimized norm-conserving Vanderbilt pseudopotential (ONCVPSP)¹⁰³ implemented by the PseudoDojo project¹⁰⁴ in PSML¹⁰⁵ format. The Brillouin zone was sampled by a Monkhorst-Pack¹⁰⁶ mesh with a k-space density greater than 0.25 Å⁻¹ along periodic direction. A vacuum layer of 30 Å was added perpendicular to the 2D plane to screen interactions from adjacent images. The convergence tolerance for the Hamiltonian matrix elements is 10⁻³ eV during the electronic iterations. The convergence tolerance for the maximum atomic forces is 0.05 and 0.02 eV Å⁻¹ in coarse and fine relaxations, respectively. Real space properties were expanded using a plane wave with a cutoff energy of 300 Ry.

PW-basis DFT

The electronic and optical properties of HHPMs were calculated using the PW-basis DFT implemented in the VASP (Vienna Ab initio Simulation Package)^107,108,109 code. Projected argument wave (PAW)¹¹⁰ pseudopotentials were used in all calculations. The exchange-correlation functionals PBE, HLE16, and LMBJ were used in electronic structure calculations. A PW cutoff energy of 600 eV was applied. The Brillouin zone was sampled using a Monkhorst-Pack mesh with a k-space density greater than 0.125 Å⁻¹ along the periodic direction. A vacuum layer of 15 Å was added perpendicular to the 2D plane to screen interactions from adjacent images. The convergence tolerance for energy was set to 10⁻⁵ eV in electronic iterations. Due to the challenging convergence of LMBJ calculations, the convergence tolerance for energy was adjusted to 5 × 10⁻⁴ eV. The electronic and optical property calculations were also performed using DFT-1/2 method⁵³ by incorporating correlation to pseudopotential implementation in the DFT-1/2 tool¹¹¹.

Dispersion corrections were included in all calculations by employing the DFT-D3 method with the Becke-Johnson damping function¹¹².

Post analysis

Bader Charge Analysis^{113,114,115,116} code was employed to calculate Bader charges based on charge density grid data. The projected COHP was calculated using Local-Orbital Basis Suite Towards Electronic-Structure Reconstruction (LOBSTER)¹¹⁷ code. For the calculation of LDOS of lateral heterojunctions, DensityTool¹¹⁸ code was utilized. The structures and partial charge densities were visualized by using Visualization for Electronic and Structure Analysis (VESTA)¹¹⁹ software.

Formulas

Logarithmic normal distribution

The distributions of band gap values of designed HHPMs show a better fitting for logarithmic normal distribution than normal distribution owning to the non-negativity of band gap. The logarithmic normal distribution function is defined as

$$\frac{1}{x\sigma \sqrt{2\pi }}\exp \left(-\frac{{(\ln x-\mu )}^{2}}{2{\sigma }^{2}}\right),$$

(1)

where μ is mean, and σ is standard deviation.

Accuracy analysis

The MAE, ME, MAPE, and MPE are defined as

$${{{\rm{MAE}}}}=\frac{1}{n}\sum\limits_{i=1}^{n}| {y}_{i}-{\hat{y}}_{i,{{{\rm{exptl}}}}}| ,$$

(2)

$${{{\rm{ME}}}}=\frac{1}{n}\sum\limits_{i=1}^{n}\left({y}_{i}-{\hat{y}}_{i,{{{\rm{exptl}}}}}\right),$$

(3)

$${{{\rm{MAPE}}}}=\frac{1}{n}\sum\limits_{i=1}^{n}\frac{| {y}_{i}-{\hat{y}}_{i,{{{\rm{exptl}}}}}| }{\hat{y}_{i,{{{\rm{exptl}}}}}},$$

(4)

$${{{\rm{MPE}}}}=\frac{1}{n}\sum\limits_{i=1}^{n}\frac{\left({y}_{i}-{\hat{y}}_{i,{{{\rm{exptl}}}}}\right)}{{\hat{y}}_{i,{{{\rm{exptl}}}}}},$$

(5)

where y_i is the predicted value, ${\hat{y}}_{i,{{{\rm{exptl}}}}}$ is the experimental value, and n is the number of data points.

Pearson correlation coefficient

The correlation coefficient between the band gap and structural parameters is calculated by Pearson correlation coefficient

$${r}_{xy}=\frac{{\sum }_{i = 1}^{n}\left({x}_{i}-\bar{x}\right)\left({y}_{i}-\bar{y}\right)}{\sqrt{\mathop{\sum }_{i = 1}^{n}{\left({x}_{i}-\bar{x}\right)}^{2}}\sqrt{\mathop{\sum }_{i = 1}^{n}{\left({y}_{i}-\bar{y}\right)}^{2}}},$$

(6)

where n is sample size, x_i and y_i are individual sample points, and $\bar{x}$ and $\bar{y}$ are sample mean.

SLME

The SLME is defined as⁸⁴

$$\eta =\frac{{P}_{{{{\rm{m}}}}}}{{P}_{{{{\rm{in}}}}}},$$

(7)

where P_m is the maximum output power density, and P_in is the total incident solar power density. P_m is obtained by maximize the power density

$$\begin{array}{ll}{P}_{\rm{m}}=\mathop{\max }\limits_{V}\{JV\}\\\!\!\qquad=\mathop{\max }\limits_{V}\left\{\left({J}_{\rm{sc}}-{J}_{0}\left({e}^{\frac{eV}{kT}}-1\right)\right)V\right\},\end{array}$$

(8)

where J is the current density, V is the voltage, J_sc is the short-circuit current density, J₀ is the reverse saturation current density, e is the elementary charge, k is the Boltzmann constant, and T is the temperature. P_in is obtained by summing the solar spectrum

$${P}_{{{{\rm{in}}}}}=\int_{0}^{\infty }E{I}_{{{{\rm{sun}}}}}(E){{{\rm{d}}}}E,$$

(9)

where E is the photon energy, I_sun is the AM1.5G solar spectrum.

Short-circuit current density J_sc is given by

$${J}_{{{{\rm{sc}}}}}=e\int_{0}^{\infty }a(E){I}_{{{{\rm{sun}}}}}(E){{{\rm{d}}}}E,$$

(10)

where a(E) is the photon absorptivity of the material giving by

$$a(E)=1-{{{{\rm{e}}}}}^{-2\alpha (E)L},$$

(11)

where α(E) is the absorption coefficient, and L is the thickness of the material. Reverse saturation current density J₀ is given by

$${J}_{0}=\frac{{J}_{0}^{{{{\rm{r}}}}}}{{f}_{{{{\rm{r}}}}}},$$

(12)

where ${J}_{0}^{{{{\rm{r}}}}}$ is the radiative recombination current density given by

$${J}_{0}^{{{{\rm{r}}}}}=e\pi \int_{0}^{\infty }a(E){I}_{{{{\rm{bb}}}}}(E,T){{{\rm{d}}}}E,$$

(13)

where I_bb is the black-body spectrum, and f_r is the fraction of radiative recombination given by

$${f}_{{{{\rm{r}}}}}=\exp \left(\frac{{E}_{{{{\rm{g}}}}}-{E}_{{{{\rm{g}}}}}^{{{{\rm{da}}}}}}{kT}\right),$$

(14)

where ${E}_{{{{\rm{g}}}}}^{{{{\rm{da}}}}}$ is direct allowed band gap, and the E_g is the band gap.

As a result, the SLME depend on the α(E), E_g, ${E}_{{{{\rm{g}}}}}^{{{{\rm{da}}}}}$, L, and T. The band gap E_g and the direct allowed band gap ${E}_{{{{\rm{g}}}}}^{{{{\rm{da}}}}}$ are obtained from the band structure. The material thickness L is assumed as 200 nm, and temperature T as 300 K. The absorption coefficient α(E) is calculated from the dielectric function

$$\alpha (E)=\frac{2E}{\hslash c}\sqrt{\frac{\left\Vert \varepsilon (E)\right\Vert -\Re \varepsilon (E)}{2}},$$

(15)

where ℏ is the reduced Planck constant, c is the speed of light in vacuum, and ε(E) is the dielectric function.