Introduction

Refractory multi-principal element alloys (RMPEAs)1, mainly composed of elements with high melting points (e.g. Mo, Nb, Ta, W, V, Hf, Ti), have attracted lots of interest due to their superior properties at elevated temperatures. For example, MoNbTaW and MoNbTaVW have yield stresses normalized by densities being two to four times higher at 1000 ∘C compared to Inconel 718 and Haynes 2302.

The fundamental plastic deformation mechanisms behind the remarkable mechanical properties of RMPEAs are extremely complicated. The effects of microstructures, e.g., lattice distortion and chemical short-range order (SRO), on RMPEAs’ deformation were extensively explored recently3,4,5,6,7. The core of the plastic deformation in RMPEAs is dislocation movement, which is intimately connected to critical resolved shear stress (CRSS) for the dislocation to move. Due to the spatial atomic disorder in RMPEAs, the CRSS is strongly location-dependent, leading to a distribution8. It has been shown that SRO enhances the average CRSS in RMPEAs9,10. Lattice distortion is another key factor that contributes to the strength of a material, and the distortion in MPEA is believed to be much more severe than that in dilute alloys11. Previous investigations showed a positive correlation between the strength and lattice distortion7,12,13. The constituent elements of the alloys are also crucial to the mechanical properties of the MPEA14,15. These studies explored the effects of local atomic environments on the strengths of MPEAs from different aspects and emphasized the importance of the factors that they considered. However, to our best knowledge, no studies to date have provided a comprehensive investigation of how multiple aspects of local atomic environments, including the local elements, SRO, and lattice distortion, affect the RMPEAs’ strength.

Due to the vast compositional space of refractory elements, it is extremely time-consuming and expensive to fabricate these alloys. The requirement to reveal the atomic-level deformation of the alloys adds additional challenges to the experimental materials characterization. Computational simulations thus become an important tool in elucidating the fundamental atomistic mechanisms behind the observed strengthening in RMPEAs. On the other hand, the high computational cost limited the density functional theory (DFT) calculations to several hundreds of atoms. Therefore, higher-scale methods such as molecular dynamics (MD) have become an important approach to studying mechanical properties and the associated underlying mechanisms16,17 in alloys. The accuracy of MD simulations primarily lies on the interatomic potentials18, most of which are unfortunately not good for RMPEAs. The recent development of machine learning interatomic potentials (ML-IAPs)19,20,21,22,23, which can reach near-DFT accuracy at several orders of magnitude lower cost than DFT, provides an opportunity. The structural and mechanical properties of MPEA have been extensively studied in recent years. For example, Kostiuchenko et al.24 used an “on lattice” low-rank ML potential to study the phase stability and transition of the single-phase MoNbTaW MPEA. Zheng et al.25 and Yin et al.6 conducted detailed research of SRO effects on dislocation glide of MoNbTi/TaNbTi and MoNbTaW RMPEA with the moment tensor potential (MTP). Dai et al.26 investigated thermal and elastic properties of high entropy (Ti0.2Zr0.2Hf0.2Nb0.2Ta0.2)B0.2 with deep learning potential. Byggmaster et al.27 trained a Gaussian approximation potential (GAP) and investigated the defects in MoNbTaVW MPEA. To go further, with an ML-IAP that balances precision and efficiency, high-throughput, systematic computations of RMPEAs are made possible. The subsequently generated consistent data can be utilized to enable the construction of reliable and accurate ML models, hence further speeding up the material property predictions.

In this work, we develop an MTP model for the refractory Mo-Nb-Ta-V-W alloy system by training on tens of thousands of data points. We demonstrate that the MTP model can achieve near-quantum accuracy across a wide range of properties, including energies, forces, elastic properties, and stacking fault energies. CRSS of both edge and screw dislocations in a large amount of different local atomic environments (around 1900) are subsequently generated. By comparing two key parameters in the solid solution theory, i.e., the atomic radius mismatch and the elastic mismatch, we show that the SRO strengthening is attributed to not only the stronger bonds between atoms but also the stronger atomic radius and elastic mismatch in the local environment. With newly designed solid solution-strengthening parameters in this work, we can predict the average CRSS and rank the parameter importance through an ML model. For the latter, it is found that the lattice distortion is the lead contributor to the CRSS of an edge dislocation, while the elastic mismatch contributes to the CRSS of a screw dislocation more than other factors.

Results

ML-IAP

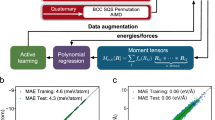
In this section, we discuss the results of the development of an ML-IAP for the Mo-Nb-Ta-V-W system. We generate the training data (see the Method section for details and Supplementary Fig. 1 for the visualization of the conformational space of the dataset) for elemental, binary, ternary, quaternary, and quinary systems, and employ a similar approach as our previous studies6,10 to fit the potential based on MTP formalism. Additional discussion about the importance of the complex composition in the training dataset can be found in Supplementary Tables 1 and 2. We choose MTP since it has an excellent balance between accuracy and computational cost among multiple ML-IAP formalisms23 and can accurately predict the dislocation-related properties in RMPEAs, including the generalized stacking fault energy10, dislocation core structures10, dislocation core energies6, and CRSS10.

Figure 1 shows a comparison of the DFT- and MTP-predicted energies and forces for both training and testing data. An excellent fit was achieved for energies and forces, i.e., with the mean absolute error (MAE) less than 3 meV/atom and 0.05 eV/Å, respectively. In addition, no bias in performance is observed for any particular chemistry system. The basic materials property predictions of the MTP model with reasonable accuracy, including lattice constants, elastic constants, phonon dispersions, are also provided in Supplementary Table 3 and Figure 2. These results demonstrate the accuracy and validity of the developed MTP model.

Fig. 1: MTP model performance for energies and forces.
figure 1

Parity plots of the MTP predictions versus DFT for (a) energies and (b) forces. For energy prediction, the MAE is 2.1 meV/atom and 2.2 meV/atom for training and testing data, respectively. For force prediction, the MAE is 0.046 eV/Å and 0.040 eV/Å, respectively.

Full size image

SRO in MoNbTaVW RMPEA

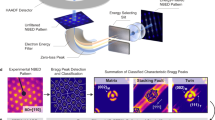
Due to the different mixing energy between pairs of atoms among the five metals, the MPEA system does not consist of completely randomly distributed atoms3. Instead, some pairs tend to attract each other, while some tend to repulse each other. To investigate the SRO effect, configurations with different atomic local environments are created, i.e., a random solid solution (RSS) configuration and configurations with different degrees of SRO. It is known that the degree of SRO will decrease as the annealing temperature increases in MPEAs25,27. Thus we selected three representative configurations that show different levels of SRO: (1) an RSS, corresponding to the equilibrium configuration at a sufficiently high temperature, (2) a room temperature (300 K) equilibrium state of SRO, and (3) a configuration with the theoretically largest SRO, i.e., equilibrium state of SRO at 0 K. To equilibrate the SRO state, we perform a hybrid MD/Monte Carlo (MD/MC) simulation to the RSS cell until reaching the respective equilibrium states (see the Method section for details).

Figure 2 plots the initial RSS and final equilibrium configurations at O K (top panels a and b) and 300 K (bottom panels d and e), respectively. As confirmed by the pairwise multi-component SRO parameters28 shown in panels c and f, the SRO at 0 K is more pronounced than that at 300 K. At either temperature, some pairs of dissimilar atoms like Mo-Ta and V-W attract each other. From 300 K to 0 K, the sign of the SRO parameters does not change, but the absolute values of almost all pairs increase. Although the overall energy reduction per atom from the random to the ordered system is relatively small, the local environment changes a lot and will influence material properties. A hybrid MD/MC simulation is also performed in a polycrystal to assess how atoms segregate at grain boundaries, which can be found in Supplementary Table 4.

Fig. 2: Crystal models before and after MC/MD simulation and the corresponding SRO parameters.
figure 2

Snapshot of the quinary system before and after the MC simulation at a, b 0 K and d, e 300 K, respectively. c and f are the corresponding tables of SRO parameters. For MC at 300 K, slices of the (110) plane before and after the MC simulations are shown at the corresponding bottom right corner to display clearer SRO effects.

Full size image

GSFE

Once the structures are constructed, we explore the mechanical properties of the MoNbTaVW RMPEA. First, we calculate the GSFE, which is strongly relative to the strength and ductility of metals29, and influences the motion of a dislocation30. The simulation is done by shifting half of the cell in the \(\left\langle 111\right\rangle\) direction on the {110} plane, with a vacuum added to the cell along the {110} plane normal such that only one stacking fault exists. The shifting in one step is 0.02 of the atomic spacing in the glide direction, and the system is relaxed along the glide plane normal following each shift. A previous study showed that relaxation in the other in-plane direction has little effect on GSFE31.

Figure 3a presents the GSFE curves for all five elements along with two quinary MPEA systems, one with SRO annealed at 300 K, the other is a random solid solution. Solid lines are MTP-based values, while the X markers are previous DFT results32,33,34,35,36,37. Overall the GSFEs for all five elements are consistent between MTP and DFT, with W being the highest and V the lowest. No local minimum in GSFE is found in any element, suggesting the absence of metastable states. The curves for the quinary have a range because multiple parallel planes were considered38. The range for the RSS system is larger than that for the SRO system, in agreement with a prior finding for dislocation properties in MoNbTaW9.

Fig. 3: MTP model prediction in GSFE and the illustration of different slip planes.
figure 3

a GSFE curves. The glide plane is {110} while the glide direction is 〈111〉. Solid line sare MTP-based values, while the X markers are previous DFT results. b The atomic ratios in two different layers are shown to illustrate the local environment fluctuation.

Full size image

CRSS

Pure metals

The CRSS for a dislocation to start moving is another essential property controlling the strength of a material39. In BCC pure metals, the CRSS of a screw dislocation is about two orders of magnitude larger than that of an edge dislocation. As a result, the strengths of BCC metals are controlled by screw dislocations40,41,42.

We calculate the CRSS of five pure metals using the periodic array of dislocation (PAD) model43. The dislocation is inserted in the center of the cell, while the Burgers vector is \(({a}_{0}/2)\left\langle 111\right\rangle\). Then a linearly incremental shear strain is applied to the system. When the strain is small, the stress increases with the strain; then at a certain strain, the stress declines sharply. At the same time, the dislocation starts to move. The CRSS is the maximum stress before the sharp decline. Table 1 summarizes the CRSS for the five elements and compares the screw dislocation to the experimental and DFT results. The predicted CRSS from MTP are calculated using both static and dynamic methods (see Method section for details). We obtain consistent results from these two methods (see Table 1). The MTP-based CRSS for screw dislocations are 2–3 times higher than that measured from experiments due to the quantum effect44, which cannot be considered in atomistic simulations. For dynamic simulations, the much larger strain rate compared to the experiment can have additional effects. While the MTP results can achieve an excellent agreement with DFT results with the same value order. The screw-to-edge ratio in CRSS ranges from about 50 to 300 based on the MTP results.

Table 1 CRSS of both screw and edge dislocations in five pure metals with comparing experiment values for screw dislocation
Full size table

RMPEAs

Here, we insert the same dislocations into the cells for RMPEAs which possess different degrees of SRO. The method to obtain CRSS in RMPEAs is similar to that for pure metals, except that multiple CRSS are calculated for each RMPEA because of the spatially varying local atomic environments. As a result, the CRSS in an RMPEA, even when atoms are randomly distributed, have a wide range. Specifically, we calculated 25 CRSS for each RMPEA.

First, we focus on the equal atomic systems, the values of which are listed in Table 2. For the screw dislocation in MoNbTaVW, the mean CRSS (1718 MPa) is higher than the prediction based on the simple rule of mixture (1593.8 MPa), in agreement with a previous study15; at some point of the system, CRSS for the quinary is higher than that for W, which possesses the highest CRSS among the five metals. For the edge dislocation, while its mean CRSS (1058 MPa) is still smaller than that for the screw dislocation, the two values become more comparable than in pure metals, suggesting that both edge and screw dislocations become important in governing the strength of the quinary. Similar patterns have also appeared in the other quaternary systems. Most of those values in systems with SRO have varying degrees of increase compared with those in random systems. The specific value distribution of the quinary system can be found in the Supplementary information with the differential-displacement maps at distinct positions to show environmental fluctuations in Supplementary Figs. 4 and 5. For further investigation of the strengthening mechanism, we calculate more non-equal atomic systems, in which one element’s concentration is adjusted from 0.5 to 1.5 with respect to other elements. All those values including screw and edge dislocation in equal and non-equal systems; random and ordered systems are shown in Fig. 4, which contains 76 systems in all. Each system goes through the same calculation as we just mentioned above. A detailed list of all alloys we have studied can be found in Supplementary Table 5. Generally, the CRSS of two types of dislocations presents an opposite pattern: a certain system with high CRSS of edge will have a relatively low value of screw and vice versa. Such a pattern suggests that the strengthening factors contributing to different dislocation types differ.

Table 2 Average CRSS and standard errors of equal atomic quinary and quaternary systems, including both screw and edge dislocations; in random and systems with SRO
Full size table
Fig. 4: Average CRSS values in each alloy/configuration with respect to the screw-to-edge ratio.
figure 4

Each alloy system contributes two data points in this figure: one for the random structure and another for the SRO structure.

Full size image

Factors contributing to the elevated CRSS in RMPEAs

One explanation for the high strength of MPEA compared with conventional metals is the solid solution strengthening mechanism. Former research has attributed the solid solution strengthening to the atomic size and elastic mismatch between solute and solvent atoms2,45,46,47,48. In conventional alloys, a solute atom with a different radius and elastic constants becomes a pinning site where the dislocation needs extra applied stress to bypass, as a result of which the material becomes stronger. In MPEAs, nearly every atom has a different size and elastic modulus from nearby atoms. Thus, severe lattice distortion arises across the entire system, and all atoms can be regarded as solute atoms. Eq (1) is the solute-specific distortion that causes the solid solution strengthening, where \({\eta }^{{\prime} }\) represents the elastic modulus mismatch and δ is the atomic size mismatch. ξ and α are constants. ξ is related to the number of active slip systems and α represents the governing type of dislocations during deformation.

$$B={(\xi \sqrt{{\{{\eta }^{{\prime} }\}}^{2}+{\{\alpha \delta \}}^{2}})}^{\frac{4}{3}}$$
(1)

First, we focus on the lattice distortion, which has been shown as a key factor in affecting material strength, dislocation mobility, and CRSS7,12,13.

Traditionally, the lattice distortion is represented by the atomic size mismatch through the following formulation48,

$$\delta =\sqrt{\sum\limits_{i=1}^{n}{c}_{i}{(1-{r}_{i}/\overline{r})}^{2}}$$
(2)

where ri and \(\overline{r}\) is the atomic radius of element i and average atomic radius, ci is the concentration of element i, and n is the total number of atomic types. However, this expression, as well as others45,49, consider only the fraction and radius of constituent atoms but not the atomic arrangement, as it assumes that the probability of each atom appearing within the nearest neighbor distance of a certain atom is the same and the local concentration is equal to the average concentration of the alloy. However, our SRO structures show clear attraction and repulsion effects, and pairs like Ta/Mo and V/W have relatively large radius misfits.

Therefore, here we use the average atomic displacement to represent the lattice distortion, i.e.,

$$d=\frac{1}{N}\sum\limits_{i=1}^{N}\left\vert {r}_{i}-{{r}_{i}}^{{{{\rm{ideal}}}}}\right\vert$$
(3)

which describes the deviation of the atoms’ sites after relaxation from their ideal sites50, and N is the total number of atoms. Table 3 presents the average atomic displacements in both RSS and SRO systems, showing a clear discrepancy that all SRO alloys have a stronger distortion except for MoNbTaW. Again, all SRO structures are constructed at 300 K.

Table 3 Average atomic displacement (in Å) for RSS and SRO systems of the quinary and different quaternaries
Full size table

Figure 5 shows the displacement vectors of different structures. In the RSS system, the displacement has a near-uniform distribution. In the SRO system, as some atoms get clustered (i.e., Mo/Nb/Ta and V/W), large distortion appears at the boundaries of different clusters and affects nearby regions, which explains why, for the same alloy, the lattice distortion in the SRO system is larger than that in the RSS system. The only exception is MoNbTaW, in which the attractive atom pairs are Ta/Mo and Nb/W, which have similar atomic volumes, 15.524/17.985 Å3 and 15.807/17.952 Å3 respectively, thus no clear cluster boundaries are observed in MoNbTaW. As such a system becomes locally ordered, the probability of a certain type of atom that is attracted by the central atom appearing in its nearest neighbor significantly increases, causing a more symmetric force field around the atom compared to a random system. Under a relatively symmetric force field, an atom will be less likely to deviate from the center position, so the lattice distortion decreases.

Fig. 5: Comparison of lattice distortion between different alloy systems.
figure 5

Relaxed structure of a random MoNbTaVW, b MoNbTaVW with SRO, c MoNbTaW with SRO. d–f are corresponding displacement vector maps with different colors indicating displacement variations from 0 to near 0.4 Å, and red circles denote high-distortion regions.

Full size image

Next, we consider another factor that contributes to the elevated CRSS in MPEAs: the elastic mismatch. Traditionally, this mismatch is quantified by46

$${\eta }_{i}=2\frac{{\mu }_{i}-{\mu }_{{{{\rm{alloy}}}}}}{{\mu }_{i}+{\mu }_{{{{\rm{alloy}}}}}}$$
(4)

where μi and μalloy are the shear moduli of element i and alloy, respectively. The shear modulus of an alloy can be estimated by

$${\mu }_{{{{\rm{alloy}}}}}=\sum\limits_{i}^{n}{c}_{i}{\mu }_{i}$$
(5)

where ci is the concentration of element i. Similar to Equation (2), the above equation does not show the difference between the random and SRO systems, as it assumes that the probability of atom pair interaction depends only on the atomic concentration. Here, we develop a new elastic mismatch parameter:

$${\eta }_{i}=2\frac{{\mu }_{i}-\sum\nolimits_{j}^{n}{p}_{ij}{\mu }_{j}}{{\mu }_{i}+\sum\nolimits_{j}^{n}{p}_{ij}{\mu }_{j}}$$
(6)

where pij is the average probability of finding an j-type atom appearing in the nearest shell around an i-type atom, as the average shear modulus around i-type atoms is calculated by weighted average. In locally ordered systems, atomic pairs with large shear modulus misfits like Ta/Mo become more likely to appear in the nearest neighbor with a relatively small, negative SRO parameter. On the other hand, the Mo/W pair with similar shear modulus is repulsive, with relatively large SRO parameters. As a result, the elastic mismatch η is also enhanced by SRO.

In addition to the two solid solution strengthening factors discussed above, the SRO itself is also a key factor for MPEA strengthening. As attractive pairs of atoms become aggregated, the bonds generally become stronger, affecting the strength of a material. To quantify the SRO effect, we can use the root mean square of SRO parameters,

$${\sigma }_{{{{\rm{SRO}}}}}=\sqrt{\frac{\sum\nolimits_{i}^{n}\sum\nolimits_{j}^{n}{a}_{ij}^{2}}{{n}^{2}}}$$
(7)

where aij are SRO parameters in Section SRO in MoNbTaVW RMPEA and can be calculated by Equation (13), which considers the degree of how the atoms are orderly arranged. A similar method to quantify SRO based on the Warren-Cowley parameters has also been used in a previous study25. Since the influence of SRO results from the changes in the bonding strength of rearranged atoms, we can quantify the SRO strengthening by a parameter describing the mixing or binding energy,

$${\sigma }_{E}^{{{{\rm{mixing}}}}}=\sum\limits_{i}^{n}{c}_{i}\sum\limits_{j}^{n}{p}_{ij}{E}_{ij}^{{{{\rm{mixing}}}}}$$
(8)
$${\sigma }_{E}^{{{{\rm{binding}}}}}=\sum\limits_{i}^{n}{c}_{i}\sum\limits_{j}^{n}{p}_{ij}{E}_{ij}^{{{{\rm{binding}}}}}$$
(9)

where pij is again the average probability of finding an j-type atom appearing in the nearest shell around an i-type atom, and Eij is the mixing or binding energy per atom pair of B2 system consisting of ij atoms, which takes the strength of bonds into account. Mixing energy (per atom) in B2 systems of N atoms is \({E}_{ij}^{{{{\rm{mixing}}}}}=(E-\frac{N}{2}{E}_{i}-\frac{N}{2}{E}_{j})/N\) where E is the total energy of B2 system, and Ei and Ej are energy per atom of i- and j-type, respectively, at their ground state (pure BCC metal). We use the B2 structure for atomic pairs in the nearest neighbor completely consisting of different elements, while a random binary alloy has mixed A-A/A-B pairs. The calculation of binding energy has the same formula except that Ei and Ej are energies of an isolated i- and j-type atom, respectively. It is worth noting that the calculations about mixing and binding use DFT instead of our potential. The mixing energy of different elements directly controls whether they are attractive or repulsive and how strong the trend is, and it’s also closely related to the energy decrease during MC swaps. On the other hand, binding energy directly describes the strength of bonds, such that CRSS which involves bonds’ breaking and rebuilding during dislocation movement will be influenced.

Once all parameters are determined, we study how they affect the CRSS. We first focus on the screw-to-edge ratio in CRSS because it was shown to influence the ductile-to-brittle transition in BCC metals51. Figure 6a shows the overall negative correlation between lattice distortion and screw-to-edge ratio in CRSS. The concentration of V, which has the smallest atomic size among all refractory elements52, in those systems is highlighted. As expected, increasing the V concentration increases lattice distortion, and the screw-to-edge ratio in CRSS tends to decrease. If we extrapolate the trend to zero lattice distortion, i.e., pure metals, the CRSS ratio between screw and edge dislocation will be extremely high, which is consistent with our findings. Relationship between CRSS and lattice distortion can also be found in Fig. 6b, where there is a slight negative/positive correlation between lattice distortion and screw-to-edge ratio in CRSS.

Fig. 6: Correlation between lattice distortion and CRSS.
figure 6

a The screw-to-edge ratio in CRSS is plotted against the lattice distortion. The color of points displays the concentration of V. b CRSS of screw and edge dislocation against the lattice distortion.

Full size image

ML model for CRSS prediction

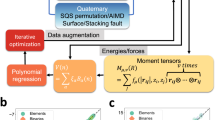
In this subsection, we construct an ML model to assess how factors discussed so far contribute to the CRSS. The model we used is XGBoost, which is an optimized distributed gradient boosting library and implements ML algorithms under the Gradient Boosting framework. We start with 5 feature parameters calculated by Eqs. (3), (6), (7), (8), (9). Since correlations may exist between these feature factors, leading to redundant features, we perform cross-validation (CV) for different combinations of the features to find the best one with the lowest test error. The prediction target is the CRSS normalized by the shear modulus. Figure 7(a) shows the root mean square error (RMSE) in CV tests for both edge and screw CRSS prediction, with the best subsets (i.e., the smallest RMSE) marked by triangles. The CV shows that if we use three feature parameters (d, η, and \({\sigma }_{E}^{{{{\rm{mixing}}}}}\) in Eqs. (3), (6), (8)), we can reach the smallest test RMSE. Adding more features would not significantly reduce RMSE. Figure 7 (b,c) is the comparison between calculated values and predicted values by XGBoost model. Data in the train set are displayed in blue while the test set in red. Features importance in Fig. 7(d,e) shows that lattice distortion contributes the most for both dislocation types as it dominates the strength of a material. For edge dislocation, the importance of lattice distortion is much higher than the second factor, modulus mismatch, while for screw dislocation, although lattice distortion is still dominant, the importance of the first and second contributors is closer.

Fig. 7: XGBoost model for CRSS prediction.
figure 7

a Different feature combinations with their corresponding RMSE in CV tests, dashed lines show the variation of the smallest RMSE with different numbers of features and the best combination is marked by triangles. b, c Comparison between calculated and predicted CRSS/G for screw and edge dislocations, blue and red points representing train and test sets. d, e Corresponding feature importance. b, d for edge dislocation while c, e for screw.

Full size image

DISCUSSION

Here we constructed an XGBoost model for CRSS prediction. All the dataset is calculated by our verified potential to ensure consistency, as different dislocation models and/or potentials will lead to significantly different results for CRSS calculations31. Thousands of calculations are conducted with different local environments of dislocations, considering different atomic ratios and/or SRO. For a given ratio and SRO, we calculate the average CRSS. A large data on our dislocation structures and calculated CRSS value are constructed, and those data can be used for further investigations like how specific elements influence the CRSS, what range of atoms will influence the CRSS, or direct prediction of CRSS from structure, etc.

Feature importance shows the CRSS of edge dislocation is controlled mostly by lattice distortion and partly by elastic mismatch and mixing energy, while lattice distortion and elastic mismatch contribute to screw dislocation’s CRSS with relatively close importance, and it’s also influenced by mixing energy. Some studies omit the influence of elastic mismatch12,45, while in our studies the elastic mismatch is of near-equal importance compared to lattice distortion for screw dislocation. These results match the traditional solid solution strengthening theory that the value of α in Equation (1) becomes larger as the importance of edge dislocations becomes greater in a material, and δ becomes more important. Besides, although lattice distortion is positively related to the yield strength of alloys, the pattern seems to be contrary to our findings for screw dislocation, as high distortion systems have relatively low CRSS for screw and high CRSS for edge, resulting in a low screw-to-edge ratio, which means the high lattice distortion prefers to enhance edge dislocation which is weaker compared to screw in BCC alloys to enhance the strength.

Mixing energy is the least important contributor for both dislocation types according to the feature importance analysis, which is also an indicator of the strength of SRO. While this work on the local atomic environment analysis shows that the contribution of SRO to CRSS is not only reflected in its direct impact, e.g., the SRO strengthening effect is often attributed to bond strength53, but we also find that rearranged atoms with SRO have improved lattice distortion and elastic mismatch. Such phenomenon results from attractive atom pairs in our systems like Ta/Mo or V/W which have large radius or shear modulus differences. A similar pattern can be found in former studies that in BCC NbHfTiZr MPEA54: Hf/Zr are observed to be rich in certain regions which have the biggest radius difference and almost the biggest shear modulus difference among the four elements. Unfortunately, the formation of SRO is rapid in material manufacturing, and there are no systematic studies yet on how to control the degree of SRO by experimental methods.

In alloy design, it is usually difficult to maximize solid solution strengthening due to the trade-off between competing effects55. Large elastic misfit needs the combination of extremely soft and stiff elements, while sniff elements tend to have an intermediate size that weakens lattice distortion or radius mismatch. Since the correlation between different parameters and dislocation types is also different, we can put particular emphasis on certain parameters and dislocation types, and design alloys for different purposes. Ductile systems can be built by combining elements with significantly different sizes which leads to high CRSS of edge dislocations and low screw-to-edge ratio, while focusing on elastic mismatch can achieve higher CRSS of screw dislocations and screw-to-edge ratio which ensures screw dislocation is governing the strength and makes an alloy even stronger. Furthermore, the selection of element pairs with large atomic size or elastic modulus misfit that we may emphasize for corresponding purposes should also have as low mixing energy as possible to further enhance the strengthening effect.

Methods

ML-IAP

Our ML-IAP is based on MTP22. The energy calculated by the MTP is the sum of the contribution by every atom, and the potential energy of each atom depends on the atomic neighbor environment:

$$E=\sum\limits_{i}{V}_{i}\left({u}_{i}\right)$$
(10)

where ui is the coordinate of the neighboring atoms within the sphere shell for atom i. The number of atoms considered around the central atom is determined by a cutoff radius Rc. Vi is a linear combination of a series of basis functions Bl(Ri) and parameters θl:

$${V}_{i}=\sum\limits_{l=1}^{m}{\theta }_{l}{B}_{l}({R}_{i})$$
(11)

where the number of functions, m, is chosen based on a balance of accuracy and computational efficiency. The basis functions B(R) are formulated by contracting a set of moment tensors to a scalar, and the moment tensors are devised as follows:

$${M}_{\mu ,\nu }(R)=\sum\limits_{j}\,{f}_{\mu }{R}_{ij}\bigotimes \ldots \bigotimes {R}_{ij}$$
(12)

where fμ is the radial distribution of the local environment around atom i and these functions are specified according to the atomic type of the neighbor atom j. Rij⨂…⨂Rij are tensors of rank υ including the angular information about the atomic environment. The moment tensors as local environment descriptors are contracted rotationally invariant, and the basis functions satisfy all physical symmetries.

Training data

A sufficiently large number of samples is the key to fitting a potential, but too much data can also result in a waste of computational time, and even overfitting. The categories of data included in the training are determined based on our previous works on the binary16 and quarternary alloys10, which have achieved success in describing the dislocation-based properties. In the meantime, during the training procedure for the quinary potential, we manually perform the iteration between fitting and validating by adjusting the training data to ensure the validity of the potential. The optimized final training dataset for a quinary system includes all the combinations from unary to quinary. Detailed descriptions of the training data are shown below,

  1. 1.

    Elemental systems

    • Snapshots from AIMD NVT simulations of the bulk 3 × 3 × 3 supercell at 300, 1000, and 3000 K, respectively. Additional snapshots are also obtained from AIMD NVT simulations at 300 K at 90% and 110% of the equilibrium 0 K volume. Interval for snapshots is 0.1 ps, 200 snapshots are taken for each element.

    • Structures for all the surfaces with a maximal Miller’s index less than 3.

    • Strained conventional cell structures, including the ground state structures, with strains from10% to 10% at 1% intervals in six different modes56.

  2. 2.

    Binary systems

    • AxB1−x solid solution structures with random atomic configuration where x ranging from 0 to 100 at% at intervals of 6.25 at% in a 2 × 2 × 2 supercell.

  3. 3.

    Ternary, quaternary, and quinary systems

    • Special quasi-random structures (SQSs)57 generated by ATAT code58 in 3 × 3 × 3, 4 × 4 × 4, 5 × 5 × 5 bulk for ternary, quaternary and quinary systems, respectively. Both the relaxed and the unrelaxed structures, including the snapshots during structural optimization, are included to improve the prediction of the forces.

    • Snapshots from AIMD NVT simulations of the SQSs at 300, 1000, and 3000 K, respectively.

Atomistic simulations

All simulations below are performed using LAMMPS59 with the newly developed MTP.

  • GSFE. The glide plane is (\(\overline{1}10\)), while the displacement is along \([\overline{1}\overline{1}1]\). The direction normal to the glide plane is set non-periodic to prevent periodic images from affecting each other. The displacement in each step is 0.02 of the atomic spacing in the glide direction. Since the energy curve is periodic, only one period is calculated.

  • CRSS. The CRSS is calculated at 0 K using the molecular statics approach. The system starts from a thin structure, with only a few layers of atoms along the dislocation line direction. For the alloy systems, the structure is a supercell about 11 × 9 × 3 nm while for elements it is about 5 × 3 × 2 nm, the second dimension is along the slip plane normal and the last dimension is along the dislocation line. The supercell for alloys is larger to ensure that the elements are uniformly arranged in a random system and display local ordering in an SRO system. The dislocation is inserted in the middle of the system by Atomsk60 after a random or locally ordered bulk is constructed. For a screw dislocation, a small tilt factor is added to transform the originally orthogonal cell to a parallelepiped to keep the periodicity along the glide direction. The dislocation’s Burgers vector is 1/2\(\left\langle 111\right\rangle\) on a glide plane {110}. It follows that an incremental strain, 10−4 for the screw dislocation and 5 × 10−5 for the edge dislocation, is applied to the system to calculate the CRSS.

  • Dislocation mobility. All the orients of the bulk and dislocation are set to be the same with CRSS calculations by molecular statics. We use much larger systems with about 23 × 12 × 8 nm for dislocation mobility calculations. Each velocity data under a certain shear stress is acquired by equilibrating the system under the target temperature which is 10 K in this work, linearly applying the shear stress, and maintaining the shear stress step by step. Dislocation line and corresponding atomic coordinates are extracted and identified by OVITO61. The CRSS can be identified between the interval stresses between which the dislocation starts to move. Detailed velocity-stress curves can be found in Supplementary Fig. 3.

  • MC/MD simulation. The single crystal is a 15 × 15 × 15 cube. The MD simulation is performed at 300K. The system initially has a random atomic distribution, and only one pair of atoms is swapped in each MD step.

SRO parameters

The chemical SRO parameter we use here is:

$${a}_{ij}^{k}=\frac{{p}_{ij}^{k}-{c}_{j}}{{\delta }_{ij}-{c}_{j}}$$
(13)

where k refers to the k-th nearest-neighbor (kNN) shell of the central atom \(i,{p}_{ij}^{k}\) is the average probability of an atom j appearing in the corresponding shell around an atom i, cj is the average concentration of atom j in the system, and δij is the Kronecker delta function:

$${\delta }_{ij}=\left\{\begin{array}{ll}1&(i=j)\\ 0&(i\,\ne\, j)\end{array}\right.$$
(14)

For pairs of the same species, a positive SRO parameter means they tend to get close to each other, while a negative parameter suggests the opposite. For pairs of different species, the tendency is the opposite, i.e., a positive SRO parameter indicates repulsion while a negative one clustering.