Introduction

Insight of chemical bonds and knowledge of molecular symmetries allow us to quickly analyze and predict the vibrational spectrum and the activity of Raman and IR modes in simple molecules. This allows the practical identification of well-known stretching and bending signatures of different chemical species. Symmetries constrain the vibrational patterns to align on high symmetry planes and axes, while determining the multiplicity of modes and their Raman or IR activity. However, the power of group theory diminishes in more complex organic molecules where few or no symmetries are present, like in complex sugars, lipids, amino acids, or proteins1,2. Interpreting the vibrational spectrum in these cases is much more challenging, as the number of Raman and IR active modes increases linearly with the number of atoms in the molecule. While intuition and experience are still fundamental assets to interpret vibrational spectra, theoretical predictions are a handy aid for experimenters. The accurate prediction of Raman and IR data often comes with major costs in the complexity of employing existing software and the computational resources required. High-level ab initio calculation needs powerful high-performance computers and a deep understanding of the theory behind these tools, while most empirical force fields lack the necessary precision. Moreover, atoms present in organic molecules are light and sensitive to sizable quantum fluctuations even at room temperature3, which can trigger the anharmonic nature of molecular bonds, as it occurs in the OH stretching3,4. While coupling quantum nuclear dynamics with advanced quantum chemistry tools to describe the electronic ground state has proven highly effective in reproducing—with high accuracy—the vibrational behavior of small molecules, its computational cost prevents its daily applications in more challenging systems.

Significant steps forward have been made thanks to the availability of machine-learning force fields for the interatomic potential, which were able to bring near chemical accuracy at a computational cost that is just a fraction of any ab initio calculation5,6,7. Of particular interest is the ANI-1ccx model8,9, trained on the GDB database of high-level coupled cluster CCSD(T) energies of organic molecules containing H, C, N, O atoms10, and the more recent ANI-2x, which extends the force-field by including S, F and Cl atomic species11, making up for ~90% of all drug-like molecules. The employment of such machine-learned force field allows the application of advanced tools to simulate the quantum nature of nuclei accounting for anharmonicity in both solids and molecules, like path-integral molecular dynamics (PIMD) (see, e.g., refs. 12,13,14). However, these calculations still remain time-consuming when run on ordinary computers. Moreover, PIMD is a static theory in which extracting the dynamical features of the vibrational spectrum remains an open challenge.

In this work, we introduce a method able to capture the quantum anharmonic dynamics of the nuclei while keeping a good description of the electronic degrees of freedom to predict and analyze the vibrational spectrum of molecules as big as small proteins, with a computational cost low enough to run on any common laptop for few hours. The method is distributed as an open-source web app named FAbulA : FAst viBroscopy of molecULes with Anharmonicity.

FAbulA combines the time-dependent Stochastic Self-Consistent Harmonic Approximation (tdSSCHA) to simulate the quantum and anharmonic motion of nuclei15 with different force fields for the interatomic potential. In the following sections, we describe the underlying methodology of tdSSCHA and the implementation of FAbulA in detail. We also present several examples of applications of the method to illustrate its capabilities.

Results

Outline of the FAbulA method

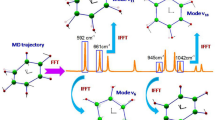
The calculation of Raman and IR spectra of a molecule is a two-step procedure: one has to (i) evaluate the frequencies and polarization modes of the atomic vibrations and (ii) simulate the molecular response to light irradiation, either inelastic Raman scattering or infrared absorption. FAbulA can compute the molecular vibrational excitations with three degrees of accuracy: (i) harmonic, (ii) static anharmonic, and (iii) dynamic anharmonic (Fig. 1).

Fig. 1: Schematic representation of the FAbulA method.
figure 1

Starting from an input molecule of known 3D structure, the method combines existing force fields with a simple capacitor model and point-charge model to build a starting dynamical matrix with an associated polarizability and polarization matrix, which are then minimized according to the SSCHA (Stochastic Self-Consistent Harmonic Approximation) theory. The SSCHA logo is reproduced with permission from the owner.

Full size image

The Harmonic spectrum is temperature-independent, and the infinite lifetime of lattice vibrations gives rise to arbitrary narrow spectral lines. The harmonic excitations are evaluated through a finite-difference approach, where the atoms are slightly displaced from their average positions, and curvature of the energy landscape is obtained from the numerical derivative of the forces. In particular, all the calculations in this work are performed using either ANI-1ccx or ANI-2x8. These are very accurate neural network force fields trained on high-quality quantum chemistry calculations and can be selected from the web interface/command line package of FAbulA (details in the Methods).

In the static anharmonic approach, FAbulA dresses the harmonic spectrum with anharmonicities triggered by quantum and thermal fluctuations of nuclei. The anharmonic shift corrects both the frequencies and polarization modes of the harmonic calculation. The procedure is a mean-field technique, where the curvature of the energy landscape is evaluated on an average region of the phase space obtained as the equilibrium ensemble of an auxiliary self-consistent Harmonic system. In particular, we adopt the SSCHA16. The overall static anharmonic spectrum is evaluated from the resulting self-consistent harmonic potential. Like in the harmonic case, phonon peaks have infinite lifetimes, but their position and intensity depend on temperature. Further details on the implementation are discussed in the Methods.

Lastly, the complete dynamical anharmonic calculation simulates the quantum dynamics of nuclei in the anharmonic potential at any given temperature. This approach goes beyond the mean field, enabling the scattering and decay of vibrations, resulting in a complex spectrum displaying the natural lifetime broadening of peaks, overtones, combinational modes, and complex satellite features. The dynamical anharmonic calculation is obtained as the linear response of the time-dependent stochastic self-consistent harmonic approximation (tdSSCHA)15,17. The computational cost of each approach is incremental, and each stage is a required starting point for the next one: the harmonic dynamical matrices are needed to initialize the SSCHA, and the self-consistent harmonic potential is required to set the equilibrium condition for the time evolution in the tdSSCHA.

The harmonic, SSCHA, and tdSSCHA runs allow for the evaluation of frequencies, polarization modes, and spectral functions of the molecule. However, to estimate the activity and intensity of each mode, we must simulate the interaction between photons and vibrations. FAbulA provides two models to compute the dipole and polarizability induced by the atomic motion, which can be employed to simulate the Raman and IR spectra. In particular, the coupling between light and the atoms in the lattice is modeled with the effective charges (Z) and Raman tensors (Ξ), representing the variation of dipole (μ) and polarizability (α) in the molecule when an atom is displaced from its equilibrium position:

$${Z}_{\alpha\, j\beta }=\frac{\partial {\mu }_{\alpha }}{\partial {R}_{j\beta }},\qquad {\Xi }_{\alpha \beta i\gamma }=\frac{\partial {\alpha }_{\alpha \beta }}{\partial {R}_{i\gamma }}.$$
(1)

The intensity of Raman and IR peaks within the harmonic and SSCHA approximation is estimated from the squared projection of the effective charge and Raman tensor on the polarization of each vibration as

$${I}_{\mu }^{({\rm{IR}})}=\sum _{j\beta \alpha }{\left(\frac{{Z}_{\alpha j\beta }{{e}_{\mu }}^{j\beta }}{\sqrt{{m}_{j}}}\right)}^{2},$$
(2)

where eμ is the polarization vector of the μ-th vibrational mode, and mj is the mass of atom j. We employ an analogous expression for the Raman, with a bit of extra care to cover the case of unpolarized light18 by estimating the so-called Placzek rotation invariats19. The dynamical IR spectrum is evaluated from the dipole autocorrelation function, while the Raman spectrum is obtained from the polarizability. Therefore, there is no predefined one-on-one assignment of each peak with the corresponding lattice vibration, but it also accounts for overtones, natural broadening, and combinational modes. The spectrum is evaluated using a Lanczos algorithm to invert the interacting anharmonic Green’s function15. More details are reported in the Methods section.

The computation of effective charges can be performed ab initio with linear response, as implemented in Quantum ESPRESSO20 for small molecules. For bigger systems, we approximate the effective charges as an isotropic charge on each atom qi,

$${Z}_{\alpha i\beta }={q}_{i}{\delta }_{\alpha \beta },$$
(3)

where the value of qi can be obtained from the input PDB structure, the topology files, or standard force-field parameters (point-charge model).

For the Raman intensities, we derived an analytical bond capacitor model, trained on a subset of ab initio estimations of small organic molecules, introduced and discussed in more detail in the Methods section. The bond capacitor model evaluates the Raman tensor for any organic molecule with a negligible computational cost compared to the calculation of vibrations.

Identification of vibrational modes from the spectrum

We tested the capability of FAbulA to evaluate the vibrational frequencies of organic molecules. Figure 2a displays the experimental Raman (left) and infrared (right) spectra of the five nucleic acids -i.e., adenine, cytosine, guanine, thymine, and uracil- as green curves in the 400–1700 cm−1 and 450–2000 cm−1 spectral ranges, respectively. Vertical blue and red lines mark the predicted active mode positions for Raman and infrared spectra, respectively. The thickness of the lines indicates the agreement between the position of the experiment and the predicted peaks. As one can see, FAbulA detects the peaks with higher spectral weight in both kinds of spectra. To determine active Raman/IR modes, we used our bond capacitor model to compute the polarizability dynamical autocorrelation and the effective charges computed ab initio (within DFPT as implemented in quantum ESPRESSO) for the dipole dynamical autocorrelation. Active modes are defined as those participating at least 0.01% of the total spectrum intensity. The unpolarized Raman spectrum of cytosine is reported in Fig. 2b, where we address the bond capacitor model efficacy. In particular, the overall relative intensity of the vibrational modes is well captured by the model, except for the 1250 cm−1 vibration, whose intensity is underestimated with respect to the experiment. Analogously, Fig. 2c reports the cytosine IR spectrum, where a similar good agreement is achieved. Overall, the FAbulA method estimates the relative intensities between the different modes at a small fraction of the computational cost required from a full ab initio simulation. In Supplementary Note 1, we report a careful test of the method versus ab initio simulation, separately assessing the impact on the vibrational spectra of the approximation of the potential energy landscape (the ANI neural-network force-field), the point-charge approximation for the IR intensity, and the bond capacitor model for the Raman tensor. Note that the obtained accuracy can be further increased considering the effect of the molecule’s surrounding environment. As discussed in Supplementary Note 2, FAbulA has the potential to simulate molecules in solution by explicitly accounting for the solvent structure. Considering cytosine embedded in a water shell allows FAbulA harmonic prediction to describe the experimental infrared spectrum of cytosine with a good approximation. FAbulA also provides the possibility to inspect visually and quantitatively (bending and stretching components) the atomic motion associated with each vibrational mode, which can be helpful in comparing the predicted Raman/IR features with similar known modes of different molecules.

Fig. 2: Comparison between experimental and predicted Raman and IR vibrational frequencies of the five main nucleobases.
figure 2

a From left to right, sticks representation of the considered nucleobasis, Raman, and infrared spectra. Green-shaded curves represent experimental Raman and infrared spectra of molecules in crystalline phase taken from the work of De Gelder37 and Bec et al.38, respectively. Blue and red vertical lines mark the positions of the active vibrational frequencies predicted by FAbulA with the SSCHA method. b Comparison between the experimental Raman spectrum of cytosine37 and the prediction of FAbulA with the SSCHA method combined with the neural-network derived-polarization matrix to determine the relative intensities. c Same as in b but for the infrared spectrum of cytosine.

Full size image

Peak relative intensity and width

While the SSCHA-based calculation provides a fast estimation of the vibrational mode positions considering anharmonic effects, it does not yield indications on the peak width. This information can be uncovered by employing the time-dependent SSCHA (see Methods for details). A comparison between the SSCHA and tdSSCHA approaches is provided in Fig. 3, where ethanol is considered as a case of study. Figure 3a, b shows the experimental Raman (panel a) and infrared (panel b) spectra of ethanol in the gas phase as green-shaded curves, together with the predictions of FAbulA using the SSCHA and tdSSCHA, respectively. As one can see, the positions of the prominent active peaks are significantly improved by employing the tdSSCHA. In addition, the time-dependent method also provides a quantitative estimation of the modes’ lifetimes, i.e., the peak linewidths, as evident, for instance, in the bending (~420 cm−1) and stretching (~920 cm−1) modes of Fig. 3b and Table 1.

Fig. 3: Comparison of FAbulA results using SSCHA or tdSSCHA method.
figure 3

a Comparison between the predicted (blue curve) and measured (green) Raman spectrum of the ethanol molecule. Experimental data for liquid ethanol are taken from ref. 39, while predictions are obtained via FAbulA with the SSCHA method. Frequencies of the four vibrational modes of higher intensity are reported. b Same as in a but using the tdSCHA method. c Same as in a but for the infrared spectrum of the ethanol molecule. Experimental data of liquid ethanol are taken from ref. 21. d Same as in b but for the infrared spectrum of the ethanol molecule.

Full size image
Table 1 Predicted vibrational modes of ethanol by FAbulA via the SSCHA, together with their percentage of stretching and bending components against the experimental Raman36 active modes and relative assignments
Full size table

In Fig. 3c, d, we reported, instead, the comparison between experimental21 and predicted absorbance infrared spectra for ethanol molecules in the gas phase. Also, the positions of predicted IR active modes are in accordance with experimental data. In particular, both relative intensities and lifetimes of the C–C stretching modes in the region ~1060 cm−1 are well reproduced by the tdSSCHA.

Temperature dependence

Being able to account for anharmonicities, FAbulA allows us to study the temperature-dependence behavior of vibrational modes. To test the capability of FAbulA, we considered the case of study of myristic acid, a common saturated fatty acid composed of 44 atoms for which the Raman active modes show a significative temperature dependence (Fig. 4). In particular, Miranda et al.22 collected unpolarized Raman spectra of myristic acid powders at different temperatures in the range of 20–300 K. At room temperature, myristic acid presents Raman active modes in the spectral range of 880–920 cm−1: one centered at ~897 cm−1 associated to the C13−C14 stretching and the other localized at ~910 cm−1 and assigned to C1–C2–C3 stretching and C1–H2 wagging. Interestingly, increasing the temperature produces three significant changes: (i) a red-shift of the 897 cm−1 and the 910 cm−1 modes, (ii) a decrease in the relative differences between the intensities of the two modes, and (iii) the disappearance of a third peak in the Raman spectrum a temperature lower than ~60 K. Figure 4c compares experimental and predicted Raman spectra for myristic acid at different temperatures. FAbulA reproduces the correct active modes and their relative intensities compared with experiments. Moreover, we successfully explain both the red-shift of the 897 cm−1 mode upon increasing the simulation temperature as an anharmonic interaction and the presence of the third mode–predicted to be a C−H2 rocking, as noted by ref. 23, disappearing upon heating. On the opposite, we do not reproduce the redshift of the 910 cm−1 mode, whose slight residual temperature dependence displayed in Fig. 4 is an effect of the stochastic sampling of the energy landscape.

Fig. 4: Temperature dependence of FAbulA results using the SSCHA method for myristic acid.
figure 4

a Balls and sticks representation of the myristic acid molecule with the associated atom nomenclature. b Comparison between predicted (blue curve) and measured (green) Raman spectrum of the myristic acid molecule. Experimental data of crystalline myristic acid are taken from ref. 37, while predictions are obtained via FAbulA with the SSCHA method. The frequencies of the two low-frequency vibrational modes of higher intensity are reported together with the corresponding atomic motion. c Comparison between experimental (left) and predicted (right) behaviors of the vibrational modes in the spectral region 850–950 cm−1 as a function of temperature. The experimental spectrum of crystalline myristic acid data is taken from Miranda et al.22. Atomic motions of the three observed peaks are shown together with their assigned modes.

Full size image

Discussion

Spectroscopy investigation of the optical properties of organic molecules is one of the easiest and most common ways to characterize a sample. In particular, Raman and IR signals help understand sample composition and provide valuable insights into the structural and chemical properties of the molecules. While experimental apparati for standard Raman and IR measurements are commonly available, tools for the rapid characterization of the measured vibrational profiles are still largely missing, and the interpretation of the observed spectra is often handwaving when not based on time-consuming numerical ab initio simulations. Indeed, over the past decades, various methods have been developed to address this problem, ranging from semi-empirical approaches to highly accurate quantum mechanical computations22. Among the latter, the self-consistent harmonic approximation has emerged as a powerful and efficient tool for the computation of anharmonic thermodynamic properties and spectra of small to medium-sized crystalline systems16. Indeed, the method has been shown to provide highly accurate prediction for condensed matter systems, and it is considered the state of the art in the field24,25,26.

In this work, we present FAbulA, a computational protocol for the fast computation of the vibrational modes of organic molecules, taking into account anharmonic effects. FAbulA is based on the union of the stochastic self-consistent harmonic approximation formalism, able to model the anharmonic fluctuations of atomic vibration4,15,16 and neural network-based force-fields for the rapid evaluation of the atomic interaction of molecules.

The main features of static FAbulA calculation include rapid evaluation of the vibrational modes of the given organic molecule, evaluation of Raman and infrared active modes, and their relative intensities, as we showed in Fig. 2 using the five nucleic bases as examples. Notably, the static approach allows for assigning the atomic motions corresponding to each vibrational mode. We benchmarked the predicted modes of ethanol with the respective assigned nuclear motions, finding that FAbulA correctly classifies all ethanol principal modes (see Table 1). Additional benchmarks of the approximation for the Raman/IR intensities, the effect of the solvent, and the atomic energy landscape are analyzed in the Supplementary Information (see Supplementary notes 1–4). In addition, considering the anharmonic effects, our method permits us to consider the temperature-dependence behavior of the found vibrational modes. We tested its potential in the case of myristic acid, where an experimental investigation of the Raman spectrum of myristic acid at different temperatures highlighted a well-defined trend of its active modes in the 880 − 920 cm−1 region, perfectly explained by the FAbulA calculations as shown in Fig. 4.

As the static approach can not provide information on mode bandwidths and overtones, we implemented a dynamical version of FAbulA, based on the time-dependent self-consistent harmonic approximation. The dynamic results systematically improve the agreement with the experimental data while simultaneously predicting the natural linewidth emerging from anharmonic scattering (see Fig. 3).

Based on combining a solid theoretical framework with neural-network algorithms to evaluate total energies and polarizability tensors efficiently, FAbulA can be applied to a wide range of organic molecules made of hundreds of atoms. Alternatively, the method can also account for the explicit effects of solvents or aggregate states thanks to the fast evaluation of the vibrational spectrum (more details in Supplementary Note 2).

Limitations of the current method comprehend the description of molecular rotations27, as the corresponding atomic motion strongly deviates from the linear vibration of a harmonic oscillator. To mitigate this issue for the free molecular rotation, we lock both the average position and the global rotation of the molecule and study only the vibration of the internal degrees of freedom. This is correct in the approximation that the global rotation of the molecule can be decoupled from the other phonons, which is true if we neglect the centrifugal force due to the rotation of the other internal vibration. Indeed, the larger the molecule, the better this approximation becomes. A different case occurs for molecules that present substructures that can freely rotate within themselves, like paracetamol, where the final methyl group (C–H3) presents rotational degrees of freedom that the SCHA method fails to describe27.

Overall, our method combines state-of-the-art computational techniques with a user-friendly interface that permits even non-expert users to calculate the vibrational properties of organic molecules and obtain quick estimations of mode motions and temperature-dependent behaviors.

We envisage that FAbulA will shorten the distance between experimenters and computational/theoretical methods, allowing for a prompt comprehension of the vibrational properties of organic molecules.

Material and methods

The FAbulA method

The harmonic spectrum is evaluated using a finite-difference approach: the molecule is relaxed in the closest local minimum of the Born-Oppenheimer energy landscape (the total energy of the molecules where the ions are at position R, assuming the electrons are always in the ground state). Then, a complete set of symmetry inequivalent atomic displacements is selected, for which we evaluate the forces f acting on the ions. We generate the remaining displacement, u, and forces by applying the symmetry operations until we have a complete Cartesian set, for which we evaluate the harmonic force-constant matrix \(\mathop{\Phi }\limits^{\,\text{(h)}\,}\) inverting the set of equations

$${f}_{\alpha }^{i}={-}\mathop{{\sum}}\limits_{\begin{array}{l}j=1,\cdots \,,N\\ \beta =1,2,3\end{array}}{\mathop{\Phi }\limits^{\,\text{(h)}\,}}_{\alpha \beta }^{ij}{u}_{\beta }^{j};$$
(4)

Latin indices identify the atom, while Greek letters are the Cartesian component. The frequencies and polarization modes are obtained by diagonalizing the force-constant matrix divided by the masses:

$$\frac{{\mathop{\Phi }\limits^{\,\text{(h)}\,}}_{\alpha \beta }^{ab}}{\sqrt{{m}_{a}{m}_{b}}}=\mathop{\sum }\limits_{\mu =1}^{3N}{\omega }_{\mu }^{2}{{e}_{\mu }}_{\alpha }^{a}{{e}_{\mu }}_{\beta }^{b},$$
(5)

where ωμ is the frequency of the μ-th mode, eμ is the polarization vector defining the pattern of the vibrations, and the cross-section of the μ-th mode with the IR or Raman probe.

The harmonic force constant matrix \(\mathop{\Phi }\limits^{\,\text{(h)}\,}\) is employed as the starting point for the static anharmonic calculation, performed with the SSCHA4,16,28,29. The SSCHA method finds the force constant matrix that minimizes the Gibbs free energy, solution of the self-consistent equations

$${\left\langle \frac{{d}^{2}V}{d{R}_{\alpha }^{i}d{R}_{\beta }^{j}}\right\rangle }_{\tilde{\rho }\left[{\mathscr{R}},\mathop{\Phi }\limits^{{\rm{(s)}}}\right]}={\mathop{\Phi }\limits^{\,\text{(s)}\,}}_{\alpha \beta }^{ij},$$
(6)
$${\left\langle \frac{dV}{d{R}_{\alpha }^{i}}\right\rangle }_{\tilde{\rho }\left[{\mathscr{R}},\mathop{\Phi }\limits^{{\rm{(s)}}}\right]}=0,$$
(7)

where V(R) is the Born-Oppenheimer energy landscape, and the averages are performed with a Monte-Carlo algorithm, where the atomic configurations are extracted with an ionic position distributed according to \(\tilde{\rho }[{\mathscr{R}},\mathop{\Phi }\limits^{\,\text{(s)}\,}]\):

$$\tilde{\rho }\left[\mathop{\Phi }\limits^{\,\text{(s)}\,},{\mathscr{R}}\right](R)=\sqrt{\frac{\det \Upsilon }{{(2\pi )}^{3N}}}\exp \left[-\frac{1}{2}\sum _{\begin{array}{c}ab=1,N\\ \alpha \beta =1,2,3\end{array}}\left({R}_{\alpha }^{a}-{{\mathscr{R}}}_{\alpha }^{a}\right){\Upsilon }_{\alpha \beta }^{ab}\left({R}_{\beta }^{b}-{{\mathscr{R}}}_{\beta }^{b}\right)\right]$$
(8)

with

$${\Upsilon }_{\alpha \beta }^{ab}=\sqrt{{m}_{a}{m}_{b}}\mathop{\sum }\limits_{\mu =1}^{3N}\frac{2{\mathop{\omega }\limits^{{\rm{(s)}}}}_{\mu }}{\hslash (2{n}_{\mu }+1)}{{\mathop{e}\limits^{{\rm{(s)}}}}_{\mu }}_{\alpha }^{a}{{\mathop{e}\limits^{{\rm{(s)}}}}_{\mu }}_{\beta }^{b}$$
(9)

where \(\mathop{\omega }\limits^{\,\text{(s)}\,}\) and \(\mathop{e}\limits^{\,\text{(s)}\,}\) are frequencies and polarization vectors of \(\mathop{\Phi }\limits^{\,\text{(s)}\,}\), while nμ is the Bose-Einstein occupation factor

$${n}_{\mu }=\frac{1}{{e}^{\beta \hslash {\mathop{\omega }\limits^{{\rm{(s)}}}}_{\mu }}-1},\qquad \beta =\frac{1}{{k}_{{\rm{b}}}T}.$$
(10)

The probability distribution for the atoms in (8) is Gaussian around the centroid position \({\mathcal{R}}\) with a width determined by the covariance matrix ϒ−1 defined in (9). Notably, the covariance matrix takes into account the quantum zero-point motion of atoms, making our method able to correctly describe quantum-anharmonicity, particularly relevant when light atoms are present.

Thanks to the Gaussian form of (8), we can extract an ensemble of randomly distributed atomic configurations according to \(\tilde{\rho }[\mathop{\Phi }\limits^{\,\text{(s)}\,},{\mathcal{R}}]\) almost instantaneously, without the need of any Metropolis or MD. These configurations evaluate the averages in (6) and (7). To speed up the self-consistency, we employ the importance sampling16,30,31 to avoid recomputing the ensemble after each iteration and integrate by parts (6) to have only the first derivatives of the Born-Oppenheimer energy landscape16,29; so that we only need to compute the forces of the atomic configurations. More details on the implementation are reported in ref. 16.

Once (6) and (7) are satisfied, we use the \(\mathop{\omega }\limits^{\,\text{(s)}\,}\) and \(\mathop{e}\limits^{\,\text{(s)}\,}\) as vibrational modes to compute the Raman and IR. This is the static anharmonic approximation, as it considers changes in the molecules due to both temperature and quantum effects, as well as a self-consistent change of the vibrational frequencies in the distribution.

The dynamical anharmonic spectrum is obtained by inserting an explicit time dependence in the probability distribution \(\tilde{\rho }[\mathop{\Phi }\limits^{\,\text{(s)}\,},{\mathcal{R}}]\) and imposing the stationary Action principle15. This procedure takes the name of time-dependent stochastic self-consistent harmonic approximation (tdSSCHA) and can be employed to evaluate the response function of the system under an external perturbation (Raman or IR). While this procedure concedes with computing the Raman or IR signal directly from the frequencies and polarization vectors in a perfectly harmonic system, this is not true in the presence of anharmonicity. In particular, scattering and interactions between different vibrational modes could result in the appearance of overtones or combinational modes, as well as change the linewidth by introducing a finite lifetime. The details of the tdSSCHA implementation are reported elsewhere15,17.

IR and Raman intensity

Raman and IR intensities depend on the response function of dipole μ and polarizability α of the molecule. In particular, the IR intensity is related to the dipole-dipole response function

$${I}_{x}^{({\rm{IR}})}(\omega){\propto} -\Im \mathop{\int}\nolimits_{-\infty}^{\infty }{e}^{-i\omega t}\left\langle {\mu}_{x}(t){\mu }_{x}(0)\right\rangle,$$
(11)

while the Raman is related to the autocorrelation of the polarizability tensor

$${I}_{xy}^{({\rm{Raman}})}(\omega ){\propto} -[n(\omega )+1]\Im \mathop{\int}\nolimits_{-\infty }^{\infty }{e}^{-i\omega t}\left\langle {\alpha }_{xy}(t){\alpha }_{xy}(0)\right\rangle .$$
(12)

The time dependence of μ and α is due to the movement of atoms in the lattice. By expanding the expression of the dipole and polarization around equilibrium, we get the one-phonon contribution to the vibrational spectra17:

$${\mu }_{x}(t)={\mu }_{x}(0)+\sum _{i\alpha }\frac{\partial {\mu }_{x}}{\partial {R}_{i\alpha }}({R}_{i\alpha }(t)-{{\mathscr{R}}}_{i\alpha })\qquad {Z}_{xi\alpha }=\frac{\partial {\mu }_{x}}{\partial {R}_{i\alpha }}$$
(13)
$${\alpha }_{xy}(t)={\alpha }_{xy}(0)+\sum _{i\beta }\frac{\partial {\alpha }_{xy}}{\partial {R}_{i\beta }}({R}_{i\beta }(t)-{{\mathscr{R}}}_{i\beta })\qquad {\Xi }_{xyi\beta }=\frac{\partial {\alpha }_{xy}}{\partial {R}_{i\beta }}$$
(14)

where Zxiα is the born effective charge, while Ξxyiβ is the Raman Tensor. Then, the IR and Raman intensity are obtained as

$$I^{({\rm{IR}})}_{x}(\omega) \propto -\sum\limits_{i\alpha j\beta}\frac{Z_{xi\alpha} Z_{xj\beta}}{\sqrt{m_i m_j}} \Im\underbrace{\int_{-\infty}^\infty e^{-i\omega t}\left\langle\sqrt {m_i} (R_{i\alpha}(t) - {\mathscr{R}}_{i\alpha})\sqrt {m_j}(R_{j\beta}(0) - {\mathscr{R}}_{j\beta})\right\rangle}_{G_{i\alpha j \beta} (\omega)}$$
(15)
$$I^{({\rm{Raman}})}_{x}(\omega) \propto -[n(\omega) + 1]\sum\limits_{i\alpha j\beta}\frac{{\Xi}_{xyi\alpha} {\Xi}_{xyj\beta}}{\sqrt{m_i m_j}} \Im\underbrace{\int_{-\infty}^\infty e^{-i\omega t}\left\langle\sqrt {m_i} (R_{i\alpha}(t) - {\mathscr{R}}_{i\alpha})\sqrt {m_j}(R_{j\beta}(0) - {\mathscr{R}}_{j\beta})\right\rangle}_{G_{i\alpha j \beta} (\omega)}$$
(16)

where Giαjβ(ω) is the dynamical vibrational Green’s function. The self-consistent harmonic Green’s function has the form

$$\mathop{G}\limits^{(s)}(\omega )={\left[{\omega }^{2}-\mathop{D}\limits^{(s)}\right]}^{-1}\qquad {\mathop{D}\limits^{(s)}}_{i\alpha j\beta }=\frac{{\mathop{\Phi }\limits^{{\rm{(s)}}}}_{i\alpha \,j\beta }}{\sqrt{{m}_{i}{m}_{j}}}$$

where the eigenvalues of the dynamical matrix \(\mathop{D}\limits^{(s)}\) determine the position of the vibrational peaks. The dynamical tdSSCHA spectrum is evaluated by computing the interacting Green’s function accounting for scattering between different atoms15.

The IR and Raman activity is determined by the projection of effective charges and Raman tensor on the polarization vector of the vibration. Usually, these quantities are evaluated ab initio using density-functional theory or Hartree-Fock, either employing linear-response32 or finite differences33,34. However, these calculations require considerable computational power for anything with more than 10 atoms. Instead, we approximate the tensorial dependences of Zxiα as an isotropic charge qi located on the atom, as usually assumed in classical force fields (as reported, for instance, in PDB or parametrization files):

$${Z}_{xi\alpha }={\delta }_{x\alpha }{q}_{i}$$
(17)

where δij is the Kronecker delta.

The Raman tensor is far more challenging to evaluate as it is a property related to the bonding network of the molecule. For this reason, we trained a Neural-Network potential on a bond capacitor model of organic molecules. A tensorial capacitor \({C}_{ijhk}^{(ij)}\) is located between each couple of bounded atoms i and j in the molecule (as indicated in the topology file). The total polarizability is evaluated as a sum over all bonds of a local quantity that depends on the atomic bonds

$${\alpha }_{xy}=\sum _{(i,j)\in \,\text{bonds}\,}\sum _{\alpha \beta }{C}_{xy\alpha \beta }^{(ij)}({R}_{i\alpha }-{R}_{j\alpha })({R}_{i\beta }-{R}_{j\beta }).$$
(18)

The Raman tensor of each atom is obtained from the derivative of the total polarizability

$${\Xi }_{xyi\alpha }=2\sum _{\beta }\sum _{(k,i)\in \,\text{bonds}\,}{C}_{xy\alpha \beta }^{(ki)}({R}_{i\beta }-{R}_{k\beta })$$
(19)

Even if the C has 36 independent components for each bond, we assume C(ij) to depend only on the atomic species of atoms i and j and their distance in the bond to distinguish between single, double, and triple bonds. Under this assumption, we neglect the role played by the environment of each bond, and the capacitor tensor gains rotational symmetry around the bond, retaining only 6 independent quantities.

The independent values of C(ij) are obtained by training a neural-network model on a small dataset of molecules to correctly reproduce the Raman tensor evaluated within DFT with LDA approximation for exchange-correlation functional.

Used dataset and chosen parameters

The 3D structures in MOL2 format of nucleic basis, ethanol, and myristic acid were taken from the ZINC database35. Molecules’ Raman and infrared spectra were calculated using the FAbulA webserver with 100,000 configurations, a maximum number of populations of 20 and the ANI-1ccx force field for the SSCHA minimization; the number of steps for the tdSCHA algorithm was set to 10,000. Finally, the following molecule-specific parameters were used: Nucleic basis: temperature was set to 300 K; Ethanol: temperature was set to 300 K; Myristic acid: temperature was set to 50, 150, 200, and 300 K.

Neural network

To get the parameters of the bond capacitor model, we implemented a multi-layer perceptron (MLP) regression algorithm via the sklearn.neural-network.MLPRegressor module within the scikit-learn library.

Webserver

The method is distributed as a free webserver, designed for seamless access and operation at: https://fabula.bio-groups.com, where users can find a complete guide to how to use the FAbulA tool.