Quantum embedding method with transformer neural network quantum states for strongly correlated materials

Abstract

The neural-network quantum states (NNQS) method is rapidly emerging as a powerful tool in quantum mechanisms. While significant advancements have been achieved in simulating simple molecules using NNQS, the ab initio simulation of complex solid-state materials remains challenging. Here in this work, we have adopted the periodic density matrix embedding theory to extend the NNQS method to deal with complex solid-state systems. Our approach notably reduces the computational problem size while maintaining high accuracy. We have validated the accuracy and efficiency of our method against traditional methodologies and experimental data in extended systems, and have investigated the magnetic ordering and charge density wave state in transition metal compounds. The findings from our research indicate that the integration of quantum embedding with intuitive chemical fragmentation can significantly enhance the NNQS simulation of realistic materials.

Introduction

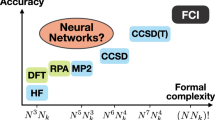
The electronic structure and properties of materials can, in principle, be determined by solving the Schrödinger equation to obtain an exact solution of the wave function. The square of this wave function represents the probability density function for finding the many electrons simultaneously. The most difficult task is finding a general way to reduce the exponential complexity of the full many-body wave function and the extraction of its most essential features. Various approaches have been developed to solve the Schrödinger equation for realistic systems. Although the full configuration interaction (FCI) method offers ground-truth results, the exponential growth of the Hilbert space limits the size of feasible simulations. To approximate the exact energy, several strategies have been devised, including perturbation theory^1,2, variational method^3,4,5,6, coupled-cluster (CC) method⁷. However, these methods can fail in numerous cases, mostly due to the inefficient expressive power of the wave function ansatz. Very recently, the neural-network quantum state (NNQS) algorithm with better expressive power has been proposed as a groundbreaking approach for tackling many-body quantum systems^8,9,10,11,12. The main idea behind NNQS is to parameterize the quantum wave function using a neural-network architecture and to optimize its parameters using the variational Monte Carlo (VMC) algorithm stochastically, and the computational cost of NNQS typically scales polynomially. However, the sampling process within Monte Carlo processes may be inefficient in certain situations with a low acceptance rate and can result in correlated samples. To address this challenge, we have presented QiankunNet^13,14 to solve the many-electron Schrödinger equation with a language model. QiankunNet adeptly harnesses the language model’s prowess to effectively capture highly non-trivial quantum correlations by integrating the attention mechanism and enhancing the sampling process through a batched autoregressive sampling strategy. Moreover, QiankunNet can incorporate essential physics knowledge into neural networks, striking a balance between respecting physics principles and enhancing computational efficiency.

The NNQS method has been successfully used to study molecular systems^{13,14,15,16,17,18}, however, the algorithmic development of the NNQS method for periodic systems is still in the early stage, and so far, most of the current studies have been limited to simple solids systems such as homogeneous electron gas¹⁹, hydrogen chain²⁰ and lithium hydride crystals²¹. This is because the necessity of approaching the thermodynamic limit (TDL)²² results in an extra dimension of computational variables compared to their molecular counterparts, which demands huge computational resources, and the complexity of electronic correlation in periodic systems requires high expressiveness of neural networks, so even using high-performance computing architectures, it is still challenging to apply them to complex materials. An important requirement to tackle complex materials is the reduction of the region treated at the highest level of accuracy, and the quantum embedding method is one of the solutions, which divides a large system into smaller fragments, and enables an accurate treatment of each fragment using a high-level computational method. There has been a lot of progress in the quantum embedding method^{23,24,25,26,27,28,29,30}. Within the quantum embedding method, density matrix embedding theory (DMET) is a promising framework because it can intrinsically allow high-level treatments for multiple fragments using a high-level theory, unlike the dynamical mean-field theory (DMFT) with active space or projection-based embedding, which have been mostly developed for one single fragment or one correlated site. DMET has been successfully applied to a variety of chemical systems, ranging from molecules to extended solid-state systems^28,29,31,32. It is particularly useful for studying systems where electron correlation significantly influences the physical and chemical properties. However, the combination of DMET with the state-of-the-art NNQS method to deal with complex materials problems is still missing.

Here in this work, we integrate the NNQS solver—QiankunNet into the DMET method to offer a balance between computational feasibility and accuracy, particularly for systems where electron correlation is critical. The schematic of the DMET-QiankunNet framework is shown in Fig. 1. In this framework, the global system is partitioned into smaller subsystems, and each fragment is treated as a subsystem (referred to as the impurity) embedded in a larger environment, with the interactions between the subsystem and its environment being carefully accounted for. The electronic structure of each subsystem is accurately solved with QiankunNet while also accounting for the effect of the rest of the system. This is achieved by constructing a local density matrix that represents the subsystem and its immediate environment. Additionally, we have employed a self-consistent periodic quantum embedding method to achieve the TDL, and we use the periodic quantum chemistry method to efficiently treat long-range interactions. Furthermore, based on the observation that embedding Hamiltonians in the quantum embedding iteration generally exhibits similar structures, the parameters for neural networks to determine the ground state of these Hamiltonians should not differ significantly. Consequently, a transfer learning strategy has been developed, whereby most Hamiltonians in the DMET iteration only require fine-tuning of the neural network. In order to demonstrate the effectiveness and accuracy of the theory, we employ the DMET-QiankunNet algorithm in a variety of periodic systems, ranging from simple to complex cases. These include the one-dimensional hydrogen chain, the diamond crystal, the investigation of magnetic ordering in four different transition metal oxides, and the study of the charge density wave (CDW) state in 1T-TiSe₂. The results of the one-dimensional hydrogen chain and the diamond crystal are compared with DMET-FCI results or DMET-CCSD results when the FCI solver reaches its limit. The results of transition metal oxides and 1T-TiSe₂ are compared with existing theoretical or experimental research. Our findings indicate that the combination of the QiankunNet NNQS solver with the DMET method enables the simulation of strongly correlated materials on a large scale with remarkable accuracy.

Fig. 1: The ab initio DMET-QiankunNet (DMET-NNQS) framework.

a The complex solid-state material is divided into an impurity along with its corresponding environment, and DMET embedding constructs an embedding Hamiltonian that encompasses the impurity orbitals and the bath orbitals. The impurity problem is subsequently solved for the many-body wave function with QiankunNet. b The mapping between orbital and qubit. c QiankunNet: The autoregressive language model takes qubits as tokens, and outputs the conditional probability p(x_i∣x < i) of the next token in the sequence. The conditional probabilities can be combined with additional parameterizations of phase information to output the complex quantum state or wave function.

Numerical results and applications

One-dimensional hydrogen chain

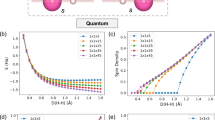
We initiate our investigation with numerical simulations of the one-dimensional equispaced hydrogen chain (1D-H). The potential energy surface (PES), with H-H distance varying from 0.6 to 2.0, is calculated. The hydrogen chain, although consisting of a simple atomic arrangement, holds significant importance in the field of strongly correlated materials. The strong electron correlation becomes significant as the H-H distance increases. Such a system provides a valuable foundation for comprehending various fundamental physical phenomena, including the insulator-to-metal transition and the antiferromagnetic Mott phase³³. The unit cell of the hydrogen chain is presumed to comprise 2 hydrogen atoms. A GTH-SVZ basis set, along with the GTH-PADE pseudo-potential, is employed. Given the small size of this system, there is no need to further partition the unit cell into fragments; each unit cell is treated as an individual fragment. Consequently, the corresponding embedding Hamiltonian contains 6 orbitals: 2 impurity orbitals, 2 virtual orbitals, and 2 bath orbitals. Two different k-point meshes (1 × 1 × 5, 1 × 1 × 11) are used. To assess the accuracy of the NNQS solver, the results are compared to the same DMET calculation using an FCI solver. For DMET-NNQS results with 5 k-points, the results are also compared to the FCI results.

Figure 2 presents the potential energy surface for a one-dimensional hydrogen chain calculated using the DMET-NNQS method and several classical approaches. In the case of 5 k-points, the DMET-NNQS method, alongside the CCSD and MP2 methods, closely aligns with FCI results when the H-H distance is less than 1.2 Å. However, as the distance approaches 2.0 Å, classical methods deviate from the FCI results. Notably, the MP2 method significantly underestimates the correlation energy, and the CCSD method yields unreasonable results for an H-H distance exceeding 1.5 Å, failing to converge beyond 1.7 Å. In contrast, the DMET-NNQS method consistently matches the FCI results across all H-H distance values. The absolute error between the DMET-NNQS method and FCI results is depicted in Fig 2c. As illustrated in the figure, the energy difference between DMET-NNQS and the FCI method ranges from −1 milli-Hartree to 3 milli-Hartree. Remarkably, for an H-H distance larger than 1.0 Å, the DMET-NNQS results fall within the realm of chemical accuracy. Moreover, the energy deviation is even smaller between the DMET-NNQS method and the DMET-FCI method, with an absolute energy difference ranging from 1 × 10⁻⁷ Hartree to 1 × 10⁻⁵ Hartree. Such high precision underscores the remarkable accuracy of the NNQS solver. In the case of 11 k-points, achieving convergence becomes more challenging for classical methods. The CCSD method fails to converge for H-H distance larger than 1.3 Å. The MP2 method consistently underestimates the correlation energy for H-H distances larger than 1.2 Å. Moreover, MP2 results for H-H distances greater than 1.8 Å deviate from the trend observed in the curve. However, the DMET-NNQS method continues to produce reasonable results even with a large number of k-points. The energy difference compared to the DMET-FCI method remains at a very low level, attesting to the method’s robustness in handling larger k-point meshes. Results for both 5 and 11 k-points predict the existence of an equilibrium structure. For all the calculated H-H distances, the energy minimum is found at 1.1 Å. After interpolation, an energy minimum is estimated to be around 1.073 Å. Previous theoretical calculations have reported the equilibrium structure of a one-dimensional hydrogen chain when hydrogen atoms are equispaced at 0.984 ų⁴ or 1.058 Ų⁰. The equilibrium distance predicted in this work is slightly larger than previously reported results. This slight difference is attributed to the different basis sets used, as the GTH-SZV basis is used in this work while the cited works used the STO-6G basis and STO-3G basis respectively. The DMET-NNQS method was employed for additional calculations, systematically varying the number of k-points in the range of 5 to 17, and extrapolating the results to Nk ⟶ ∞. Detailed outcomes can be found in the Supplementary Information.

Fig. 2: The Potential energy surface for a one-dimensional hydrogen chain calculated with DMET-NNQS in comparison with several other classical methods.

Two different k-point meshes are used: a 1 × 1 × 5 and b 1 × 1 × 11. c Energy discrepancy of the Results: A comprehensive comparison is presented, contrasting DMET-NNQS results obtained with 5 k-points against both DMET-FCI and FCI results. Additionally, the DMET-NNQS outcomes with 11 k-points are exclusively compared with DMET-FCI results. The shaded area refers to the realm of chemical accuracy.

Bulk diamond

Our simulation is then extended to a realistic 3D material, the diamond crystal, to assess the performance of DMET-NNQS in a larger system. The structure of the primitive cell of the diamond crystal is depicted in Fig. 3e, each unit cell comprises two carbon atoms. As the GTH pseudo-potential and GTH-DZVP basis set are employed, each carbon atom contains 2s2p3s3p3d, totaling 13 atomic orbitals. In this section, three distinct fragmentation schemes are defined to evaluate the performance when different atomic orbital sets are assigned to the impurity. In every scheme the two carbon atoms are partitioned into two different fragments and different atomic orbitals are included in the impurity: (1) 2s2p, (2) 2s2p3s3p, and (3) 2s2p3s3p3d. Orbitals not included in the impurity are evaluated at the Hartree-Fock level. A series of unit cell energies is calculated by varying the lattice constant ‘a’. All mean-field calculations in this section utilize a 3 × 3 × 3 k-point mesh.

Fig. 3: Potential energy surfaces of diamond with different orbitals included in the impurity.

a DMET-NNQS results with different orbital sets defined in the impurity. Detailed results are presented when the impurity comprises b 2s2p, c 2s2p3s3p, and d 2s2p3s3p3d orbitals of the carbon atoms. e Structure of bulk diamond.

The results of this calculation are shown in Fig. 3. A comparison between DMET-NNQS results with different orbital partition schemes indicates that by including more orbitals in the impurity, more correlation energy can be recovered. The absolute correlation energy calculated with the DMET-NNQS method, when only 2s2p orbitals are included in the impurity, only accounts for 63.06% of the correlation energy obtained by DMET-NNQS calculation, which includes all the orbitals (2s2p3s3p3d). For DMET-NNQS results with 2s2p3s3p orbitals included in the impurity, the percentage increases to 67.65%. These results emphasize that including more orbitals in the impurity partition leads to greater accuracy. While this may not hold significant implications for diamonds, as the 3d orbitals of carbon atoms are barely occupied, it becomes crucial for more complex systems, particularly those containing transition metals. This aspect will be explored further in the section “Transition metal oxides”. Fig. 3b depicts the DMET-NNQS results with 2s2p orbitals of the carbon atoms included in the impurity, alongside the DMET results with an FCI solver. It is evident that the DMET-NNQS results align closely with the DMET-FCI method. The average deviation between the two methods is 2.12 × 10⁻⁴ Hartree, which again shows the high accuracy of the NNQS solver. The DMET-NNQS results with 2s2p3s3p orbitals and all orbitals included in the impurity are compared to the same DMET calculations with the CCSD solver as shown in Fig. 3c, d. It is clear that the DMET-NNQS method recovers more correlation energy than the DMET-CCSD method because the NNQS solver provides more accurate results than the CCSD solver. The NNQS solver still demonstrates remarkable accuracy for Hamiltonians with a large number of orbitals. All three DMET-NNQS calculations yield an equilibrium structure with a lattice constant of 2.55 Å, slightly larger than the expected value of 2.527 Å. The task of predicting the equilibrium lattice constant has been essentially achieved. To further improve the results, it would be necessary to use a larger and more complete basis set for the calculation. Another potential way to improve the results is to use the Birch-Murnaghan equation of state (EOS)³⁵ to obtain the results of thermodynamic limit (TDL), as is done in Cui’s work³⁰.

Transition metal oxides

Transition metal oxides (TMOs) constitute a class of compounds with pivotal roles in diverse scientific and technological realms, owing to their intriguing electronic and magnetic properties. The applications of TMOs span catalysis, energy storage, and electronic devices. Furthermore, the intricate interplay between the electronic, magnetic, and structural properties of TMOs has fueled the exploration of cutting-edge technologies, including spintronics. Understanding the magnetic order of transition metal oxides is of great importance due to its profound impact on the material’s overall properties.

Three different transition metal oxides (VO₂, MnO, and NiO) are simulated with the DMET-NNQS method to predict the magnetic order. VO₂ has a rutile structure, as is shown in Fig. 4a. Each transition metal atom is coordinated with six oxygen atoms, forming an octahedral arrangement. MnO and NiO both have a rock salt structure, with the cations and anions arranged in a face-centered cubic lattice. Such a structure exhibits two different antiferromagnetic orders. The transition metals can be anti-ferromagnetically arranged in the [001] or [111] direction, defined as AFI and AFII order, respectively. MnO and NiO are proven to have an AFII order, with the arrangement of transition metal atoms shown in Fig 4b. To simplify the calculation, a smaller primitive cell is used. The primitive cell comprises only two transition metal atoms and two oxygen atoms but is still capable of describing the AFII order. For the sake of consistency, all four TMO’s are partitioned into fragments with the same scheme: For every transition metal atom, its 4s and 3d orbitals, together with the 2s 2p orbitals of a nearby oxygen atom, formed one fragment. Orbitals included in the impurity are shown in Fig. 4d. This fragmentation scheme includes all the valence orbitals near the Fermi level. Orbitals not included in the impurity fragments are put into a third fragment and are solved with a CCSD solver.

Fig. 4: Structures of TMOs included in this study.

a Rutile structure of VO₂. b AFII magnetic order for MnO and NiO. The gray and yellow atoms represent transition metal atoms with opposite magnetic moments, respectively. c Primitive cell which contains two transition metal atoms that are used for computation. d Orbitals included in the impurity (4s, eg, and t2g orbitals for transition metal atoms; 2s and 2p orbitals for oxygen atoms).

The results of DMET-NNQS simulations are shown in Table 1. We also include findings from previous research, both experimental and theoretical. DMET-NNQS simulations predict that the stable magnetic order of VO₂ is ferromagnetic, with an energy advantage of 105.54 meV, falling between the DFT-PBE and DFT-LDA+U results. Each V atom is predicted to have a magnetic moment of 1.043 μ_B, consistent with the DFT-PBE result. Besides the rutile structure, VO₂ has two other monoclinic phases, but we do not delve into this topic here. For MnO and NiO, the DMET-NNQS method correctly predicts the AFII order to be the stable magnetic order. The experimental magnetic moment for MnO ranges from 4.58 to 4.79 μ_B, and we obtain a slightly higher magnetic moment of 4.866 μ_B. The calculated energy difference for NiO falls within a reasonable range, and the predicted magnetic moment of NiO is consistent with experimental results. In summary, for all three transition metal oxides, the DMET-NNQS method predicts the correct magnetic order and provides accurate estimations of the energy difference and magnetic moment.

Table 1 Results of ΔE (defined as E_FM − E_AFM per formula unit, in meV), magnetic moment (μ_B), and stable magnetic order in comparison with other theoretical or experimental results

CDW state in 1T-TiSe₂

Transition metal dichalcogenides (TMDs) have garnered significant attention in recent years due to their unique electronic and optoelectronic properties, particularly when reduced to nanosheets or monolayers. Among the extensively studied TMDs, 1T-TiSe₂ stands out as a notable example, experiencing a resurgence in interest. This compound, characterized by a layered structure, exhibits a quasi-two-dimensional nature with Ti octahedrally coordinated by six Se atoms in successive Se-Ti-Se sandwiches. Below a critical temperature of 200 K, 1T-TiSe₂ undergoes a commensurate CDW state with a 2 × 2 × 1 superstructure.

The CDW state is a collective electron phenomenon observed in low-dimensional electronic systems. The CDW state disrupts the original translational symmetry, leading to a periodic redistribution of charge density, commonly referred to as CDW instability. Previous research has revealed the potential origin of the CDW instability of 1T-TiSe₂³⁶. As is shown in Fig. 5, in the band structure of 2 × 2TiSe₂ supercells, the electron and hole pockets are folded at the Γ and M points, with no emergence of a gap in the spectrum. The CDW distortion helps open a gap near E_f, which helps stabilize the whole system. The CDW state in 1T-TiSe₂ is of particular significance and has garnered much attention, given its intricate connection to superconductivity. Studies have shown that superconductivity can be induced in 1T-TiSe₂ by Cu intercalation or pressure, leading to the suppression of the CDW. This CDW state has been subject to intense theoretical and experimental scrutiny for over three decades. Understanding the properties of the CDW state in 1T-TiSe₂ offers valuable insights into the physics of these intriguing materials and holds promise for diverse applications in electronic devices and beyond.

Fig. 5: Structure and the corresponding schematic band structure.

a 1 × 1 unit cell of 1T-TiSe_2, b 2 × 2 super cells, and c the CDW distorted structure. d Calculated electron density distribution of 3d electrons in Ti atom. e Electron density distribution of Se electrons (certain background electron density is removed to make the figure more apparent). Boxes with Dashed lines in d and e indicate the charge density of a 2 × 2 supercell.

We employ The DMET-NNQS method to investigate the CDW instability in 1T-TiSe₂ by comparing the energy and electron density between the normal-ordered 1T-TiSe₂ and the distorted CDW order. The normally ordered 1T-TiSe₂ belongs to a hexagonal crystal lattice with the $P\overline{3}m1$ space group. A 2 × 2 × 1 supercell has lattice constant a = 7.08Å, the four Ti atoms occupy (0, 0, 0.5), (0.5, 0, 0.5), (0.5, 0, 0.5), (0.5, 0.5, 0.5) sites and the eight Se atoms take (1/6, 1/3, z), (1/6, 5/6, z), (2/3, 1/3, z), (2/3, 5/6, z), (1/3, 1/6, −z), (1/3, 2/3, −z), (5/6, 1/6, −z), (5/6, 2/3, −z) sites, z refers to the distance between the Ti layer and Se layer and is set to 1.532 Å bases on structures of previous works. A vacuum layer of 15 Å is employed. The CDW order is constructed by inducing distortion toward a well-ordered 2 × 2 × 1 TiSe₂ supercell. Figure 5c illustrates the direction of distortion for each atom in the structure. Notably, the Ti atoms and the Se atoms experience different levels of distortion. Experimental evidence suggests that the distortion ratio on the Ti atom and Se atom δTi/δSe is approximately 3.0, in this simulation, δTi and δSe are set to 0.012a and 0.004a respectively. For both normally ordered and distorted structures, a 3 × 3 × 1 k-point mesh is used.

For both structures, the same fragmentation partition scheme is applied. Every Ti atom and every Se atom is treated as a single fragment. For Ti atoms, 3d4s4p orbitals are contained in the fragment, and for Se atoms, 4s4p4d5s5p orbitals form the impurity fragment. Orbitals not defined in the fragments together form the last fragment and are solved with a CCSD solver. Surprisingly, in the Hartree-Fock calculation, which serves as the starting point for the DMET-NNQS method, the CDW instability is not predicted. The normal state exhibits a lower Hartree-Fock energy, with an energy difference of 1.96 meV. However, the CDW instability is predicted by the DMET-NNQS method, with the CDW state exhibiting an energy difference of −18.08 meV compared to the normal state, consistent with the results of previous DFT calculations with GGA exchange potential³⁶. The discrepancy in results between HF and DMET-NNQS methods suggests that certain electron correlation is not captured at the HF level. To comprehend the origin of the CDW instability, a detailed analysis of electron occupation or electron density is imperative. In the DMET procedure, 1-particle and 2-particle density matrices are calculated based on wave functions produced by the NNQS solver. These density matrices bring us essential information like electron occupation of orbitals and electron density of the system can be calculated. Figure 5c illustrates the electron density of 3d electrons for Ti atoms, indicating that undisturbed Ti atoms have fewer 3d electrons, whereas distorted Ti atoms have a higher concentration. Figure 5d illustrates the electron density above the 1T-TiSe₂ layer, revealing the electron density distribution of Se atoms at the top layer. In contrast to Ti atoms, the undistorted Se atoms exhibit a maximum in electron density, while the distorted ones show a minimum. This pattern of maximum and minimum electron density aligns with the scanning tunneling microscopy (STM) figures from previous research³⁷. The observed electron density difference for both Ti and Se atoms suggests that as the CDW distortion brings the distorted atoms closer, it strengthens the coupling between Ti 3d orbitals and Se 4p orbitals, potentially serving as a source of CDW instability. The periodic electron density redistribution is successfully captured with the DMET-NNQS method.

Efficiency of transfer learning strategy

In this study, we have carefully designed the transfer learning strategy introduced in the section “Transfer learning strategy in DMET-NNQS”. Learning rates and convergence tolerances are configured separately for transfer and non-transfer scenarios. The model transfer order of two iterations in DMET (named as μ iteration and u iteration respectively) is shown as follows:

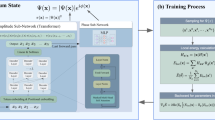
Where (i,j) refers to the i-th u iteration and j-th μ iteration. For the (0,0)-th iteration, the initial learning rate is set to 1.0, and it adjusts to smaller values during the learning process. A convergence criterion of 1 × 10⁻⁶ Hartree is employed. For the subsequent iteration steps that involve transfer learning, the learning rate is set to 3 × 10⁻⁵, with a convergence tolerance of 1 × 10⁻⁸ Hartree. Figure 6a illustrates the schematic of such a parameter transfer process and the number of epochs required for convergence in different iteration steps for a DMET-NNQS calculation using the transfer learning strategy. Apart from the first iteration, which requires approximately 8000 epochs to converge, subsequent iteration steps that load the model from the previous iteration only necessitate a few hundred epochs to achieve convergence. In the later stages of the μ iteration, the NNQS solver typically only needs tens of epochs.

Fig. 6: The schematics of three different transfer learning scenarios used in this study are presented, along with the corresponding histogram showing the number of epochs required for convergence with the transfer learning strategy.

The neural-network icons represent the NNQS solver and the green arrows indicate the direction to transfer neural-network parameters. a In the DMET iteration process, each μ iteration step involves loading the model from the preceding step, and similarly, each u iteration loads the model from the previous step. b Transfer learning is applied to embedding Hamiltonians generated by the hydrogen chain with varying H-H distance values. c Transfer learning is utilized between similar fragments in bulk diamonds.

The transfer learning strategy can also be applied to similar embedding Hamiltonians from different fragments or different chemical systems. For instance, in the computation of the potential energy surface of a one-dimensional hydrogen chain, calculations are performed with varying H-H distances. Although the variations in H-H distance will result in different values of one- and two-body integrals, the structures of the embedding Hamiltonians are only slightly altered, allowing them to be solved with the same NNQS model. Figure 6b depicts the effectiveness of such a model transfer. By loading the model from a different but similar model, the number of epochs required to converge is reduced from 8000 epochs to no more than 2000 epochs for the initial DMET iteration step. The third transfer learning scenario involves the transfer between similar fragments. For instance, in the calculation of a diamond, two carbon atoms in the unit cell are divided into two different fragments. Since the Hamiltonians for these two fragments are similar, transfer learning can be used. Figure 6c illustrates the schematic of such a transfer learning process and the efficiency of this strategy.

In summary, the implementation of the transfer learning strategy significantly enhances the efficiency of the DMET-NNQS algorithm, making it several tens of times more efficient. A series of similar structures would require only one single comprehensive NNQS training, significantly reducing the computational cost of solving all the embedding Hamiltonians. The notable increase in efficiency makes it feasible to perform DMET-NNQS calculations on much larger systems.

Performance of DMET-NNQS

In this section, we evaluate the performance of the DMET-QiankunNet method. We first compare the DMET-QiankunNet calculation with the direct calculation with the QiankunNet-Solid method³⁸ to demonstrate the benefit of the quantum embedding method. We use the hydrogen chain with different k-point numbers as an example. The unit cell of the hydrogen chain contains 2 hydrogen atoms, and the H-H distance is fixed to 1.0 Å. We collect the average one-step GPU time for both methods to show their performance. For both methods, the calculations are performed using one NVIDIA A100 GPU. The GPU times are gathered and shown in Table 2. It is clear that the DMET-QiankunNet method gives a significantly lower time. Because for the hydrogen chain with 2 hydrogen atoms, the QiankunNet method would have to solve a Hamiltonian with 2 × N_k orbitals, while the DMET-QiankunNet method only needs to solve embedding Hamiltonians with 4 orbitals. In addition to shorter per-step computation times, the DMET-QiankunNet method typically requires significantly fewer steps to achieve convergence.

Table 2 One-step GPU times (ms) for NNQS method and DMET-NNQS method for Hydrogen chain with different k-point numbers (N_k)

We have chosen four calculations with characteristic embedding Hamiltonian size and collected their wall times to show the performance of the DMET-QiankunNet method on systems with different sizes. The selected system includes: 1D Hydrogen chain, bulk Diamond with 2s2p orbitals as impurity orbitals and 2s2p3s3p orbitals included in the impurity respectively, and the ferromagnetic order of NiO. The chosen systems have embedding Hamiltonians with 8,16,24,40 spin-orbitals respectively. The time cost of the QiankunNet solver and the total time is listed in Table 3. The results show that the QiankunNet solver takes most of the time. Time cost besides the QiankunNet solver is mainly the calculation of the two-particle reduced density matrices (2-RDM). The scaling of 2-RDM is $O({N}_{u}^{2}{N}_{o})$, so for large systems with numerous unique samples, the computation of the 2-RDM also consumes a significant amount of time. However, for the experiments conducted in this work, the majority of computation time is still dominated by the QiankunNet solver.

Table 3 QiankunNet solver time (s) and total time (s) for DMET-QiankunNet method with four different systems calculated in this work

Discussion

This study introduces an innovative NNQS approach for simulating solid-state materials. Utilizing the DMET method and partitioning at the orbital level, we demonstrate the feasibility of ab initio NNQS simulations for complex electronic structures. Our approach represents a significant advancement in the NNQS method for strongly correlated solids, especially those containing 3d transition metals. To validate our method’s accuracy, we investigated systems such as the 1D hydrogen chain and cubic diamond, and the strongly correlated electronic structure of transition metal complexes. The agreement of our results with classical approaches and previous studies highlights the accuracy and potential of our approach.

By dividing orbitals into impurity and environment components, the DMET method offers an efficient way to partition a periodic system into fragments, which significantly reduces computational cost. Furthermore, the DMET method provides a viable approach to consider correlations between these fragments. This fragmentation scheme is not only more accurate but also more reasonable compared to direct fragmentation methods such as the fragment molecular orbital (FMO)^39,40,41 method or the many-body expansion (MBE) method^42,43, which often struggle to handle periodic systems effectively. Compared to the extensively developed dynamical mean-field theory (DMFT)^23,24, DMET offers a similar representation of physics but at significantly lower computational costs. However, it is still challenging for the DMET method to accurately evaluate properties related to excited states, which limits its applicability in certain scenarios.

The current DMET-NNQS method faces size limitations. For large systems, we have two options: increasing the fragment size or partitioning the system into more fragments. However, larger fragments require more memory for the NNQS solver, thus constraining the maximum fragment size to the VRAM of the GPU used. Conversely, partitioning the system into too many fragments complicates the convergence of the DMET algorithm. Overcoming these limitations necessitates further development of the DMET-NNQS method.

The results in this work demonstrate the feasibility of the DMET-NNQS method in dealing with transition metal atoms. Many similar materials are known to exhibit strong electron correlation effects. Looking forward, we plan to apply our method in studying strongly correlated materials, such as high-temperature superconducting cuprates and catalysis, where the accurate treatment of electron correlations is critical. These applications would require an a priori partitioning of active orbitals based on chemical intuition, with systematic expansion of each correlating fragment for convergence of properties of interest.

Methods

In this section, we explain the pivotal steps of the DMET-NNQS method. We begin with a concise introduction to the DMET method. Given the comprehensive coverage of the DMET method for both molecular and periodic systems in prior publications, we will not delve into every detail of the DMET method. In the subsequent section, we will begin by outlining the methodology for solving the Hamiltonian using the NNQS solver. Subsequently, an overarching workflow of the DMET-NNQS method is presented, providing a comprehensive overview and introducing the transfer learning strategy in the DMET-NNQS method. Further elaboration and in-depth discussion will follow, offering detailed insights.

Quantum chemistry Hamiltonians

The primary objective of ab initio quantum chemistry calculation is to solve the static Schrödinger equation $H\left\vert \Psi \right\rangle =E\left\vert \Psi \right\rangle$ to get the ground state $\left\vert \Psi \right\rangle$ and the ground-state energy E of the many-body interacting Hamiltonian:

$$\hat{H}=-\mathop{\sum }\limits_{i=1}^{N}\frac{1}{2}{\nabla }_{i}^{2}-\mathop{\sum }\limits_{i=1}^{N}\mathop{\sum }\limits_{A=1}^{M}\frac{{Z}_{A}}{| {{\bf{r}}}_{i}-{{\bf{R}}}_{A}| }+\mathop{\sum }\limits_{i=1}^{N}\mathop{\sum }\limits_{j > i}^{N}\frac{1}{| {{\bf{r}}}_{i}-{{\bf{r}}}_{j}| }$$

(1)

where N, M denote the total number of electrons and nuclei, ∇_i is the single particle kinetic operator of the i-th electron, r_i indicates the electronic coordinates, R_A and Z_A indicate the coordinates and charges of the A-th nucleus in the molecule. As shown in ref. ¹³, we have transformed the Hamiltonian in Eq. (1) into many-spin Hamiltonian $H=\mathop{\sum }\nolimits_{i = 1}^{{N}_{h}}{c}_{i}{P}_{i}$, where each P_i is the tensor product of Pauli spin operators {I, σ_x, σ_y, σ_z} of length N, referred to as a Pauli string, and c_i is a real coefficient. N_h denotes the total number of Pauli strings. For quantum chemistry Hamiltonians, N_h often scales as O(N⁴), which means that for each input bitstring x, there could exist $O({N}^{4})\,{\bf{x}}^{\prime}$ s with nonzero ${H}_{{\bf{x}}{\bf{x}}^{\prime} }$. As a result for large N, evaluating the local energy can be very expensive, and storing all the ${\bf{x}}^{\prime}$ s that are nontrivially coupled to x could use a large amount of memory, we have proposed an efficient scheme for the local energy calculation with a highly compressed data structure for the Hamiltonian together with a fused design of nonzero Hamiltonian entry evaluation and local energy calculation¹⁴.

Density matrix embedding theory

The density matrix embedding theory (DMET) assesses the interaction between the impurity and the environment using the density matrix. Once the impurity is identified, the DMET method focuses on the off-diagonal part of the density matrix, which contains information about the interaction between the impurity orbitals and environment orbitals. Specifically, singular value decomposition (SVD) is applied to the off-diagonal segment of the density matrix, denoted as D_IJ:

$${D}_{IJ}=\mathop{\sum }\limits_{\kappa }^{{d}_{\kappa }}{{\bf{U}}}_{I\kappa }{\lambda }_{\kappa }{{\bf{V}}}_{\kappa J}^{\dagger },I\in env,J\in imp$$

(2)

I is subscript for environmental orbitals and J is subscript for impurity orbitals. SVD result gives the diagonal matrix of singular values λ_κ, the number of singular values is denoted as N_κ. Leveraging the outcomes of SVD, the extensive environment can be condensed to a set of merely N_κ virtual orbitals, denoted as the bath orbitals. U_Iκ in Eq. (2) is exactly the transformation matrix from environment to bath orbitals. The SVD result of the density matrix forms the core of the DMET algorithm.

In practice, the DMET algorithm for a periodic system starts with the mean-field calculation of the system, usually a Hartree-Fock or a DFT calculation, yielding Bloch wave functions. Considering the preference for performing the DMET method in a localized real space basis, it is imperative to conduct the localization of Bloch wave functions. In this work, we employ intrinsic atomic orbitals for this purpose. Following this, it is imperative to identify the impurity and the environment or partition the localized orbitals into fragments. When concentrating on a specific fragment, orbitals in other fragments collectively constitute the environment. For each fragment impurity, SVD (Eq. (2)) is applied to the density matrix on a localized basis. The outcome of this process provides the transformation matrix C from localized orbitals to bath orbitals:

$${C}^{{\rm{LO}},{\rm{bath}}}=\left[\begin{array}{cc}{\bf{I}}&{\bf{0}}\\ {\bf{0}}&{{\bf{U}}}_{I,\kappa }\end{array}\right]$$

(3)

Where the impurity part remains the same and the environment orbitals are reduced to N_κ bath orbitals with U_I,κ. Based on mean-field results and the transformation matrix, the embedding Hamiltonian can be constructed (detailed information can be found in ref. ³⁰):

$${\hat{H}}_{{\rm{emb}}}=\sum _{pq}{h}_{pq}{a}_{p}^{\dagger }{a}_{q}+\sum _{pqrs}{v}_{qs}^{pr}{a}_{p}^{\dagger }{a}_{r}^{\dagger }{a}_{s}{a}_{q}$$

(4)

Here, h_pq and ${v}_{qs}^{pr}$ are one- and two-electron integrals. a^† and a are the creation and annihilation operators. p, q, r, s are subscripts for embedding orbitals. The embedding Hamiltonians for all fragments are subsequently solved with the NNQS solver, yielding the ground-state wave function, from which the 1-particle and 2-particle reduced density matrices are computed. Information from all fragments is amalgamated to construct a comprehensive picture.

To ensure self-consistency, the DMET algorithm undergoes two iterations. The first iteration focuses on electron number convergence, which ensures the total electron number aligns with the original electron number in the system. To achieve this, an additional global potential is introduced into the embedding Hamiltonian:

$${\hat{H}}_{new}^{{\rm{emb}}}\leftarrow {\hat{H}}_{old}^{{\rm{emb}}}-\mu \sum {\hat{a}}_{p}^{\dagger }{\hat{a}}_{p}$$

(5)

The global potential μ is induced as an extra one-electron term in the embedding Hamiltonian. By adjusting the value of the global potential, the algorithm seeks to find the optimal value that achieves electron number convergence. This iteration is referred to as μ iteration in the following paper. The second iteration is employed to enhance the self-consistent construction of the bath orbitals. This is achieved by updating the Fock operator in the mean-field calculation with a correlation potential u. A lost function is used to optimize a better correlation potential u by minimizing the matrix norm between the mean-field density matrix ${D}_{pq}^{{\rm{mf}}}(u)$ and the one-particle density matrix solved with NNQS solver ${D}_{pq}^{{\rm{NN}}}$.

$$min \sum _{pq}{\left[{{D}^{mf}_{pq}}(u)-{{D}^{NN}_{pq}}\right]}^{2}$$

(6)

Such an iteration improves the result of the mean-field calculation and refines the construction of bath orbitals. The second iteration is identified as the u iteration below. Upon the completion of the self-consistent iterations, the physical properties of interest can be obtained.

QiankunNet: the NNQS method based on transformer architecture

In our previous work¹³, a transformer-based neural-network architecture (QiankunNet) was used as the variational ansatz to directly solve the many-electron Schrödinger equation under the second quantized formalism, which significantly improves the accuracy of first-principles calculations compared to existing Fermionic ansatz.

Using QiankunNet as a representation for the ground state, expressed as $\vert {\psi }_{\vec{\theta}}\rangle$, where ${\vec{\theta}}$ signifies the parameters undergoing optimization, the system’s energy can be articulated as a function dependent on ${\vec{\theta}}$. In the second quantized formalism, with a basis set (single-electron quantum states or spin-orbitals) introduced, the many-electron wave function can be written as a linear combination of configurations

$$\vert {\psi}_{\vec{\theta}}\rangle =\mathop{\sum}\limits_{{\rm{x}}}\langle {\bf{x}}| {\psi }_{\vec{\theta}}\rangle \vert {\bf{x}}\rangle =\mathop{\sum}\limits_{{\rm{x}}}{\psi }_{\vec{\theta}}({\bf{x}})\vert {\bf{x}}\rangle$$

(7)

where each configuration is represented by an occupation number vector (‘configuration string’) $\vert {\bf{x}}\rangle =\{{x}_{1},{x}_{2},\ldots {x}_{N}\}$ with x_i ∈ {0, 1} denoting whether the i-th spin orbital is occupied or not, then we have,

$$\begin{array}{ll}E(\vec{\theta })=\frac{\langle {\psi }_{\vec{\theta }}| H| {\psi }_{\vec{\theta }}\rangle }{\langle {\psi }_{\vec{\theta }}| {\psi }_{\vec{\theta }}\rangle }=\frac{{\sum }_{{\bf{x}},{\bf{x}}^{\prime} }\langle {\psi }_{\vec{\theta }}| {\bf{x}}\rangle \langle {\bf{x}}| H| {\bf{x}}^{\prime} \rangle \langle {\bf{x}}^{\prime} | {\psi }_{\vec{\theta }}\rangle }{{\sum }_{{\bf{y}}}\langle {\psi }_{\vec{\theta }}| {\bf{y}}\rangle \langle {\bf{y}}| {\psi }_{\vec{\theta }}\rangle }\\ \qquad\;\;\;\;=\frac{{\sum }_{{\rm{x}}}{E}_{loc}({\bf{x}}){p}_{\vec{\theta }}({\bf{x}})}{{\sum }_{{\bf{y}}}{p}_{\vec{\theta }}({\bf{y}})}={{\mathbb{E}}}_{p}[{E}_{loc}({\bf{x}})]\end{array}$$

(8)

Here, x, ${\bf{x}}^{\prime}$, and y represent distinct bitstrings. In the second line of Eq. (8), the concept of local energy, denoted as E_loc(x), is established as:

$${E}_{loc}({\bf{x}})=\mathop{\sum}\limits_{{\bf{x}}^{\prime}}{H}_{{\bf{x}}{\bf{x}}^{\prime} }{\psi}_{\vec{\theta}}({\bf{x}}^{\prime})/{\psi}_{\vec{\theta}}({\bf{x}})$$

(9)

In this context, ${H}_{{\bf{x}}{\bf{x}}^{\prime} }=\langle {\bf{x}}| H| {\bf{x}}^{\prime} \rangle$ signifies the matrix element, and ${\psi }_{\vec{\theta}}({\bf{x}})=\langle {\bf{x}}| {\psi}_{\vec{\theta}}\rangle$ represents the probability amplitude for the wave function hypothesis $\vert{\psi}_{\vec{\theta}}\rangle$ in the $\vert {\bf{x}}\rangle$ basis. Additionally, the expression ${p}_{\vec{\theta}}({\bf{x}})=| {\psi}_{\vec{\theta}}({\bf{x}}){| }^{2}$ is used to denote the probability.

Accurately calculating Eq. (8) is typically unfeasible due to the vast, exponentially large set of varying bitstrings. Nevertheless, an approximate assessment of Eq. (8) can be achieved by drawing samples from the probability distribution ${p}_{\vec{\theta}}({\bf{x}})$, thereby acquiring a collection of N_s samples, labeled as $\{{{\bf{x}}}^{1},{{\bf{x}}}^{2},\ldots ,{{\bf{x}}}^{{N}_{s}}\}$, followed by their subsequent averaging:

$$\tilde{E}({\vec{\theta}})=\frac{1}{{N}_{s}}\mathop{\sum}\limits_{i=1}^{{N}_{s}}{E}_{loc}({{\bf{x}}}^{i})$$

(10)

In this instance, $\tilde{E}({\vec{\theta}})$ is employed rather than $E({\vec{\theta}})$ to underscore that it is merely an estimation of the actual value. Consequently, if one can effectively draw samples from ${p}_{\vec{\theta}}({\bf{x}})$ (feasible when ${\psi}_{\vec{\theta}}({\bf{x}})$ can be efficiently calculated for each x), and identify those significant ${H}_{{\bf{x}}{\bf{x}}^{\prime} }$ values along with corresponding ${\bf{x}}^{\prime}$, then a more efficient evaluation of Eq. (8) is achievable. Employing a gradient-based optimizer can expedite these calculations compared to methods that don’t use gradients. Using the gathered samples, it is possible to estimate the gradient of Eq. (8) through automatic differentiation, as suggested in¹⁶:

$$\begin{array}{l}{\nabla }_{\vec{\theta}}\tilde{E}=2{\rm{Re}}\left({{\mathbb{E}}}_{p}\left[\left({E}_{loc}({\bf{x}})\right.\right.\right.\\\qquad\;\left.\left.\left.-\,{{\mathbb{E}}}_{p}\left[{E}_{loc}({\bf{x}})\right]\right){\nabla}_{\vec{\theta}}\ln \left({\Psi }_{\vec{\theta}}^{*}({\bf{x}})\right)\right]\right)\end{array}$$

(11)

In a comparable manner, ${\nabla}_{\vec{\theta}}\tilde{E}$ serves as an approximation for the precise gradient ${\nabla}_{\vec{\theta}}E$. Subsequent to this, the parameters ${\vec{\theta}}$ are updated using ${\nabla}_{\vec{\theta}}\tilde{E}$ in conjunction with the optimizer, culminating in the completion of a single cycle of the variational Monte Carlo algorithm (VMC).

Transfer learning strategy in DMET-NNQS

The comprehensive workflow of the DMET-NNQS method is depicted in Fig. 7. As indicated in the figure, the DMET algorithm generates a series of embedding Hamiltonians tailored to a specific system. These embedding Hamiltonians are solved using the NNQS solver, yielding the ground-state energies and wave functions. The wave functions then generate one-particle and two-particle reduced density matrices, which are crucial components for the two self-consistent iterations in the DMET method. The iteration continues until a specified convergence criterion is achieved.

Fig. 7: Flowchart of the DMET-NNQS algorithm, featuring the DMET method outlined in blue boxes and the NNQS solver in green boxes.

Yellow boxes indicate information exchange between them.

A significant problem in the entire DMET-NNQS process is that the two iterations of DMET produce numerous embedding Hamiltonians for the NNQS solver, leading to a substantial increase in computational time for the entire algorithm. Our observation indicates that the two iteration processes do not result in substantial modifications to the one- and two-body integrals in the Hamiltonian, suggesting that all Hamiltonians in the iteration share similar structures. As a result, the parameters for generating the ground state wave function in neural networks are not expected to differ significantly. Our analysis further suggests that the neural-network parameters obtained from the previous iteration can serve as ideal initial parameters for the next iteration. Thus the final parameters for each DMET iteration are saved, and in the subsequent DMET iteration, the entire neural network is reconstructed using these saved parameters. Furthermore, considering that the initial parameters (except in the first iteration) require only merely steps toward reaching the optimal parameters, we can set the learning rate of the neural network to a relatively low value. Additionally, more stringent convergence criteria can be imposed. These adjustments contribute to the faster and more accurate convergence of the NNQS solver. Apart from transfer learning within DMET iterations, transfer learning can significantly enhance efficiency whenever Hamiltonians exhibit a certain degree of similarity. For instance, this applies to Hamiltonians derived from various fragments or even different systems, provided that the orbitals within these fragments share similar structural characteristics. The utilization of transfer learning significantly enhances the algorithm’s efficiency, and detailed results are presented in the section “Efficiency of transfer learning strategy”.

Implementation and computational details

In this work, we used QiankunNet as the NNQS solver and developed an interface to the libdmet code developed by Cui et al.³⁰. We followed the general workflow provided with libdmet and made necessary modifications to the code. All mean-field calculations in this work were conducted using the PySCF package^44,45, with the Hartree-Fock method in periodic boundary conditions serving as the starting point for DMET iterations. GTH pseudo-potentials were used to replace core electrons, and corresponding GTH basis sets were utilized. For systems lacking d electrons, the GTH-DZVP basis set was applied, whereas the GTH-DZVP-MOLOPT-SR basis set was used for systems containing d electrons. The two-electron integrals were computed using the GDF module in PySCF. In all DMET calculations, the intrinsic atomic orbital (IAO) method was employed as the localization method. Classical quantum chemistry methods such as CC and CI were also implemented using the PySCF package.

We compiled the NNQS transformer using a hybrid of single-precision and double-precision, on the Intel Xeon Scale 8358 CPU and NVIDIA A100 PCIe 80 GB. Pytorch 1.13 was used, which has been deeply integrated with the underlying runtime and computing libraries.