DenseGNN: universal and scalable deeper graph neural networks for high-performance property prediction in crystals and molecules

Abstract

Modern generative models based on deep learning have made it possible to design millions of hypothetical materials. To screen these candidate materials and identify promising new materials, we need fast and accurate models to predict material properties. Graphical neural networks (GNNs) have become a current research focus due to their ability to directly act on the graphical representation of molecules and materials, enabling comprehensive capture of important information and showing excellent performance in predicting material properties. Nevertheless, GNNs still face several key problems in practical applications: First, although existing nested graph network strategies increase critical structural information such as bond angles, they significantly increase the number of trainable parameters in the model, resulting in a increase in training costs; Second, extending GNN models to broader domains such as molecules, crystalline materials, and catalysis, as well as adapting to small data sets, remains a challenge. Finally, the scalability of GNN models is limited by the over-smoothing problem. To address these issues, we propose the DenseGNN model, which combines Dense Connectivity Network (DCN), hierarchical node-edge-graph residual networks (HRN), and Local Structure Order Parameters Embedding (LOPE) strategies to create a universal, scalable, and efficient GNN model. We have achieved state-of-the-art performance (SOAT) on several datasets, including JARVIS-DFT, Materials Project, QM9, Lipop, FreeSolv, ESOL, and OC22, demonstrating the generality and scalability of our approach. By merging DCN and LOPE strategies into GNN models in computing, crystal materials, and molecules, we have improved the performance of models such as GIN, Schnet, and Hamnet on materials datasets such as Matbench. The LOPE strategy optimizes the embedding representation of atoms and allows our model to train efficiently with a minimal level of edge connections. This substantially reduces computational costs and shortens the time required to train large GNNs while maintaining accuracy. Our technique not only supports building deeper GNNs and avoids performance penalties experienced by other models, but is also applicable to a variety of applications that require large deep learning models. Furthermore, our study demonstrates that by using structural embeddings from pre-trained models, our model not only outperforms other GNNs in distinguishing crystal structures but also approaches the standard X-ray diffraction (XRD) method.

Introduction

In the almost infinite design space of chemistry, only 10⁵ crystal structures have been synthesized and characterized, forming a very limited region of the potential material space. To push the boundaries of existing material properties and explore a broader material design space, one of the most promising approaches is the generative design paradigm based on deep learning (DL). In this approach, existing materials are fed into deep generative models based on neural networks, which learn atomic assembly rules to form stable crystal structures and use these rules to generate chemically viable hypothetical structures or compositions^1,2,3. Although these material candidates can be rapidly generated in the hundreds or thousands, a fast and accurate model for predicting material properties is required to screen the most promising materials for further description of their properties, whether through first-principles density functional theory (DFT) or molecular dynamics calculations or through experiments. After all these steps, unique materials can be found in the unknown design space.

Currently, machine learning (ML) models have become one of the most promising methods in materials discovery, offering higher prediction accuracy and speed compared to first-principles calculations⁴. ML models based on composition or structure can successfully predict material properties, with their performance heavily influenced by the choice of ML algorithms, features, and the quality and quantity of available datasets. Among these screening models, composition-based ML models^5,6,7 have the advantage of speed and the ability to screen large-scale hypothetical compositions generated by DL models⁸. However, almost all material properties strongly depend on the structure of the material, so structure-based material prediction models typically have higher prediction accuracy. They can be used to screen known material structure repositories, such as ICSD⁹ or the (MP) Database¹⁰, or the structures of hypothetical crystal materials created by modern generative DL models^11,12,13,14. Currently, there are two main classes of ML methods for predicting material properties based on structure, which are divided into those based on heuristic features and those based on DL models that learn features. Although heuristic feature-based ML models^15,16 have shown some success in various applications, such as formation energy prediction¹⁷ and ion conductivity screening¹⁸, extensive benchmark studies have shown that GNNs outperform them in material performance prediction¹⁹. GNNs are used to process graph-structured data and are closely related to geometric DL. In addition to research on social and citation networks and knowledge graphs, chemistry is one of the main driving forces behind GNN development. GNNs can be viewed as an extension of convolutional neural networks to handle irregularly shaped graph structures. Their architecture allows them to directly work on natural input representations of molecules and materials, which are chemical graphs composed of atoms and bonds, or even the three-dimensional structure or point cloud of atoms. Therefore, GNNs can fully represent materials at the atomic level²⁰ and have the flexibility to incorporate physical laws²¹ and phenomena at larger scales, such as doping and disorder. Using this information, GNNs can learn valuable and information-rich internal material representations for specific tasks, such as predicting material properties. Thus, GNNs can complement or even replace handcrafted feature representations widely used in the natural sciences.

Since 2018, various GNN models have been proposed to improve prediction performance, such as CGCNN²², SchNet²⁰, MEGNet²³, iCGCNN²⁴, ALIGNN²⁵, and coGN²⁶, among others. These architectures all use structure graph representation as input, also incorporating slightly different additional information, convolution operators, and neural network architectures^20,23,24. Despite this progress, there are still major problems with the application of GNNs in the fields of chemistry and materials: First, nested graph networks like ALIGNN and coNGN²⁶ have substantially more trainable parameters, leading to higher training costs compared to non-nested graph networks. These nested graph networks maintain their advantages only on some crystal datasets. Therefore, it is necessary to develop strategies that can effectively embed information on many-body interactions such as bond angles and local geometric distortions outside of nested graph networks. Second, there exists an imbalance in research and model development efforts across the fields of materials science, molecular science, and chemistry. Extending existing GNN models to broader application areas (such as spanning molecular, crystal materials, and catalysis fields) may be challenging and require further development of GNN models. At the same time, the data released by Matbench official website²⁷ currently shows that GNNs generally perform worse on small datasets compared to the MODNet²⁸, which incorporates traditional feature engineering²⁹. Thirdly, the strategy for constructing graph representations of input structures is a key factor affecting the performance and training cost of GNNs. The coGN proposes asymmetric unit cells as representations, reducing the number of atoms by utilizing all symmetries of the crystal system to minimize the number of nodes in the crystal graph. This reduces the time required to train large GNNs without sacrificing accuracy. However, the method of reducing the number of atoms does not effectively optimize edge connections in some material datasets, such as the perovskites dataset in Matbench, where using all symmetry does not reduce the average number of nodes. Finally, most message-passing GNNs currently suffer from oversmoothing problems, in which the representation vectors of all nodes of a graph become indistinguishable as the number of graph convolution (GC) layers increases^30,31,32,33, limiting the increase in GC layers. As the number of layers increases, the model performance decreases.

In this work, we propose DenseGNN, a GNN model that combines DCN, HRN, and LOPE to overcome oversmoothing problems, support the construction of very deep GNNs, and avoid the performance degradation problems present in other models. Our model allows for highly efficient training at the level of minimal edge connections. We also apply the DCN and LOPE strategies to GNNs in the fields of computers, crystal materials, and molecules, achieving performance improvements on almost all models in the Matbench dataset. Our contributions in this paper can be summarized as follows:

• We overcome the main bottlenecks of GNNs in predicting material properties and propose a novel DCN-based GNN architecture. This architecture updates edge, node, and graph-level features simultaneously during the message-passing process through DCN and residual connection strategies, achieving more direct and dense information propagation, reducing information loss during propagation in the network, overcoming oversmoothing problems, and supporting the construction of very deep GNNs. Additionally, it better utilizes feature representations from preceding layers, improving network performance and generalization.

• DenseGNN outperforms the latest coGN, ALIGNN, and M3GNet³⁴ on most benchmark datasets for crystal, and molecules materials, while also demonstrating higher learning efficiency on experimental small datasets.

• We apply our DCN and LOPE strategies to GNNs in fields such as computers, crystal materials, and molecules, achieving notable performance improvements on all GNNs in the Matbench material dataset.

• Many important material properties (especially electronic properties such as band gaps) are very sensitive to structural features such as bond angles and local geometric distortions. Therefore, effectively learning these many-body interactions is crucial. Current strategies mainly involve building nested graph networks based on bond graphs to introduce bond angle information, but this method has high training costs. By incorporating LOPE and optimizing atomic embeddings, we minimize edge connections, reduce training time for large GNNs while maintaining accuracy.

• We demonstrate the improvement in the ability to distinguishing crystal structures by utilizing pre-trained model structural embeddings compared to other GNNs, approaching the standard XRD method.

Results

Model architecture description

In the architecture of DenseGNN, the first block is an edge-node-graph input embedding block, as shown in Fig. 1, which independently embeds atom/node, bond/edge, and global state/graph features. We employed k-nearest neighbors (KNN) as a default preprocessing method for edge selection, with the parameter k set to either 12 or 6 to achieve optimal test results. Figure 1 illustrates the high-level architecture of the GNN, but does not specifically instantiate the update functions ϕ_E, ϕ_V, ϕ_G, and aggregation functions ρ_E → _V, ρ_V → _G, ρ_E → _G. The ϕ_E function utilizes 32 Gaussian functions uniformly distributed in the [0, 8] Å range to expand edge distances. As only distance information is used, this embedding is E(3)-invariant. The initial representations are projected into a 128-dimensional embedding space and implemented through a single Multilayer Perceptron (MLP) network. The ϕ_V function embeds atomic features (including LOPE, atomic number, atomic mass, atomic radius, ionization state, and oxidation state) into a 128-dimensional space. The ϕ_G function updates the attributes at the molecule/crystal level or state (e.g., the system’s temperature). A more detailed explanation of the embedding block can be found in the Fig. 2.

Fig. 1: An overview of the DenseGNN architecture.

This figure illustrates the architecture of DenseGNN, which is divided into three main components. Firstly, the input embedding block handles atom/node, bond/edge, and global state/graph features through independent embeddings. Edge selection uses K-nearest neighbors (KNN) with k = 12 or 6. Edge distances are modeled using 32 Gaussian functions within an 8 Å range to ensure E(3)-invariance. Initial representations are projected into a 128-dimensional space via an MLP. The second component includes T = 5 sequential graph convolution processing blocks, each with distinct learnable parameters, updating edge, node, and graph-level features using DCNs and HRNs. The final component is a readout module that combines node, edge, and graph features to produce graph-level predictions of crystal properties through a single-layer MLP with linear activation. The model consistently uses a 128-dimensional feature space and swish activation in MLPs. Training utilizes an Adam optimizer with a linear learning rate scheduler over 300 epochs.

Fig. 2: Representation of local chemical environment in crystal structure.

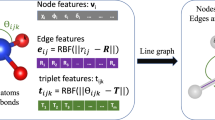
This figure illustrates the representation of the local chemical environment of atoms within a crystal structure. Nodes represent individual atoms, and edges signify the connections between them. These nodes and edges are embedded with vectors that encapsulate the characteristics of the constituent atoms, including their Local Structure Order Parameters Embedding (LOPE) and the correlations with their neighboring atoms. Additionally, a graph state vector is depicted, which accumulates the molecular or crystalline level attributes.

In the second block of the Fig. 1, we implemented a sequentially connected structure consisting of T = 5 GC processing blocks, each with independent learnable parameters and identical configuration. In each block, edge, node, and graph-level features are updated synchronously and are connected through DCNs respectively, achieving a comprehensive optimization of the local chemical environment of the atoms. A more detailed explanation of the edge-node-graph update can be found in the Fig. 3.

Fig. 3: Input graph and attribute update steps in DenseGNN.

This figure illustrates the input graph for DenseGNN and the process of updating node, edge, and graph attributes. The input graph consists of node attributes, edge attributes, and optional graph attributes. During the first update step, edge attributes are updated based on information from the nodes forming the edges, the graph attributes, and the previous edge attributes. In the subsequent steps, node attributes are updated incorporating information from the edge attributes and graph attributes, while graph attributes are updated considering information from both node and edge attributes. This iterative update process optimizes the representation of the graph structure and its associated features.

In the third block of the Fig. 1, we designed an independent readout module that aggregates node, edge, and graph features into graph-level features and inputs them into a single-layer MLP with a linear activation function to generate the final predictions of crystal properties. Throughout the hidden representations of the GNN, we uniformly used a 128-dimensional feature space. Unless specified otherwise, we used the common swish activation function in the MLPs. The GNN is trained using an Adam optimizer with a linear learning rate scheduler for 300 epochs.

Figure 2 elaborates on the embedding block part of Fig. 1, illustrating the representation of the local environment around atoms in a crystal structure. In this crystal graph, nodes, and edges are embedded with vectors, which characterize the constituent atoms and their correlations with neighboring atoms. The local chemical environment of the nodes is represented by concatenating the features of the constituent atoms and the LOPE. The edge vectors capture the local structural information of the crystal graph by selecting KNN or using a parameter-free Voronoi method. Each edge is also embedded with a vector ${e}^{k}(i,j)$, which contains the distance information between adjacent atoms i and j within the crystal unit cell. To account for the periodicity of the crystal, multiple edges between atoms i and j can exist, indexed by k. Each node in the crystal graph is connected to its 6 or 12 nearest neighbors (DenseGNN performs better under this parameter.). Finally, g is a graph state vector storing the molecule/crystal level or state attributes (e.g., the temperature, charge of the system). In the input part of DenseGNN, the graph state vector is not mandatory and can be omitted depending on the specific use case.

The LOPE feature reflects the local environment and coordination of atoms around specific positions in the materials/molecular system. It consists of atomic embeddings and orientation-resolved embeddings, obtained by calculating the product integral of the radial distribution function (RDF) and a Gaussian window function. The atomic embeddings provide information about the local atomic environment, such as the density and distribution of neighboring atoms, by weighted summing the distances between the central atom and adjacent atoms. The orientation-resolved embeddings take into account the direction of neighboring atoms in relation to the central atom, providing a more detailed description of the local atomic environment, which includes orientation and anisotropy information. By introducing LOPE, we optimized the embedding representation of atoms, which is different from the nested graph strategy of ALIGNN as it includes bond angle information. This method avoids the high training cost of nested graph network strategies like ALIGNN, DimeNetPP and coNGN while maintaining model accuracy, thereby improving training efficiency.

$${e}_{{ij}}^{t+1}={e}_{{ij}}^{t}+\sum _{j,k}\sigma \left([{v}_{i}^{t}\,\bigoplus {v}_{j}^{t}\bigoplus {u}_{{ij}}^{t}\bigoplus {e}_{{ij}}^{t}]{W}_{1}^{t}+{b}_{1}^{t}\right)$$

(1)

$${v}_{i}^{t+1}={v}_{i}^{t}+\sum _{j,k}\sigma \left([{v}_{i}^{t}\,\bigoplus {u}_{{ij}}^{t}\bigoplus {e}_{{ij}}^{t}]{W}_{2}^{t}+{b}_{2}^{t}\right)$$

(2)

$${u}_{{ij}}^{t+1}={u}_{{ij}}^{t}+\sum _{j,k}\sigma ([{v}_{i}^{t}\,\bigoplus {u}_{{ij}}^{t}\bigoplus {e}_{{ij}}^{t}]{W}_{3}^{t}+{b}_{3}^{t})$$

(3)

Equations 1, 2, and 3 correspond to ϕ_E, ϕ_V and ϕ_G in Fig. 1, respectively, detailing the edge-node-graph update process in DenseGNN during training. Below, we will explain the update process step by step.

• 1. Edge feature update: The edge update function ϕ_E combines features of the receiver and sender nodes, global state, and edges, transforms them through a three-layer MLP network, and updates edge features through residual networks and activation functions.

• 2. Node feature update: For each node, we first aggregate the updated edge features, then concatenate the aggregated node features with the global state and original node features, transform them through a single-layer MLP network ϕ_V, and update node features through residual networks and activation functions.

• 3. Graph feature update: For each graph, we sum or average the updated edge and node features, then concatenate the aggregated graph features with the global state, transform them through a single-layer MLP network ϕ_G, and update graph features through residual networks and activation functions. To ensure efficient flow of information between blocks, we adopted the design concept of DCN, directly connecting all blocks to each other.

Each block not only receives features from all preceding blocks but also passes its own node, edge, and graph features to subsequent blocks. This design introduces L(L + 1)/2 connections in the network, rather than the traditional L connections in the architecture. This feature of DCN not only improves the flow of information and gradients, making the network easier to train, but also allows each layer to directly access gradients from the loss function and original input signal, thereby achieving implicit deep supervision³⁵. This helps in training deeper network architectures and overcoming over-smoothing problems in GNNs. Additionally, dense connections have a regularization effect, helping to reduce overfitting on tasks with small training set sizes. Figures. 1 and 12 schematically illustrate this architectural layout.

We noticed that dense connections may slow down model inference speed. However, factors affecting model training and inference speed primarily include three aspects: the method for constructing crystal/molecular graphs, the model’s hyperparameter settings (such as learning rate and batch size), and the model’s training parameters. On the Matbench and Jarvis DFT datasets, we compared DenseGNN with reference models and found that, with consistent hyperparameter settings, regardless of whether the radius-based or KNN method is chosen, DenseGNN requires fewer edges than reference models such as MEGNet, SchNet, CGCNN, and coGN. This compensates for the dense connections in the DCN. Additionally, in Supplementary Fig. S1, we provide a low-parameter version of DenseGNN, DenseGNN-Lite, maintaining the DCN and LOPE strategies, using a crystal graph based on KNN, and no longer using the graph state. By optimizing the edge-node update strategy, we significantly reduce the model’s parameters while only slightly decreasing the model’s performance, which remains superior to recent coGN in most cases.

Overall, the DenseGNN stands out for its simplicity, containing only MLP as update functions and mean or max aggregation functions, without the complex edge gate control or attention-based message passing mechanisms found in CGCNN, ALIGNN, or GeoCGNN³⁶. By introducing the mechanism of DCN, we successfully constructed a very deep GNN architecture while avoiding performance degradation problems, enhancing the scalability of GNNs.

Model comparison and analysis

To ensure the performance evaluation of DenseGNN is both fair and accurate, we have taken a series of measures to ensure comparisons with other SOTA models are conducted under equal conditions. This includes training all models on the same dataset, using appropriate training and optimal hyperparameters, and employing the same cross-validation methods. We implemented all models based on the Keras Graph Convolution Neural Networks (KGCNN)³⁷ framework and set the hyperparameters for all models in a unified json configuration file. All models’ hyperparameters are specified in JSON files, which can be referenced at https://github.com/dhw059/DenseGNN/tree/main/training/hyper. All models were trained for 300 epochs. To comprehensively evaluate the performance of different versions of DenseGNN, we tested them on multiple datasets, including molecular property datasets (QM9, LipopDataset, FreeSolvDataset, and ESOLDataset)^{38,39,40,41,42}, catalysis datasets (Open Catalyst Project, OC22)⁴³, and solid-state material datasets (Matbench and JARVIS-DFT)^27,44. These datasets are widely used to evaluate the performance of models in various material property prediction tasks, with detailed descriptions provided in the dataset description section. For the Matbench dataset, we adopted the official default training-validation-testing split strategy. As for the JARVIS-DFT and QM9 datasets, we employed an 80%:10%:10% split strategy, aligning with the split used for the coGN and MEGNet datasets. The difference between DenseGNN-KNN and DenseGNN-Voronoi lies in the edge selection method, with the former using a KNNs approach and the latter a Voronoi-based approach. DenseGNN-Lite, as shown in Fig. S1, is a streamlined version of DenseGNN that maintains performance while substantially reducing the number of training parameters.

The comparison results on the 8 regression task datasets in Matbench are shown in Fig. 4, using the mean absolute error (MAE) metric. The results for ALIGNN, SchNet, M3GNet, MODNet, coGN, and coNGN are from previous benchmark studies. DenseGNN and DenseGNN-Voronoi performed better on almost all material property prediction tasks, especially showing substantial advantages on small datasets like Jdft2d, Phonons, and Dielectric. It is worth noting that, compared to ALIGNN, MODNet, and coNGN, the architecture of DenseGNN neither introduces bond angles through nested graph networks like ALIGNN and coNGN, nor incorporates traditional domain knowledge databases like Matminer²⁹ at input as MODNet does. Instead, it cleverly fuses DCN, HRN, and the LOPE strategy, optimizing the network structure for efficient information flow and feature reuse. By introducing atomic embeddings for local chemical environment information, DenseGNN avoids increasing training costs, enhances model performance.

Fig. 4: Comparison of test MAE results on MatBench datasets.

This figure compares the MAE results of different versions of DenseGNN on the MatBench datasets against the previous models, including SchNet, MODNet, ALIGNN, and recent models like M3GNet, coGN, and coNGN. Notably, ALIGNN, coNGN, and M3GNet belong to the category of nested graph networks and incorporate angle information. The properties evaluated include e_form (eV/atom), gap (eV), perovskites (eV/unit cell), log_kvrh (log10(GPa)), log_gvrh (log10(GPa)), dielectric (unitless), phonons (1/cm), and jdft2d (meV/atom). The best results, data size, and relative improvements are highlighted in bold. Asterisks (*) denote cases where training parameters were not provided or no training was performed.

Evaluation on the QM9 molecular property dataset (130,829 molecules) showed that DenseGNN achieved competitive results on multiple tasks compared to other reference models, such as SchNet, MEGNet, enn-s2s⁴⁵, ALIGNN, and DimeNet++⁴⁶, especially in tasks like Highest Occupied Molecular Orbital (HOMO) and energy gap (Δϵ), as shown in Fig. 5. DenseGNN outperformed ALIGNN in most tasks and approached the performance of DimeNet++. DenseNGN implements the DCN strategy within the nested graph networks framework of coNGN, and it shows competitive results, surpassing DimeNet++ on most tasks, highlighting the importance of the DCN strategy and angle information for molecular property prediction. Note that we did not include models like EquiformerV2 in the baseline comparisons primarily because these models require significantly larger parameter counts and hardware resources; for example, EquiformerV2 has 122 million parameters, whereas our model has only 3.10 million parameters. Supporting Information Fig. S2 shows the test error of DenseNGN on the IS2RES task in the OC22 challenge, demonstrating its competitive performance in direct OC22-only predictions compared to models such as SchNet, DimeNet++, PaiNN, and GemNet.

Fig. 5: Comparison of test MAE results on QM9 datasets.

This figure compares the Test MAE of the QM9 datasets among various models: DenseGNN, DenseNGN, MEGNet, SchNet, enn-s2s, ALIGNN, and DimeNet++ (DN++). Among these, DenseNGN is a nested graph network that incorporates angle information, allowing the model to learn more accurate local chemical environment information. DenseNGN implements the DCN strategy within the nested graph networks framework of coNGN. The best results are highlighted in bold. A dash (-) indicates that the MAE results were not provided for certain comparisons.

In Fig. 6, we demonstrate that on the JARVIS-DFT dataset, DenseGNN outperforms the recent coGN model in most property prediction tasks. Further, in Supporting Information Fig. S3, we compare DenseNGN (a nested graph network version of DenseGNN that includes angular information) on the JARVIS-DFT dataset with other nested graph network models such as coNGN, ALIGNN, and DimeNet++. DenseNGN shows superior results. These results further confirm the effectiveness of the DCN and LOPE strategies in enhancing material property prediction performance. Supporting information Fig. S4 present the MAE comparison results of DenseGNN and DenseNGN with reference models on LipopDataset, FreeSolvDataset, and ESOLDataset. DenseGNN again demonstrates its competitive performance across different property prediction tasks.

Fig. 6: Comparison of test MAE results on JARVIS-DFT datasets.

This figure compares the Test MAE of the JARVIS-DFT datasets among different versions of DenseGNN and previous models such as coGN, CGCNN, Matminer, and CFID. These models do not belong to the category of nested graph networks and do not include angle information. The best results and relative improvements are highlighted in bold. A dash (-) indicates training failure due to insufficient computational resources or missing information. An asterisk (*) denotes that the training parameters were not provided or no training was performed. The figure also provides the train/validation/test split ratios for each dataset.

In Supporting information Fig. S5 showcases the performance comparison of DenseGNN-Lite against reference models on experimental small datasets. These datasets, sourced from matminer (https://github.com/dhw059/DenseGNN/datasets/dataset_metadata.json), have sample sizes ranging from 100 to 3000, covering various scales of experimental data. The results demonstrate that DenseGNN-Lite exhibits very high learning efficiency on these experimental small datasets, learning and adapting to the data more rapidly than reference models and providing superior prediction results. Figure S6 further confirms DenseGNN’s learning efficiency in scenarios with small data volumes. This figure displays the learning curves for the OptB88vdW formation energy and bandgap models, with uncertainty values representing the standard error of the 5-fold cross-validation iterations. DenseGNN shows rapid learning ability, quickly converging to low prediction errors even when experimental data is scarce, further validating its learning efficiency and prediction accuracy on small datasets. Taken together, the results in Figs. S5 and S6 demonstrate that DenseGNN models not only excel on computational datasets but also show efficient learning capabilities and good predictive performance on experimental small datasets. This is particularly important in materials science research, where experimental data is often limited and DenseGNN’s ability to exploit limited data for more accurate predictions has significant practical implications. Figures S7–S11 present the test results of DenseGNN, DenseGNN-Lite, and DenseNGN on the Matbench, Jarvis-DFT, and QM9 datasets.

Ablation study

To gain a deeper understanding of the contributions of each component in the DenseGNN to the prediction accuracy MAE, we conducted a series of ablation experiments. We selected the DFT Voigt-Reuss-Hill average bulk modulus(log kvrh) and the peak frequency of phonon DOS(phonons) as the experimental datasets. The experimental results are summarized in Table 1. Overall, the impact of the DCN component on the prediction results exceeded that of the LOPE component, leading to decrease of 23.44% and 29.21% in log kvrh and phonons predictions, respectively, while the decrease from the LOPE component were 7.81% and 8.43%, respectively. When only replacing the GC component in DenseGNN with Schnet-GC and GIN-GC, we observed a substantial decrease in prediction accuracy. On the log kvrh and phonons datasets, the prediction accuracy decreased by 7.03%, 11.52%, and 17.87%, 22.69%, respectively. Furthermore, we attempted to increase the number of GC layers in DenseGNN, and the results indicated that for log kvrh and phonons predictions, the prediction accuracy increased by 4.30% and 6.95%, respectively. Although adding more GC layers may lead to oversmoothing problems, the combination of DCN and LOPE resulted in a substantial performance improvement in our DenseGNN. Additionally, with an increase in model depth, accuracy also improved, indicating that more GC layers can more effectively capture embedding features and utilize features of higher-order neighbors. Table S1 in the supporting information presents the results of all models in ablation experiments on the jdft2d (exfoliation energy), phonons, dielectric (refractive index), perovskites (perovskite formation energy), as well as log gvrh and log kvrh (logarithm of DFT Voigt-Reuss-Hill average shear modulus and bulk modulus) datasets.

Table 1 Ablation study MAE results for DenseGNN components

In Supplementary Figs. S12–S15, conduct ablation experiments to confirm the role of each component in the model. Figure S12 demonstrates the effect of varying the number of hidden units on the DenseGNN model’s performance on the JARVIS-DFT OptB88vdW formation energy and bandgap datasets. The results show that as the number of hidden features increases from 64 to 256, the model’s parameter and training time increase, but the model’s MAE improves. Figure S13 explores the impact of changing the number of Graph Convolutional Network (GCN) layers on the DenseGNN model’s performance on the same datasets. The results indicate that as the number of GCN layers increases, the model’s parameters and training time increase, but the model’s MAE improves. Figure S14 investigates the effect of altering the number of DCN layers on the DenseGNN’s performance. The results show that as the number of DCN layers increases, the model’s parameters and training time increase, but the model’s MAE improves. The results in Fig. S15 show that introducing the DCN strategy reduces the MAE test error of Schnet, PAiNN and DimeNet++ on the QM9 dataset, validating the strategy’s ability to optimize the performance of current models. In the Supplementary Figs. S16–S19 provide the original 5-fold train and test results. Through these ablation experiments, we not only confirmed the role of each component in DenseGNN but also showcased how the DCN and LOPE strategies work together to improve the model’s predictive accuracy and deepen its learning capabilities.

Our DCN and LOPE strategy improve GNN models in different fields

Our ablation experiments highlighted the crucial roles of DCN and LOPE strategy in enhancing model performance. While numerous models have been proposed for computer, molecular, and materials fields, their performance often deteriorates when transferred to the crystal materials domain. To validate the effectiveness and generality of the DCN and LOPE strategy, we fused DCN and LOPE strategy into representative models from these three fields. We selected GraphSAGE⁴⁷, GAT⁴⁸, and GIN⁴⁹ for the computer domain; AttentiveFP⁵⁰, PAiNN⁵¹, and HamNet⁵² for the molecular domain; and CGCNN, MEGNet, and Schnet for the materials domain. These models cover spatial convolutions, message passing, 3D geometric message passing, attention mechanisms, and graph transformers, among others, in the realm of GNNs.

As shown in Fig. 7, we compared the MAE results of Schnet, HamNet, and GIN models in their original state and after fusing DCN and LOPE strategy on six Matbench regression datasets (ranging from 312 to 18,928 samples). The experimental results demonstrate performance improvements across all datasets for all models. Particularly, the enhancement of model performance by DCN exceeded that of LOPE, aligning with the findings of the ablation experiments, notably prominent in models from the molecular and computer fields such as HamNet and GIN. This further confirms the impact of DCN and LOPE strategy in enhancing model cross-domain performance, demonstrating their versatility and scalability. Supplementary Fig. S20 presents the MAE results comparison of representative models from the three fields fused with DCN strategy on the six Matbench datasets.

Fig. 7: Test MAE changes after fusing DCN and LOPE strategies.

This figure compares the test MAE changes for GNN models on six different property datasets in Matbench after fusing the DCN and LOPE strategies. a–f correspond to the test MAE results on Phonons, Perovskites, Jdft2d, Log gvrh, Dielectric, and Log kvrh datasets, respectively. The models include GIN from the computer domain; HamNet from the molecular domain; and SchNet from the materials domain. The MAE results show improvements across all datasets for all models after fusing DCN and LOPE strategies. Specifically, DCN showed greater enhancement than LOPE, particularly in models from the molecular and computer domains like HamNet and GIN.

In the Matbench test results, notably on small datasets such as Jdft2d, Phonons, and Dielectric, the SchNet fused with DCN and LOPE achieved decrease in MAE. Similarly, the HamNet model exhibited notable performance improvements in Phonons and Dielectric properties, with MAE errors decreased by 23.93% and 18.26%, respectively. For the GIN model, the most performance improvements were observed on the Phonons and Perovskites datasets, with MAE errors reduced by 41.15% and 38.78%, while the decrease in MAE for other properties ranged from 3% to 10%. These results underscore the effectiveness of DCN and the LOPE strategy in enhancing the performance of models transferred from other fields to the materials domain, offering a new technical solution to address the challenge of extending existing GNNs to broader application fields.

Fusion of DCN to address the over-smoothing problems of GNNs

In view of the prevalent oversmoothing problem in existing message-passing GNNs, we explored whether the DCN and LOPE strategies could address this problem of and enable them to benefit from deeper GC layers. In previous studies on DeeperGATGNN⁵³, it was found that existing GNN models such as SchNet, CGCNN, MEGNet, and GATGNN experience a significant performance decline after adding a certain number of GC layers, leading to inaccurate property predictions. The DGN and skip connections strategies proposed in the paper did not effectively improve the scalability of models other than DeeperGATGNN, almost all models experienced a substantial performance decrease after 20 GC layers. Based on this, we implemented the DCN and LOPE strategies to the Schnet, HamNet, and GIN models across different fields and studied the scalability of these models and their deep versions (DeeperDenseGNN, DeeperSchnet, DeeperHamNet, and DeeperGIN). We conducted this study using six Matbench datasets, with all experiments employing 300 epochs and 5-fold cross-validation, training each model with 5, 10, 15, and 20 GC layers, and evaluating their scalability.

The results in Table 2 show that DeeperSchNet exhibited a performance improvement of approximately 3% to 9% across the six datasets as the number of GC layers increased from 10 to 20, indicating that our strategies effectively improved the scalability of the model. For instance, on the Perovskites dataset, the MAE decreased from 0.0321 with 20 GC layers to 0.0294 with 5 GC layers, and there was no decrease in MAE with 30 GC layers. DeeperDenseGNN, DeeperHamNet, and DeeperGIN also showed similar results, with these models demonstrating an improvement in MAE across all test datasets as the number of GC layers increased. DeeperDenseGNN improved by ~4% to 7%, DeeperHamNet by ~3% to 8%, and DeeperGIN by ~5% to 9%. Particularly, the DCN and LOPE strategies performed better on the GIN, with the MAE decreasing even with over 20 layers. Further testing of DeeperGIN with 30, 40, 50, and 60 GC layers revealed a continued decrease in MAE, especially notable on smaller datasets such as Jdft2d and Phonons (with sample sizes of 636 and 1265, respectively), showing improvements from 8.87% and 7.66% to 10.89% and 9.80%, respectively.

Table 2 Impact of network depth on MAE

Our DCN and LOPE strategies improved the scalability of models in various fields. All these models showed a decrease in MAE across all datasets at 20 GC layers. Furthermore, even beyond 30 GC layers (see shaded area in Table 2 and Supplementary Fig. S21), no model exhibited a performance decline, indicating the potential for further increasing the number of GC layers. Due to computational resource constraints, we did not continue to increase the number of layers. A key point is that our models could scale to over 60 GC layers, with performance still slightly improving, especially on smaller datasets. This suggests that with more training samples for deeper training, we have the potential to achieve better results. In summary, our experiments with 60 GC layers demonstrate that DCN and LOPE strategies can improve the scalability of models in multiple fields, with model performance not deteriorating with an increase in GC layers, demonstrating strong robustness against overfitting.

Optimizing edges connectivity for efficiency improvement

In GNNs, the nested graph networks strategy enhances the model’s expressive power by incorporating angle information, but it also leads to a significant increase in the number of training parameters, thereby raising training costs. To improve efficiency, we explore more efficient methods for constructing input graphs. The selection of edge connections directly impacts model performance. As highlighted in coGN, GNNs that rely solely on relative distance information cannot distinguish geometric shapes with different angles. By strategically adding additional connections between nodes (where differences in angles can also be expressed through the distances between these additional connections, refer to Fig. S24), GNNs can distinguish these shapes without relying on angle information, thus avoiding an increase in parameters. However, an excessive number of edge connections can lead to a decline in model performance.

Supplementary Fig. S22 compares DenseGNN, coGN, MEGNet, SchNet, and CGCNN on 12 Matbench and Jarvis-DFT datasets, examining the changes in test set MAE as the average number of edges per graph increases using common graph construction methods such as radius-based and KNN approaches. The results demonstrate that, regardless of whether the graphs are constructed using radius-based or KNN methods, DenseGNN requires the fewer average edges to achieve the better MAE results. Fig. 8 compares all reference models and the DenseGNN on the Jarvis-DFT formation energy dataset, focusing on the graph parameters (including total edges, average edges per graph, total nodes, and average nodes per graph) when each model is at its optimal edges selection method for constructing crystal graphs. It also compares the models’ total parameters, trainable parameters, MAE on the test set, and training and inference times per epoch. From this figure, we draw the following conclusions: First, the model parameters and the number of edges required for optimal performance by DenseGNN are lower compared to nested graph networks like ALIGNN, DimeNetPP, and coNGN. Therefore, under consistent training and testing hyperparameters (such as batch size, learning rate, and optimizer parameters), DenseGNN has the shortest training and inference times. Second, for non-nested graph networks such as SchNet, CGCNN, MEGNet, and coGN, we optimized the information passing and updating strategies for edges-nodes-graphs in DenseGNN while keeping the DCN and LOPE strategies intact. This led to the development of DenseGNN-Lite, which significantly reduced the number of trainable parameters, as shown in Fig. S1. At its optimal performance, DenseGNN-Lite uses the fewer number of edges, with an average of only 124 edges per graph. Consequently, under consistent training and testing hyperparameters, DenseGNN-Lite has much shorter training and inference times.

Fig. 8: Comparison of models performance on Jarvis-DFT formation energy dataset.

This figure compares the performance of baseline models, DenseGNN, and DenseGNN-Lite on the Jarvis-DFT formation energy dataset. It displays crystal graph parameters (total edges, average edges per graph, total nodes, average nodes per graph) for each model using their optimal edge selection methods. Additionally, it shows the total model parameters, trainable parameters, MAE results on the test set, and the training and inference time per epoch. The nested graph networks, whose parameter counts exceed those of DenseGNN and DenseGNN-Lite. All tests were conducted on a 4090 GPU with consistent batch size, learning rate, and other settings. The average time per epoch for training and inference was calculated using the mean from 20 epochs.

Thanks to the DCN and LOPE strategies, DenseGNN achieves competitive performance with a lower number of required edges, thereby increasing model efficiency. The coGN strategically increases the number of edge connections using the KNN method to improve the distinguishability of the graph, and uses crystal symmetry to reduce the number of nodes in the graph to balance the number of edge connections. However, the reliance on symmetry to reduce the number of edges in the crystal/molecular graph may fail in real-world materials research, where disordered materials such as molecules and polymers are frequently encountered. As shown in Fig. 9, across six Matbench properties, DenseGNN exhibits a substantially reduced number of edge connections compared to other reference models. For the perovskites, coGN uses all symmetries in constructing asymmetric unit graphs but does not reduce the average number of nodes (refer to Fig. S23). Furthermore, coGN requires a higher number of edge connections (optimal k parameter of 24) to achieve optimal model performance and enhance graph discriminability (refer to Fig. S24). Therefore, under the optimal MAE edges selection strategy, the required number of edges for coGN significantly increases. Fig. 10 compares the graph parameters, total parameters, trainable parameters, and MAE results on the test set for coGN, DenseGNN, and DenseGNN-Lite models on the Perovskites dataset, when each model is at its optimal edges selection method for constructing crystal graphs. It reveals that, on the perovskites dataset, DenseGNN and DenseGNN-Lite have the shortest training and inference times per epoch. Supplementary Information Table S2 provides a comparison of all edges and nodes for DenseGNN, SchNet, CGCNN, MEGNet, and coGN on the Matbench dataset.

Fig. 9: Comparison of edge connections among models on Matbench datasets.

This figure compares the edge connections among DenseGNN, SchNet, CGCNN, MEGNet, and coGN models using their optimal edge selection methods on six Matbench datasets. coGN constructs asymmetric unit graphs that fully utilize the symmetry of the crystal structure but struggles to reduce the number of nodes on the Perovskites dataset. Consequently, under the optimal MAE edges selection strategy (KNN = 24), the required number of edges for coGN significantly increases.

Fig. 10: The performance comparison of DenseGNN and coGN on perovskites dataset.

This figure compares coGN, DenseGNN, and DenseGNN-Lite on the perovskites dataset from Matbench. It displays crystal graph parameters (total edges, average edges per graph, total nodes, average nodes per graph) for each model using their optimal edge selection methods. Additionally, it presents the total model parameters, trainable parameters, MAE results on the test set, and the training and inference time per epoch. The average time per epoch for training and inference was calculated using the mean from 20 epochs.

Crystal structure distinguishment improvement

Our approach involves extracting structural embeddings from specific layers of pre-trained models and utilizing a similarity calculation strategy similar to the standard XRD method to distinguish among over 8970 silicon-containing compounds from the Materials Project (MP) database⁵⁴. As depicted in Fig. 11, our DenseGNN has shown significant improvement in distinguishing structures compared to the MEGNet. The horizontal coordinates of each colored point in the figure represent the similarity between structures, with a resolution of 0.1 and divided into 10 categories ranging from 0 to 1, where structures become increasingly similar from left to right. Figure 11a depicts the classification results of silicon-containing structures using the standard XRD method, while Fig. 11b presents the classification results based on the structural embeddings derived from the MEGNet pre-trained on the bandgap dataset from the MP database²³. Figure 11c showcases the classification results using the structural embeddings obtained from our DenseGNN pre-trained on the same dataset. The gray points in the figure represent structures where the pre-trained models’ classifications are inconsistent with the standard XRD results.

Fig. 11: Performance comparison in structural distinction of silicon-containing compounds.

This figure compares the performance of different methods in classifying silicon-containing compounds. a shows classification results using the standard XRD method. b displays classification results from a pre-trained MEGNet model, and (c) shows the classification results from a pre-trained DenseGNN model. Gray dots indicate misclassified structures compared to XRD results.

It is evident that the DenseGNN has shown a significant improvement in classification accuracy compared to the MEGNet. The classification accuracy of MEGNet is less than 40% (with the majority of errors occurring on the right side of the figure, involving highly similar structures, which aligns with common knowledge that very similar structures are indeed challenging to distinguish), while the accuracy of DenseGNN has nearly doubled, reaching approximately 80%. This results highlights the superior performance of our model in distinguishing material structures.

Discussion

In this study, we propose the DenseGNN to address a series of problems in material property prediction faced by existing GNNs. Despite the introduction of various GNNs such as CGCNN, MEGNet, ALIGNN, and coGN since 2018, which have made substantial achievements in aspects like global state variable representation, incorporation of bond angle information, and optimization of crystal graph edge connections, there are still some problems that need to be overcome. First, we observe that nested graph networks like ALIGNN and coGN, while effective in certain cases, are limited in their widespread application due to high training costs and advantages on only specific datasets. To tackle these problems, we introduce LOPE to optimize the atomic embedding representation and edge connectivity, effectively learn multi-body interactions such as bond angles and local geometric distortions, and achieve minimal edge connections. This reduces the training time required for larger GNNs without sacrificing accuracy. Second, we introduce the DenseGNN model to address the problems of extending GNN to diverse applications in materials, molecular, and chemical fields. We specifically focus on the generalization ability and performance trade-offs of existing GNN models across different fields. While GNNs perform well on specific domain datasets, they often struggle to maintain consistent performance when applied across different fields, limiting their potential in broader fields. DenseGNN is fused with DCN, HRN, and the LOPE strategy, leading to performance improvements across multiple fields. DenseGNN not only achieves optimal performance on benchmark datasets in molecular, crystal materials, and catalysis fields, demonstrating its versatility and scalability across different fields, but also outperforms existing coGN and MODNET on small datasets, showcasing its exceptional generalization capabilities across various datasets. Third, we apply our DCN and LOPE strategies to GNN in fields such as computer science, crystalline materials, and molecules, resulting in performance improvements on the Matbench dataset. Finally, we address the problems of over-smoothing in GNNs, which is a major barrier to increasing the number of model layers. The DenseGNN overcomes this problem by fusing the DCN design, enabling the construction of very deep networks while avoiding performance degradation.

The DenseGNN has achieved success in the fields of materials science, molecular, and chemistry, demonstrating its advantages in handling complex many-body interactions and improving training efficiency. Despite the outstanding performance of DenseGNN on benchmark datasets in multiple domains, we recognize that there are still some potential problems and challenges that need to be addressed in future research. First, the deep network structure of DenseGNN may face higher computational complexity when dealing with large-scale graph data. To overcome this challenge, future research can explore more efficient structural graph optimization strategies and model architecture designs to reduce the computational cost. Additionally, the “black box” nature of DL models also limits the interpretability of the model. Therefore, developing new visualization tools and techniques to aid in understanding the decision-making process of DenseGNN will be crucial in improving the transparency of the model. Although DenseGNN is versatile, further optimization or integration of domain-specific pre-training knowledge may be necessary in specific domains. Developing customized DenseGNN tailored to the data characteristics and application requirements of specific domains will help improve the model’s performance on specific tasks. In conclusion, the introduction of the DenseGNN model provides a new perspective and tool for the application of GNN in multiple domains. By addressing these problems mentioned above, we look forward to DenseGNN achieving broader applications in future research and driving scientific advancements in related fields.

Methods

Data description

The JARVIS-DFT dataset was developed using the Vienna ab initio simulation package. Most properties are calculated using the OptB88vdW⁵⁵ functional. For a subset of the data, we use TBmBJ⁵⁶ to get a better bandgap. We use density functional perturbation theory⁵⁷ to predict piezoelectric and dielectric constants with electronic and ionic contributions. The linear response theory-based⁵⁸ frequency based dielectric function was calculated using OptB88vdW and TBmBJ, and the zero energy values are used to train ML models. The TBmBJ frequency-dependent dielectric function is used to calculate the maximum efficiency limited by the spectrum (SLME)⁵⁹. The magnetic moment is calculated using spin-polarized calculations considering only ferromagnetic initial configurations and ignoring any DFT + U effects. Thermoelectric coefficients such as the Seebeck coefficient and power factor are calculated using the BoltzTrap software⁶⁰ with a constant relaxation time approximation. The exfoliation energy of van der Waals bonded two-dimensional materials is calculated by calculating the energy difference between each atom in the bulk phase and the corresponding monolayer. Spin orbit spillage⁶¹ is computed as the disparity between material wavefunctions with and without the inclusion of spin-orbit coupling effects. All JARVIS-DFT data and classical force field inspired descriptors (CFID)⁶² are generated using the JARVIS-Tools software package. The CFID baseline model is trained using the LightGBM software package⁶².

Matbench is an automated benchmark testing platform specifically designed for the field of materials science, designed to evaluate and compare the most advanced ML algorithms that predict various solid material properties. It provides 13 carefully curated ML tasks that cover a wide range of inorganic materials science, including the prediction of various material properties such as electronics, thermodynamics, mechanics to thermal properties of crystals, two-dimensional materials, disordered metals, etc. The datasets for these tasks come from different density functional theories and experimental data, with sample sizes ranging from 312 to 132,000. The platform is hosted and maintained by the MP, providing a standardized evaluation benchmark for the field of materials science.

QM9 provides molecular properties calculated by DFT, such as HOMO, lowest unoccupied molecular orbital, energy gap, zero-point vibrational energy, dipole moment, isotropic polarizability, electron spatial extent, internal energy at 0 K, internal energy at 298 K, enthalpy at 298 K, Gibbs free energy at 298 K, and heat capacity. LipopDataset: Lipophilicity is an important feature that affects the membrane permeability and solubility of drug molecules. This lipophilicity dataset is curated from the ChEMBL database, providing experimental results of octanol/water partition coefficients (logD at pH 7.4) for 4200 compounds. FreeSolvDataset: The FreeSolv dataset consists of experimental and computationally derived solvation free energies of small molecules in water, along with their experimental values. Here, we utilize a modified version of the dataset that includes the SMILES strings of the molecules and their corresponding experimental solvation free energy values. ESOLDataset: The Delaney (ESOL) dataset is a regression dataset containing structures and water solubility data of 1128 compounds. This dataset is widely used to validate the ability of ML models to directly estimate solubility from molecular structures encoded as SMILES strings.

The OC22 dataset focuses on oxide electrocatalysis. A crucial difference between OC22 and OC20 is that the energies in OC22 are DFT total energies. DFT total energies are more challenging to predict but offer the most generality and are closest to a DFT surrogate, providing flexibility to study property prediction beyond adsorption energies. Similar to OC20, the tasks in OC22 include S2EF-Total and IS2RE-Total.

DenseGNN implementation and training

DCN

We described the process of densely connecting all GC layers based on the DCN strategy as shown in Fig. 12. In comparison to ResNet, DCN proposes a more aggressive dense connection mechanism: that is, each layer will connect to all preceding layers, specifically, each layer will take all preceding layers as additional inputs. For example, the input of x_E’ in layer T₂ includes not only x_E from layer T₂, but also x_E from preceding layer T₁ and x_E’, all concatenated along the last dimension. Unlike ResNet, where each layer is connected to a preceding layer through element-wise addition shortcut connections, in DCN, each GC layer concatenates with all preceding layers at the edge-node-graph level and serves as input to the next layer. For a network with k GC layers, DCN includes a total of k(k + 1)/2 connections, which is a dense connection compared to ResNet. Additionally, DCN directly connects feature maps from different layers, enabling feature reuse and improving efficiency, which is the main difference between DCN and ResNet. In the formula representation, the output of a traditional network at the k-th layer is:

$${x}_{k}={H}_{k}({x}_{k-1})$$

Fig. 12: Dense connection process in DenseGNN.

This figure illustrates the process of densely connecting all GC layers based on the DCN strategy in DenseGNN. Each GC layer densely connects the edge-node-graph representations to those in all preceding GC layers. This design enables each GC layer to fully leverage feature information from preceding layers, facilitating effective feature reuse. By concatenating the feature maps of all layers, the shortest information propagation path is achieved. All dense connection channels are highlighted in red.

For ResNet, an identity function from the preceding layer input is added:

$${x}_{k}={H}_{k}({x}_{k-1})+{x}_{k-1}$$

In DCN, all preceding layers are concatenated as input:

$${x}_{k}={H}_{k}\left([{x}_{0},{x}_{1},....,{x}_{k-1}]\right)$$

Here, ${H}_{k}(.)$ represents the non-linear transformation function in the GC layer, which is a composite operation that include a series of connection operations, a 3-layer MLP network, residual operations, and the Swish activation function, applied to the edges, nodes, and graph objects, achieving synchronous updates of edge-node-graph features.

In this study, we innovatively integrate the design philosophy of DCN with GNN to enhance the performance of GNN in material property prediction tasks. The core of this fusion strategy lies in the dense connectivity feature of DCN, which brings advantages to the GNN model. First, the dense connectivity strategy of DCN ensures that each layer of GC in DenseGNN can directly access the feature information of all preceding GC layers. This design allows each GC layer to fully utilize the information of edges, nodes, and graph levels, achieving efficient information propagation, reducing the risk of information loss, enhancing network training efficiency, and achieving more precise feature representation. Second, DCN concatenates edge, node, and graph-level features in the channel dimension, enabling direct information propagation between GC layers. This design not only simplifies the network structure but also accelerates the flow of information between GC layers. This direct information flow mechanism helps improve the GNN’s ability to capture complex graph structural features, especially in dealing with large-scale graph data, enabling more effective feature extraction and pattern recognition. Last, DCN’s feature reuse mechanism improve the learning ability of the GNN model. This design allows the network to access and utilize feature information from all preceding GC layers at each layer, thereby improving the model’s ability to capture data patterns. Additionally, as feature reuse reduces the need for additional parameters, it helps reduce the model’s complexity and the risk of overfitting.

In summary, the fusion of DCN with GNN not only improves the model’s performance but also improve the robustness and generalization ability of the model in handling complex graph data. This fusion strategy provides a new perspective for research in the field of materials science, with the potential to drive the discovery of new materials.

LOPE

We employed LOPE to represent node features, optimizing the atomic embedding representation, and enhancing the performance of DenseGNN in material property prediction. LOPE includes atomic embeddings and orientation-resolved embeddings, calculated through the product integration of RDFs and Gaussian window functions to describe the local atomic environment. The computation process of LOPE is as follows:

1. Initialization of parameters: we set the directions, Gaussian window widths, and cutoff distances. The direction parameter can be None or specific coordinate axes (such as ‘x’, ‘y’, ‘z’), while the Gaussian window width is typically a list of floating-point numbers defining different window widths. The cutoff distance is a threshold used to determine the interaction range between atoms.

2. Neighbor atoms and distance calculation: For a given atom in the structure, we calculate all its neighboring atoms and determine the distances between them.

3. Direction-dependent processing: If direction-dependent fingerprints need to be computed, we calculate the displacement of each neighboring atom relative to the central atom.

4. Calculation of the cutoff function: We use the cutoff function ${\rm{f}}({\rm{r}})$ to limit the interactions between atoms, where ${\rm{f}}({\rm{r}})$ is $0.5[\cos (\frac{{\rm{\pi }}{\rm{r}}}{{\rm{Rc}}})+1]$ when the distance ${\rm{r}}$ is less than the cutoff distance ${\rm{Rc}}$, and 0 when ${\rm{r}}$ is greater than or equal to ${\rm{Rc}}$.

5. Calculation of Gaussian windows: For each Gaussian window width value, we compute the Gaussian window function, which is the product of the exponential function of the distance squared divided by the Gaussian window width, multiplied by the cutoff function ${\rm{Rc}}$.

6. Calculation of fingerprints: Based on the direction parameter, we compute the atomic fingerprints. For non-directional fingerprints, we sum all window function values. For directional fingerprints, we multiply the window function by the corresponding component of displacement, and then sum them.

7. Output results: Finally, we horizontally stack all computed fingerprint vectors to form the final feature vector.

The introduction of the LOPE strategy improved the efficiency of the DenseGNN in material data learning. This strategy optimizes the atomic embedding representation, allowing the model to achieve efficient training with minimal edge connections while maintaining prediction accuracy. Furthermore, benefiting from the effectiveness of LOPE, the DenseGNN can construct deeper networks with up to 60 layers, and as the network depth increases, the model performance shows a steady improvement trend.

Implementation details

In this study, we utilized the TensorFlow and Keras DL frameworks to construct all models. During the implementation process, we relied on a series of important libraries, including KGCNN, Python Materials Genomics (Pymatgen)⁶³, the RDKit open-source cheminformatics toolkit⁶⁴, and PyXtal⁶⁵. The training of all models was trained on an NVIDIA RTX 4090 24GB GPU. Regarding the model parameter settings, the default cutoff radius for Schnet, CGCNN, and MEGNet was set to 6 angstroms. The default cutoff radius for HamNet and GIN was set to 5 angstroms, while the maximum number of neighbors for nodes (excluding self, as self-loops are allowed) was limited to 17. When dealing with edges in the graph, we first computed the distance matrix between nodes, then selected edges based on the cutoff radius as a threshold, limiting the number of neighbors to within the default value of 17. For DenseGNN, we employed the KNN edge selection method, with the parameter k set to 12 for optimal performance. The KNN method relies on the number of neighbors k, but edge distances may vary with changes in crystal density. Subsequently, we applied a Gaussian kernel function to extend edge lengths and used them as the edge features of our model’s graph. For the node features of DenseGNN, we introduced the LOPE representation as a 24-dimensional vector added to the node features. To evaluate model performance, we used the MAE as the standard evaluation metric, which is the common evaluation method for material property prediction and the primary evaluation metric used in this study for all models and Matbench benchmark tests. We assessed the performance of all models based on specific experimental designs using 5-fold cross-validation and hold-out testing methods.