Introduction

Over the past decades, the electronic structure simulation of molecular and solid-state systems has assumed an increasingly important role in the research and development of new materials. While the exact computation of ground and excited-state properties poses an exponentially scaling problem through the solution of the Schrödinger equation, many methods have been developed to various degrees of approximation rendering their implementation feasible. In particular, density functional theory (DFT) has established itself as a cheap yet effective means for the simulation of a wide range of systems of interest. However, due to its nature, it falls short in the description of problems that contain strongly correlated electrons. In general, the accurate description of such systems requires methods that consider multiple configuration state functions (CSFs) in order to capture the complex entanglement between the electrons. These methods of greater accuracy come at increasingly higher computational costs approaching the theoretical exponential scaling of the exact solution, therefore limiting their applicability to problems of relatively small sizes.

In the past decade, significant progress has been made in the development of quantum computers, which provide access to a new computational paradigm that promises to overcome this exponential barrier1,2. This feat can be achieved by encoding the exponentially scaling wave function (WF) in a polynomial number of qubits, the fundamental processing units of a quantum computer, which enables the efficient representation of an otherwise inaccessible computational space. Many algorithms have been developed to leverage this representation for the computation of ground and excited-state properties of chemical systems3. However, these algorithms exceed the quantum computational capabilities of state-of-the-art devices when applied to large problems. On one hand, this is due to the deep quantum circuits that arise when encoding a fermionic WF in a set of qubits, while ensuring the physical nature of the generated superposition. The long runtime of such quantum circuits exceeds the decoherence times of the available hardware, resulting in the accumulation of errors that require error correction to be feasible before we can gain any significant results3. On the other hand, algorithms that trade the execution of a single long quantum circuit for a (variational) optimization problem involving many shorter circuits quickly become infeasible; in particular when targeting systems that are beyond the current capabilities of classical computational hardware4.

As a short-term solution to these limitations, combined with the interest of the computational chemistry and materials science communities to leverage this new computing platform, we have seen in recent years increasing efforts in the development of new hybrid quantum-classical algorithms. In particular, many embedding methods have been adapted or newly developed to leverage the quantum resources for the treatment of embedded fragments, where, in many cases, the computation of a small region of a larger system is offloaded to the quantum computer, while the rest is carried out on classical hardware5,6,7,8,9,10,11,12,13. These efforts have been very important for exploring the current practical limitations of noisy devices and for benchmarking quantum computational approaches for the simulation of chemical and solid-state systems. Crucially, embedding methods also provide the means to systematically scale the problems of interest alongside the development of quantum computing hardware, such that the infrastructure and resources invested now will eventually allow to reach system sizes and an accuracy beyond what is currently feasible.

Adding to these efforts, this work presents a general framework for the implementation of active space (AS) embedding methods. In particular, we show how quantum computing can be used to find the ground and excited states within an active space embedding into a mean-field level of theory calculation. While the framework to do so is general, in this work, building upon earlier work by some of the authors5, we extend the range-separated DFT embedding scheme to allow embedding not only into molecular but also into periodic environments. We do so by extending the CP2K package14 with our proposed interface to couple to any AS solver. To leverage quantum computing for the treatment of the AS, we choose Qiskit Nature15,16 as the solver.

The communication between the two codes is handled through message passing permitting future extensions as well as providing a scalable path towards quantum-centric supercomputing.

The rest of this paper is structured as follows. In the section “Results,” we start by presenting the general theory underlying the periodic active space embedding framework based on multiconfigurational range-separated DFT. We then elaborate on the details of the implementation and integration of CP2K and Qiskit Nature, before we present the results obtained by applying the developed methodology to study the optical properties of the neutral oxygen vacancy in magnesium oxide. Finally, in the section “Discussion,” we discuss the results obtained in this work and draw conclusions. Complete details about the methods can be found in the section “Methods”.

Results

Any active space embedding approach, where a subset of electrons and orbitals of a system—the fragment—are embedded in an effective potential generated by the remaining electrons of the systems and all the ion cores—the environment—may be implemented in the general framework presented in this work. Here, we use the framework of multiconfigurational range-separated density functional theory (rsDFT)17,18,19,20,21,22,23,24 and the Gaussian and plane waves (GPW) approach25, whereby the embedding potential is obtained from a mean-field method, while the fragment Hamiltonian is solved with a correlated wave function ansatz. The approach and infrastructure we have developed are completely general; it can treat both molecular and periodic systems, it supports spin-polarized and unpolarized calculations, describes the core electrons explicitly or through pseudopotentials, and can be combined with both classical WF and quantum circuit ansatzes alike.

Periodic active space embedding

To introduce the framework for AS embedding methods, we start with the second-quantized electronic Hamiltonian in the Born-Oppenheimer approximation. This can be written in atomic units as

$$\hat{H}=\sum _{pq}{h}_{pq}{\hat{a}}_{p}^{\dagger }{\hat{a}}_{q}+\frac{1}{2}\sum _{pqrs}{g}_{pqrs}{\hat{a}}_{p}^{\dagger }{\hat{a}}_{r}^{\dagger }{\hat{a}}_{s}{\hat{a}}_{q}+{\hat{V}}_{nn}\,,$$
(1)

where \({\hat{V}}_{nn}\) is the Coulomb repulsion between the nuclei, while hpq and gpqrs are one- and two-electron integrals given by

$${h}_{pq}=\left\langle {\psi }_{p}({\bf{x}})| \hat{h}| {\psi }_{q}({\bf{x}})\right\rangle \,,$$
(2)
$${g}_{pqrs}=\left\langle {\psi }_{p}({\bf{x}}){\psi }_{r}({\bf{x}}^{\prime} )| \hat{g}| {\psi }_{q}({\bf{x}}){\psi }_{s}({\bf{x}}^{\prime} )\right\rangle \,.$$
(3)

The variable x (\({\bf{x}}^{\prime}\)) is a compound variable for the electron coordinates in space, r (\({\bf{r}}^{\prime}\)), and its spin degree of freedom. The operators \(\hat{h}\) and \(\hat{g}\) in Eqs. (2) and (3) account for the kinetic energy of the electrons, the electron-nuclear attraction, and the electron-electron repulsion, and are defined as

$$\hat{h}({\bf{r}})=-\frac{1}{2}{\nabla }^{2}+\sum _{P}\frac{-{Z}_{P}}{| {\bf{r}}-{{\bf{R}}}_{P}| }\,,$$
(4)
$$\hat{g}({\bf{r}},{\bf{r}}^{\prime} )=\frac{1}{| {\bf{r}}-{\bf{r}}^{\prime} | }\,,$$
(5)

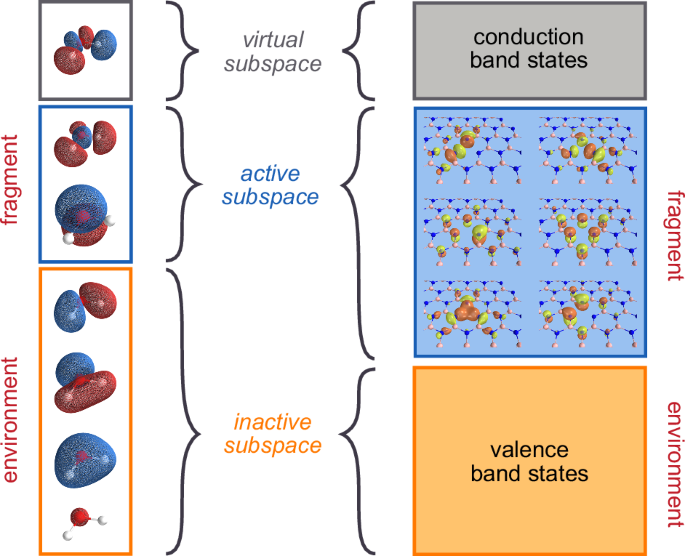
where P labels the ion cores, while ZP and RP denote the corresponding nuclear charges and nuclear positions, respectively. The indices p, q, r, s label general one-particle functions (spin-orbitals), whose corresponding sums appearing in Eq. (1) run through the entire basis set. The operator \({\hat{a}}_{p}^{\dagger }\) (\({\hat{a}}_{p}\)) is a creation (annihilation) operator adding (removing) an electron to (from) spin-orbital ψp(x). In an embedding approach like the one presented here, the fragment of interest is defined in terms of an active space consisting of a handful of active electrons and active orbitals. All the electrons that are not part of the AS typically occupy the low-energy states of the system and are called inactive orbitals; see Fig. 1 for an example of AS selection in molecules and materials. Once the AS has been identified, a corresponding embedded fragment Hamiltonian can be defined in a manner completely analogous to Eq. (1), that is

$${\hat{H}}^{{\rm{frag}}}=\sum _{uv}{V}_{uv}^{\text{emb}\,}{\hat{a}}_{u}^{\dagger }{\hat{a}}_{v}+\frac{1}{2}\sum _{uvxy}{g}_{uvxy}{\hat{a}}_{u}^{\dagger }{\hat{a}}_{x}^{\dagger }{\hat{a}}_{y}{\hat{a}}_{v}\,,$$
(6)

with the only difference that the sums are limited to the active orbitals, labeled by the indices u, v, x, y, and that the one-electron integrals, hpq, have been replaced by the elements of an embedding potential, \({V}_{uv}^{\,\text{emb}\,}\). This potential accounts for the interactions between the inactive and active electrons in addition to the contributions from the one-electron integrals. Notice that until this point, this formulation is completely general; we have not yet specified how to compute the embedding potential. In principle, one could define an operator that explicitly accounts for all many-body interactions between the inactive and active subsystems, though probably, this would result in a methodology that is computationally as expensive as solving directly the entire problem with such an approach. Therefore, in practice, the embedding potential introduces approximations to describe the low-energy degrees of freedom and the interactions between active and inactive subsystems. For example, one such option would be to use the Hartree-Fock (HF) approximation for the inactive electrons, such that the active electrons only interact with the inactive ones in a mean-field manner. In this case, \({V}_{uv}^{\,\text{emb}\,}\) would simply correspond to the elements of the Fock matrix. Similarly, as we will discuss in more detail in the next section, describing the environment using DFT translates into an embedding potential similar to the Kohn-Sham (KS) one. It is important to realize that, in general, \({V}_{uv}^{\,\text{emb}\,}\) always depends on the inactive electronic degrees of freedom, but possibly also on the active subsystem, in which case the resulting embedding scheme has to be solved self-consistently (see Fig. 2).

Fig. 1: Examples of possible active and inactive space selections for an isolated and periodic system alike.
figure 1

The left column depicts the qualitative molecular orbitals of a water molecule. The right column depicts the molecular orbitals localized around the positively charged boron vacancy in hexagonal boron nitride. In both cases, only a small number of orbitals is included in the active space: for water, it is spanned by the HOMO-LUMO pair, while for boron nitride, by the localized defect orbitals.

Full size image
Fig. 2: Workflow diagram depicting the interaction of CP2K and Qiskit Nature.
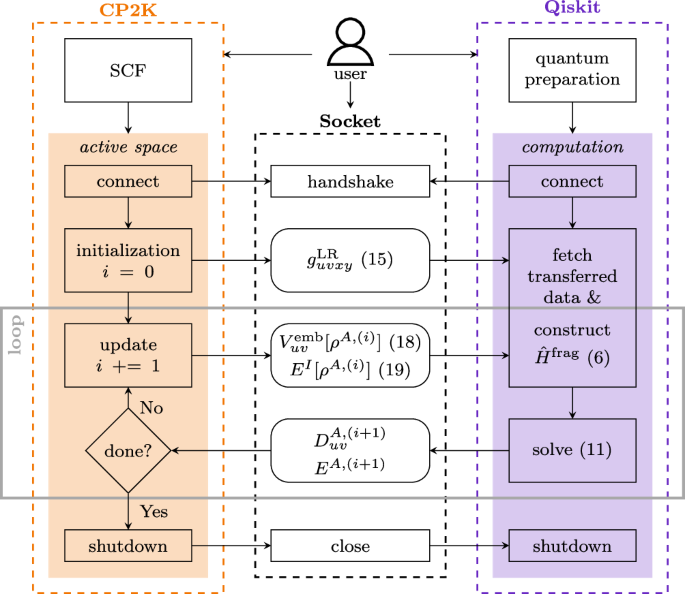
figure 2

The user configures the two classical processes and the socket for the IPC. Each process then follows the computational steps (rectangular boxes) outlined inside their respective frames. The data that gets computed and transferred is indicated by the rounded boxes. Numbers in parentheses refer to the respective equations in this manuscript. The self-consistent embedding requires a loop which is highlighted by the gray box. This loop is terminated based on the decision (diamond shape) taken by the CP2K process.

Full size image

To compute the total energy of the system, we can start from the expectation value of Eq. (1) with respect to the total WF of the system, that is

$$E=\left\langle \Psi | \hat{H}| \Psi \right\rangle =\sum _{pq}{h}_{pq}{D}_{pq}+\frac{1}{2}\sum _{pqrs}{g}_{pqrs}{d}_{pqrs}+{V}_{nn}\,,$$
(7)

where

$${D}_{pq}=\left\langle \Psi | {\hat{a}}_{p}^{\dagger }{\hat{a}}_{q}| \Psi \right\rangle \,,$$
(8)
$${d}_{pqrs}=\left\langle \Psi | {\hat{a}}_{p}^{\dagger }{\hat{a}}_{r}^{\dagger }{\hat{a}}_{s}{\hat{a}}_{q}| \Psi \right\rangle \,,$$
(9)

are the elements of the one- and two-particle reduced density matrices (RDMs), D and d, respectively. By separating the one-particle RDM (1-RDM) into inactive and active components, D = DI + DA, and factorizing the elements of the inactive two-particle RDM (2-RDM) into a product of 1-RDMs (see Appendix A.1 and A.2 of Rosssmannek et al.5 for a detailed derivation), we can express the total energy as a sum of inactive and active parts, E = EI + EA, with

$${E}^{I}=\sum _{ij}\left({h}_{ij}+{V}_{ij}^{\,\text{emb}}\right){D}_{ij}^{I}+{V}_{nn}\,,$$
(10)

and

$${E}^{A}=\sum _{uv}{V}_{uv}^{\,\text{emb}\,}{D}_{uv}^{A}+\frac{1}{2}\sum _{uvxy}{g}_{uvxy}{d}_{uvxy}^{A}\,.$$
(11)

In Eq. (10) and (11), the indices i, j label inactive orbitals, and the superscripts I and A on the density-matrix elements emphasize to which subspace they belong (even though the indices and sums implicitly account for that information). At last, notice that the choice of one-particle functions is completely general: one can choose localized molecular orbitals in the case of molecules, crystalline orbitals, or Wannier functions in solid-state systems, or a combination thereof, e.g., to describe point defects in materials.

To extend the formalism to periodic range-separated DFT embedding, the first ingredient is the definition of the one-particle embedding potential, with elements

$${V}_{pq}^{\,\text{emb}}={F}_{pq}^{I,\text{LR}}+{V}_{H,pq}^{\text{SR}\,}[{\rho }^{I}]+{V}_{H,pq}^{\,\text{SR}\,}[{\rho }^{A}]+{V}_{xc,pq}^{\,\text{SR}\,}[\rho ]\,,$$
(12)

where the elements of the inactive long-range Fock operator are defined as

$${F}_{pq}^{I,\,\text{LR}}={h}_{pq}+{V}_{H,pq}^{\text{LR}\,}[{\rho }^{I}]+{V}_{\,\text{HFX},pq}^{\text{LR}\,}[{\rho }^{I}]\,,$$
(13)

along with the classical Hartree potential, VH[ρ], the exact Hartree-Fock exchange potential, VHFX[ρ], and the DFT exchange-correlation potential, Vxc[ρ], evaluated over the indicated electron densities, ρI, ρA and ρ = ρI + ρA (see the Supplementary Information (SI) for the explicit definition of these operators in a one-particle basis). The two-electron integrals over the Coulomb operator are split into long-range (LR) and short-range (SR) components,

$$\hat{g}={\hat{g}}^{\omega ,\text{LR}}+{\hat{g}}^{\omega ,\text{SR}}\,$$
(14)
$$=\frac{\,\text{erf}\,(\omega | {\bf{r}}-{\bf{r}}^{\prime} | )}{| {\bf{r}}-{\bf{r}}^{\prime} | }+\frac{\,\text{erfc}\,(\omega | {\bf{r}}-{\bf{r}}^{\prime} | )}{| {\bf{r}}-{\bf{r}}^{\prime} | }$$
(15)

which give rise to the superscripts LR and SR in Eqs. (12) and (13). The range separation is obtained with the error function and its complement (as indicated by Eq. (15)), where ω is the range-separation (RS) parameter of units \({a}_{0}^{-1}\).

In practice, two issues arise for the direct computation of the inactive energy and embedding potential according to Eqs. (10) and (12). First, it is computationally disadvantageous when the inactive subsystem becomes very large. Second, for periodic calculations, the sums concerning the electron-electron, electron-nuclear, and nuclear-nuclear interactions are conditionally convergent, and cannot be easily separated into inactive and active components. Hence, we express the inactive terms indirectly as the difference between the total system and the (localized) active subsystem. We can achieve this by defining the inactive 1-RDM and electron density as DI = D − DA and ρI = ρ − ρA, respectively. Reformulating Eq. (13) by replacing ρI = ρ − ρA, yields

$$\begin{array}{l}{F}_{pq}^{I,\,\text{LR}}={F}_{pq}^{\text{tot}\,}\,-\,{V}_{H,pq}^{\,\text{SR}\,}[\rho ]-{V}_{xc,pq}^{\,\text{SR}\,}[\rho ]\\ \qquad\quad\;\;\;-\,{V}_{H,pq}^{\,\text{LR}\,}[{\rho }^{A}]-{V}_{\,\text{HFX},pq}^{\text{LR}\,}[{\rho }^{A}]\,,\end{array}$$
(16)

where the total rsDFT Fock operator is defined as

$${F}_{pq}^{\,\text{tot}\,}={h}_{pq}+{V}_{H,pq}[\rho ]+{V}_{\,\text{HFX},pq}^{\text{LR}\,}[\rho ]+{V}_{xc,pq}^{\,\text{SR}\,}[\rho ]\,.$$
(17)

Inserting the same relation for the inactive electron density as well as Eq. (16) into Eq. (12) results in

$${V}_{pq}^{\,\text{emb}}={F}_{pq}^{{\rm{tot}}}-{V}_{H,pq}^{\text{LR}\,}[{\rho }^{A}]-{V}_{\,\text{HFX},pq}^{\text{LR}\,}[{\rho }^{A}]\,.$$
(18)

We can proceed analogously for the expression of the inactive energy, obtaining

$${E}^{I}={E}^{{\rm{tot}}}-\sum _{uv}{F}_{uv}^{{\rm{tot}}}{D}_{uv}^{A}+{E}_{H}^{\text{LR}\,}[{\rho }^{A}]+{E}_{\,\text{HFX}}^{\text{LR}\,}[{\rho }^{A}]\,.$$
(19)

The active energy component that is needed to compute the total energy, E = EI + EA, simply corresponds to the ground state of the fragment Hamiltonian, Eq. (6). Owing to the similar structure of Eqs. (1) and (6) essentially any electronic structure method can be used in combination with our embedding scheme. In practice, because the space spanned by the active orbitals and electrons is relatively small, exact diagonalization or a good approximation thereof is the method of choice. Electronically excited states can also be targeted by the embedding method, either by directly calculating the spectrum of \({\hat{H}}^{{\rm{frag}}}\) or by linear response. However, one has to be careful that the inactive subspace is normally optimized for the ground state, unless some form of state-averaging or orbital optimization similar to classical multiconfigurational quantum chemical methods is introduced26,27. As will be discussed in the next section, we have used quantum circuit ansatzes to obtain the ground and excited states energies of Eq. (6). Owing to the dependence of the embedding potential to the AS electron density, ρA, the method chosen to get the spectrum of \({\hat{H}}^{{\rm{frag}}}\) should also provide this quantity (more generally, it should provide the 1-RDM). Crucially, this dependence of Vemb on ρA implies that our embedding approach requires a self-consistent solution, whereby an updated active density is obtained at each iteration, which is used to build a refined embedding potential and updated inactive energy that accounts for the feedback of the active subsystem on the environment degrees of freedom. A scheme depicting this self-consistent loop is shown in Fig. 2, when discussing the implementation details in the section “Quantum-classical interface implementation”.

Finally, it should be emphasized that Eqs. (18) and (19) are valid for both the molecular and periodic embedding settings, at least when invoking the Γ point approximation, since only the computation of the total Fock operator and energy are affected by this change. Hence, in practice, the presented methodology is a generalization of multiconfigurational rsDFT to periodic systems sampled at the Γ point. Furthermore, we point out the limiting cases provided by the RS scheme: they allow us to recover the common HF embedding scheme (i.e., complete active space configuration interaction) as ω approaches infinity as well as KS-DFT as ω approaches zero. This can be seen in Eqs. (18) and (19), where the standard KS case is evident as all LR terms simply disappear. The common HF embedding is also evident from Eq. (17), in which the only DFT-specific term for the exchange-correlation interaction, \({V}_{xc}^{\,\text{SR}\,}\), vanishes.

Quantum-classical interface implementation

In this section, we present the implementation details of the integration of CP2K14 and Qiskit Nature15,16. The developments of this work have been released as part of CP2K v2024.1, Qiskit Nature v0.7.0, as well as a separate module handling more specific parts of the integration called qiskit-nature-cp2k28. In the first part, we discuss the technical aspects and challenges. Later, we review the future scalability and extensibility of this design.

Interfacing CP2K with Qiskit Nature for the implementation of an iterative embedding scheme poses a number of challenges. While CP2K is primarily written in Fortran and provides the means to efficiently run highly parallelized simulations in a variety of computational setups, Qiskit Nature (and the underlying Qiskit Qiskit software development kit (SDK)) is mostly developed in Python and has not yet (at the time of writing) reached a computational maturity comparable to CP2K. When Qiskit Nature was coupled to other Python-based computational programs in the past, they could easily share the same Python runtime execution environment and, thus, share all data directly in memory5,13. For the integration discussed here, this was not possible in such a straightforward manner. Instead, our implementation relies on a message passing protocol in order to exchange data between the two codes. Particularly, for this initial implementation, the messages and data are sent over a socket file. This is inspired by a similar architecture used by the i–Pi project29. Additional technical details are available in the SI.

A socket is an application programming interface (API) used for inter-process communication (IPC). Using this protocol, it is possible for the communicating processes to run on the same physical machine or different ones connected via the internet. The calculation proceeds identically in both scenarios, with the only difference being the latency of the communication. However, this is not of concern to us, since the rate-limiting factor of the communication is (in any case) the bandwidth of the connection to the quantum hardware. This is also a reason for the choice of using the socket API for the communication rather than a tighter integration of the two codes using ctypes. While the latter is likely to have a performance advantage, the ease of further implementations to couple to other codes outweighs. Additionally, the computation of the AS solution is also likely to outweigh the cost of communication.

Figure 2 summarizes the computational workflow of our integration between CP2K and Qiskit Nature. The diagram depicts a user who has to configure three parts of their calculation; the CP2K and Qiskit (Nature) processes depicted on the left and right, respectively, as well as the socket itself via which the messages are passed between the two codes. Both computational codes will start in parallel. While CP2K starts out by finding a low-level solution to the entire system (SCF), Qiskit can use this time to perform certain preparational tasks that are unique to the execution of quantum computing hardware and do not require problem-specific data. For both programs, the user has full flexibility to leverage their respective capabilities during these initial steps. Upon completion of their respective steps, both codes will synchronize by performing a handshake through the socket. If either process reaches this point before the other, it awaits the other one. CP2K reaches this point inside its active space module, which was released as part of CP2K v2024.1. The input to this module configures the active fragment to be embedded into its environment and computes the one- and two-body terms of the AS Hamiltonian (i.e., the fragment Hamiltonian). It allows both single-shot and iterative embedding routines to be performed. In Fig. 2 we have depicted the final rsDFT embedding protocol. However, some of the components do not change throughout the course of the self-consistent embedding. These can be pre-computed only once during the initialization procedure. A key example is the LR-electron-repulsion integrals (ERIs) (cf. Eqs. (3) and (15)). Therefore, these only have to be transferred to the Qiskit process once. Components that depend on the active density of the current iteration, ρA,(i), have to be updated and exchanged during every iteration of the loop indicated by the gray frame in Fig. 2. During every such iteration, Qiskit Nature constructs the Hamiltonian of the active fragment (cf. Eq. (6)) using the LR-ERIs and embedding potential, \({V}_{uv}^{\,\text{emb}\,}[{\rho }^{A,(i)}]\), (cf. Eq. (18)). It then proceeds with finding the ground-state solution to this Hamiltonian using the quantum circuit ansatz specified by the user. Upon completion, it will return the active energy, EA,(i+1), and active 1-RDM, \({D}_{uv}^{A,(i+1)}\), to the CP2K process. CP2K will then perform a convergence check based on the total energy, E = EI + EA,(i+1). If convergence has not been reached, CP2K and Qiskit will return back to their respective steps of the embedding protocol to proceed with another iteration. If this check succeeds, both processes will be signaled to terminate. During their shutdown procedures, both processes may perform additional post-processing steps. For example, Qiskit Nature may compute additional properties using the final ground-state WF including the computation of excited-state energies.

At this point one might wonder how scalable this design is for the future. Indeed, the transfer of the two-body integrals is the limiting factor here. If CP2K and Qiskit Nature were able to leverage a shared memory, this would alleviate the need for transfer completely. However, only up to the point where the mapped qubit Hamiltonian needs to be transferred to the QPU (quantum processing unit). Until we have a direct high-bandwidth connection between the CPU and QPU, this transfer of data will remain the rate-limiting factor. Therefore, within the scope of this more general problem, we deem the current implementation and design as scalable. Furthermore, future improvements to aid in the transfer of data to the QPU that will be implemented into the quantum stack will be accessible directly to the end-users of our integration because it only serves as a middleman between the two codes.

Once again, we emphasize that the presented architecture provides a general framework for the implementation of active space embedding approaches. From a software perspective, any two codes may be coupled via the described interface. From a theoretical perspective, it is straightforward to implement other embedding approaches into an existing implementation. For example, a projection-based embedding approach such as this earlier work by some of the authors13 can simply be implemented by adding a new subroutine to CP2K to compute the embedding potential without requiring any further changes to the integration protocol or the AS solver.

Optical properties of the oxygen vacancy in MgO

To test our implementation we have studied the optical properties of the F0-center (neutral oxygen vacancy) in magnesium oxide, whose nature remains unclear despite the many experimental30,31,32,33 and computational34,35,36,37,38,39,40,41 studies carried out in the past decades. This data will allow us to compare the accuracy of the periodic rsDFT embedding with respect to both experimental spectra as well as state-of-the-art ab initio methods.

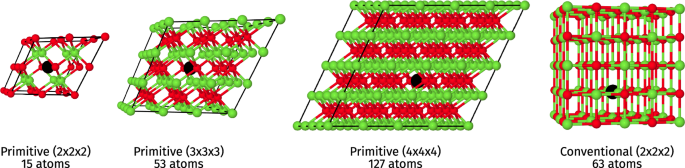
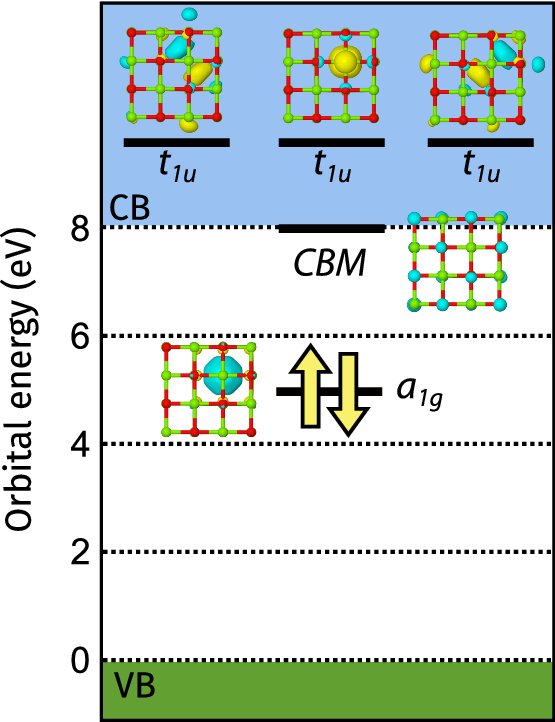
We have considered four different supercell sizes: the 2 × 2 × 2, 3 × 3 × 3 and 4 × 4 × 4 supercells constructed from the primitive unit cell, and the 2 × 2 × 2 supercell constructed from the conventional unit cell; see Fig. 3. The embedding calculations were performed by including 2 electrons and 5 orbitals (10 spin-orbitals in total) in the AS, which are shown within the band structure diagram in Fig. 4 (and are reproduced with higher resolution in the SI). Four of the five active orbitals are localized at the vacancy and are labeled according to the (localized) octahedral symmetry around the defect (Oh point group). The remaining orbital included corresponds to the conduction band minimum (CBM) and is a fully delocalized conduction s-band, which we label as CBM in the following. The ground state energy of the embedded fragment Hamiltonian was obtained using the variational quantum eigensolver (VQE) algorithm4 with a quantum unitary coupled cluster singles and doubles (q-UCCSD) ansatz42, and the excited states were obtained using the quantum equation of motion (qEOM) approach43. A brief review of the most important quantum computing concepts is provided in the section “Quantum computing”, along with detailed information on the computational settings used for these calculations in section “Computational details”.

Fig. 3: The four supercells used in the calculations.
figure 3

Magnesium atoms are in green, oxygen atoms are in red, the oxygen vacancy is colored in black.

Full size image
Fig. 4: Band diagram of the F0-center in magnesium oxide.
figure 4

The closed-shell A1g singlet-spin ground state is depicted, with two electrons occupying a defect orbital labeled a1g within the gap. Singlet and triplet excitons occur when an electron from the mid-gap orbital is excited either to the fully delocalized CBM state or to one of the three t1u defect orbitals within the conduction band (CB).

Full size image

A neutral oxygen vacancy in MgO introduces a 1 s-type localized defect orbital at mid-gap that is doubly occupied in the 1A1g electronic ground state. We shall call this orbital the mid-gap orbital. Three more defect-localized degenerate one-particle states of t1u symmetry (p-like orbitals) appear within the conduction band. These three orbitals are energetically slightly above the CBM, which corresponds to the delocalized s-band. The four orbitals localized at the oxygen vacancy and the CBM one are shown in Fig. 4 and are believed to be responsible for the optical properties of defective MgO; for this reason, we included them in the active space of our embedding calculation, along with the 2 electrons occupying the mid-gap defect state.

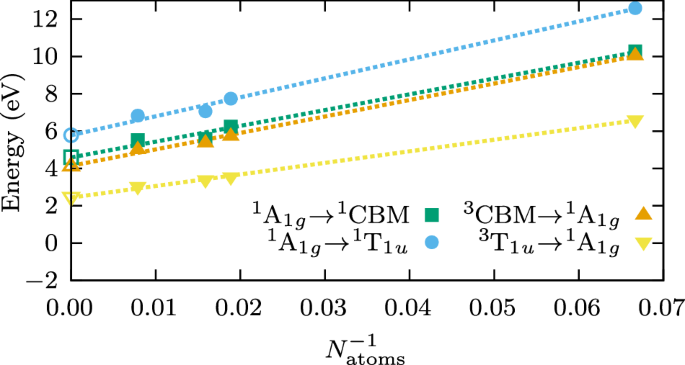
Experimentally, it is well established that the absorption peak of the F0-center is at 5.03 eV, which is extremely close to that of the F+-center (that is, a positively charged oxygen vacancy) at 4.96 eV30,31. We identified the vertical excitation energies corresponding to the transition of one electron from the mid-gap orbital to either the CBM or the t1u orbitals, denoted as 1A1g → 1CBM and 1A1g → 1T1u, respectively. In Fig. 5, we show in blue and green the energies obtained for these states as a function of the number of atoms in the supercell. Notice that the energies calculated with our embedding method are obtained directly from many-body wave functions, thus they account for electron-hole interactions and the exciton binding energy. We performed an extrapolation to the thermodynamic limit (TDL) assuming a \({N}_{\text{atoms}}^{-1}\) convergence to correct for finite-size effects, which is shown as dashed lines in Fig. 5. Our best estimates are reported at the bottom of Table 1, along with all the energies obtained for the different supercell sizes. The transition to the 1CBM state is predicted to be 4.60 eV, while for the (triply degenerate) one to the 1T1u state, we get 5.78 eV. The experimental absorption peak at 5.03 eV corresponds to the 1A1g → 1T1u, as the excitation to the CBM is dipole-forbidden; we, therefore, overestimate the experimental value by 0.75 eV. This result can be compared to a number of other computational studies on the F0-center in magnesium oxide, which have been performed with a large variety of methods from both the solid-state physics and quantum chemistry communities. From Table 2 we can see that most of the quantum chemistry methods overestimate the absorption to the localized 1T1u state, while FN-DMC36 and G0W0-BSE35 reproduce the experimental absorption peak, despite the fact that they likely target the CBM state rather than the defect one. This may suggest that the transition to the 1T1u obtained with those methods is possibly overestimating the experimental absorption maximum. Our calculations consistently predict a blue-shifted absorption by ~0.5 eV compared to the embedded-BSE@DDH of Vorwerk et al.39. While normally, the small (2,5) AS could be a reason for this, the AS convergence study reported in the SI suggests otherwise, as virtually the same results are obtained with 8 electrons in 60 orbitals. We, therefore, ascribe the blue-shift to the lack of orbital relaxation in the environment, which is optimized for the ground state only. In passing, we also note that the observed weak dependence on the active space size in our calculations is due to the RS parameter used in this work, \(\omega =0.14{a_0^{-1}}\). A larger value of ω would increase the importance of the active space size, as shown in the SI for \(\omega =0.4{a_0^{-1}}\), highlighting the sensitivity of the method to the value used for the RS parameter. Therefore, it is important to choose an active space that is not only relevant to the physical problem at hand, but that is also converged with respect to the value of ω. A more detailed discussion about this is available in the section “Methods” of the SI. Interestingly, density-matrix embedding theory40 predicts the absorption to the CBM state to be higher than the one to the localized state, perhaps owing to the missing extrapolation to the TDL. The only method that underestimates the absorption is TDDFT, with an absorption peak centered at 4.85 eV37.

Fig. 5: Vertical absorption and emission energies as a function of the (inverse) number of atoms in the supercell.
figure 5

Filled green squares and blue circles correspond to calculated singlet absorption energies, while filled upside-orange and downside-yellow triangles correspond to calculated triplet emission energies. Dashed lines are linear extrapolation curves to the TDL, whose value is marked with a corresponding empty symbol.

Full size image
Table 1 Optical singlet absorption energies (in eV) of the F0-center in MgO
Full size table
Table 2 Comparison of predicted optical absorption and photoluminescence energies (in eV) obtained with different computational methods
Full size table

The photoluminescence (PL) of defective MgO is considerably more complicated than the absorption, and several interpretations have been brought forward throughout the years. The main source of ambiguity is the vicinity of the absorption peaks of the F0, F+, and F2+ centers, which are all likely to be excited by incoming irradiation at 5 eV, significantly complicating the assignment of the emission bands to the correct point defect and electronic state. Experimentally, there are two very distinct peaks visible in the PL spectrum, one at 2.3 eV and one at 3.2 eV32,33. The former has been associated with an emission from the F0-center, while the latter to an emission from the F+-center32,33. The initial explanation for the long-lived nature of the 2.3 eV band was based on temperature-dependent experiments carried out on samples prepared in different ways and containing different concentrations of F0-centers and hydrogen impurities. The proposed mechanism involves the escape of an electron in the conduction band upon excitation of the F0-center, leaving behind a positively charged oxygen vacancy, an F+-center. Hydrogen impurities in the sample then act as traps for the mobile electrons, which may be thermally released back at a later time into the conduction band. Two processes can happen with the released electrons: they may encounter F+-centers left behind after the absorption process, in which case they recombine in an excited 1T1u state of the F0-center that quickly emits light, or they may be recaptured by H− traps, slowing down the overall emission process. An alternative, more straightforward interpretation is that the emission band is simply due to triplet phosphorescence from a localized 3T1u state at the defect, accessed via inter-system crossing from the excited 1T1u state. This second interpretation is the most accepted explanation in recent computational studies, corroborated by calculations based on advanced ab initio methodologies37,38,39,40 (in contrast to the first interpretation based on older semi-empirical methods and experiments32,33).

In light of this analysis, we also investigate the second pathway as the leading emission process and compute the photoluminescence from the relaxed 3T1u structure and state. Our results are shown by the orange and yellow lines in Fig. 5 and listed in Table 3. The predicted value for the emission from the localized triplet state is 2.44 eV and is in very good agreement with the experimental value of 2.3 eV. In particular, we are much closer to this value than other methodologies, which consistently predict higher energies for this emission band as shown in the last column of Table 2. The better accuracy of this value with respect to experiment compared to the singlet excitation energy obtained for the absorption to the 1T1u state is likely due to the relaxed inactive orbitals, which have been optimized for this state in the reference SR local density approximation (LDA) SCF calculation. These should provide a better embedding potential compared to that for the excited singlet state, whose inactive orbitals were optimized for the closed-shell ground state. Nevertheless, one has to be careful when comparing different theoretical works, since these focused on different states or mechanisms. The work by Vorwerk et al.39 reported 2.93 eV as the PL from the F+-center, hence to be compared with the experimental value of 3.2 eV. The earlier work based on FN-DMC36 and G0W0-BSE35 reported the emission from the singlet state (whether the CBM or T1u state is unclear), and have concluded that the assignment from the experimental studies should be re-evaluated, with the 3.2 eV peak assigned to the F0-center rather than the F+ center. All the works using approaches based on quantum chemistry methods, that is NEVPT2-DMET, EOM-CCSD, TDDFT, and CASPT2, analyze the transition 3T1u → 1A1g like us and compare their results against the 2.3 eV band34,37,38,40. Here, we do the same, and we get the best theoretical result so far, which corroborates the experimental assignment of the 2.3 eV band to the F0-center, though originating from a different mechanism than the originally proposed one. While this is not conclusive evidence, the competing interpretation relies on emission from the singlet state, 1T1u → 1A1g, which is normally expected to be higher in energy than the corresponding triplet one, hence further away from the experimental value.

Table 3 Photoluminescence energies (in eV) of the F0-center in MgO
Full size table

Discussion

We developed a general framework for hybrid quantum-classical molecular and periodic embedding calculations based on an orbital space separation of the system into fragments and environments. This framework has been implemented in the CP2K package, leveraging many of its functionalities and taking advantage of its high parallel efficiency. The modular nature of the implementation allows us to easily develop several types of embedding schemes and to couple different solvers to obtain ground and excited states energies and properties of the embedded fragment Hamiltonian. It supports both classical wave function and quantum circuit ansatzes, and the communication between CP2K and the solver is handled by sockets, which seamlessly integrate within current supercomputing facilities but are also ready for a more quantum-centric high-performance computing vision.

To demonstrate the potential of the new framework in practice, we have implemented a range-separated DFT embedding scheme that enables the study of both finite and extended systems. This approach is essentially an extension of multiconfigurational range-separated DFT to periodic boundary conditions and relies on the range-separation of the two-electron integrals in long- and short-range components. Within this approach, any correlated wave function method can, in principle, be coupled with DFT in a self-consistent scheme, whereby the former is used to obtain the spectrum of a fragment Hamiltonian and the latter to construct an embedding potential generated by the environment degrees of freedom. In particular, as part of this work, we have implemented an interface to Qiskit Nature28 that allows to map the fermionic fragment Hamiltonian to a qubit Hamiltonian, whose ground and excited states can be obtained with the quantum algorithm of choice.

The developed rsDFT embedding scheme has a wide application scope, allowing the investigation of both strongly correlated molecular systems, as well as localized electronic states in materials, such as those arising from vacancies and impurities. To this end, we have demonstrated its accuracy and applicability by studying the optical properties of the neutral oxygen vacancy in MgO, whereby both defect-localized and delocalized states have been treated on equal footing, and the low-lying spectrum of the embedded fragment Hamiltonian has been calculated by VQE and qEOM, in combination with the q-UCCSD ansatz. Our calculations for the absorption spectrum predict a peak at 5.78 eV, a value that overestimates the experimental result by 0.75 eV, but which lies in the same ballpark as other sophisticated computational approaches. On the other hand, the predicted PL emission of 2.44 eV from the 3T1u state almost perfectly matches with the experimentally measured signal at 2.3 eV, and provides new evidence on a system that has eluded state-of-the-art ab initio approaches for the last decade. While the accuracy of the method for the absorption leaves room for improvement, and the excellent agreement for the emission is certainly helped by favorable error compensation, the present study shows that current hybrid quantum-classical algorithms can reach an accuracy similar to that of classical state-of-the-art ab initio methodologies for problems beyond simple model systems.

Many possible future directions are envisioned based on this work. On one hand, the periodic rsDFT embedding scheme can be extended in several ways. For instance, introducing orbital optimization would allow the incorporation of the feedback from the correlated active space wave function onto the inactive long-range component; this would be particularly important for accounting for the changes in the environment when targeting states other than the ground state. Furthermore, it would make the embedding scheme truly variational, significantly simplifying the calculation of analytical forces. State-averaging would also be a useful extension, allowing a more balanced description of several states simultaneously. This is fundamental in cases where near-degeneracies are prominent, such as in molecules and materials containing open-shell transition metals. While optimally tuned short-range LDA performed well in this study, implementing more SR functionals will provide alternatives to cases where LDA is not sufficiently accurate.

Future directions that are not strictly tied to the rsDFT embedding scheme are also envisaged. For instance, one possibility is to implement orbital localization schemes based on maximally localized Wannier functions and pair natural orbitals, which would allow the study of pristine solid-state materials, where localized states do not arise naturally due to symmetry-breaking of the supercell. Owing to the local nature of electron correlation, orbital localization could also simplify the construction of hardware efficient ansatzes, thereby potentially increasing the maximum size of the active space. Additionally, CP2K can be interfaced with other classical active space solvers, such as those based on selected configuration interaction, which would also allow the study of larger fragment Hamiltonians solely on classical hardware.

Finally, the use of quantum computing will allow scaling the size of the active space to sizes beyond what can be treated with purely classical methods. While the practical applicability of this may not lie within the foreseeable future, recent advancements show a promising trend of hybrid quantum-classical algorithms to treat non-trivially sized active spaces44. The flexible framework presented in this work enables researchers to leverage these developments directly, opening up many possible application avenues for the future.

Methods

In this section, we first review the core quantum computing ingredients needed to obtain the embedded fragment Hamiltonian eigenvalues, and then we report the detailed computational settings used for the embedding calculations.

Quantum computing

We leverage quantum computing to find the ground and excited-state solutions of the embedded fragment Hamiltonian (cf. Eq. (6)). We do so through the means of the newly developed integration between CP2K14 and Qiskit Nature15,16 which we discussed in more detail in section “Quantum-classical interface implementation”. In recent years, quantum computing has made significant progress in emerging as a new computational paradigm that promises great advances for the simulation of chemistry and material science problems3. In particular for the latter, the ability to treat localized fragments embedded into periodic systems using quantum computing platforms is particularly appealing. While we rely on state-of-the-art hybrid quantum-classical algorithms such as the VQE4 and qEOM43, the presented embedding framework is not coupled to these choices and can leverage any advancements in the field of quantum computing that are yet to come. This also holds for the modular integration of the two computational codes, as shown earlier in section “Quantum-classical interface implementation”. In this section, we briefly review the theoretical foundations of the quantum computational tools used throughout this work.

In order to simulate a fermionic system on a quantum computer, one must first map the second-quantized Hamiltonian (cf. Eq. (6)) into a form that the quantum computer can work with. Since the fundamental operational unit of a quantum computer is a two-level system, a so-called qubit, the translation routines are referred to as fermion-to-qubit mappings. Many such mappings exist45,46,47,48,49,50, but in this work, we employ the parity mapping47. It maps the fermionic creation, \({\hat{a}}_{p}^{\dagger }\), and annihilation, \({\hat{a}}_{p}\), operators acting on spin-orbital, p, to a tensor product of identities, \({\mathcal{I}}\), and Pauli matrices, \(\{{\hat{\sigma }}_{p}^{X},{\hat{\sigma }}_{p}^{Y},{\hat{\sigma }}_{p}^{Z}\}\), which correspond to the principal single-qubit rotations along the Cartesian axes. The mapping can be written as

$${\hat{a}}_{p}\to \left(\mathop{\otimes }\limits_{q=1}^{{p-2}}{{\mathcal{I}}}_{q}\right){\hat{\sigma }}_{p-1}^{z}{\hat{\sigma }}_{p}^{-}\left(\mathop{\otimes }\limits_{q=p+1}^{{M}}{\hat{\sigma }}_{q}^{X}\right)\,,$$
(20)
$${\hat{a}}_{p}^{\dagger }\to \left(\mathop{\otimes }\limits_{q=1}^{{p-2}}{{\mathcal{I}}}_{q}\right){\hat{\sigma }}_{p-1}^{z}{\hat{\sigma }}_{p}^{+}\left(\mathop{\otimes }\limits_{q=p+1}^{{M}}{\hat{\sigma }}_{q}^{X}\right)\,,$$
(21)

where \({\hat{\sigma }}^{\pm }=({\hat{\sigma }}^{X}\pm i{\hat{\sigma }}^{Y})/2\) are the so-called ladder operators. This mapping encodes the parity information, that is, the number of occupied fermionic modes up to a given index modulo 2, into the qubit at that given index. This is called the parity basis of the qubits and can be interpreted as the dual to the occupation basis, the basis of the common Jordan-Wigner mapping45, in which the occupation of every fermionic mode is directly encoded in the corresponding qubit. The advantage of the parity mapping, and the reason that we employ it here, is a trivially arising symmetry for particle-number preserving Hamiltonians. In such cases, two qubits, namely the middle and last one, carry redundant information, and, thus, may be removed from the system without loss of information. This is known as the two-qubit reduction47.

The resulting qubit Hamiltonian is a weighted sum of the form1

$${\hat{H}}^{{\rm{qu}}}=\sum _{p}{c}_{p}{\hat{P}}_{p}\,,$$
(22)

where each Pauli string, \({\hat{P}}_{p}\), is a tensor product of identities and Pauli matrices. Crucially, the number of unique terms in \({\hat{H}}^{{\rm{qu}}}\) scales as \({\mathcal{O}}({M}^{4})\), just like the number of two-body interactions in the original second-quantized Hamiltonian, Eq. (6).

The VQE4 is a hybrid quantum-classical algorithm to find the ground state of any Hamiltonian. It has gained a widespread interest as an alternative to quantum phase estimation (QPE) since it is more amenable to near-term quantum computers. It does so by replacing the execution of a single long-running quantum circuit with the sampling of many shorter-duration circuits. The fundamental principle of the VQE is based on the expectation value computation of an observable, \(\hat{O}\), with respect to some reference state, Ψ, as

$$\left\langle \hat{O}\right\rangle =\frac{\left\langle \Psi | \hat{O}| \Psi \right\rangle }{\left\langle \Psi | \Psi \right\rangle }\,.$$
(23)

Finding the ground state of a Hamiltonian, \(\hat{H}\), amounts to using a parameterized ansatz for the WF, Ψ(θ), and variationally optimizing the parameters, θ, with respect to the expectation value, \(\left\langle \hat{H}\right\rangle\). In recent years, many variants of the VQE algorithm have been developed (see, for instance, refs. 51,52,53,54), which oftentimes leverage specific structures found in particular ansatzes for the WF. Since we are only simulating the execution of quantum circuits on classical computers, we do not require improved circuit depths or other benefits brought about by these algorithm variants. Thus, we employ the unaltered VQE algorithm.

Choosing an ansatz for the VQE algorithm is a difficult task. On one hand, it has to be expressive enough to contain the true ground state in its parameterized subspace of the entire Hilbert space. On the other hand, it should be limited in its circuit depth implementation to ensure that it can be executed on near-term quantum computers. Both of these properties can be achieved by means of hardware efficient ansatzes (HEAs), which can even be tailored to respect the limited qubit connectivity of the quantum computing hardware. However, optimization of such ansatzes can be challenging due to the large number of variational parameters55. Moreover, chemical problems, such as the ones we are interested in here, are constrained to the Fock space that often exhibits additional symmetries, further restricting the size of the subspace containing the true physical ground state. Therefore, chemistry-inspired ansatzes have been developed which are designed to explore only this physical subspace, a famous example of which is the quantum unitary coupled cluster (q-UCC) ansatz42. Its major drawback is the significant circuit depth overhead associated with the implementation of these constraints. Nonetheless, it is still orders of magnitude cheaper than an implementation of the QPE algorithm42.

Many different (hybrid) quantum algorithms exist for the computation of excited states43,56,57; in this work, we rely on the qEOM method43. It has the advantage that, once a ground-state solution has been found, one only needs to perform additional measurements on this optimized WF. Other algorithms, however, may require an entire new optimization procedure to be completed for each targeted excited state56.

The fundamental idea of qEOM relies on a classical computer solving the equations of motion while a quantum computer is used for the measurement of the matrix elements that go into the system of equations. When including only single and double excitations in the operator basis, the measurement cost of these matrix elements scales just like the measurement cost of the Hamiltonian expectation value with its number of terms \({\mathcal{O}}({M}^{4})\). This can be seen from the expectation values that give rise to the excitation energies that we are after

$${E}_{0n}=\frac{\left\langle 0\left| \left[{\hat{O}}_{n},\hat{H},{\hat{O}}_{n}^{\dagger }\right]\right| 0\right\rangle }{\left\langle 0\left| \left[{\hat{O}}_{n},{\hat{O}}_{n}^{\dagger }\right]\right| 0\right\rangle }\,,$$
(24)

where \(\left\vert 0\right\rangle\) denotes the ground state and \({\hat{O}}_{n}^{\dagger }=\left\vert n\right\rangle \left\langle 0\right\rangle\) is the excitation operator from the ground state to the n-th excited state (and \({\hat{O}}_{n}\) is the matching de-excitation operator). For more details we refer the interested reader to the original paper by Ollitrault et al.43.

Computational details

In the calculations of the neutral oxygen vacancy in magnesium oxide we have used four supercells. For each supercell size, we have first optimized the cell parameters and geometry of the pristine system with spin-unpolarized KS-DFT and the Perdew, Burke, and Ernzerhof (PBE) functional58, together with the geometrical response valence triple-ζ basis set59 and correlation-consistent polarization functions (ccGRB-T basis set in CP2K). The core electrons were described by the Goedecker-Teter-Hutter pseudopotential optimized for the PBE functional60,61,62. The DFT calculations were performed within the GPW approach25,63, using plane-wave absolute and relative cutoffs of 1000 and 50 Rydberg, respectively, and a 4-layer grid for the numerical integration.

To create the vacancy, we removed a single oxygen atom from each optimized pristine supercell and relaxed again the geometry of all systems with the same settings as just discussed, while keeping the cell parameters fixed. Note that the ground state of the F0-center in MgO is closed-shell, and therefore spin-unpolarized DFT describes it well. To perform the rsDFT embedding calculations, we reduced the basis set to a double-ζ plus polarization (ccGRB-D) for all atoms but the six magnesium ones surrounding the vacancy, for which we kept the triple-ζ basis. In addition, we have also added the triple-ζ basis functions of oxygen at the vacancy site, calculated as the center of mass of the six coordinated magnesium atoms. Furthermore, we changed the pseudopotential to the one optimized for hybrid functionals. We used the LDA functional in its SR form64,65,66 in combination with a truncated Coulomb potential67 for the LR HF component of the functional, using a truncation radius of 4.25 Å. We shall note that a truncation radius between 4 Å and 6 Å has been shown to provide total energies essentially converged to an accuracy of microHartree/atom67,68. Therefore, we expect that the use of a fixed truncation radius with an increasing supercell size does not introduce significant errors, especially considering that we target relative rather than absolute energies. The choice of LDA is a constraint of our current implementation, but it nevertheless provides very good accuracy in combination with the optimal tuning procedure. The development of SR generalized gradient approximation (GGA) and meta-GGA density functionals is left for future work. The RS parameter was set to \(0.14{a}_{0}^{-1}\), which was optimally tuned by matching the bandgap of the largest pristine supercell to the experimental bandgap value of 7.77 eV69. This is significantly smaller than the optimal value suggested by Fromager et al.21 for molecules, \(\omega =0.4\,{a}_{0}^{-1}\), and is ascribed to two reasons. First, the value in ref. 21 was chosen to best divide dynamic and static electron correlation components, rather than a fit to best reproduce molecular properties. Second, the absence of core electron density due to the use of a pseudopotential alleviates the constraints on ω, and a smaller value is expected to be a good approximation in combination with the LDA functional21. At last, a value of \(0.14{a}_{0}^{-1}\) is in line with the range generally used in optimally tuned RS hybrid functionals as well70,71.

As the active space solver for the embedded fragment Hamiltonian we have used the VQE algorithm4 with a q-UCCSD ansatz42. For the latter, we employ its original formulation involving two Trotterizations1,42 matching the implementation provided by the Qiskit Nature package16. The absorption and emission excitation energies were obtained by calculating the lowest ten excitonic states of singlet and triplet spin symmetry, respectively, using the qEOM approach43. The absorption energies were obtained at the ground state geometry, and the qEOM approach was used on top of the ground state AS embedding calculation with restricted orbitals and a spin-unpolarized short-range density functional. For the photoluminescence, we used instead the relaxed geometry of the 3T1u excited state, which was optimized using time-dependent density functional theory (TDDFT) within the Tamm-Dancoff approximation (TDA)72,73 on top of the 1A1g ground state DFT calculation. The other computational settings were the same as those used for the ground state geometry relaxation. The calculation of the triplet energies was carried out with qEOM on top of a triplet AS embedding calculation with unrestricted orbitals and a spin-polarized SR density functional. The AS embedding calculations for both singlet and triplet states converged to an energy change of 1 × 107Eh.

As discussed in the section “Optical properties of the oxygen vacancy in MgO”, the active space size selected was of 2 electrons in 5 orbitals. We should note that the q-UCCSD ansatz for 2 electrons is equivalent to an exact diagonalization, which we confirm by also performing all calculations using the classical full configuration interaction (FCI) solver of PySCF74. To ensure that the energies calculated with such a small AS are converged with respect to its size, we have performed a systematic study increasing the AS up to 8 electrons in 60 orbitals. We have found that for this system and our choice of \({\omega =0.14\,{a}_{0}^{-1}}\), the energies do not change significantly with respect to AS size (see section 4 of the SI for all the details of this test and a thorough discussion). This shows that the use of RS DFT allows for a very compact expansion of the long-range wave function, especially in combination with a small value of ω. A direct consequence of this, and the closed-shell nature of the ground state, is such that the energetic contribution of the embedding on top of the reference SRLDA is minimal, and so is the change in the ground state electron density due to the self-consistence cycles.

Finally, for the main results of this work, the quantum circuits were simulated without the addition of artificial noise using Qiskit15 (version 0.45), though, we performed a number of simulations, including sampling noise. These results are discussed in section 6 of the SI.

The SI provides additional theoretical and technical information on the embedding method, along with absorption and emission energies calculated with TDDFT (section 5).