Hybrid improper ferroelectricity in a Si-compatible CeO₂/HfO₂ artificial superlattice

Abstract

Hybrid improper ferroelectrics (HIFs), characterized by ferroelectric polarization arising from the rotation of two symmetry inequivalent antiferrodistortive modes, exhibit exotic properties such as T-independent dielectric constants and robustness against depolarizing field. Here, using first-principles simulations, we report a new $P{2}_{1}$ phase in a Si-compatible CeO₂/HfO₂ superlattice that exhibits remarkably robust hybrid improper ferroelectricity, induced by the in-plane oxygen rotations of two antiferrodistortive distortion modes. These non-polar distortions are coupled with a polar distortion through a trilinear coupling in the superlattice, stabilizing ferroelectricity as the competing ground state with the assistance of epitaxial strain. The estimated out-of-plane polarization ($P=30.3\,\mu C/c{m}^{2}$) is switchable with a remarkably small energy barrier of 8.5 meV/atom and relatively smaller coercive field relative to bulk HfO₂, expected to reduce the operational voltage of ferroelectric devices. Our discovery may offer unexpected opportunities for innovating high-performance, low-voltage devices, and promising advancements in next-generation CMOS compatible oxide-based electronics.

Introduction

Hybrid improper ferroelectricity was first experimentally reported in 2008 in the PbTiO₃/SrTiO₃ superlattice¹, further demonstrated in many layered perovskite Ruddlesden-Proper phases such as Ca₃Mn₂O₇², (Ca,Sr)₃Ti₂O₇³, (Sr,Ca)₃Sn₂O₇⁴, Sr₃Zr₂O₇⁵ and Ca_0.69Sr_0.46Tb_1.85Fe₂O₇⁶. Since then, it has garnered considerable attention in the field of ferroelectricity due to its exotic applications in the next generation nanoelectronics. In the recent past, using first-principles simulations, symmetry analysis and various experiments, a number of HIF materials have been found^{7,8,9,10,11,12}. Most HIFs have been discovered in Ruddlesden-Proper phases^13,14, Dion-Jacobson layered perovskites¹⁵, perovskite superlattices¹⁶, as well as metal-organic molecular perovskites^17,18. The potential to cross-couple order parameters within HIFs makes them highly interesting for materials designed for multiferroics. However, their presence has not yet been extensively studied in Si-compatible oxides, limiting their application in device manufacturing.

The discovery of ferroelectricity in HfO₂¹⁹ has gained widespread attention in both academia and industry due to its unprecedented ferroelectric properties such as scale-free²⁰ polarization and compatibility with complementary metal-oxide-semiconductor (CMOS) technologies²¹. Ferroelectricity in HfO₂ is observed in its orthorhombic ${Pca}{2}_{1}$ phase which can be stabilized in thin films through chemical doping^22,23,24, external strain²⁵ and interfacial effects with electrodes. Furthermore, other ferroelectric phases were experimentally confirmed in the fluorite-oxide such rhombohedral $R3m$ phase by interstitial of Hf atom in HfO₂²⁶ and ${Pnm}{2}_{1}$ phase in the ZrO₂²⁷. In recent years, to optimize the crucial characteristics of its ferroelectric films, extensive research has focused on HfO₂/ZrO₂^28,29,30 superlattices to enhance the ferroelectric properties of HfO₂-based materials. Moreover, attempts have been made to create CeO₂/HfO₂^31,32,33,34 (CHO) superlattices, leveraging the structural similarities between CeO₂ and HfO₂, aiming to improve the properties of HfO₂-based materials. Recently, the hybrid-improper ferroelectricity was proposed in a the ${Pc}$ phase of CHO superlattice³⁴, where it is quite sensitive to epitaxial strain and can be suppressed under positive epitaxial strain. In contrast, we introduce a new $P{2}_{1}$ phase in the CHO superlattice that exhibits remarkable stability of hybrid-improper ferroelectricity across a wide range of epitaxial strains.

In this work, employing a combination of phonon analysis, phenomenological theory and first-principles simulations, we report a new ferroelectric phase in CHO superlattice which strongly exhibits the characteristics of hybrid improper ferroelectricity. This phase possesses an out of plane polarization of $P=30.3\,\mu C/c{m}^{2}$ which can be switched at remarkably low energy barrier of 8.5 meV/atom (of 27.2 meV/atom in bulk HfO₂), significantly reduces the coercive field that potentially improves the facile polarization switching in this superlattice. The alternate layers of Hf and Ce atoms, which have different atomic sizes, are separated by oxygen layers along the z-direction enhance the phonon softness of antiferroelectric distortion rotation of oxygen atoms in the xy-plane. These distortions cause a trilinear coupling with the polar distortion mode and lead to the stabilization of hybrid improper ferroelectricity in the $P{2}_{1}$ symmetry phase of CHO superlattice. Surprisingly, $P{2}_{1}$ phase is identified as the competing ground state in the epitaxial growth on the YSZ substrate. The coupling of polar mode with combination of antiferroelectric distortions is not only used for multiferroics but also plays a critical role in tuning the coercive field. Additionally, a sizable dielectric constant (ε = 27) will be less sensitive to temperature, as demonstrated in perovskite HIF superlattices. We believe that our results will open new avenues for exploring HIFs in the CMOS-compatible oxide materials, leading to the development of low-voltage and high-performance ferroelectric-based devices, such as ferroelectric random-access memory (FeRAM) and ferroelectric field-effect transistor (FeFET).

Results

Modeling of CHO superlattice

We commence our analysis by designing an artificial superlattice composed of alternating layers of CeO₂ and HfO₂, called CHO superlattice, along the z-direction in the high-symmetry cubic ${Fm}\bar{3}m$ structure of HfO₂ (Supplementary Fig. 1a). The CHO superlattice consists of a total of six atoms (one Ce, one Hf, and four O atoms) in its primitive unit cell (Supplementary Fig. 1b), optimized in the tetragonal phase which exhibits $P4/{mmm}$ symmetry. In the $P4/{mmm}$ phase, the c lattice parameter along the superlattice direction increases significantly compared to bulk HfO₂. Moreover, oxygen atoms in this phase shift away from the Ce atomic layers while moving closer to the Hf atomic layer (Supplementary Fig. 1b), deviating from their respective high-symmetry positions in the cubic phase. This shift is attributed to the relatively larger atomic size of Ce compared to Hf.

Symmetry analysis of distortion modes

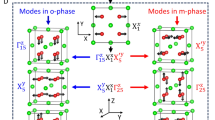
The phonon dispersion (Fig. 1a) of the $P4/{mmm}$ phase reveals that out of plane polarization can emerge in the CHO superlattice by the condensation of polar ${\Gamma }_{z}^{{\prime} }({\Gamma }_{4}^{-})$ distortion mode (Fig. 1b). However, this polar mode is found to be quite hard with its positive frequency of ${\omega }_{{\Gamma }_{z}^{{\prime} }}=$ 221.4 $c{m}^{-1}$, unable to condense on its own. Interestingly, two antiferrodistortive ${A}_{{xy}}({A}_{4}^{+})$ and ${A}_{{xy}}^{{\prime} }\,({A}_{1}^{-})$ modes are also present in this phonon dispersion at the cell doubling A ($1/2,\,1/2,\,1/2)$ point; the ${A}_{{xy}}$ mode with significantly larger instability with frequency of ${\omega }_{{A}_{{xy}}}=-210\,{c}{m}^{-1}$ and ${A}_{{xy}}^{{\prime} }$ mode is quite stable with frequency of ${\omega }_{{A}_{{xy}}^{{\prime} }}=192\,{c}{m}^{-1}$. The ${A}_{{xy}}$ mode induces the antiferrodistortive rotation of oxygen atoms in the xy-plane such these atoms rotate in opposite directions across the Hf layer, while rotating in the same direction across the Ce layer (Fig. 1c). In contrast to the ${A}_{{xy}}$, the ${A}_{{xy}}^{{\prime} }$ mode rotates oxygen atoms in the same direction across the Hf layer and in opposite direction across the Ce layer (Fig. 1d). The symmetries of ${A}_{{xy}}$, ${A}_{{xy}}^{{\prime} }$ and polar ${\Gamma }_{z}^{{\prime} }$ modes exhibit a trilinear coupling (Supplementary Eq. 1) among them which play a pivotal role to the stabilization of hybrid improper ferroelectricity in the CHO superlattice.

Fig. 1: Phonon dispersions and atomic displacements associate with the modes responsible for HIF in the P4/mmm structure of CeO₂/HfO₂ and PbTiO₃/SrTiO₃ superlattice.

Phonon dispersion of the $P4/{mmm}$ phase of the superlattice composed alternate layers of CeO₂ and HfO₂ along z-direction (a), atomic displacements (depicted with black arrows) associated to its polar ${\Gamma }_{z}^{{\prime} }$ (b), unstable ${A}_{{xy}}$ (c) and stable ${A}_{{xy}}^{{\prime} }$ (d) modes. Phonon dispersion of the same prototype ${P}_{4}/{mmm}$ phase of PbTiO₃/SrTiO₃ (e), its atomic displacements associated to unstable polar ${\Gamma }_{z}^{{\prime} }$ (f), unstable ${M}_{{xy}}^{{\prime} }$ (g) and stable non-polar ${M}_{{xy}}$ (h) modes. The subscripted x, y and $z$ in the mode depicts the direction of atomic displacements in their respective modes.

This hybrid improper ferroelectricity is quite similar in nature to that observed in the perovskite PbTiO₃/SrTiO₃ superlattice¹. In contrast to CHO superlattice, the two antiferroelectric distortive ${M}_{{xy}}\,$(${M}_{2}^{+}$) and ${M}_{{xy}}^{{\prime} }$ (${M}_{4}^{-}$) modes belong to M (1/2, 1/2, 0) point of its high symmetry $P4/{mmm}$ phase of the perovskite superlattice. The phonon dispersion (Fig. 1e) of $P4/{mmm}$ phase of PbTiO3/SrTiO3 superlattice reveals polar instability of ${\omega }_{{\Gamma }_{z}^{{\prime} }}=-102\,{c}{m}^{-1}$ at ${\Gamma }_{z}^{{\prime} }$ (${\Gamma }_{3}^{-}$) mode and antipolar distortive instability of ${\omega }_{{M}_{{xy}}^{{\prime} }}=-60\,{c}{m}^{-1}$ in the ${M}_{{xy}}^{{\prime} }$ mode, while only ${M}_{{xy}}$ mode shows the positive frequency of ${\omega }_{{M}_{{xy}}}=29\,{{c}{m}^{-1}}$. The atomic displacements of polar ${\Gamma }_{z}^{{\prime} }$, ${M}_{{xy}}^{{\prime} }$ and ${M}_{{xy}}$ modes are shown in Fig. 1f–h. Interestingly, the condensation of ${\Gamma }_{z}^{{\prime} }$, ${M}_{{xy}}^{{\prime} }$ and ${M}_{{xy}}$ was found to be adequate to stabilize the ferroelectricity in the PbTiO₃/SrTiO₃ superlattice due to their strong trilinear coupling¹. In contrast, in CHO superlattice, the ${\Gamma }_{z}^{{\prime} }$, ${A}_{{xy}}$ and ${A}_{{xy}}^{{\prime} }$ distortion modes are not sufficient to energetically stabilize the ferroelectric phase.

To identify the origin of the insufficiency of these three modes to stabilize the ferroelectricity, we first estimated the energy landscapes of each of ${A}_{{xy}}$, ${A}_{{xy}}^{{\prime} }$ and ${\Gamma }_{z}^{{\prime} }$ modes, individually, taking $P4/{mmm}$ as a reference structure (Fig. 2a, b). As expected, the energy landscape of unstable ${A}_{{xy}}$ mode shows a double well, while it is parabolic for both stable ${A}_{{xy}}^{{\prime} }$ and ${\Gamma }_{z}^{{\prime} }$ modes. The condensation of unstable ${A}_{{xy}}$ mode in the $P4/{mmm}$ transforms it into $I4/{mcm}$ phase (Supplementary Figs. 2 and 3a). Furthermore, we estimated the field-induced phase transition of non-polar $I4/{mcm}$ to the polar phase by performing atomic position relaxation of the structures obtained with fixed distortion amplitude of ${\Gamma }_{z}^{{\prime} }$ mode in the former phase. It was observed that the energy of the phase increases as expected when freezing of a stable ${\Gamma }_{z}^{{\prime} }$ mode. The induced polar phase structure adopts a polar tetragonal $I4{cm}$ structure (Fig. 2c), which relaxes back to $I4/{mcm}$ phase upon removal of constraint. The distortion mode decomposition of $I4{cm}$ phase reveals that it includes amplitudes of ${A}_{{xy}}$, ${A}_{{xy}}^{{\prime} }$ and ${\Gamma }_{z}^{{\prime} }$ modes, where the emergence of ${A}_{{xy}}^{{\prime} }$ mode is the result of their trilinear coupling ${b}_{1}{Q}_{{\Gamma }_{z}^{{\prime} }}{Q}_{{A}_{{xy}}^{{\prime} }}{Q}_{{A}_{{xy}}}$ (Supplementary Eq. 1), where ${b}_{1}$ denotes the coupling constant.

Fig. 2: Energy profiles and distortion modes contribution in the hybrid improper ferroelectric phase of the CHO superlattice.

a Estimated energy landscapes of reference $P4/{mmm}$ structure as a function of the amplitudes of ${A}_{{xy}}$ (black open circles), ${A}_{{xy}}^{{\prime} }$ (red open squares), ${\Gamma }_{z}^{{\prime} }$ (green open up-triangles) and ${M}_{z}$ (blue open down-triangles) modes. b Energy landscapes of the $P4/{mmm}$ (green open up-triangles) and $P{2}_{1}$ (pink stars) as a function of polar ${\Gamma }_{z}^{{\prime} }$ mode. c Energy landscapes of $I4/{mcm}$ phase as a function of polar ${\Gamma }_{z}^{{\prime} }$ mode with by atomic relaxation keeping other modes to be zero in initial structure (green open up-triangles) and by full relaxation keeping ${M}_{z}$ mode non-zero in initial structure (pink stars). d Emerged other phonon modes in the full relaxed $I4/{mcm}$ structure as a function of ${\Gamma }_{z}^{{\prime} }$ mode with non-zero amplitude of ${M}_{z}$ mode. The sharp jump in the amplitude of newly emerged modes at the ${Q}_{\Gamma }$ = 0.027 Å (black dashed ellipse) depicts the domination of ${Pm}$ phase while at ${Q}_{\Gamma }$ = 1.33 Å (pink dashed ellipse), $I4/{mcm}$ structure transforms into the polar $P{2}_{1}$ structure. e List of the amplitudes of distortion modes which are condensed in the $P4/{mmm}$ to $P{2}_{1}$ structural transformation.

Strikingly, using the group theory and phonon mode symmetry analysis we anticipated that the stable ${M}_{z}({M}_{5}^{+})$ distortion mode in $P4/{mmm}$ phase (Fig. 2a, Supplementary Fig. 4a and 4e) could play a pivotal role in stabilizing ferroelectricity in the CHO superlattice, as it exhibits trilinear couplings with all three modes ${A}_{{xy}}$, ${A}_{{xy}}^{{\prime} }$ and ${\Gamma }_{z}^{{\prime} }$ (Supplementary Eq. 1). To validate our anticipation, we further estimated the energy landscape of $I4/{mcm}$ structure at different fixed amplitudes of ${\Gamma }_{z}^{{\prime} }$ mode, by fully optimizing the structure with non-zero amplitude of ${M}_{z}$ mode. Surprisingly, we found that the energy of the distorted structure becomes lower than that of $I4/{mcm}$. At an amplitude of 0.133 Å of ${\Gamma }_{z}^{{\prime} }$ mode, we identified the lowest energy ferroelectric structure, which adopts the space group symmetry of $P{2}_{1}$ phase (Supplementary Fig. 3c). We further decomposed the changes in atomic positions relative to the reference $P4/{mmm}$ structure into the distortion modes of later structure (Supplementary Eq. 2) using the scheme introduced by the Reyes-Lillo et al.³⁵, extracted the distortion modes amplitude at each value of ${\Gamma }_{z}^{{\prime} }$ along this energy landscape. This analysis revealed that not only ${M}_{z}$ mode but also six other distortion modes ${A}_{{xy}}^{{\prime} }$, ${Z}_{x}({Z}_{5}^{+})$, ${Z}_{x}^{{\prime} }({Z}_{5}^{-})$, ${M}_{{My}}^{{\prime} }({M}_{5}^{-})$, ${Z}_{{Mx}}({Z}_{5}^{+})$ and ${Z}_{{Mx}}^{{\prime} }({Z}_{5}^{-})$ (Supplementary Fig. 4) emerge in the $P{2}_{1}$ phase. Thus, we identified a total of nine modes in the polar $P{2}_{1}$ structure. The amplitudes of these distortion modes, condensed in the ferroelectric $P{2}_{1}$ phase, are listed in Fig. 2e, its lattice parameters and energetics are listed in Supplementary Table 1.

We also observed a sudden increase in the amplitudes of ${A}_{{xy}}$, ${Z}_{{Mx}}^{{\prime} }$, ${Z}_{x}^{{\prime} }$ and ${M}_{{My}}$ modes at ${Q}_{\Gamma }$ = 0.027 Å (Fig. 2d), indicating the dominance of these modes which locally stabilize an intermediate nonpolar ${Pm}$ phase governed by the trilinear couplings among these four modes (Supplementary Eq. 1). The modes which are not condensed in the ${Pm}$ phase are linearly dependent on the amplitude of polar distortion mode (Fig. 2d). We estimated an out of plane polarization of $P=30.3\,\mu C/c{m}^{2}$ in the $P{2}_{1}$ phase of CHO superlattice. Furthermore, we estimated its dielectric constant ${\varepsilon }_{r}=27$ which is 1.5 times higher than that of of ${Pca}{2}_{1}$ phase of HfO₂ (${\varepsilon }_{r}=$18), and fairly temperature independent³⁶ in contrast to proper ferroelectrics which is expected because the primary order parameter is not a polar mode and not directly couple with the external electric field in HIFs.

Surprisingly, we also note that CHO superlattice exhibits two distinct FE $P{2}_{1}$ phases, both of them differ fundamentally in terms of their structures, energetics and ferroelectric properties. The FE $P{2}_{1}$ phase presented in this work has 24 atoms in its primitive unit cell and exhibits polarization along the superlattice direction (Fig. 3a and Supplementary Fig. 5c). In contrast, the FE $P{2}_{1}$ phase reported by Zhao, H. J. et al.³⁴ contains 12 atoms in its primitive unit cell (denoted as $P{2}_{1}$-12 phase), shows polarization perpendicular to the superlattice direction (Supplementary Fig. 5b). Interesitnly, only FE $P{2}_{1}$ phase with 24 atoms exhibits hybrid improper ferroelectricity due to xy-plane oxygen rotations in its primary order parameter ${A}_{{xy}}$ mode (Fig. 1c) and its tri-linear coupling with ${A}_{{xy}}^{{\prime} }$ (Fig. 1d) and polar ${\Gamma }_{z}^{{\prime} }$ modes (Fig. 1b). While $P{2}_{1}$-12 phase emerges as a distortion of the ${Pca}{2}_{1}$ phase of pure HfO₂ (Supplementary Fig. 5a) when the superlattice is vertically aligned³³. In the $P{2}_{1}$-12 phase, the in-plane oxygen rotations are missing in the primary order parameter ${X}_{2}^{{\prime} }$ mode (Supplementary Fig. 6d). As a result, this phase does not exhibit hybrid improper ferroelectricity and remains a distortive phase of ${Pca}{2}_{1}$ phase of pure HfO₂. Importantly, the $P{2}_{1}$ phase with 24 atoms is significantly lower in energy at any value of epitaxial strain compared to the $P{2}_{1}$-12 phase (Supplementary Fig. 5d), making the former phase energetically favorable, while the latter remains a high-energy phase. Thus, from this point forward, we focus on the ferroelectric properties of the $P{2}_{1}$ phase, unless specified otherwise.

Fig. 3: Results of polarization switching in the P2₁ phase.

The atomic structures of up-polarized (U) $P{2}_{1}$ structure (a), two of its symmetry equivalents down-polarized ${D}_{1}$ (b) and ${D}_{2}$ (c) structures. The red sheds oxygen layers in these atomic structures show the ferroelectric (FE) layers while without sheds are spacer layers, while up and down red arrows shows the polarization directions in the respective polar $P{2}_{1}$ phases. d Shows the estimated energy barriers along polarization switching pathways from up- and down-polarized $P{2}_{1}$ phases in CHO superlattice (black open circles and red open squares), and in pristine HfO₂ (blue open diamonds). The switching barrier from U to D₁ was estimated to be 12.3 meV/atom (black line) which is 2.3 times lower than bulk HfO₂ (green dotted line), the lowest among all four pathways. e Estimated hysteresis in polarization switching between up- and down-polarization phases in CHO and pristine HfO₂. The estimated coercive field ${E}_{c}$ = 7.96 MV/cm is almost 20% smaller than that of bulk HfO₂. f and (g) show the mode reversal in the U to D₁ and D₂ polarization switching, respectively.

We now compare the distortion modes involved in $P{2}_{1}$ and ${Pca}{2}_{1}$ phases in CHO superlattice and pristine HfO₂, respectively. Interestingly, we found that six out of nine modes involved in $P{2}_{1}$ phase (Supplementary Fig. 4) differ from those eight modes (Supplementary Fig. 6) condensed in the ${Pca}{2}_{1}$ phase of pristine HfO₂. While only the ${M}_{z}$ (Supplementary Fig. 4e) and ${M}_{{My}}^{{\prime} }$ (Supplementary Fig. 4h) modes are identical to the ${Y}_{5}^{z}$ (Supplementary Fig. 6f) and ${Y}_{3}^{{\prime} y}$ (Supplementary Fig. 6i) modes, which are common to both the $P{2}_{1}$ phase of CHO and the ${Pca}{2}_{1}$ phase of pristine HfO₂. Moreover, pristine HfO₂ also found to be a proper ferroelectric taking Pbcn as the reference structure³⁷, and also observed experimentally³⁸. The $P{2}_{1}$ phase remains a hybrid improper ferroelectric if one take Pbcn as a reference structure in the CHO superlattice. This is because the $P{2}_{1}$ phase (24 atoms in the unit cell) is a cell-doubling structure of Pbcn (12 atoms in the unit cell). Therefore, without the condensation of Z-point zone-boundary modes (as the unit cell expands along the z-direction) in the Pbcn phase, the polar mode alone unable to the transform Pbcn phase into $P{2}_{1}$ phase (Supplementary Note-1).

Polarization switching mechanism and coercive field

Using the symmetrical invariant analysis (Supplementary Eq. 1), we found that the up-polarization phase of $P{2}_{1}$ can be switched into four different down-polarized (D₁, D₂, D₃ and D₄) phases which are symmetrically identical to U phase (Fig. 3a–c and Supplementary Fig. 7). For reference we maintained the positive amplitudes of distortion modes condensed in U phase (Fig. 2e). According to invariant symmetry (Supplementary Eq. 1), four modes (${\Gamma }_{z}^{{\prime} }$, ${A}_{{xy}}^{{\prime} }$, ${M}_{z}$, ${Z}_{x}$ and ${Z}_{{Mx}}$) reverse their sign in D₁ phase and five modes (${\Gamma }_{z}^{{\prime} }$, ${A}_{{xy}}^{{\prime} }$, ${M}_{z}$, ${Z}_{x}^{{\prime} }$, ${M}_{{My}}^{{\prime} }$ and ${Z}_{{Mx}}^{{\prime} }$) modes change their signs in D₂ phase (Fig. 2e). In the D₃ phase, ${\Gamma }_{z}^{{\prime} }$, ${A}_{{xy}}$, ${M}_{z}$, ${Z}_{x}^{{\prime} }$ and ${Z}_{{Mx}}^{{\prime} }$ mode switch their signs while in D₄ phase ${\Gamma }_{z}^{{\prime} }$, ${A}_{{xy}}$, ${Z}_{x}$, ${M}_{{My}}^{{\prime} }$ and ${Z}_{{Mx}}$ change their signs (Fig. 2e). Our nudged elastic band (NEB) calculations estimated the energy barriers of the homogeneous polarization switching from up-polarized U phase to four different down-polarized D₁, D₂, D₃ and D₄ phases as 12.3 meV/atom, 15.1 meV/atom, 22.3 meV/atom and 38.8 meV/atom, respectively (Fig. 3d and Supplementary Fig. 7d). Among these, the barrier from U to D₁ switching is remarkably small which can further reduce the polarization switching voltages relative to the bulk HfO₂.

We now estimate the coercive field using the simplified phenomenological Landau theory where we fit the energy barriers of polarization switching in a quadratic free energy function as follows³⁹,

$$F=\frac{{F}_{0}}{{P}_{s}^{4}}{\left({P}^{2}-{P}_{s}^{2}\right)}^{2}+{E}_{e}P,$$

(1)

where ${F}_{o}$ is the energy barrier of polarization switching, ${P}_{s}$ is the spontaneous polarization of polar ${P2}_{1}$ phase, while P and ${E}_{e}$ are polarization and external electric field. The energy barriers of all four switching pathways are well fitted by Eq. (1) at ${E}_{e}=0$ (Fig. 3d and Supplementary Fig. 7d). By solving Eq. (1) in thermodynamical equilibrium conditions³⁹, we found the dependency of coercive field on energy barrier and spontaneous polarization as follows,

$${E}_{c}=\frac{8}{3\sqrt{3}}\left(\frac{{F}_{0}}{{P}_{s}}\right).$$

(2)

It is now clear from Eq. (2) that the coercive field is proportional to the ratio of polarization switching barrier and spontaneous polarization. Furthermore, to estimate the hysteresis we numerically solve the following Landau-Khalatnikov equation⁴⁰:

$$\rho \left(\frac{\partial P}{\partial t}\right)=-\left(\frac{\partial F}{\partial P}\right),$$

(3)

where $\rho$ is kinetic coefficient. By solving Eq. (3), we estimated hysteresis for all four switching pathways (Fig. 3e and Supplementary Fig. 7e), and found that the estimated ${E}_{c}\,$= 7.96 MV/cm for U to D₁ switching pathway is the smallest among them as expected because its energy barrier also the smallest. Interestingly, we found that the coercive field in polarization switching reduces only 20% relative to bulk-HfO₂ (${E}_{c}=10.58{MV}/{cm}$), even though its energy barrier reduces almost 60%. This is due to the estimated spontaneous polarization being 56.1 $\mu C/c{m}^{2}$ in HfO₂, whereas in CHO it is 30.3 $\mu C/c{m}^{2}$. It should be noted that the phenomenological theory tends to overestimate the coercive field relative to experiments because it does not account for external factors such as strain and domain effects, which reflects in our results too as coercive field for HfO₂ is estimated 10.58 MV/cm which is almost five times higher than of experimental value^41,42. However, despite overestimating the coercive field, the Landau theory provides a qualitative understanding of the coercive field and reveals its critical dependency on the ratio of energy barrier and spontaneous polarization in ferroelectric materials.

To understand the origin of the different energy barriers along four different pathways, we further examined the intermediate paths and reversal of distortion modes along these pathways. We found that in U to D₁ polarization switching pathway, the four modes ${A}_{{xy}}$, ${Z}_{x}^{{\prime} }$, ${M}_{{My}}^{{\prime} }$ and ${Z}_{{Mx}}^{{\prime} }$, which do not reverse their sign, are not suppressed at the intermediate phase (Fig. 3f) due to their strong trilinear couplings (${b}_{7}{Q}_{{A}_{{xy}}}{Q}_{{M}_{{My}}^{{\prime} }}{Q}_{{Z}_{x}^{{\prime} }}$ and ${b}_{8}{Q}_{{A}_{{xy}}}{Q}_{{M}_{{My}}^{{\prime} }}{Q}_{{Z}_{{Mx}}^{{\prime} }}$(Supplementary Eq. 1)). This intermediate phase is identified as a non-polar ${Pm}$ structure which has slightly lower energy relative to $I4/{mcm}$ phase (Supplementary Table 1), resulting in the lowest energy barrier among all four pathways. The amplitudes of distortion modes condensed in the ${Pm}$ phase are listed in Supplementary Table 2. While in U to D₂ switching pathway, only ${A}_{{xy}}$ remains nonzero and the rest of the modes become zero at intermediate phase (Fig. 3g). Therefore, the transition occurs through a tetragonal phase ($I4/{mcm}$) which is stabilized by the condensation of only ${A}_{{xy}}$ mode. Furthermore, in U to D₃ and D₄ polarization switching, the ${A}_{{xy}}$ mode also switch its sign. Thus, it is mandatory to suppress this mode in intermediate phase, resulting in significantly higher energy barriers in these two pathways (Supplementary Fig. 7f, g). Thus, our polarization switching calculations suggest that U to D₁ polarization switching is energetically feasible.

Relative stabilities of different phases of CHO superlattice

To compare the relative stability of $P{2}_{1}$ phase with other phases of CHO superlattice along z-direction, we further optimized nonpolar tetragonal ($P{4}_{2}/{mnc}$), polar orthorhombic (${Pca}{2}_{1}$) and nonpolar monoclinic ($P{2}_{1}/c$) phases of HfO₂ in this superlattice. Here it is important to note that in tetragonal, orthorhombic and monoclinic phases of bulk HfO₂, the unstable ${X}_{2}^{{\prime} x}$ mode of cubic phase is the primary order parameter³³. The tetragonal $P{4}_{2}/{mnc}$ phase of bulk HfO₂ optimized in this superlattice into the ${Pban}$ symmetry phase (Supplementary Fig. 8a). Interestingly, the orthorhombic ${Pca}{2}_{1}$ optimized into a ${Pc}$ (Supplementary Fig. 8b) phase which is also a ferroelectric phase and have spontaneous polarization along xz-direction, Zhao, H. J. et al³⁴ also reported this FE ${Pc}$ phase in CHO superlattice. While monoclinic $P{2}_{1}/c$ phases optimized into the $P\bar{1}$ symmetry (Supplementary Fig. 8c), which is found to be the lowest energy phase in the CHO superlattice. The relative energies of all the phases (Supplementary Table 1) indicates that the $P{2}_{1}$ phase is a metastable phase in the bulk CHO.

Epitaxial strain effects

To explore the possibilities of stabilizing the polar $P{2}_{1}$ phase as the ground state, we conducted epitaxial strain calculations using YSZ substrate’s in plane lattice parameters in the different phases of CHO superlattice. We optimized polar $P{2}_{1}$, $I4/{mnc}$, ${Pban}$, ${Pc}$, $P\bar{1}$ and $P4/{mmm}$ phases at various epitaxial strains taking in plane experimental lattice parameters of YSZ substrate as reference (a = b = 5.185 Å)⁴³, clamping the in-plane lattice parameters while fully relaxed atomic positions, c-lattice parameters and lattice angles α and β in all considered phases. The epitaxial strain diagram (Fig. 4a) illustrates that the ground state strongly depends on the epitaxial strain as its negative value almost equally stabilizes $P{2}_{1}$ and ${Pc}$ phases while between zero to 3.5% ${Pc}$ become the competing ground state and at any strain above 3.5% stabilizes $P\bar{1}$ phase stabilizes as the ground state. Whereas the $I4/{mnc}$, ${Pban}$ and $P4/{mmm}$ phases remain high energy phases across all epitaxial strain values. Moreover, the in plane lattice parameters mismatch between $P{2}_{1}$ (Supplementary Table 1) and YSZ substrate ranges from −2% to −3%, which is considered small enough to expect epitaxial growth on the YSZ substrate. Interestingly, this mismatch is negative, and since CHO is a prototype fluorite oxide, epitaxial growth is likely to occur with relative ease. This is because a negative lattice mismatch results in better alignment between the substrate’s lattice parameters and the fluorite phase⁴⁴. Thus, we believe that the FE $P{2}_{1}$ phase can epitaxially grow on the YSZ substrate easily through controlled layer-by-layer epitaxy techniques.

Fig. 4: Epitaxial strain results from different phases of the CHO superlattice along z-direction.

a The relative stabilities of various phases of the CHO superlattice are shown as a function of epitaxial misfit strain, with respect to the equilibrium cubic lattice constant of 5.185 Å for YSZ. The ferroelectric $P{2}_{1}$ phase is a competing ground state at negative misfit strain compared to the ferroelectric ${Pc}$ phase. b The polarization of the $P{2}_{1}$ phase remains robust against epitaxial strain, while that of the ${Pc}$ phase is suppressed at misfit strains of 4% and above. c The polarization switching barrier for the $P{2}_{1}$ phase (black line) is 8.5 meV/atom at 0% misfit strain, which is more than two times lower than that of 17.4 meV/atom barrier of the ${Pc}$ phase. d The estimated hysteresis reveals a further reduction in the coercive field of the $P{2}_{1}$ phase at 0% misfit strain relative to the ${Pc}$ phase at the same misfit strain.

Furthermore, the comparative analysis of the $P{2}_{1}$ phase with its counterpart ferroelectric Pc phase in the CHO superlattice reveals that both the $P{2}_{1}$ and Pc³⁴ phases share a common $P4/{mmm}$ reference structure (Supplementary Fig. 1a). However, in contrast to the $P{2}_{1}$ phase, where the second most unstable ${A}_{{xy}}$ mode leads the ferroelectric transformation, the transformation from $P4/{mmm}$ to Pc is driven by the most unstable ${M}_{{xy}}^{{\prime} }({M}^{1-})$ mode, along with eight other secondary modes (${M}^{3+}$, ${\Gamma }_{z}^{-}$, ${\Gamma }_{x}^{-}$, ${M}_{y}^{5-}$, ${M}_{y}^{5+}$, ${M}^{4-}$, ${M}^{2+}$ and ${\Gamma }_{2}^{5+}$) (Supplementary Fig. 9). Among all the modes involved in $P4/{mmm}$ to $P{2}_{1}$ and Pc transformation only three modes, polar ${\Gamma }_{z}^{-}({\Gamma }_{z}^{{\prime} })$, nonpolar ${M}_{z}({M}_{5}^{5+})$ and nonpolar ${M}_{{My}}^{{\prime} }({M}_{y}^{5-})$, are common between the $P{2}_{1}$ and Pc phases.

Surprisingly, the Polarization in the $P{2}_{1}$ phase is robust against a wide range of epitaxial strains as the polarization does not deviate much with respect to epitaxial strain (Fig. 4b). In contrast, in the Pc phase, the polarization is highly sensitive to epitaxial strain and suppressed above 4% misfit strain from the YSZ superlattice (Fig. 4b). Interestingly, the polarization switching barrier of 8.5 meV/atom at 0% misfit strain in the $P{2}_{1}$ phase is remarkably small compared to 17.4 meV/atom in the Pc phase (Fig. 4c), resulting in a much lower coercive field in the $P{2}_{1}$ phase (Fig. 4d). Since the YSZ substrate is widely used for epitaxially growing HfO₂-based ferroelectric thin films, our results reveal that the $P{2}_{1}$ phase can be more favorable for robust ferroelectricity and reducing the coercive field in epitaxially grown CHO superlattices.

Discussion

In summary, we have discovered a new hybrid-improper ferroelectric $P{2}_{1}$ phase in the CeO₂/HfO₂ superlattice which exhibits a spontaneous polarization of 30.3 $\mu C/c{m}^{2}$ along the direction of the superlattice and remarkably small energy barrier of 8.5 ${meV}/{atom}$ for polarization switching. We demonstrated that the trilinear couplings of antiferrodistortive modes with polar modes contribute to the stabilization of $P{2}_{1}$ phase. Furthermore, our atomic scale calculations suggest that this phase can be experimentally realized in the epitaxial growth on the YSZ substrate. The hybrid-improper ferroelectricity in the $P{2}_{1}$ phase is remarkably robust across a wide range of epitaxial strains, making it well-suited for growth in epitaxial thin films. This new ferroelectric phase may catalyze comparative studies on hybrid-improper ferroelectricity between perovskites and Si-compatible oxides. Moreover, our prediction on the Si-compatible HIFs with low coercive field and robust ferroelectricity will open new avenues for designing next-generation memory devices with facile switching and low power consumption.

Methods

Computational details

The first-principles calculations in this work are carried out within the density functional theory (DFT) based on a plane-wave pseudopotential scheme as implemented in the Vienna Ab-initio Simulation Package (VASP)^45,46,47. We used the projector augmented-wave (PAW)⁴⁸ pseudopotential with a generalized gradient approximation (GGA) and Perdew-Burke-Ernzerhof (PBE)⁴⁹ form of exchange-correlation energy functional, and $5{s}^{2}5{p}^{6}6{s}^{2}5{d}^{2}$ electronic states of Hf, $4{f}^{1}5{s}^{2}5{p}^{6}5{d}^{1}6{s}^{2}$ states of Ce and 2${s}^{2}2{p}^{4}$ states of O as valence states. We also used PBEsol functional to estimate lattice parameters and energetics of each structure in the superlattice. The energy cutoff to truncate the plane-wave basis sets in representing Kohn-Sham wave functions were set to 500 eV. In self-consistent Kohn-Sham calculations with conventional unit cells, Brillouin zone integrations were sampled on uniform meshes, using Monkhorst-Pack (MP)⁵⁰, of 8 × 8 × 8, and 8 × 8 × 2 for cell doubled 24 atoms unit cell. In the structural optimization, the convergence criteria for total energy were set to 10⁻⁷ eV, and for total forces it was 10⁻³ eV/Å. We use density functional perturbation theory (DFPT) in VASP to determine the lattice-dynamical properties of HfO₂ and CHO superlattice.