Introduction

So far, studies on compressed binary hydrides (i.e., H-rich materials) have revealed the possibility of achieving compounds exhibiting a superconducting state at near-room temperature1. Among a huge number of candidates that have been explored, the ones that can be regarded as the most interesting are H3S with critical temperature Tc = 203 K2,3, LaH10 with Tc = 250 K4, YH9 with Tc = 243 K5, YH6 with Tc = 224 K6 and CaH6 with Tc = 215 K7,8. Although these values of Tc are relatively high, the pressure required to achieve a stable superconducting state is still too high from the practical point of view. Therefore, searching for high-Tc hydrides at lower or, ideally, ambient pressure remains a significant challenge9,10,11,12.

To date, the superconductivity of nearly all elements from the periodic table forming binary compounds with hydrogen has been systematically explored. Based on a wealth of theoretical and experimental reports from numerous studies, several approaches have been proposed that could be valuable in the search for even more remarkable superconductors. For example, efforts to classify hydrogen-rich superconductors by their structural, chemical, and electronic properties concluded that only materials exhibiting highly symmetrical structures and a high density of states (DOS) at the Fermi level can achieve high Tc9,10,13,14. However, as later found, these conditions, while necessary, were not sufficient for that purpose. A different approach was proposed by Belli et al. who explored a database of 178 binary hydride superconductors to elucidate the origin of their high Tc15. They discovered that Tc is strongly correlated with the networking value, which is multiplied by both the hydrogen fraction and the cubic root of the fraction of the DOS at the Fermi energy contributed by the hydrogen atoms. Very recently, Wrona et al.16 conducted a deep study of a database exceeding 580 binary hydrides exhibiting superconducting properties. Among the parameters examined, the ratio of the total molecular weight of heavier atoms to the total mass of all hydrogen atoms in the hydride’s chemical formula (MX/MH) was recognized as the most valuable indicator for identifying new promising superconductor candidates. Namely, the highest Tc is associated with the lowest MX/MH ratio. It was also shown that the probability of discovering superconductors with Tc above 200 K within the range 0 < MX/MH < 15 is as high as 28%.

Such a comprehensive understanding of binary hydrides now paves the way for the exploration of another promising group of materials: ternary hydrides. Compared to binary hydrides, ternary hydrides offer a broader spectrum of chemical compositions, resulting in more diverse structures that harness the unique properties of various elements. The extensive knowledge gained from studying binary hydrides is invaluable in selecting candidates for further theoretical and numerical analysis. Introducing new elements into well-characterized binary hydrides could, therefore, be a highly effective strategy for constructing ternary hydrides, potentially leading to the discovery of novel superconducting materials with enhanced properties17,18.

Very recent theoretical calculations have allowed the discovery of a series of ternary superhydrides exhibiting high critical temperatures at relatively low stabilization pressures in such systems as La-Y-H19,20, La-Ce-H21,22,23, La-Mg-H24, La-Be-H25, La-B-H26,27, Ce-Ca-H28, K-B-H29,30, Sc-Y-H31, Mg-C-H32, Mg-P-H33, Mg-Pt-H34, La-Be-H35, Sc-C-H36, Ac-Be-H37, Th-Be-H38, La-Th-H39, Y-Ce-H23, Ba-Si-H40. For instance, \(Fm{\bar{3}}m\)-LaBeH8 was predicted to be thermodynamically stable above 98 GPa, and dynamically stable down to 20 GPa with a Tc of approximately 185 K25. Very recently, LaBeH8 has been successfully synthesized, and a sharp drop in resistivity to zero at 110 K at 80 GPa and a characteristic shift in Tc driven by a magnetic field have been observed35. Another noteworthy example comes with ref. 41 where the authors introduced extra electrons of Li dopant in MgH16. As a result, Tc of about 470 K was reported for Li2MgH16, albeit under a pressure of 250 GPa.

An outstanding report of superconductivity in Lu-H-N at 294 K and 1 GPa gave promise for long-awaited ambient-condition superconductors. Unfortunately, none of the further studies have confirmed the credibility of this finding42,43,44,45,46. Nevertheless, subsequent advancements emerged alongside other research attempts. Namely, few works predicted numerically superconductive properties under ambient pressure of such materials as KCdH3 (23.4 K)47, Li2CuH6 (80 K)48, Mg(BH4)2 (140 K)49, Mg2IrH6 (160 K)50. These discoveries indicate the immense potential of novel hydrides and given that there are probably more than 1700 stable ternary hydrogen-rich systems9, a vast landscape remains unexplored for finding even more exciting materials exhibiting superconducting properties.

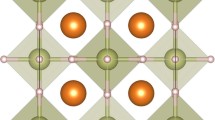
This work employed first-principles calculations to search for superconductivity in compressed (0−100 GPa) XC2H8, where X denotes the elements from the 13th–17th group. From a chemical perspective the 13th group elements can form electron-deficient hydrides, 14th group elements can form electron-precise hydrides and 15th–17th group elements can form electron-rich hydrides. Moreover, the choice of carbon in the chemical formula is motivated by evidence from other studies indicating that the carbon atom has been identified as a promising candidate for the stabilization of the \(Fm{\bar{3}}m\) structure18,36. From the investigated elements only Ga, In, Tl, Sn, Pb, Sb, Bi, Te, and Po inserted at X position in \(Fm{\bar{3}}m\)-XC2H8 exhibit superconducting properties. Among them, \(Fm{\bar{3}}m\)-SbC2H8 exhibits the highest critical temperature of 73 K at a pressure of 100 GPa which is correlated with its high-symmetry crystal structure, high density of states at the Fermi level (1.27 states/eV), large phonon frequencies (301 meV) and strong electron–phonon coupling constant (1.02).

Methods

First-principles calculations

First-principle studies for all ternary hydrides analyzed in this paper were performed within the density functional theory (DFT) implemented in the Quantum-Espresso computational package51,52 with plane wave pseudopotential method and generalized gradient approximation of Perdew, Burke, and Ernzerhoff (GGA-PBE)53 for exchange-correlation interaction. For all elements, the ultrasoft pseudopotentials54,55 were used with kinetic energy cutoffs of 80 Ry for the wave functions and 1000 Ry for charge density, to ensure their convergences. All lattice parameters and atomic positions were fully relaxed as a function of pressure using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-Newton algorithm56. The coordinates were optimized until each atom’s maximum force was smaller than 0.001 eV/Å with energy and pressure convergence of 10−5 eV and 10−8 kbar, respectively. For structural relaxation, calculations of the density of states (DOS), and electronic properties, a Monkhorst–Pack k-point grid57 of 28 × 28 × 28 was utilized. The density-functional perturbation theory (DFPT)58 was applied to compute the phonon band structures, electron–phonon coupling (EPC), and Eliashberg spectral functions with the 7 × 7 × 7 q-point grid.

Migdal–Eliashberg approach

Due to the high values of the EPC constants (~1), the Migdal–Eliashberg approach was used to determine the superconducting properties of ternary compounds XC2H8. The main input to the Eliashberg equations is the spectral α2F(ω) function, which is defined as

$${\alpha }^{2}F(\omega )=\frac{1}{2\pi N({\varepsilon }_{F})}\sum\limits _{{\bf{q}}\nu }\delta (\omega -{\omega }_{{\bf{q}}\nu })\frac{{\gamma }_{{\bf{q}}\nu }}{\hslash {\omega }_{{\bf{q}}\nu }}$$
(1)

with

$$\begin{array}{l}{\gamma }_{{\bf{q}}\nu }\,=\,2\pi {\omega }_{{\bf{q}}\nu }\sum\limits _{ij}\displaystyle\int\frac{{d}^{3}k}{{\Omega }_{BZ}}| {g}_{{\bf{q}}\nu }({\bf{k}},i,j){| }^{2}\delta ({\varepsilon }_{{\bf{q}},i}-{\varepsilon }_{F})\\\qquad\qquad \times\, \delta ({\varepsilon }_{{\bf{k}}+{\bf{q}},j}-{\varepsilon }_{F}),\end{array}$$
(2)

where N(εF), γqν, and gqν(k, i, j) are the density of states at the Fermi level εF, phonon linewidth, and electron–phonon matrix element, respectively. The Eliashberg function is a part of the electron–phonon interaction pairing kernel given by

$${\lambda }_{n,m}=2\mathop{\int}\nolimits_{0}^{\infty }d\omega \frac{\omega }{{\left({\omega }_{n}-{\omega }_{m}\right)}^{2}+{\omega }^{2}}{\alpha }^{2}F\left(\omega \right).$$
(3)

The isotropic Migdal–Eliashberg equations for the superconducting order parameter function \({\varphi }_{n}=\varphi \left(i{\omega }_{n}\right)\) and the electron mass renormalization function \({Z}_{n}=Z\left(i{\omega }_{n}\right)\) are defined as follows59,60,61:

$${\varphi }_{n}=\frac{\pi }{\beta }\sum \limits_{m=-M}^{M}\frac{{\lambda }_{n,m}-{\mu }^{* }\theta \left({\omega }_{c}-| {\omega }_{m}| \right)}{\sqrt{{\omega }_{m}^{2}{Z}_{m}^{2}+{\varphi }_{m}^{2}}}{\varphi }_{m},$$
(4)
$${Z}_{n}=1+\frac{1}{{\omega }_{n}}\frac{\pi }{\beta }\sum\limits_{m=-M}^{M}\frac{{\lambda }_{n,m}}{\sqrt{{\omega }_{m}^{2}{Z}_{m}^{2}+{\varphi }_{m}^{2}}}{\omega }_{m}{Z}_{m},$$
(5)

where μ* denotes the Coulomb pseudopotential, specifying depairing interaction between electrons, for which we have used two widely accepted values of 0.1 and 0.15. The superconducting order parameter is defined by the ratio Δn = φn/Zn and the superconducting transition temperature Tc is estimated from the simple relation Δn=1(μ*, T = Tc) = 0. The Heaviside step function θ is determined by a cutoff frequency, whose value is set to ten times the maximum phonon frequency, and the value of β is specified by β = 1/kBT, where kB is the Boltzmann constant. The Eliashberg equations were solved iteratively in a self-consistent manner using in-house developed code. The maximum error tolerance between two successive iterations was set at 10−10. The convergence was controlled by the sufficiently high number of Matsubara frequencies: \({\omega }_{n}=\left(\pi /\beta \right)\left(2n-1\right)\), where n = 0, ±1, ±2, …, ±M and M = 110018,62,63,64.

After solving the Eliashberg equations, the free energy difference between the superconducting and normal state (ΔF) can be calculated using the formula65:

$$\begin{array}{ll}\Delta F\,=\,-2\pi TN({\epsilon }_{F})\mathop{\sum }\limits_{n=1}^{M}\left(\sqrt{{\omega }_{n}^{2}+{\Delta }_{n}^{2}}-\left\vert {\omega }_{n}\right\vert \right)\\ \qquad\quad\times \,\left({Z}_{n}^{S}-{Z}_{n}^{N}\frac{\left\vert {\omega }_{n}\right\vert }{\sqrt{{\omega }_{n}^{2}+{\Delta }_{n}^{2}}}\right),\end{array}$$
(6)

where symbols \({Z}_{n}^{S}\) and \({Z}_{n}^{N}\) represent the wave function renormalization factor for the superconducting (Δn=1 ≠ 0) and normal (Δn=1 = 0) states, respectively. Based on (ΔF), the specific heat difference between the superconducting and normal states (ΔC = CS − CN) was estimated in the following way:

$$\Delta C=-T\frac{{d}^{2}\Delta F}{d{T}^{2}}.$$
(7)

The specific heat in the normal state is expressed as CN = γT, where the Sommerfeld constant (γ) is defined as \(\gamma =(2/3){\pi }^{2}\left(1+\lambda \right){k}_{B}^{2}N({\varepsilon }_{F})\).

Results and discussion

As the prediction of ternary crystal structures is challenging and computationally expensive, we mainly focused on the stability and superconductivity of the well-known sodalite-like clathrate structure with a high symmetry \(Fm{\bar{3}}m\) space group. This structure has been identified as responsible for the high critical temperatures in several binary hydrides such as LaH10 (Tc = 260 K)66,67, ThH10 (Tc = 161 K)68,69 or CeH10 (Tc = 115 K)70. In the ternary system, the \(Fm{\bar{3}}m\) structure contains hydrogen atoms at 32f (0.62, 0.62, 0.62) positions, and heavier atoms occupying 8c (0.25, 0.25, 0.25) and 4a (0, 0, 0) sites. In our case, 8c (0.25, 0.25, 0.25) position has always been occupied by C atoms. The motivation for this choice is, as shown in other papers18,36, that carbon is a promising candidate for the stabilization of \(Fm{\bar{3}}m\) structure. Additionally, we considered five other structures: I4/mmm, P42nm, Fd3m, \(P{\bar{4}}\) and I41/amd, that can form XC2H8 stoichiometry, and we verified which one is the most favorable in terms of energy for p-block elements substituted as X.

The aforementioned crystal structures were predicted in our recent work, where we utilized the particle swarm optimization (PSO) methodology, implemented in the CALYPSO code71,72, to search for low-energy crystalline configurations in the ternary hydride ScC2H836. Moreover, The ground state structures were carefully tested based on a combination of enthalpy minimization and dynamic stability criteria. Given the complexity and time-intensive nature of identifying low-energy structures, this study builds on our previous findings by focusing on the most promising configurations. By selecting these pre-identified, energetically favorable structures, we streamline our analysis while ensuring robust consideration of optimal configurations from prior optimization efforts.

For 16 from 25 investigated compounds (XC2H8, where X = B, C, N, O, F, Al, Si, P, S, Cl, Ge, As, Se, Br, I, and At), the calculated enthalpies indicated that the \(Fm{\bar{3}}m\) structure is energetically unfavorable over the entire analyzed range of pressure (0−100 GPa). Furthermore, the structures with the lowest energy are dynamically unstable and do not exhibit superconducting properties. Interestingly, four of these compounds (AlC2H8, SiC2H8, GeC2H8, AsC2H8) exhibit superconducting properties in energetically unfavorable \(Fm{\bar{3}}m\) space groups. These two types of systems are shown in Fig. 1 with different colors: red for compounds that do not show superconducting properties at all and blue for systems that are superconductors in the \(Fm{\bar{3}}m\) space group, but it is not energetically favorable. Noteworthy is that Jiang et al.32 demonstrated that \(Fm{\bar{3}}m\)-AlC2H8 is a superconductor with a critical temperature as high as 67 K at 80 GPa. However, their conclusion about the stability of the \(Fm{\bar{3}}m\) structure was based solely on comparing its enthalpy with the decomposition enthalpies. Our analysis, detailed in Supplementary Fig. 9, reveals that for the AlC2H8 system, the most energetically favorable are the Fd3m (0–40 GPa) and I41/amd (40–100 GPa) crystal structures. However, these configurations are dynamically unstable and do not exhibit superconductivity. The remaining nine elements, marked with green in Fig. 1, provide an energetically stable \(Fm{\bar{3}}m\) structure, at least in most of the pressure range analyzed. The minimum pressure at which the system achieves energetic stability can be determined from the enthalpy difference curves (in relation to the \(Fm{\bar{3}}m\) structure), as shown in Fig. 2. As can be seen, the lowest stabilization pressure (12 GPa) is observed for InC2H8 and TlC2H8, while above 50 GPa all of the 9 compounds obtained are stable. For all the systems obtained, in terms of their energetic stability, we also confirmed the dynamic stability, based on the non-existence of negative phonon modes (see calculated phonon dispersion in Supplementary Fig. 5).

Fig. 1: The matrix of elements from the 13th to 17th group used as X for searching for superconducting properties in XC2H8.
figure 1

Red, blue, and green colors denote the no-superconducting XC2H8 systems, XC2H8 superconducting in the \(Fm{\bar{3}}m\) phase that is not energetically favorable, and \(Fm{\bar{3}}m\)-XC2H8 superconducting and stable, respectively.

Full size image
Fig. 2: Relative enthalpies (ΔH) and crystal structures of the considered XC2H8 compounds.
figure 2

Relative enthalpies of a GaC2H8, b InC2H8, c TlC2H8, d SnC2H8, e PbC2H8, f SbC2H8, g BiC2H8, h TeC2H8, and i PoC2H8, with respect to the \(Fm{\bar{3}}m\) structure from 0 to 100 GPa. The following crystal structures were considered: \(Fm{\bar{3}}m\), P42nm, \(P{\bar{4}}\), Fd3m, I41/amd, I4/mmm. The arrows point to the pressures where the \(Fm{\bar{3}}m\) ternaries are predicted to be energetically stable.

Full size image

The calculated electronic band structures and projected density of states (DOS) of \(Fm{\bar{3}}m\)-SbC2H8 at 100 GPa are presented in Fig. 3a. The valence and conduction bands overlap, indicating that the system exhibits metallic behavior. This feature was also observed in the other studied \(Fm{\bar{3}}m\)-XC2H8 (X = Ga, In, Tl, Sn, Pb, Bi, Te, Po) superconductors (see calculated electronic band structures in Supplementary Figs. 2 and 3). The electronic density of states near the Fermi level, N(εF), is crucial for understanding many properties of metallic systems. A high N(εF) value typically leads to a broad spectrum of unusual and exciting electronic, magnetic, and structural properties. However, too large a value of N(εF) can also compromise the stability of the material, making experimental synthesis challenging. In some cases, losing initial stability is not detrimental, because it can transform the system into a stable magnetic or superconducting state73. According to the Bardeen–Cooper–Schrieffer (BCS) theory74, high-Tc superconductivity requires a high density of states near the Fermi level, strong electron–phonon coupling, and high phonon frequencies75. As shown in Fig. 3a, the density of states (DOS) of \(Fm{\bar{3}}m\)-SbC2H8 exhibits a relatively high value at the Fermi level (1.27 states/eV), with comparable contributions from H, C, and Sb atoms. This elevated DOS is primarily due to the presence of a flat electronic band near the L point. A high density of states at the Fermi level can significantly enhance the electron–phonon coupling constant, which is crucial for the superconducting properties of the material. The results for all investigated systems are summarized in Table 1.

Fig. 3: The electronic and phonon properties.
figure 3

a Electronic band structures and partial density of states and b phonon dispersion and projected phonon density of states for SbC2H8 at 100 GPa.

Full size image
Table 1 Thermodynamic properties of \(Fm{\bar{3}}m\)-XC2H8 obtained using the DFT methods and Eliashberg approach with μ* = 0.1
Full size table

The electronic localization function (ELF) is a tool used to visualize the probability of finding localized electrons in a material, such as in bonds or around atoms76,77. ELF values range from 0 to 1, with values close to 1 signifying regions of high electron localization and values near 0 indicate electron delocalization. When analyzing the electronic properties of the XC2H8 systems, it is important to note that X is usually a metal, except for the metalloids Sb and Te. These two elements exhibit distinct characteristics, especially in the distribution of ELF, as shown in Supplementary Fig. 4. The differences in ELF can be attributed to the higher ionization energy and electronegativity of Sb and Te compared to the metallic elements. These properties lead to variations in electron localization and bonding behavior within the system. The ELF can also be related to ionization energy and electronegativity. Higher ELF values near the nucleus or bonds typically correspond to higher ionization energy, as electrons are more tightly bound. Similarly, high ELF values in bonding regions suggest higher electronegativity, as these atoms more effectively localize electrons. Although the ELF patterns among the various compounds exhibit general similarities, the compounds containing Sb and Te display distinct electron localization due to their metalloid nature, which influences their bonding characteristics compared to metals.

In our analysis of the \(Fm{\bar{3}}m\)-XC2H8 systems, we calculated the phonon dispersion curves, projected phonon density of states (PhDOS), Eliashberg spectral functions α2F(ω), and electron–phonon integral λ(ω). These quantities provide crucial insights into the vibrational properties of the system and how these vibrations influence the superconducting transition temperature. As shown in Figs. 3b and 4a for \(Fm{\bar{3}}m\)-SbC2H8 at 100 GPa, and in Supplementary Fig. 5 for other systems at 60 GPa, the low-frequency phonon modes, particularly those involving the heavier X atoms (such as Sb), are important for the electron–phonon coupling and for the superconducting state. The phonon band structure reveals three acoustic modes with zero frequency at the Γ point, characteristic of stable crystal structures. The positive phonon frequencies confirm the dynamical stability of the \(Fm{\bar{3}}m\) structure. In XC2H8 systems, the heavier X atoms contribute predominantly to low-frequency phonon modes (below 35 meV), while the lighter H atoms dominate the high-frequency region (above 90 meV). The C atoms, with intermediate mass, influence the mid-frequency region (35–90 meV). In all investigated systems, the maximum phonon frequencies assume large values of ~300 meV. We note that high phonon frequencies can favor high-temperature superconductivity. This principle is crucial in searching for new high-temperature superconductors, particularly materials with light atoms exhibiting higher phonon frequencies. Hydrogen-rich compounds are a prime example of such materials. The low-frequency modes, particularly those originating from heavier X atoms, play a vital role in enhancing the electron–phonon interaction, as they contribute significantly to the Eliashberg spectral function and the electron–phonon coupling constant λ. In turn, a stronger electron–phonon interaction leads to a higher Tc. This relationship underlines the importance of tuning the atomic composition of these compounds to achieve high-temperature superconductivity, especially by incorporating appropriate heavy X atoms that enhance low-frequency phonon contributions.

Figure 4a shows the isotropic Eliashberg spectral function and the cumulative electron–phonon coupling parameter, λ(ω), obtained by integrating α2F(ω)/ω over ω. This integration yields a total λ of 1.02. For \(Fm{\bar{3}}m\)-SbC2H8 at 100 GPa, the contribution to electron–phonon coupling arises from acoustic modes, predominantly induced by Sb, which account for 22% of the total λ(ω), while carbon-related vibrations contribute 35%, and hydrogen-related vibrations account for 43%. From a physical point of view, the incorporation of carbon modifies the phonon spectra, which is crucial for enhancing the electron–phonon coupling constant.

Fig. 4: Eliashberg spectral function, energy gap, and specific heat difference.
figure 4

a Eliashberg spectral function α2F(ω) and EPC coefficient λ(ω), b, c superconducting energy gap (in meV) as a function of temperature and temperature-dependent specific heat difference between the superconducting and normal state (in J/mol K) for \(Fm{\bar{3}}m\)-SbC2H8 at 100 GPa for two values of Coulomb pseudopotential μ* = 0.1 (red lines) and μ* = 0.15 (blue lines).

Full size image

To obtain the key characteristics of the superconducting state, we solved the Eliashberg equations self-consistently at different temperatures on both the imaginary and the real frequency axes. This approach enables a thorough analysis of the superconducting properties and captures the details of electron–phonon interactions, which are essential for understanding critical phenomena, such as the behavior of the superconducting energy gap Δ or specific heat. Figure 4b presents the resulting Δ versus temperature curve for \(Fm{\bar{3}}m\)-SbC2H8 at 100 GPa. The curve illustrates the gradual decrease in Δ(T) as the temperature increases, indicating a typical superconducting phase transition, where the energy gap vanishes at Tc. Based on these data, we estimated Tc to be 73 K (60.7 K) and the universal dimensionless ratio 2Δ(0)/kBTc to be 4.05 (3.99) for μ* equals 0.1 (0.15). The results for all investigated systems are presented in Supplementary Fig. 8 and listed in Table 1 and Supplementary Table I. As shown, the larger the value of the electron–phonon coupling, the higher the 2Δ(0)/kBTc ratio. In all cases, the obtained results significantly exceed the BCS gap ratio value of 3.5374. It is important to note that for systems containing elements from the 15th and 16th groups, there is a sharp increase in the critical temperature in response to rising pressure. This is correlated with an increase in the electron–phonon coupling constant (for other systems, EPC decreases with pressure) and a sharp widening of the superconducting energy gap.

Moreover, the specific heat difference of \(Fm{\bar{3}}m\)-SbC2H8 at 100 GPa between the superconducting and normal states as a function of temperature has been calculated using Eq. (7) and displayed in Fig. 4c. The abrupt jump in the specific heat at Tc indicates that superconductivity is induced by a second-order phase transition. This specific heat jump, denoted by the vertical dashed line, is calculated to be 1.54 J/mol K (1.20 J/mol K). This result allows us to determine the dimensionless relative jump of the specific heat ΔC(Tc)/γTc equals 1.75 (1.65) for μ* equals 0.1 (0.15). Also, in this case, the results obtained strongly exceed the universal value of 1.43 predicted by the BCS theory74.

It should be noted that seven of the superconductors identified in this study have not been discovered in previous research. The \(Fm{\bar{3}}m\)-GaC2H8 was described by Jiang et al.32, where it was found to be stable in the same pressure range as in our analysis. The pressure dependence of the critical temperature is also similar and shows an increase at 60 GPa32. The \(Fm{\bar{3}}m\)-TeC2H8 has been analyzed by Zhang et al., however, in a different pressure range (100−300 GPa)78. Our findings complement these results, confirming the Tc = 49.4 K obtained at 100 GPa78.

The pressures required to induce the superconducting state in hydrogen-rich compounds present significant challenges for synthesis. However, recent advancements in high-pressure experimental techniques, such as diamond anvil cells (DAC) and laser-heating methods, have enabled the achievement of the extreme pressures necessary for synthesizing these superconductors. For example, superconducting hydrides like H3S and LaH10 have been successfully synthesized at pressures exceeding 150 GPa using DACs, demonstrating that superconductivity in hydride materials can be experimentally studied2,4. Additionally, ongoing experimental efforts are focused on synthesizing compounds similar to those explored in our theoretical analysis. Studies on ternary hydrides, such as Li5MoH11 and LaBeH8, have revealed superconducting properties under high-pressure conditions, highlighting the potential for synthesizing analogous compounds35,79. Since the pressures predicted for the synthesis of the compounds in this study are relatively low, current high-pressure synthesis techniques are well-equipped to achieve these conditions. This provides a feasible path for the experimental validation of the theoretical predictions presented in this work.

Discussion

This study employs first-principles calculations and the strong-coupling Migdal–Eliashberg approach to explore superconductivity in XC2H8 compounds, focusing on X elements from the 13th to 17th groups of the periodic table. It was found that nonmetals from these groups do not form stable compounds with superconducting properties. In contrast, superconductivity was observed in almost all analyzed p-block metals (Ga, In, Tl, Sn, Pb, Bi, and Po) when substituted as X in the energetically favorable \(Fm{\bar{3}}m\)-XC2H8 structure. The situation is more diverse for metalloids. Although most metalloids (Si, Ge, As, Sb, Te) can form a superconducting system in the \(Fm{\bar{3}}m\) structure, this structure is often energetically unfavorable (as in the cases of Si, Ge, and As). At pressures below 20 GPa, stability in the \(Fm{\bar{3}}m\) structure is achieved by three systems: GaC2H8, InC2H8, and TlC2H8, all containing elements from the 13th group of the periodic table. Among these, GaC2H8 reaches the highest critical temperature of 36 K at a pressure of 20 GPa. In particular, across the investigated pressure range, SbC2H8 demonstrates the highest critical temperature of 73 K at 100 GPa, attributed to its stable high-symmetry structure, high density of states at the Fermi level, large phonon frequencies, and strong electron–phonon coupling. By solving the Eliashberg equations, we not only determined the critical temperatures but also quantitatively analyzed key thermodynamic properties of the investigated systems, including the energy gap and specific heat jump. These results provide detailed insights into the superconducting behavior of the compounds and offer specific predictions that can be directly verified through experimental measurements. The advancements in high-pressure synthesis techniques, such as diamond anvil cells and laser heating, make it feasible to validate these theoretical predictions. With the capability to achieve the relatively low pressures required for synthesizing the identified compounds, this research not only enhances our understanding of hydrogen–carbon-based structures but also serves as an inspiration for future experimental investigations into new superconducting hydrides.